文章信息
- 艾永乐, 李帅
- AI Yongle, LI Shuai
- 基于PSIM的单相H桥三电平性能研究
- Study of single-phase H bridge three-level performance based on PSIM
- 武汉大学学报(工学版), 2019, 52(4): 337-343
- Engineering Journal of Wuhan University, 2019, 52(4): 337-343
- http://dx.doi.org/10.14188/j.1671-8844.2019-04-009
-
文章历史
- 收稿日期: 2018-05-24
随着光伏发电等新能源的大量投入,电力系统对逆变器的性能提出了更高要求,而调制方式是决定逆变电路的重要因素[1].对正弦脉宽调制技术(SPWM)的不断改进,在一定程度上提高了直流电压的利用率,减少了交流侧THD(Total Harmonic Distortion).由于空间矢量脉宽调制(SVPWM)技术具有易于数字化实现和电压利用率高等优点,与SPWM调制技术相比,其被广泛地应用及研究[2].
研究表明,SVPWM调制技术具有SPWM调制技术所不具备的优势[3-6];文献[7]提出了一种通用H桥级联SVPWM算法,对SVPWM算法进行改进,结果表明改进后的级联SVPWM算法降低了计算工作量.文献[8, 9]通过Matlab/Simulink仿真分析与理论推导,对比分析SVPWM调制与SPWM调制,发现了它们的内在联系.文献[10-12]使用DSP芯片,进行实物验证,验证了SVPWM调制方式具有控制算法简单、速度快和实现简单等优点.本文使用通用的H桥逆变电路作为研究模型和实验主电路,对单相(H桥使用的)SVPWM进行详细的数学推导,使用双重傅里叶分析来研究SVPWM调制技术的性能;通过PSIM搭建仿真模型进行验证分析,利用其能产生C代码的功能,不但解决了编写C代码的难题,同时有利于算法和模型的修改,极大地缩短了科研周期.
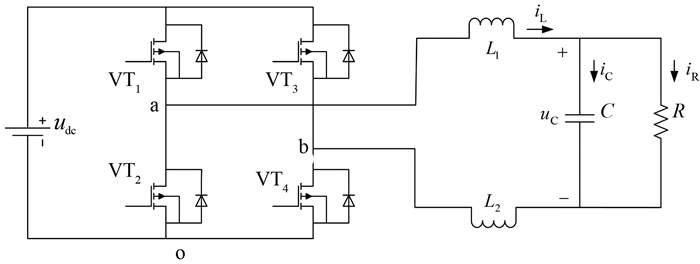
1 单相SVPWM算法的数学推导本文以单相H桥逆变电路作为研究对象,对SVPWM算法进行推导分析.单相H桥逆变电路的主电路结构拓扑图如图 1所示.
|
| 图 1 主电路结构拓扑图 Fig. 1 Topology diagram of main circuit |
图 1中, VT1和VT2为桥臂S1;VT3和VT4为桥臂S2.
为方便研究分析,定义开关函数Sk为
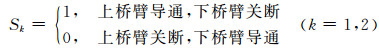 (1)
(1)
分析图 1可知,对于每一个桥臂都有2种电平(0,udc)输出,对于H桥有3种电平(-udc,0,udc)输出,对于4个开关管有4种不同的组合.4个开关管的状态组合对应的开关函数Sk值和H桥输出电压如表 1所示.
| VT1 | VT2 | VT3 | VT4 | S1 | S2 | uab |
| on | off | on | off | 1 | 1 | 0 |
| on | off | off | on | 1 | 0 | Udc |
| off | on | on | off | 0 | 1 | Udc |
| off | on | off | on | 0 | 0 | 0 |
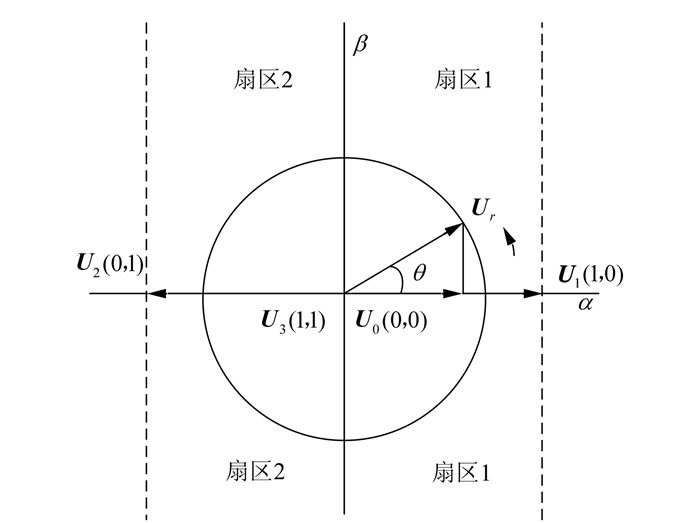
与三相SVPWM算法类同,单相SVPWM算法也为通过扇区的判断、矢量作用时间的计算和SVPWM的产生来实现[8],其中SVPWM矢量合成图如图 2所示.
|
| 图 2 单相SVPWM矢量合成图 Fig. 2 Single phase SVPWM vector composite graph |
图 2中U0(0,0)和U3(1,1)为零矢量;Ur为合成矢量,以角度θ=ωt旋转;图中分为2个扇区(扇区1、2),对应着合成矢量Ur的正负.设开关周期为TS,在图 2中1,2两个扇区内,根据伏秒平衡原理有
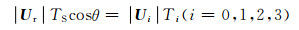 (2)
(2)
式中:Ui为i矢量;Ti为Ui有效的作用时间.
所以,矢量U1、U2的在一个开关周期中的作用时间为
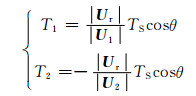 (3)
(3)
式中:T1为矢量U1的作用时间;T2为矢量U2的作用时间.
又因为|U1|=|U2|=Udc,所以
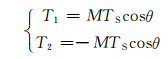 (4)
(4)
式中: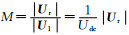
为了尽量减少开关动作频率,降低损耗,使得每次只动作1只开关管,所以在两区域内适量应用零矢量U0(0, 0)和U3(1, 1);为了使产生的输出电压波形具有最小的THD,利用“对称原则”对作用矢量进行布置[6].定义其开关顺序如表 2所示.
| 扇区 | 桥臂的开关顺序(S1,S2) |
| 1 | 0, 0→1, 0→1, 1→1, 0→0, 0 |
| 2 | 0, 0→0, 1→1, 1→0, 1→0, 0 |
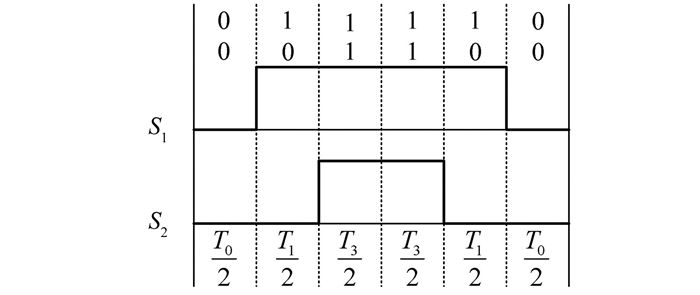
当合成矢量Ur在扇区1内时,在一个开关周期内,由表 2定义开关顺序,建立扇区1开关函数波形如图 3所示.
|
| 图 3 扇区1内的开关函数波形 Fig. 3 Switch function waveform in sector 1 |
图 3中,定义:
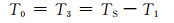 (5)
(5)
式中:T0为矢量U0的作用时间;T3为矢量U3的作用时间.
所以由式(4)知,VT1、VT3的开通时间为
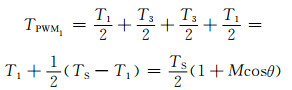 (6)
(6)
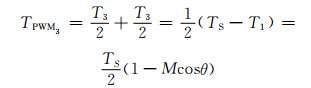 (7)
(7)
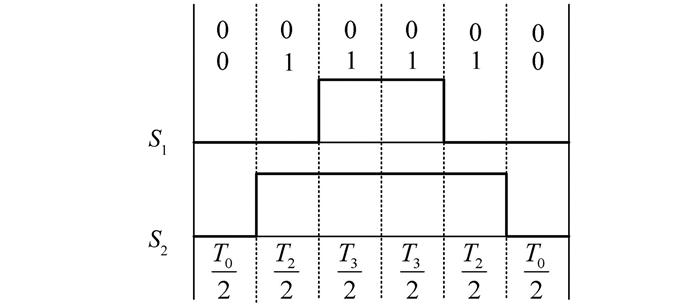
同上,建立扇区2开关函数波形如图 4所示.
|
| 图 4 扇区2内的开关函数波形 Fig. 4 Switch function waveform in sector 2 |
图 4中,定义:
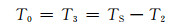 (8)
(8)
所以由式(4)知,VT1、VT3的开通时间为
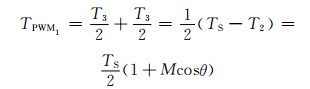 (9)
(9)
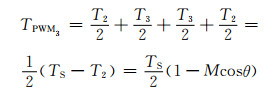 (10)
(10)
所以,在整个区域中,即θ∈[0, 2π],VT1和VT3的开通时间为
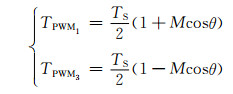 (11)
(11)
因此,输出电压为
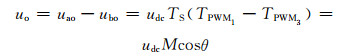 (12)
(12)
式中:uao为交流侧端口a-o间电压;ubo为交流侧端口b-o间电压;udc为直流电源的电压值.
2 基于PSIM的仿真电路的建立和C代码的产生H桥逆变电路作为一种广泛应用的逆变电路,具有实现简单(仅需要4个开关管)、便于构造、性能稳定等优点[13].本文根据图 1所示的电路拓扑建立PSIM仿真主电路.PSIM仿真主电路各元件参数为:直流侧电压udc=70 V,VT1、VT2、VT3和VT4选择MOSFET型的开关管,滤波电感L1=L2= 660 μH,滤波电容C=10 μF,负载电阻R=10 Ω.
2.1 搭建SVPWM算法模型由图 2可知,扇区的划分规则为:扇区1,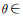
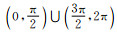
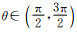
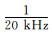
|
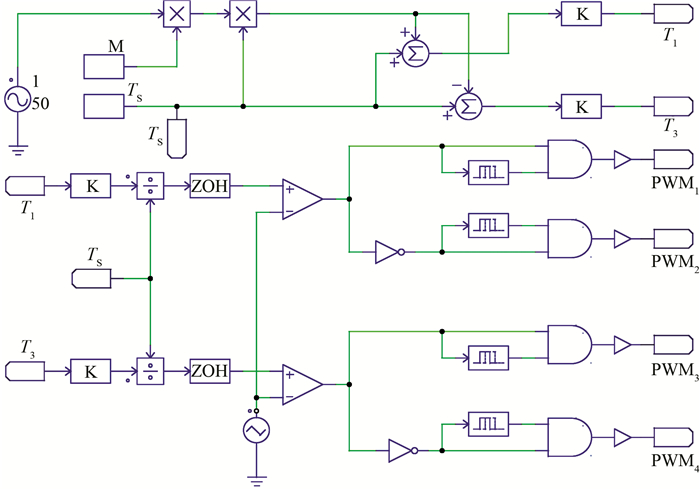
| 图 5 SVPWM算法模型图 Fig. 5 Model diagram of SVPWM algorithm |
由式(12)可知,输出的电压波形为u0=uPWM1- uPWM3,根据式(11)、(12)和图 5画出此SVPWM调制方式具体的开关模式示意图如图 6所示
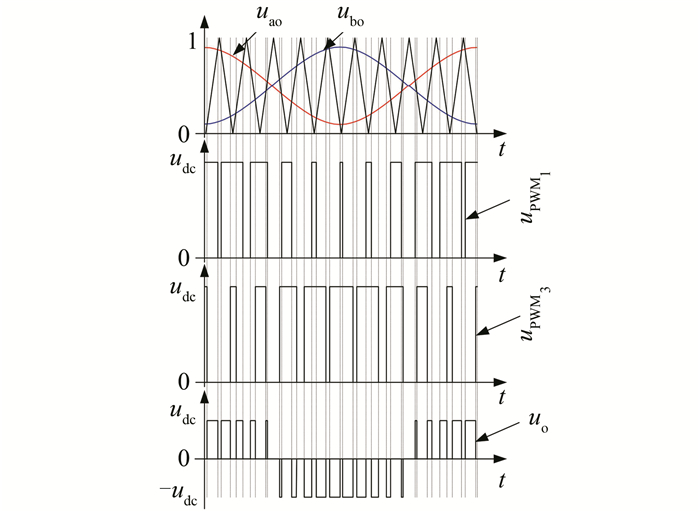
|
| 图 6 开关模式示意图 Fig. 6 Sketch of switching mode |
对于工程研究人员来说,C代码的编写、修改和查错可谓是一件繁琐的工作.而PSIM具有的C代码自动生成功能[15],可将不太熟悉C语言编程的研究人员从繁琐的编程工作中解放出来.PSIM中集成了TMS320F28335功能模块,用户可以直接用这些功能块搭建仿真电路.本次实验搭建的产生SVPWM的C代码功能模块图如图 7所示,在图 7中使用了F28335的ADC模块、串行通信模块、PWM生成模块和PWM中断模块以及GPIO模块;该功能模块图与图 5对应,可以当作图 5的数字离散型模型图.

|
| 图 7 C代码产生功能模块图 Fig. 7 C code generation function module diagram |
文献[16, 17]介绍了SPWM双重傅里叶级数谐波分析.本文使用双重傅里叶级数谐波分析法对基于SVPWM形式的输出电压进行谐波分析,首先要建立基于SVPWM形式的输出电压的傅里叶级数表达式,由图 1、6可知:
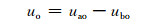 (13)
(13)
其中
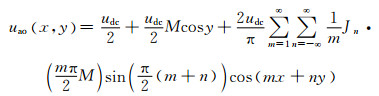 (14)
(14)
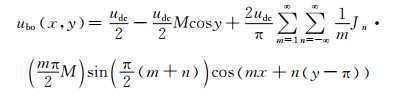 (15)
(15)
所以
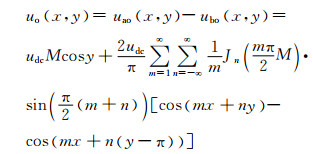 (16)
(16)
其中,式(14)~(16)中的(x,y)为
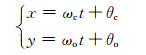 (17)
(17)
式中:ωc和θc分别是载波的角频率和初相角;ωo和θo分别是调制波的角频率和初相角.
由式(16)可以看出该调制方式没有载波谐波.其中对于式(16)右边最后一项,有
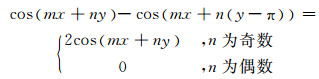 (18)
(18)
这说明,载波谐波的边带谐波没有基波偶数倍的边带谐波,只有奇数倍谐波,即
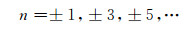
而对于式(16)最后第2项,有
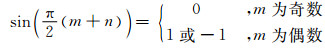 (18)
(18)
这说明,对于载波谐波的边带谐波只有在载波偶数倍处才有,即
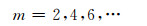
综上分析说明, SVPWM调制方式有倍频的效果,且主要谐波分布在载波偶数倍附近.
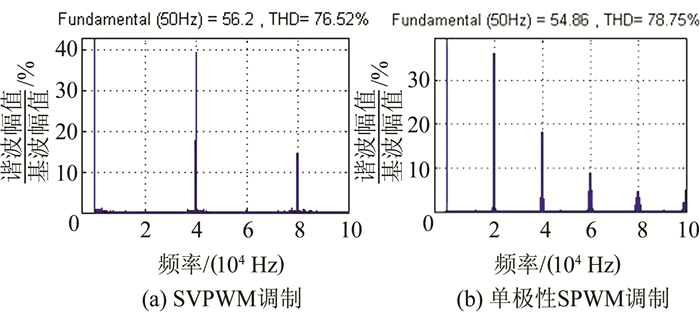
4 仿真与实验结果 4.1 仿真结果分析为对比研究分析SVPWM调制方式,在相同参数(即:载波频率为20 kHz,调制比M=0.8)下,同时搭建单极性SPWM调制方式的逆变电路.最后得到的仿真结果以文本的形式保存,然后导入到Matlab中进行快速傅里叶分析.其中PWM波形式(即uab)的输出电压的傅里叶分析如图 8所示.
|
| 图 8 快速傅里叶分析 Fig. 8 Fast Fourier analysis |
由图 8可知,在SVPWM调制方式下,THD降低了,同时主要的谐波变为载波频率的偶数倍附近,这与上述谐波分析符合.理论上SVPWM调制方式可以降低1倍的开关损耗;同时也有利于对低频大功率逆变进行设计[3],减小LCL或LC滤波器电感电容的体积,降低成本.
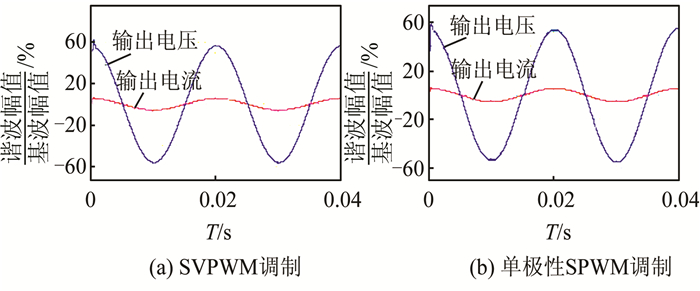
经过LC滤波器后得到的输出电压和输出电流结果如图 9所示.
|
| 图 9 输出电压电流 Fig. 9 Output voltage current |
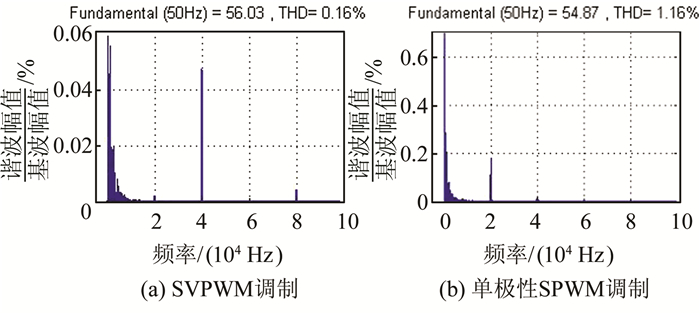
由图 10可以看出在相同的条件下(即:相同的调制比、载波和LC滤波器),SVPWM调制方式比单极性SPWM调制方式的输出电压THD小.
|
| 图 10 输出电压FFT频谱图 Fig. 10 Output voltage FFT spectrogram |
本次实验的实验平台为基于TI公司的TMS320F28335控制核心的实验台.通过图 7产生的C代码下载到DSP中;实验中的PWM1、PWM3以及PWM1-PWM3波形如图 11所示.

|
| 图 11 PWM波形图 Fig. 11 PWM waveform |
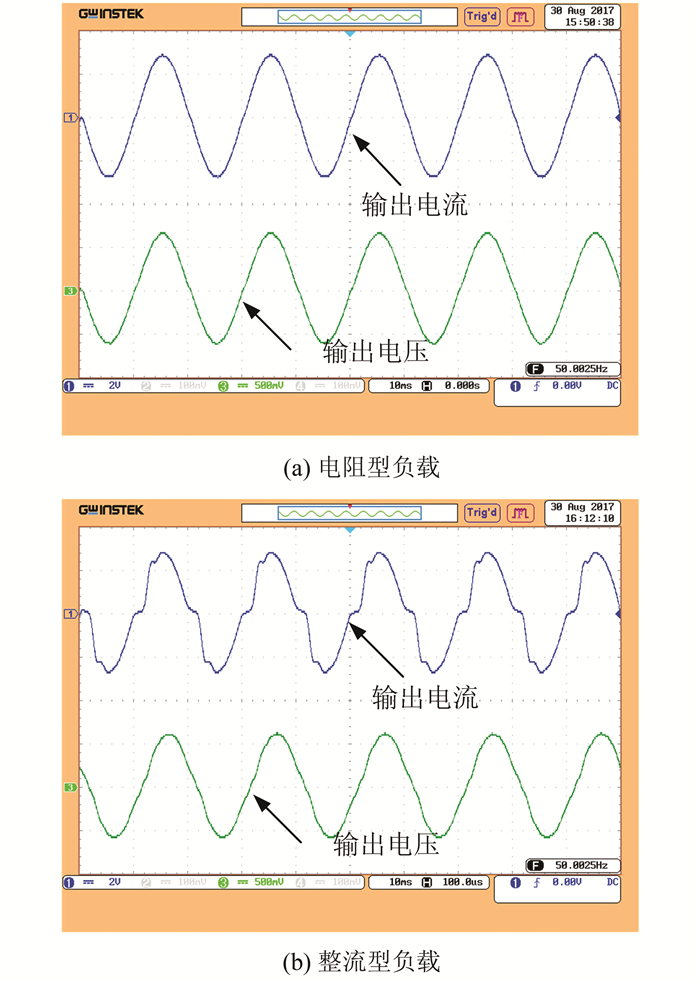
由图 5知MOS管VT1和VT2的PWM驱动信号是1对加死区的互补信号,MOS管VT3和VT4的PWM驱动信号是1对加死区的互补信号;对图 11所示的PWM驱动信号施加开关管(VT1~VT4)得到PWM波形式的输出电压,再经LC滤波器滤波后的输出电压(Uo)和输出电流(Io)波形图如图 12所示.
|
| 图 12 输出电压、电流波形图 Fig. 12 Waveform of output voltage and current |
图 12中波形为输出电压经过0.012 5倍的衰减,输出电流经过0.8倍的衰减;同时为检验逆变器性能的稳定性,对逆变器进行了电阻型和整流型2种不同的负载实验;从图 12可以看出2种负载电压波形无明显变化.
5 结论1) 通过对SVPWM调制方式的算法进行推导,适当地添加零矢量,发现SVPWM调制方式有倍频的效果,这有利于滤波器体积的减小,降低成本.
2) 通过与单极性SPWM调制方式对比分析,发现SVPWM调制方式交流侧输出电压THD明显减少.
3) PSIM仿真软件的使用解决了编写C代码的难题,同时有利于算法和模型的修改,极大地缩短了科研周期.
| [1] |
周磊, 郭前岗, 周西峰, 等. 基于三电平的优化SVPWM算法研究[J]. 微型机与应用, 2016, 35(22): 88-91. Zhou Lei, Guo Qiangang, Zhou Xifeng, et al. Research on an improved SVPWM algorithm for a three-level inverter[J]. Microcomputer & Its Applications, 2016, 35(22): 88-91. |
| [2] |
王晓刚, 张杰. 基于开关电感的增强型Z源三电平逆变器[J]. 电力系统保护与控制, 2015, 43(16): 65-72. Wang Xiaogang, Zhang Jie. Enhanced Z-source three-level inverter based on switched-inductor[J]. Power System Protection and Control, 2015, 43(16): 65-72. DOI:10.7667/j.issn.1674-3415.2015.16.010 |
| [3] |
张纯江, 贲冰, 王晓寰, 等. 基于三电平SVPWM扇区过渡问题的技术研究[J]. 电力电子技术, 2016, 50(4): 67-69, 74. Zhang Chunjiang, Ben Bing, Wang Xiaohuan, et al. Research on three-level SVPWM sector transition problem[J]. Power Electronics, 2016, 50(4): 67-69, 74. DOI:10.3969/j.issn.1000-100X.2016.04.019 |
| [4] |
谭兴国, 王辉, 张黎, 等. 具有电压补偿的四开关并网逆变器等效SVPWM控制方法[J]. 电力系统保护与控制, 2014, 42(1): 1-8. Tan Xingguo, Wang Hui, Zhang Li, et al. An equivalent SVPWM control method with voltage compensation for four-switch inverter[J]. Power System Protection and Control, 2014, 42(1): 1-8. |
| [5] |
张辑, 田洪, 魏荣宗, 等. 降低H/NPC变换器开关损耗的三段式SVPWM算法[J]. 电力电子技术, 2016, 50(10): 11-13. Zhang Ji, Tian Hong, Wei Yongzong, et al. Three segment SVPWM algorithm aiming at low switching losses for H/NPC converter[J]. Power Electronics, 2016, 50(10): 11-13. DOI:10.3969/j.issn.1000-100X.2016.10.004 |
| [6] |
袁佳歆, 薛钢, 赵震, 等. 三相逆变器无死区最优矢量控制研究[J]. 电力系统保护与控制, 2014, 42(24): 18-24. Yuan Jiaxin, Xue Gang, Zhao Zhen, et al. New optimal dead-time elimination for three-phase voltage source inverters[J]. Power System Protection and Control, 2014, 42(24): 18-24. DOI:10.7667/j.issn.1674-3415.2014.24.004 |
| [7] |
吴瑕杰, 熊成林, 冯晓云. 一种适用于单相级联H桥型变换器的通用型多电平空间矢量PWM算法[J]. 电工技术学报, 2017, 32(14): 127-136. Wu Xiajie, Xiong Chenglin, Feng Xiaoyun. An universal multilevel space vector pulse-width modulation algorithm for single-phase cascaded H-bridge converter[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 127-136. |
| [8] |
宋文胜, 冯晓云. 一种单相三电平SVPWM调制与载波SPWM内在联系[J]. 电工技术学报, 2012, 27(6): 131-138. Song Wensheng, Feng Xiaoyun. Relationship between single phase three-level SVPWM and carrier SPWM[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 131-138. |
| [9] |
李宁, 王跃, 雷万钧, 等. 三电平NPC变流器SVPWM策略与SPWM策略的等效关系研究[J]. 电网技术, 2014, 38(5): 1283-1290. Li Ning, Wang Yue, Lei Wanjun, et al. Research on equivalent relations between two kinds of SVPWM strategies and SPWM strategy for three-level neutral point clamped converter[J]. Power System Technology, 2014, 38(5): 1283-1290. |
| [10] |
陆原, 胡丙辉, 张军伟, 等. 基于SVPWM调制的三段式算法研究[J]. 电力系统保护与控制, 2016, 44(6): 68-75. Lu Yuan, Hu Binghui, Zhang Junwei, et al. A three-segment algorithm research based on SVPWM modulation[J]. Power System Protection and Control, 2016, 44(6): 68-75. |
| [11] |
任先文, 王坤, 张俊丰, 等. 基于TMS320F28335的SVPWM实现方法[J]. 电力电子技术, 2010, 44(7): 76-78. Ren Xianwen, Wang Kun, Zhang Junfeng, et al. The method of SVPWM realization based on TMS320F28335[J]. Power Electronics, 2010, 44(7): 76-78. DOI:10.3969/j.issn.1000-100X.2010.07.031 |
| [12] |
罗颜, 张逸成. 基于DSP的单相SVPWM技术及其应用[J]. 电气自动化, 2009, 31(4): 30-32, 36. Luo Yan, Zhang Yicheng. DSP-based single phase SVPWM technique and its application[J]. Electrical Automation, 2009, 31(4): 30-32, 36. DOI:10.3969/j.issn.1000-3886.2009.04.010 |
| [13] |
Angirekula B N V M. Modeling, analysis and control of single phase DC-AC multilevel converters[D]. USA: Tennessee Technological University, 2014: 27-57.
|
| [14] |
郭天勇, 赵庚申, 程如岐, 等. 基于Matlab的单相Z源逆变器的SVPWM仿真研究[J]. 南开大学学报(自然科学版), 2009, 42(4): 34-37. Guo Tianyong, Zhao Gengshen, Cheng Ruqi, et al. SVPWM simulation of single-phase Z-source inverter based on Matlab[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis, 2009, 42(4): 34-37. |
| [15] |
刘生建, 马桂芳, 邱晓芬. 基于PSIM和MATLAB/Simulink的Buck电路的联合仿真[J]. 淮阴师范学院学报(自然科学版), 2017, 16(3): 33-36. Liu Shengjian, Ma Guifang, Qiu Xiaofen. Co-simulation of buck circuit based on PSIM and MATLAB/Simulink[J]. Journal of Huaiyin Teachers College(Natural Science Edition), 2017, 16(3): 33-36. |
| [16] |
刘永迪, 李虹, 张波, 等. 基于双重傅里叶级数的混沌SPWM频谱量化分析[J]. 物理学报, 2014, 63(7): 68-77. Liu Yongdi, Li Hong, Zhang Bo, et al. Spectrum calculation of chaotic SPWM signals based double Fourier series[J]. Acta Physica Sinica, 2014, 63(7): 68-77. |
| [17] |
Song W, Feng X, Xiong C, et al. Single phase three-level SVPWM algorithm and its relationship with carrier-based PWM with zero-sequence voltage injection[C]// IEEE Power Electronics and Motion Control Conference, 2012: 1646-1651.
|
 2019, Vol. 52
2019, Vol. 52




