文章信息
- 刘晴, 倪玉芳, 曹志先
- LIU Qing, NI Yufang, CAO Zhixian
- 考虑下渗的一维河道水流数学模型
- One-dimensional hydrodynamic modelling of river floods with severe infiltration
- 武汉大学学报(工学版), 2019, 52(6): 471-481
- Engineering Journal of Wuhan University, 2019, 52(6): 471-481
- http://dx.doi.org/10.14188/j.1671-8844.2019-06-001
-
文章历史
- 收稿日期: 2018-10-12
河道洪水演算分析研究洪水波在河道中的运动规律,是水文预报的重要组成部分,对防洪减灾和水资源的综合利用有着重要的现实意义.但对于常年断流、河水与地下水长期处于脱节状态的河道,一旦行洪下渗非常强烈,渗漏量会很大.河道渗漏直接影响着行洪流量的大小,因此,再使用传统的不考虑河道下渗的洪水演进模拟模型,无法准确模拟真实的洪水运动.
关于已有的考虑渗漏的河道水流数学模型,齐春英等[1]从质量守恒原理出发,推导了考虑渗漏的明渠非恒定流连续方程,并结合水文学方法,建立了适用于平原河道的考虑沿程渗漏的明渠非恒定流河道洪水流量演算模型.Morin等[2]使用基于运动波方程的河道水流数学模型模拟了干旱半干旱地区存在下渗情况的河道上的洪水演进.Costa等[3]将地表水流连续性方程与地下水流动方程耦合求解,模拟了干旱地区河道的洪水演进过程.Hutton等[4]采用Green-Ampt入渗公式计算入渗率,并与运动波模型结合对短渠道中的洪水过程进行了模拟.Noorduijn等[5]将扩散波方程与Philip入渗公式结合,模拟了人工河槽渗流通量的空间变化.程亮等[6]采用霍顿下渗公式描述河道下渗,推导出了河道下渗流量计算公式,并与基于马斯京根法的天然河道洪水演进模型进行耦合,构建了强烈下渗条件下天然河道洪水演进模拟模型.
本文基于完整的圣维南方程,开发了考虑渗漏的河道一维水流数学模型,其中,下渗率采用Green-Ampt公式进行计算.本文采用有限体积法离散控制方程,利用SLIC数值格式计算数值通量,并使用坡面产流实验结果对该模型进行了初步验证.最后,模型被应用于浊漳河西南源实际河道洪水模拟中.
1 数学模型 1.1 控制方程圣维南方程的积分形式可以根据流体运动的基本守恒定律推导得出[7].在液体密度为定值,且不存在旁侧入流的情况下,有
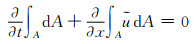 (1)
(1)
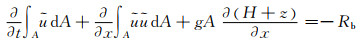 (2)
(2)
式中:t为时间;x为顺水流方向的坐标;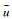
方程中各积分项分别表示如下:过水断面面积A=∫AdA;流量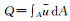
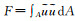
 (3)
(3)
考虑河道入渗,采用水面宽度的变化反映下渗面随着洪水涨落的变化,利用平均水面宽度和下渗率乘积计算单位长度下渗量[6].同时考虑降雨, 处理方式与入渗的处理方式相类似,采用平均水面宽度和降雨强度的乘积计算单位长度降雨产流.故方程(3)写作:
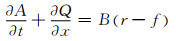 (4)
(4)
其中:r为降雨强度;f为入渗率;B为河道平均水面宽度.
使用动量修正系数β将动量通量F与流量以及过水断面面积联系起来,即
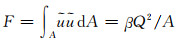 (5)
(5)
故动量方程(2)的微分形式可写作:
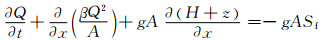 (6)
(6)
在考虑入渗的情况下,由于入渗水流不会对阻力项产生影响,因此动量方程仍采用式(6).
综上所述,考虑渗漏的圣维南方程写作:
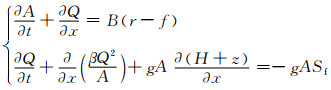 (7)
(7)
应用曼宁糙率公式计算河床阻力坡度:
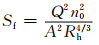 (8)
(8)
式中:Rh为水力半径;n0为综合糙率系数.
根据Sf可得相应的床面剪切应力τb=γhSf,式中γ为清水容重.
1.2.2 下渗率本文采用Green-Ampt模型计算河道下渗率.Green-Ampt公式写作[8]:
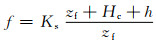 (9)
(9)
式中:f为地表入渗率;Ks为土壤饱和导水率;zf为概化湿润锋深度;Hc为Green-Ampt压力水头;h为土壤表面积水深度.
当地表积水很小时,h≈0,则式(9)可改写为
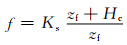 (10)
(10)
概化湿润锋深度zf可以根据累积入渗量确定,具体表示为Fs=(θs-θi)zf,代入式(10),可得到反映下渗率和累计下渗量的关系式:
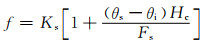 (11)
(11)
式中:θs为饱和含水率;θi为初始含水率;Fs为累计入渗深度.
由入渗量Fs(t)和下渗率f(t)的关系:
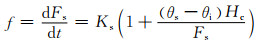 (12)
(12)
通过求解微分方程(12)以得到Fs关于时间t的隐式方程:
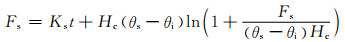 (13)
(13)
对式(13)采用二分法迭代求解得到累计入渗深度Fs,进而通过式(12)求得入渗强度f.式中入渗相关参数主要取决于土壤实测资料.
1.3 数值算法 1.3.1 控制方程离散将控制方程写作向量形式:
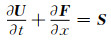 (14)
(14)
其中:
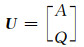 (15)
(15)
 (16)
(16)
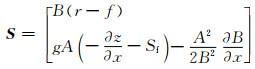 (17)
(17)
 (18)
(18)
其中:U为守恒变量;F为通量变量;S为源项向量.
雅克比矩阵A有2个特征值:
 (19)
(19)
采用有限体积法离散控制方程,源/汇项计算采用龙格库塔方法:
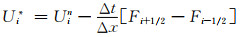 (20)
(20)
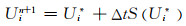 (21)
(21)
其中:Δx为空间步长;Δt为时间步长;上标n为时间节点号;下标i为空间节点号;Fi+1/2和Fi-1/2为相邻单元交界面上的通量.
本文模型计算为显式格式.为了保证计算稳定,时间步长须满足CLF稳定性条件:
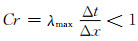 (22)
(22)
式中:Cr为克朗数; λmax为最大特征速度.
1.3.2 数值通量计算本文采用TVD-SLIC方法计算数值通量Fi+1/2[9],具体步骤如下:
1) 数据重构
记原始变量向量W=[A, Q]T,用符号q代表向量W中任意一个元素.可按照一定空间梯度计算得到2个相邻的有限控制体计算单元交界面x=xi+1/2两侧的变量值qi+1/2L和qi+1/2R,即
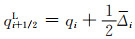 (23)
(23)
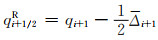 (24)
(24)
式中:Δi和Δi+1是有坡度限制的变量空间梯度,本文采用MINBEE坡度限制器计算,即
 (25)
(25)
式中:Δi-1/2=qi-qi-1;Δi+1/2=qi+1-qi.
2) 交界面两侧半个时间步长的演化
| 参数 | LQ1/% | 峰值 | 累计 | ||||||
| 流量/(m3·s-1) | ε1, Q/% | ε2, Q/% | 累计量/m3 | ε1, V/% | ε2, V/% | ||||
| 率定参数 | 18.9 | 3.969 | 0.0 | 25.5 | 2 446 063 | 0.0 | 0.03 | ||
| Hc/m | 0.4 | 14.2 | 3.985 | 0.4 | 26.0 | 2 473 300.75 | 1.1 | 1.1 | |
| 0.8 | 19.0 | 3.954 | -0.4 | 25.0 | 2 420 069.25 | -1.1 | -1.0 | ||
| n | 0.015 | 18.9 | 4.108 | 3.5 | 29.8 | 2 476 405.5 | 1.2 | 1.3 | |
| 0.035 | 19.3 | 3.985 | -2.4 | 22.4 | 2 390 523 | -2.3 | -2.2 | ||
| s | 1/3 | 19.1 | 3.922 | -1.2 | 24.0 | 2 353 227.5 | -3.8 | -3.8 | |
| 1 | 12.4 | 4.017 | 1.2 | 27.0 | 2 533 525.5 | 3.6 | 3.6 | ||
通过数据空间重构,可得到交界面两侧的重构变量Wi+1/2L和Wi+1/2R,进而可计算得到Ui+1/2L和Ui+1/2R.对Ui+1/2L和Ui+1/2R可按照下式进行半个时间步长上的演化,从而达到时间的二阶精度:
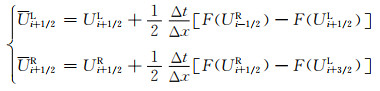 (26)
(26)
3) FORCE通量计算
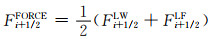 (27)
(27)
式中:Lax-Friedrichs通量Fi+1/2LF和Lax-Wendroff通量Fi+1/2LW计算方法为
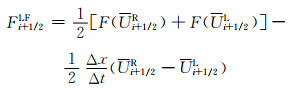 (28)
(28)
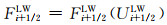 (29)
(29)
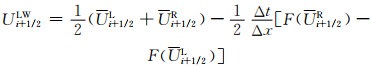 (30)
(30)
1) 上游边界条件对于一维问题,只有水流进口边界条件时,上游给定流量或流量过程,然后根据特征线求解水深和流速.
控制方程的特征线为
 (31)
(31)
对应特征方程为
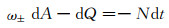 (32)
(32)
其中: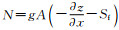
对于上游边界点,由适用于逆特征线的方程,结合上游边界条件联立求解,即可解得上游边界水流变量.
2) 下游边界条件
对于下游边界点,由适用于顺特征线的方程,结合下游边界条件联立求解,即可解得下游边界水流变量.
进行洪水演进模拟时,边界条件是建立洪水演进数学模型的关键问题之一.本文扩展计算区域,保证计算时间内形成的洪水未达到计算区域的边界,从而避免了边界条件.虽然该处理方法增加了计算量,但保证了区域内水流按照其固有物理规律运动,具有普适性[10].
2 模型初步验证Lima[11]在长1 m、宽0.5 m、坡度为0.1的土质坡面上进行坡面产流实验.实验使用的是经过数周自然风干的干燥土壤,将其通过5.6 mm筛网后松散均匀地放置于水槽中形成土坡.实验采用的降雨强度为恒定的0.003 74 mm/s,历时为15 min.
实验采用的坡面有2种土壤类型,分别是来自荷兰林堡的壤土以及来自葡萄牙阿连特茹的黏壤土.反映2种土样物理特性的参数初始含水率θi、饱和含水率θs、土粒密度ρs和土壤容重ρ等均根据实验测定,土壤饱和导水率Ks和土壤水分扩散率Ds则是通过估算得到的.反映2种土样物理特性的参数列于表 1.
| 土壤类型 | 壤土 (来自Limburg) |
黏壤土 (来自Alentejo) |
| 初始含水率θi | 0.010 7 | 0.006 |
| 饱和含水率θs | 0.506 | 0.411 |
| 土粒密度ρs/(kg·m-3) | 2 640 | 2 730 |
| 土壤容重ρ/(kg·m-3) | 1 150 | 1 370 |
| Ks/(10-6 m·s-1) | 1.67 | 0.113 4 |
| Ds/(10-6 m2·s-1) | 13.3 | 5.0 |
为了评价模型性能,将计算结果与实验室测量值进行比较.计算时Hc取为常数0.02 m,空间步长Δx=0.05 m.
为了定量比较计算值和观测值的整体误差,引入无量纲差异指标L1范数:
 (33)
(33)
其中:Lh1和LQ1分别为水深和流量的L1范数;hc和h0分别为计算和观测水深;Qc和Q0分别为计算和观测流量.
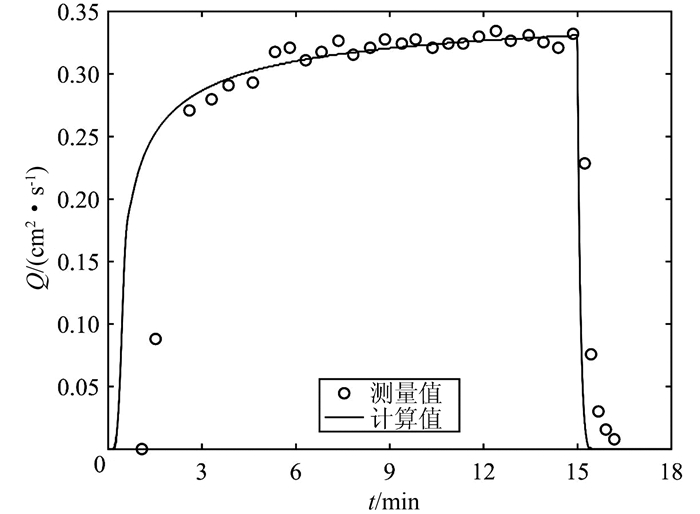
图 1显示的是使用本文所建立的模型模拟历时15 min、强度为0.003 74 mm/s的降雨在坡度为0.1的壤土土坡上形成的坡面流的单宽流量过程线与实测单宽流量过程的对比结果.从图中可以看出,模拟结果与实验观察结果基本符合.定量而言,LQ1为14.06%.
|
| 图 1 壤土土坡上计算单宽流量过程与实验观测流量比较 Fig. 1 Computed discharge hydrograph and measured data for the loam soil |
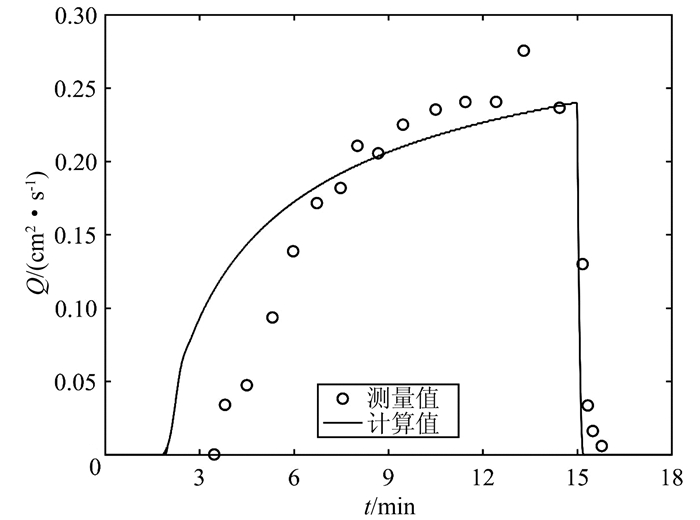
图 2为粘壤土土坡模拟结果与实验值单宽流量过程比较.从图中可以看出,模拟结果与实验观察结果符合良好.定量而言,LQ1为8.77%.从整体误差来看,黏壤土土坡上的模拟结果要优于在壤土土坡上的模拟结果.
|
| 图 2 黏壤土土坡上计算单宽流量过程与实验观测流量比较 Fig. 2 Computed discharge hydrograph and measured data for the clay loam soil |
浊漳河属海河流域漳卫河水系,流域呈扇形分布于山西省的晋中市、长治市和河北、河南两省交界地区,在山西省境内流域面积共11 169 km2.浊漳河上游分为南源、西源与北源,南源发源于长子县西南部的发鸠山,流向为南—北,经上党盆地入襄垣县境;西源发源于沁县北部,流向由东南而正东,在襄垣县甘村与南源汇合;北源发源于榆杜县北部的三仙瑙,流向由北而南,出武乡县关河水库后流向东南.西、南源在甘村汇合后,向东北流约26 km,在襄垣县小峧与北源汇合,流向为东—东南—正东,长90 km,经黎城、潞城于平顺县马塔村出山西境.
浊漳河流域东靠太行山脉,西倚太岳山,北屏北万山,南有丹朱岭,中心为上党盆地,流域为四周高中间低的高原盆地地形.地层地貌形态大体分为4种:石山区(31%)、土石山区(25.8%)、丘陵区(26.4%)、河谷平川区(16.8%),其中,北源关河水库以上为砂页岩土石山区,以下多为黄土丘陵区;西源后湾水库以上为砂页岩丘陵区;南源绛河以上为砂页岩土石山区,陶清河、石子河为灰岩山区,长治一带为高原盆地;三大水库以下右岸一般为灰岩而左岸多为古老石英砂岩地区.另外,在西南源汇合后的西宁静—小峧为断裂带及奥陶系灰岩,属漏水带.坝址以下至石梁水文站也有部分灰岩出露,河槽中砂卵石覆盖层由上而下逐渐加厚,形成又一漏水带.流域植被受地形、气候等因素影响,各地状况差异较大,西、南源山区有比较有利的地层条件,地形坡度相对较缓,多为中等密闭度的灌木林,水土流失较为轻微,加上众多大、中、小型水库的拦截,泥沙出境较少.北源植被条件较差,特别是关河水库以下黄土丘陵区,水土流失较严重.
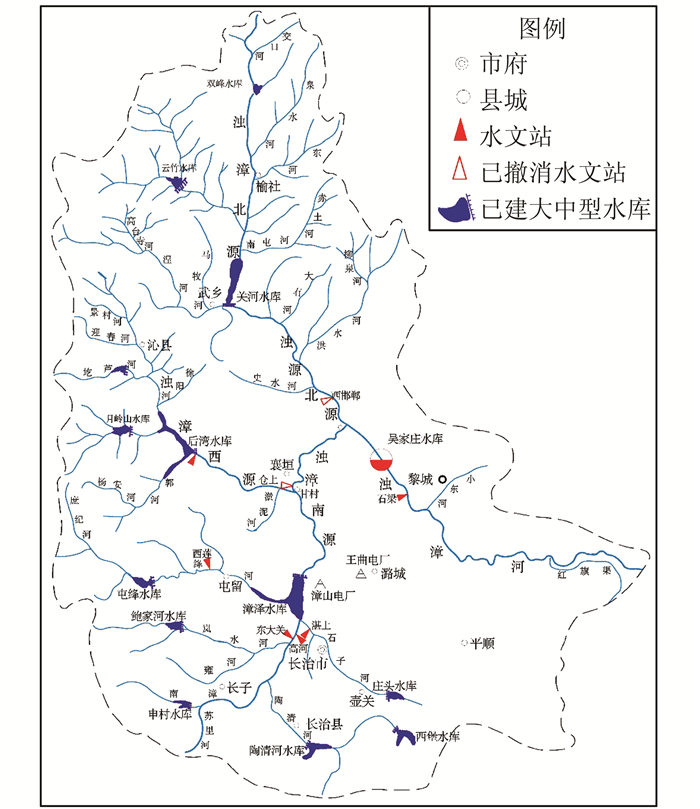
|
| 图 3 浊漳河流域水系图 Fig. 3 Watershed system diagram |
根据水文地质勘察成果,浊漳河干流石梁站以上河道的渗漏地段初步划分为2段,即西南源会合后的西宁静-小峧断裂带(简称“上段”)和三源汇合后的吴家庄-石梁站沙砾石覆盖层段(简称“下段”).这里采用西南源会合后的西宁静-小峧断裂带(即“上段”)渗漏损失实测数据来验证模型.
根据土壤资料可知西宁静-小峧断裂带为奥陶纪灰岩,土壤孔隙率为0.16~0.52,这里取平均值作为饱和土壤体积含水量,即θs=0.34.
初始体积含水量(或前期土湿)对非湿润地区产汇流过程有重要影响.本次计算考虑3种不同的初始土壤体积含水量,分别为饱和含水量的1/3、2/3和1,即θi/θs=1/3,θi/θs=2/3,θi/θs=1,对应于干旱、半干旱和湿润情况[12].
分析时除了采用前面的Lh1和LQ1范数评估计算值与实测值的整体差异外,还引入相对差异ε1, Q=Qc/QC-1×100%,ε2, Q=Qc/Qo-1×100%,ε1, V=Vc/VC-1×100%,ε2, V=Vc/Vo-1×100%进行峰值流量以及下游断面累计流量差异的定量比较,其中Qc、QC、Qo分别为计算峰值流量、率定参数条件下的计算峰值流量和观测峰值流量,Vc、VC、Vo分别为计算下游断面累计流量、率定参数条件下的计算下游断面累计流量和由观测流量计算得出的下游断面累计流量.
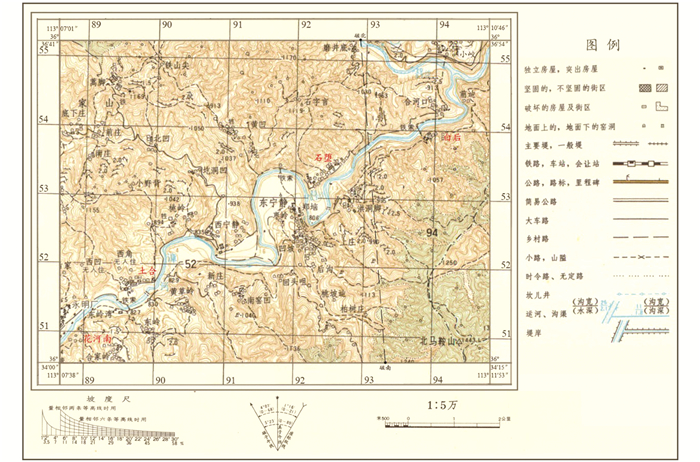
|
| 图 4 计算区域示意图 Fig. 4 Computational domain |
根据土壤资料得土壤饱和入渗率Ks=7.42×10-6 m/s,模型率定的Hc=0.6 m,n=0.025 s/m1/3,前期土壤半干旱, θi/θs=2/3.
使用以上参数,采用考虑下渗的圣维南方程模拟花河南-白后段洪水演进过程.计算初始条件为干河床,入口断面洪量为1958年11月8~30日花河南实测洪水过程,如图 5所示.出口小峧断面流量为0.相对高程基准面取为花河南河床高程.将白后断面计算结果与白后实测数据进行对比,结果如图 6所示.

|
| 图 5 花河南来流过程 Fig. 5 Inflow for the Huahenan |
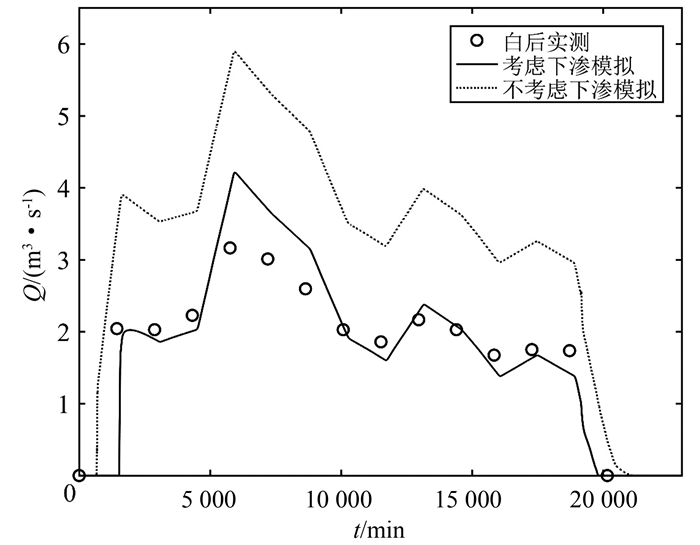
|
| 图 6 白后断面洪水流量模拟结果 Fig. 6 Discharge hydrograph for the Baihou |
从图 6中可以看出, 考虑下渗的模拟结果与实测结果基本吻合,而不考虑下渗的模拟结果与实测结果间存在较大偏差.另外, 考虑下渗情况下白后断面的累计量模拟值为2 446 063 m3, 实测值为2 445 305 m3, 累计量的模拟值与实测值非常接近,ε2, V=0.03%.考虑下渗情况下白后断面的最大流量模拟值为3.969 m3/s, 实测值为3.163 m3/s, 最大流量的模拟值与实测值也相差不大.白后断面计算流量和实测流量的整体误差LQ1为18.9%.
由以上结果可知:河道渗漏对河道洪水演进的影响十分显著,主要表现在其对洪峰流量有明显的削弱作用,且考虑下渗情况下下游断面的见水时间有明显推迟,洪水历时缩短.因此,在对强渗漏地区(如灰岩地区)进行洪水演进的模拟和预报时需要考虑河道下渗的影响.
图 7为花河南-白后段考虑下渗和不考虑下渗情况下的水深、流速、床面剪切应力的模拟结果对比.从模拟结果可以看出,考虑下渗情况下的水深、流速明显小于不考虑下渗情况下的水深和流速.相应地,考虑下渗情况下的床面剪切应力也明显小于不考虑下渗情况下的床面剪切应力.又因为无因次床面剪切力,即希尔兹数Θ=τb/(γs-γ)d是描述泥沙起动的判据之一,因此,考虑下渗情况下对河床变形情况进行模拟的结果也会不同于不考虑下渗情况下的模拟结果.
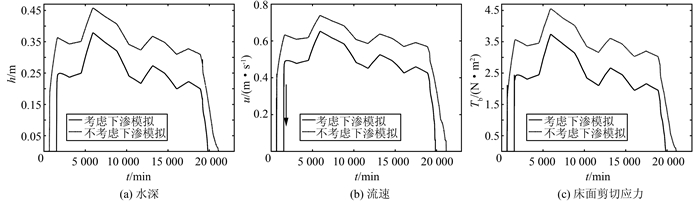
|
| 图 7 白后断面模拟结果 Fig. 7 Simulated results of Baihou |
图 8为花河南-白后段洪水传播120 h后考虑下渗和不考虑下渗情况下的沿程水深、水位、流速以及床面剪切应力的对比.从图中可以看出,沿程水深、流速与床面剪切应力的变化趋势大体相同,且考虑下渗情况下的水深、流速以及床面剪切应力均小于不考虑下渗情况下的对应量.

|
| 图 8 花河南-白后段T=120 h时水深、流速以及床面剪切应力对比 Fig. 8 Profiles of depth, velocity, bed shear stress at 120 h for the Huahenan-Baihou |
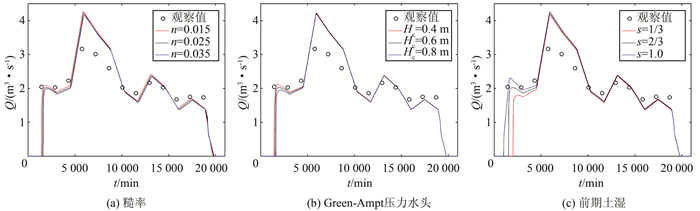
糙率是模型中重要的参数,直接影响洪水的传播过程.为了研究其对洪水过程的影响,糙率取值分别为0.015,0.025,0.035.从图 9(a)可以看出,糙率越大,峰值流量越小,峰值流量出现时间越晚.类似地,糙率越小,峰值流量越大,峰值流量出现时间越早.定量而言,当糙率变为0.015和0.035时,峰值流量分别变为4.108 m3/s(+3.5%)和3.985 m3/s(-2.4%),同时,LQ1分别变为18.9%和19.3%.
|
| 图 9 各因素对白后断面流量过程影响 Fig. 9 Impact of each factors on discharge hydrograph for the Baihou |
Green-Ampt压力水头是入渗公式中的重要参数,直接影响下渗率的大小.为了研究其对洪水过程的影响,Green-Ampt压力水头分别取值为0.4、0.6、0.8 m.从图 9(b)可以看出,Green-Ampt压力水头越大,峰值流量越小,白后断面累计流量越少.类似地,Green-Ampt压力水头越小,峰值流量越大,白后断面累计量越大.定量而言,当Green-Ampt压力水头变为0.4、0.8 m时,峰值流量分别变为3.985 m3/s(+0.4%)和3.954 m3/s(-0.4%),白后断面累计量分别变为2 473 300.750 m3(+1.1%)和2 420 069.250 m3(-1.1%),同时,LQ1分别变为14.2%和19.0%.
前期土湿是入渗模型中的重要参数,直接影响下渗率的大小.为了研究其对洪水过程的影响,土壤初始含水量与饱和含水量比值s分别取值为1/3、2/3、1.0.从图 9(c)可以看出,前期降雨越充分(s越大,s=θ0/θs),峰值流量越大,白后断面累计量越大.定量而言,当s变为1/3、1.0时,峰值流量分别变为3.922 m3/s(-1.2%)和4.017 m3/s(+1.2%),白后断面累计量分别变为2 353 227.5 m3(-3.8%)和2 533 525.5 m3(+3.6%),同时,LQ1分别变为19.1%和12.4%.
3.4 土合-石堕段 3.4.1 计算结果根据土壤资料得土壤饱和入渗率Ks=3.83×10-5 m/s,模型率定的Hc=0.6 m,n=0.025,前期土壤半干旱θi/θs=2/3.
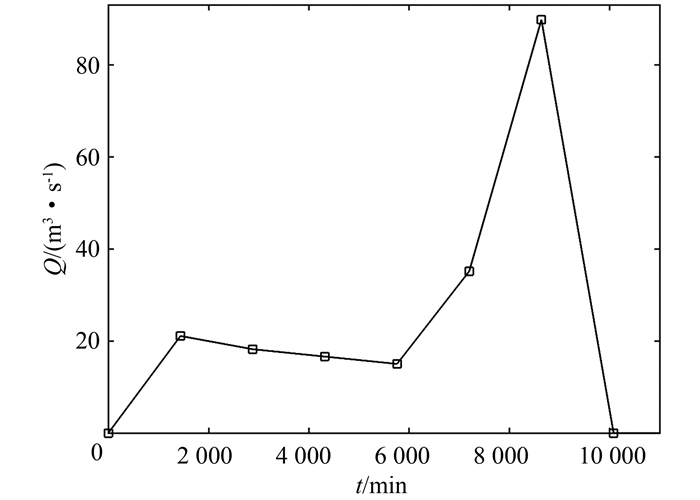
使用以上参数,采用考虑下渗的圣维南方程模拟土合-石堕段洪水演进过程.计算初始条件为干河床,入口断面流量为1992年11月6~21日土合实测洪水过程,如图 10所示.出口小峧断面流量为0.相对高程基准面取为土合河床高程.将石堕断面计算结果与石堕实测数据进行对比,结果如图 11(a)所示.
|
| 图 10 土合来流过程 Fig. 10 Inflow for the Tuhe |

|
| 图 11 石堕断面模拟结果 Fig. 11 Simulated results of the Shiduo |
从图 11(a)中可以看出, 考虑下渗的模拟结果与实测结果基本吻合,而不考虑下渗的模拟结果与实测结果间存在较大偏差.另外, 石堕断面的累计量模拟值为12 255 106 m3, 实测值为122 522 27 m3, 累计洪量的模拟值与实测值非常接近,ε2, V=0.02%.石堕断面的最大流量模拟值为74.205 m3/s, 实测值为74.071 m3/s, 最大流量的模拟值与实测值也相差不大,ε2, Q=0.2%.石堕断面计算流量和实测流量的整体误差LQ1为13.3%.
图 11(b)~(d)为土合-石堕段考虑下渗和不考虑下渗情况下的水深、流速、河床剪切应力的模拟结果对比.从模拟结果可以看出,考虑下渗情况下的水深明显小于不考虑下渗情况下的水深.相应地,考虑下渗情况下的床面剪切应力也要小于不考虑下渗情况下的床面剪切应力.
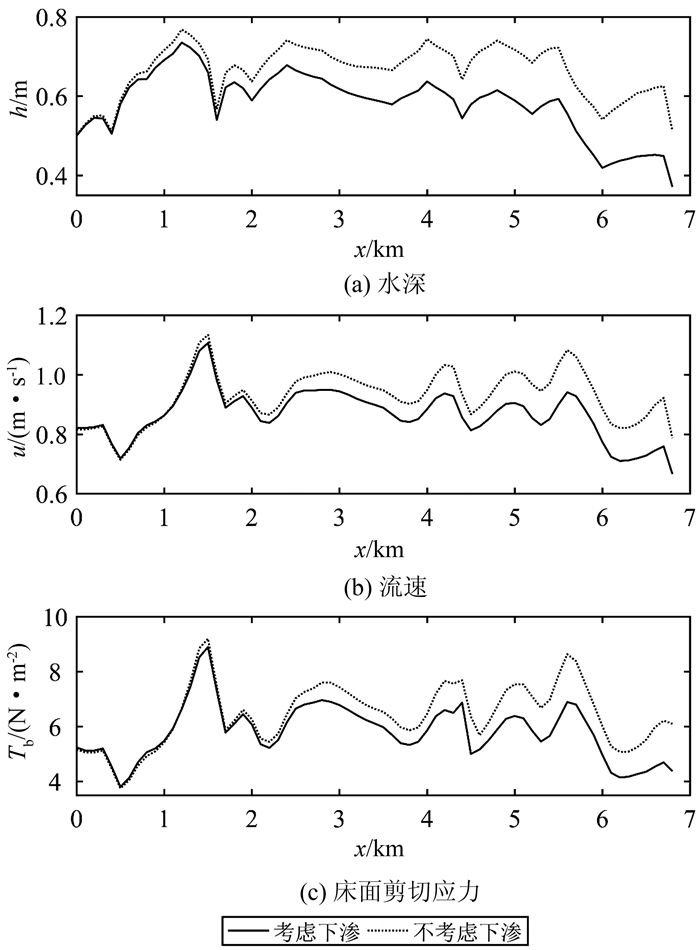
图 12为土合-石堕段洪水传播72 h后考虑下渗和不考虑下渗情况下的沿程水深、流速以及床面剪切应力的对比.从图中可以看出,沿程水深、流速与床面剪切应力的变化趋势大体相同,且考虑下渗情况下的水深、流速以及床面剪切应力均小于不考虑下渗情况下的对应量.
|
| 图 12 土合-石堕段T=72 h时水深、流速以及床面剪切应力对比 Fig. 12 Profiles of depth, velocity and bed shear stress at 72 h for the Tuhe-Shiduo |
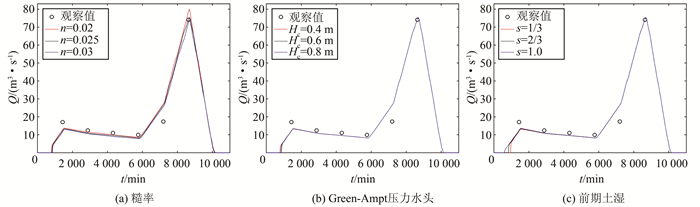
计算时将糙率分别取为0.015、0.025、0.035.从图 13(a)可以看出,糙率越大,峰值流量越小,峰值流量出现时间越晚.类似地,糙率越小,峰值流量越大,峰值流量出现时间越早.定量而言,当糙率变为0.015和0.035时,峰值流量分别变为80.877 m3/s(+8.9%)和71.074 m3/s(-0.5%),同时,LQ1分别变为16.2%和16.4%.
|
| 图 13 各因素对石堕断面流量过程影响 Fig. 13 Impact of several factors on discharge hydrograph for the Shiduo |
计算时将Green-Ampt压力水头分别取为0.4、0.6、0.8 m.从图 12(b)可以看出,Green-Ampt压力水头越大,峰值流量越小,石堕断面累计量越少.类似地,Green-Ampt压力水头越小,峰值流量越大,石堕断面累计量越大.定量而言,当Green-Ampt压力水头变为0.4、0.8 m时,峰值流量分别变为74.215 m3/s(+0.01%)和74.195 m3/s (-0.01%),石堕断面累计量分别变为12 280 380 m3(+0.2%)和12 230 332 m3(-0.2%),同时,LQ1分别变为13.2%和13.4%.
计算时将土壤初始含水量与饱和含水量比值s分别取为1/3、2/3、1.0.从图 13(c)可以看出,前期降雨越充分(土壤初始含水量与饱和含水量比值s=θ0/θs越大),峰值流量越大,石堕断面累计量越大.定量而言,当s变为1/3、1.0时,峰值流量分别变为74.175 m3/s(-0.04%)和74.236 m3/s(+0.04%),石堕断面累计量分别变为12 182 399 m3(-0.6%)和12 333 456 m3(+0.6%),同时,LQ1分别变为13.6%和13.1%.分析结果见表 3所示.
| 参数 | LQ1/% | 峰值 | 累计 | ||||||
| 流量/(m3·s-1) | ε1, Q/% | ε2, Q/% | 累计量/m3 | ε1, V/% | ε2, V/% | ||||
| 率定参数 | 13.3 | 74.205 | 0.0 | 0.2 | 12 255 106 | 0.0 | 0.02 | ||
| Hc/m | 0.4 | 13.2 | 74.215 | 0.01 | 0.2 | 12 280 380 | 0.2 | 0.2 | |
| 0.8 | 13.4 | 74.195 | -0.01 | 0.2 | 12 230 332 | -0.2 | -0.2 | ||
| n | 0.015 | 16.2 | 80.877 | 8.9 | 9.2 | 13 160 919 | 7.39 | 7.4 | |
| 0.035 | 16.4 | 71.074 | -0.5 | -4.0 | 11 506 249 | -6.1 | -6.1 | ||
| s | 1/3 | 13.6 | 74.175 | -0.04 | 0.1 | 12 182 399 | -0.6 | -0.6 | |
| 1 | 13.1 | 74.236 | 0.04 | 0.2 | 12 333 456 | 0.6 | 0.7 | ||
本文基于完整的圣维南浅水方程,结合Green-Ampt公式建立了考虑下渗的河道水流数学模型.通过坡面产流实验算例对模型进行初步验证,数值计算结果与实测数据吻合良好,表明本文模型可以较好地模拟坡面产流过程.使用本文模型对典型渗漏区域洪水,即浊漳河西南源的2场典型场次洪水进行数值模拟,模拟结果与实测流量过程吻合良好,而不考虑下渗的传统模型计算结果与实测流量过程差异很大,且计算结果表明河道下渗对洪峰流量、洪水总量、洪水历时均有影响.参数敏感性分析表明模型中糙率n、土壤湿度s、湿润锋吸力等参数均对计算结果有一定影响.
今后的研究可以在本文模型的基础上考虑泥沙输移及河床变形,建立考虑下渗的浅水泥沙形态动力学模型,用以研究典型渗漏区域的泥沙输移与河床变形过程.
| [1] |
齐春英, 刘克岩. 沿程渗漏河道的洪水流量演算模型[J]. 水文, 1997, 17(6): 27-30. Qi Chunying, Liu Keyan. Flood flow routing model for river course with on-way seepage[J]. Journal of China Hydrology, 1997, 17(6): 27-30. |
| [2] |
Morin E, Grodek T, Dahan O, et al. Flood routing and alluvial aquifer recharge along the ephemeral arid Kuiseb River, Namibia[J]. Journal of Hydrology, 2009, 368(1): 262-275. |
| [3] |
Costa A C, Bronstert A, Araújo J C D. A channel transmission losses model for different dryland rivers[J]. Hydrology & Earth System Sciences, 2011, 16(4): 1111-1135. |
| [4] |
Hutton C J, Brazier R E, Nicholas A P, et al. On the effects of improved cross‐section representation in one‐dimensional flow routing models applied to ephemeral rivers[J]. Water Resources Research, 2012, 48(4): 4509. |
| [5] |
Noorduijn S L, Shanafield M, Trigg M A, et al. Estimating seepage flux from ephemeral stream channels using surface water and groundwater level data[J]. Water Resources Research, 2014, 50(2): 1474-1489. DOI:10.1002/2012WR013424 |
| [6] |
Cheng Liang, Wang Zongzhi, Hu Siyi, et al. Flood routing model incorporating intensive streambed infiltration[J]. Science China Earth Sciences, 2015, 58(5): 718-726. DOI:10.1007/s11430-014-5018-x |
| [7] |
Cao Zhixian, Meng Jian, Pender G, et al. Flow resis tance and momentum flux in compound open channels[J]. Journal of Hydraulic Engineering, 2006, 132(12): 1272-1282. DOI:10.1061/(ASCE)0733-9429(2006)132:12(1272) |
| [8] |
朱昊宇, 段晓辉. Green-Ampt入渗模型国外研究进展[J]. 中国农村水利水电, 2017(10): 6-12. Zhu Haoyu, Duan Xiaohui. Research progress of Green-Ampt soil water infiltration model in foreign countries[J]. China Rural Water & Hydropower, 2017(10): 6-12. DOI:10.3969/j.issn.1007-2284.2017.10.002 |
| [9] |
Toro E F. Shock-capturing methods for free-surface shallow flows[M]. Chichester: John Wiley, 2001.
|
| [10] |
Huang Wei, Cao Zhixian, Qi Wenjun, et al. Full 2D hydrodynamic modelling of rainfall-induced flash floods[J]. Journal of Mountain Science, 2015, 12(5): 1203-1218. DOI:10.1007/s11629-015-3466-1 |
| [11] |
Lima J L M P. Model kininf for overland flow on pervious surface[M]. Overland Flow: Hydraulics and Erosion Mechanics, 2001.
|
| [12] |
Mlv M, Todini E, Libralon A. A Bayesian decision approach to rainfall thresholds based flood warning[J]. Hydrology & Earth System Sciences Discussions, 2005, 2(6): 413-426. |
 2019, Vol. 52
2019, Vol. 52




