文章信息
- 黄震, 傅鹤林, 张加兵, 袁维, 洪开荣
- HUANG Zhen, FU Helin, ZHANG Jiabing, YUAN Wei, HONG Kairong
- 基于模糊-证据理论的盾构隧道施工风险综合评价
- Comprehensive evaluation of shield tunnel construction risk based on fuzzy-evidence theory
- 武汉大学学报(工学版), 2019, 52(8): 694-702
- Engineering Journal of Wuhan University, 2019, 52(8): 694-702
- http://dx.doi.org/10.14188/j.1671-8844.2019-08-006
-
文章历史
- 收稿日期: 2018-07-07
2. 中国电建集团中南勘测设计研究院, 湖南 长沙 410014;
3. 中铁隧道集团有限公司,河南 洛阳 471009
2. Hydro China Zhongnan Engineering Corporation, Changsha 410014, China;
3. China Railway Tunnel Group Co., Ltd., Luoyang 471009, China
在北京、上海、广州等特大城市中,轨道交通系统承担了城市公共客运总量的40%~50%,而盾构法作为城市轨道交通的主要工法,其施工总长度占据了城市轨道线路总长的50%~70%[1, 2].由于盾构隧道穿梭于城市复杂地层中,且周边存在重要构筑物及密集活动人群,使得盾构隧道在设计、施工及服役环境中存在许多不确定风险因素,这些因素构成了盾构隧道建设和运营安全的潜在风险源.针对这些风险源,选择合理的评价方法来指导工程风险决策尤为重要.为此,近年来我国学者对盾构隧道的风险评价方法进行了研究,王明卓、彭铭等[3, 4]通过监测项目指标与盾构隧道结构状态之间关系,对盾构隧道进行风险评价.姚浩等[5]采用模糊综合评价模型对软土地区土压式盾构掘进施工风险进行评估.谢壮[6]采用层次—模糊综合评估法对花岗岩球状风化体段盾构施工进行风险因素的评估.郑俊杰等[7]结合模糊故障树理论,提出用模糊成本重要度的指标来评价盾构隧道施工风险因素对成本的影响,进而得出盾构施工需要规避的风险.陈自海等[8]采用模糊综合评判法对杭州某地铁盾构隧道施工进行风险评价.张姣[9]采用贝叶斯网络模型对地铁盾构隧道施工进行风险评估.王公忠等[10]利用模糊层次分析法对台山核电站海底隧道泥水平衡盾构施工风险因素进行分析、评价.
上述风险评价方法大都集中于不确定风险综合评估,指标权重建立在专家评估的基础上.由于认知局限,专家评定出较为模糊的结果,因此,Kangari等[11]、Chen等[12, 13]采用模糊数学方法对评价结果进行量化处理,但模糊算子的选取具有随意性,缺乏合理性证明.为解决盾构隧道风险评价不确定性推理与决策的问题,采用证据理论可以提高评价结果的置信度[14, 15].证据理论利用信用函数进行不确定性推理,无需得到先验概率,因此相比于贝叶斯方法更显优越,其合成规则能够高效地融合不确定信息,该方法目前已广泛应用于传感信息数据融合.
由于缺乏长期盾构隧道施工风险的统计资料,并且施工环境及地层条件具有较强的地域性和特殊性,施工风险指标评价主要通过专家评语进行评价.因此,本文基于盾构隧道施工风险评价指标体系,提出模糊-证据理论的风险综合评价模型,利用专家对风险指标的评价结果,对盾构隧道的施工风险进行决策.
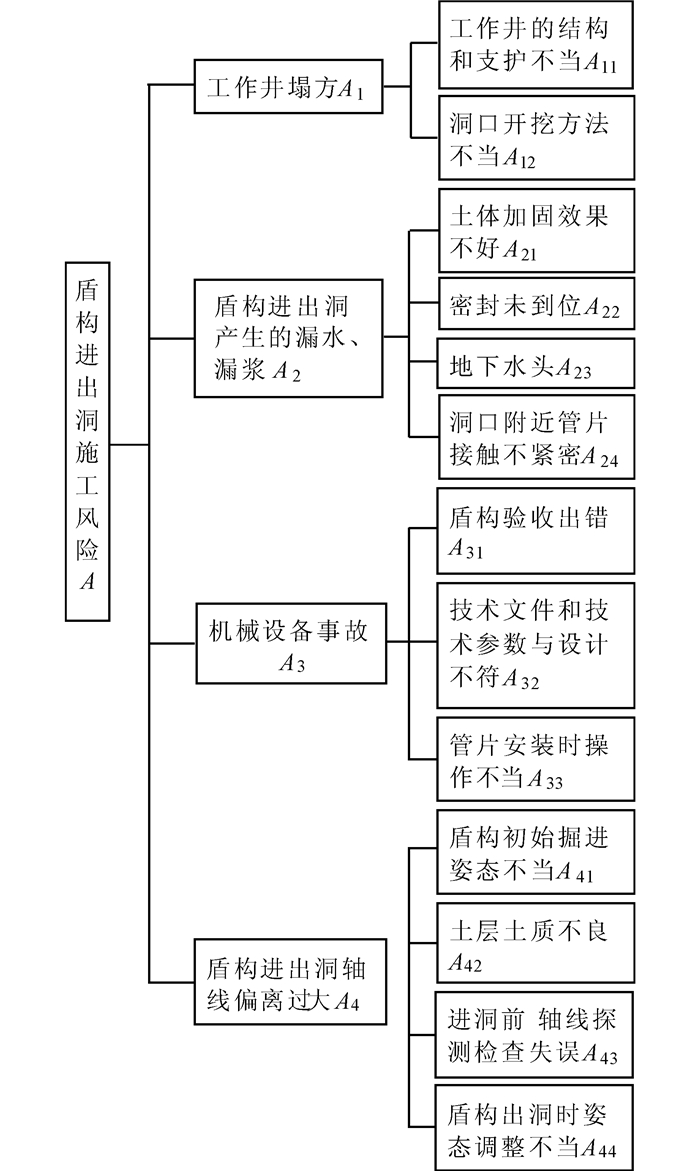
1 盾构隧道施工风险评价指标体系盾构隧道施工风险评价的首要任务是建立风险评价指标体系,这些评价指标将作为风险评价证据.为此,本文结合盾构隧道施工风险因素及实际工况,建立隧道盾构进出洞及盾构推进过程的2级风险评价指标体系.由于隧道盾构进出洞与推进过程均为风险顶上事件,风险评价方法过程相同,因此,本次研究以盾构隧道进出洞风险事故为例进行风险评价,其第1层指标为主因素,共4个,第2层指标为子因素,共13个,如图 1所示.
|
| 图 1 盾构进出洞施工风险指标体系 Fig. 1 Risk index system of shield tunnel construction |
1967年Dempster[16]首次提出证据理论,后由Shafer[17]在此基础上进一步发展,证据理论简称为D-S理论.证据理论采用信任函数度量不知道引起的不确定性事物,是一种不确定性推理方法.
2.1 基本概念定义 1 设U为某个需要解决事件所有可能取值的集合,表示为U={x1, x2, …, x3},且集合中的元素两两互斥,称U为事件的识别框.2U称为U的幂集,有2n个元素,则基本概率分配函数m:2U→[0, 1]满足下式时,称m(A)为A的基本概率赋值,m也称为对U中子集的赋值的函数:
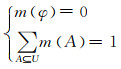 (1)
(1)
定义 2 信任函数Bel:2U→0, 1,且满足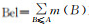
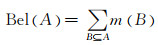 (2)
(2)
定义 3 似然函数PL:2U→[0, 1],且PL(A)=1-Bel(-A),PL函数也称为上限函数,表示对A怀疑程度:
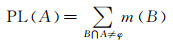 (3)
(3)
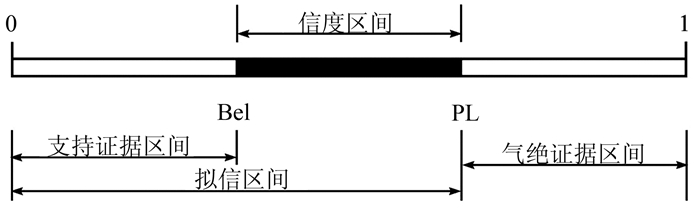
Bel(A)和PL(A)构成了A的信度区间,图 2中反映了证据理论对A的不确定性描述.
|
| 图 2 模糊证据理论对事件的不确定性描述 Fig. 2 Description of uncertainty of events by fuzzy-evidence theory |
设m1, m2, …, mn分别为n个证据在同一识别框U上对应的基本概率分配函数,焦元分别为Aij,其中i=1, 2, …, n,表示证据个数, j=1, 2, …, s,表示证据信度结构中焦元个数.证据组合规则为
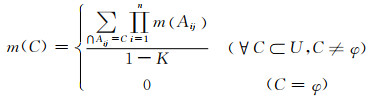 (4)
(4)
式中, 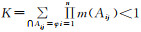
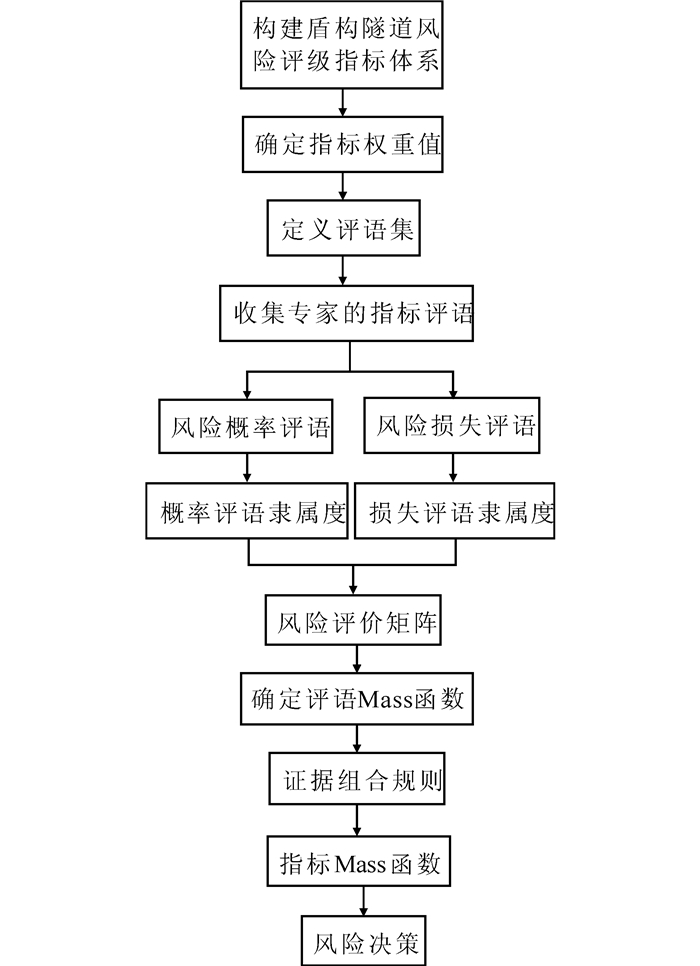
评价基本思路:依据证据理论,在构建盾构隧道施工风险评价指标体系的基础上,确定风险等级识别框,将风险评价指标作为证据,逐层对指标评语转化Mass函数,最后依据风险等级信度进行决策.其中风险等级识别框的建立是证据判断的先决条件,依据人们对事物的辨别能力,定义风险等级识别框U={1级,2级,3级,4级,5级},识别框中的元素用Rq(q=1, 2, 3, 4, 5与元素对应,风险发生概率由低到高),评价具体流程如图 3所示.
|
| 图 3 基于证据理论的盾构隧道施工风险评价流程 Fig. 3 Flowchart of risk assessment of shield tunnel construction based on fuzzy-evidence theory |
风险评价指标权重通常采用层次分析法进行计算,利用“1~9”比较标度法对指标进行量化,但这种标度方法不能真实地反映客观情况,例如,i比j稍微重要,则利用“1~9”标度法得到i与j的重要性比为0.75:0.25,这个结果明显不符合实际评判思维.为了避免这种不合理的情况,本文基于梯形模糊数[18]的指标权重确定方法,采用的梯形模糊数标度等级赋值如表 1所示.
| 两元素i与j重要性比较 | “1~9”法标度值 | 改进法 | 量化结果 |
| 同等重要 | 1 | 5/5 | 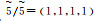
|
| 稍微重要 | 3 | 6/4 | 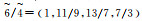
|
| 明显重要 | 5 | 7/3 | 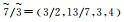
|
| 强烈重要 | 7 | 8/2 | 
|
| 极为重要 | 9 | 9/1 | 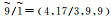
|
说明:梯形模糊数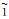
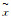
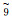
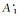
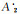
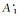
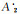
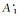
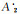
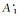
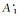
计算过程如下:
1) 将Y个专家对同一指标集进行两两比较,分别给出判断矩阵R(e)=(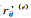
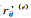
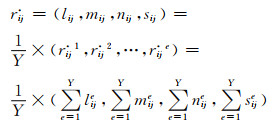 (5)
(5)
2) 通过下式计算模糊评价值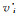
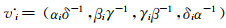 (6)
(6)
其中
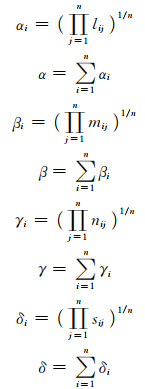
3) 通过下式计算各指标模糊评价值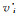
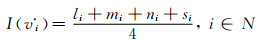 (7)
(7)
4) 将式(7)采用归一化处理方法,计算得到k层指标相对上一层的权重:
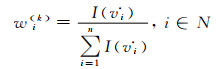 (8)
(8)
1) 定义评语集
专家通过评语集对风险概率和风险损失进行评价,定义评语集为h={极大、很大、较大、一般、较小、很小、极小},评语集中的元素用ht表示,t=7~1,依据风险概率及损失程度由大到小,ht对应的分值f=7~1,Ahtf为f对于ht的隶属度.
| ht | f | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 极小 | 1 | 0.75 | 0 | 0 | 0 | 0 | 0 |
| 很小 | 0.25 | 1 | 0.75 | 0 | 0 | 0 | 0 |
| 较小 | 0 | 0.25 | 1 | 0.75 | 0 | 0 | 0 |
| 一般 | 0 | 0 | 0.25 | 1 | 0.25 | 0 | 0 |
| 较大 | 0 | 0 | 0 | 0.75 | 1 | 0.25 | 0 |
| 很大 | 0 | 0 | 0 | 0 | 0.75 | 1 | 0.25 |
| 极大 | 0 | 0 | 0 | 0 | 0 | 0.75 | 1 |
2) 指标评语Mass函数
定义风险损失C特征集ΘC={5级,4级,3级,2级,1级},特征集中的元素用Cd表示(d=5~1),C5~C1风险损失逐渐减小.通过定义f为特征集Cd的论域,BCdf为f对Cd的隶属度,建立Cd与ht的关系.特征集定义见表 3[20].
| Cd | f | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| C1 | 1 | 0.75 | 0 | 0 | 0 | 0 | 0 |
| C2 | 0 | 0.25 | 1 | 0.5 | 0 | 0 | 0 |
| C3 | 0 | 0 | 0.25 | 1 | 0.5 | 0 | 0 |
| C4 | 0 | 0 | 0 | 0.25 | 1 | 0.5 | 0 |
| C5 | 0 | 0 | 0 | 0 | 0 | 0.75 | 1 |
专家Y(Y=1,2,…,e)依据自己经验及知识对模糊评语ht映射到Cd中的广义隶属函数为
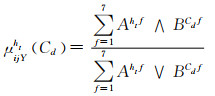 (9)
(9)
式中:μijYht(Cd)表示模糊评语ht与Cd匹配度,取值范围为[0, 1];∧表示Min运算,∨表示Max运算.
依据归一化原理,定义ΘC为风险损失等级识别框,专家Y对指标Aij的评语在ΘC上的Mass函数为
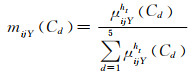 (10)
(10)
定义风险损失P特征集ΘP={5级,4级,3级,2级,1级},特征集中的元素用Po表示(o=5~1),P5~P1风险损失逐渐减小.依据上述原理,可得专家Y对模糊评语ht映射到Po中的广义隶属函数μijYht(Po)和指标Aij的评语在ΘP上的Mass函数:
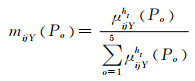 (11)
(11)
上述Mass函数mijY(Cd)、mijY(Po)表示Cd、Po发生的概率.依据文献[21]以及风险函数关系式(R=f(C, P)),建立函数:
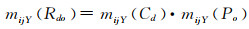 (12)
(12)
式中,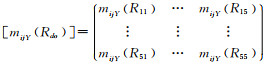
本文中Cd、Po、Rq的风险特征集均为5级,参考文献[21, 22]中风险矩阵,见表 4,将mijY(Rdo)映射到各个风险等级上.定义专家Y对模糊评语ht映射到Rq中的Mass函数为
| 风险矩阵 | 风险损失Cd | |||||
| C1 | C2 | C3 | C4 | C5 | ||
| 风险概率Po | P1 | R1 | R1 | R2 | R3 | R4 |
| P2 | R1 | R2 | R3 | R3 | R4 | |
| P3 | R1 | R2 | R3 | R4 | R4 | |
| P4 | R2 | R3 | R3 | R4 | R5 | |
| P5 | R2 | R3 | R4 | R5 | R5 | |
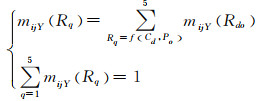 (13)
(13)
3) 指标Mass函数合成
由于各专家自身的认识和偏好的差异,给出的指标评语在某种程度上存在不可靠性,因此,本文采用折扣系数法[23]对指标评语的Mass函数进行折扣修正.设专家Y对指标评语的权重为wY,修正Mass函数为
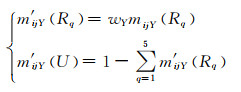 (14)
(14)
式中,0≤wY≤1,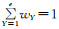
专家Y对指标评语的权重wY的计算公式为
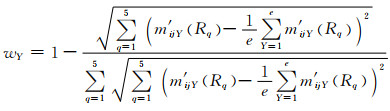 (15)
(15)
依据盾构隧道进出洞施工风险评价指标层次结构图,对所有的指标合成Mass函数为
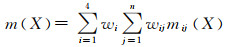 (16)
(16)
式中:X为U的子集;m(X)为子集的发生概率;mij(X)为第1层指标i中第j个子指标的发生概率;wi为第1层指标i的权重;wij为第1层指标i中第j个子指标的权重;ni为第1层指标i下的子指标数.
通过式(4)将各位专家的修正后Mass函数进行合成,其中mij(X)为式(16)合成的指标Aij的Mass函数:
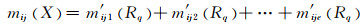 (17)
(17)
工程上通常采用表 5[22]所示的风险接受准则对风险等级进行判定,并给出相应的工程决策.风险准则中的风险等级与本文建立的风险等级识别框中的元素Rq是对应关系,风险等级用区间数进行估值,并提出不同风险等级有不同的工程决策.
| 等级 | 概率区间 | 接受准则及工程决策 |
| 1级 | [0,0.2) | 可忽略,正常管理及巡视 |
| 2级 | [0.2,0.4) | 可容许,需加强管理及巡视 |
| 3级 | [0.4,0.6) | 可接受,加强防范及监测,制定预防措施 |
| 4级 | [0.6,0.8) | 不可接受,需要采取控制措施,预警方案 |
| 5级 | [0.8,1] | 拒绝接受,停止作业,规避风险,采取应急预案 |
定义风险等级信度区间为
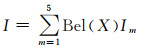 (18)
(18)
式中,Im为表 5中的概率区间,Im=[Im-, Im+),I=[I-, I+).
本文引用文献[24]中提出的区间数贴近度进行风险决策,Im与I区间数贴近度为
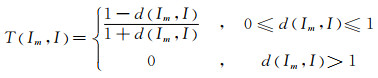 (19)
(19)
式中,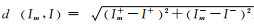
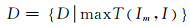 (20)
(20)
确定风险等级后,再依据接受准则表进行工程决策.
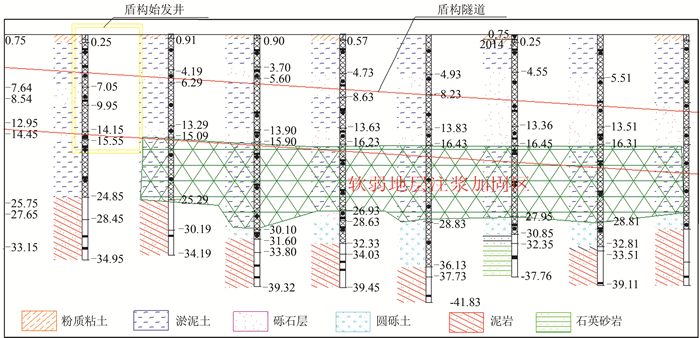
4 工程案例分析佛山~东莞城际铁路狮子洋隧道,盾构段长4 900 m,盾构直径13.46 m,采用泥水平衡盾构.始发井和接收井的平面尺寸分别为28.8 m×29.1 m,它们位于邻近狮子洋入海口,地层由上至下为人工填土层、第4系海相沉积及冲击层、基岩层,地下承压水头较大,地下水丰富,这些不利因素成为了盾构隧道进出洞施工安全的风险源.从进洞始发段地质剖面图 4可看出,该盾构始发段淤泥土层很厚,而淤泥土具有含水率高、空隙比大、易产生流变等特性,加之泥水平衡盾构洞口土体的稳定性对盾构始发和接收极为重要,稍有不慎将引起盾构轴线偏离过大、基座变形损坏、洞口水土流失、土体坍塌、泥水平衡建立困难等风险事故.因此,狮子洋隧道进出洞施工风险评价结果将对工程风险决策具有重要的指导作用.
|
| 图 4 进洞地质纵断面图 Fig. 4 Geological profile of tunnel entry |
依据盾构隧道进出洞施工风险评价指标体系,结合专家对指标集的两两重要性对比结果,利用梯形模糊数方法计算得到第1层指标权重A=[0.032,0.624,0.308,0.036],第2层指标权重A1=[0.708,0.292],A2=[0.641,0.031,0.297,0.031],A3=[0.062,0.062,0.876],A4=[0.064,0.776,0.064,0.096],从指标权重计算结果可知,盾构隧道进出洞漏水、漏浆、机械设备事故是引起风险的主要因素.
4.2 指标Mass函数专家依据评语集为h={极大、很大、较大、一般、较小、很小、极小},用ht表示,t=7~1,对指标进行评价,共收集到若干专家评语,选取有代表性的专家评语进行统计分析,结果如表 6所示.采用本文描述的指标评语转化Mass函数的方法,将表 6中的指标评语转化为指标Mass函数,结果见表 7.
| 指标 | 专家评语(风险损失,风险概率) | ||||
| 1 | 2 | 3 | 4 | 5 | |
| A11 | h5,h3 | h5,h4 | h6,h3 | h5,h4 | h5,h5 |
| A12 | h4,h3 | h3,h2 | h3,h3 | h3,h4 | h4,h2 |
| A21 | h5,h5 | h6,h4 | h5,h6 | h5,h5 | h5,h4 |
| A22 | h6,h3 | h5,h2 | h4,h3 | h5,h3 | h6,h2 |
| A23 | h5,h4 | h4,h3 | h5,h4 | h4,h4 | h4,h3 |
| A24 | h3,h3 | h3,h2 | h2,h2 | h2,h3 | h4,h2 |
| A31 | h5,h2 | h6,h1 | h5,h1 | h5,h2 | h7,h1 |
| A32 | h6,h2 | h5,h3 | h7,h1 | h5,h1 | h6,h3 |
| A33 | h4,h3 | h5,h4 | h4,h2 | h5,h2 | h4,h3 |
| A41 | h4,h4 | h5,h5 | h4,h3 | h4,h5 | h4,h3 |
| A42 | h3,h5 | h4,h6 | h3,h6 | h4,h4 | h4,h5 |
| A43 | h6,h2 | h5,h3 | h5,h2 | h5,h3 | h6,h3 |
| A44 | h3,h4 | h4,h3 | h5,h4 | h4,h4 | h4,h3 |
| 指标 | 指标Aij的Mass函数值 | |||||
| R1 | R2 | R3 | R4 | R5 | U | |
| A11 | 0.102 3 | 0.438 1 | 0.363 2 | 0.093 1 | 0 | 0.003 3 |
| A12 | 0.008 7 | 0.312 0 | 0.539 2 | 0.138 9 | 0 | 0.001 2 |
| A21 | 0.093 1 | 0.392 3 | 0.217 4 | 0.293 4 | 0 | 0.003 8 |
| A22 | 0.005 1 | 0.516 5 | 0.402 8 | 0.073 2 | 0 | 0.002 4 |
| A23 | 0.105 7 | 0.243 2 | 0.542 4 | 0.105 3 | 0 | 0.003 4 |
| A24 | 0.073 2 | 0.129 4 | 0.555 4 | 0.239 1 | 0 | 0.002 9 |
| A31 | 0.304 2 | 0.218 4 | 0.437 4 | 0.034 1 | 0 | 0.005 9 |
| A32 | 0.248 5 | 0.308 7 | 0.393 0 | 0.044 5 | 0 | 0.005 3 |
| A33 | 0.003 4 | 0.411 3 | 0.490 5 | 0.093 8 | 0 | 0.001 0 |
| A41 | 0.060 3 | 0.587 1 | 0.272 3 | 0.077 2 | 0 | 0.003 1 |
| A42 | 0.015 5 | 0.602 3 | 0.336 7 | 0.041 4 | 0 | 0.004 1 |
| A43 | 0.315 1 | 0.309 8 | 0.358 2 | 0.010 1 | 0 | 0.006 8 |
| A44 | 0.049 2 | 0.740 2 | 0.184 0 | 0.023 9 | 0 | 0.002 7 |
依据式(16)、(17)对表 7中的指标函数进行合成,合成结果如表 8所示.
| 指标 | R1 | R2 | R3 | R4 | R5 | U |
| A1 | 0.075 0 | 0.401 3 | 0.414 5 | 0.106 5 | 0 | 0.002 7 |
| A2 | 0.093 5 | 0.343 7 | 0.330 2 | 0.229 0 | 0 | 0.003 6 |
| A3 | 0.037 2 | 0.393 0 | 0.481 2 | 0.087 0 | 0 | 0.001 6 |
| A4 | 0.040 8 | 0.595 8 | 0.319 3 | 0.040 0 | 0 | 0.004 1 |
利用信任函数计算出Rq信度值为{0.073 67,0.369 8,0.379 0,0.174 5,0},根据区间贴近度方法,计算出风险概率区间与风险等级信度区间的贴近度为{0,0.333 6,0.480 6,0,0}.因此,依据式(20)判定狮子洋隧道进出洞的施工风险等级属于3级风险,且出现风险等级为1级、4级、5级的可能性较小.因此,该项目施工风险可接受,但需要对土样本进行颗分实验,确保泥水循环系统性能,并对始发段软土地层进行加固处理,加强地层变形及地下水位的监测,以降低盾构始发与接收施工的风险等级.
为了验证基于模糊-证据理论的施工风险综合评价方法的有效性,笔者采用文献[5]提出的盾构隧道施工风险模糊综合评价方法,结合本文中的评价指标体系,对该隧道盾构施工整体风险进行评价,评价结果与本文基于模糊-证据理论的隧道施工综合评价结果一致,如表 9所示.此外,该评价结果与狮子洋隧道施工安全风险评估报告结果相吻合,进一步说明了基于模糊-证据理论的盾构隧道施工风险评价方法的可行性.
由表 9可知本文所提的方法与模糊综合评价方法之间的差异,其中在风险因素的权重比较方面梯形模糊数更加符合实际评判思维.风险是风险概率和风险损失的函数,因此在风险表述中,本文同时考虑了风险损失和风险概率;在专家评价结果量化中,模糊评价方法主要是通过定量估值打分,具有一定的随意性,而本文主要将评语转化为Mass函数进行处理,消除了随意性的影响.在综合评判原则方面,本文主要结合区间贴近度进行表述,较最大隶属度原则更为科学合理.
5 结论1) 由于证据理论可以提高评价结果的置信度,本文结合盾构隧道施工风险评价指标体系,提出了基于模糊-证据理论的盾构隧道施工风险综合评价方法, 通过对狮子洋盾构隧道进出洞施工风险评价,验证了该方法的实用性及有效性.
2) 考虑到“1~9”标度法不能合理反映评价的客观情况,引入梯形模糊数函数确定指标的权重.同时基于风险函数关系式,建立了反映风险损失和风险概率的指标评语Mass函数,并采用折扣系数法对指标评语Mass函数进行修正,利用加权函数逐层合成指标Mass函数.最终,结合指标权重计算风险信度区间.该过程可实现程序化,便于今后盾构隧道施工的风险评价.
3) 通过引入区间贴近度建立了盾构隧道风险等级的决策方法.利用风险准则中的风险等级概率区间及风险等级信度区间的贴近程度,反映了专家组综合评价结果.
| [1] |
张新金, 刘维宁, 路美丽, 等. 北京地铁盾构法施工问题及解决方案[J]. 土木工程学报, 2008, 41(10): 93-99. Zhang Xinjin, Liu Weining, Lu Meili, et al. Problems and solutions of shield tunneling for Beijing metro[J]. China Civil Engineering Journal, 2008, 41(10): 93-99. DOI:10.3321/j.issn:1000-131X.2008.10.014 |
| [2] |
徐顺明.广州轨道交通盾构隧道施工控制测量的研究[D].武汉: 武汉大学, 2011. Xu Shunming. On the control survey in the shield tunnel construction of Guangzhou rail traffic[D]. Wuhan: Wuhan University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10486-1013047506.htm |
| [3] |
王明卓, 黄宏伟. 基于横向收敛变形的盾构隧道风险评价研究[J]. 现代隧道技术, 2014, 51(S1): 5-9. Wang Mingzhuo, Huang Hongwei. Risk assessment of shield tunnel based on horizontal convergence[J]. Modern Tunnelling Technology, 2014, 51(S1): 5-9. |
| [4] |
彭铭, 黄宏伟, 胡群芳, 等. 基于盾构隧道施工监测的动态风险数据库开发[J]. 地下空间与工程学报, 2007, 3(7): 1255-1260. Peng Ming, Huang Hongwei, Hu Qunfang, et al. A risk database designed for dynamic risk management in shield tunneling from monitoring date[J]. Chinese Journal of Underground Space and Engineering, 2007, 3(7): 1255-1260. |
| [5] |
姚浩, 周红波, 蔡来炳, 等. 软土地区土压盾构隧道掘进施工风险模糊评估[J]. 岩土力学, 2007, 28(8): 1753-1756. Yao Hao, Zhou Hongbo, Cai Laibing, et al. Fuzzy synthetic evaluation on construction risk of EPBS during tunnelling in soft soil area[J]. Rock and Soil Mechanics, 2007, 28(8): 1753-1756. DOI:10.3969/j.issn.1000-7598.2007.08.043 |
| [6] |
谢壮.花岗岩球状风化体地段地铁盾构施工风险分析与控制[D].长沙: 中南大学, 2010. Xie Zhuang. Risk analysis and control of metro shield construction in the area of the spherical weathered granite[D]. Changsha: Central South University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10533-2010188771.htm |
| [7] |
郑俊杰, 林池峰, 赵冬安, 等. 基于模糊故障树的盾构隧道施工成本风险评估[J]. 岩土工程学报, 2011, 33(4): 501-508. Zheng Junjie, Lin Chifeng, Zhao Dongan, et al. Risk assessment of shield tunnel construction cost using fuzzy fault tree[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(4): 501-508. |
| [8] |
陈自海, 陈建军, 杨建辉. 基于模糊层次分析法的盾构隧道施工风险分析[J]. 地下空间与工程学报, 2013, 9(6): 1427-1432. Chen Zihai, Chen Jianjun, Yang Jianhui. Risk analysis of tunnel shield machine driving in construction process based on fuzzy AHP[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(6): 1427-1432. |
| [9] |
张姣. 基于贝叶斯网络的地铁盾构隧道工程风险评估方法[J]. 城市轨道交通研究, 2014(3): 30-34. Zhang Jiao. Risk assessment of metro shield tunnel construction based on Bayesian network[J]. Urban Mass Transit, 2014(3): 30-34. |
| [10] |
王公忠, 刘星魁, 李凤琴. 层次分析法的海底隧道盾构施工风险评价[J]. 辽宁工程技术大学学报:自然科学版, 2015, 34(11): 1240-1243. Wang Gongzhong, Liu Xingkui, Li Fengqin. Evaluation of risks of shield construction of submarine tunnel with analytic hierarchy process[J]. Journal of Liaoning Technical University: Natural Science, 2015, 34(11): 1240-1243. |
| [11] |
Kangari R, Riggs L S. Construction risk assessment by linguistics[J]. IEEE Transactions on Engineering Management, 1989, 36(2): 126-131. DOI:10.1109/17.18829 |
| [12] |
Chen S J, Chen S M. Fuzzy risk analysis based on similarity measures of generalized fuzzy numbers[J]. IEEE Transactions on Fuzzy Systems, 2003, 11(1): 45-56. DOI:10.1109/TFUZZ.2002.806316 |
| [13] |
Chen S J, Chen S M. Fuzzy risk analysis based on measures of similarity between interval -valued fuzzy numbers[J]. Computers and Mathematics with Applications, 2008, 55(11): 1670-1685. |
| [14] |
Guo Huawei, Shi Wenkang, Deng Yong. Evaluating sensor reliability in classification problems based on evidence theory[J]. IEEE Transactions on Systems, Man and Cybernetics, 2006, 36(5): 970-981. DOI:10.1109/TSMCB.2006.872269 |
| [15] |
Lefevr E, Colot O, Vannoorenbe Rghe O. Belief functions combination and conflict management[J]. Information Fusion, 2002, 3(2): 149-162. DOI:10.1016/S1566-2535(02)00053-2 |
| [16] |
Dempster A P. Upper and lower probabilities induced by a multi-valued mapping[J]. Annals of Mathematical Statistics, 1967, 38: 325-339. DOI:10.1214/aoms/1177698950 |
| [17] |
Shafer G. A Mathematical Theory of Evidence[M]. Princeton: Princeton University Press, 1976.
|
| [18] |
刘雨华. 基于梯形模糊数的指标权重确定方法的应用研究[J]. 南京信息工程大学学报:自然科学版, 2009, 1(4): 369-372. Liu Yuhua. Study on application of the method of determining index weights based on trapezoidal fuzzy numbers[J]. Journal of Nanjing University of Information Science and Technology: Natural Science Edition, 2009, 1(4): 369-372. |
| [19] |
Wang J, Yang J B, Sen P. Safety analysis and synthesis using fuzzy sets and evidential reasoning[J]. Reliability Engineering and System Safety, 1995, 47: 103-117. DOI:10.1016/0951-8320(94)00053-Q |
| [20] |
杨萍, 刘卫东. 基于证据理论的群决策层次评价方法研究[J]. 系统工程与电子技术, 2002, 24(2): 42-44. Yang Ping, Liu Weidong. Study on group decision making in the hierarchical evaluation process based on evidential reasoning[J]. Systems Engineering and Electronics, 2002, 24(2): 42-44. DOI:10.3321/j.issn:1001-506X.2002.02.014 |
| [21] |
杜修力, 张雪峰, 张明聚, 等. 基于证据理论的深基坑工程施工风险综合评价[J]. 岩土工程学报, 2014, 36(1): 155-161. Du Xiuli, Zhang Xuefeng, Zhang Mingju, et al. Risk synthetic assessment for deep pit construction based on evidence theory[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 155-161. |
| [22] |
中华人民共和国建设部. 地铁及地下工程建设风险管理指南[M]. 北京: 中国建筑出版社, 2007. Ministry of Construction P R China. Guidelines of Risk Management for the Construction of Tunnel and Underground Works[M]. Beijing: China Architecture & Building Press, 2007. |
| [23] |
Fabre S, Appriou A, Briattet X. Presentation and description of two classification methods using data fusion based on sensor management[J]. Information Fusion, 2001, 2(1): 49-71. DOI:10.1016/S1566-2535(00)00018-X |
| [24] |
杨春玲, 张传芳, 许文翠. 基于区间数贴近度的不确定多属性决策模型[J]. 数学的实践与认识, 2010, 40(21): 148-154. Yang Chunling, Zhang Chuanfang, Xu Wencui. A model based on similarity degree of interval number for uncertain multi-attribute decision-making[J]. Journal of Mathematics in Practice and Theory, 2010, 40(21): 148-154. |
 2019, Vol. 52
2019, Vol. 52



