文章信息
- 蔡芳, 程永光, 张晓曦
- CAI Fang, CHENG Yongguang, Zhang Xiaoxi
- 保证调压室水位波动三维CFD模拟准确性的方法
- Approaches to guarantee accuracy of 3D CFD simulations of surge tank wave
- 武汉大学学报(工学版), 2016, 49(3): 390-396
- Engineering Journal of Wuhan University, 2016, 49(3): 390-396
- http://dx.doi.org/10.14188/j.1671-8844.2016-03-012
-
文章历史
- 收稿日期: 2015-06-05
调压室是水电站和泵站系统的重要平压建筑物,过渡过程中调压室水位波动的准确计算是调压室尺寸设计和布置优化的基础[1].目前调压室水位波动计算主要采用一维方法,在多数情况下能获得准确结果[2].不过当调压室内水流三维效应明显,如长廊式调压室内水流纵向振荡和阻抗孔部位有立轴漩涡时[3],采用三维CFD进行计算分析势在必行.
调压室水力特性的三维CFD模拟处于起步阶段,目前主要侧重于恒定工况下的阻抗系数预测[4]和体型优化[5].虽有一些针对过渡过程中室内不良流态三维模拟成果[3],但模拟对象一般取调压室局部,将管道流量变化过程作为已知条件施加在边界上.近期有学者开展了将管道系统与调压室结合起来进行三维计算的尝试[6~7],但研究表明,全三维模拟所得结果与实验或实测数据的吻合程度较差,其原因亟待研究.
本文旨在探讨如何保证CFD模拟调压室水位波动的准确性.首先讨论影响调压室水位波动的因素,然后针对每种因素分析CFD设置或模型选取方法,总结保证计算准确性的措施,最后通过实例应用展示这些措施的有效性.
1 影响调压室水位波动的基本因素针对图 1所示的典型水电站简单式调压室系统,取引水隧洞为脱离体,根据牛顿第二定律和连续条件,得到以调压室水位和隧洞流速为变量的动量方程和连续方程[1]:

|
| 图 1 水电站简单式调压室示意图 Figure 1 Sketch map of the simple surge tank in hydropower station |
其中:V为引水隧洞瞬时流速,流向调压室为正;Z为以库水位为基准的调压室瞬时水位,向上为正;hw为系统水头损失;L为引水隧洞的长度;f为引水隧洞面积;F为调压室断面面积;QT为压力管道流量;g为重力加速度;t为时间.
动量方程等号左端表示引水隧洞中的水流惯性,右端第二项表示系统的水头损失;连续方程左端与引水隧洞面积有关,右端第一项与调压室断面面积有关.所以,调压室水位波动的基本影响因素是系统的水流惯性和阻力,以及引水隧洞与调压室的断面面积.对于阻抗式调压室,系统的水流惯性除了包括引水隧洞的惯性外,还应包括连接管的惯性,当调压室断面面积不大时还应包括调压室内的水流惯性;系统阻力除了包括引水隧洞的沿程损失外,还应包括进水口、连接管和阻抗孔等局部损失.
采用一维数值方法模拟调压室水位波动过程时,水库给定水位条件,调压室作为单独的边界处理.当采用三维CFD模拟时,通过软件平台实现,水库进口处给定水位边界、压力管道给定流量边界、调压室顶部为自由水面边界、引水隧洞管壁边界需要特别处理.
综上分析,若要采用三维CFD方法准确模拟调压室水位波动过程,应重点探索如何准确模拟系统水流惯性、水头损失和合理设置各种边界条件.
2 影响CFD模拟水位波动准确性的主要因素分析 2.1 水位波动特性基本定义可用波动周期T、最高水位Zmax、最低水位Zmin和衰减系数c来描述理想调压室的水位波动过程(图 2).波动周期表征调压室水位波动快慢,本文分析中主要针对前4个周期的平均值.最高和最低水位用于校核和优化调压室体型,这里取以调压室初始水位为基准的相对值;可用衰减系数判断衰减特性,c值越大波动衰减越快.波动周期和最高(最低)涌浪主要取决于引水隧洞水流惯性以及引水隧洞与调压室的断面面积比,衰减速度主要取决于系统的阻力.

|
| 图 2 调压室水位波动过程基本参数定义示意图 Figure 2 Basic parameters definition of surge tank wave |
为突出基本影响因素,本文以简单式调压室为例进行分析.鉴于用一维方法计算简单式调压室波动的准确性较高,且经过了大量工程验证,本文的三维结果要与一维结果比较来判断准确性.定义εT、εZmax、εZmin和εc分别为波动周期、最高水位、最低水位和波动衰减因子的相对误差,即一维与三维结果的绝对误差与一维结果的比值,如周期相对误差定义为
其中:T3D表示三维CFD所得周期;T1D表示一维方法所得周期.
2.2 水体惯性模拟的准确性如图 3所示的U形管中的水柱振荡与调压室水位波动的物理本质一致,都体现了水体惯性能、动能和势能的相互转化过程.这里用此算例来验证CFD模拟水体惯性的准确性.水柱沿管轴线的长度是L,初始时U形管两端水位不平衡,在重力作用下水柱产生周期性振荡.水柱振荡周期T仅与水柱长度L有关,其关系为:$T=2\pi \sqrt{L/2g}$ [8].本文CFD模拟中选用无粘性三维流动方程,通过VOF方法来捕捉自由液面.将所得周期与解析解对比(图 3),可知CFD模拟结果与理论公式一致,相对误差在0.5%以内,说明CFD方法可准确模拟调压室水位波动过程中水体惯性的影响.

|
| 图 3 模拟所得U形管水柱振荡周期 Figure 3 Simulation results of the oscillating period of the water in U-tube |
系统的阻力影响调压室水位波动的衰减速度,包括引水隧洞的沿程水头损失、调压室与引水隧洞间的局部水头损失以及进水口的局部水头损失,下面分别讨论.
1) 管道沿程水头损失
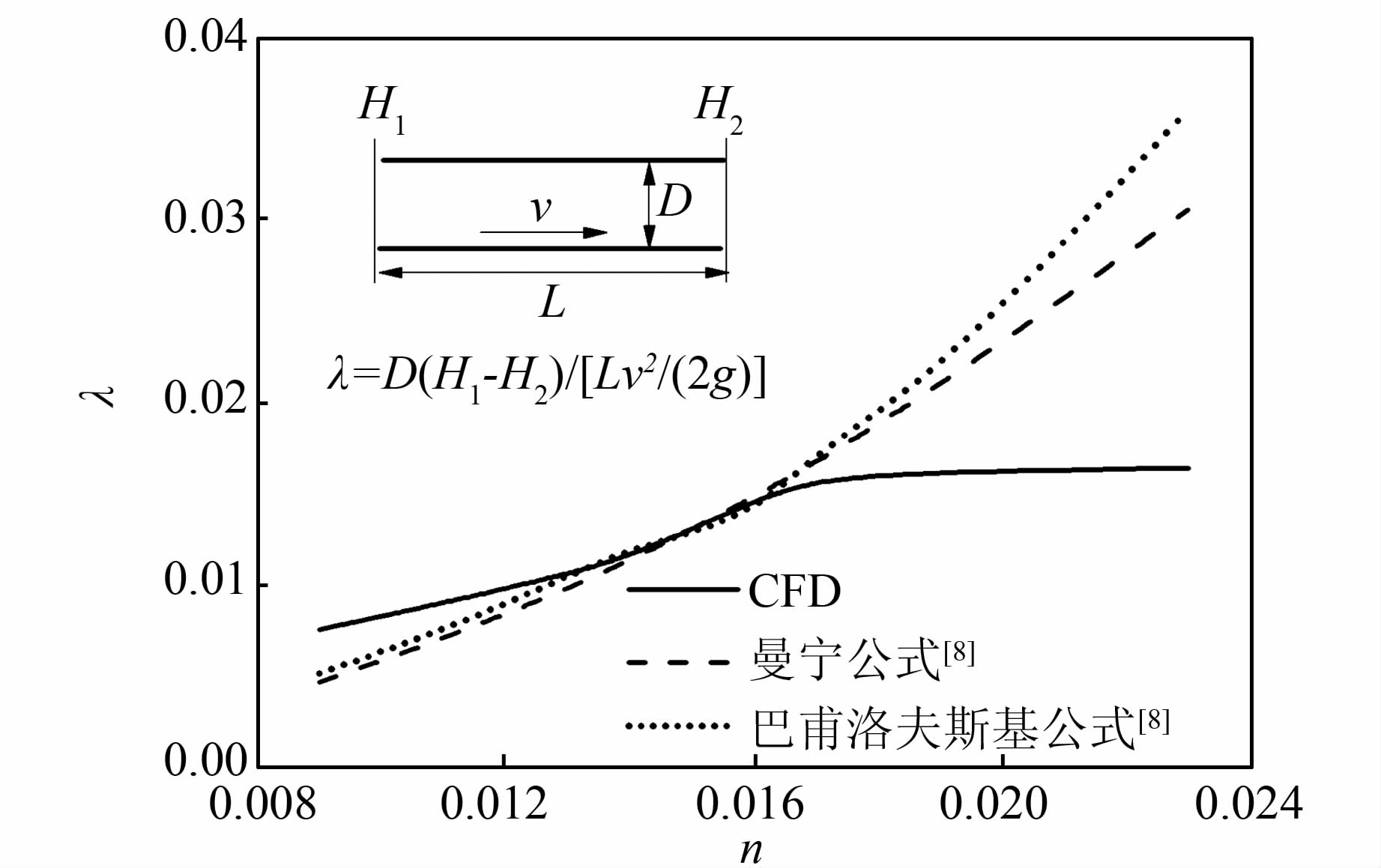
用CFD计算管道流动时,须划分壁面边界层,给定糙率系数,选定合适的湍流模型和边壁函数.这里用CFD模拟等径直管在不同糙率下的水头损失系数,通过与经验公式对比来验证沿程水头损失计算的准确性.直管长500 m,直径10 m,糙率n∈[0.009,0.023].采用计算水头损失较好的Realizable k-ε湍流模型[9]和标准壁面函数,并用公式$n={{\Delta }^{1/6}}/\left( 7.66\sqrt{g} \right)$中的当量粗糙度Δ设定Fluent中常用糙率参数KS,CS取值0.5.计算网格数量经过网格无关性验证,且边界层网格符合标准壁面函数要求.CFD模拟结果与常用经验公式(曼宁公式和巴普洛夫斯基公式)[10]结果对比如图 4所示,可见模拟值与经验值整体的吻合度不高.在n∈0.013,0.017范围内CFD结果与两种经验值基本重合,但离开此范围后,三者偏差即开始增大.虽然两种经验公式的结果也不完全重合,但趋势一致,最大相对误差未超过15%.而随着糙率的减小或增大,CFD结果与两种经验值的差别逐渐加大,n=0.023时最大误差可达50%以上.这说明用CFD计算长管道沿程水头损失的准确性较差.
|
| 图 4 模拟所得管道沿程水头损失系数 Figure 4 Simulation results of piping frictional head losses |
为了分析管道沿程水头损失对调压室水位波动的影响,这里选择不同长度的引水隧洞进行调压室水位波动计算.隧洞糙率n=0.009,调压室与隧洞面积比为1∶1,水库边界为带自由水面的水库边界(后面详述).所得周期、最高水位、最低水位和衰减因子与一维结果对比如表 1所示.可见,无论引水隧洞长短,CFD计算所得调压室水位波动周期均十分准确,进一步证实了CFD模拟水体惯性的准确性.但随着隧洞长度变长,CFD所得水位振幅,特别在第二振幅(对应最低水位)和衰减因子的误差显著增大.这说明常规CFD方法无法准确模拟管道沿程水头损失,从而影响调压室水位波动的幅值和衰减特性,在隧洞较长时可能带来较大误差.
| 隧洞长度L/m | 方法 | T/s | εT/% | Zmax/m | εZmax/% | Zmin/m | εZmin/% | c | εc/% |
| 50 | 1D | 15.58 | 0.47 | 1.973 | 4.97 | -1.796 | 1.82 | 0.007 8 | 6.41 |
| 3D | 15.65 | 2.071 | -1.764 | 0.008 3 | |||||
| 100 | 1D | 21.00 | 0.81 | 3.150 | 3.10 | -2.631 | 6.94 | 0.006 0 | 8.33 |
| 3D | 21.17 | 3.053 | -2.814 | 0.005 5 | |||||
| 500 | 1D | 45.32 | 0.54 | 7.043 | 3.55 | -6.783 | 13.49 | 0.004 3 | 34.88 |
| 3D | 45.56 | 7.302 | -5.977 | 0.002 8 |
2) 局部水头损失
进水口、隧洞和调压室相接处,阻抗式调压室的阻抗孔等的局部水头损失对调压室涌浪有重要影响.用CFD模拟与调压室相关的局部水头的准确性已在文献[4, 5, 11]中得到验证,大体结论是:一般来说,CFD模拟得到的局部水头损失系数的误差小于20%,当网格划分较好和选择合适计算模型时,也可将误差控制在10%以内.
本文选取调压室与隧洞面积比不同的工况,在其他条件不变条件下进行三维数值模拟.该组算例主要反映进水口的阻力以及调压室与隧洞之间的阻力对调压室水位波动的影响.一维计算中流入进水口损失系数取0.5,流出进水口损失系数取1.0,隧洞与调压室连接处损失系数按文献[1]中的实验值选取,并且考虑了调压室内水体惯性和流速.三维计算中调压室的隧洞长度取100 m,直径为1 m,壁面糙率n=0.由表 2可以看出,4种工况CFD模拟的最高和最低涌浪的幅值与一维结果相比误差较小,都在工程允许误差范围内,说明了三维CFD模拟局部水头损失的准确性.虽然衰减因子误差稍大,但不一定全归咎于三维模拟的误差,因为依经验取值的损失系数也可能存在误差.所以,可以认为CFD能较好反映局部水头损失对调压室涌浪的影响.
| 面积比 | 方法 | T/s | εT/% | Zmax/m | εZmax/% | Zmin/m | εZmin/% | c | εc/% |
| 1 | 1D | 20.99 | 1.00 | 2.98 | 2.92 | -2.83 | 4.09 | 0.003 1 | 16.12 |
| 3D | 21.20 | 3.07 | -2.96 | 0.003 6 | |||||
| 2 | 1D | 29.09 | 1.03 | 2.14 | 3.32 | -2.01 | 3.83 | 0.003 1 | 3.23 |
| 3D | 29.39 | 2.21 | -2.09 | 0.003 0 | |||||
| 5 | 1D | 45.24 | 1.55 | 1.35 | 2.07 | -1.23 | 3.58 | 0.003 1 | 6.45 |
| 3D | 45.94 | 1.38 | -1.27 | 0.002 9 | |||||
| 7 | 1D | 53.52 | 1.20 | 1.14 | 1.75 | -1.02 | 3.53 | 0.003 0 | 10.00 |
| 3D | 54.16 | 1.16 | -1.06 | 0.002 7 |
综上所述,采用常规三维CFD方法可以较准确地模拟水力系统的局部水头损失,但难以准确模拟管道的沿程水头损失,从而导致调压室水位波动振幅和衰减特性模拟的准确性降低.为此,推荐采用一维管道与三维局部耦合的计算方法[12, 13].这一方法将计算区域按流态分为两部分,渐变流区域(管道)用一维方法计算,急变流区域(调压室)用三维方法计算,既能保留一维方法计算管道的准确性,又可以结合三维方法模拟复杂流动的优势,是进行三维水力过渡过程模拟的较佳选择.
2.4 水库边界条件的设定在三维CFD计算中,水库边界条件的设定至关重要.为了实现水库边界的水位恒定,可通过2类方法设定:直接模拟水库法和进口直接给定压力法.前者模拟体积较大的水库,水库面积与进口面积之比也较大(后面算例取10∶1),除了能保证水位基本恒定外,还可较准确地模拟进水口的局部水头损失.后者直接在进水口断面上设定压力条件,计算量小.直接模拟水库法可分为自由水面和刚盖2种,进口直接给定压力法可分为静压分布、均压分布2种,这4种方法示意于图 5.

|
| 图 5 4种水库边界条件设定方法示意图 Figure 5 Sketch map of four kinds of reservoir boundary conditions |
现比较4种水库边界设定方法的准确性.三维模拟中,引水隧洞长为100 m,调压室与隧洞断面面积比1∶1,为了消除沿程损失的影响,一维计算中沿程阻力系数设为0,三维计算亦采用上一节已验证过的无粘性的三维流动方程结合VOF方法.
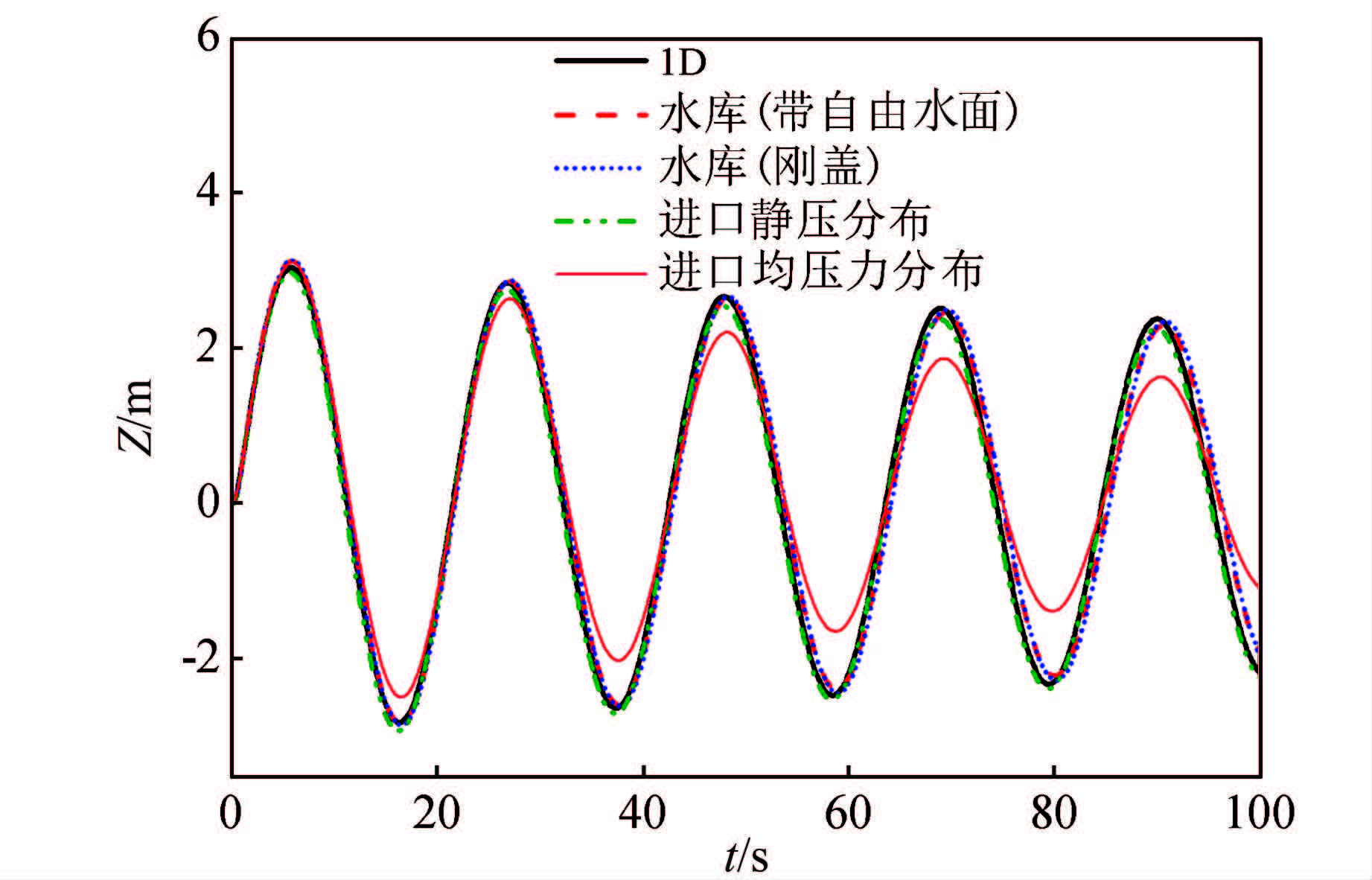
计算所得水位波动过程线见图 6.可知,除了进口均压分布法,其他3种方法的结果与一维计算结果吻合.表 3对比了调压室水位波动的周期、极值和衰减因子.对于波动周期,4种方法所得结果均十分准确,误差在1.0%以下;对于最高水位,4种方法的结果也很好;对于最低水位,均压力分布法误差较大,其余方法的误差均不超过3.0%;对于衰减因子,4种方法所得结果误差均超过了10.0%,均压分布法误差达到144.83%,准确性很差.
|
| 图 6 4种水库边界设定方法的调压室水位波动过程线 Figure 6 Simulation results of surge tank wave under four kinds of reservoir boundaries |
| 方法 | T/s | εT/% | Zmax/m | εZmax/% | Zmin/m | εZmin/% | c | εc/% |
| 1D | 21.05 | 0 | 3.041 | 0 | -2.805 | 0 | 0.002 9 | 0 |
| 带自由水面的水库 | 21.20 | 0.71 | 3.128 | 2.86 | -2.815 | -0.36 | 0.003 6 | 24.14 |
| 带刚盖的水库 | 21.23 | 0.86 | 3.140 | 3.26 | -2.840 | -1.25 | 0.003 4 | 17.24 |
| 进口静压分布 | 20.97 | -0.38 | 2.976 | -2.14 | -2.855 | -1.78 | 0.003 3 | 13.79 |
| 进口均压分布 | 21.11 | 0.29 | 3.105 | 2.10 | -2.481 | 11.55 | 0.007 1 | 144.83 |
因此,若主要关注最大最小涌波水位,不关注衰减快慢,可采用模拟部分水库法或进口给定静压分布法来处理水库边界,应避免使用进口给定均压分布的方法.考虑到模拟水库法需要消耗更多计算资源,一般可推荐使用静压分布法.
若实际水库较小(模型试验中的模型水库)或为渠道(尾水河道或渠道),则水库水面或渠道水位的波动对调压室波动有影响,这时需要按实际情况模拟全部水库或渠道.
3 实例计算 3.1 计算条件某水电站采用“两机一室一洞”的尾水布置方式,同一水力单元的2条尾水支洞共用一个阻抗式长廊式调压室,并由室下的对称岔管与尾水洞相连.需计算下游低水位2台机同时甩负荷工况的调压室水位波动过程,用以校核调压室内淹没水深是否符合设计要求.由于尾水隧洞较长,这里采用一维管道与三维调压室耦合的方法[12, 13]进行模拟.
计算区域如图 7所示.其中三维区域主要包括尾水管、调压室及部分尾水洞,总长209 m,其体型及边界条件设置如图 8所示.三维模拟通过Fluent软件平台实现,用VOF方法追踪自由液面,湍流模型选用Realizable k-ε模型.一维区域为三维区域出口到尾水水库,长592 m,用特征线法计算,通过Fluent软件的用户自定义函数(User Defined Function,UDF)[12]实现.1D-3D边界采用部分重叠耦合法(POC)[12, 13],也通过UDF实现.

|
| 图 7 整体计算区域示意图 Figure 7 Sketch map ofwhole calculation domain |

|
| 图 8 调压室部分三维体型及边界条件示意图 Figure 8 Sketch map of three-dimensional section and boundary conditions |
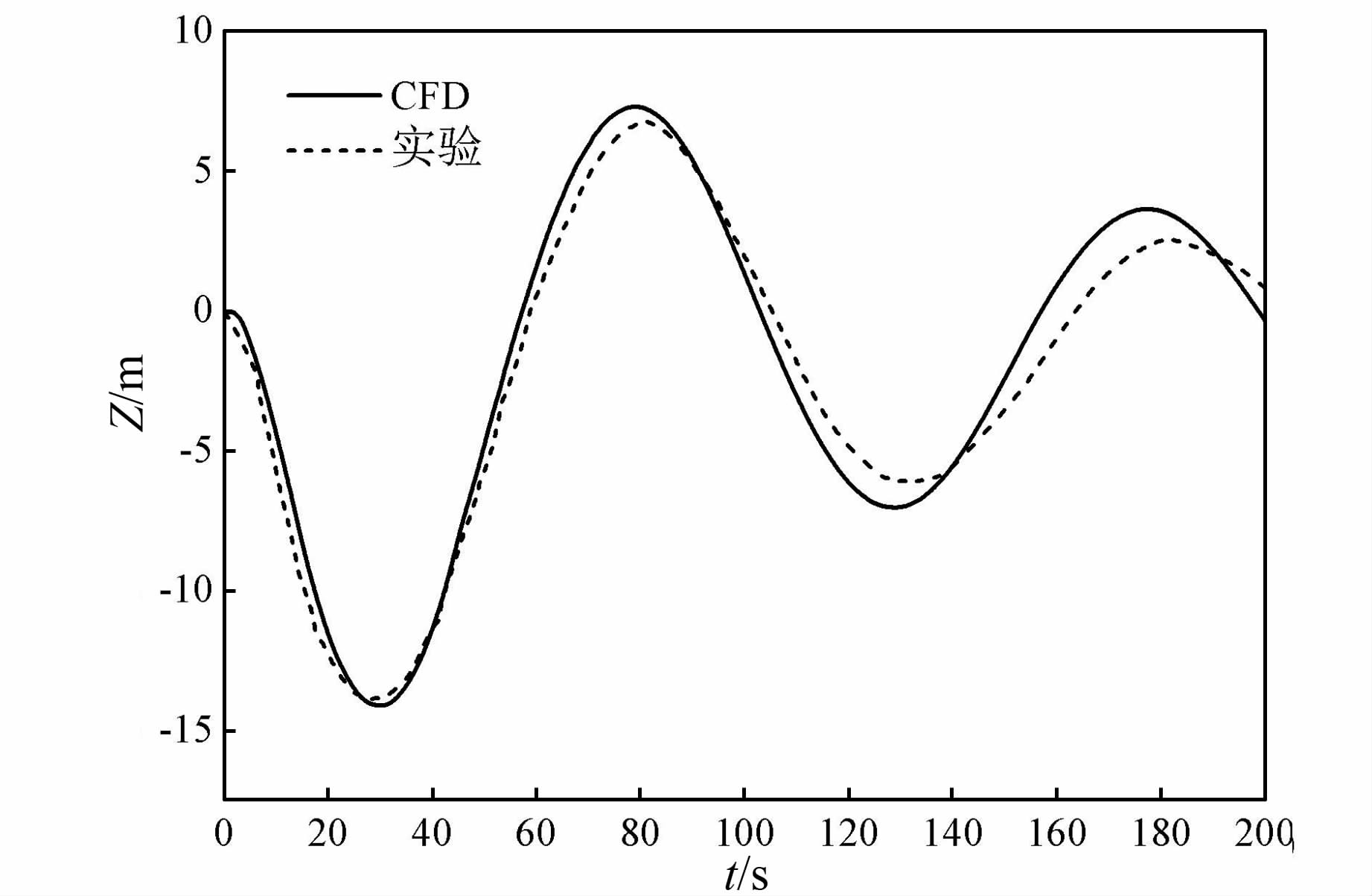
图 9是水位波动过程线,表 4是关键参数.数据表明一维与三维耦合方法模拟所得调压室水位波动过程与模型试验所得结果吻合很好,波动周期、最高水位、最低水位和衰减因子相对误差均在8.0%以内,准确性较好.
|
| 图 9 一维与三维耦合模拟结果与模型试验水位波动过程对比 Figure 9 Comparisons of simulation results and experimental data of surge tank wave in real hydropower station |
| 参数 | T/s | Zmax/m | Zmin/m | c |
| 实验 | 101.76 | -14.01 | 6.81 | 0.008 0 |
| 1D-3D | 98.66 | -14.11 | 7.31 | 0.007 5 |
| 相对误差/% | 1.69 | 0.70 | 7.34 | 6.48 |
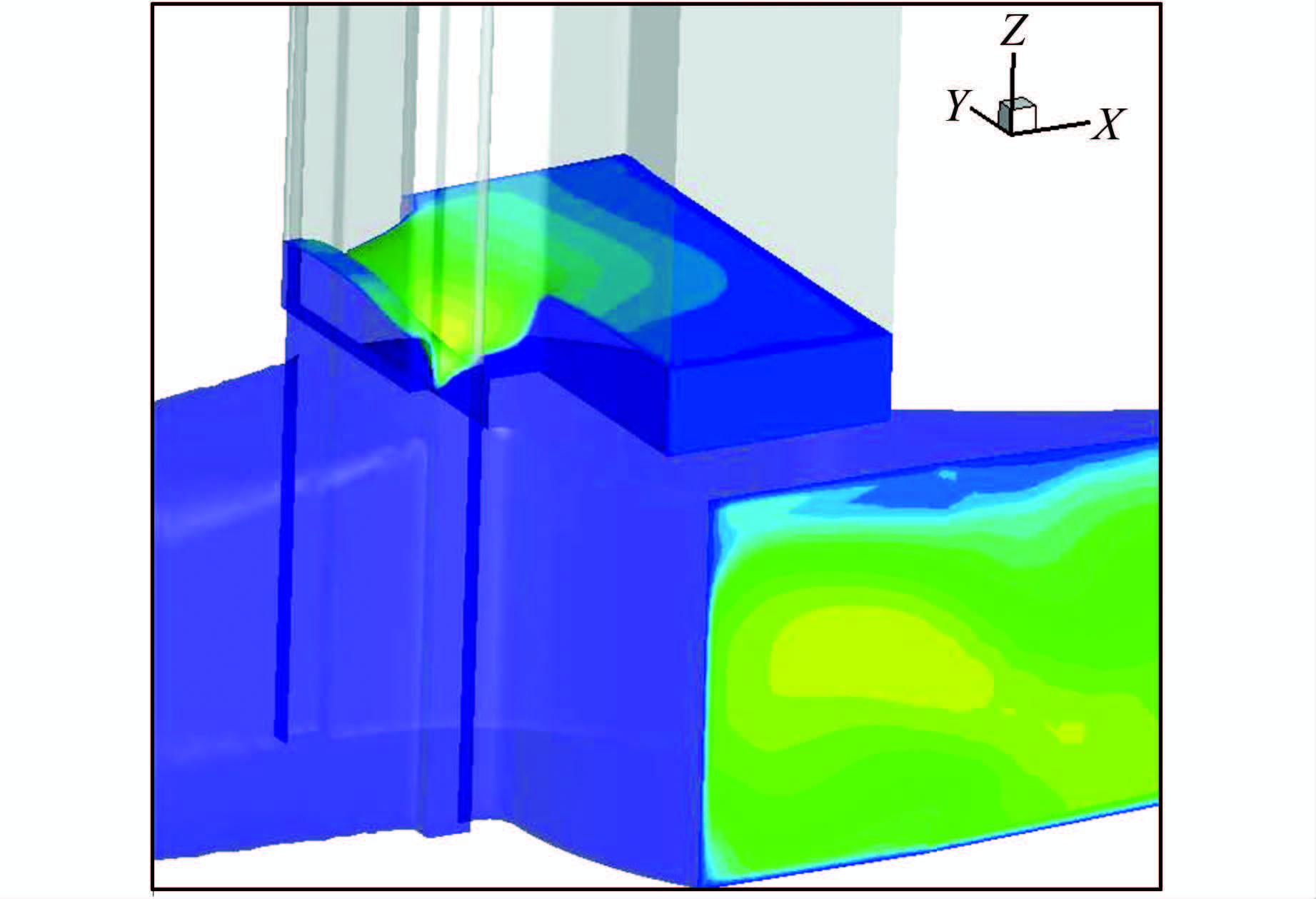
三维计算的目的不是得到与一维计算或模型实验一致的水位波动过程,而是要分析调压室内的水流流态.图 10中展示了最低水位时刻t=13.0 s的水面形态,可见阻抗孔部位水位下降,出现漩涡形态.
|
| 图 10 调压室室内水流流态展示 Figure 10 Flow patterns in surge tank |
本文从水体惯性、系统阻力、水库边界设定3个方面讨论了保证三维CFD模拟调压室水位波动准确性的问题.结果表明,常规CFD方法可以准确模拟水体惯性和局部水头损失,但模拟沿程水头损失的准确度不高,故在隧洞较长时,用CFD模拟整个调压室系统的准确性降低.水库边界的处理方法中,模拟部分水库法效果较好,另外直接给定进口静压分布也能满足要求.所以,在隧洞较长的条件下,推荐采用一维管道与三维调压室耦合的方法来模拟调压室水位波动,这种方法可发挥一维计算效率高、三维模拟可研究流态的优点,推动三维CFD方法在调压室吸气漩涡、溢流和水位纵向振荡等问题的深入研究.
| [1] |
刘启钊, 胡明.
水电站调压室[M]. 北京: 中国水利水电出版社, 2010.
Liu Qizhao, Hu Ming. Surge Chamber in Hydropower Station[M]. Beijing: China Water & Power Press, 2010. |
| [2] |
陈玲, 鞠小明, 杨济铖. 水电站调压室涌浪水位多种计算方法比较[J].
中国农村水利水电, 2013(9): 158–161.
Chen Ling, Ju Xiaoming, Yang Jicheng. The methods of calculating the surge water level of surge chambers[J]. China Rural Water and Hydropower, 2013(9): 158–161. |
| [3] |
邓淞苡, 张剑, 程永光, 等. 长廊式调压室流态CFD分析及吸气旋涡消除措施研究[J].
水力发电学报, 2009(4): 130–136.
Deng Songyi, Zhang Jian, Cheng Yongguang, et al. Flow characteristics of long corridor shaped surge tank and elimination of the air entraining vertical vortices : CFD simulation and analysis[J]. Journal of Hydroelectric Engineering, 2009(4): 130–136. |
| [4] |
程永光, 杨建东. 用三维计算流体力学方法计算调压室阻抗系数[J].
水利学报, 2005(7): 787–792.
Cheng Yongguang, Yang Jiandong. Hydraulic resistance coefficient determination of throttled surge tanks by means of computational fluid dynamics[J]. Journal of Hydraulic Engineering, 2005(7): 787–792. |
| [5] |
程永光, 刘晓峰, 杨建东. 大型尾水调压室底部交汇型式CFD分析与优化[J].
水力发电学报, 2007(5): 68–74.
Cheng Yongguang, Liu Xiaofeng, Yang Jiandong. Optimization of the converging type of conduit of tailrace surge tank by CFD method[J]. Journal of Hydroelectric Engineering, 2007(5): 68–74. |
| [6] |
刘飞, 杨建东, 李进平. CFD在调压室涌浪水位模拟中的应用[J].
中国农村水利水电, 2011(9): 123–126.
Liu Fei, Yang Jiandong, Li Jinping. The application of 3D numerical simulation to calculating the waves in surge tanks[J]. China Rural Water and Hydropower, 2011(9): 123–126. |
| [7] |
陈世凡,周大庆. 基于弱可压缩流体模型的抽蓄电站引水系统甩负荷过渡过程数值模拟[C]//第6届全国水利机械及其系统学术会议, 2013.
Chen Shifan, Zhou Daqing. Numerical simulation of load rejection of pumped storage power station water diversion system based on weakly compressible flow model[C]//6th National Water Machinery and Systems Conference, 2013. |
| [8] | Oertel Herbert. Prandtl's Essentials of Fluid Mechanics[M]. New York: Springer, 2004. |
| [9] | ANSYS Inc. ANSYS FLUENT 12.0 Theory Guide[R]. ANSYS, Inc. Canonsburg, PA, 2009. |
| [10] |
赵昕, 张晓元, 赵明登, 等.
水力学[M]. 北京: 中国电力出版社, 2009.
Zhao Xin, Zhang Xiaoyuan, Zhao Mingdeng, et al. Hydraulics[M]. Beijing: China Electric Power Press, 2009. |
| [11] |
华富刚, 秦柳燕. 水电站调压室内三维湍流场数值模拟[J].
水利水电科技进展, 2007(5): 47–49.
Hua Fugang, Qin Liuyan. Numerical simulation of 3D turbulent flow in surge tanks of hydropower station[J]. Advances in Science and Technology of Water Resources, 2007(5): 47–49. |
| [12] | Zhang Xiaoxi, Cheng Yongguang. Simulation of hydraulic transients in hydropower systems using the 1D and 3D coupling approach[J]. Journal of Hydrodynamics, 2012, 24(4): 595–604. DOI:10.1016/S1001-6058(11)60282-5 |
| [13] | Zhang Xiaoxi, Cheng Yongguang, Yang Jiandong, et al. Simulation of the load rejection transient process of a Francis turbine by using a 1D-3D coupling approach[J]. Journal of Hydrodynamics, 2014, 26(5): 715–724. DOI:10.1016/S1001-6058(14)60080-9 |
 2016, Vol. 49
2016, Vol. 49




