文章信息
- 周鹏华, 徐礼华, 谷雨珊, 吴敏, 许明耀, 黄乐
- ZHOU Penghua, XU Lihua, GU Yushan, WU Min, XU Mingyao, HUANG Le
- 钢管与其核心自应力自密实高强混凝土的粘结性能
- Experimental study on bond behavior of self-stressing and self-compacting high strength concrete filled steel tube
- 武汉大学学报(工学版), 2018, 51(9): 782-789
- Engineering Journal of Wuhan University, 2018, 51(9): 782-789
- http://dx.doi.org/10.14188/j.1671-8844.2018-09-006
-
文章历史
- 收稿日期: 2017-07-24
钢管高强混凝土结构以其承载力高、抗震性能优越、延性好、耐火性能好、施工简便、经济合理等一系列优点而广泛应用于高层(超高层)建筑、桥梁建筑中,但钢管混凝土易出现脱空、蜂窝麻面等质量缺陷,而自应力自密实混凝土良好的流动性和微膨胀特性能有效改善这类工程问题,对于钢管混凝土这种难以振捣的结构具有重要的工程意义.
相对于其他结构材料而言,钢管混凝土研究还很不充分,尤其是粘结性能研究更少,还存在一些亟需研究和解决的关键科学和技术问题,如钢管内核心混凝土密实程度、钢管与其核心混凝土的粘结等.
Okamura H[1]的研究结果表明,自密实混凝土尤其适合于不方便浇筑的结构,并且其综合经济效益可观.在同等条件下,自密实混凝土的强度与普通混凝土相当,但弹性模量稍低, 干燥收缩较大, 抗碳化能力较强.粘结性能是钢管混凝土构件的一个重要特性,粘结应力的存在使得钢管与核心混凝土之间能够进行荷载传递,从而能够良好地共同工作.影响钢管与其核心混凝土间粘结强度的因素有很多,如钢管内壁粗糙程度、截面形式、混凝土龄期和强度、钢管径厚比、构件长细比、混凝土浇注方式等.很多学者考虑这些影响因素,对钢管柱界面粘结性能进行了研究,薛立红、蔡绍怀[2-4]采用钢管内壁进行机械除锈和手工除锈两种方式进行处理,得出机械除锈试件粘结破坏荷载较低的结论;文献[5]进行光圆钢筋表面凹凸程度对粘结强度的影响试验研究,结果表明,当严重锈蚀的钢筋表面凹凸差为0.08~0.1 mm、新轧制的钢筋凹凸差为0.03 mm时,前者的粘结强度超过后者的3倍; Morishita[6]对圆形钢管混凝土试件、八边形钢管混凝土试件、方形钢管混凝土试件分别进行了研究,发现八边形截面试件钢管与混凝土之间的粘结性能介于圆形截面和方形截面之间,即其粘结强度总体上高于方形钢管混凝土,但低于圆钢管混凝土; Virdi和Dowling[7]通过5组15个不同长细比、不同混凝土浇筑方式的钢管混凝土试件试验研究,发现钢管混凝土构件的粘结强度随构件长细比增大而增大,混凝土浇筑方式对粘结强度的影响很大.通过6组18个不同径厚比的钢管混凝土试验研究,发现钢管的径厚比对粘结强度有影响,但其变化规律不明显;Virdi和Dowling[8]对28个由不同混凝土龄期和强度组成的钢管混凝土试件进行了试验研究,结果表明,粘结强度与混凝土强度的关系不大; Roeder[9]等对钢管与其核心混凝土之间的粘结强度进行了理论分析和试验研究,15个圆形钢管混凝土试件试验研究表明,钢管与核心混凝土之间的粘结强度随径厚比的增大越来越低.Shakir-Khali[10, 11]考虑截面形式(圆形、方形、矩形)、界面长度、界面情况(普通界面、界面涂润滑剂、界面之间加抗剪螺栓)、加载方式(分级加载至破坏荷载、分级加循环荷载值破坏)、支承类型(直接将钢管放在刚性底板上、钢管支承在钢管壁上焊接的侧向支承以模拟节点受力)等多种因素,通过短柱粘结滑移试验研究了钢管与核心混凝土之间的粘结强度.
综上所述,目前关于钢管与混凝土粘结性能研究大多集中于钢管与普通混凝土之间的粘结问题,关于钢管与自应力自密实高强混凝土的粘结性能研究尚未见诸报道.本文考虑自应力值、混凝土强度和界面长度3种影响因素,设计制作22根钢管自应力自密实高强混凝土柱试件和1根钢管自密实混凝土柱试件,通过推出试验,研究钢管与其核心自应力自密实高强混凝土的粘结性能,建立钢管自应力自密实高强混凝土界面抗剪粘结强度计算公式,为工程应用提供参考.
1 试验概况 1.1 试验原材料及其力学性能试验中水泥采用亚东P.O. 52.5硅酸盐水泥,膨胀剂采用中国建筑材料科学研究院研制的天津爆鸣系列的HCSA混凝土膨胀剂,其膨胀能高、膨胀快,与减水剂、水泥等具有良好适应性,适用于配制高性能混凝土.减水剂选用中建聚羧酸高效减水剂,粗骨料采用粒径 < 20 mm的天然碎石.为了保证混凝土的流动性,添加Ⅰ级麻城粉煤灰和湖北武新S95矿粉.试件用钢管均采用外径159 mm、壁厚3.92 mm的无缝圆钢管.
通过同条件下成型养护的150 mm立方试块按GB/T50081-2002《普通混凝土力学性能试验方法》测得混凝土强度,每组3个试块取其平均值.所配混凝土的塌落度和扩展值分别为240 mm和50 mm左右,没有发现离析现象.
根据文献[12],每组钢管制作3个试件,通过拉伸试验测得钢管的力学性能参数,如表 1所示.
| 试件编号 | 含钢率 | 屈服强度/MPa | 极限抗拉强度/MPa | 弹性模量/MPa | 泊松比 | 延伸率/% |
| 159×3.92 | 0.106 | 367.35 | 484.96 | 2.03×105 | 0.275 | 24.7 |
混凝土配合比共设计7组,如表 2所示.混凝土采用强制式单卧轴搅拌机搅拌,通过漏斗将混凝土灌入钢管中.为了保证混凝土有足够的空间在钢管内部被推出,保留50 mm高的空钢管不浇筑.混凝土浇筑之前,在钢管外表面中部贴4个3 mm×2 mm的应变片,并将其与应变仪连接.自混凝土浇筑起开始实时记录钢管的应变.待混凝土初凝后,在试件顶部涂抹环氧树脂进行密封养护,以防止混凝土水分蒸发.试件在室内常温养护28 d.
| 试件编号 | 水泥/kg | Ⅰ粉煤灰/kg | 硅灰[13]/kg | 微珠[14]/kg | 矿粉/kg | 膨胀剂/kg | 河沙/kg | 碎石/kg | 水/kg | 减水剂/% |
| C60 | 336 | 84 | - | 56 | 84 | - | 750 | 950 | 150 | 2.0 |
| C60 Ⅰ | 336 | 28 | - | 56 | 84 | 56 | 750 | 950 | 150 | 2.0 |
| C60 Ⅱ | 336 | 30 | - | 56 | 60 | 78 | 750 | 950 | 146 | 2.0 |
| C70 Ⅰ | 380 | 86 | 40 | - | 34 | 60 | 750 | 950 | 138 | 2.3 |
| C70 Ⅱ | 380 | 86 | 40 | - | 22 | 72 | 750 | 950 | 138 | 2.3 |
| C80 Ⅰ | 410 | 100 | 48 | - | 10 | 62 | 750 | 950 | 135 | 2.8 |
| C80 Ⅱ | 410 | 100 | 46 | - | - | 74 | 750 | 950 | 135 | 2.8 |
| 注:Ⅰ表示目标自应力值为3 MPa,Ⅱ表示目标自应力值为5 MPa. | ||||||||||
本文考虑自应力值、混凝土强度和界面长度3种影响因素,每种因素均考虑3种水平:自应力值(0.3 MPa、5 MPa)、混凝土强度(C60、C70、C80)和钢管与混凝土界面长度(300 mm、500 mm、700 mm),设计22根钢管自应力自密实高强混凝土柱试件和1根钢管自密实混凝土柱试件.根据试验侧重点和概率统计知识,部分试件设计3根,试件编号及参数见表 3.
| 试件编号 | 直径×壁厚/(mm×mm) | 自应力目标值/MPa | 混凝土立方体抗压强度fc/MPa | 钢管长度L/mm |
| C1S1L2-1 | 159×3.92 | 3 | 70 | 550 |
| C1S2L2-2 | 159×3.92 | 5 | 70 | 550 |
| C2S1L1-3-1 | 159×3.92 | 3 | 60 | 350 |
| C2S1L1-3-2 | 159×3.92 | 3 | 60 | 350 |
| C2S1L1-3-3 | 159×3.92 | 3 | 60 | 350 |
| C2S1L2-4-1 | 159×3.92 | 3 | 60 | 550 |
| C2S1L2-4-2 | 159×3.92 | 3 | 60 | 550 |
| C2S1L2-4-3 | 159×3.92 | 3 | 60 | 550 |
| C2S2L3-5-1 | 159×3.92 | 3 | 60 | 750 |
| C2S2L3-5-2 | 159×3.92 | 3 | 60 | 750 |
| C2S2L3-5-3 | 159×3.92 | 3 | 60 | 750 |
| T2-11 | 159×3.92 | 0 | 60 | 550 |
| C2S2L1-6-1 | 159×3.92 | 5 | 60 | 350 |
| C2S2L1-6-2 | 159×3.92 | 5 | 60 | 350 |
| C2S2L1-6-3 | 159×3.92 | 5 | 60 | 350 |
| C2S2L2-7-1 | 159×3.92 | 5 | 60 | 550 |
| C2S2L2-7-2 | 159×3.92 | 5 | 60 | 550 |
| C2S2L2-7-3 | 159×3.92 | 5 | 60 | 550 |
| C2S2L3-8-1 | 159×3.92 | 5 | 60 | 750 |
| C2S2L3-8-2 | 159×3.92 | 5 | 60 | 750 |
| C2S2L3-8-3 | 159×3.92 | 5 | 60 | 750 |
| C3S1L2-9 | 159×3.92 | 3 | 80 | 550 |
| C3S2L2-10 | 159×3.92 | 5 | 80 | 550 |
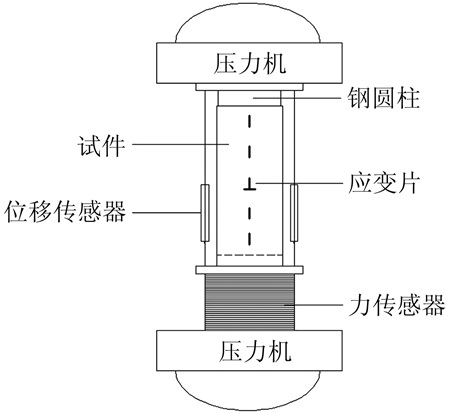
试验在武汉大学土木建筑工程学院土木工程试验中心的500 t压力机上进行,采取推出试验,加载装置如图 1所示.在加载之前,将试件上表面打磨平整,在试件上方放置一个大小与核心混凝土面积一致的圆钢柱,通过压力机施力,使得核心混凝土从圆钢管中推出.为了防止出现荷载偏心,当试件放置到试验机上后,降下上部加载板,再次检查构件是否对中,然后开始缓慢加载.采取分级加载制度,在计算极限荷载值的60%范围内,每级加载量为极限荷载的10%;当实测荷载-滑移曲线的线性阶段结束时,每级荷载改为计算极限荷载值的5%.加载速度为0.5 kN/s,每级持荷2~3 min.当核心混凝土与下部加载板接触、承载力快速上升时,停止试验.
|
| 图 1 加载与测量装置简图 Fig. 1 Test setup |
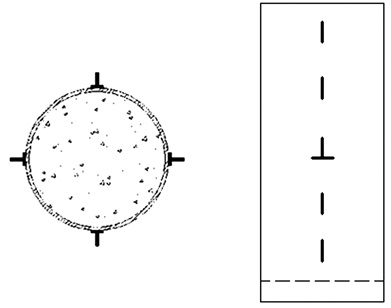
本文试验在轴向方向放置两个位移传感器,以测取试件的轴向位移.每个试件布置12个尺寸为3 mm×2 mm的应变片(如图 2所示),为了监测混凝土的膨胀变形以测得混凝土的自应力,在钢管中部的外壁分别沿纵向和环向方向各贴4个应变片;为了获取钢管与核心混凝土粘结力沿高度的分布,顺着某一轴向方向再均匀分布4个应变片.轴向位移和钢管应变均用东华DH3816N进行数据采集.
|
| 图 2 测点布置 Fig. 2 Arrangement of strain gages |
钢管自应力自密实高强混凝土柱的推出破坏形态如图 3所示,钢管与核心混凝土发生相对滑移,图 3(a)为推出后钢管上端情形,图 3(b)为推出后钢管下端情形,推出过程中界面处混凝土被压碎.在加载初期,荷载增长较快,位移计读数很小,钢管外壁应变缓慢增长,试件没有明显的变化.随着荷载的增加,会发出“嗵嗵”的声音,说明核心混凝土被压实并且即将产生滑移,此时位移计和应变仪的示数依旧增长缓慢;之后会听到比较明显的响声,此时位移计和应变仪的示数开始快速增长,承载力开始快速下降;随着荷载的继续施加,承载力会逐渐趋于稳定,直到核心混凝土接触到钢管底部时,承载力开始回升.整个试验过程中,钢管保持稳定,未出现局部变形或者屈曲,钢管外壁应变均匀增长,呈现线性变化趋势,核心混凝土也未出现压碎和破坏现象.

|
| 图 3 破坏形态 Fig. 3 Failure modes |
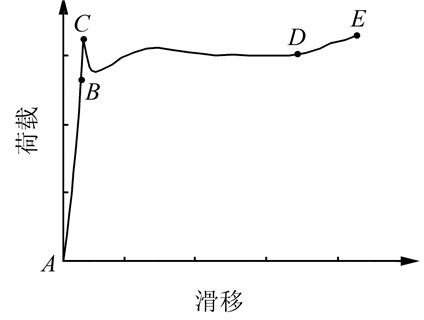
钢管自应力自密实高强混凝土柱的荷载-滑移曲线与钢管普通混凝土柱一致,如图 4所示,曲线可分为胶结段(AB)、滑移段(BC)、摩擦段(CD)和上升段(DE).在AB段,混凝土与钢管之间主要是化学胶结力,该力只存在于无相对滑移的状态下;在BC段,随着荷载稍微增大,试件两端局部范围内的钢管与核心混凝土之间开始出现微小滑动,化学胶结力被破坏,混凝土与钢管开始有滑移的趋势,混凝土界面上晶体颗粒挤压并且开始咬合在一起,在此过程中机械咬合力产生;CD段为摩擦段,也是主要的滑移段,在此阶段化学胶结力完全消失,主要是摩擦阻力和残余机械咬合力,该力同时也是钢管与混凝土之间粘结力的主要部分.在此阶段中会发现曲线有向上波动的现象,因为在试验过程中,随着荷载的增加,核心混凝土的横向变形也随之增加,钢管对核心混凝土的约束作用也增大,使得界面的摩阻力增加,最终提高构件的承载力;DE段为曲线上升段,承载力回升是由于核心混凝土已经被推到钢管底部,整个试件开始承担施加的荷载.
|
| 图 4 典型荷载-滑移曲线 Fig. 4 Typical load-displacement curve |
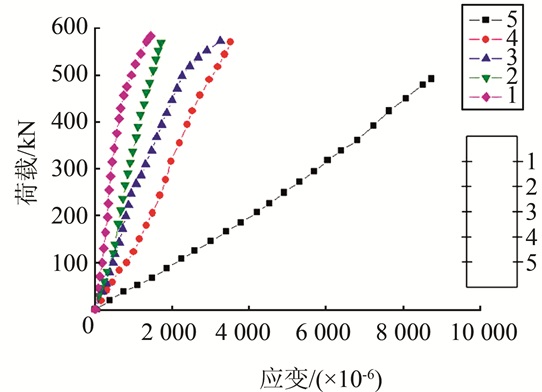
钢管外表面应变沿界面高度的分布如图 5所示,混凝土从1至5方向推出从图中可以看出:钢管纵向应变沿钢管高度方向呈三角形分布;钢管上部应变很小,随着传递距离的增加,核心混凝土所承受的轴向荷载也逐渐通过钢管和混凝土之间的界面粘结传递给钢管;钢管底部变形明显大于上部,这是由于底部没有浇筑混凝土,整体刚度较小,导致变形较大;钢管的变形在整个过程呈线性,且是连续的,说明在极限荷载之前,钢管和混凝土之间并没有出现粘结破坏.
|
| 图 5 钢管应变沿界面高度分布 Fig. 5 Strain distribution of steel tube along the height |
从图 5可以看出,粘结力在钢管与混凝土界面上的传递是不均匀的,因此界面上某一点的粘结强度的确定很困难.钢管混凝土的粘结强度是与粘结破坏荷载相对应的,与粘结破坏荷载相对应的剪应力被定义为抗剪粘结强度τu,该临界状态是滑移开始迅速发展的起点,同时也是控制钢管与混凝土共同作用而不发生较大滑移的临界点,可以作为粘结破坏的标志.在钢管混凝土界面剪力传递设计中,认为界面的粘结力沿钢管混凝土界面是均匀分布的.圆钢管混凝土界面的抗剪粘结强度计算公式为
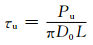 (1)
(1)
式中:τu为界面抗剪粘结强度;Pu为构件推出试验极限荷载;D0为圆钢管内径;L为钢管与混凝土界面长度.本文抗剪粘结强度试验值根据式(1)计算,如表 4所示.
| 试件编号 | 直径×壁厚/(mm×mm) | 自应力值S | fc/MPa | L/mm | 承载力Pu | 抗剪粘结强度试验值τ/MPa | 本文计算值/MPa | 本文计算值/试验值 | 文献计算值/MPa |
| C1S1L2-1 | 159×3.92 | 2.73 | 76.4 | 550 | 449 | 1.89 | 1.98 | 1.04 | 0.62 |
| C1S2L2-2 | 159×3.92 | 4.86 | 77.2 | 550 | 508 | 2.14 | 2.13 | 0.99 | 0.62 |
| C2S1L1-3-1 | 159×3.92 | 3.05 | 64.8 | 350 | 204 | 1.43 | 1.35 | 0.94 | 0.57 |
| C2S1L1-3-2 | 159×3.92 | 2.96 | 64.8 | 350 | 195 | 1.37 | 1.26 | 0.92 | 0.57 |
| C2S1L1-3-3 | 159×3.92 | 3.10 | 64.8 | 350 | 203 | 1.42 | 1.36 | 0.96 | 0.57 |
| C2S1L2-4-1 | 159×3.92 | 2.87 | 64.8 | 550 | 284 | 1.20 | 1.26 | 1.05 | 0.57 |
| C2S1L2-4-2 | 159×3.92 | 3.02 | 64.8 | 550 | 296 | 1.25 | 1.26 | 1.01 | 0.57 |
| C2S1L2-4-3 | 159×3.92 | 2.95 | 64.8 | 550 | 298 | 1.26 | 1.26 | 1.00 | 0.57 |
| C2S2L3-5-1 | 159×3.92 | 3.15 | 64.8 | 750 | 381 | 1.15 | 1.26 | 1.10 | 0.57 |
| C2S2L3-5-2 | 159×3.92 | 3.13 | 64.8 | 750 | 375 | 1.13 | 1.16 | 1.03 | 0.57 |
| C2S2L3-5-3 | 159×3.92 | 3.01 | 64.8 | 750 | 392 | 1.18 | 1.26 | 1.07 | 0.57 |
| C2S2L1-6-1 | 159×3.92 | 5.06 | 64.8 | 350 | 298 | 2.09 | 2.03 | 0.97 | 0.57 |
| C2S2L1-6-2 | 159×3.92 | 5.04 | 64.8 | 350 | 302 | 2.12 | 2.02 | 0.95 | 0.57 |
| C2S2L1-6-3 | 159×3.92 | 5.10 | 64.8 | 350 | 305 | 2.14 | 2.08 | 0.97 | 0.57 |
| C2S2L2-7-1 | 159×3.92 | 4.78 | 65.2 | 550 | 461 | 1.94 | 1.83 | 0.94 | 0.57 |
| C2S2L2-7-2 | 159×3.92 | 4.97 | 65.2 | 550 | 464 | 1.96 | 1.91 | 0.98 | 0.57 |
| C2S2L2-7-3 | 159×3.92 | 4.89 | 65.2 | 550 | 458 | 1.93 | 1.83 | 0.95 | 0.57 |
| C2S2L3-8-1 | 159×3.92 | 5.03 | 64.8 | 750 | 581 | 1.75 | 1.85 | 1.06 | 0.57 |
| C2S2L3-8-2 | 159×3.92 | 4.96 | 64.8 | 750 | 598 | 1.80 | 1.91 | 1.06 | 0.57 |
| C2S2L3-8-3 | 159×3.92 | 4.99 | 64.8 | 750 | 590 | 1.78 | 1.84 | 1.03 | 0.57 |
| C3S1L2-9 | 159×3.92 | 2.87 | 84.8 | 550 | 574 | 2.42 | 2.45 | 1.01 | 0.66 |
| C3S2L2-10 | 159×3.92 | 4.91 | 85.1 | 550 | 597 | 2.52 | 2.58 | 1.02 | 0.66 |
| T2-11 | 159×3.92 | 0 | 66.9 | 550 | 249 | 1.05 | 1.15 | 1.10 | 0.58 |
测取钢管外壁纵向和环向应变, 进行理论分析和计算得到混凝土自应力值.由于自应力混凝土在钢管中体积膨胀产生相互作用力,混凝土和钢管的受力分析如图 6所示.
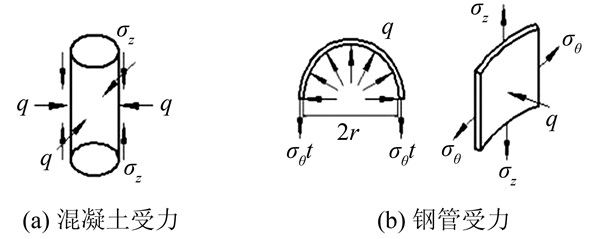
|
| 图 6 钢管与混凝土受力示意图 Fig. 6 Stress diagram of concrete and steel tubes |
由广义胡克定律可知:
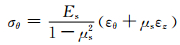 (2)
(2)
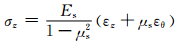 (3)
(3)
式中:σθ、σz分别是钢管环向和轴向应力;εθ、εz分别为实测环向和轴向应变;Es、μs分别为钢管的弹性模量和泊松比.
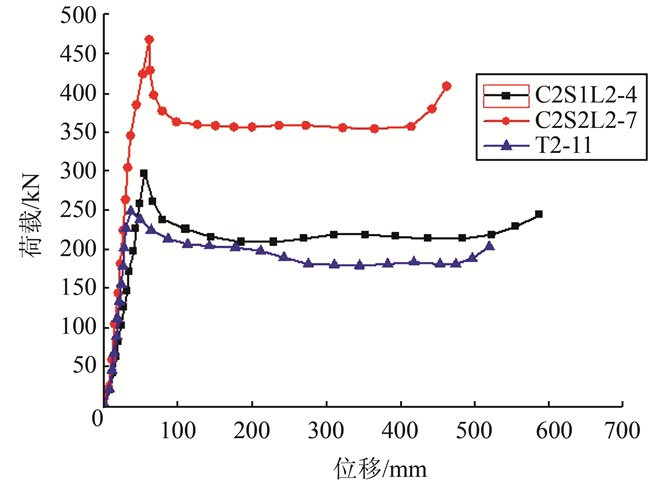
由图 6(b)可得:2σθt=2rq,由轴向平衡条件可得Asσz=Acσcz,其中:r为钢管内径;t为钢管壁厚.
由以上公式可推出核心混凝土轴向压应力为
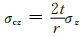 (4)
(4)
测得轴向应变和纵向应变,即可得到钢管混凝土的自应力值,其结果见表 4.
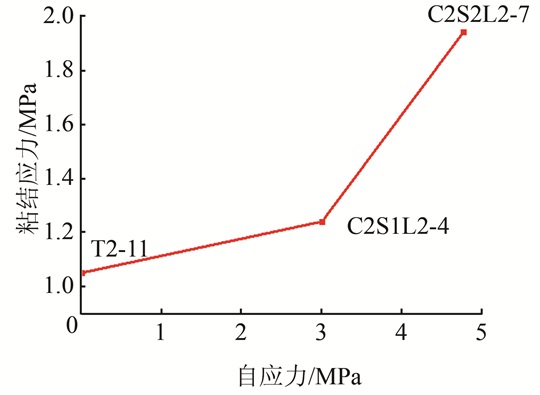
3.3 抗剪粘结强度的影响因素 3.3.1 自应力值图 7、8分别为不同自应力试件的荷载-滑移曲线、抗剪粘结强度与自应力值的关系曲线.从图中可知,钢管自应力混凝土的抗剪粘结强度高于普通钢管混凝土,这主要是由于自应力提供了初始侧向约束,使得核心混凝土在加载之前已经处于3向受压状态,提高了界面之间的摩阻力,最终导致粘结强度的提高.但值得注意的是,与钢管自应力自密实高强混凝土柱比较,钢管自密实混凝土T2-11在极限荷载之后承载力下降较少,这是由于自应力混凝土在钢管约束条件下,其脆性有所提高,导致构件延性有所下降.通过对比还可以发现,钢管自应力自密实高强混凝土柱在摩擦段通常会出现上升波动段,这是由于随着荷载的增加,核心混凝土的横向变形也随之增加,钢管对核心混凝土的约束作用也增大,增强了构件的性能,从而使构件的承载力出现回升的现象.
|
| 图 7 不同自应力试件的荷载-滑移曲线 Fig. 7 Load-displacement curve of specimens with different self-stresses |
|
| 图 8 抗剪粘结强度与自应力值的关系 Fig. 8 Relationship between bond stress and self-stress |
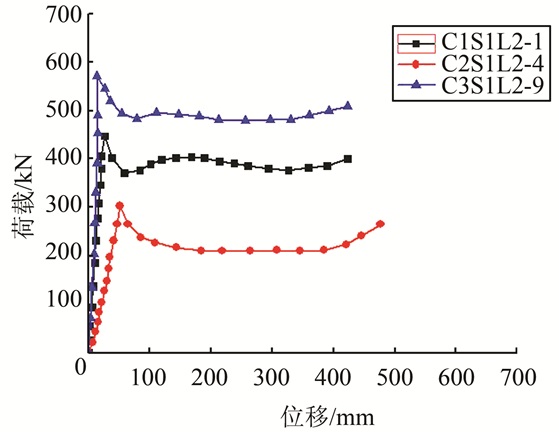
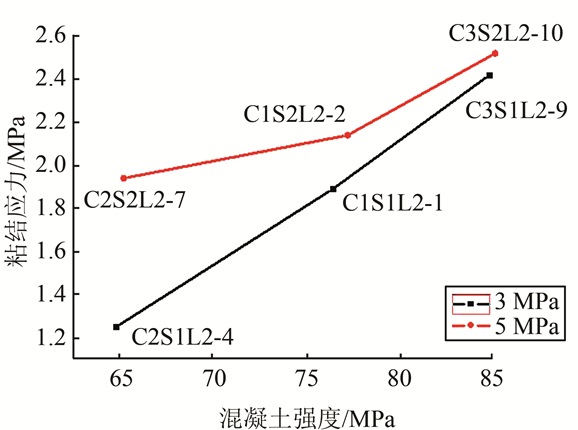
为分析混凝土强度对试件粘结性能的影响,绘制了不同混凝土强度试件的荷载-滑移曲线对比图和抗剪粘结强度与混凝土强度的关系曲线,分别如图 9、10所示.从图中可以看出,随着混凝土强度的提高,试件抗剪粘结强度有所提高.对比试件C1S1L2-1和C2S1L2-4可以发现,当混凝土强度从64.8 MPa提高到76.4 MPa,粘结强度提高了70%.在提高混凝土骨料-水泥砂浆界面过渡区研究中,文献[15]通过推出试验得出结论:界面强度与界面厚度和硅粉数量有关.与普通混凝土相比,掺加硅灰强度越高的混凝土,界面厚度越薄,相应粘结强度也越高.同时, 在电镜下观察掺有硅灰的混凝土,可以发现水泥石空隙中有晶体生长,硅灰颗粒很细小、可均匀地填充混凝土微孔,从而增强混凝土的化学胶结力和机械咬合力[3].机械咬合力是粘结力的主要组成部分,其大小取决于钢管表面的粗糙程度以及混凝土的抗剪强度.摩阻力与接触面的摩擦系数和法向压力的大小成正比,由于混凝土中添加膨胀剂,使得核心混凝土从初始阶段起就受到由钢管提供的较大的法向力,从而提高了摩阻力,因此, 混凝土-钢管界面的粘结强度得到了提高.但峰值之后,混凝土强度越高的试件承载力下降越快,分析其原因:一是在相同含钢率情况下,混凝土强度的增大导致套箍系数的降低;二是高强混凝土本身的脆性所致.
|
| 图 9 不同混凝土强度试件的荷载-滑移曲线 Fig. 9 Load-displacement curves of specimens with different concrete strengths |
|
| 图 10 抗剪粘结强度与混凝土强度的关系 Fig. 10 Relationship between bond stress and concrete strength |
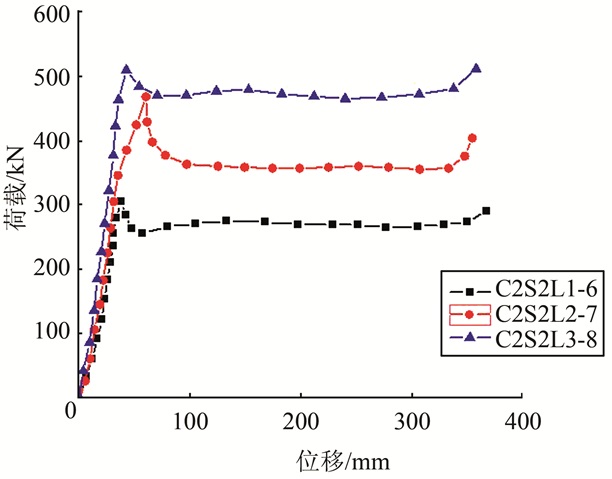
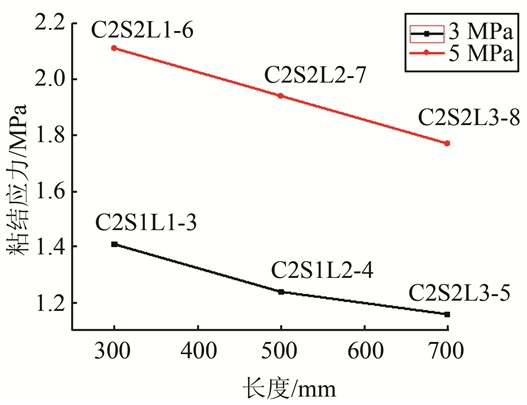
图 11、12分别为不同界面长度试件的荷载-滑移曲线、抗剪粘结强度与自应力值的关系曲线.从图中可以看出,3组试件的荷载-滑移曲线形状基本相同,其抗剪粘结极限承载力随着界面长度的增加而增加,但粘结强度与界面长度则近似呈线性减小的关系.这主要是由于随着界面长度的增加,钢管与混凝土间相互接触的面积增大,承载能力也增大,但同时,其粘结应力的分布却愈加不均匀,导致最终的计算粘结强度越小.康希良等人[16]对2组13个试件进行了偏心推出试验,试验结果同样表明,在相同偏心率的条件下,当长细比满足7.28 < 4L/D < 21.8时,粘结强度随长细比的增大而减小,结论与本文试验结果一致.
|
| 图 11 不同界面长度试件的荷载-滑移曲线 Fig. 11 Load-displacement curves of specimens with different embedded lengths |
|
| 图 12 抗剪粘结强度与界面长度的关系 Fig. 12 Relationship between bond stress and embedded length |
前述分析表明,抗剪粘结强度与自应力值、混凝土强度和界面长度有着紧密的联系.由于前两者的影响程度更为显著,本文提出的抗剪粘结强度计算公式仅考虑混凝土强度和自应力值两个因素.
目前钢管混凝土结构设计与施工规范中并没有提出钢管混凝土粘结强度的计算方法,更没有钢管自应力自密实高强混凝土柱粘结强度的计算公式,蔡绍怀[17]分3批制作了32个试件,混凝土强度为40 MPa左右,所用钢管均为φ165 mm×5 mm直缝焊接管,钢管高度为300、500、700和900 mm,基于此试验结果,该课题组提出粘结强度与混凝土强度的关系可以表达为
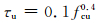
基于本课题试验结果,考虑自应力值、混凝土强度的影响因素,最终提出钢管自应力自密实高强混凝土柱粘结强度的计算公式.
以自应力值和核心混凝土强度作为变量,对试验结果进行回归分析,可得粘结强度的经验公式:
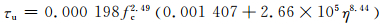 (5)
(5)
式中:fc为核心混凝土抗压强度;η为自应力水平[16],即混凝土自应力与抗压强度的比值.试验值和计算值的对比如表 4所示,计算值/试验值的平均值为1.01.与文献公式τu=0.1fcu0.4得到的计算值作对比可知,自应力可以大幅度提高钢管混凝土界面的粘结强度.
4 结论本文通过22根钢管自应力自密实高强混凝土柱和1根钢管自密实混凝土柱试件的推出试验,研究界面粘结性能,分析自应力值、混凝土强度和界面长度对粘结性能的影响,得出如下主要结论:
1) 与钢管自密实混凝土柱相似,钢管自应力自密实高强混凝土柱的荷载-滑移曲线可以分为4个阶段,即胶结段、滑移段、摩擦段和上升段.在摩擦段,自应力使得钢管在加荷之前就提供了侧向约束,从而使钢管自应力自密实高强混凝土柱试件的承载力出现上升现象.
2) 自应力自密实混凝土增强了混凝土与钢管界面间化学胶结力和机械咬合力,进而提高了摩阻力.
3) 钢管自应力自密实高强混凝土柱的抗剪粘结强度随着自应力值的增大而增大,随混凝土强度的提高而提高;随着界面长度的增大而减小,且粘结强度与界面长度的关系可以近似表达为线性关系.
4) 基于试验数据,参考相关文献,本文提出钢管自应力自密实高强混凝土抗剪粘结强度的计算公式,该公式可为工程设计提供参考.
| [1] |
Okamura H. Self-compacting high-performance concrete[J]. Concrete International, 1997, 19(7): 50-54. |
| [2] |
薛立红, 蔡绍怀. 钢管混凝土柱组合界面的粘结强度(上)[J]. 建筑科学, 1996a, 12(3): 22-28. Xue Lihong, Cai Shaohuai. Bond strength at the interface of concrete-filled steel tube columns[J]. Building Science, 1996a, 12(3): 22-28. |
| [3] |
薛立红, 蔡绍怀. 钢管混凝土柱组合界面的粘结强度(下)[J]. 建筑科学, 1996b, 12(4): 19-23. Xue Lihong, Cai Shaohuai. Bond strength at the interface of concrete-filled steel tube columns[J]. Building Science, 1996b, 12(4): 19-23. |
| [4] |
薛立红, 蔡绍怀. 荷载偏心率对钢管混凝土柱组合界面粘结强度的影响[J]. 建筑科学, 1997, 13(2): 22-25. Xue Lihong, Cai Shaohuai. The influence of load eccentricity on bond strength at the interface of concrete-filled steel tube columns[J]. Building Science, 1997, 13(2): 22-25. |
| [5] |
Park R, Paulay T. Reinforced Concrete Structures[M]. New Zealand, 1975.
|
| [6] |
Morishita Yo, Tomii M, Yoshimura K. Experimental studies on bond strength in concrete filled circular steel tubular columns subjected to axial loads[J]. Transactions of Japan Concrete Institute, 1979b(Ⅰ): 359-366. |
| [7] |
Virdi K S, Dowling P J. Bond strength in concrete filled steel tubes[C]// IABSE Proceeding, P-33/80, 1980: 125-139.
|
| [8] |
Virdi K S, Dowling P J. Bond strength in concrete filled steel tubes[R]. CESLIC Report CCⅡ, Department of Civil Engineering, Imperial College, London, 1975.
|
| [9] |
Roeder C W, Cameron B, Brown C B. Composite action in concrete filled tubes[J]. Journal of Structural Engineering, ASCE, 1999, 125(5): 477-484. DOI:10.1061/(ASCE)0733-9445(1999)125:5(477) |
| [10] |
Khalil H S. Push-out strength of concrete-filled steel hollow sections[J]. Structural Engineer, 1993, 71(13): 230-233. |
| [11] |
Khalil H S. Resistance of concrete-filled steel tubes to push-out force[J]. Structural Engineer, 1993, 71(13): 234-243. |
| [12] |
GB/T 2975-1998钢及钢产品力学性能试验取样位置及试样制备[S]. GB/T 2975-1998 Steel and Steel Products-Location and Preparation of Test Pieces for Mechanical Testing[S]. |
| [13] |
杨玉喜, 刘学全. 硅灰在混凝土中的作用[J]. 黑龙江交通科技, 2007, 30(6): 51-55. Yang Yuxi, Liu Xuequan. The effect of silica fume in the concrete[J]. Communications Science and Technology Heilongjiang, 2007, 30(6): 51-55. DOI:10.3969/j.issn.1008-3383.2007.06.030 |
| [14] |
袁启涛, 唐玉超, 罗作球, 等. 微珠在C50, C55商品混凝土中的应用研究[J]. 混凝土与水泥制品, 2014, 7: 21-24. Yuan Qitao, Tang Yuchao, Luo Zuoqiu, et al. Study on the beads used in C50, C55 commodity concrete[J]. China Concrete and Cement Products, 2014, 7: 21-24. |
| [15] |
Caliskan, Sinan. Aggregate/mortar interface: Influence of silica fume at the micro-and macro-level[J]. Cement and Concrete Composites, 2003, 25(4): 557-564. |
| [16] |
康希良, 赵鸿铁, 薛建阳, 等. 钢管混凝土套箍机理及组合弹性模量的理论分析[J]. 工程力学, 2007, 24(11): 121-125. Kang Xiliang, Zhao Hongtie, Xue Jianyang, et al. Theoretic analysis for hooping mechanism and composite elastic modulus of CFST members[J]. Engineering Mechanics, 2007, 24(11): 121-125. DOI:10.3969/j.issn.1000-4750.2007.11.021 |
| [17] |
蔡绍怀. 现代钢管混凝土结构[M]. 北京: 人民交通出版社, 2007. Cai Shaohuai. Modern Steel Tube Confined Concrete Structures[M]. Beijing: China Communications Press, 2007. |
| [18] |
徐磊.钢管自应力免振混凝土轴压柱设计理论研究[D].大连: 大连理工大学, 2005. Xu Lei. Research on the design theory for self-stressing and self-compacting concrete filled steel tube column under axial load[D]. Dalian: Dalian University of Technology, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10141-2006021893.htm |
 2018, Vol. 51
2018, Vol. 51




