文章信息
- 朱庆东, 黄小玲, 陈明祥, 谭星舟
- ZHU Qingdong, HUANG Xiaolin, CHEN Mingxiang, TAN Xingzhou
- 工字钢剪切键埋件的试验研究与有限元分析
- Research and finite element analysis on the embedded part of H-steel shear key
- 武汉大学学报(工学版), 2018, 51(3): 239-244
- Engineering Journal of Wuhan University, 2018, 51(3): 239-244
- http://dx.doi.org/10.14188/j.1671-8844.2018-03-009
-
文章历史
- 收稿日期: 2017-11-20
2. 武汉大学土木建筑工程学院,湖北 武汉 430072;
3. 武大巨成结构股份有限公司,湖北 武汉 430077
2. School of Civil and Architectural Engineering, Wuhan University, Wuhan 430072, China;
3. Wuda Jucheng Structure Co., Ltd., Wuhan 430077, China
设计电厂主厂房结构时,从施工工期、楼层结构净空等方面考虑,有时将钢筋混凝土框架结构的混凝土次梁改为钢次梁.对这种混合结构的节点连接,传统的做法是将钢次梁简支于混凝土主梁的挑耳上,后来也有将钢次梁直接插入钢筋混凝土主梁内.前者主梁施工支模复杂,铰接构造易引起后浇混凝土板开裂;后者受力有所改善,但主梁绑扎钢筋和支模不便,因此有必要探讨其他的节点结构型式[1].
本文提出采用型钢预埋件连接型式,即借鉴纯锚筋式埋件连接便于施工的优点,用一定数量的型钢替代部分锚筋进而提高埋件抗剪承载力,以解决锚筋式埋件连接在承载力上的不足.型钢埋件缺乏设计依据,有必要对其进行试验研究和理论计算分析,为工程应用提供参考.
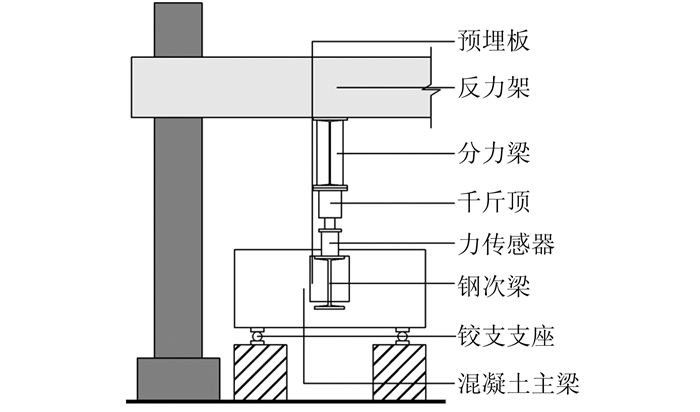
1 试件的设计参考实际工程案例设计试验模型,试件参数见表 1[2, 3], E1埋件为含工字钢剪切键埋件,E2埋件为纯锚筋埋件,锚筋选用Φ16,工字钢选用I10.锚筋抗剪强度参考《混凝土结构设计规范》[4]计算,工字钢剪切键抗剪强度参考《预埋件设计手册》[5]计算.试验装置如图 1所示,钢筋混凝土简支梁长1.2 m,截面300 mm×800 mm,选用C35混凝土.试验以30 kN/40 kN/50 kN的步长加载[6],按照工程惯例,埋件与混凝土间缝隙达到2 mm时,判定节点破坏.
| 编号 | 简图 | 锚板尺寸/mm(长/宽/高) | 锚筋数量 | 工字钢数量 | 设计抗剪强度/kN |
| E1-1 |  |
300/200/10 | 4 | 1 | 168 |
| E2-1 |  |
300/200/10 | 7 | 0 | 171 |
| E1-2 |  |
400/200/10 | 6 | 1 | 218 |
| E2-2 |  |
400/200/10 | 9 | 0 | 210 |
| E1-3 |  |
400/200/10 | 6 | 2 | 309 |
| E2-3 |  |
400/200/10 | 12 | 0 | 280 |
|
| 图 1 试件加载装置图 Figure 1 Experimental loading equipment |
1) 在制作试件时预留了3个150 mm×150 mm×150 mm混凝土立方块,完成混凝土的养护后,对试块进行抗压强度试验,测得立方块抗压强度为35.1 MPa,抗拉强度为3.5 MPa.
2) 经过拉拔试验, 钢筋、钢板的强度指标见表 2所示.
| 种类 | 牌号 | 直径或厚度/mm | 抗拉强度/MPa | 抗剪强度/MPa | 弹性模量/GPa |
| 主梁纵筋 | HRB335 | 28 | 332.0 | 203 | |
| 锚筋 | HRB335 | 16 | 333.6 | 204 | |
| 主梁箍筋 | HPB300 | 16 | 303.5 | 210 | |
| 锚板 | Q345B | 10 | 346.7 | 185.4 | 206 |
| 工字钢腹板 | Q345B | 4.5 | 350.2 | 186.1 | 206 |
型钢与锚筋组合的埋件为一种新的型式,缺少现成的计算公式,由试验只能得到设计规格埋件的破坏形态和承载力,难以推广到其他规格.本文采用现行的钢筋混凝土有限元理论建立数值模型,将计算结果与试验进行对比,探讨埋件的破坏机理,可以为其他规格的埋件设计提供借鉴[7].
该预埋件结构只涉及到2种材料:钢材和混凝土,埋件在加载过程中钢材或混凝土会发生破坏,本构关系采用ABAQUS程序推荐的本构关系进行分析.型钢、钢筋与混凝土之间的交接面也可能发生拉脱或滑移,这种破坏形态模拟参数选取困难,本文尝试利用混凝土的破坏来达到模拟界面破坏的效果[8, 9].
3.1 材料本构模型混凝土受压应力-应变曲线采用下式[10]:
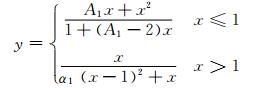 (1)
(1)
式中:y=σ/fc;x=ε/εc;fc为混凝土轴心抗压强度,fc=0.4fcu7/6;εc为混凝土受压峰值应变,εc=383fcu7/18×10-6;参数A1的物理意义为混凝土弹性模量与峰值割线模量比值, A1=9.1fcu-4/9; fcu为混凝土立方体抗压强度;α1=0.15.
混凝土受拉应力-应变曲线采用下式[11]:
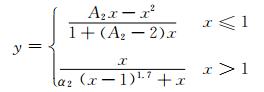 (2)
(2)
式中:y=σ/ft;x=ε/εt;ft为混凝土轴心抗拉强度,ft=0.24fcu2/3;εt为混凝土受拉峰值应变,εt=33fcu1/3×10-6;参数A2的物理意义为混凝土弹性模量与峰值割线模量比值,A2=1.306;α2=1+3×10-4 fcu2; fcu为混凝土立方体抗压强度.
钢材采用理想弹塑性模型,弹性模量、抗拉强度和抗剪强度参照表 2.
3.2 单元类型混凝土采用8节点六面体单元C3D8R单元;锚板和工字钢采用4结点四边形壳单元S4R单元;纵筋和箍筋采用3结点二次三维桁架单元T3D3单元;锚筋采用3结点二次空间梁单元B32单元.埋件单元网格划分见图 2[12].
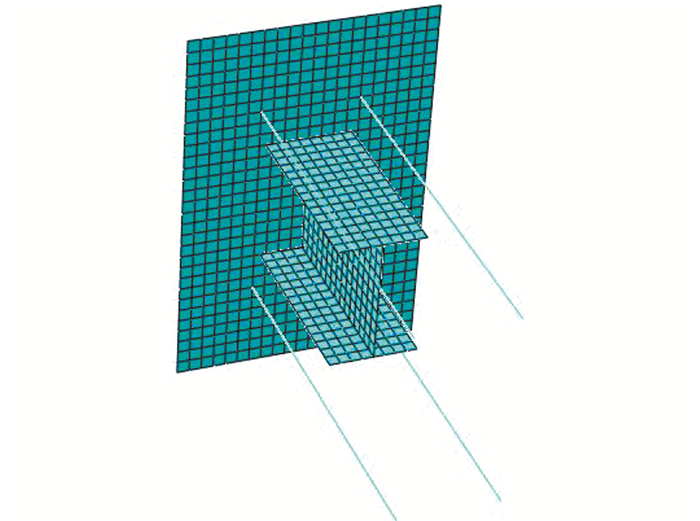
|
| 图 2 埋件单元网格划分 Figure 2 The finite mesh elements of embedded part |
锚板与混凝土的界面模型由法线方向的接触和切线方向的黏结滑移2部分构成.切线方向的接触列式为罚函数列式,锚板与混凝土界面摩擦系数取0.5,并采用有限滑移,而法线方向的接触采用硬接触.接触单元为surface-to-surface,其中锚板单元为主面,混凝土单元为从面[13].
锚板与锚筋、工字钢剪切键、钢次梁的约束形式为tie.箍筋、纵筋、锚筋、工字钢剪切键与混凝土的约束形式为embedded region,其中内置区域为箍筋、纵筋,主体区域为混凝土[14].
4 试验与有限元模拟 4.1 试验结果与有限元模拟结果各梁加载试验结果与有限元模拟结果见表 3, 总体上E1埋件的极限承载力大于E2埋件, 工字钢剪切键有助于提高埋件的抗剪承载力.
| 编号 | 有限元模拟极限荷载/kN | 试验破坏荷载/kN | 有限元模拟与试验结果比值 |
| E1-1 | 195 | 215 | 0.907 |
| E2-1 | 185 | 205 | 0.902 |
| E1-2 | 265 | 300 | 0.883 |
| E2-2 | 245 | 275 | 0.891 |
| E1-3 | 350 | 430 | 0.814 |
| E2-3 | 330 | 390 | 0.846 |
E1-1受力情况与破坏形式较有代表性,以E1-1为例描述加载过程中的试验现象.
E1-1加载至90 kN时,埋件下方混凝土出现一条细微竖向裂缝; 当加载至175 kN时,埋件开始出现滑移,锚板顶部与混凝土之间出现0.5 mm缝隙; 继续加载,缝隙逐渐加宽;当加载至215 kN时,缝隙扩大至2 mm,且锚板顶部明显向外翘起约0.5 mm,判定埋件受剪已达到极限状态,停止加载.加载过程中混凝土裂缝不断增加、扩展,最终裂缝宽度达到0.6 mm.
4.3 工字钢剪切键与锚筋的应力试件破坏时,预埋件顶层锚筋应力和工字钢剪切键腹板剪应力最大,其荷载-应力曲线如图 3.从图 3中可以看出:
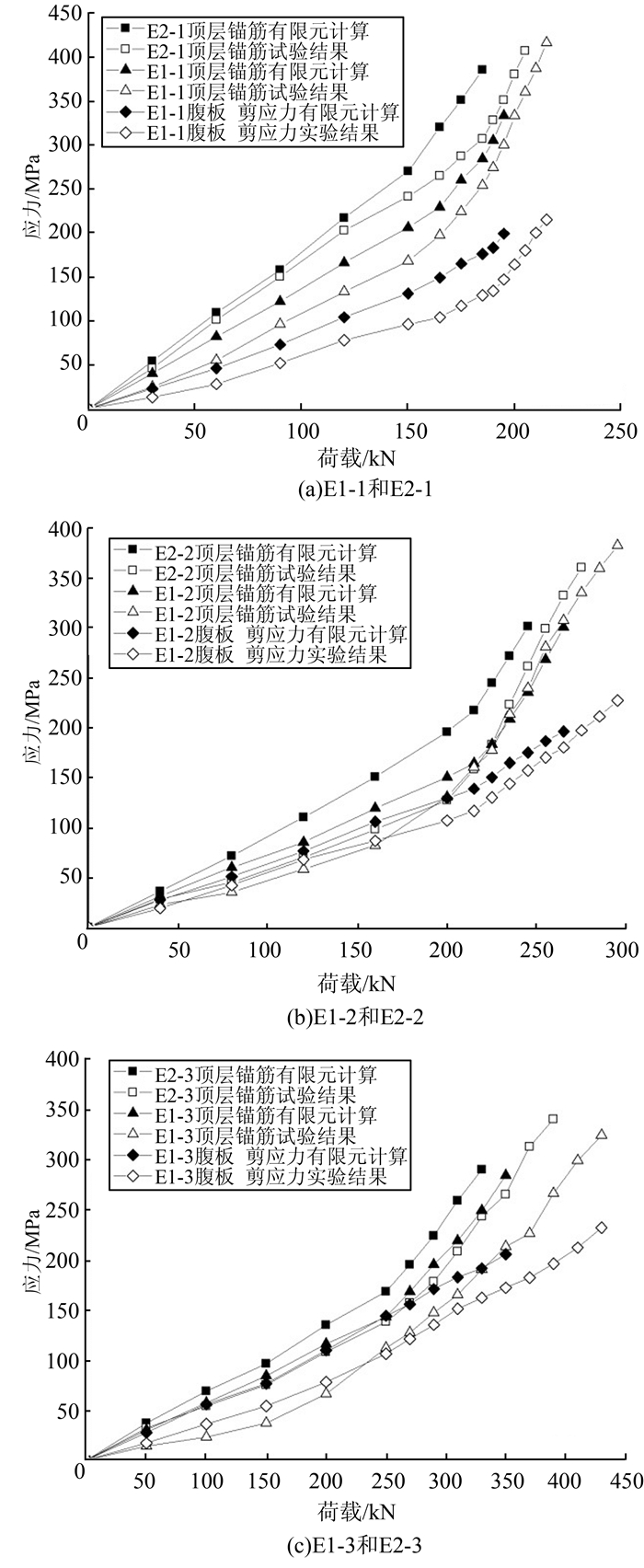
|
| 图 3 荷载-应力曲线 Figure 3 Load-stress curves |
1) 观察顶层锚筋应力与腹板剪应力的试验结果曲线,荷载较小时,荷载与应力表现出线性关系;荷载接近150/200/250 kN时,锚筋出现相对滑移,荷载-应力曲线段斜率上升;荷载接近210/275/430 kN时,曲线段斜率进一步上升,顶层锚筋屈服,工字钢剪切键腹板屈服,埋件破坏.
2) 相同荷载作用下,E2埋件的顶层锚筋应力大于E1埋件,这是由于E2埋件全部剪切荷载由锚筋承担,顶层锚筋承担的剪切力相对大,而E1埋件很大一部分剪切荷载由工字钢剪切键承担,顶层锚筋承担的剪切力相对较小,故纯锚筋预埋件中钢筋更易屈服.
3) 有限元模拟曲线与试验测量曲线变化趋势总体一致.
图 4为极限荷载下E1-1埋件工字钢剪切键的剪应力分布云图,从中可以看出节点破坏时,工字钢腹板最大剪应力为196 MPa,超过腹板抗剪强度186.1 MPa,故工字钢腹板已经屈服,与试验结果一致;而工字钢剪切键的上下翼缘剪应力较低.图 5为极限荷载下E1-1埋件锚筋的拉应力分布云图,从中可以看出预埋件节点破坏时,锚筋与锚板连接区域拉应力最大,为336 MPa,超过锚筋抗拉强度333.6 MPa,与试验结果一致,E1埋件破坏始于工字钢腹板和锚筋屈服.图 4、图 5中工字钢剪切键、锚筋左侧与锚板相连[15].
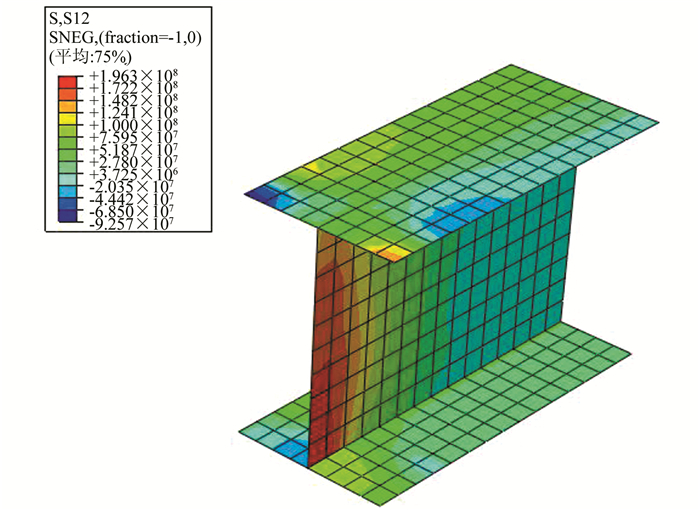
|
| 图 4 剪应力云图 Figure 4 Nephogram of shear stresses |
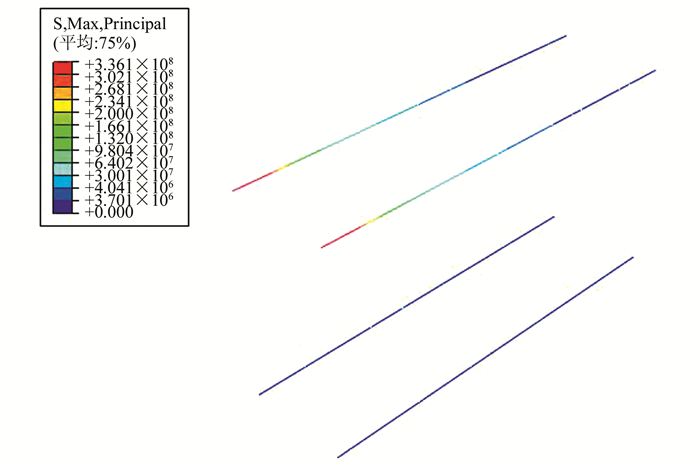
|
| 图 5 拉应力云图 Figure 5 Nephogram of tensile stresses |
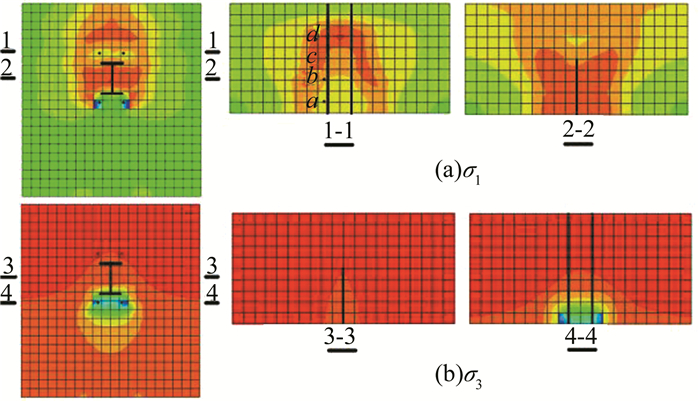
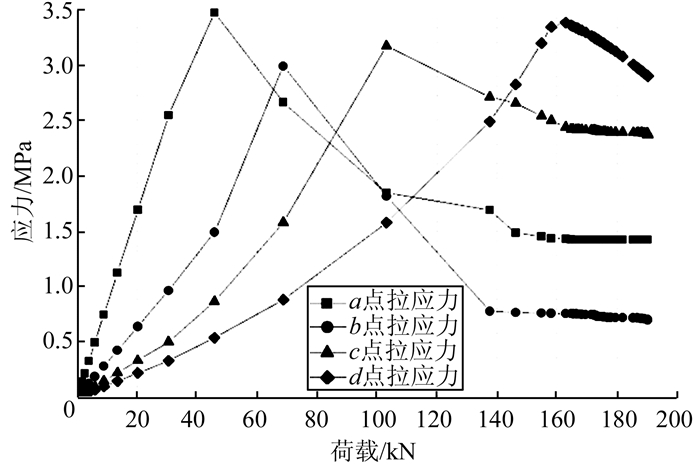
图 6为E1-1混凝土主应力云图(σ1>σ2>σ3).图 7为图 6中1-1剖面图上a、b、c、d 4点的荷载-应力曲线.
|
| 图 6 E1-1主应力云图 Figure 6 Nephograms of principal stresses of E1-1 |
|
| 图 7 a、b、c、d点荷载-应力曲线 Figure 7 Load-stress curves of a、b、c、d |
观察σ1应力云图可知:混凝土所受最大拉应力为3.47 MPa,接近C35混凝土极限抗拉强度3.5 MPa.在1-1剖面上(抗拉锚筋位置)产生最大拉应力的部位在梁截面中间区域而不在靠近锚板侧(锚板在下侧),表明锚板侧锚筋附近的混凝土拉应力超出极限抗拉强度,混凝土开裂,拉应力释放,最大拉应力位置向背离锚板方向转移,体现了锚板侧锚筋与混凝土之间的连接失效.
观察σ3应力云图可知:混凝土所受最大压应力约为3.1 MPa,未达到C35混凝土极限抗压强度35.1 MPa,故混凝土未压坏,表明在混凝土内埋入工字钢剪切键,工字钢的翼缘可以将压力分摊给混凝土,不致于在混凝土内产生过大的局部压应力.
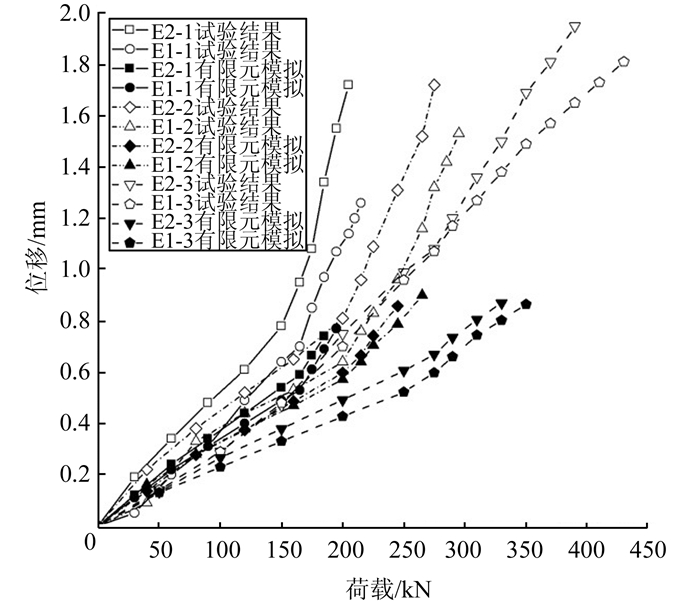
4.5 埋件与主梁的相对位移图 8反映了埋件与主梁竖直方向的相对位移在荷载作用下的变化情况.相同荷载作用下,E1的相对位移明显低于E2,工字钢剪切键的抗剪刚度高于钢筋剪切键,工字钢剪切键有助于提高埋件的抗剪刚度.
|
| 图 8 荷载-埋件相对位移曲线 Figure 8 Load-relative displacement curves of embedded parts |
1) 用型钢代替部分锚筋的预埋件是一种新的型式,试验研究和有限元分析表明,含工字钢剪切键埋件的抗剪刚度和极限剪切承载力均优于纯锚筋埋件.
2) 工字钢剪切键埋件的破坏始于工字钢腹板和锚筋屈服,属于塑性破坏,满足安全性要求.
3) 有限元模拟结果展现了埋件的破坏过程,有限元计算破坏荷载为试验破坏荷载的0.81~0.91倍,采用有限元分析对该新型埋件设计具有指导意义.
4) E1埋件的工字钢剪切键和锚筋应力随荷载变化趋势基本一致,E1埋件破坏时,工字钢剪切键与锚筋均已屈服,它们能较好地协同工作.
| [1] |
预埋件专题研究组. 预埋件的受力性能及设计方法[J].
建筑结构学报, 1987(3): 36–50.
Embedded Parts Research Group. Load-bearing capacity and design method of embedded elements[J]. Journal of Building Structures, 1987(3): 36–50. |
| [2] |
赵均, 刘建成, 杜修力, 等. 混凝土墙体与钢梁连接的穿筋预埋件性能试验研究[J].
北京工业大学学报, 2008(5): 487–491.
Zhao Jun, Liu Jiancheng, Du Xiuli, et al. Experimental study on the behavior of the sandwich-like embedded anchor in the concreted with steel beam[J]. Journal of Beijing University of Technology, 2008(5): 487–491. |
| [3] |
王清湘, 朱耀国. 大直径锚筋预埋件纯剪、拉剪作用下的试验研究[J].
建筑结构学报, 2008(s1): 281–286.
Wang Qingxiang, Zhu Yaoguo. Experimental study on mechanical behavior of big-diameter anchor bar embedded part under shear and tension-shear[J]. Journal of Building Structures, 2008(s1): 281–286. |
| [4] |
GB 50010-2010混凝土结构设计规范[S].
GB 50010-2010 Code for Design of Concrete Structures[S]. |
| [5] |
严正庭, 严捷.
预埋件设计手册[M]. 北京: 中国建筑工业出版社, 1994.
Yan Zhengting, Yan Jie. Embedded Part Design Manual[M]. Beijing: China Architecture & Building Press, 1994. |
| [6] |
GB 50152-92混凝土结构试验方法标准[S].
GB 50152-92 Standard Test Method for Concrete Structure[S]. |
| [7] |
雷拓, 钱江, 刘成清. 混凝土损伤塑性模型应用研究[J].
结构工程师, 2008, 2(22): 22–27.
Lei Tuo, Qian Jiang, Liu Chengqing. Application of damaged plasticity model for concrete[J]. Structural Engineers, 2008, 2(2): 22–27. |
| [8] | Lubliner J, Oliver J, Oller S, et al. A plastic-damage model for concrete[J]. International Journal of Solids and Structures, 1989, 25(3): 299–326. DOI:10.1016/0020-7683(89)90050-4 |
| [9] |
江见鲸, 陆新征, 叶列平.
混凝土结构有限元分析[M]. 北京: 清华大学出版社, 2005.
Jiang Jianjing, Lu Xingzheng, Ye Lieping. Finite Element Analysis of Concrete Structures[M]. Beijing: Tsinghua University Press, 2005. |
| [10] |
余志武, 丁发兴. 混凝土受压力学性能统一计算方法[J].
建筑结构学报, 2003(4): 41–46.
Yu Zhiwu, Ding Faxing. Unified calculation method of compressive mechanical properties of concrete[J]. Journal of Building Structures, 2003(4): 41–46. |
| [11] |
丁发兴, 余志武. 混凝土受拉力学性能统一计算方法[J].
华中科技大学学报:城市科学版, 2004, 21(3): 29–34.
Ding Faxing, Yu Zhiwu. Unified calculation method of mechanical properties of concrete in tension[J]. Journal of Huazhong University of Science and Technology: Urban Science Edition, 2004, 21(3): 29–34. |
| [12] | ABAQUS Theory Manual V6. 10[S]. ABAQUS Inc, 2010. |
| [13] |
丁发兴, 周林超, 余志武, 等. 钢管混凝土轴压短柱非线性有限元分析[J].
中国科技论文在线, 2009(7): 472–479.
Ding Faxing, Zhou Linchao, Yu Zhiwu, et al. Nonlinear finite element analysis of axially loaded concrete-filled steel tubular stub columns[J]. Sciencepaper Online, 2009(7): 472–479. |
| [14] | ABAQUS User's Manual[S]. ABAQUS Inc, 2007. |
| [15] |
朱耀国, 王清湘. 预埋件受剪性能数值分析[J].
大连理工大学学报, 2014(2): 210–214.
Zhu Yaoguo, Wang Qingxiang. Finite element analysis of shear performances of embedded parts[J]. Journal of Dalian University of Technology, 2014(2): 210–214. DOI:10.7511/dllgxb201402009 |
 2018, Vol. 51
2018, Vol. 51



