文章信息
- 余敏, 谢佳新, 查晓雄, 徐礼华, 黄伟军
- YU Min, XIE Jiaxin, ZHA Xiaoxiong, XU Lihua, HUANG Weijun
- 实空心钢管混凝土抗剪承载力统一计算方法
- A unified formula for solid and hollow concrete-filled steel tube columns under shear
- 武汉大学学报(工学版), 2017, 50(6): 829-835
- Engineering Journal of Wuhan University, 2017, 50(6): 829-835
- http://dx.doi.org/10.14188/j.1671-8844.2017-06-005
-
文章历史
- 收稿日期: 2016-04-20
2. 哈尔滨工业大学深圳研究生院, 广东 深圳, 518055
2. Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, China
目前钢管混凝土在实际工程已有大量的应用,常见的是实心钢管混凝土,即在钢管中浇灌混凝土而形成[1].同时随着行业的发展,也出现了空心钢管混凝土,空心钢管混凝土是采用离心法浇筑管内混凝土并通过蒸汽养护制成,混凝土部分为中空,主要用于输变电塔,目前也开始向民用建筑中推广[2].从几何构造上看实心钢管混凝土可以看成空心钢管混凝土的特例,即空心率等于0的情况.根据钟善桐教授的“钢管混凝土统一理论”[3],实心和空心钢管混凝土的性质应该是连续变化的,在承载力计算公式方面应该有统一的计算公式.因此,进行实心和空心钢管混凝土的统一计算研究有理论和实际价值.
目前关于钢管混凝土的研究多针对实心构件,对于抗剪承载力亦是如此.如:王建伟等[4]、肖从真等[5]、郭淑丽等[6]从剪跨比、轴压比等方面进行研究和分析,分别提出了钢管混凝土抗剪承载力公式;傅中秋等[7]从混凝土类型、混凝土强度以及空钢管的受力性能差异等方面分析了钢管混凝土的抗剪性能;Jones等[8]、吴波等[9]、韩林海等[10]、蔡健等[11]基于抗剪强度和轴压承载力提出了多种不同的钢管混凝土构件的抗剪承载力计算方法.而关于实心和空心钢管混凝土在各种受力情况下的统一计算研究也有部分成果,例如:黎玉婷等给出了复杂应力下钢管混凝土构件承载力计算的统一相关方程公式[12];Yu等[13-15]基于厚壁圆筒理论和Perry公式提出了实、空心统一的钢管混凝土轴压强度和稳定承载力计算公式,并基于平均温度将常温公式扩展到了高温下;余敏等[16]基于弹性和塑性理论分析推导给出了实心和空心统一的钢管混凝土抗扭承载力计算公式.同时目前规范GB 50936[17]中给出了钢管混凝土在压、弯、剪、扭共同作用下的承载力计算公式,但是其中实心和空心钢管混凝土的抗剪承载力公式过于复杂.
因此,为实现实心和空心钢管混凝土抗剪承载力的统一计算,采用数值和理论相结合的方法对钢管混凝土的抗剪承载力进行研究,最终给出实心和空心完全统一的抗剪承载力计算公式,并通过和试验的对比证明公式的有效性.为钢管混凝土的统一计算理论和工程实践提供参考.
1 有限元模型及验证有限元方法在钢管混凝土压、弯、剪、扭等研究中被广泛应用,目前相关的材料参数取值、单元类型及接触行为已经有大量的研究,相关模拟技术相对比较成熟.因此采用有限元法对钢管混凝土在纯剪荷载作用下的性能进行模拟,为简化公式的建立和参数确定提供数据支持.
1.1 材料本构关系1) 混凝土的本构关系
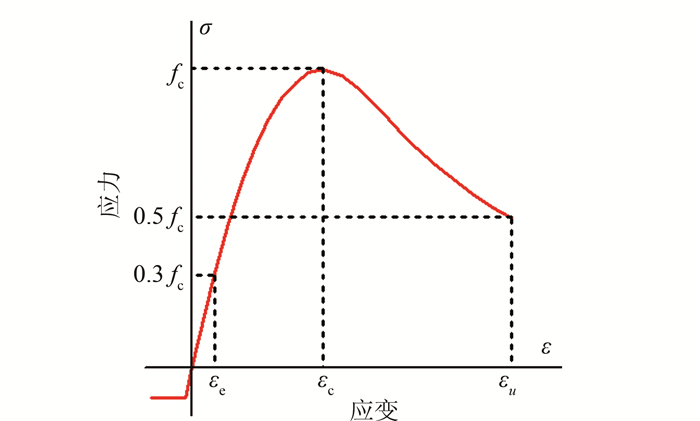
混凝土采用弹塑性损伤本构模型,其中单轴应力-应变曲线采用混凝土规范GB 50010[18]中推荐的公式,弹性模量取0.3fc处的割线模量.受拉部分做了适当的简化,取抗压强度的1/10,以便于计算收敛,见图 1.
|
| 图 1 混凝土本构关系模型 Figure 1 Constitutive model of concrete |
2) 钢材的本构关系
钢材采用双折线模型[16],硬化模量取弹性模量的0.01,屈服准则采用Von Mises应力准则.
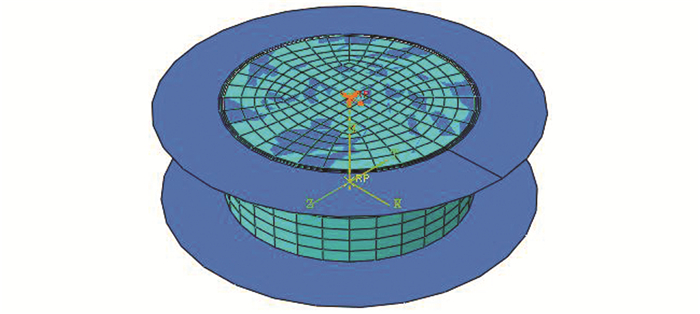
1.2 有限元模型及其试验验证钢管和核心混凝土一般采用单面自动接触和完全约束接触,在此不考虑钢管与混凝土间的滑动,采用tie接触.为了方便施加剪力,构件上下表面各和1块刚壳体连接,构件上下表面和刚壳之间也采用tie连接.加载方式为位移加载.有限元模型及网格划分见图 2.
|
| 图 2 抗剪计算有限元模型 Figure 2 Finite element model of shear |
为验证上述有限元模型的合理性,对文献[19]中的2个受剪构件S21-C2-1和S31-C2-1进行了有限元模拟,试件尺寸等信息见表 1.
| 试件编号 | D/mm | l/mm | t/mm | fc/MPa | fy/MPa |
| S21-C2-1 | 166 | 232 | 4.4 | 32.4 | 345 |
| S31-C2-1 | 165 | 232 | 3 | 32.4 | 408 |
| 注:D、l、t分别为钢管的外径、实际长度和壁厚;fc为实测混凝土轴心抗压强度值;fy为钢材屈服强度的实测值. | |||||
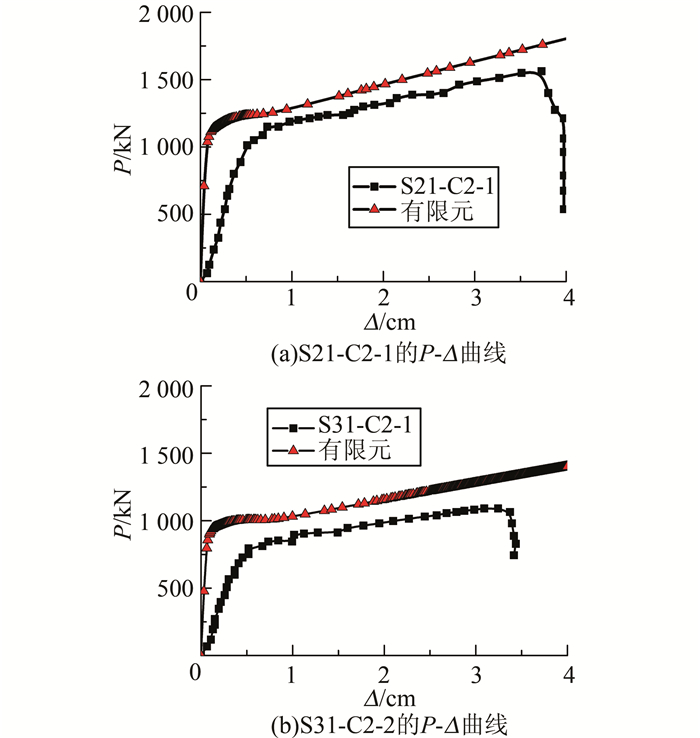
钢管混凝土纯剪构件的有限元计算和试验得到的荷载-位移曲线的比较如图 3所示.
|
| 图 3 有限元计算和试验的比较 Figure 3 Comparison between finite element calculation and experiment |
从图 3的比较发现,构件P-Δ曲线的计算结果与实测结果总体上趋势一致,但是曲线初期刚度的计算结果与试验结果存在一定的差别,即计算变形总体小于实测结果.可能的原因是试验得到的跨中位移值包含了支座处钢管受压变形而产生的位移,从而使得实测位移值偏大,这和其他学者如韩林海教授[20]的模拟结果情况类似.根据文献[20]取τ-γ曲线上剪应变达10 000 με时的剪力为抗剪强度.对于本研究比较关心的抗剪承载力,试验结果和模拟结果比较接近.综上所述,本文所采用的有限元模型可以用于计算钢管混凝土的抗剪承载力.
2 抗剪承载力的分析 2.1 影响因素影响钢管混凝土抗剪承载力的因素包括材料强度和几何尺寸.对于实心钢管混凝土,如钢管外径D、混凝土强度fck、钢材强度fy和套箍系数等影响已有研究.而对于空心钢管混凝土,主要是多了一个参数空心率ψ,其定义为混凝土中空心的面积Ak除以混凝土面积Ac与空心部分面积之和,即ψ=Ak/(Ac+Ak).因此本文重点分析空心率ψ对钢管混凝土抗剪承载力的影响.
采用上述有限元模型,分析空心率ψ对平均剪切应力(即截面剪力除以截面总面积τ=V/Asc)和剪切应变(γ=Δ/L)曲线的影响规律.模型的基本条件为:钢管外径D=400 mm、钢管壁厚t=D/50=8 mm、混凝土等级为C40、钢材采用Q345、构件长度为320 mm.根据韩林海教授[20]的研究,极限剪切应力取γ=20 000 με时对应的剪应力.
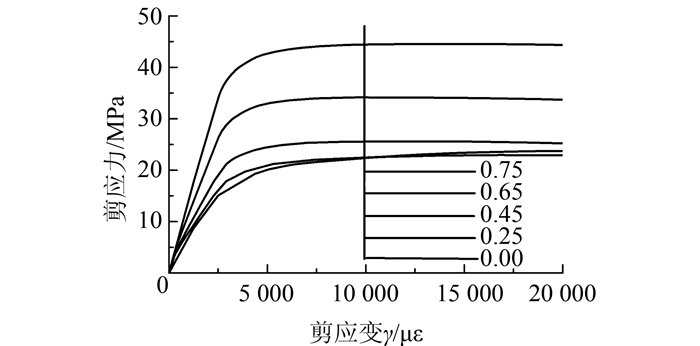
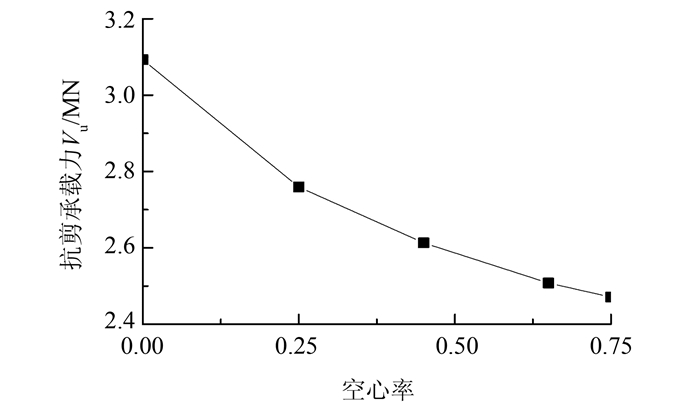
图 4给出了不同空心率时钢管混凝土纯剪τ-γ曲线.可见,在其他参数不变的情况下,随着ψ的提高,钢管混凝土的弹性段剪切刚度和极限抗剪强度逐渐增大.这主要是随着空心率的增大,钢材在抗剪承载力中的比重越来越大,剪切强度越接近钢材的抗剪强度.图 5为对应的抗剪承载力随空心率的变化图,由图可知,随着空心率的增大,虽然截面的极限抗剪强度越来越大,但是总体的抗剪承载力却是越来越低,这是因为随着混凝土面积的减小,混凝土部分的抗剪承载力也在降低,该影响不能忽略.
|
| 图 4 不同空心率下τ-γ曲线 Figure 4 τ-γ curves with different hollow ratios |
|
| 图 5 抗剪承载力随空心率的变化曲线 Figure 5 Variation curve of shear bearing capacity with hollow ratio |
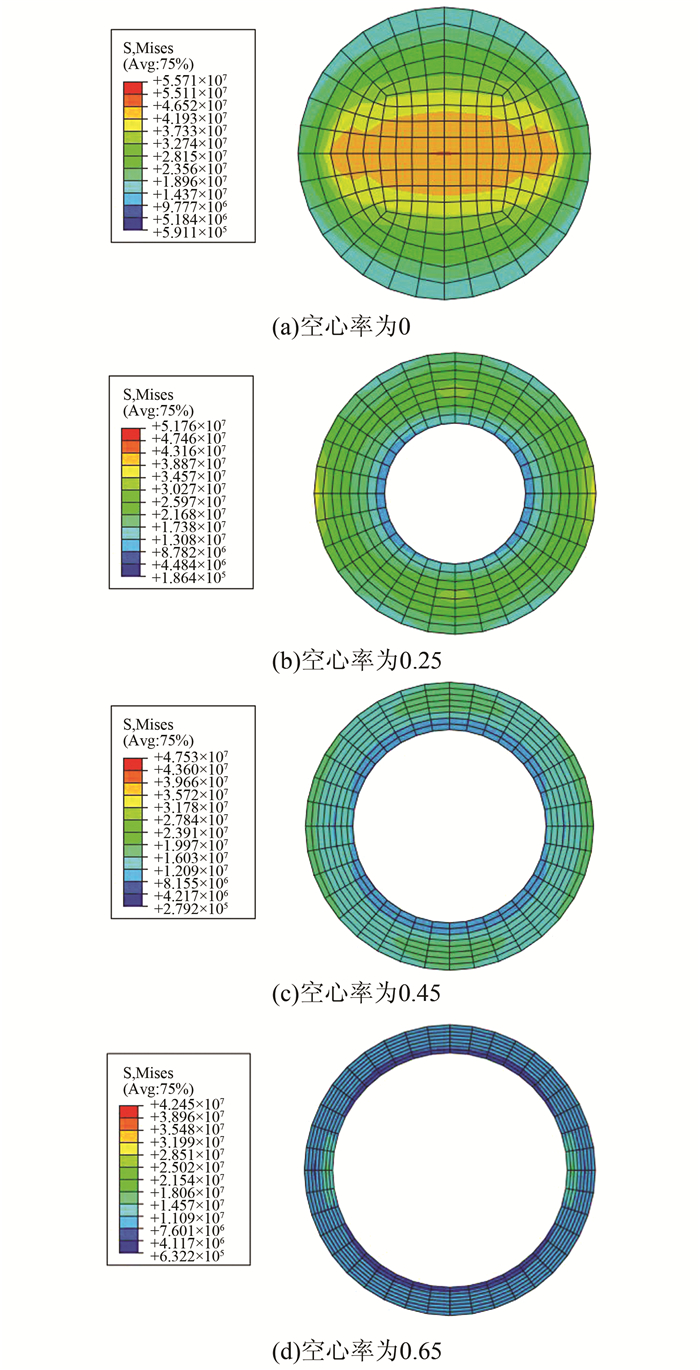
为了进一步分析空心率对混凝土部分抗剪能力的影响,分别提取了不同空心率下的核心混凝土应力分布云图,见图 6.由图 6可以看出,随着空心率的增大,应力分布逐渐均匀.
|
| 图 6 不同空心率下核心混凝土的剪应力云图 Figure 6 Shear stress nephograms of core concrete under different hollow ratios |
根据上述有限元分析的结果可知:钢管混凝土构件的核心混凝土受到钢管的约束,避免或减缓了钢材的局部屈曲,钢管壁的稳定性显著提高,而钢管对核心混凝土起到了支撑作用,因此在构件受到剪切作用时,钢材和混凝土都能保持其稳定性,从而有利于构件抗剪.所以可以将钢管混凝土看作是2种材料组合以后的构件,同时具有2种材料的特性.
目前我国的钢管混凝土设计规范GB50936[17]中给出了实心和空心钢管混凝土抗剪承载力公式:
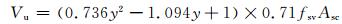 (1)
(1)
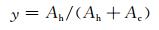 (2)
(2)
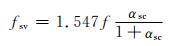 (3)
(3)
该公式基于钟善桐教授的统一理论建立,在实心抗剪承载力的公式的基础上乘上一个考虑空心率的回归系数,公式总体比较复杂,也缺少理论基础.
另一个比较有代表性的是蔡绍怀[21]提出的计算方法,按照将钢管混凝土抗剪承载力分成钢管和混凝土两部分的方法,提出了一种简单的计算方法,但是只适合实心钢管混凝土:
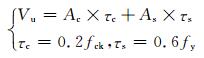 (4)
(4)
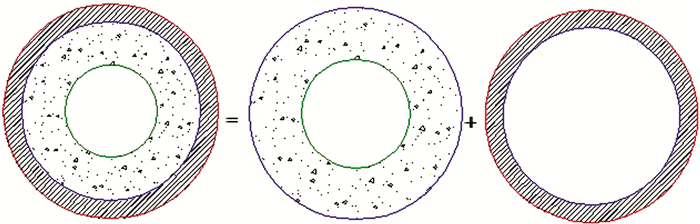
该公式根据极限平衡条件,将钢管和核心混凝土二者的极限受剪承载力予以叠加,有一定的理论基础.因此对于空心钢管混凝土将采用该方法,计算示意图见图 7.
|
| 图 7 空心钢管混凝土抗剪计算方法示意图 Figure 7 Calculation method of shear bearing capacity of hollow concrete-filled steel tube |
在式(4)的基础上,为得出适用于实、空心钢管混凝土的抗剪承载力计算公式,同时考虑到空心率对混凝土应力分布不均匀的影响,将核心混凝土的平均极限受剪强度乘上一个空心率修正系数α,则对于空心钢管混凝土有
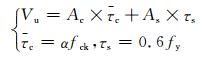 (5)
(5)
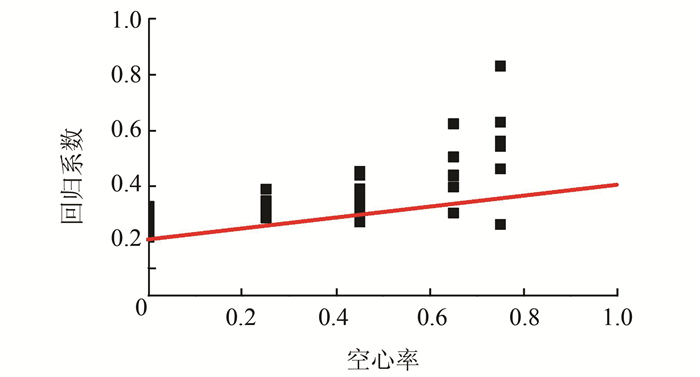
采用上述公式并结合有限元计算结果,最终给出空心率修正系数α随着空心率的变化关系,见图 8.可以得出:空心率修正系数α随空心率的增大而增大.为了简单假定其为线性关系,同时为了保证空心率等于0时,可以退化为实心的公式,在此设α=0.2(1+aψ).
|
| 图 8 回归系数与空心率关系 Figure 8 Relationship between regression coefficient and hollow ratio |
同时,根据作者先前的研究[16],对于实心和空心钢管混凝土的统一抗扭承载力计算公式,其中正好包含有0.2(1+ψ)fckAc+0.6fyAs的部分.同时考虑到混凝土所承担的只是部分剪力,从偏于安全和保证公式形式简单等综合因素考虑取a=1,即α=0.2(1+ψ).最终取实心和空心钢管混凝土的统一的抗剪承载力计算公式为
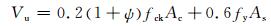 (6)
(6)
式中:ψ为钢管混凝土的空心率,实心时取0;Ac为混凝土截面面积;fck为混凝土轴心抗压强度;As为钢管截面面积;fy为钢材屈服强度.
当空心率为0时为实心混凝土,公式可退化为蔡绍怀提出的计算公式,而且可以和作者先前提出的抗扭承载力公式建立联系,从而形成系统性的结果,关于公式的精度在下节说明.
2.2.2 抗剪承载力计算公式的验证在有限元模拟的基础之上,通过搜集前人所做的钢管混凝土试验的试验数据,对上述公式进行核对.借用了徐春丽等[5]、郭淑丽[6]、吉伯海等[22]和钱稼茹等[23]的试验数据与本文所给出的抗剪承载力计算公式的计算结果进行了比较,其结果见表 2.比值的平均值为1.159 1,方差为0.076 8.从对比的数据不难看出,计算值和试验值的误差不大,在容许范围内,证明了公式的有效性.
| 来源 | 序号 | 编号 | 外径 D/m |
钢管厚度 ts/m |
混凝土厚 度tc/m |
钢管强度 fy/MPa |
混凝土强度 fck/MPa |
抗剪承载力/(MN·m) | 实验值/ 计算值 |
|
| 试验值 | 计算值 | |||||||||
| 徐 春 丽 等 |
1 | S11-C1-1 | 0.160 | 0.005 5 | 0.074 5 | 377.00 | 25.900 | 0.625 0 | 0.693 8 | 0.900 8 |
| 2 | S11-C2-1 | 0.160 | 0.005 5 | 0.074 5 | 377.00 | 32.400 | 0.675 0 | 0.716 5 | 0.942 1 | |
| 3 | S11-C3-1 | 0.160 | 0.005 5 | 0.074 5 | 377.00 | 29.500 | 0.650 0 | 0.706 4 | 0.920 2 | |
| 4 | S21-C1-1 | 0.166 | 0.004 4 | 0.078 6 | 345.00 | 25.900 | 0.515 0 | 0.562 6 | 0.915 3 | |
| 5 | S21-C2-1 | 0.166 | 0.004 4 | 0.078 6 | 345.00 | 32.400 | 0.568 0 | 0.587 9 | 0.966 2 | |
| 6 | S21-C3-1 | 0.166 | 0.004 4 | 0.078 6 | 345.00 | 29.500 | 0.525 0 | 0.576 6 | 0.910 5 | |
| 7 | S31-C1-1 | 0.165 | 0.003 0 | 0.079 5 | 408.00 | 25.900 | 0.375 0 | 0.476 4 | 0.787 2 | |
| 8 | S31-C2-1 | 0.165 | 0.003 0 | 0.079 5 | 408.00 | 32.400 | 0.415 0 | 0.502 2 | 0.826 4 | |
| 9 | S31-C3-1 | 0.165 | 0.003 0 | 0.079 5 | 408.00 | 29.500 | 0.385 0 | 0.490 7 | 0.784 7 | |
| 10 | S11-C1-2 | 0.160 | 0.005 5 | 0.074 5 | 377.00 | 25.900 | 0.728 0 | 0.693 8 | 1.049 3 | |
| 11 | S11-C2-2 | 0.160 | 0.005 5 | 0.074 5 | 377.00 | 32.400 | 0.750 0 | 0.716 5 | 1.046 8 | |
| 12 | S11-C3-2 | 0.160 | 0.005 5 | 0.074 5 | 377.00 | 29.500 | 0.780 0 | 0.706 4 | 1.104 2 | |
| 13 | S21-C1-2 | 0.166 | 0.004 4 | 0.078 6 | 345.00 | 25.900 | 0.630 0 | 0.562 6 | 1.119 7 | |
| 14 | S21-C2-2 | 0.166 | 0.004 4 | 0.078 6 | 345.00 | 32.400 | 0.658 0 | 0.587 9 | 1.119 3 | |
| 15 | S21-C3-2 | 0.166 | 0.004 4 | 0.078 6 | 345.00 | 29.500 | 0.675 0 | 0.576 6 | 1.170 6 | |
| 16 | S31-C1-2 | 0.165 | 0.003 0 | 0.078 0 | 408.00 | 25.900 | 0.480 0 | 0.476 4 | 1.007 6 | |
| 17 | S31-C2-2 | 0.165 | 0.003 0 | 0.078 0 | 408.00 | 32.400 | 0.485 0 | 0.502 2 | 0.965 8 | |
| 18 | S31-C3-2 | 0.165 | 0.005 5 | 0.077 0 | 408.00 | 29.500 | 0.495 0 | 0.490 7 | 1.008 8 | |
| 郭 淑 丽 等 |
1 | C1-1 | 0.12 | 0.002 | 0.058 | 338.00 | 21.346 | 0.222 0 | 0.195 4 | 1.136 3 |
| 2 | C1-2 | 0.12 | 0.002 | 0.058 | 338.00 | 21.346 | 0.253 0 | 0.195 4 | 1.295 0 | |
| 3 | C1-3 | 0.12 | 0.002 | 0.058 | 338.00 | 21.346 | 0.318 0 | 0.195 4 | 1.627 7 | |
| 4 | C1-4 | 0.12 | 0.002 | 0.058 | 338.00 | 21.346 | 0.328 0 | 0.195 4 | 1.678 9 | |
| 5 | C2-1 | 0.12 | 0.002 | 0.058 | 338.00 | 21.346 | 0.366 0 | 0.195 4 | 1.873 4 | |
| 6 | C2-2 | 0.12 | 0.002 | 0.058 | 338.00 | 21.346 | 0.285 0 | 0.195 4 | 1.458 8 | |
| 7 | C2-3 | 0.12 | 0.002 | 0.058 | 338.00 | 21.346 | 0.180 0 | 0.195 4 | 0.921 3 | |
| 8 | C2-4 | 0.12 | 0.002 | 0.058 | 338.00 | 21.346 | 0.170 0 | 0.195 4 | 0.870 1 | |
| 9 | C3-1 | 0.12 | 0.002 | 0.058 | 338.00 | 38.465 | 0.339 0 | 0.231 5 | 1.464 1 | |
| 10 | C4-1 | 0.12 | 0.002 | 0.058 | 415.00 | 21.346 | 0.370 0 | 0.229 6 | 1.611 5 | |
| 吉 伯 海 等 |
1 | S1-C1 | 0.165 | 0.003 | 0.079 5 | 336.00 | 31.490 | 0.456 0 | 0.301 7 | 1.511 2 |
| 2 | S1-C2 | 0.165 | 0.003 | 0.079 5 | 366.00 | 27.135 | 0.462 0 | 0.312 8 | 1.477 1 | |
| 3 | S1-C3 | 0.165 | 0.003 | 0.079 5 | 336.00 | 30.954 | 0.440 0 | 0.300 6 | 1.463 9 | |
| 4 | S2-C1 | 0.165 | 0.004 | 0.078 5 | 315.00 | 31.490 | 0.488 5 | 0.352 8 | 1.384 7 | |
| 钱 稼 茹 等 |
1 | A1 | 0.194 | 0.005 5 | 0.091 5 | 330.00 | 36.180 | 1.002 5 | 0.833 7 | 1.202 5 |
| 2 | B1 | 0.194 | 0.007 5 | 0.089 5 | 422.00 | 36.180 | 1.204 7 | 1.294 0 | 0.931 0 | |
| 3 | A2 | 0.194 | 0.005 5 | 0.091 5 | 330.00 | 47.570 | 1.118 1 | 0.893 5 | 1.251 3 | |
| 4 | B2 | 0.194 | 0.007 5 | 0.089 5 | 422.00 | 47.570 | 1.427 7 | 1.351 3 | 1.056 5 | |
| 5 | A3 | 0.194 | 0.005 5 | 0.091 5 | 330.00 | 56.280 | 1.166 9 | 0.939 3 | 1.242 3 | |
| 6 | B3 | 0.194 | 0.007 5 | 0.089 5 | 422.00 | 56.280 | 1.453 8 | 1.395 1 | 1.042 0 | |
1) 建立了钢管混凝土在纯剪荷载作用下的有限元模型,并基于试验验证了有限元模型的合理性.
2) 分析了空心率对钢管混凝土抗剪承载力和截面应力分布的影响,并结合极限平衡条件提出了实心和空心统一的钢管混凝土抗剪承载力计算公式.
3) 通过与试验结果进行比较分析,证明了抗剪统一公式的有效性,该工作可为钢管混凝土的相关工程设计和规范修订提供参考.
| [1] |
钟善桐.
钢管混凝土结构[M]. 第3版. 北京: 清华大学出版社, 2003.
Zhong Shantong. The Concrete-filled Steel Tubular Structure[M]. Third Edition. Beijing: Tsinghua University press, 2003. |
| [2] |
查晓雄.
空心和实心钢管混凝土结构[M]. 北京: 科学出版社, 2010.
Zha Xiaoxiong. Hollow and Solid Concrete-filled Steel Tubular Structures[M]. Beijing: Science Press, 2010. |
| [3] |
钟善桐.
钢管混凝土统一理论——研究与应用[M]. 北京: 清华大学出版社, 2006.
Zhong Shantong. Unfied Theory of Concrete-filled Steel Tube——Research and Appilacation[M]. Beijing: Tsinghua University Press, 2006. |
| [4] |
王建伟, 王文博. 钢管混凝土柱抗剪承载力计算[J].
工业建筑, 2011(S1): 337–338.
Wang Jianwei, Wang Wenbo. The calculation of shearing resistance of concrete-filled steel tube column[J]. Industrial Construction, 2011(S1): 337–338. |
| [5] |
肖从真, 蔡绍怀, 徐春丽. 钢管混凝土抗剪性能试验研究[J].
土木工程学报, 2005, 38(4): 5–11.
Xiao Congzhen, Cai Shaohuai, Xu Chunli. Experimental study on shear resistance performance of concrete filled steel tube columns[J]. China Civil Engineering Journal, 2005, 38(4): 5–11. |
| [6] |
郭淑丽. 钢管混凝土柱抗剪承载力公式[J].
福建建材, 2011(8): 1–3.
Guo Shuli. The formula of shear bearing capacity of concrete filled steel tubular columns[J]. Fujian Building Materials, 2011(8): 1–3. |
| [7] |
傅中秋, 吉伯海, 余振鹏, 等. 核心混凝土对钢管混凝土受剪性能影响的试验[J].
交通科学与工程, 2013(4): 40–46.
Fu Zhongqiu, Ji Bohai, Yu Zhenpeng, et al. Experimental study on the influence of core concrete on concrete filled steel tube shear performance[J]. Traffic Science and Engineering, 2013(4): 40–46. |
| [8] | Jones M H, Wang Y C. Shear and bending behaviour of fin plate connection to concrete filled rectangular steel tubular column-development of a simplified calculation method[J]. Journal of Constructional Steel Research, 2011, 67(3): 348–359. DOI:10.1016/j.jcsr.2010.10.006 |
| [9] |
吴波, 许喆, 刘琼祥, 等. 薄壁钢管再生混合柱的抗剪性能试验[J].
土木工程学报, 2010(9): 12–21.
Wu bo, Xu Zhe, Liu Qiongxiang, et al. Test of the shear behavior of thin-wall steel tubular columns filled with demolished concrete segments/lumps[J]. China Civil Engineering Journal, 2010(9): 12–21. |
| [10] | Han L H, Tao Z, Yao G H. Behaviour of concrete-filled steel tubular members subjected to shear and constant axial compression[J]. Thin-Walled Structures, 2008, 46(7-9): 765–780. DOI:10.1016/j.tws.2008.01.026 |
| [11] |
蔡健, 梁伟盛, 林辉. 方钢管混凝土柱抗剪性能试验研究[J].
深圳大学学报(理工版), 2012, 29(3): 189–194.
Cai Jian, Liang Weisheng, Lin Hui. Experimental study on shear resistance performance of concrete filled square steel tubular columns[J]. Journal of Shenzhen University(Natural Sciences & Engineering), 2012, 29(3): 189–194. |
| [12] |
黎玉婷, 查晓雄. 空、实心钢管混凝土构件复杂受力下统一公式——压-弯-剪-扭相关方程[J].
工业建筑, 2011, 41(6): 9–14.
Li Yuting, Zha Xiaoxiong. Unified equations for solid and hollow concrete-filled tube columns under complex stress:correlation equations[J]. Industrial Construction, 2011, 41(6): 9–14. |
| [13] | Yu Min, Zha Xiaoxiong, Ye Jianqiao, et al. A unified formulation for hollow and solid concrete-filled steel tube columns under axial compression[J]. Engineering Structures, 2010, 32(4): 1046–1053. DOI:10.1016/j.engstruct.2009.12.031 |
| [14] | Yu Min, Zha Xiaoxiong, Ye Jianqiao, et al. A unified formulation for circle and polygon concrete-filled steel tube columns under axial compression[J]. Engineering Structures, 2013, 49: 1–10. DOI:10.1016/j.engstruct.2012.10.018 |
| [15] | Yu Min, Zha Xiaoxiong, Ye Jianqiao, et al. A unified method for calculating fire resistance of solid and hollow concrete-filled steel tube columns based on average temperature[J]. Engineering Structures, 2014, 71: 12–22. DOI:10.1016/j.engstruct.2014.03.038 |
| [16] |
余敏, 谢佳新, 石正浩. 实、空心钢管混凝土抗扭承载力统一计算方法[J].
钢结构, 2016(9): 20–24.
Yu min, Xie Jiaxin, Shi Zhenghao. A unified formula for hollow and solid concrete-filled steel tube columns under torsion[J]. Steel Structure, 2016(9): 20–24. |
| [17] |
中华人民共和国住房和城乡建设部. GB 50936-2014钢管混凝土结构技术规范[S]. 北京: 中国建筑工业出版社, 2014.
Ministry of Housing and Urban-Rural Development of the People`s Republic of China. GB 50936-2014 Technical Code for Concrete Filled-steel Tubular Structures[S]. Beijing: China Architecture & Building Press, 2014. |
| [18] |
中华人民共和国住房和城乡建设部. GB 50010-2010混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2011.
Ministry of Housing and Urban-Rural Development of the People's Republic of China. GB 50010-2010 Code for Design of Concrete Structures [S]. Beijing: China Architecture & Building Press, 2011. |
| [19] |
徐春丽. 钢管混凝土柱抗剪承载力试验研究[D]. 青岛: 山东科技大学, 2004.
Xu Chunli. Research of test on the shear resistance of concrete-filled steel tube column[D]. Qingdao: Shandong University of Science and Technology, 2004. http://d.wanfangdata.com.cn/Thesis/Y671322 |
| [20] |
韩林海.
钢管混凝土结构——理论与实践[M]. 第2版. 北京: 科学出版, 2007.
Han Linhai. Concrete-Filled Steel Tubular Structures——Theory and Application[M]. 2nd Edtion. Beijing: Science Press, 2007. |
| [21] |
蔡绍怀.
现代钢管混凝土结构[M]. 北京: 人民交通出版社, 2007.
Cai Shaohuai. Modern Steel Tube Confined Concrete Structure[M]. Beijing: China Communication Press, 2007. |
| [22] |
吉伯海, 傅中秋, 瞿涛, 等. 钢管轻集料混凝土抗剪承载力试验研究[J].
土木工程学报, 2011(12): 25–33.
Ji Bohai, Fu Zhongqiu, Qu Tao, et al. Experimental study of the shear strength of lightweight aggregate concrete filled steel tube[J]. China Civil Engineering Journal, 2011(12): 25–33. |
| [23] |
钱稼茹, 崔瑶, 方小丹. 钢管混凝土柱受剪承载力试验[J].
土木工程学报, 2007(5): 1–9.
Qian Jiaru, Cui Yao, Fang Xiaodan. Shear strength tests of concrete filled steel tube columns[J]. China Civil Engineering Journal, 2007(5): 1–9. |
 2017, Vol. 50
2017, Vol. 50




