文章信息
- 魏文礼, 李小欢, 洪云飞, 刘玉玲
- WEI Wenli, LI Xiaohuan, HONG Yunfei, LIU Yuling
- 三角形波浪底板消力池自由水跃水力特性的数值模拟
- Numerical simulation study of hydraulic characteristics of free hydraulic jump on triangular corrugated beds of stilling basin
- 武汉大学学报(工学版), 2017, 50(2): 207-212, 227
- Engineering Journal of Wuhan University, 2017, 50(2): 207-212, 227
- http://dx.doi.org/10.14188/j.1671-8844.2017-02-008
-
文章历史
- 收稿日期: 2016-04-20
在水利工程泄水建筑物的消能中底流消能是最常用的方式之一,为减少工程造价及提高消能效率,应尽量使消力池长度缩短,为加强紊动混掺作用可在池内设置各种消能工,例如把光滑底板改成三角形底板.
在20世纪70年代,Rajaratnam等[1]、Leutheusser等[2]通过试验研究了波浪形底板消力池的水跃长度和共轭水深.研究结果表明:光滑底板上水跃的长度明显大于波浪形底板上的长度,同时跃后水深大于波浪形底板的水深,有明显的消能效果.Ead等[3-5]研究了波浪形底板消力池,结果表明:跃后水深及水跃长度比光滑底板均明显减小.Carollo[6]等研究了粗糙底板上水跃的水力特性,他们得出结论:水跃长度及跃后水深在布设粗糙底板时均有所减小,底板粗糙度和弗劳德数与水跃长度有关.Pagliara等[7]对不同介质的粗糙底板上的水跃进行研究,通过在常规水跃方程上添加校正系数,来表示统一和不统一的粗糙底板上的水跃.Bejestan等[8]研究了菱形粗糙底板对水跃的影响,结果表明这种形状的底板跃后水深比光滑底板减少了24%,水跃长度减少了40%.Abbaspour等[9]对波状床面上的水跃进行研究,得出:与光滑底板上的水跃相比,跃后水深减小了20%;弗劳德数对跃后水深和水跃长度有较大的影响.Elsebaie等[10]测量了5种形状(正弦、三角形、矩形和2种坡脚的梯形)波浪底板水跃的相关参数,并进行分析研究,研究结果表明,各形状的波浪底板跃后水深基本都比光滑底板跃后水深小50%以上,而且波浪底板表面的切应力比光滑底板大15倍之多.程香菊等[11]采用RNG k-ε紊流模型和VOF方法追踪自由水面,对波浪形底板上水跃的形成过程进行了数值模拟,模拟结果与试验数据吻合较好,表明所用数值模型能够较好地模拟水跃水流.戴会超等[12]采用k-ε紊流模型对淹没水跃进行了模拟,得出:自由液面高度及雷诺应力和文献[13]的试验结果吻合较好,表明弗劳德数的增加将会使紊动动能和紊动能耗散率及水跃长度有所增加,选取适当的弗劳德数有利于减小跃后水深和水跃长度.张春财等[14]对光滑底板上的水跃进行了数值模拟,上下游自由液面的捕捉采用VOF法,得出:弗劳德数较低时,随弗劳德数的减小水跃长度、断面平均流速、跃后水深及底面压强都有所减小,紊动能、耗散率和水跃消能率变化不大.张志昌等[15]据已有文献应用N-S方程推导了波浪形消力池流速及水跃长度的计算公式.
综上,到目前国内外对波浪形底板消力池的模型实验研究较多,但对三角形底板消力池研究的文献却很少.本文根据实验资料,采用数值模拟方法,研究了三角形波浪底板消力池上自由水跃的流场、速度场、横断面最大流的速衰减规律、紊动能、耗散率的分布规律等.
1 数学模型 1.1 湍流模型以本文选用RNG k-ε湍流模型,其控制方程[16]如下.
连续方程:
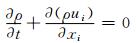 (1)
(1)
动量方程:
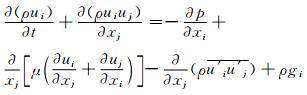 (2)
(2)
雷诺应力方程:
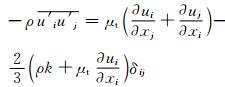 (3)
(3)
式中:t是时间;xi是沿i方向的空间坐标(i=1、2、3);ui是沿i方向的时均速度分量;μt为湍动黏度;μ和ρ分别为流体分子黏性系数和密度;p为压强;gi为i方向的重力加速度;k为湍动动能;δij是Kronecker函数:δij=1(i=j),δij=0(i≠j).
k和ε的方程分别为
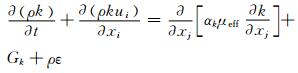 (4)
(4)
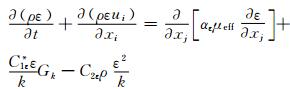 (5)
(5)
其中,μeff=μ+μt,μt=ρCμk2/ε,Cμ=0.084 5,αk=αε=1.39,C1ε*=C1ε-η(1-η/η0)/(1+βη3),C1ε=1.42,C2ε=1.68,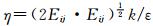
以上方程组构成了求解流场分布规律的封闭方程组,根据实际工况施加相应的边界条件后,构成该方程组的定解问题.
1.2 VOF方法VOF方法[17]常用来处理自由液面,通过对流体和网格体积比函数Fw(xi, t)的研究来确定自由面,Fw(xi, t)=1,则表示该单元被液体充满;当Fw(xi, t)=0,则表示它是一个空单元;若Fw(xi, t)∈(0, 1),则表示该单元部分充满液体.
描述Fw的控制方程为
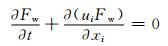 (6)
(6)
引入VOF后,ρ、μ是Fw(xi, t)的函数,其表达式为
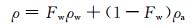 (7)
(7)
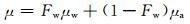 (8)
(8)
式中:ρa为空气密度;ρw为水的密度;μw为水分子粘性系数;μa为空气分子粘性系数.
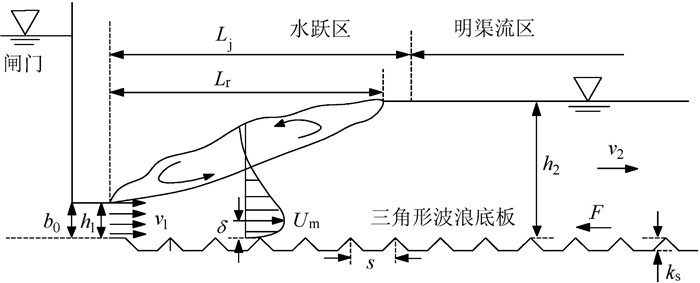
2 数值模拟 2.1 计算区域及实验参数三角形波浪底板消力池自由水跃的纵断面如图 1所示,闸门的上游底板与三角形底板上波峰的位置高程相同.
|
| 图 1 三角形波浪底板上自由水跃示意图 Figure 1 Schematic view of free hydraulic jump on triangular corrugated beds |
图 1中,h1为跃前断面的平均水深;h2为跃后断面的平均水深;b0为闸门开度;Lr为水跃的漩滚长度;Lj为水跃长度;s为波长;ks为粗糙高度;v1为跃前断面的平均流速;v2为跃后断面的平均流速横;F为床面摩阻力;Um为横断面最大流速;δ为边界层厚度.
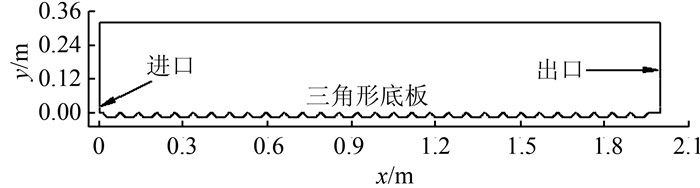
根据文献[10]的实验资料:试验水槽的长宽高分别为9、0.295、0.32 m,横断面为三角形的条状塑料板等间距安装在水槽底部,形成三角形波浪底板,波浪底板沿水流方向的波长是6.5 cm,从波峰到波谷的高度是1.8 cm,三角形横断面的2个边角坡度都是45°.水槽末尾用闸门控制水槽尾水深,使水槽内形成自由水跃.经过适当简化,建立波浪形底板消力池的二维数值模型,如图 2所示.
|
| 图 2 二维计算区域 Figure 2 Two-dirnensional computational region |
本文对6种工况的三角形波浪底板消力池上的自由水跃进行了数值模拟.所有工况底板的波长和粗糙度都相同,且等于模型试验中的尺寸:s=6.5 cm,ks= 1.8 cm,闸孔开度也相同,h1=b0=2.5 cm.各工况的相关参数如表 1所示.
| 工况 | v1/(m·s-1) | Fr1 | h2/cm | Lj/m |
| A | 2.04 | 4.1 | 8.0 | 0.17 |
| B | 2.48 | 5.0 | 9.2 | 0.23 |
| C | 2.84 | 5.7 | 10.5 | 0.35 |
| D | 3.17 | 6.4 | 12.1 | 0.40 |
| E | 3.46 | 7.0 | 14.1 | 0.43 |
| F | 3.73 | 7.5 | 14.7 | 0.50 |
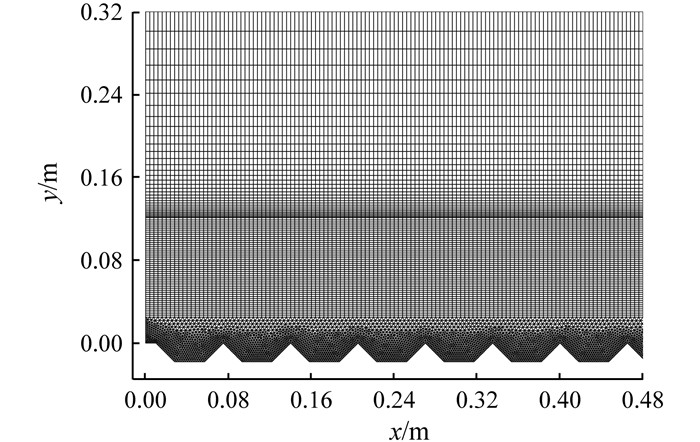
采用GAMBIT软件建模和进行网格划分.对于水跃流场,由于流场速度高、变化快,为了提高精度,同时也由于描述自由表面的需要,整体采用结构化网格进行划分:在三角形底板表面附近采用三角形网格,在水体区采用等大小的矩形网格,水面附近采用渐变网格,计算区域网格如图 3所示.
|
| 图 3 二维计算区域局部网格 Figure 3 Partial computational mesh for two-dimensional region |
进口边界和出口边界分别为速度进口和压力出口,顶面与空气接触,采用压力进口.设工作压强为101 325 Pa,相对压强为0.闸门、边壁和底板为固体壁面,使用标准壁面函数法确定.
使用VOF法捕捉自由液面的,气液两相流时均方程采用RNG湍流模型封闭,采用有限体积法离散控制方程,采用PISO算法求解速度与压力耦合方程.时间步长设为0.000 2 s,计算收敛时进出口流量差小于0.01 m3/s.
2.4 结果分析和讨论 2.4.1 模型验证把模拟计算的水面线与实测值进行比较,结果如图 4所示.从图中看出,在水跃末端工况B、D、E、F的模拟计算值比实测值稍微偏高;在明渠流区工况D、F的模拟计算值比实测值略高,这可能是在实验过程中,由于水面波动引起的测量误差造成的.从整体比较看,模拟计算的水面线与实测值吻合较好,证明了数值模拟结果的正确性.
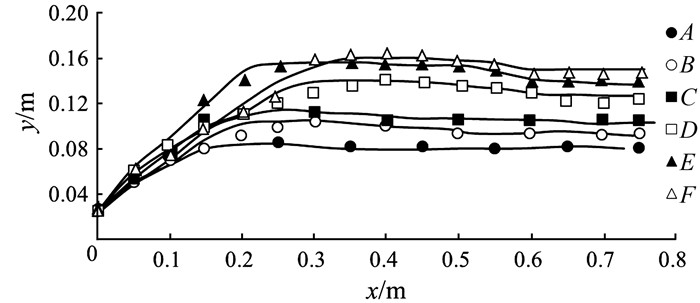
|
| 图 4 模拟计算的水面线与实测值的比较(散点代表实验值,实线代表对应的模拟计算值) Figure 4 Comparisons of simulation water surface profiles with experimental values(splashes represent for experimental values, solid lines represent for simulation results corresponding) |
以工况D为例,流线分布如图 5所示,流线密的地方代表流速大,流线稀疏的地方表示流速小[18].从流线图看出,高速水流从闸孔流出后,水流由急流状态过度到缓流状态,形成水跃,在水跃区水深沿水流方向逐渐增大,水流在水跃区上部作剧烈漩滚,漩涡方向为逆时针,在漩滚下方形成急剧扩散的主流,大量空气被表面漩涡卷入,主流与漩滚不断发生能量交换,流体质点之间发生频繁的碰撞,导致该区域产生较大的能量损失,该区域即为水跃的主要消能区.
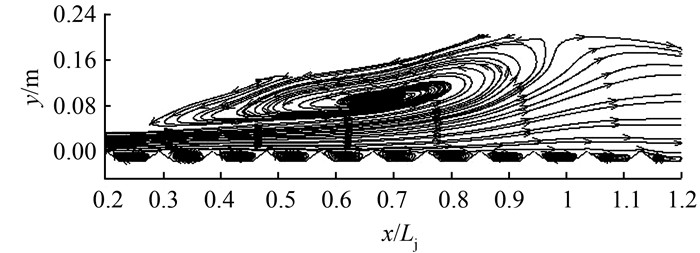
|
| 图 5 D工况自由水跃的流线分布图 Figure 5 Streamline distributions of free hydraulic jump under D condition |
另外,从图 5中可以看出,三角形底板表面附近产生有小漩涡.漩涡分布在底板的凹陷处,沿顺时针方向旋转,并且沿程逐渐减小.D工况底板表面附近局部漩涡放大后如图 6所示,其他各工况类似,产生这些小漩涡的原因[19],是由于水的粘性和边壁的摩擦,引起流速不均匀分布,相邻流层间的液体流速不同,导致流层间产生内摩擦力.靠近底板的水流,流层上面是急速扩散的主流,加于它的切应力方向是顺流方向的,流层下面是底板,加之切应力方向与流向相反.因此流层所受的总切应力,构成力矩,使流层顺时针方向旋转.主流沿程流速不断减小,从而施加于该流层上方顺流方向的切应力也沿程减小,故漩涡的尺寸沿程减小.底板附近的漩涡使得流场紊动加剧,因此消能率相对于光滑底板更高.
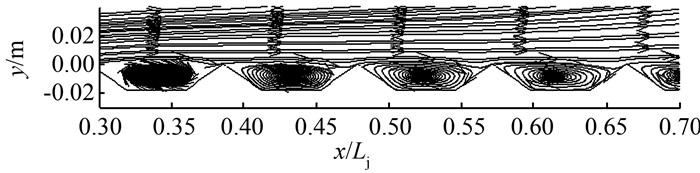
|
| 图 6 D工况底板表面漩涡局部放大图 Figure 6 Partial amplification of vortexes on beds under D condition |
图 7显示工况E横断面上的流速矢量沿程分布.由图可知,流速在水跃区各断面从底板开始逐渐增大到最大值Um,然后逐渐减小到零,再往上流速变为负值,边界层δ厚度为不同断面上流速最大值Um处到底板的间距,从图 7中可以看出,水跃区各横断面上最大流速位置到底板的距离逐渐增大,即边界层δ厚度沿程增大,到达x/Lj=1.2附近时,δ达到最大.到明渠流区,横断面上流速分布规律为:从底板开始逐渐增大,到水面附近达到最大值,流速分布沿程不再变化,且没有负值.

|
| 图 7 E工况横断面流速矢量图 Figure 7 Velocity vectogram of transverse section under E condition |
图 8显示工况E各横断面平均流速和最大流速沿程分布,从图中可知,在水跃区横断面平均流速和最大流速都沿程逐渐减小,但沿流向断面平均流速与最大流速之差先增大后变小,在x/Lj=0.4附近差值达到最大.这是由于在水跃区横断面平均流速沿程开始下降的快然后下降的慢,而横断面最大流速开始下降的较慢然后变快的缘故.到x/Lj=1后,即明渠流区,沿流向最大流速与断面平均流速变化不明显.
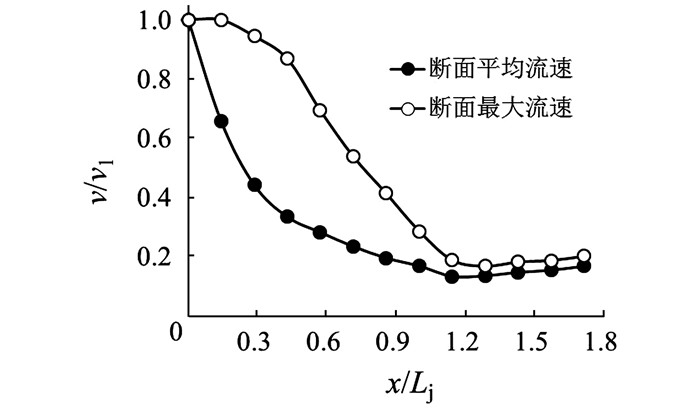
|
| 图 8 E工况横断面平均流速和最大流速沿程分布 Figure 8 Mean velocity and maximum velocity distribution of different transverse section under E condition |
不同工况横断面最大速度沿程衰减曲线如图 9所示.从图中看到,Fr1越小,横断面最大流速衰减的距离越短,反之衰减的距离越长.但是不同Fr1下横断面最大流速沿程衰减规律相似:从闸门开始,从v1逐渐减小到一个最小值,然后沿程几乎不变.到x=0.9 m之后,各工况横断面最大流速都达到稳定值,沿程几乎无变化.
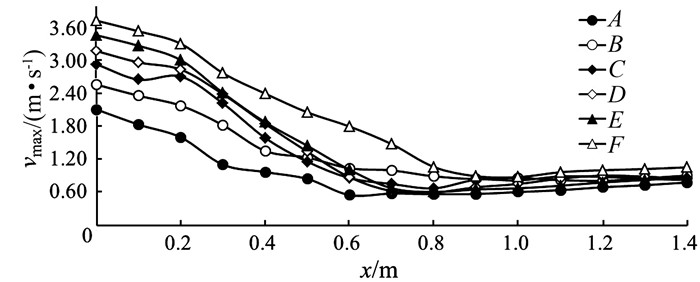
|
| 图 9 不同工况横断面最大流速沿程衰减图 Figure 9 The decay of the maximum velocity with the longitudinal distance under different conditions |
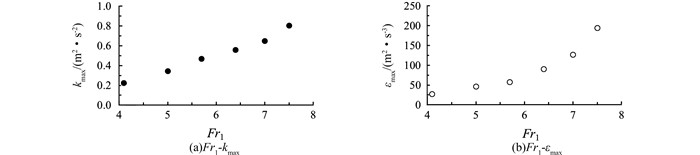
由图 10可知,紊动动能k最大值发生在闸门出口附近区域.从图 11可见,耗散率ε主要分布在水跃区前部和三角形底板波峰附近,可见三角形底板增加了流场的耗散率,从而提高了水跃的消能率.由图 12(a)可知,紊动能k最大值与Fr1呈线性关系,当Fr1由4.1增加到7.0时,k由0.222 m2/s2增加到0.647 m2/s2.此外,在水跃漩滚区紊动动能k变化较大,在明渠中紊动动能k的值变化较小.
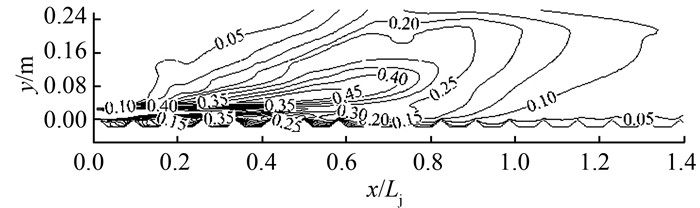
|
| 图 10 工况E水跃区及明渠流区紊动能k的等值线分布(单位:m2/s2) Figure 10 Contour map of k in hydraulic jump and channel flow region under E condition (unit: m2/s2) |
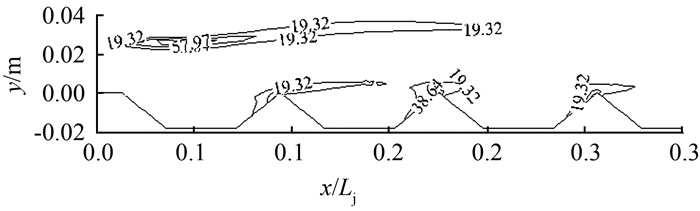
|
| 图 11 工况E水跃区耗散率ε的等值线分布(单位:m2/s3) Figure 11 Contour map of ε in hydraulic jump region under E condition (unit: m2/s3) |
|
| 图 12 紊动能最大值kmax和耗散率最大值εmax与Fr1的关系 Figure 12 Relation between kmaxand εmax with Fr1 |
由图 12(b)可知,耗散率随Fr1的增大而增大,当Fr1由4.1增加到7.5时,紊动耗散率由26.85 m2/s3增加到194.23 m2/s3,变化较大,当Fr1增大时紊动能耗散率也增大.紊动能耗散率ε在闸门附近变化最大.
2.4.5 消能率的变化理论消能率η的计算公式[14]:
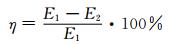 (9)
(9)
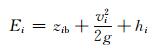 (10)
(10)
式中:Ei表示断面单位重量液体所具有的总能量,i=1, 2,分别表示跃前及跃后断面;zib为渠道底面标高;vi为断面平均流速;hi为断面平均水深.
实际消能率的计算公式:
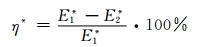 (11)
(11)
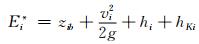 (12)
(12)
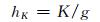 (13)
(13)
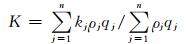 (14)
(14)
式中:Ei*为考虑紊动能后单位水体的平均能量;hK为断面平均紊动能水头;K为断面平均紊动能;kj为流体质点的紊动动能; ρj为液体密度;qj为各质点对应的单宽净流量.
表 2为不同工况下的消能率,由表 2可知,实际消能率与理论消能率均随Fr1的增加而增加;且Fr1大于4.1时消能率都超过了50%,当Fr1=7.5时,实际效能率达到73.28%,表明三角形波浪底板上自由水跃的消能率很高,可考虑应用到实际工程中.比较理论消能率和实际消能率,结果表明考虑紊动能的实际消能率比理论值稍微偏小,η与η*的差值为0.31%~0.65%,可以忽略不计.
| 工况 | Fr1 | η | η* | η-η* |
| A | 4.1 | 51.19 | 50.53 | 0.65 |
| B | 5.0 | 58.11 | 57.62 | 0.49 |
| C | 5.7 | 65.07 | 64.67 | 0.31 |
| D | 6.4 | 68.02 | 67.64 | 0.37 |
| E | 7.0 | 71.13 | 70.64 | 0.48 |
| F | 7.5 | 73.70 | 73.28 | 0.42 |
本文采用数值模拟的方法研究了三角形波浪底板消力池上的自由水跃,模拟计算的水面线与实测值比较,二者吻合较好,表明所选数值模型可较好模拟水跃现象.
此外,研究发现:
1) 波浪形底板表面凹陷处有漩涡产生,漩涡沿顺时针方向旋转,且漩涡尺寸沿程逐渐减小.
2) 在水跃区,沿流向断面平均流速与最大流速的差值先增大后减小,并且不同Fr1时横断面最大流速沿程衰减规律相似.
3) 三角形底板能增加流场的耗散率,并且紊动能和耗散率的最大值随进口断面弗劳德数的增大而增大.
4) 理论消能率和实际消能率均随进口断面弗劳德数的增加而增大.
| [1] | Rajaratnam N. Hydraulic jumps on rough beds[J]. Transactions of the Institution of Chemical Engineers, Canada, 1968, 11(A-2): 1–8. |
| [2] | Leutheusser H J, Schiller E J. Hydraulic jump in a rough channel[J]. Water Power & Dam Construction, 1975(5): 25–34. |
| [3] | Ead S A, Rajaratnam N, Katopodis C. Turbulent open-channel flow in circular corrugated culverts[J]. Journal of Hydraulic Engineering, 2000, 126(10): 750–757. DOI:10.1061/(ASCE)0733-9429(2000)126:10(750) |
| [4] | Ead S A, Rajaratnam N. Hydraulic jumps on corrugated beds[J]. Journal of Hydraulic Engneering, 2002, 128(7): 656–663. DOI:10.1061/(ASCE)0733-9429(2002)128:7(656) |
| [5] | Ead S A, Rajaratnam N. Plane turbulent wall jets on rough boundaries with limited tailwater[J]. Journal of Engineering Mechanics, 2004, 130(10): 1245–1250. DOI:10.1061/(ASCE)0733-9399(2004)130:10(1245) |
| [6] | Carollo F G, Ferro V, Pampalone V. Hydraulic jumps on rough beds[J]. Journal of Hydraulic Engineering, 2007, 133(9): 989–999. DOI:10.1061/(ASCE)0733-9429(2007)133:9(989) |
| [7] | Pagliara S, Lotti I, Palermo M. Hydraulic jump on rough bed of stream rehabilitation structures[J]. Journal of Hydro-environment Research, 2008, 2(1): 29–38. DOI:10.1016/j.jher.2008.06.001 |
| [8] | Bejestan M S, Neisi K. A new roughened bed hydraulic jump stilling basin[J]. Asian Journal of Applied Sciences, 2009, 2(5): 436–445. DOI:10.3923/ajaps.2009.436.445 |
| [9] | Abbaspour A, Dalir H A, Farsadizadeh D, et al. Effect of sinusoidal corrugated bed on hydraulic jump characteristics[J]. Journal of Hydro-environment Research, 2009, 3(2): 109–117. DOI:10.1016/j.jher.2009.05.003 |
| [10] | Elsebaie I H, Shabayek S. Formation of hydraulic jumps on corrugated beds[J]. International Journal of Civil & Environmental Engineering, 2010, 10(1): 37–47. |
| [11] |
程香菊, 陈永灿. 波浪形底板上水跃的数值模拟[J].
水利学报, 2005, 36(10): 1252–1257.
Cheng Xiangju, Chen Yongcan. Numerical simulation of hydraulic jumps on corrugated beds[J]. Journal of Hydraulic Engineering, 2005, 36(10): 1252–1257. DOI:10.3321/j.issn:0559-9350.2005.10.020 |
| [12] |
戴会超, 王玲玲. 淹没水跃的数值模拟[J].
水科学进展, 2004, 15(2): 184–188.
Dai Huichao, Wang Lingling. Refined simulation of submerged jump[J]. Advances in Water Science, 2004, 15(2): 184–188. |
| [13] | Long D, Stefller P M, Rajaratnam N. LDA study of flow structure in submerged hydraulic jumps[J]. Journal of Hydraulic Research, 1990, 28(4): 437–460. DOI:10.1080/00221689009499059 |
| [14] |
张春财, 杜宇. 低佛氏数水跃紊流数值模拟研究[J].
西北农林科技大学学报(自然科学版), 2012, 40(1): 227–234.
Zhang Chuncai, Du Yu. Numerical simulation study on turbulence of hydraulic jump with low Froude number[J]. Journal of Northwest A&F University(Natural Science Edition), 2012, 40(1): 227–234. |
| [15] |
张志昌, 傅铭焕, 赵莹, 等. 波浪形底板消力池自由水跃特性的探讨[J].
应用力学学报, 2013, 30(6): 870–875.
Zhang Zhichang, Fu Minghuan, Zhao Ying, et al. Study on properties of free hydraulic jump on corrugated beds of stilling basin[J]. Chinese Journal of Applied Mechanics, 2013, 30(6): 870–875. DOI:10.11776/cjam.30.06.D064 |
| [16] |
魏文礼, 戴会超.
紊流模型理论及工程应用[M]. 西安: 陕西科学技术出版社, 2006: 75-77.
Wei Wenli, Dai Huichao. Turbulence Model Theory and Engineering Applications[M]. Xi'an: Shaanxi Science and Technology Press, 2006: 75-77. |
| [17] | Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201–225. DOI:10.1016/0021-9991(81)90145-5 |
| [18] | Long D, Stefller P M, Rajaratnam N. LDA study of flow structure in submerged hydraulic jumps[J]. Journal of Hydraulic Research, 1990, 28(4): 437–460. DOI:10.1080/00221689009499059 |
| [19] |
吴持恭.
水力学[M]. 第4版. 北京: 高等教育出版社, 2008: 127-131.
Wu Chigong. Hydraulics[M]. 4th Edition. Beijing: Higher Education Press, 2008: 127-131. |
 2017, Vol. 50
2017, Vol. 50



