武汉大学学报(工学版)   2016, Vol. 49 Issue (2): 161-167

文章信息

林琳, 史良胜, 宋雪航
LIN Lin, SHI Liangsheng, SONG Xuehang
地下水参数反演的确定性集合卡尔曼滤波方法
A deterministic ensemble Kalman filter method for inversing hydrogeological parameters
武汉大学学报(工学版), 2016, 49(2): 161-167
Engineering Journal of Wuhan University, 2016, 49(2): 161-167
http://dx.doi.org/10.14188/j.1671-8844.2016-02-001

文章历史

收稿日期: 2015-08-18
 Abstract              PDF               Figures               Tables
引用本文 0
林琳, 史良胜, 宋雪航. 地下水参数反演的确定性集合卡尔曼滤波方法[J]. 武汉大学学报(工学版), 2016, 49(2): 161-167.
LIN Lin, SHI Liangsheng, SONG Xuehang. A deterministic ensemble Kalman filter method for inversing hydrogeological parameters[J]. Engineering Journal of Wuhan University, 2016, 49(2): 161-167.
地下水参数反演的确定性集合卡尔曼滤波方法
林琳, 史良胜, 宋雪航     
武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072
收稿日期: 2015-08-18
作者简介: 林琳（1981-），女，博士，主要从事土壤水和地下水运移研究，E-mail:linlin.wh@whu.edu.cn.
基金项目: 国家自然科学基金资助项目(编号：51279141,51479144).
摘要: 由于地下水流动的发生环境通常非常复杂，通过稀少的钻孔资料难以对含水层特征进行准确的描述，而数据同化技术可以利用地下水位等动态数据反演出含水层的特征.为减小大尺度问题的抽样误差，提出了以确定性抽样技术为基础的卡尔曼滤波方法，讨论了确定性卡尔曼滤波方法在强烈非均匀介质和大尺度问题中的应用效果.研究结果表明：确定性卡尔曼滤波方法生成了唯一的样本集合，避免了传统集合卡尔曼滤波方法预测结果的不确定性；该方法能够缓解小样本条件下的系统方差快速衰减现象，并在强烈非均质介质中表现出良好的计算性能；结合局部化技术，确定性集合卡尔曼滤波方法能够很好地解决大尺度地下水系统的参数反演问题.
关键词： 地下水     数据同化     卡尔曼滤波     抽样    
A deterministic ensemble Kalman filter method for inversing hydrogeological parameters
LIN Lin, SHI Liangsheng, SONG Xuehang     
State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
Abstract: he circumstance of groundwater flow is very complex; and the sparse borehole data can not provide a detailed description to aquifer properties. Data assimilation technique is commonly used to infer the properties according to dynamic observation data such as piezometric head. In this study, the ensemble Kalman filter method based on deterministic sampling technique is proposed to reduce the sampling error. The ability of deterministic ensemble Kalman filter is discussed for strongly heterogeneous porous media and large-scale groundwater problem. The results show that deterministic ensemble Kalman filter method generates unique sample ensemble; so it avoids the estimation uncertainty that traditional enesemble Kalman filter suffers. The proposed method alleviates the rapid decrease of system variance when the sample size is not sufficiently large. It is able to obtain satisfactory hydraulic conductivity with few realizations even for strongly heterogeneous porous media. By combining with localization technique, this method can efficiently deal with the inverse modeling in large-scale application.
Key words: groundwater     data assimilation     Kalman filter     sampling    

地下水的许多参数需要高成本的钻孔实验来获得，由于空间变异性的存在，很难通过稀疏的钻孔数据对含水层特性进行准确的描述，因此参与数值模拟的参数通常具有一定的不确定性.在地下水系统中，观测井的压力水头和污染物浓度等信息较易获得；观测井的数量虽然有限，但我们可通过持续的观测来获得水头和浓度的动态变化过程.许多研究试图利用这些动态的数据并结合静态数据(即含水层特性的钻孔数据或其他取样数据)来进行反演运算和条件模拟.Franssen等[1]的研究表明，通过浓度的观测值可以准确地反演出含水层的渗透系数并改进水流和溶质运移的预测.史良胜等[2]以KLPC算法为基础，分析了降雨观测值对水头、流速和水动力弥散系数的影响；史良胜等[3]进一步讨论了在同时具有边界条件、补给和渗透系数等观测值时地下水的流动状态.以上文献均采用反演运算和条件模拟等方法来预测观测条件下的地下水流和污染物运移过程.数据同化方法本质上属于条件模拟的一种，即以具有一定误差的观测资料作为模拟的约束条件进行条件模拟，这样可以减少地下水系统的不确定性.该方法与传统的反演运算和条件模拟的区别在于前者根据实时的观测来实时地更新对地下水系统的描述.数据同化可定义为：在每个分析周期(即观测周期，水位的观测通常以旬为周期)，将系统状态当前的观测值(可以是水头的观测值、溶质浓度、流速、降雨、蒸发等)和模型预测结果相结合，为当前状态提供一个“最优”估计.该估计过程实际上在平衡观测值和预测值的不确定性，而估计的结果将被作为最新的系统状态用于下个分析周期的运算.

数据同化方法特别是集合卡尔曼滤波方法目前在天气预报、石油工程和海洋动力学等多个学科得到了广泛的应用[4-6].集合卡尔曼滤波方法是一种基于贝叶斯理论的顺序性Monte Carlo方法，该方法通过一定数量的样本来近似系统状态的统计矩.在实际应用中特别是大尺度的问题中，采用的样本数与系统的自由度相比通常非常少，而过少的样本可能会导致所谓的方差低估现象.方差低估现象是指随着同化步的增加，当样本数远小于系统的自由度时，分析协方差(数据同化之前的协方差函数)的质量会逐渐恶化，且由样本估计到的方差将逐渐被低估[7].理论上，这种方差低估现象在样本数足够多的时候可以消失，但非线性问题高昂的求解成本决定了样本数通常仅为数十个或上百个.为克服因样本不足而导致的方差低估现象，常规的解决方案包括协方差膨胀技术[8, 9]和样本选择技术[10, 11]，其中前者通过人为地放大协方差以抵消方差的低估；后者通过选择特定的样本来更加精确地逼近理论条件下的协方差矩阵.

本文提出了一种基于新的样本选择技术的数据同化方法，并将其拓展至地下水问题，重点探讨了在强烈非均匀介质中该方法的应用效果；不同于传统的随机样本，本文模型采用了确定性样本，克服了预测结果不确定性的弊端.同时，针对大型地下水问题，本文结合局部化技术，分析了局部化技术在反演大尺度水力传导度场时起到的作用.

1 地下水非恒定流和集合卡尔曼滤波方法 1.1 地下水非恒定流

本文以非均匀介质中二维非恒定流为研究基础，运动方程可表示为

${S_y}\frac{{\partial h\left( {{\bf{x}},t} \right)}}{{\partial t}} = \nabla \cdot \left[ {{K_s}\left( {\bf{x}} \right)\nabla h\left( {{\bf{x}},t} \right)} \right] + g\left( {{\bf{x}},t} \right)$    (1)

式中：Sy为给水度；h(x,t)为压力水头；Ks(x)为饱和水力传导度；g(x,t)为源汇项.不失一般性，饱和水力传导度为未知的空间函数，并假设源汇项和给水度为确定性参数.定义如下的观测值向量d：

${\bf{d}} = {\bf{H}}{{\bf{S}}^t} + {\bf{e}}$    (2)

其中：St为由水头值和水力传导度值组成的联合状态向量，若某地下水系统有Nd个节点，则该向量的维度为2Nd，通常又称2Nd为自由度；H为观测算子，反映了观测值和状态变量之间的对应关系；e为观测误差.数据同化的目标在于根据动态和静态的观测数据获得对状态变量的最优估计.本文同时忽略了方程(1)可能具有的模型误差.

1.2 集合卡尔曼滤波方法

Evensen[12]首先提出了集合卡尔曼滤波方法，该方法是标准卡尔曼滤波算法的一种近似算法.由于标准卡尔曼滤波算法需要获得协方差矩阵的解析表达式，它目前仅适用于线性问题.集合卡尔曼滤波方法则利用若干样本实现来估计系统状态的统计矩，具有计算流程简单、适用于非线性问题和大尺度问题等优点.对于每个样本进行如下更新：

$\begin{array}{l} {\bf{S}}_k^a\left( i \right) = {\bf{S}}_k^f\left( i \right) + {\bf{K}}\left( i \right)\left( {{{\bf{d}}_k}\left( i \right) - {\bf{HS}}_k^f\left( i \right)} \right),\\ k = 1, \cdots ,{N_e} \end{array}$    (3)

式中：k为样本的编号；dk(i)为扰动的观测；Ne为样本大小；上标“a”和“f”分别表示同化过程和预测过程；K为卡尔曼积，定义如下，

${\bf{K}}(i) = {\bf{P}}_{}^f(i){{\bf{H}}^T}{\left[ {{\bf{HP}}_{}^f(i){{\bf{H}}^{\mathop{\rm T}\nolimits} } + {\bf{R}}(i)} \right]^{ - 1}}$    (4)

式中：R(i)为观测误差协方差矩阵；Pf(i)为预测状态向量的协方差矩阵，按如下公式计算获得：

$\begin{array}{l} {{\bf{P}}^f}\left( i \right) \approx \frac{1}{{{N_e} - 1}}\sum\limits_{k = 1}^{{N_e}} {\left\{ {\left[ {{\bf{S}}_k^f\left( i \right) - \left\langle {{{\bf{S}}^f}\left( i \right)} \right\rangle } \right]{{\left[ {{\bf{S}}_k^f\left( i \right) - \left\langle {{{\bf{S}}^f}\left( i \right)} \right\rangle } \right]}^{\rm{T}}}} \right\}} \\ \left\langle {{{\bf{S}}^f}\left( i \right)} \right\rangle \approx \frac{1}{{{N_e}}}\sum\limits_{k = 1}^{{N_e}} {{\bf{S}}_k^f\left( i \right)} \end{array}$    (5)

由于集合卡尔曼滤波方法本质上是Monte Carlo算法，随机场均值按照Ne-1/2的速度收敛，因此为提高一位有效数字的均值精度，样本大小Ne则需要增加100倍.这导致了高精度的集合卡尔曼滤波模拟需要非常大的Ne.同时注意到，当系统的自由度(本文为2Nd)远大于样本大小Ne时，通过式(5)估计的协方差和均值将明显偏离于理论的协方差和均值，且估计的方差将明显小于理论方差[7].在大尺度的地下水问题中，运行一个样本带来的昂贵的计算成本限制了可采用的样本大小.

2 确定性抽样方法

为便于下文阐述，本文以Karhunen-Loève (KL)展开法为例说明样本生成过程，关于KL展开法的细节请参照文献[13].对于二阶平稳场，当协方差函数已知时，KL展开可表示为

$U\left( {\bf{x}} \right) = \left\langle {U\left( {\bf{x}} \right)} \right\rangle + \sum\limits_{i = 1}^\infty {\sqrt {{\lambda _i}} {f_i}\left( {\bf{x}} \right){\xi _i}} $    (6)

式中：λi和fi(x)分别为特征值和特征函数；ξi为一系列相互独立的随机变量.传统随机场样本生成方法首先产生服从标准正态分布的随机数xi，然后组成随机向量：

${{\bf{\xi }}_k} = \left( {x_1^k,x_2^k, \cdots ,x_N^k} \right),k = 0,1, \cdots ,N$    (7)

对式(6)取M维截断，并将式(7)代入式(6)则可获得随机场U(x)的N个实现.随机数xi是随机产生的，如上生成的随机场样本因此具有很大的随意性.由于选取样本的差异，在执行集合卡尔曼滤波方法时(式(3)~(5))也可能出现截然不同的计算结果；特别在样本数量非常少时，不同的样本集合可能反演出迥异的水力传导度[7].下文我们将通过算例阐释该现象.

Stroud数值积分技术已被应用于随机偏微分方程的求解[14].常用的Stroud-2和Stroud-3方法是指对于不高于2阶和3阶多项式的数值积分均精确的数值积分方法.Xiu[15]最近将Stroud-2 拓展到多维非对称积分式，并整理了不同权重函数下(即随机变量的概率密度函数)的积分点配置方案.虽然不同的权重函数有截然不同的Stroud选点方法，但Stroud方法选出的数值积分点是等权重的.具体来说，对于一个M维多项式的数值积分，Stroud-2 和Stroud-3分别有M+1和2M个等权重的积分点.针对高斯随机变量，分别给出Stroud-2 和Stroud-3积分点算法.

Stroud-2：定义第k个积分点为如下向量形式：

${{\bf{\xi }}_k} = \left( {\xi _1^k,\xi _2^k, \cdots ,\xi _N^k} \right),k = 0,1, \cdots ,N$    (8)

式中各元素可表示为

$\begin{array}{l} \xi _{2r - 1}^k = \sqrt 2 \cos \frac{{2rk\pi }}{{N + 1}},\xi _{2r}^k = \sqrt 2 \sin \frac{{2rk\pi }}{{N + 1}},\\ r = 1,2, \cdots ,\left[ {N/2} \right] \end{array}$    (9)

式中：N/2为不大于N/2的最大整数，如果N为奇数则取ξNk=-1k.

Stroud-3：定义第k个积分点为如下向量形式：

${{\bf{\xi }}_k} = \left( {\xi _1^k,\xi _2^k, \cdots ,\xi _N^k} \right),k = 1,2, \cdots ,2N$    (10)

式中各元素满足

$\begin{array}{l} \xi _{2r - 1}^k = \sqrt 2 \cos \frac{{\left( {2r - 1} \right)k\pi }}{N},\xi _{2r}^k = \sqrt 2 \sin \frac{{\left( {2r - 1} \right)k\pi }}{N},\\ r = 1,2, \ldots ,\left[ {N/2} \right] \end{array}$    (11)

式中：N/2为不大于N/2的最大整数，如果N为奇数则取ξNk=-1k.

同理，将式(8)和式(10)代入式(6)则可获得随机场U(x)的N个实现.由于ξk是按照Stroud积分规则生成的确定性值，由此生成的每个随机场样本也是确定性的.将获得的确定性样本代入式(3)~(5)即可进行数据同化模拟，我们将该方法称为确定性集合卡尔曼滤波方法.该方法样本集合的大小将取决于截断维数M和积分精度.下文将讨论这两个因素对同化效果的影响.

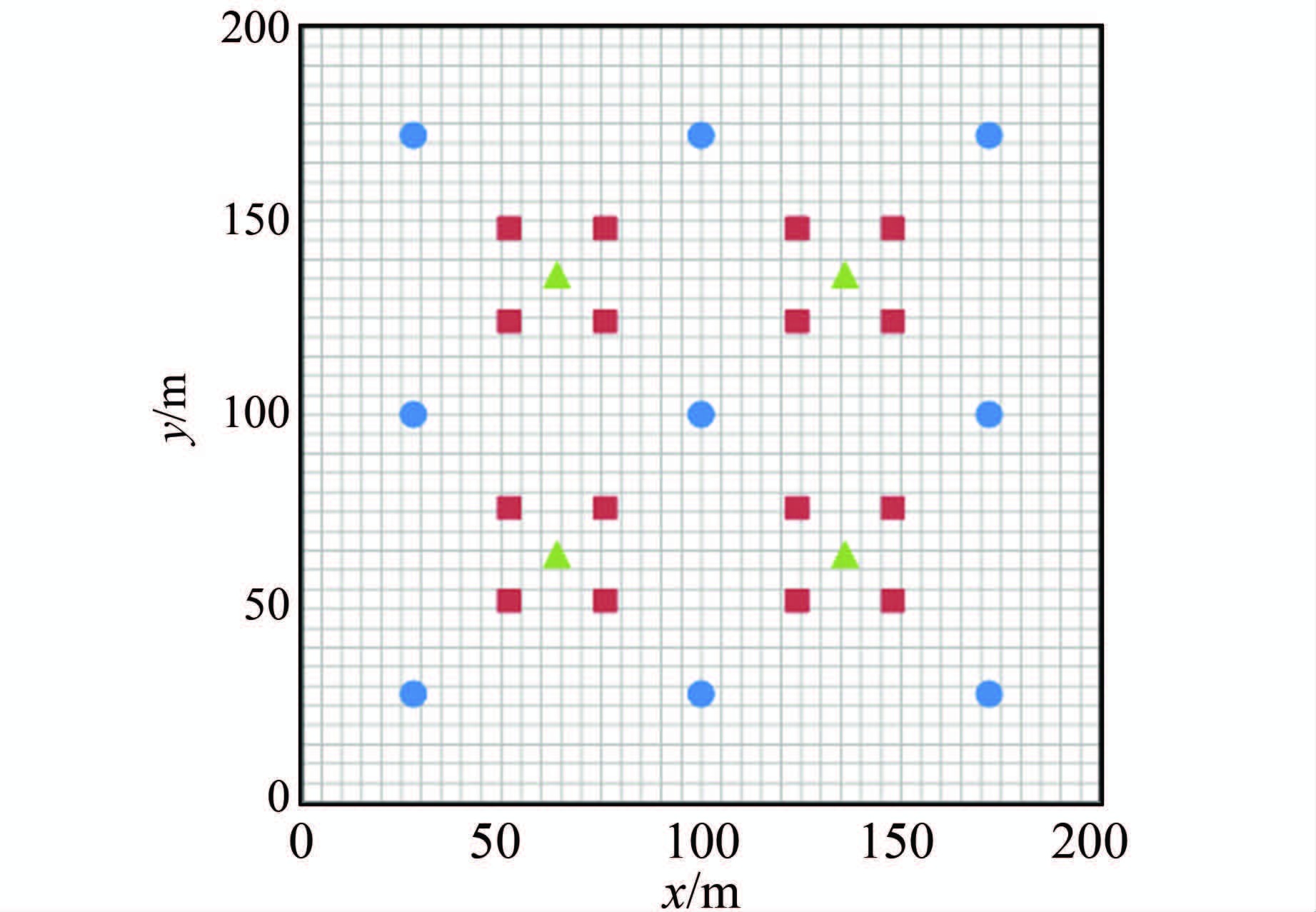
3 算例分析

模拟区域大小为200 m×200 m，平面上共布置有4口流量为2.5 m3/d的抽水井、25个水头h观测点和16个Ks观测点，如图 1所示.图中：16个方点为饱和水力传导度Ks观测点；16个方点和9个圆点是水头h观测点；4个三角形的点是抽水井.研究区域含水层厚度为20 m，初始地下水埋深为4 m，左右两侧边界的定水头值为16 m，上下边界为隔水边界.研究区域的横向和纵向均匀离散为51个节点，共2 601个节点.总模拟时长为200 d，每10 d采集一次水头观测值，即有20个同化步，每个同化步长为10 d.按照lnKs场的均值为-1 m/d，方差为1和相关长度为20 m为条件，采用传统随机场生成方法产生若干随机场，选择任一随机场作为真实水力传导度(参照场)，Ks观测信息直接从参照场中提取.然后以该参照场为基础，设计一虚拟的地下水流动，即按上文给定的边界条件和初始计算出各观测时刻的水头值，并以计算出的观测点处的水头值

图 1 模拟区域及观测点布置 Figure 1 Illustration of the simulation area and the observation points
图选项

作为动态观测值.在获得观测数据后，下文将分别以传统的集合卡尔曼滤波方法和本文提出的确定性方法来反演水力传导度.如上所述，传统方法采用随机生成的lnKs场(<Y>场)样本来执行数据同化过程，本文算法则采用Stroud积分规则生成的样本.

3.1 同化效果比较

本文采用均方根误差RMSE(Root Mean Square Error)来评估数据同化的效果，定义如下：

${\rm{RMSE}} = \sqrt {\frac{1}{P}\sum\limits_{i = 1}^P {{{\left[ {E\left( {Y\left( {{{\bf{x}}_i}} \right)} \right) - {Y^t}\left( {{{\bf{x}}_i}} \right)} \right]}^2}} } $    (12)

式中：P为格点的数目，本文为2 601个；E(Y(xi))为每个格点同化后的均值；Yt(xi)为每个格点的参照值.RMSE越小，表示由数据同化方法反演出的水力传导度越接近于真实值，即数据同化效果越好.为评估系统方差随同化步的变化规律，对于某样本集合，定义平均标准差ASD (Average Standard Deviation)表示为

$ASD = \sqrt {\frac{1}{{N \cdot P}}\sum\limits_{j = 1}^N {\sum\limits_{i = 1}^P {{{\left[ {Y\left( {{\bf{x}}_i^j} \right) - E\left( {Y\left( {{{\bf{x}}_i}} \right)} \right)} \right]}^2}} } } $    (13)

式中：P为格点的数目；N为样本大小.ASD实际上反映了系统的不确定性，随着同化步的增加，ASD将逐渐减小；当N足够大时，ASD能够真实地反映出系统不确定性的变化；但由于实际问题N通常取值较小，ASD通常会出现快速减小的假象，即出现低估系统不确定性的现象.

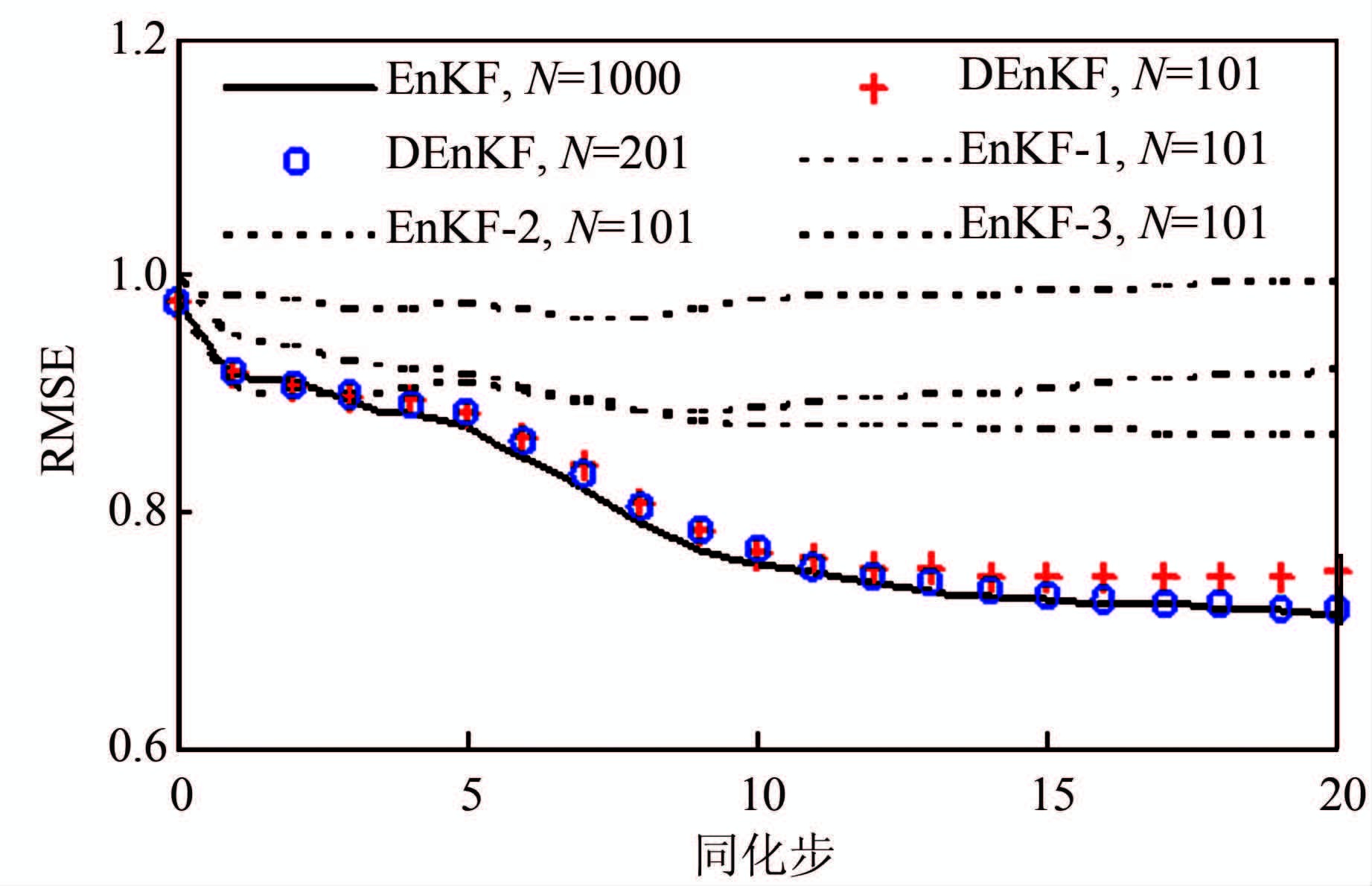
为简洁起见，下文将确定性集合卡尔曼滤波记为DEnKF (Deterministic Ensemble Kalman Filter).图 2给出了DEnKF和EnKF在不同样本大小下的RMSE图，其中EnKF(N=1 000)被作为参照的数据同化结果，即认为当N=1 000时，样本已经足够多，因此可以忽略EnKF引入的统计误差.在DEnKF模拟中，采用Stroud-2积分规则获取确定性样本，截断维数分别取 M=100和200，对应的样本大小分别为N=101和N=201.下文将比较截断维数对同化效果的影响.同时，为对比DEnKF和EnKF，我们运行样本大小同样为101但基于三个不同样本集合的EnKF模拟.由于每个集合是随机生成的，不同集合的EnKF可能得到截然不同的结果.由图 1可知，当N=101时，DEnKF与参照EnKF(N=1 000)的RMSE非常接近；当增加N至201时，DEnKF得到的RMSE更加接近于参照EnKF的结果，但改善程度并不明显.然而，在样本大小同样为101时，三个不同集合的EnKF获得的RMSE都远远偏离于参照结果，且每个集合得到的RMSE都不相同.该现象表明，在样本过小时，传统的EnKF并不能够取得满意的计算效果，而且模拟的结果本身也存在不确定性，然而DEnKF则取得了良好的模拟效果.

图 2 RMSE对比图 Figure 2 Comparison of RMSE
图选项

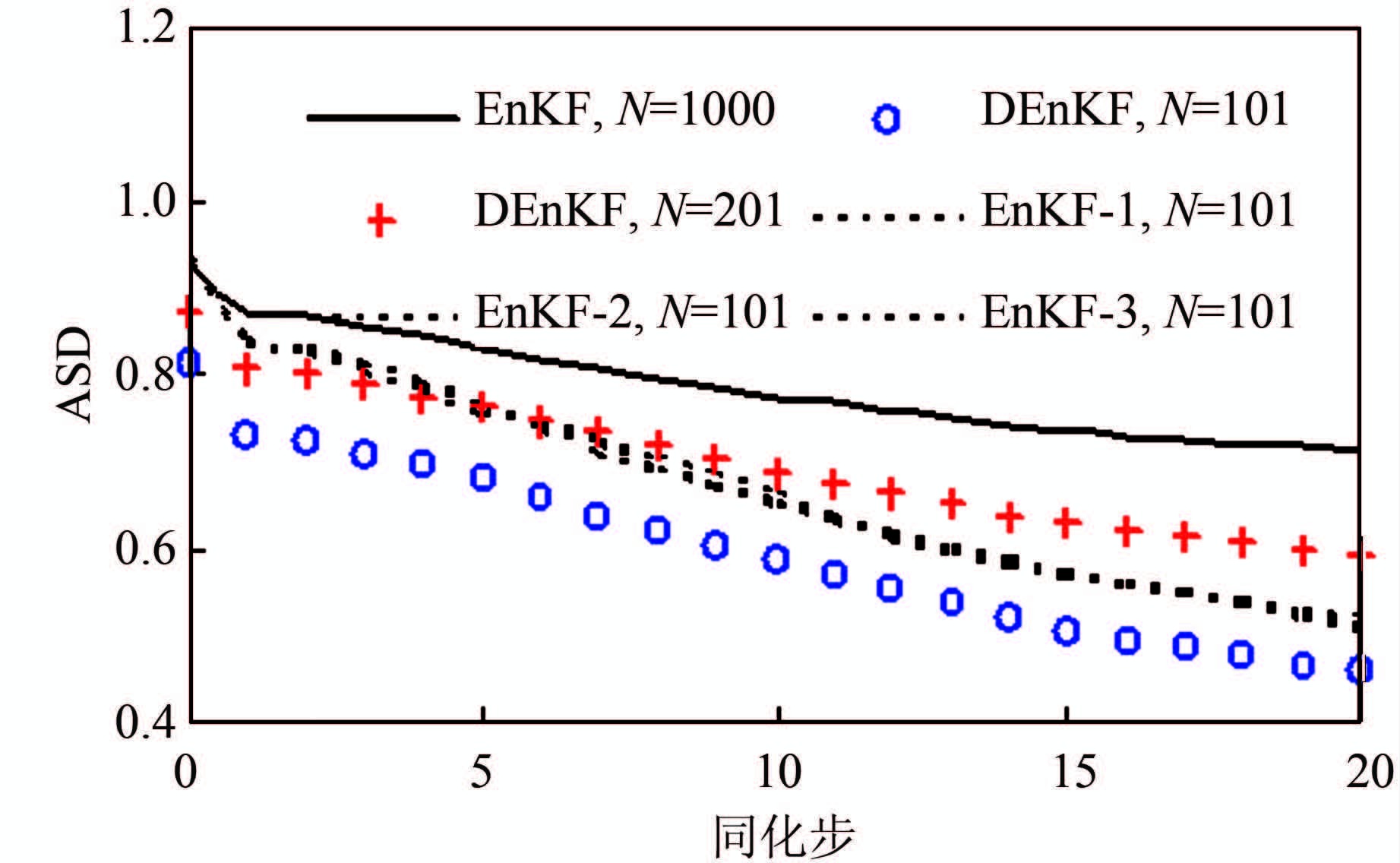
图 3显示了平均标准差ASD随同化步的变化情况.从图中可以看出，对于不同样本大小的EnKF，在初始时刻(t=0)系统均具有十分接近的方差；但当样本大小N=101时，方差开始迅速减小，逐渐偏离于参照的ASD曲线(N=1 000).因此，当样本大小不够大时，EnKF将出现低估系统不确定性的现象.Furrera and Bengtssonb[7] 详细探讨了该现象，并提出了若干解决方案.相比EnKF在初始时刻的标准差(N=101和1 000时，标准差均为0.93)，DEnKF方法在t=0时具有较小的方差(N=101和201时，标准差分别为0.81和0.87)，即DEnKF方法在初始时刻就忽略了随机场的细节；截断维数越小，忽略的细节也越多，初始时刻的不确定性也越小.当N=101时，DEnKF算法在t=0～20 d内ASD从0.81降至0.46，降幅为0.35，该降幅小于N=101时EnKF算法的降比(约为0.42)；当N=201时，DEnKF算法在t=0～20 d内ASD从0.87降至0.59，降幅为0.28，十分接近于参照EnKF的降比(0.22).该现象表明，即使在样本非常小的条件下DEnKF算法也可避免严重的方差低估现象，一方面这是由于DEnKF的样本具有优越的统计特性，另外一方面是由于DEnKF算法在初始时刻就忽略了随机场的细节而关注于大尺度的不确定性.

图 3 ASD对比图 Figure 3 Comparison of ASD
图选项

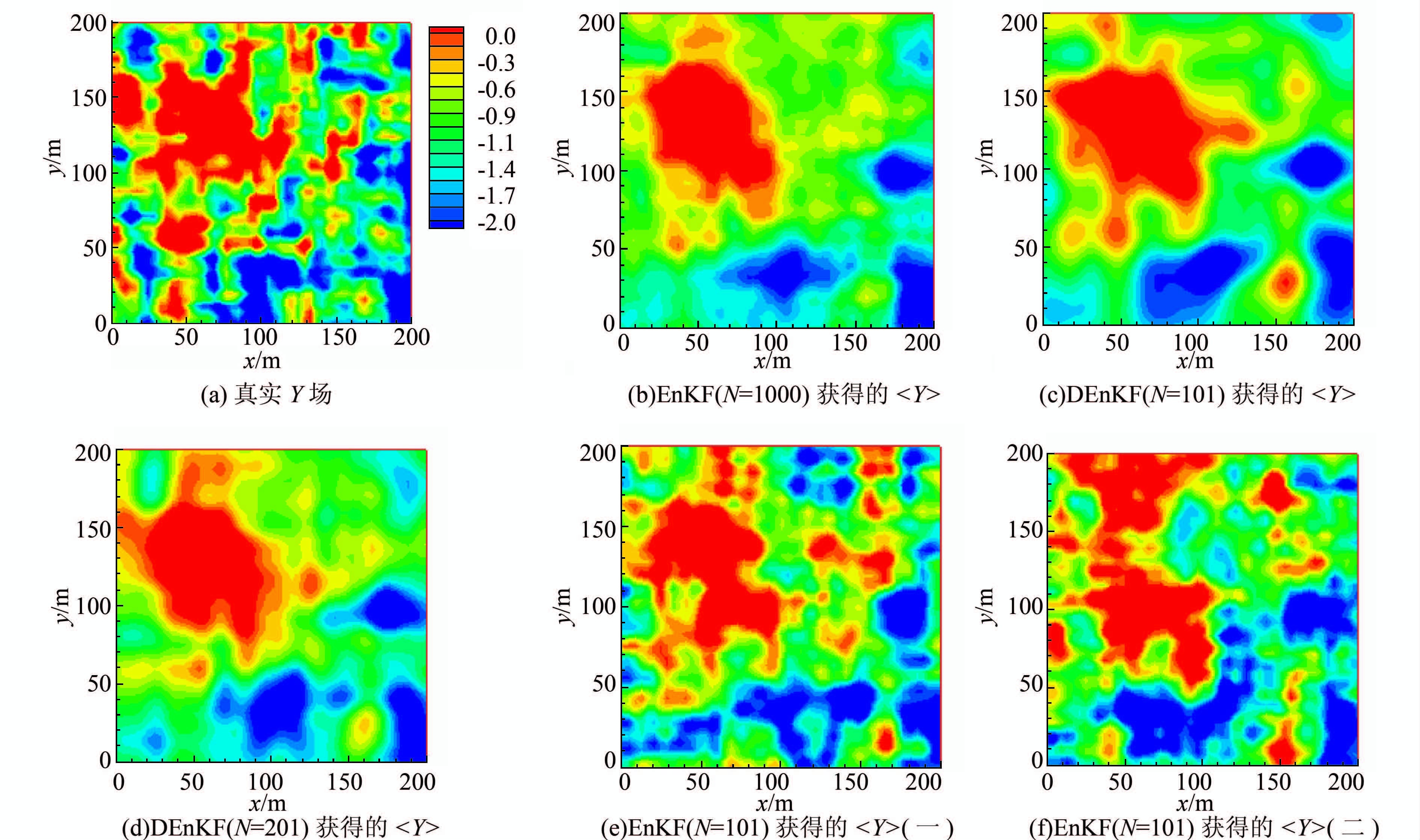
图 4给出了不同算法得到的<Y>.可以看出DEnKF在N=101(图 4(c))和201(图 4(d))时均获得了与参照解(图 4(b))十分接近的<Y>场；而当样本较小时(N=101)，不同序列的EnKF则会获得截然不同的<Y>场，如图 4(e)和4(f)所示.

图 4 不同算法和不同配置条件下反演出的<Y>分布图 Figure 4 The contours of the <Y> field inversed from different algorithms and conditions
图选项
3.2 强烈非均匀介质

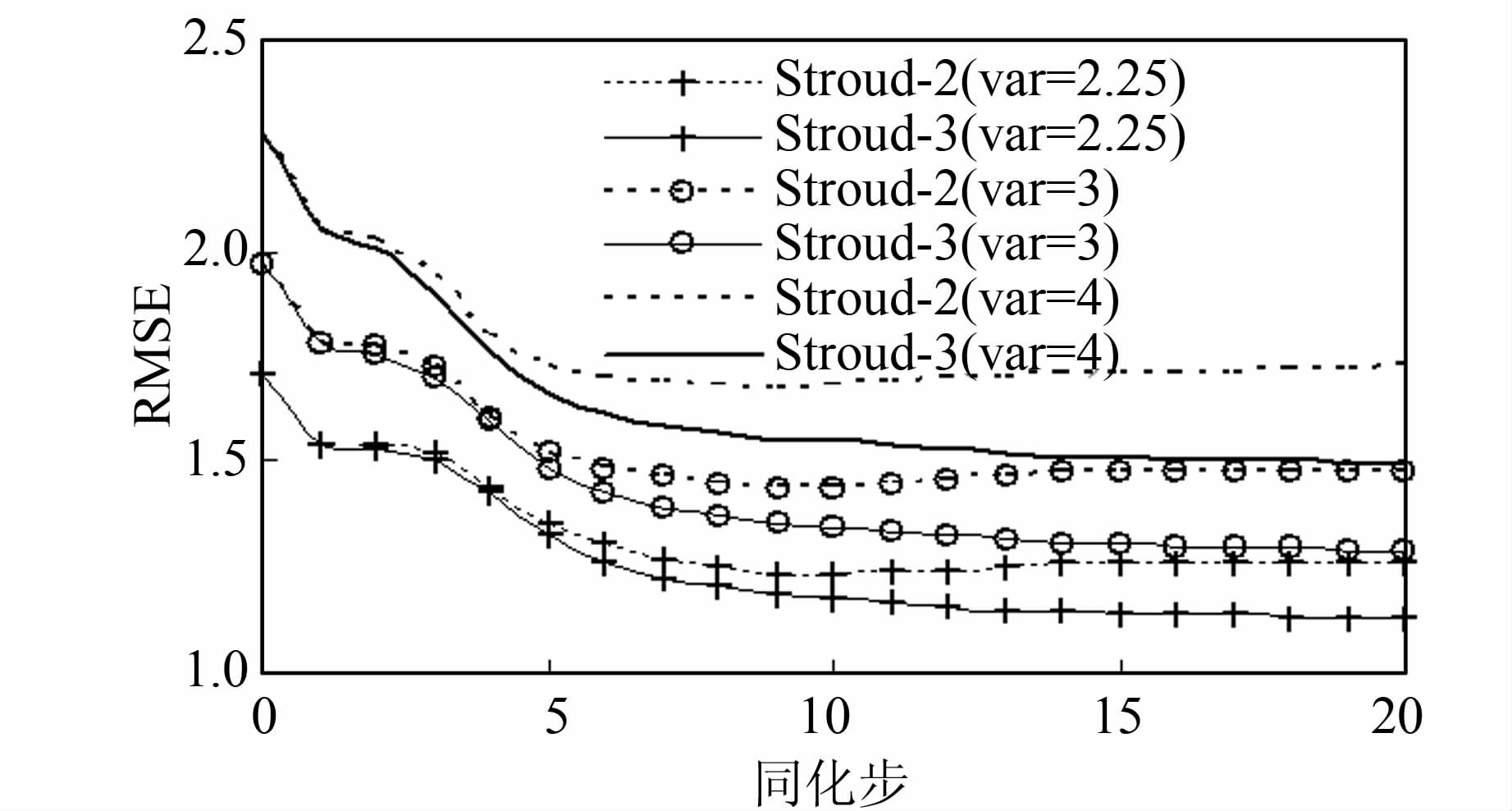
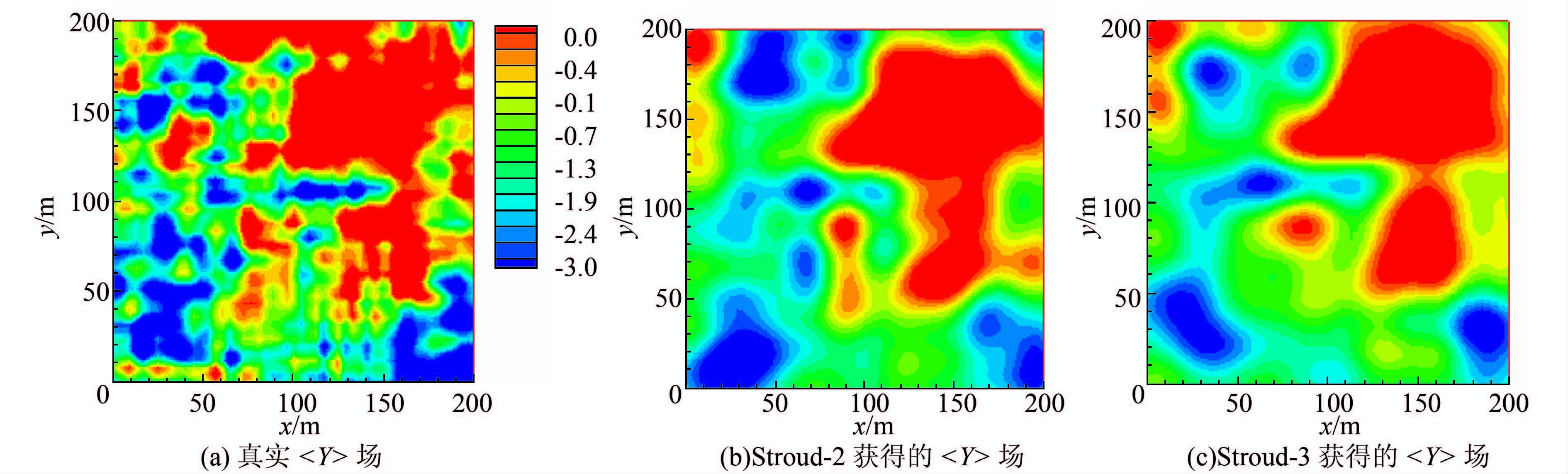
为检验DEnKF算法在强烈非均匀介质中的计算能力，增加方差至2.25、3和4，对应的水力传导度随机场变异系数分别达到291%、437%和732%，算例中其他参数保持不变.图 5给出了3种方差条件下基于Stroud-2积分和Stroud-3积分的DEnKF方法的RMSE图.可以看出当方差为2.25时，DEnKF (Stroud-2) 产生的RMSE曲线在前10个同化步逐渐下降，但随后略有上升并趋于平稳；DEnKF (Stroud-3)仍表现出良好的计算特性，随着水头动态观测数据的加入，RMSE曲线仍呈现出下降趋势.比较不同方差下Stroud-2和Stroud-3对应的RMSE曲线可知，随着方差的增加，DEnKF (Stroud-2) 和DEnKF (Stroud-3)产生的RMSE曲线表现出更大的差异.方差为2.25时，在第10个同化步Stroud-2和Stroud-3对应的RMSE曲线相对差异已达到5%，而方差为3和4时，分别在第7和第6同化步，两者相对差异达到5%.因此，随着介质不均匀性的增强，低阶确定性同化方法在较晚同化步会出现计算精度恶化的现象，此时需要借助更高阶积分规则来生产样本集合.高阶积分规则虽然增加了样本的大小 (在该算例中，Stroud-2和Stroud-3对应的样本数分别为101和200)，但上文结果表明，即使方差达到4，DEnKF尤其是基于Stroud-3积分规则的集合卡尔曼滤波方法仍能够反演出合理的水力传导度.图 6进一步对比了方差为3时DEnKF方法模拟出的<Y>场和参照场.

图 5 不同强弱的非均匀介质中DEnKF获得的RMSE曲线 Figure 5 RMSE calculated by DEnKF under different levels of heterogeneous media
图选项
图 6 方差为4时DEnKF获得的<Y>分布图 Figure 6 The contours of the <Y> field by DEnKF with the variance of 4
图选项
3.3 大尺度非均匀介质

为检验DEnKF算法在大尺度非均匀介质中的计算性能，设方差为2.25，并取相关长度为8 m，其他参数保持不变，则问题转变为一个大尺度问题.在大尺度问题中，当N不够大时式(5)通常产生伪协方差，下文将结合局部化技术来执行确定性集合卡尔曼滤波模拟.采用局部化技术，对协方差矩阵(5)中每个元素修正如下[9, 16]：

${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over p} _{ij}} = {p_{ij}}{c_{ij}}$    (14)

式中：pij为协方差矩阵(5)的元素；cij 为指数衰减因子，可表示为

${c_{ij}} = c\left( {{{\bf{x}}_i},{{\bf{x}}_j}} \right) = \exp \left( {\frac{{ - {d_{ij}}}}{\theta }} \right)$    (15)

式中：dij为点 xi 和点 xj之间的距离，θ可近似表示为

$\theta \approx \frac{\lambda }{4}\left( {\sqrt {9 + 8N} - 5} \right)$    (16)

式中：λ为先验的相关长度；N为样本大小.

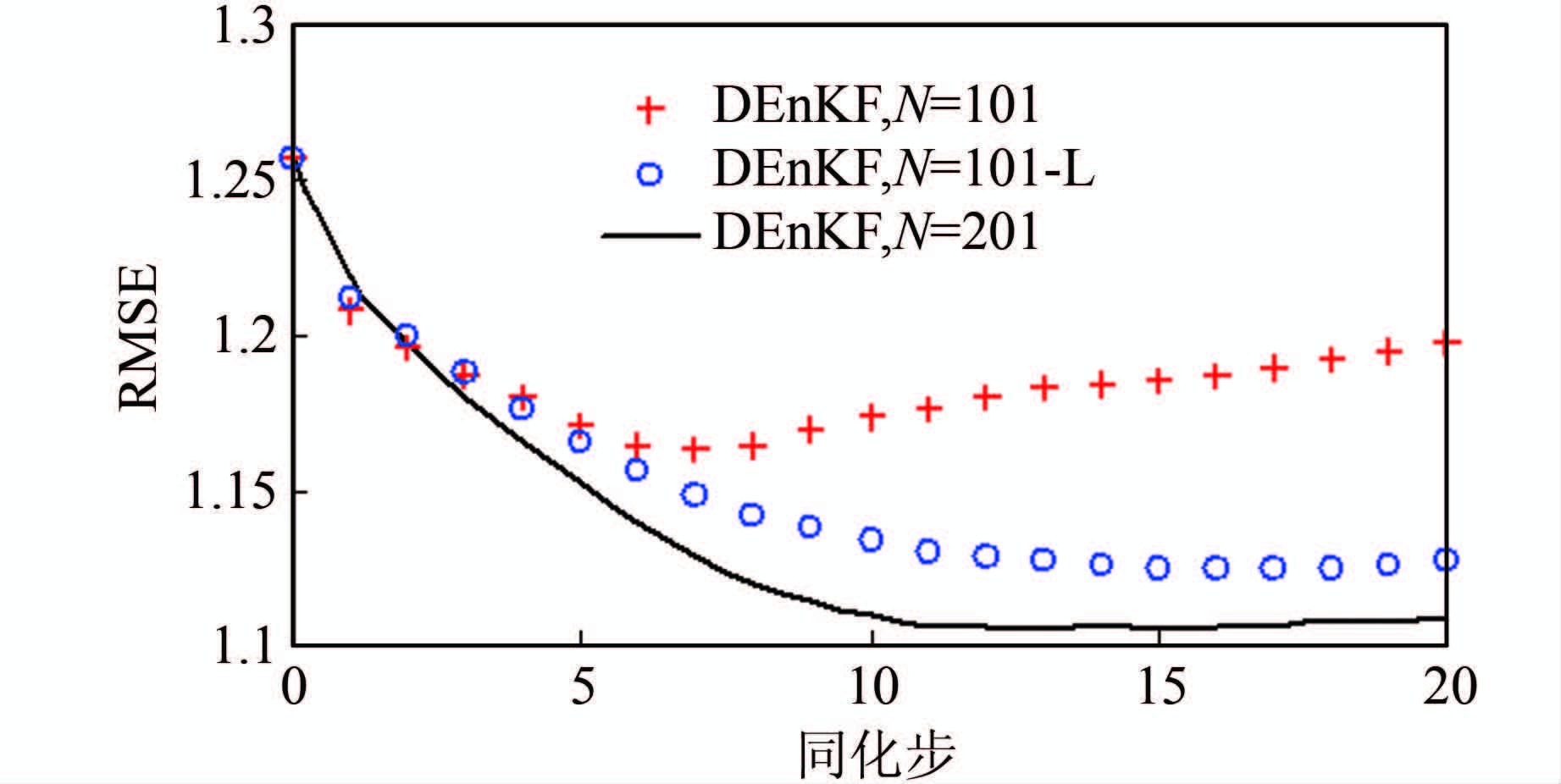
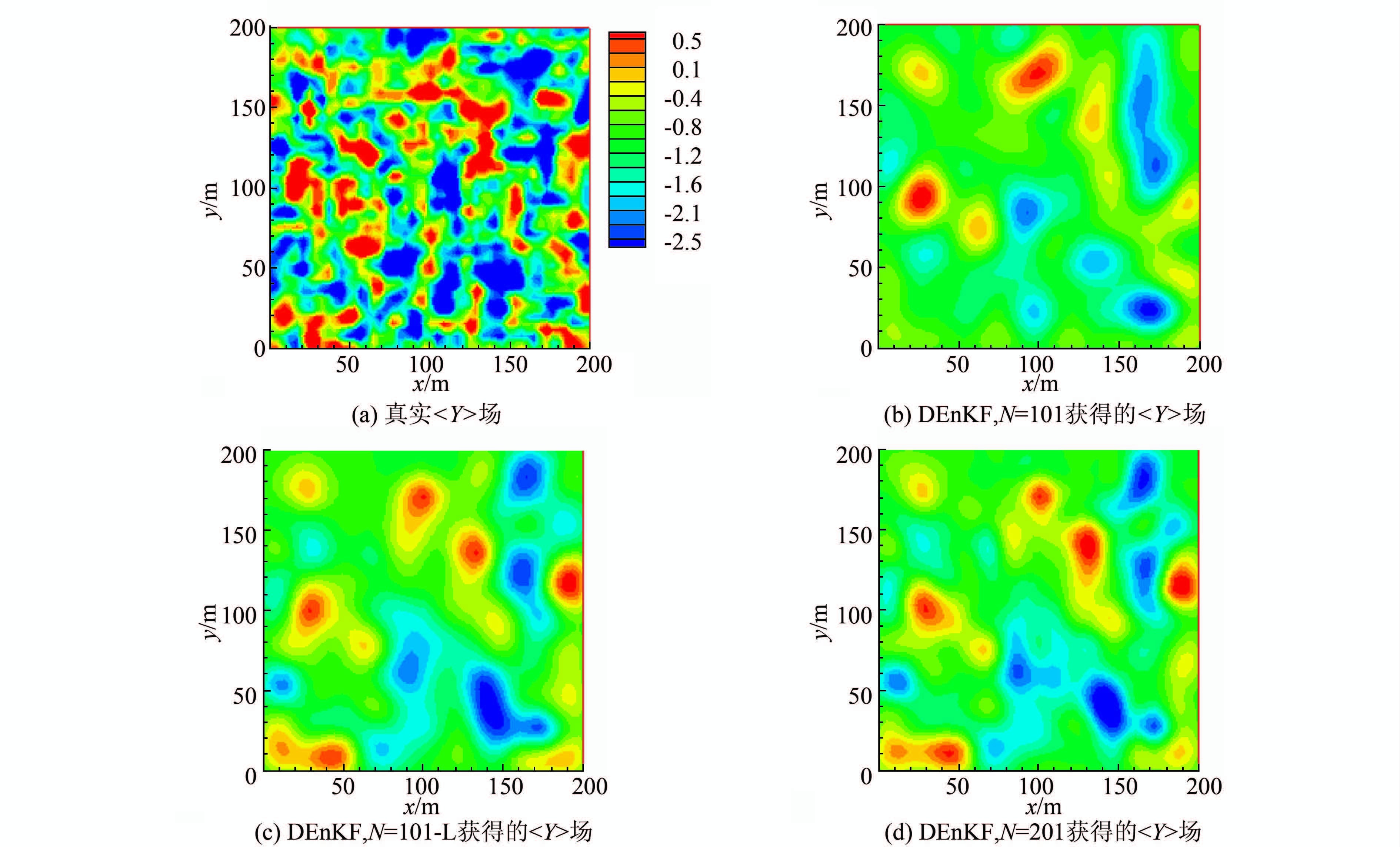
图 7给出了基于Stroud-2积分规则的DEnKF算法在采用局部化和没有采用局部化技术时获得的RMSE图，图中“DEnKF,N=101-L”表示样本大小为101时，结合局部化技术获得的结果.从图中可以看出相比于“DEnKF,N=101”，在样本大小同样为101时，局部化技术可以显著地改进模拟精度.由于该问题尺度较大，提高截断维数可以提高数据同化的效果，如图中“DEnKF,N=201”(对应的截断维数为200)获取的RMSE曲线明显低于“DEnKF,N=101”(对应截断维数为100)的曲线.有趣的是，采用局部化技术后虽然样本大小仅为101，但结合局部化技术的DEnkF获得结果与不采用局部化技术但样本大小为201的结果非常接近.因此，局部化技术可以进一步缓解数据同化方法对样本大小的依赖.图 8进一步展示了该现象，其中“DEnKF,N=101-L”和“DEnKF,N=201”反演出相似的水力传导度，而两者结果都优于“DEnKF,N=101”的结果.文献[16]将局部化技术在标准集合卡尔曼滤波方法中应用于小集合情况下一般问题的参数估计能力进行了讨论，而本研究将局部化技术应用于确定性集合卡尔曼滤波方法下的大尺度非均匀介质中，应用范围更加广泛.

图 7 结合局部化技术DEnKF获得的RMSE曲线 Figure 7 RMSE from DEnKF with the localization technique
图选项
图 8 方差为2.25时DEnKF获得的<Y>分布图 Figure 8 The contours of the <Y> field by DEnKF with the variance of 2.25
图选项
4 结论

本文建立了基于确定性抽样技术的地下水系统数据同化方法，将Stroud积分方法与集合卡尔曼滤波方法相结合，缓解了经典集合卡尔曼滤波方法在小样本条件下发生的方差低估现象.主要研究成果包括：1)基于Stroud理论的确定性集合卡尔曼滤波方法具有等权重的样本，执行过程和基于Monte Carlo理论的同化方法具有完全相同的执行过程；该方法可直接调用常用的地下水代码Modflow，便于实现与经典地下水软件的无缝链接；2)基于Stroud理论的确定性集合卡尔曼滤波方法只存在一个集合，反演出的水力传导度具有唯一性，而传统的同化方法则可能反演出截然不同的水力传导度，从而具有较大的预测不确定性；3)当样本过小时，传统方法通常会导致系统方差快速衰减，本文方法在初始时刻忽略了对水力传导度细节的描述，关注于大尺度的不确定性，缓解了系统方差的非正常衰减；4)随着含水层不均匀性的增加，基于确定性抽样技术的数据同化方法需要采用更高阶的积分规则；但研究结果表明在方差为3的条件下，本文算法仍然取得了良好的模拟效果；5)结合局部化技术，确定性集合卡尔曼滤波方法能够很好地解决大尺度地下水系统的数据反演.

参考文献
[1] Franssen H J H, Gómez-Hernández J, Sahuquillo A. Coupled inverse modeling of groundwater flow and mass transport and the worth of concentration data[J]. Journal of Hydrology, 2003, 281(4): 281–295. DOI:10.1016/S0022-1694(03)00191-4
[2] 史良胜, 杨金忠, 蔡树英. 基于降雨空间变异的潜水运动随机模拟方法Ⅱ——条件模拟[J]. 水利学报, 2007, 38(5): 524–528.
Shi Liangsheng, Yang Jinzhong, Cai Shuying. Stochastic simulation of groundwater flow subject to spatial variable precipitation II——Conditional simulation[J]. Journal of Hydraulic Engineering, 2007, 38(5): 524–528.
[3] 史良胜, 廖卫红, 杨金忠, 等. 地下水流动的条件模拟[J]. 四川大学学报(工程科学版), 2009(6): 452–465.
Shi Liangsheng, Liao Weihong, Yang Jinzhong. The conditional simulation of groundwater flow[J]. Journal of Sichuan University (Engineering Science Edition), 2009(6): 452–465.
[4] Verlaan M, Heemink A W. Nonlinearity in data assimilation applications: a practical method for analysis[J]. Month Weather Rev., 2001, 129: 1578–1589. DOI:10.1175/1520-0493(2001)129<1578:NIDAAA>2.0.CO;2
[5] Geir N, Johnsen L M, Aanonsen S I, Vefring E H. Reservoir monitoring and continuous model updating using ensemble Kalman filter[J]. SPE Journal, 2003, 10(1): 66–74.
[6] Evensen G. The ensemble Kalman filter: theoretical formulation and practical implementation[J]. Ocean Dynam., 2003, 53: 343–367. DOI:10.1007/s10236-003-0036-9
[7] Furrer R, Bengtsson T. Estimation of high-dimensional prior and posterior covariance matrices in Kalman filter wariants[J]. J. Multivariate Analysis, 2007, 98: 227–255. DOI:10.1016/j.jmva.2006.08.003
[8] Anderson J L. An adaptive covariance inflation error correction algorithm for ensemble filters[J]. Tellus A, 2007, 59(2): 210–224. DOI:10.1111/tea.2007.59.issue-2
[9] Wang X, Hamill T M, Whitaker J S, Bishop C H. a comparison of hybrid ensemble transform Kalman filter-optimum interpolation and ensemble square root filter analysis schemes[J]. Mon. Weather Rev., 2007, 135: 1055–1076. DOI:10.1175/MWR3307.1
[10] Evensen G. Sampling strategies and square root analysis schemes for the EnKF[J]. Ocean Dyn., 2004, 54: 539–560. DOI:10.1007/s10236-004-0099-2
[11] Wen X H, Chen W H. Practical issues on real-time reservoir updating using ensemble Kalman filter[J]. SPEJ, 2007, 12(2): 156–166. DOI:10.2118/111571-PA
[12] Evensen G. Sequential data assimilation with a nonlinear quasigeostrophic model using Monte Carlo methods in forecast error studies[J]. J. Geophys. Res., 1994, 99(C5): 10143–10162. DOI:10.1029/94JC00572
[13] Ghanem R, Spanos P. Stochastic Finite Elements: A Spectral Approach[M]. New York: Springer-Verlag, 1991.
[14] Xiu D, Hesthaven J S. High-order collocation methods for differential equations with random inputs[J]. SIAM Journal of Scientific Computing, 2005, 27(3): 1118–1139. DOI:10.1137/040615201
[15] Xiu D. Efficient collocational approach for parametric uncertainty analysis[J]. Communications in Computational Physics, 2007, 2(2): 293–309.
[16] 南统超, 吴吉春. 集合卡尔曼滤波估计水文地质参数的局域化修正[J]. 水科学进展, 2010, 21(5): 613–621.
Nan Tongchao, Wu Jichun. Localization corrections for the estimation of hydrogeological parameters using ensemble Kalman filter[J]. Advances in Water Science, 2010, 21(5): 613–621.