武汉大学学报(工学版)   2016, Vol. 49 Issue (3): 365-371

文章信息

肖雪, 王修贵, 谭丹, 王兵, 巴乾, 白雪
XIAO Xue, WANG Xiugui, TAN Dan, WANG Bing, BA Qian, BAI Xue
几种计算渠道渗漏损失的经验公式比较
Comparison of empirical formulas for calculating canal seepage loss
武汉大学学报(工学版), 2016, 49(3): 365-371
Engineering Journal of Wuhan University, 2016, 49(3): 365-371
http://dx.doi.org/10.14188/j.1671-8844.2016-03-008

文章历史

收稿日期: 2015-12-24
 Abstract              PDF               Figures               Tables
引用本文 0
肖雪, 王修贵, 谭丹, 王兵, 巴乾, 白雪. 几种计算渠道渗漏损失的经验公式比较[J]. 武汉大学学报(工学版), 2016, 49(3): 365-371.
XIAO Xue, WANG Xiugui, TAN Dan, WANG Bing, BA Qian, BAI Xue. Comparison of empirical formulas for calculating canal seepage loss[J]. Engineering Journal of Wuhan University, 2016, 49(3): 365-371.
几种计算渠道渗漏损失的经验公式比较
肖雪1,2, 王修贵1, 谭丹3, 王兵4, 巴乾5, 白雪6     
1. 武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072;
 2.  长江科学院水资源所，湖北 武汉 430010;
 3. 中工武大设计研究有限公司，湖北 武汉 430074;
 4.  新疆伊犁自治州水利局，新疆 伊犁 835000;
 5. 新疆伊犁自治州喀什河流域管理处，新疆 伊犁 835000;
 6.  新疆水利水电勘测设计研究院，新疆 乌鲁木齐 830000
收稿日期: 2015-12-24
作者简介: 肖雪（1990-），女，硕士研究生，主要从事灌区规划方面研究，E-mail:x_xiaoxue@126.com.
通讯作者: 王修贵（1962-），男，教授，博士生导师，主要从事农田排水及水管理研究，E-mail:wangxg@whu.edu.cn
基金项目: “十二五”国家科技支撑计划项目（编号：2012BAD08B03）；国家自然科学基金项目（编号：51379153）.
摘要: 灌溉渠道渗漏损失的确定对于正确计算灌溉水利用系数具有重要的作用.分析影响渠道渗漏损失的主要因素，对几种常见的计算渠道渗漏损失的经验公式进行分析，并以新疆伊犁喀什河下游灌区内的典型渠道为实例分别利用各类经验公式计算渠道渗漏量.结果表明：几种经验公式和理论公式均可转换为相同的形式，通用形式反映了渠道断面形式和水力特性、土壤因素对渠道渗漏的影响.实例研究表明，经验公式的转换形式与理论公式中的流量或水深指数越接近，其计算精度越高；其中莫里兹公式和考斯加可夫公式的计算精度较高，而Ingham公式和Molesworth公式的计算精度较低；考斯加可夫公式形式最为简单，计算时要求渠道资料较少，且计算精度高，因此优先推荐使用.
关键词： 渠道渗漏损失     影响因素     经验公式     理论公式     实例计算    
Comparison of empirical formulas for calculating canal seepage loss
XIAO Xue1,2, WANG Xiugui1, TAN Dan3, WANG Bing4, BA Qian5, BAI Xue6     
1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;
 2. Yangtze River Scientific Research Institute, Wuhan 430010, China;
 3. CAMCE WHU Design and Research Co., Ltd, Wuhan 430074, China;
 4. Xinjiang Yili Kazakh Autonomous Prefecture Water Resources Bureau, Yili 835000, China;
 5. Xinjiang Yili Kazakh Autonomous Prefecture, Kashigaer River Basin Management Section, Yili 835000, China;
 6. Xinjiang Water Conservancy and Hydropower Survey, Design and Research Institute, Urumqi 830000, China
Abstract: The estimation of the leakage loss of the irrigation canal plays an important role in calculating the utilization coefficient of irrigation water accurately. On the basis of analyzing the main factors influencing the canal seepage loss, several empirical formulas for calculating the canal seepage loss are compared. Then, taking the typical canal in the irrigation area in the lower reaches of Kashi River in Yili Autonomous Prefecture of Xinjiang Autonomous Region for example, seepage losses are calculated by various empirical formulas respectively. The results show that these empirical formulas and the theoretical formula can be converted into the same form, which reflects the influence of the canal section form, hydraulic characteristics and soil factors on the canal seepage. In addition, the closer the index in the converted form of empirical formula is to that of theoretical formula, the higher accuracy will be. The empirical formulas of Moritzs and Kostiakov have higher calculation accuracy; while the formulas of Ingham and Molesworth have lower calculation accuracy. Because of the Kostiakov formula with simple form, few data needed and high accuracy, it is preferably recommended to use in the irrigation area.
Key words: anal seepage loss     influencing factors     empirical formula     theoretical formula     examples calculation    

渠道渗漏损失是指在渠道输配水过程中，通过渠床表面渗入渠床土体而损失的水量.正确估算渠道的渗漏损失量是计算渠道水利用系数的关键.由于影响渠道渗漏的因素甚多，目前尚无通用的渠道渗漏损失计算公式.一些经验公式是基于渠道现场试验及统计分析得出的[1]，例如戴维斯和威尔逊总结的衬砌渠道计算公式，印度采用的对土质渠床损失水量计算的经验公式等.国内广泛采用的是考斯加可夫公式[2]，一些学者还为提高计算精度对公式进行了改进，例如门宝辉[3]假定渠道单位流量在单位流程上的损失量不变，利用积分的方法对该公式进行了改进；谢崇宝等[4]将该公式与其他经验公式相结合，提出与渠道断面尺寸、土壤类型等因素均相关的改进经验公式.本文首先分析了影响渠道渗漏量的各种因素，选取国内外常用的几种计算渠道渗漏经验公式，分析了各公式之间的联系，并以新疆伊犁喀什河下游灌区的实测资料为基础，对各个公式的计算结果进行了对比验证，为分析计算渠道渗漏损失和测算渠道水利用系数提供参考.

1 渠道渗漏的主要影响因素分析

计算渠道渗漏损失的经验公式一般是在对实测资料进行统计分析的基础上，选取某些主要影响因素作为变量进行推导或率定.影响渠道渗漏的主要因素，可分为以下几类.

1) 渠床土壤

不同土壤的渗透性不同[5, 6].土壤越粘重，土粒间孔隙就越小，水流渗漏的阻力越大、水力传导度越小，因此重质土壤的渠床渗漏量小于轻质土壤.渠道渗漏量公式中常用渗透系数反映不同土壤的渗透性[7, 8].

2) 断面形式及水力特性

主要包括湿周、水深、流速和流量等水力参数[1, 9].湿周越大，渗漏面积越大，渗流量越大；水深与渠床土壤水势梯度正相关，因而与渗漏通量正相关.同时渠道水深也与湿周正相关，进而影响渗漏量.

流速对渠道渗漏的影响主要体现在两个方面：当流量一定时，流速越大，渠道过水断面越小，水流渗漏面积也越小，渗流量随之变小；流速越大，相同水量的水流停留时间越短，则渗漏损失越小.

流量对渠道渗漏也有较大影响.对相同断面形式的渠道而言，渠道流量越大时，水深和渠道渗漏面积越大，因此渠道渗漏量越大.

实际上这些因素彼此关联，相互影响，实际中难以进行明确区分，均属于渠道的断面形式及水力特性，因此，不同的公式所采用的参数有所不同[1, 10, 11].

3) 地下水埋深

渠道在输水过程中的渗漏可分为两个不同的阶段，即自由渗漏和顶托渗漏.自由渗漏的损失量主要取决于渠道的渠床土壤性质和渠道断面尺寸.顶托渗漏的损失量基本上是由地下水埋深决定的，受渠道断面尺寸影响较小.当灌区地下水位较高时，渠道水受地下水顶托作用较大，减少了渠道水下渗的水力梯度和储水空间，对渠道水的下渗起到抑制作用[12]，理论计算时，采用地下水位与渠内水位的差值为变量估算渗漏量[8]，但由于地下水位的时空不稳定性，资料难以获取，实际计算时，先计算自由渗漏，对有地下水位顶托的情况再采用折减系数修正[13, 14].

4) 衬砌条件

不同衬砌条件的防渗效果不同，与普通土渠相比，一般采用粘土夯实、混凝土衬砌和塑料薄膜衬砌的渠道渗漏损失量能分别减少45%、70%和80%左右[15].理论计算时，需要测试衬砌材料的厚度、渗透系数和土壤的分层厚度、渗透系数，并结合地下水埋深和渠道的断面形式等计算渗漏量[8].因所需的资料往往难以获取，故在实际计算时，常常先根据渠床土质计算无衬砌时的渗漏量，再乘以衬砌折减系数[1, 14]得到衬砌条件下的渗漏量.

2 各类经验公式理论分析 2.1 各类经验公式简介

由于计算渠道渗漏的理论公式所需的资料在实际应用时难以收集，因此，在实际应用中广泛采用经验公式，通过选取主要影响因素作为变量来计算渠道渗漏量.现行的经验公式主要有[1, 10, 11](本文将原公式中各参数或变量的单位均转换为国际单位制)：

戴维斯-威尔逊(Davison-Wilson)公式：

$S=\frac{0.45{{C}_{1}}P{{H}^{1/3}}}{4\times {{10}^{3}}+3.65\sqrt{v}}$    (1)

美国垦务局(USBR)莫里兹公式：

$S=0.01154{{C}_{2}}\sqrt{Q/v}$    (2)

Ingham公式：

$S=0.001{{C}_{3}}PH$    (3)

Molesworth公式：

$S={{C}_{4}}P\sqrt{R}$    (4)

考斯加可夫(Kostiakov)公式：

$S=A{{Q}_{0}}^{1-m}/100$    (5)

式中：S为单位渠长渗漏损失，m3/s/km；P为湿周，m；H为渠道水深，m；v为渠道水流流速，m/s；R为平均水力深度，即渠道过水断面面积与水面宽度的比值，m；Q为平均流量，m3/s；Q0为渠道净流量，m3/s；C1、C2、C3、C4为常数[1]；A、m为土壤透水性参数[1, 2].

上述5种经验公式将流量、水深、湿周、流速中的一种或几种影响因素作为变量来计算渠道渗漏量.5种经验公式各有特点.

1) 戴维斯-威尔逊公式选择渠道湿周、水深和流速作为变量，反映了渠道渗漏与湿周、水深的正相关关系和与流速的负相关关系.该公式是针对衬砌渠道提出来的，不同衬砌形式对渠道渗漏的影响主要通过常数C1来体现.

2) 莫里兹公式选择流量和流速作为变量来确定渠道渗漏量，公式中的Q/v也就是渠道过水断面的面积，反映了渗漏量与渠道过水断面面积的正相关关系.常数C2则体现了渠床土壤对渗漏的影响.

3) Ingham公式反映了湿周和渠道水深与渠道渗漏量的正相关关系.该公式在应用时，需要根据实验率定常数C3.

4) Molesworth公式反映了渗漏量与湿周、渠道水力半径和土壤之间的关系.其中，反映土壤质地的常数C4，现有文献仅提供了粘土和砂土两种土质的取值，其他土质则需根据实测资料确定.

5) 考斯加可夫公式形式简单，仅考虑了土壤和流量对渠道渗漏的影响，且采用2个土壤参数A、m来反映渠床土壤的影响.在实际应用时，需要根据渠床土壤质地来确定它们参数值.

2.2 理论分析

基于达西定律，渠道自由渗漏量的理论公式一般形式为[7]

$q=k\left( b+aH \right)$    (6)

式中：q为渠道单位长度的渗漏量；k为渠床的渗透系数；b为渠底宽度，m；a为根据渗流理论推导得来的系数，与边坡系数β和渠道宽深比α有关，其他符号意义同前.

前面介绍5种经验公式可分为3类：第1类通过水深、湿周等渠道断面几何尺寸来确定损失量，如Ingham公式和Molesworth公式；第2类是通过渠道流量来计算，如考斯加可夫公式；第3类是通过渠道的几何尺寸及流速来计算，如戴维斯-威尔逊公式.实际上，在渠道水流运动中，水深、湿周、流速和流量有如下关系：

$Q=\left( \alpha +\beta \right){{H}^{2}}v$    (7)
$P=\left( \alpha +2\sqrt{1+{{\beta }^{2}}} \right)H$    (8)
$v=C\sqrt{Ri}=\frac{1}{n}\sqrt[6]{R}\cdot \sqrt{Ri}=\chi {{H}^{2/3}}$    (9)

式中：α为与渠道设计水深对应的宽深比，等于b/H；β为边坡系数；χ为系数，设计渠道时底坡i和糙率n一定，χ与宽深比α和边坡系数β有关；其余符号意义同前.

根据式(7)、(8)、(9)，对计算渠道渗漏的理论公式和几种经验公式作如下变换.

理论公式：

$\begin{align} & q=k\left( b+aH \right)\text{=}k\left( \alpha +a \right)H \\ & =\frac{k\left( \alpha +a \right)}{{{\left[ \left( \alpha +\beta \right)\chi \right]}^{3/8}}}{{Q}^{3/8}} \end{align}$    (10)

戴维斯-威尔逊公式：

$\begin{align} & S=\frac{0.45{{C}_{1}}\left( \alpha +2\sqrt{1+{{\beta }^{2}}} \right)}{4\times {{10}^{3}}+3.65\sqrt{v}}{{H}^{^{4/3}}} \\ & =\frac{0.45{{C}_{1}}\left( \alpha +2\sqrt{1+{{\beta }^{2}}} \right)}{\left( 4\times {{10}^{3}}+3.65\sqrt{v} \right)\sqrt{\left( \alpha +\beta \right)\chi }}{{Q}^{1/2}} \end{align}$    (11)

莫里兹公式：

$\begin{align} & S=0.01145{{C}_{2}}\sqrt{Q/v}=0.01145{{C}_{2}}\sqrt{\alpha +\beta }H \\ & =\frac{0.01145{{C}_{2}}{{\left( \alpha +\beta \right)}^{1/8}}}{{{\chi }^{3/8}}}{{Q}^{3/8}} \end{align}$    (12)

Ingham公式：

$\begin{align} & S=0.001{{C}_{3}}PH=0.001{{C}_{3}}\left( \alpha +2\sqrt{1+{{\beta }^{2}}} \right){{H}^{2}} \\ & =\frac{0.001{{C}_{3}}\left( \alpha +2\sqrt{1+{{\beta }^{2}}} \right)}{{{\left[ \left( \alpha +\beta \right)\chi \right]}^{3/4}}}{{Q}^{3/4}} \end{align}$    (13)

Molesworth公式：

$\begin{align} & S={{C}_{4}}P\sqrt{R}={{C}_{4}}\frac{{{\left( \alpha +\beta \right)}^{1/2}}\left( \alpha +2\sqrt{1+{{\beta }^{2}}} \right)}{{{\left( \alpha +2\beta \right)}^{1/2}}}{{H}^{3/2}} \\ & =\frac{{{C}_{4}}\left( \alpha +2\sqrt{1+{{\beta }^{2}}} \right)}{{{\left( \alpha +2\beta \right)}^{1/2}}{{\left( \left( \alpha +\beta \right){{\chi }^{9}} \right)}^{1/16}}}{{Q}^{9/16}} \end{align}$    (14)

考斯加可夫公式：

$\begin{align} & S=\frac{A{{\left[ \left( \alpha +\beta \right)\chi \right]}^{1-m}}}{100}{{H}^{8\left( 1-m \right)/3}} \\ & =\frac{A{{Q}^{1-m}}}{100} \end{align}$    (15)

式(10)~(15)中符号意义同前.从上述各种公式的转化可看出，计算渠道渗漏的理论公式(6)和几种经验公式均可归纳为以下2种通用形式：

$S=N{{Q}^{\delta }}或S={{N}^{'}}{{H}^{\gamma }}$    (16)

式中：δ、γ分别为流量指数和水深指数，各公式的流量指数和水深指数汇总见表 1；N、N′为系数，与渠床的土壤渗透系数k有关，同时也与渠道断面具体尺寸和过水能力有关.

表 1 各类公式的流量指数和水深指数 Table 1 Values of flow indices and depth indices of different empirical formulas
公式名称 流量指数δ 水深指数γ
理论公式 3/8 1
戴维斯-威尔逊公式 1/2 4/3
莫里兹公式 3/8 1
Ingham公式 3/4 2
Molesworth公式 9/16 3/2
考斯加可夫公式 1-m 8(1-m)/3
注：表中的m为土壤的透水参数.
表选项

结合前面对渠道渗漏影响因素的分析，在经验公式转化为通用形式后，对比可看出：

1) 转化后的经验公式均包括宽深比α、边坡系数β、水深H(或流量Q)这几种变量以及一个系数，与理论公式一致.其中宽深比α、边坡系数β为渠道断面尺寸，水深H(或流量Q)为渠道水流水力特征参数，可见经验公式都考虑了渠道断面和水力特性这两类影响因素.

2) 4种经验公式均考虑了土壤对渠道渗漏的影响，在公式中均是通过常数项来体现，例如莫里兹公式、Ingham公式以及Molesworth公式中的C2~C4值和考斯加可夫公式中的A值，可见经验公式对土壤因素的考虑比较简单.

3) 5种经验公式均为计算自由渗漏的公式，考虑地下水位顶托渗漏流的影响时，一般是在自由渗漏的基础上乘以一个地下水顶托系数来进行修正.

4) 仅戴维斯-威尔逊公式考虑了衬砌因素对渠道渗漏的影响，且通过常数项来体现.其他4种公式对衬砌因素均未考虑.

几种经验公式均可转换成式(16)的形式，与理论公式的形式一致.但由于各公式的适用条件及选择的主要影响因素不同，每种公式的参数(C1~C4、A、m等)在计算时需根据实际情况来确定.

3 实例计算

伊犁喀什河下游灌区位于新疆伊犁河北岸，东西长132.0 km，南北平均宽18.5 km，控制面积20.8万hm2，有效灌溉面积9.4万hm2.灌区自东向西年降水量337~148 mm，年蒸发量1 600~2 117 mm，年平均温度8.3~9.9℃，年日照时数2 700~2 800 h.灌区灌溉系统完善，渠道分为总干渠、干渠、支渠、斗渠和农渠5级.总干渠2条，总长12.9 km；干渠4条，总长189.5 km；支渠352条，总长919.7 km；总干渠、干渠和支渠的渠系配套建筑物394座.灌区人口82万，属大(2)型灌区，粮油产量占自治州38%以上，是自治州主要粮、油、甜菜等作物生产基地.正确计算该灌区内渠道渗漏损失量，确定各级渠道水利用系数及全灌区灌溉水利用系数，对进一步明确节水改造工程重点、全面提高用水效率具有重要的意义.

根据灌区内渠道情况，选择中间无支流、长度满足要求且未衬砌的代表性渠段，观测上、下游两个断面同一时段的流量，其差值即为损失流量.根据所选取的典型土渠渠段及测流数据，分别利用各种经验公式计算典型渠道单位渠长的输水损失.由于戴维斯-威尔逊公式仅适用于衬砌渠道，故在此不讨论.根据该地区土壤志中典型断面的粒径分析和现场经验判断，渠床土壤存在分层和分布不均的情况，难以准确确定各渠段及各层土质，本文根据实测资料推求每种公式相应的土壤参数，再代入公式中计算单位渠长渗漏损失.计算结果见表 2.表 2中，Q1为上游断面流量；Q2为下游断面流量；L为测流渠段长度；SM、SI、SMO、SK分别为采用莫里兹公式、Ingham公式、Molesworth公式及考斯加可夫公式计算的单位渠长输水损失量；S实表示根据实际测流资料计算的单位渠长输水损失量.各类公式计算的不同级别渠道的平均值见图 1.计算结果与实测值的误差分析见表 3.

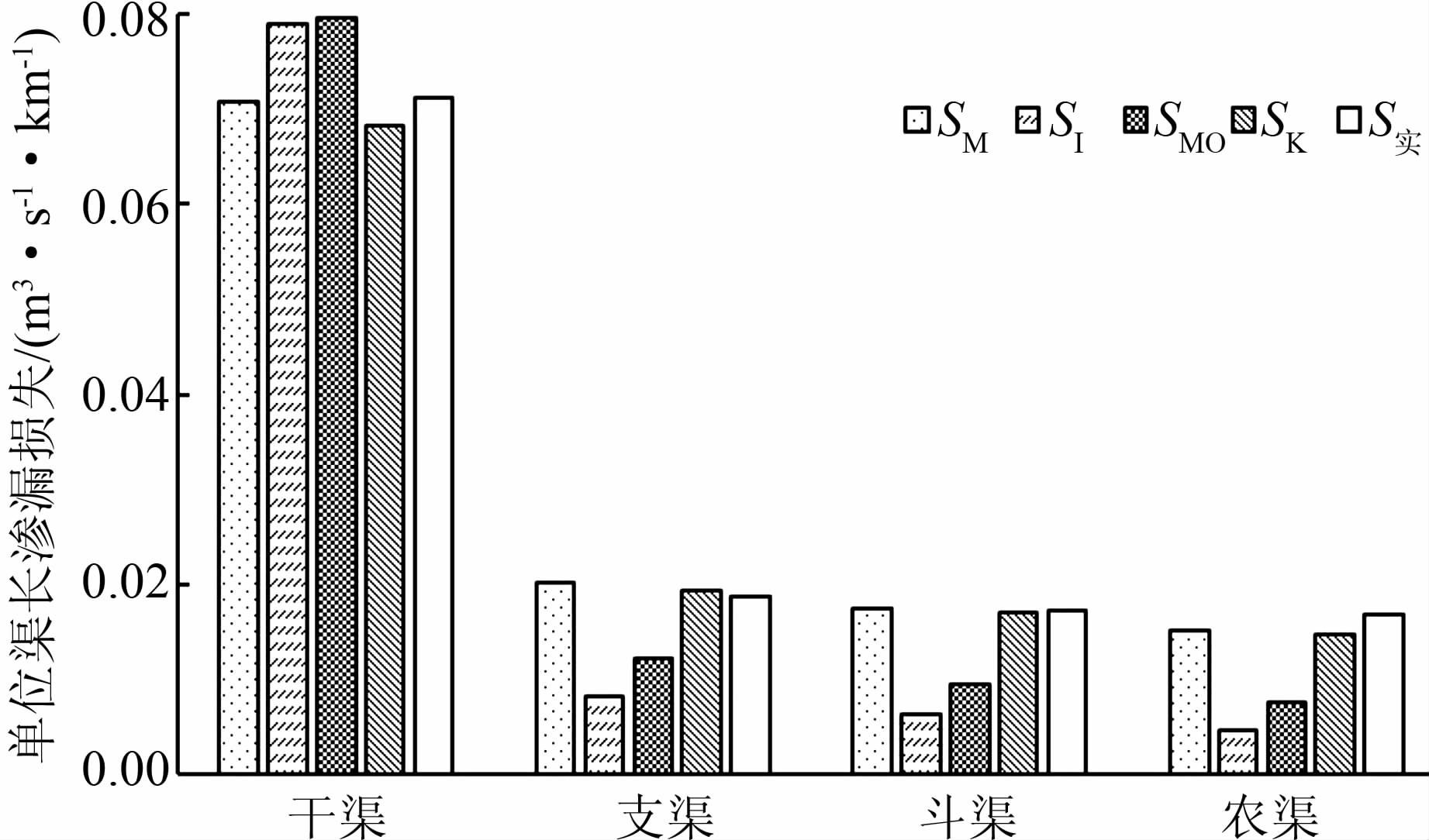
图 1 不同经验公式和实测计算结果对比图 Figure 1 Calculation results of different empirical formulas and measurement
图选项
表 2 典型渠道单位渠长渗漏损失量计算结果 Table 2 Calculation results of seepage losses of unit length of typical canal
渠道 编号 Q1/
(m3·s-1)		 Q2/
(m3·s-1)		 L/
km		 Q平均/
(m3·s-1)		 SM/(m3·
s-1·km-1)		 SI/(m3·
s-1·km-1)		 SMO/(m3·
s-1·km-1)		 SK/(m3·
s-1·km-1)		 S实/(m3·
s-1·km-1)
干渠 1 7.720 6.574 17.150 7.147 0.069 5 0.075 9 0.077 7 0.066 9 0.066 8
2 8.560 7.200 18.000 7.880 0.071 9 0.082 1 0.081 5 0.069 5 0.075 6
平均 8.140 6.887 17.575 7.514 0.070 7 0.079 0 0.079 6 0.068 2 0.071 2
支渠 1 0.150 0.130 1.450 0.140 0.015 8 0.004 1 0.008 3 0.014 9 0.013 8
2 0.446 0.362 3.100 0.404 0.023 1 0.009 8 0.014 3 0.022 3 0.027 1
3 0.172 0.139 3.600 0.156 0.016 4 0.004 4 0.008 7 0.015 5 0.009 2
4 0.100 0.086 1.010 0.093 0.013 7 0.002 9 0.006 8 0.012 7 0.013 9
5 0.400 0.336 2.100 0.368 0.022 3 0.009 1 0.013 6 0.021 5 0.030 5
6 0.947 0.820 7.200 0.884 0.030 7 0.018 9 0.022 0 0.030 1 0.017 6
平均 0.369 0.312 3.077 0.341 0.020 3 0.008 2 0.012 3 0.019 5 0.018 7
斗渠 1 0.450 0.378 1.700 0.414 0.022 8 0.011 3 0.014 1 0.022 5 0.042 4
2 0.116 0.090 1.950 0.103 0.013 7 0.003 5 0.006 5 0.013 2 0.013 3
3 0.213 0.180 4.100 0.197 0.017 3 0.006 0 0.009 3 0.016 9 0.008 0
4 0.196 0.161 2.110 0.179 0.016 7 0.005 5 0.008 8 0.016 3 0.016 6
5 0.249 0.222 2.615 0.236 0.015 6 0.004 7 0.007 9 0.015 2 0.013 0
6 0.163 0.133 2.300 0.148 0.018 5 0.007 0 0.010 3 0.018 1 0.010 3
平均 0.231 0.194 2.463 0.213 0.017 4 0.006 3 0.009 5 0.017 0 0.017 3
农渠 1 0.187 0.153 2.500 0.170 0.016 4 0.005 6 0.008 5 0.016 0 0.013 6
2 0.182 0.155 2.500 0.169 0.016 3 0.005 5 0.008 5 0.015 9 0.010 8
3 0.124 0.093 2.100 0.109 0.013 9 0.003 8 0.006 7 0.013 5 0.014 8
4 0.181 0.138 1.890 0.160 0.016 0 0.005 3 0.008 2 0.015 6 0.022 8
5 0.100 0.084 0.710 0.092 0.013 1 0.003 3 0.006 1 0.012 6 0.022 5
平均 0.155 0.125 1.940 0.140 0.015 1 0.004 7 0.007 6 0.014 7 0.016 9
表选项

由表 2、表 3和图 1可知：

表 3 各类经验公式计算结果与实测值相对误差分析 Table 3 Relative error analysis of results of different empirical formulas and measurement
渠道类别 SM/(m3·
s-1·km-1)		 SM相对
误差/%		 SI/(m3·
s-1·km-1)		 SI相对
误差/%		 SMO/(m3·
s-1·km-1)		 SMO相对
误差/%		 SK/(m3·
s-1·km-1)		 SK相对
误差/%		 S实/(m3·
s-1·km-1)
干渠 0.070 70.68 0.079 010.96 0.079 611.86 0.068 24.22 0.071 2
支渠 0.020 38.75 0.008 256.11 0.012 334.15 0.019 54.31 0.018 7
斗渠 0.017 40.93 0.006 363.32 0.009 545.12 0.01701.43 0.017 3
农渠 0.015 110.47 0.004 772.17 0.007 654.99 0.014 712.75 0.016 9
平均相对误差 5.21 50.63 36.52 5.68
表选项

1) 4种经验公式计算的单位渠长渗漏损失都随着流量的减小而减小.

2) 就Ingham公式和Molesworth公式而言，其干渠单位渠长渗漏损失计算结果略大于实测值，相对误差分别为10.96%和11.86%，均大于其余两种公式.支、斗、农渠的单位渠长渗漏损失计算结果均小于实测值，且流量越小，两者相对误差越大.农渠的计算结果相对误差分别高达72.17%和54.99%.

3) 莫里兹公式和考斯加可夫公式计算干、支、斗、农渠的结果与实测结果相近.随着流量的减小，两种公式的计算结果与实测值的相对误差逐渐增大.

4) 利用4种公式对同一级渠道的单位渠长渗漏损失进行计算时，计算结果与实测值的平均相对误差从小到大依次为：莫里兹公式(5.21%)、考斯加可夫公式(5.68%)、Molesworth公式(36.52%)、Ingham公式(50.63%).即莫里兹公式的计算精度最高，考斯加可夫公式计算精度次之，Molesworth公式和Ingham公式误差较大.

结合前面对经验公式进行的理论分析，4种经验公式计算结果产生不同误差的主要原因在于公式形式的不同.首先，计算精度较好的莫里兹公式和考斯加可夫公式均选择流量作为变量，而计算误差较大的Molesworth公式和Ingham公式选择的是水深、湿周等渠道断面几何尺寸作为变量；其次，4种经验公式转化成通用形式后其流量指数和水深指数均不同(见表 1)，其中，理论公式(式(6)、式(10))流量指数和水深指数分别为0.375和1；莫里兹公式也分别为0.375和1，该公式计算的结果平均相对误差最小，计算精度最高；考斯加可夫公式在实例计算中流量指数取值为0.383，水深指数为1.021，计算精度次之.由此可见，当经验公式的流量指数和水深指数越接近理论公式的流量指数0.375和水深指数1，公式计算的结果平均相对误差越小，计算精度越高.

4 结论和建议

1) 渠道渗漏的影响因素主要包括渠床土壤、渠道断面形式和水力参数、衬砌条件和地下水埋深.常用的几种计算渠道渗漏的经验公式选取了流量、流速、渠道水深、湿周及土壤等影响渠道渗漏的主要因素中的一种或几种作为变量来计算渠道渗漏量.

2) 5种经验公式各有特点.戴维斯-威尔逊公式仅适用于衬砌渠道，而其他4种公式主要用于计算土渠渗漏量，也可通过考虑衬砌系数来计算衬砌渠道.考斯加可夫公式的形式最为简单，应用时仅需每条渠道的流量资料，而莫里兹公式、Ingham公式和Molesworth公式还需收集渠道的断面资料，计算湿周、流速等水力参数，在渠道数量多且同一渠道流量变化较大的灌区，因资料收集和分析计算的工作量较大，应用受到限制.

3) 几种主要的经验公式均可转换成与理论公式一致的通用形式：S=NQδ或S=N′Hγ，N、N′系数中包含了宽深比α、边坡系数β和土壤常数C.转化成通用形式后可看出，每种经验公式均反映了渠道断面尺寸和水力特性的影响，对土壤因素影响通过常数项来体现，对衬砌因素和地下水的影响均未考虑(戴维斯-威尔逊公式用于计算衬砌渠道渗漏除外).同时经实例计算验证，经验公式中流量指数δ或水深指数γ越接近于理论公式，其计算渠道渗漏结果越可靠.

4) Ingham公式和Molesworth公式在渠道流量较大时，其计算结果与实测值相对误差较小，但随着流量的减小，相对误差越来越大，计算结果可靠性较低.莫里兹公式和考斯加可夫公式在计算典型渠道单位渠长输水损失时，计算结果与实测值相近，相对误差较小，具有较高的可靠性.

5) 几种经验公式各有优点和不足，当渠道数量多、渠道断面资料有限时，可选择考斯加可夫公式；如果渠道资料较为详细，则优先选择莫里兹公式；Ingham公式和Molesworth公式在本实例计算中的相对误差较大.

需要说明的是，本文仅仅基于新疆伊犁喀什河下游灌区的土渠实测资料来比较几种公式的计算精度，关于衬砌条件下的研究还有待于更多的资料来验证.

致谢: 伊犁喀什河下游灌区管理处的迪力木拉提、龙跃辉、甫拉提等人员参与了实际资料的测试工作.
参考文献
[1] 克拉茨D B. 灌溉渠道衬砌[M]. 何丕承, 译. 北京: 水利出版社, 1980.
Kratz D B. The Irrigation Canal Lining[M]. Beijing: China Hydraulic Press, 1980.
[2] 考斯加可夫A H. 土壤改良原理[M]. 陈益秋, 译. 北京: 中国工业出版社, 1965.
Kostiakov A H. Soil Improvement Schematic[M]. Beijing: China Building Industry Press, 1965.
[3] 门宝辉. 渠道流量损失及水利用系数公式的探讨[J]. 中国农村水利水电, 2000(2): 33–34.
Men Baohui. Study of the formula of channel flow loss and water use coefficient[J]. China Rural Water and Hydropower, 2000(2): 33–34.
[4] 谢崇宝, LanceJ M, 崔远来, 等. 大中型灌区干渠输配水渗漏损失经验公式探讨[J]. 中国农村水利水电, 2003(2): 20–22.
Xie Chongbao, Lance J M, Cui Yuanlai, et al. Discussion on the empiric formula for water-transportation-and-allocation seepage loss of main canal of large-and-middle-sized irrigation district[J]. China Rural Water and Hydropower, 2003(2): 20–22.
[5] 李红星, 樊贵盛. 影响非饱和土渠床入渗能力主导因素的试验研究[J]. 水利学报, 2009, 40(5): 630–634.
Li Hongxing, Fan Guisheng. Experimental study on main factors influencing the infiltration capacity of unsaturated earth canal[J]. Journal of Hydraulic Engineering, 2009, 40(5): 630–634.
[6] 侯慧敏, 戴星亮, 王之君. 不同土壤结构对渠道输水损失的影响研究[J]. 甘肃科技, 2009, 25(4): 44–47.
Hou Huimin, Dai Xingliang, Wang Zhijun. Research on the influence of different soil structure on the channel water loss[J]. Gansu Science and Technology, 2009, 25(4): 44–47.
[7] 张蔚榛. 地下水与土壤水动力学[M]. 北京: 中国水利水电出版社, 1996.
Zhang Weizhen. Groundwater and Soil Water Dynamics[M]. Beijing: China Water & Power Press, 1996.
[8] 野村安治·井上光弘, 刘新平, 王丹. 灌溉渠道的渗漏损失[J]. 水资源与水工程学报, 1990(3): 99–105.
YeCun Anzhi, Liu Xinping, Wang Dan. The irrigation channel leakage loss[J]. Journal of Water Resources and Water Engineering, 1990(3): 99–105.
[9] 李红星, 樊贵盛. 渠道水深对渠床渗漏量影响研究[J]. 太原理工大学学报, 2007, 38(1): 56–59.
Li Hongxing, Fan Guisheng. Study of the influence of canal water depth on canal seepage[J]. Journal of Taiyuan University of Technology, 2007, 38(1): 56–59.
[10] 雷声隆, 罗强, 张瑜芳, 等. 防渗渠道输水损失的估算[J]. 灌溉排水学报, 2003, 22(3): 7–10.
Lei Shenglong, Luo Qiang, Zhang Yufang, et al. Estimating seepage loss of lined canal[J]. Journal of Irrigation and Drainage, 2003, 22(3): 7–10.
[11] 罗玉峰, 崔远来, 郑祖金. 河渠渗漏量计算方法研究进展[J]. 水科学进展, 2005, 16(3): 444–449.
Luo Yufeng, Cui Yuanlai, Zheng Zujing, et al. Research progress on methods of quantifying seepage from rivers and canals[J]. Advances In Water Science, 2005, 16(3): 444–449.
[12] 阿费爾扬诺夫C Φ, 李心铭. 关于地下水位的深度对渠道渗漏的影响[J]. 人民长江, 1955(9): 45–46.
Afar Stoyanov C Φ, Li Xinming. The influence of the depth of the underground water level on canal seepage[J]. Yangtze River, 1955(9): 45–46.
[13] GB 50288-99灌溉与排水工程设计规范[S]. 北京: 中国计划出版社, 1999.
GB 50288-99 Code for Design of Irrigation and Drainage Engineering[S]. Beijing: China Planning Press, 1999.
[14] 郭元裕. 农田水利学[M]. 北京: 中国水利水电出版社, 1997.
Guo Yuanyu. Irrigation and Drainage[M]. Beijing: China Water & Power Press, 1997.
[15] 高峰, 黄修桥, 王景雷, 等. 渠道防渗与灌溉用水有效利用系数关系分析[J]. 中国水利, 2009(3): 22–24.
Gao Feng, Huang Xiuqiao, Wang Jinglei, et al. Relationship between canal lining and effective utilization coefficient of irrigated water[J]. China Water Resources, 2009(3): 22–24.