文章信息
- 刘琦, 龙新平, 陈正文, 薛胜雄, 季斌
- LIU Qi, LONG Xinping, CHEN Zhengwen, XUE Shengxiong, JI Bin
- 90°弯管液固两相流动冲蚀磨损的数值模拟
- Numerical simulation of erosion damage in liquid-solid elbow flow
- 武汉大学学报(工学版), 2018, 51(5): 443-450
- Engineering Journal of Wuhan University, 2018, 51(5): 443-450
- http://dx.doi.org/10.14188/j.1671-8844.2018-05-012
-
文章历史
- 收稿日期: 2017-11-29
2. 中国舰船研究设计中心,湖北 武汉 430072;
3. 合肥通用机械研究院,安徽 合肥 230031
2. China Ship Development and Design Center, Wuhan 430072, China;
3. Hefei General Machinery Research Institute, Hefei 230031, China
冲蚀磨损是一种普遍的磨损破坏形式,它是指固体表面材料与含有固体颗粒的流体介质相接触并发生相对运动时所导致固体材料损耗的现象.冲蚀磨损根据流体介质的不同又可以具体细分为液固冲蚀磨损和气固冲蚀磨损两大类.由于细微的固体颗粒广泛存在于流体介质中,因此冲蚀磨损是众多工程应用中一种常见的且具有共性的现象,通常它会造成一系列工程问题,带来巨大的经济损失,甚至导致严重的失效事故.弯管是管道系统中的常用部件,弯管部位的磨损速率要比直管段高出50倍[1],它是管道系统中最容易出现失效的管件;流体在弯管处的流动状态将发生改变,会呈现比较丰富的流动现象,具有一定的代表性.因此,本文最终选用90°弯管几何体作为研究对象.
近年来,基于CFD的磨损预测研究得到国内外学者的广泛关注,其在石油化工、机械制造等领域也逐渐得到广泛应用.Edwards等人[2]对气固两相流通过弯管和三通管的磨损进行了模拟分析,结果表明增大弯管曲率半径或者使用带堵头的三通管替代弯管都能有效减小磨损.丁矿等人[3]采用E/CRC磨损模型对直角弯管内液固两相流动造成的磨损进行了模拟分析,结果表明在弯管转角处以及弯管下游的管道内侧壁面的磨损较为严重.
目前,大量的相关研究工作都是基于流场计算正确、磨损模型合理的大前提下开展的,而针对磨损计算方案本身的研究并不充分.针对这一现状,本文以90°弯管为研究对象,主要针对碰撞模型和磨损模型对磨损预测的影响进行研究,以期深入了解各参数变量对磨损计算的影响规律,建立一套合理可靠的磨损预测方案,为后续的工程应用提供理论支撑.
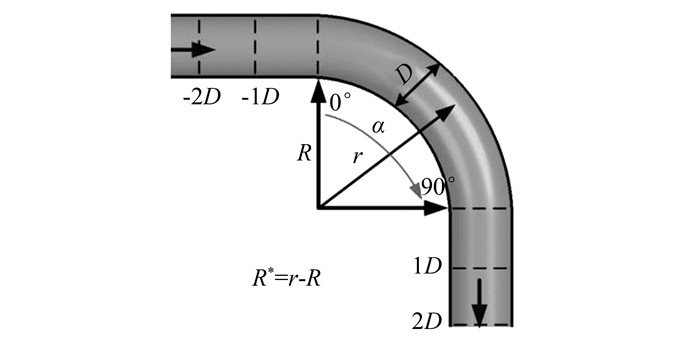
1 计算模型和数值方法本文采用Zeng等人[4]的实验数据进行磨损预测对比,弯管结构如图 1所示.由于该实验中固体颗粒的体积分数较低,因此采用欧拉-拉格朗日方法对液固两相流动进行求解,将流体相视为连续的介质,在欧拉坐标系下对其控制方程进行求解,将颗粒相视为离散的介质,利用拉格朗日法对每个颗粒进行追踪求解,并做出以下假设:1)不考虑颗粒之间的相互作用,并忽略颗粒自身的旋转作用;2)颗粒具有相同的密度和粒径,忽略粒径分布的影响;3)忽略由磨损导致的弯管壁面几何形状的改变.
|
| 图 1 90°弯管模型示意图 Fig. 1 Sketch of 90° elbow geometry |
流动的运动规律受到质量守恒以及动量守恒这两大物理定律的支配,因此连续相的控制方程由质量守恒方程和Navier-Stokes方程构成,流体对颗粒的作用通过Navier-Stokes方程的源项体现.在对控制方程进行雷诺时均处理时,会多出一项所谓的代表湍流效应的雷诺应力项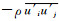
基于拉格朗日坐标系,可由牛顿第二定律直接导出颗粒运动的控制方程:
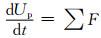 (1)
(1)
式中,∑F表示颗粒运动过程中受到的单位质量下的合外力.根据所计算的工况,本文将考虑颗粒的拖曳力、压力梯度力以及虚拟质量力.其中,单位质量颗粒所受的拖曳力可以表达为
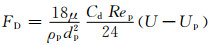 (2)
(2)
式中: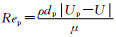
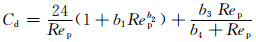 (3)
(3)
式中,各参数由下式确定:
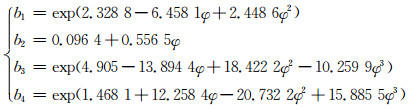 (4)
(4)
其中:φ=s/S为所谓的形状因子,s表示与真实颗粒(球形或非球形颗粒)同体积的球体固体颗粒的当量表面积,S表示真实固体颗粒的实际表面积.因此,当形状因子φ=1时,颗粒为严格意义上的球体,φ越小,表示颗粒的形状越不圆整.φ < 1时,HL关联式的拖曳力系数大于球形颗粒的拖曳力系数,并且当φ越小时,相同颗粒雷诺数下的拖曳力系数值越大.
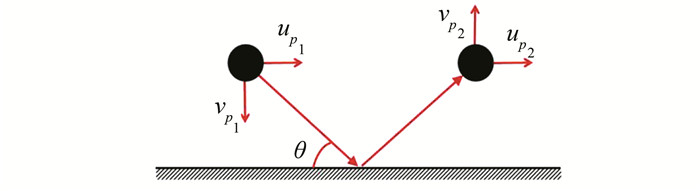
1.3 碰撞模型颗粒在流场中进行运动时,可能会与壁面发生碰撞从而改变其运动状态.固体颗粒与壁面发生碰撞前后速度分布如图 2所示,一般可以采用碰撞弹性恢复系数来描述颗粒在与壁面发生碰撞前后的速度变化.弹性恢复系数是由法向分量en和切向分量et来表示,其表达式如下:
|
| 图 2 颗粒与壁面碰撞示意图 Fig. 2 Sketch of particle impact on wall |
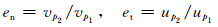 (5)
(5)
式中,en和et分别表示颗粒在与壁面发生碰撞前后,在垂直于壁面方向和平行于壁面方向(即法向和切向)动量的改变率.因此,当恢复系数同时都为1时,表示颗粒与壁面发生的碰撞为完全弹性碰撞.在真实情况下,由于颗粒的入射角度不同,颗粒与壁面发生碰撞后的法向和切向动量大小将发生不同程度的改变.
Grant和Tabakoff[6]基于碰撞试验提出了一个得到广泛应用的碰撞模型,表示如下:
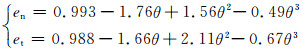 (6)
(6)
式中,θ表示固体颗粒与壁面发生撞击时的冲击角度.
Forder[7]经过研究提出一个考虑颗粒与壁面碰撞前后的能量损失的碰撞模型,其表达式为
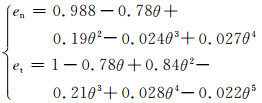 (7)
(7)
Sommerfeld和Huber[8]认为颗粒与壁面碰撞导致的动量损失主要发生在法向方向,切向方向颗粒的速度变化可以忽略,因此提出一个新的壁面碰撞模型:
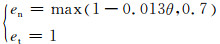 (8)
(8)
Neilson和Gilchrist[9]对气固两相流的磨损情况开展了一系列试验研究,提出一个新的磨损预测公式,该公式由切削磨损和变形磨损两部分构成:
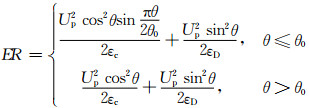 (9)
(9)
式中:θ0为过渡角度,取值为45°;εc和εD分别为切削系数和变形系数,分别取值3.332×107和7.742×107.为便于表述,本文将该模型命名为Neilson磨损模型.
Albert[10]通过大量试验得出一个针对碳钢和铝材的磨损预测模型,该模型的通用形式为
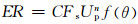 (10)
(10)
式中:C为与壁面材料布氏硬度相关的常系数;Fs为固体颗粒的形状系数,当颗粒为规整的球形时取值为0.2,半球形颗粒取值为0.53,带有尖角的颗粒其取值为1.0;Up为颗粒的撞击速度;n为速度指数,该模型中取值为1.73;f(θ)为碰撞角函数,其具体表达式为
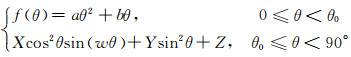 (11)
(11)
式(11)中的经验系数取值与壁面材料的状态和性质相关.
DNV研究人员[11]通过大量试验研究提出一个适用于多种材料的磨损预测公式,采用Albert模型的形式可以将其表达为
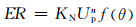 (12)
(12)
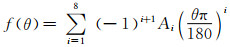 (13)
(13)
式中,对于碳钢,KN取值为2.0×10-9,速度指数取值为2.6.
Oka等人[12, 13]基于大量试验数据,将冲蚀磨损的几个重要因素进行归纳总结,提出了一个新的磨损预测方程:
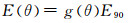 (14)
(14)
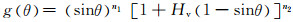 (15)
(15)
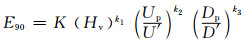 (16)
(16)
式中:n1 = s1(Hv)q1;n2 =s2(Hv)q2;k2 = 2.3(Hv)0.038;Hv为材料的Vickers数,表征材料的硬度;U′为颗粒参考速度,取值为104 m/s;颗粒基准直径D′=326 μm.
Zhang等人[14]的研究发现,Albert磨损模型中的速度指数1.73偏小,基于试验数据将速度指数修正为2.41,并提出一个新的碰撞角函数:
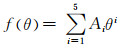 (17)
(17)
式中,经验系数见文献[19].
Vieria等人[15]基于气固两相流的磨损试验,提出了一个新的磨损计算公式:
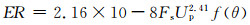 (18)
(18)
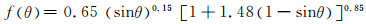 (19)
(19)
Peng等人[16]基于大量数值模拟结果拟合出一个磨损预测公式:
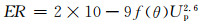 (20)
(20)
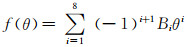 (21)
(21)
上述7种磨损模型都可以转化为如下形式:
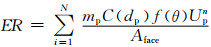 (22)
(22)
式中:mp为颗粒质量流量;C(dp)为与颗粒性质相关的函数,根据颗粒形状、硬度等计算出来同为定值;f(θ)为碰撞函数;Up为颗粒的碰撞速度;n为速度指数;Aface为碰撞壁面的面积.本文采用商业软件Ansys Fluent进行计算分析,该软件是一款得到广泛应用的通用性较强的CFD软件包[17, 18],上述碰撞模型和磨损模型通过UDF接口导入软件.
1.5 90°弯管网格划分为了对磨损预测方案的可靠性进行评估,采用Zeng等人[7]的实验数据作为基准.如图 1所示,定义R*=r-R,因此当R*/D=0时表示弯管的内侧壁面,当R*/D=1时表示外侧壁面,弯管入口处为0°,弯管出口处为90°.该实验采用X65碳钢材料90°弯管,其管径D为50 mm,曲率半径为76.9 mm,实验中采用的流体介质为水,弯管进口流速为4 m/s.在数值模拟中,为了减小入口流动对模拟结果的影响,将弯管进口的直管段延长15D;同时,为了减小出口处可能出现的回流影响从而使得计算更加稳定,将弯管出口的直管段延长10D.
本文采用SST k-ω湍流模型,该模型在边界层采用标准k-ω模型进行计算,逐渐过渡到边界层外层以后采用k-ε模型进行计算.为了能够准确捕捉到壁面附近存在较大梯度的流场信息,需要在黏性底层布置10层左右的边界层网格,并且越靠近壁面网格就越细密.采用网格数为100万、130万和180万的3套网格进行了计算,比较了3种不同网格数量下流体在60°弯管截面处的速度分布.结果表明100万的网格数量能够得到网格无关的数值解.最终采用的计算网格如图 3所示.
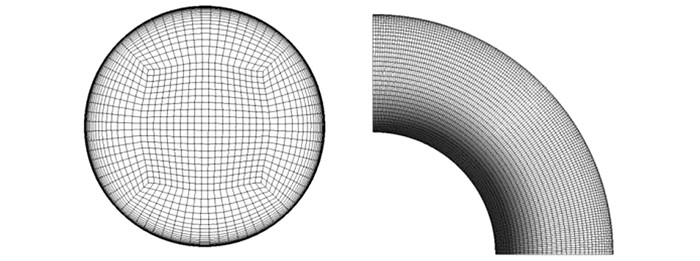
|
| 图 3 弯管网格划分情况 Fig. 3 Sketch of elbow section meshing |
进行网格无关性验证之后,表明已经可以得到不再随着网格数增加而发生显著变化的流场结果.同样,在计算磨损时其结果应该是统计意义上的平均值,也就是说所得到的磨损速率不再随着统计颗粒数目的增加而发生明显的变化.因此,需要对颗粒数目进行相应的无关性分析及验证.图 4所示为颗粒数目无关性验证结果,随着统计的颗粒数目的增加,磨损速率逐渐趋于定值,当颗粒数目超过12万时,无量纲最大磨损速率不再发生显著变化.因此,后续的计算中计算磨损速率时,统计的颗粒数目为13万到15万左右,这已经能够满足颗粒无关性的要求.
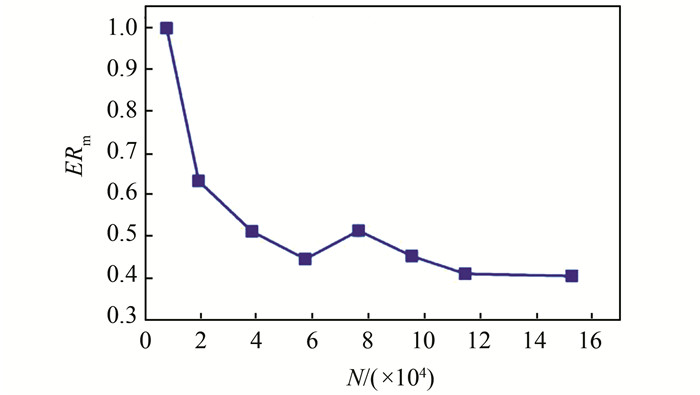
|
| 图 4 颗粒数目无关性分析 Fig. 4 Independence analysis of particle number |
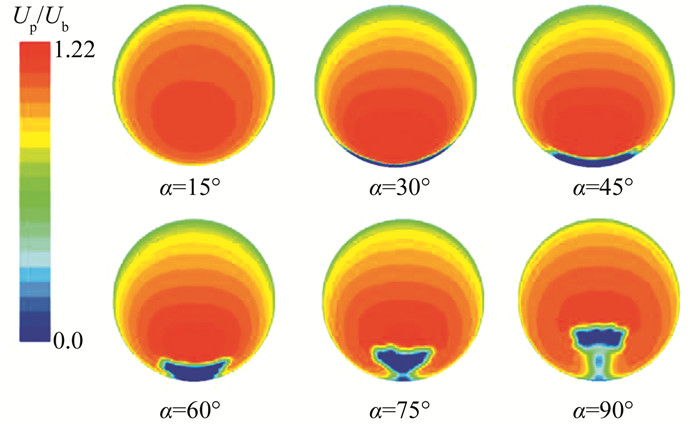
图 5所示为弯管不同截面处的颗粒速度分布情况,随着弯管角度的不断增大,颗粒速度分布在弯管内侧逐渐出现低速区,这个低速区不断从弯管内侧壁面增大收缩,到了出口截面已经发展到靠近弯管中心的区域.值得注意的是,图 5是通过统计颗粒经过每个网格的速度之和然后求取其平均值得到的.因此,图中蓝色区域速度近似等于0,并不是表示此处的颗粒速度为0,而是表明颗粒没有从该区域经过,或者表示颗粒从该区域通过的概率极低,也即代表颗粒真空区.
|
| 图 5 弯管不同截面处颗粒速度分布 Fig. 5 Contour maps of particle velocity at different sections of elbow |
图 6所示为颗粒与壁面碰撞速度的分布情况.图中弯管内侧的蓝色区域表示颗粒与壁面没有发生碰撞,该区域主要分布在弯管内侧.颗粒与壁面的最大碰撞速度为1.37 m/s,最大碰撞速度主要分布在弯管出口处的两侧壁面,这可能是由于弯管截面上形成的二次流动拖拽颗粒运动所导致的.

|
| 图 6 颗粒与壁面碰撞速度分布 Fig. 6 Contour maps of particle impact velocity |
本文基于SST湍流模型计算的流场采用不同的碰撞模型对颗粒的运动轨迹进行积分,并统计15万颗粒的运动规律,最后将颗粒与壁面的碰撞信息利用Oka磨损模型进行计算,以探讨碰撞模型对磨损预测的影响.
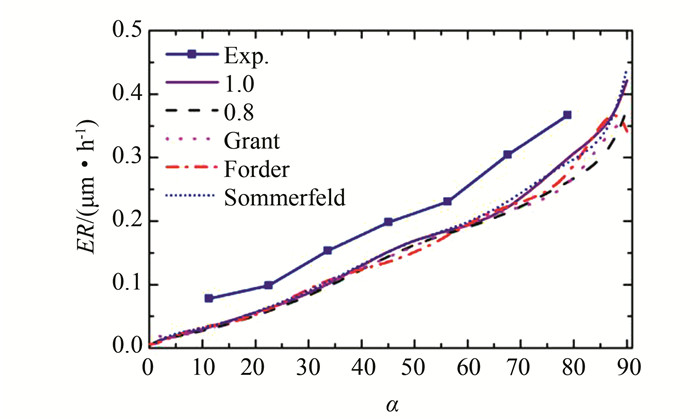
图 7所示为采用不同碰撞模型计算的弯管最外侧壁面的磨损分布情况.其中“1.0”表示法向恢复系数与切向恢复系数都为1,也即代表颗粒与壁面的碰撞为完全弹性碰撞,发生碰撞前后的能量没有损失;“0.8”表示法向和切向恢复系数都为0.8,也即表示颗粒与壁面发生碰撞前后动量损失20%;另外3种分别为前述Grant壁面碰撞模型、Forder壁面碰撞模型和Sommerfeld壁面碰撞模型.随着弯管角度的增加,这5种壁面碰撞恢复系数的设置所得的磨损预测结果都相应增大,只有Forder模型在85°以后出现微小的下降趋势.Grant模型在85°以后的预测结果区域平缓,而Sommerfeld模型在85°以后的磨损预测结果有斜率增大.这些差异相对较小,因此不排除是由于出口处颗粒运动趋于复杂的运动规律的随机性造成的.在0到30°的区域,所有模型的预测结果都能很好重合;在30°到90°区间,曲线开始出现分离,但是其偏差相对较小,并且所有模型的预测结果都与实验值呈现相同趋势.
综上所述,在本算例中碰撞模型的选择对最终磨损预测的影响并不明显,因此可以忽略碰撞模型对磨损计算带来的差异.在后面的计算分析中,壁面模型都采用得到广泛应用的Grant模型.
|
| 图 7 基于不同壁面碰撞模型弯管外侧壁面磨损分布 Fig. 7 Predicted erosion profile by different rebound models |
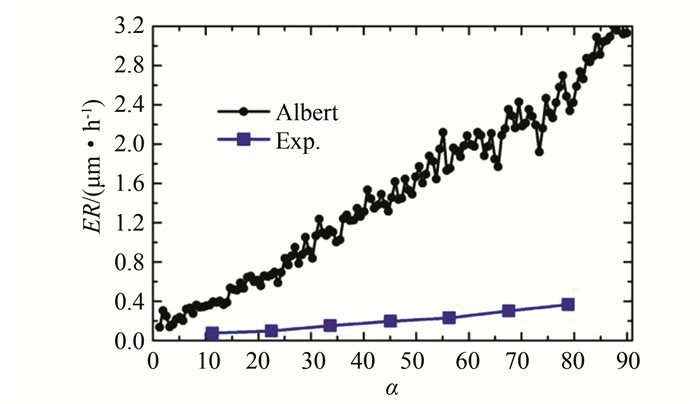
图 8所示为Albert磨损模型的磨损计算结果分布,其预测结果远远大于实验测量值,这是因为Albert磨损公式中的速度指数为1.73,但这并不是最佳值.Zhang等人[14]通过研究发现,Albert模型中的速度指数1.73虽然在一定条件的算例下可以得到较好的预测结果,但是在极大多数情况下采用该指数值计算得到的磨损量要比实际测量值高出很多倍.基于Zeng等人[4]的实验数据,本算例的计算结果也证实了Albert磨损模型远远高估了磨损预测值.
|
| 图 8 基于Albert磨损模型弯管外侧壁面磨损分布 Fig. 8 Predicted erosion profile based on Albert model |
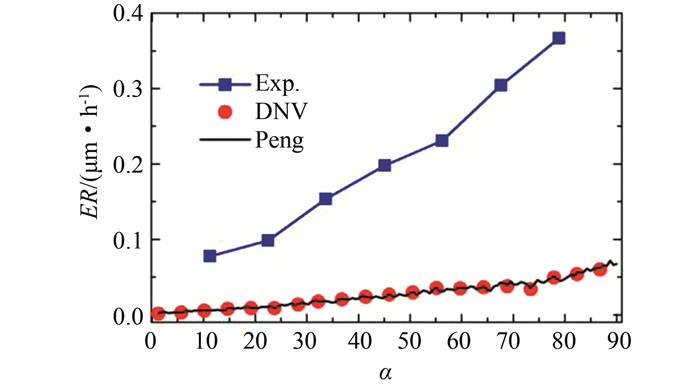
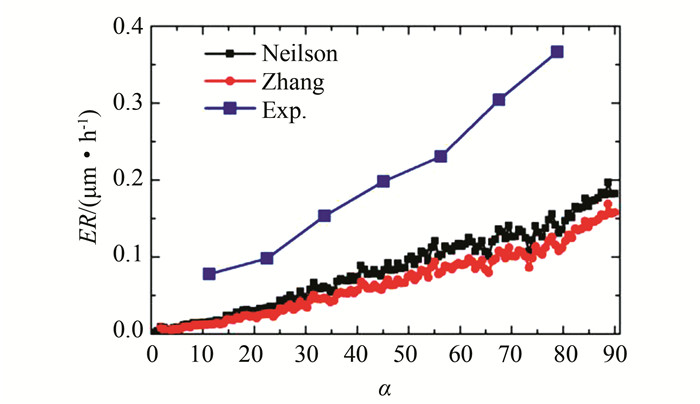
图 9所示为采用DNV磨损模型和Peng磨损模型的计算结果,可以发现这两种模型都大大低估了磨损值.有趣的是Peng模型和DNV模型的预测结果具有高度一致性,这是因为Peng模型是基于DNV模型进行大量数值模拟的预测结果拟合得到的.Neilson模型和Zhang模型的磨损预测结果如图 10所示,这两种模型都能较好地预测出弯管磨损的趋势,但是其磨损数值都相应偏小.
|
| 图 9 基于DNV磨损模型和Peng磨损模型弯管外侧壁面磨损分布 Fig. 9 Predicted erosion profile based on DNV model and Peng model |
|
| 图 10 基于Neilson磨损模型和Zhang磨损模型弯管外侧壁面磨损分布 Fig. 10 Predicted erosion profile based on Neilson model and Zhang model |
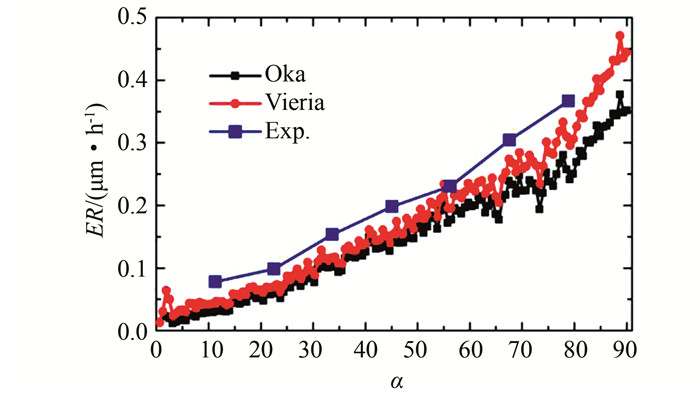
图 11所示为Oka模型和Vieria模型的预测结果,这2种磨损模型也都能较好地计算出弯管部分的磨损趋势,同时其预测的磨损值大小也与实验结果相近,其中Vieria模型与实验值更为接近,因此后续计算分析将采用该磨损模型.
|
| 图 11 基于Oka磨损模型和Vieria磨损模型弯管外侧壁面磨损分布 Fig. 11 Predicted erosion profile based on Oka model and Vieria model |
通常,颗粒的形状并不是严格意义上的球形,有的是椭球形,有的颗粒甚至带有尖角,因此考虑颗粒的形状对磨损预测的影响具有重要意义.通过设置4种不同的形状因子参数,将颗粒的形状影响通过颗粒控制方程中的拖曳力项进行考虑,在对颗粒轨迹进行积分运算后提取出颗粒与壁面碰撞的信息,并将其整合到磨损模型中进行磨损计算.
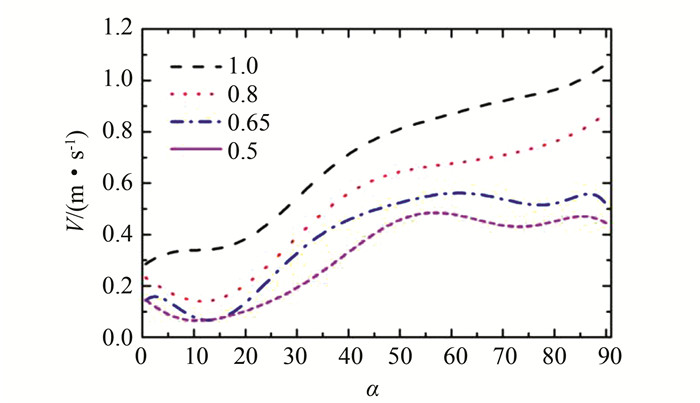
图 12所示为不同形状因子下碰撞速度分布曲线.当颗粒为球形时,在相同弯管角度下其碰撞速度最大;随着颗粒形状因子的减小,也即表示当颗粒越不规整时,其与壁面的碰撞速度越小.由拖曳力计算公式可知,当颗粒越不规整时,也即表示颗粒的形状因子越小时,在相同条件下其拖曳力系数值越大,这就说明液体对颗粒的作用也就越强烈,颗粒运动与流体流动的跟随性更好,因此颗粒在流体的拖拽下与壁面发生碰撞的速度越小.
|
| 图 12 不同形状因子弯管外侧壁面碰撞速度分布 Fig. 12 Predicted impact velocity using different shape factors |
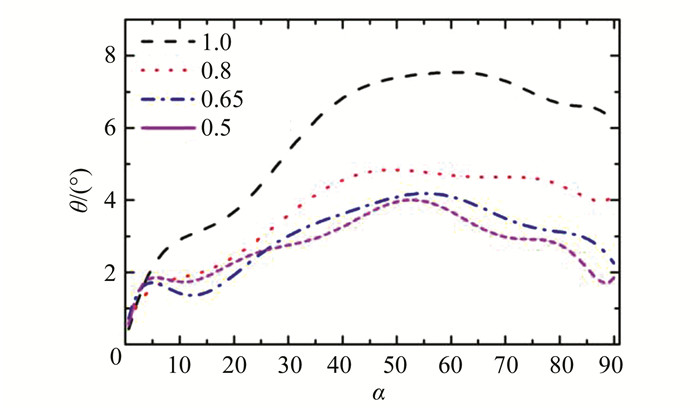
如图 13所示,随着形状因子的减小,颗粒与弯管外侧壁面的碰撞角度也相应减小.形状因子为1时的碰撞角度最大,形状因子为0.8时碰撞角度有明显减小,进一步降低形状因子后碰撞角度的减小幅度明显减小.
|
| 图 13 不同形状因子弯管外侧壁面碰撞角度分布 Fig. 13 Predicted impact angle usingdifferent shape factors |
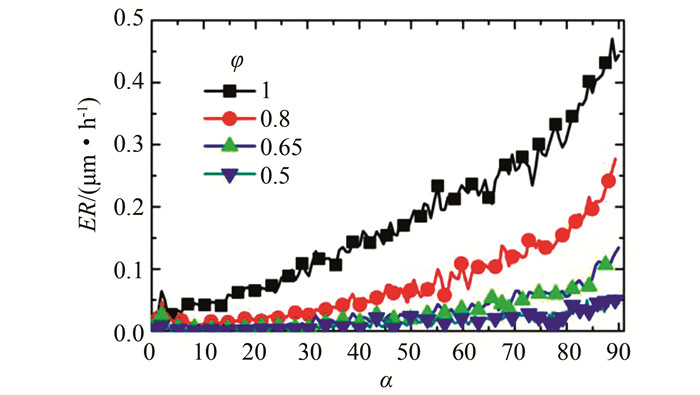
如图 14所示,弯管外侧壁面的磨损随着弯管角度的增加总体呈现增大的趋势.在相同的弯管角度下,形状因子越小颗粒对壁面造成的磨损也相应越小.结合上述分析,颗粒越不规整,其与流体的相互作用越强烈,颗粒与流体也就具有更佳的跟随性,颗粒与外侧壁面也就越不容易发生碰撞,颗粒与壁面的碰撞速度和碰撞角度呈现下降趋势,这就最终导致外侧壁面磨损程度的降低.
|
| 图 14 不同形状因子弯管外侧壁面磨损分布 Fig. 14 Predicted erosion profile using different shape factors |
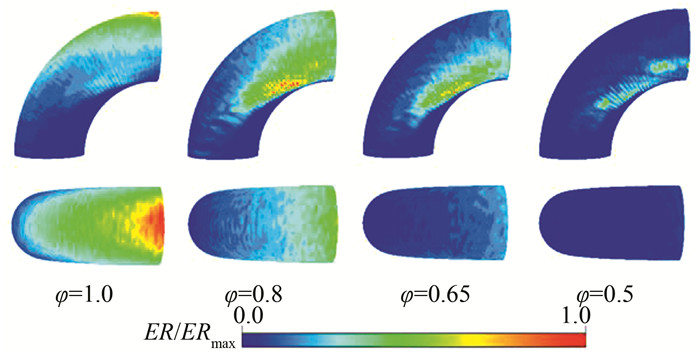
图 15给出了不同形状因子下弯管壁面的磨损分布情况,随着颗粒形状因子的减小,弯管壁面的磨损程度总体呈现下降趋势.当形状因子为0.8时,最大磨损率发生在弯管侧面;形状因子为0.65时,最大磨损率同样发生在侧面,但是此时最大磨损的区域相应减小;降低形状因子为0.5时,弯管外侧壁面已经几乎没有发生磨损,只有弯管侧面有一部分较小的磨损区域.
|
| 图 15 不同形状因子弯管壁面磨损预测分布 Fig. 15 Contour maps of predicted erosion using different shape factors |
本文以90°弯管为研究对象,采用数值模拟的方法对弯管内部的流场特性进行了分析,并对弯管内固液两相流的磨损预测方法进行了深入研究,探讨了碰撞模型、磨损模型和颗粒形状对磨损预测的影响规律,主要结论如下:
1) 基于CFD的磨损计算所统计的颗粒数目会对结果产生显著影响,本文的案例表明,当统计的颗粒数目超过12万时,磨损量不再随着颗粒数目的增加而发生明显变化.
2) 在碰撞模型的选择方面,采用5种不同的碰撞恢复系数进行了计算分析,结果表明,在本算例中碰撞模型的选择对最终磨损预测的影响并不明显,可以忽略碰撞模型对磨损计算带来的差异.
3) 对7种磨损模型分别进行了计算评估,结果表明,Albert磨损模型极大地高估了弯管的磨损情况,DNV磨损模型、Peng磨损模型、Zhang磨损模型以及Neilson磨损模型都较大地低估了弯管的磨损情况,Oka磨损模型和Vieria磨损模型与实验值最为接近.
4) 颗粒形状会对磨损预测产生重要影响,本文的算例表明,随着颗粒形状因子的减小,颗粒与壁面的相互作用减弱,磨损呈现下降趋势.
| [1] |
Tilly G P. Erosion caused by impact of solid particles[J]. Treatise on Materials Science & Technology, 1979, 13: 287-319. |
| [2] |
Edwards J K, Mclaury B S, Shirazi S A. Modeling solid particle erosion in elbows and plugged Tees[J]. Journal of Energy Resources Technology, 2001, 123(4): 277-284. DOI:10.1115/1.1413773 |
| [3] |
丁矿, 朱宏武, 张建华, 等. 直角弯管内液固两相流固体颗粒冲蚀磨损分析[J]. 油气储运, 2013, 32(3): 241-246. Ding Kuang, Zhu Hongwu, Zhang Jianhua, et al. Erosion wear analysis of solid particles in liquid-solid two-phase flow of right-angle bend pipe[J]. Oil and Gas Storage and Transportation, 2013, 32(3): 241-246. |
| [4] |
Zeng L, Zhang G A, Guo X P. Erosion-corrosion at different locations of X65 carbon steel elbow[J]. Corrosion Science, 2014, 85: 318-330. DOI:10.1016/j.corsci.2014.04.045 |
| [5] |
Haider A, Levenspiel O. Drag coefficient and terminal velocity of spherical and nonspherical particles[J]. Powder Technology, 1989, 58(1): 63-70. DOI:10.1016/0032-5910(89)80008-7 |
| [6] |
Grant G, Tabakoff W. Erosion prediction in turbomachinery resulting from environmental solid particles[J]. Journal of Aircraft, 1975, 12(5): 471-478. DOI:10.2514/3.59826 |
| [7] |
Forder A, Thew M, Harrison D. A numerical investigation of solid particle erosion experienced within oilfield control valves[J]. Wear, 1998, 216(2): 184-193. DOI:10.1016/S0043-1648(97)00217-2 |
| [8] |
Sommerfeld M, Huber N. Experimental analysis and modelling of particle-wall collisions[J]. International Journal of Multiphase Flow, 1999, 25(6-7): 1457-1489. DOI:10.1016/S0301-9322(99)00047-6 |
| [9] |
Neilson J H, Gilchrist A. Erosion by a stream of solid particles[J]. Wear, 1968, 11(2): 111-122. DOI:10.1016/0043-1648(68)90591-7 |
| [10] |
Ahlert K R. Effects of Particle Impingement Angle and Surface Wetting on Solid Particle Erosion of AISI 1018 Steel[M]. University of Tulsa, 1994.
|
| [11] |
Veritas D N. Erosive Wear in Piping Systems[S]. 1996.
|
| [12] |
Oka Y I, Okamura K, Yoshida T. Practical estimation of erosion damage caused by solid particle impact: Part 1: Effects of impact parameters on a predictive equation[J]. Wear, 2005, 259: 95-101. DOI:10.1016/j.wear.2005.01.039 |
| [13] |
Oka Y I, Yoshida T. Practical estimation of erosion damage caused by solid particle impact : Part 2: Mechanical properties of materials directly associated with erosion damage[J]. Wear, 2005, 259: 102-109. DOI:10.1016/j.wear.2005.01.040 |
| [14] |
Zhang Y, Reuterfors E P, Mclaury B S, et al. Comparison of computed and measured particle velocities and erosion in water and air flows[J]. Wear, 2007, 263: 330-338. DOI:10.1016/j.wear.2006.12.048 |
| [15] |
Vieira R E, Mansouri A, Mclaury B S, et al. Experimental and computational study of erosion in elbows due to sand particles in air flow[J]. Powder Technology, 2015, 288: 339-353. |
| [16] |
Peng W, Cao X. Numerical prediction of erosion distributions and solid particle trajectories in elbows for gas-solid flow[J]. Journal of Natural Gas Science & Engineering, 2016, 30: 455-470. |
| [17] |
肖惠民. 基于数值波浪水槽的波力直驱水轮机前导流口体型优选[J]. 武汉大学学报(工学版), 2017, 50(1): 125-128. Xiao Huimin. Configuration selection of front guide inlet for direct driving turbine based on numerical wave tank[J]. Engineering Journal of Wuhan University, 2017, 50(1): 125-128. |
| [18] |
杨秀萍, 任军, 张喆, 等. 正弦风场新月形覆冰导线动态气动力特性[J]. 武汉大学学报(工学版), 2017, 50(2): 285-289. Yang Xiuping, Ren Jun, Zhang Zhe, et al. Dynamic aerodynamic characteristics of iced conductor with crescent shape under sine wind field[J]. Engineering Journal of Wuhan University, 2017, 50(2): 285-289. |
 2018, Vol. 51
2018, Vol. 51




