文章信息
- 瞿合祚, 李晓明, 陈陈, 何乐
- QU Hezuo, LI Xiaoming, CHEN Chen, HE Le
- 基于卷积神经网络的电能质量扰动分类
- Classification of power quality disturbances using convolutional neural network
- 武汉大学学报(工学版), 2018, 51(6): 534-539
- Engineering Journal of Wuhan University, 2018, 51(6): 534-539
- http://dx.doi.org/10.14188/j.1671-8844.2018-06-011
-
文章历史
- 收稿日期: 2016-12-15
随着电力电子技术在电力系统各个环节的广泛应用,间歇性分布式电源的大量接入,用户负荷愈加多样化,冲激性和非线性负荷比例的提高等增加了电能质量扰动事件发生的可能性,对电力系统安全稳定运行产生较大危害.为了治理电能质量扰动,准确有效的扰动分类识别是重要的一步.
电能质量信号数据通常是对监测点的电压或电流波形进行恒定高频采样得到的一维数据.解决电能质量扰动分类问题的传统方法均是基于特征提取和模式分类两个步骤建立起电能质量扰动分类算法.特征提取通常是对扰动信号的时域或频域特征进行分析概括,提炼出较为显著的特征,主要采取的方法有短时傅立叶变换[1]、小波变换[2]、S变换[3]等.模式分类方面具有较多成熟的算法,如支持向量机[3-4]、k近邻[5]、神经网络、决策树[4]等.如文献[3]将聚类分析与S变换相结合提取电能质量扰动信号的特征,再使用直接支持向量机作为分类器;文献[4]采用傅立叶变换结合动态测度以及S变换提取扰动特征,作为决策树和支持向量机的分类特征进行扰动的识别.
传统方法存在的主要问题就是特征的提取需要人工参与,其特征提取是一个基于模型的过程,且该过程没有统一的方法指导,因而许多时候在做了大量工作后得到的特征并不能获得理想效果.如果能基于样本进行数据挖掘和深度学习,直接对扰动信号进行自适应的特征提取,势必会减小扰动分类算法的设计难度.
本文研究的是7类基本电能质量扰动的分类,包括骤升、中断、骤降、谐波、振荡、冲激和闪变.这7种扰动信号在时域上存在能用自然语言表述的显著特征和差异,而通过自然语言描述的波形特征,事实上是人脑对波形图像进行复杂抽象并理解后表达出来的事物特征[6],若能模仿人类大脑识别电能质量扰动特征的机理和过程,在一定程度上能实现特征的自适应提取.
当前深度学习理论中的卷积神经网络就是一种能够对原始图像进行直接学习的算法,被广泛应用于人脸识别、文字识别和目标跟踪等领域[7-8].本文尝试使用卷积神经网络对电能质量扰动信号样本进行学习,如何将一维电能质量信号转换为二维图像形式是运用CNN的关键问题.若直接将扰动信号的波形以一维形式打印渲染至图像作为样本,并使用卷积神经网络进行学习.由于此时图像尺度过大,势必会导致CNN的卷积核增大或网络层数增大,从而加大网络训练的时间和难度.因此,为了采用卷积神经网络进行电能质量扰动信号的分类,需要提出一种合适的方法将扰动信号的信息以图像的形式表现出来.
为了减小人工选取特征的难度,本文尝试运用卷积神经网络对电能质量扰动事件进行深度学习,进而提出一种时域信号的二维映射方法,并采用灰度表达对应信号采样点的值.然后以卷积神经网络LeNet-5[9]为基础确定合适的卷积神经网络结构,仿真结果证明了采用卷积神经网络进行电能质量扰动事件分类的有效性,且能避免人工进行特征提取的过程.
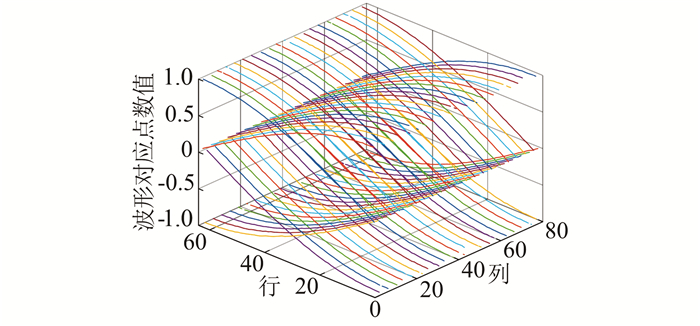
1 一维信号的二维映射方法电能质量扰动信号具有较强的周期性,因而可对一维扰动信号采样数据进行等长截取,并将其映射成二维矩阵中的行或列,实现信号的二维重构[10],如图 1所示.对一维信号进行二维映射能有效减小信号的尺度大小,使得扰动特征的分布更为聚集,有利于采取卷积神经网络进行扰动的特征学习和扰动识别.
|
| 图 1 截取一维信号重组成二维矩阵 Fig. 1 Restructure 1D signal to 2D matrix |
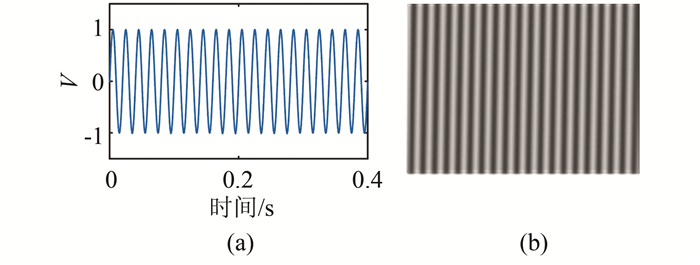
采用该映射方式能使较长的一维扰动信号以较小尺度的二维矩阵形式展现.对基频50 Hz的信号以12 800 Hz采样频率采样5 120点作为样本,以该样本为例进行二维映射.对图 2(a)中的一维信号的每64个采样点作为一列进行截断共得80列,最终映射结果为64行80列的二维矩阵(如图 1所示).本文采用灰度化的方式对所得到的二维矩阵进行可视化,即将原始信号值映射至离散灰度空间G={g|0≤g≤255, g∈Z},考虑到归一化扰动信号的采样值主要在区间[-2, 2]内,在映射前先对采样值做限制处理使之在区间[-2, 2]内.将一维信号x(n)映射至二维灰度图g(i, j)的过程如下:
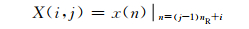 (1)
(1)
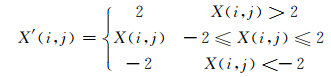 (2)
(2)
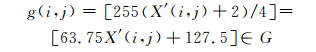 (3)
(3)
|
| 图 2 一维信号映射成二维灰度图 Fig. 2 Mapping 1D signal to 2D grayscale image |
其中:g(i, j)表示灰度图中第i行第j列的像素点的灰度值;nR表示二维矩阵的行数;[●]表示按四舍五入取整.
映射结果如图 2所示。
2 电能质量扰动信号的二维灰度表示参考文献[11],本文在Matlab下建立了7种基本电能质量扰动信号模型,如表 1所示.基波频率f0为50 Hz,采样频率fs为12.8 kHz,T为工频周期,u(t)为单位阶跃函数,每个样本的采样点数为5 120,即20个基波周期,时长0.4 s.为适应不同幅值的信号,电压幅值为归一化幅值,实际应用中相当于以电压峰值为基准的标幺值.按照前述方式对一维扰动信号样本进行截断重组和灰度化,映射为64行80列的二维灰度图,如图 3(a)~(g)所示依次为暂升、中断、暂降、谐波、振荡、冲激和闪变信号的一维图(左)和二维灰度图(右),所有左图的横坐标均表示时间.
| 信号类型 | 信号模型 | 参数 |
| 标准信号(C0) | v(t)=sin(ωt) | ω=2πf0 |
| 电压暂升(C1) | v(t)={1+k[u(t2)-u(t1)]}sin(ωt) | 0.1≤k≤0.9, 0.5T≤t2-t1≤30T |
| 电压中断(C2) | v(t)={1-k[u(t2)-u(t1)]}sin(ωt) | 0.9<k≤1, 0.5T≤t2-t1≤30T |
| 电压暂降(C3) | v(t)={1-k[u(t2)-u(t1)]}sin(ωt) | 0.1≤k≤0.9, 0.5T≤t2-t1≤30T |
| 谐波(C4) | 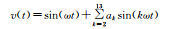 |
0.01<ak<0.2 |
| 暂态振荡(C5) | v(t)=sin(ωt)+ae-λ(t-t1)sin(βωt)u(t-t1) | 0.05<α<1, 15<λ<130, 14≤β<30 |
| 瞬态冲击(C6) | v(t)=sin(ωt)+a[u(t1)-u(t2)] | a>0.8, 1 ms<t2-t1<3 ms, |
| 电压闪变(C7) | v(t)=[1+αsin(βωt)]sin(ωt) | 0.05<α<0.2, 0.1<β<0.5 |

|
| 图 3 电能质量扰动事件波形和二维灰度图 Fig. 3 Wave and grayscale image of PQD |
在二维灰度图中,对应于电压暂升事件的部分灰度所能达到的最强明暗程度均会更明显,如图 3(a)中间部分条纹相较于两边的条纹,对比度提高.电压中断的电压有效值在短时间降低至10%有效值以下,相应地二维灰度图中电压中断发生时像素的灰度值在区间[121,134]内,对比度较低,故中断事件在二维灰度图中表现为一块较均匀的灰色区.电压暂降与电压中断类似,暂降事件对应像素的灰度取值在区间[70,185]内,此时对比度强于中断,弱于正常时刻,在二维图中相较于正常部分其颜色较浅.谐波的存在会对灰度图产生整体的影响,在二维图中部分区域的对比度会提高,另一部分的对比度则会降低,且这种影响在整个二维图中都有体现,主要表现为行方向的低对比度和高对比度条纹.发生振荡时相邻采样点的波形取值发生剧烈的变化,故对应的相邻像素点的灰度也会发生剧烈变化,使原本变化较为平滑的条纹呈现出马赛克状的变化区域,如图 3(e).当冲激发生时,在一两个采样点处的采样值会接近或超过阈值,使得相应的像素块的灰度突然降至0附近,或升至255附近,在二维图中会出现一个黑斑或亮斑.电压闪变,即电压幅值发生周期性的低频波动,闪变时在二维灰度图中以单根条纹为整体,会发生周期性的明暗变化,如图 3(g).
通过上述分析可知,扰动事件在二维灰度图中通常表现为行或列方向上的线形奇异或局部的点形奇异,对这些奇异性的提取是进一步扰动分类的基础.将电能质量扰动信号映射至二维灰度图中进行分析具有单纯进行一维波形分析不具有的优点.一维波形只能在单一时间尺度上考查,不利于直接识别周期扰动事件,而二维灰度图能在行方向和列方向上都进行考查,提高周期数据间的相关性.在一维情况下,单一采样点的相关数据为2,而在二维情况下则为8[10],这有利于充分挖掘不同扰动事件的特征.
3 卷积神经网络CNN由卷积层神经元和池化层神经元构成,其中卷积层通过对输入信号的所有局部进行卷积提取局部特征,其同一特征图的神经元共享权值;池化层,也称下采样层,对每个特征图进行独立操作,如平均池化或最大池化,通过池化层能有效减小特征分辨率,减小需要优化的网络参数的数量.将卷积神经网络的基本结构进行堆叠,前一层的输出作为后一层的输入,即构成卷积神经网络,具有深度学习的能力[12].
3.1 卷积层卷积层在前一层输出的特征图上移动一个卷积核与图的不同区域进行卷积操作,卷积的结果加上偏置后输出为该层的特征图.卷积层的形式如下式所示:
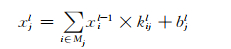 (4)
(4)
其中:l表示层数;Mj表示前一层中与当前层第j个特征图有连接的特征图集合;xjl为第l层输出的第j个特征图;xil-1为第l-1层输出的第i个特征图;kijl为第l层的第j个特征图与前一层第i个特征图之间的卷积核;bjl为第l层第j个特征图的偏置.
3.2 池化层卷积层的操作导致特征图个数增加,使得特征维数膨胀.为了降低特征维数和训练难度,在卷积层后加入池化层.池化层起到二次特征提取的作用,相当于对不同位置的特征进行统计,提高了模型的泛化能力,不容易过拟合.池化层操作如下式所示:
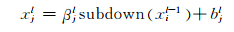 (5)
(5)
其中:subdown(·)表示池化下采样函数;βjl为比例偏置;bjl为加性偏置.
3.3 激活函数对池化层输出的特征图使用非线性函数作为激活函数,以避免神经网络模型表达能力不够的问题.传统卷积神经网络中通常采用sigmoid等饱和非线性函数[13],但由于饱和非线性函数的收敛速度慢,甚至反向传播阶段出现梯度消失问题,因此本文选取不饱和非线性激活函数ReLu(rectified linear units)[14]作为CNN的激活函数,如下式所示:
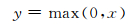 (6)
(6)
本文采用误差反向传递法则训练卷积神经网络.训练样本从输入层开始不断经过卷积、池化和激活在输出层输出样本的分类特征图O.根据式(7)计算分类特征图与样本的实际标签T的误差:
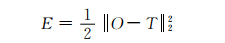 (7)
(7)
按照微分链式法则将误差逐层从输出层传递至输入层,采用随机梯度下降算法[15]相应地更新各层的卷积核和偏置系数.详细推导过程参见文献[16].
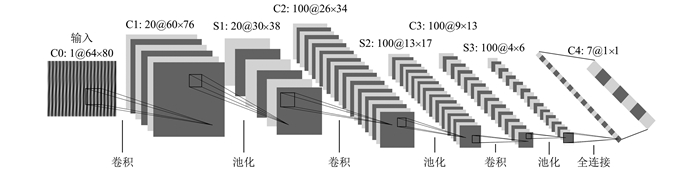
4 本文的CNN结构本文以卷积神经网络LeNet-5的结构为基础[17],通过大量尝试,最终确定采用如图 4所示的网络结构.该卷积神经网络共含有4个卷积层,3个池化层,1个输出层,除输入层外每一层均需要对权值进行训练.图 4中“C0:1@64×80”表示输入层为1个64×80特征图,C1、C2、C3和C4表示卷积层,分别含有20、100、100、7个卷积核,卷积核大小分别为5×5、5×5、5×5和4×6.S1、S2、S3表示池化层,均采用最大池化方式,池化窗大小均为2×2.在CNN中层与层间的分辨率递减,但是每层所含的特征平面数递增,这样有助于识别更多的抽象特征.卷积神经网络最终输出的是一个7×1的向量,该向量表示输入样本属于对应标签的可能性大小.
|
| 图 4 电能质量扰动识别的卷积神经网络结构 Fig. 4 Network architecture of CNN for recognition of PQD |
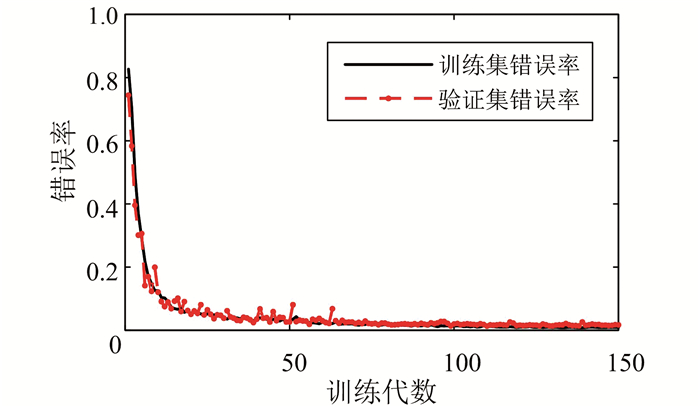
采用Matlab生成表 1所示的扰动信号,正常信号和每类扰动各生成1 200个随机样本,共9 600个样本.每类扰动分别叠加信噪比(SNR)为30、40和50 dB的高斯白噪声,每种类型扰动选取800个构成训练集,200个构成验证集,其余的构成测试集,验证集的设置可以避免卷积神经网络过拟合.将所有训练样本映射至二维灰度图形式作为卷积神经网络的输入,通过训练使CNN的分类错误率降低,如图 5所示.
|
| 图 5 卷积神经网络训练误差曲线 Fig. 5 Error curve of training CNN |
在训练开始阶段错误率较高.经过约11代训练学习后错误率快速减小至低于0.1.之后错误率的降低速度不断降低,网络参数不断进行微调,在大约100代训练后训练集错误率趋于稳定, 大约为0.5%,验证集错误率稳定于0.9%左右.从训练集和验证集上的错误率变化曲线可以看出,两者的变化趋势和数值基本一致,网络没有出现过拟合和欠拟合问题.
5.2 分类效果为了进一步验证将卷积神经网络应用于电能质量扰动分类的有效性,在不同的噪声强度下,分别对比进行了测试,分类准确率结果如表 2所示.
| 扰动类型 | SNR/dB | ||
| 30 | 40 | 50 | |
| 正常C0 | 1.000 | 1.000 | 1.000 |
| 暂升C1 | 0.995 | 1.000 | 1.000 |
| 中断C2 | 0.940 | 0.950 | 0.975 |
| 暂降C3 | 0.915 | 0.925 | 0.940 |
| 谐波C4 | 1.000 | 1.000 | 1.000 |
| 振荡C5 | 0.985 | 0.995 | 0.985 |
| 冲激C6 | 1.000 | 1.000 | 1.000 |
| 闪变C7 | 1.000 | 1.000 | 1.000 |
| 总体 | 0.978 8 | 0.983 8 | 0.987 5 |
由表 2可以看出,从总体上看,卷积神经网络在不同的噪声强度下对扰动分类的总体准确率均较高,至少为98.88%,说明基于卷积神经网络的电能质量扰动分类方法具有较强的噪声鲁棒性.但是从单一扰动角度看,该方法对电压暂降的分类效果稍有欠缺,准确率为91.0%~95.0%.对于暂升、谐波、振荡、冲激和闪变这5类扰动分类效果较好,至少为98.5%.
为了进一步分析电压暂降分类效果欠佳的原因,以信噪比40 dB的情况为例,将各类扰动的详细分类结果列于表 3.可见卷积神经网络主要在区分电压中断和电压暂降两类扰动时会发生混淆.主要原因在于暂降事件和中断事件对应的二维灰度图间的唯一差别是,两者在扰动发生时相应像素点的灰度值区间不同.其中电压中断在区间[121,134]内,暂降在区间[70,185]内,当所发生的电压暂降比较严重时,卷积神经网络对这两种扰动的区分能力会减弱.
| 类型 | C0 | C1 | C2 | C3 | C4 | C5 | C6 | C7 |
| C0 | 200 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C1 | 0 | 200 | 0 | 0 | 0 | 0 | 0 | 0 |
| C2 | 0 | 0 | 190 | 10 | 0 | 0 | 0 | 0 |
| C3 | 0 | 1 | 14 | 185 | 0 | 0 | 0 | 0 |
| C4 | 0 | 0 | 0 | 0 | 200 | 0 | 0 | 0 |
| C5 | 0 | 0 | 0 | 0 | 0 | 199 | 1 | 0 |
| C6 | 0 | 0 | 0 | 0 | 0 | 0 | 200 | 0 |
| C7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 200 |
1) 本文提出一种电能质量扰动分类新方法.采用卷积神经网络对扰动事件的原始二维灰度图进行深度学习,能有效地自适应提取扰动的特征,CNN提取特征的过程是自局部到全局的过程.在不同噪声情况下,卷积神经网络对扰动均能获得至少97.57%的分类准确率,具有较好的抗噪能力.
2) 该算法与以往方法的不同之处在于其得到的分类器不是基于事先确定的扰动模型,而是通过对扰动样本进行深度学习得到的,是一种基于数据的方法,能更好地契合样本的特征.
3) 由于CNN对严重电压暂降事件和电压中断事件的区分能力有待提高,接下来的研究将考虑引入其他辅助分类特征.进一步的研究将尝试通过改进卷积网络的结构、引入其他分类器等方式提升CNN的性能,并考虑将其推广运用于电能质量复合扰动的分类.
| [1] |
徐健, 张语勍, 李彦斌, 等. 短时傅里叶变换和S变换用于检测电压暂降的对比研究[J]. 电力系统保护与控制, 2014, 42(24): 44-48. Xu Jian, Zhang Yuqing, Li Yanbin, et al. Comparative study of STFT and S transform on detecting voltage sag[J]. Power System Protection and Control, 2014, 42(24): 44-48. DOI:10.7667/j.issn.1674-3415.2014.24.008 |
| [2] |
Dwivedi U D, Singh S N. Enhanced detection of power-quality events using intra and interscale dependencies of wavelet coefficients[J]. IEEE Transactions on Power Delivery, 2010, 25(1): 358-366. DOI:10.1109/TPWRD.2009.2027482 |
| [3] |
檀何凤, 刘政怡. 基于标签相关性的K近邻多标签分类方法[J]. 计算机应用, 2015, 35(10): 2761-2765. Tan Hefeng, Liu Zhengyi. Multi-label K nearest neighbor algorithm by exploiting label correlation[J]. Journal of Computer Applications, 2015, 35(10): 2761-2765. |
| [4] |
徐志超, 杨玲君, 李晓明. 基于聚类改进S变换与直接支持向量机的电能质量扰动识别[J]. 电力自动化设备, 2015, 35(7): 50-58, 73. Xu Zhichao, Yang Lingjun, Li Xiaoming. Power quality disturbance identification based on clustering-modified S-transform and direct support vector machine[J]. Electric Power Automation Equipment, 2015, 35(7): 50-58, 73. |
| [5] |
陈华丰, 张葛祥. 基于决策树和支持向量机的电能质量扰动识别[J]. 电网技术, 2013(5): 1272-1278. Chen Huafeng, Zhang Gexiang. Power quality disturbance identification using decision tree and support vector machine[J]. Power System Technology, 2013(5): 1272-1278. |
| [6] |
Marr D, Poggio T, Hildreth E C, et al. A computational theory of human stereo vision[J]. Readings in Cognitive Science, 1988, 204(1156): 534-547. |
| [7] |
Chowdhury A R, Lin T Y, Maji S, et al.One-to-many face recognition with bilinear CNNs[C]// IEEE Winter Conference on Applications of Computer Vision, IEEE Computer Society, 2016: 1-9. http://www.researchgate.net/publication/303563889_One-to-many_face_recognition_with_bilinear_CNNs
|
| [8] |
Collobert R, Weston J.A unified architecture for natural language processing: deep neural networks with multitask learning[C]// International Conference, Helsinki, Finland, June, 2008: 160-167. http://dl.acm.org/citation.cfm?id=1390177
|
| [9] |
Lécun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [10] |
何永远.基于小波和脊波的二维电能质量扰动信号检测与压缩[D].北京: 北京化工大学, 2010. He Yongyuan.2D power quality disturbances detection and compression based on wavelet and ridgelet[D].Beijing: Beijing University of Chemical Technology, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1673648 |
| [11] |
张杨, 刘志刚. 一种基于时频域多特征量的电能质量混合扰动分类新方法[J]. 中国电机工程学报, 2012, 32(34): 83-90. Zhang Yang, Liu Zhigang. A new method for power quality mixed disturbance classification based on time-frequency domain multiple features[J]. Proceedings of the CSEE, 2012, 32(34): 83-90. |
| [12] |
Hubel D H, Wiesel T N. Receptive fields, binocular interaction and functional architecture in the cat's visual cortex[J]. Journal of Physiology, 1962, 160(1): 106-154. DOI:10.1113/jphysiol.1962.sp006837 |
| [13] |
Glorot X, Bengio Y.Understanding the difficulty of training deep feedforward neural networks[C]// International Conference on Artificial Intelligence and Statistics, Brookline, MA: 2010: 249-256. https://www.researchgate.net/publication/215616968_Understanding_the_difficulty_of_training_deep_feedforward_neural_networks
|
| [14] |
Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks[J]. Journal of Machine Learning Research, 2011, 15: 315-323. |
| [15] |
Bottou L. Large-scale machine learning with stochastic gradient descent[C]// Proceedings of COMPSTAT2010, Physica-Verlag HD, 2010: 177-186. https://www.researchgate.net/publication/228671354_Large-scale_machine_learning_with_stochastic_gradient_descent
|
| [16] |
Strigl D, Kofler K, Podlipnig S.Performance and scalability of GPU-based convolutional neural networks[C]// Euromicro International Conference on Parallel, Distributed and Network-Based Processing, IEEE, 2010: 317-324. https://www.computer.org/csdl/proceedings/pdp/2010/3939/00/3939a317-abs.html
|
| [17] |
Anil R, Manjusha K, Kumar S S, et al.Convolutional neural networks for the recognition of malayalam characters[C]// Proceedings of the 3rd International Conference on Frontiers of Intelligent Computing: Theory and Applications (FICTA) 2014, Springer International Publishing, 2015: 493-500. https://link.springer.com/chapter/10.1007%2F978-3-319-12012-6_54
|
 2018, Vol. 51
2018, Vol. 51



