文章信息
- 杨小明, 崔雪, 周斌, 彭政
- YANG Xiaoming, CUI Xue, ZHOU Bin, PENG Zheng
- 基于粒子群优化支持向量机的短期负荷预测
- Research on short term load forecasting based on particle swarm optimization-support vector machine
- 武汉大学学报(工学版), 2018, 51(8): 715-720
- Engineering Journal of Wuhan University, 2018, 51(8): 715-720
- http://dx.doi.org/10.14188/j.1671-8844.2018-08-008
-
文章历史
- 收稿日期: 2018-01-10
负荷预测是电力领域的重要工作,它不仅是保证电网安全稳定运行的前提,更是发电厂商与售电公司报价的依据.随着配电网改造升级的推进以及需求侧响应的发展,分布式电源、电动汽车及各种储能装置在用户侧开始出现,用户可以根据电能需求结合实时电价调整用电需求;同时,售电市场逐步开放使得各电力企业处于同一个市场竞争环境之中,其竞争与合作使电价和负荷的相互影响也变得更加明显[1].因此,负荷的准确预测不仅是经济调度的基础,也是售电市场制定电价的前提.准确的负荷预测对电力系统安全运行、经济调度和市场有序进行具有重要意义.
近些年,由于电力市场化改革的深入与科学技术的迅速进步,新的预测方法层出不穷.国内外学者在长期的研究与实践中,不断探索电力系统负荷预测的新方法,各种数学模型不断涌现,人工智能技术迅速发展,从而出现了不少新的预测方法.短期负荷预测的方法主要有:以时间序列为代表的传统数理统计预测方法,以神经网络为代表的经验非线性预测方法,以支持向量机为代表的统计学习理论预测方法.
目前支持向量机理论已被广泛应用于负荷预测领域,并且成为解决非线性回归问题的一种非常有效的方法,与传统的预测方法相比,它在预测结果的精确度上以及模型算法的运算效率上有着明显的优势,因此,国内外很多学者对其做了广泛而深入的研究[2-6].
对于支持向量机来说,核函数及其参数直接决定了它的最终性能.为了获得性能优良的核函数,使用多个核函数,并通过模型训练获得其最优组合作为最终的核函数,是一种行之有效的方法.文献[3]表明,采用高斯核函数与多项式核函数按照一定的权重进行组合而得到的最终核函数具有优良的学习能力与泛化性能.
在给定样本的情况下,采用不同的模型相关参数组合在相当大的程度上影响着支持向量机模型的预测能力.目前,国内具有相当丰富的把智能优化算法引入支持向量机的参数寻优过程的相关研究文献.文献[4]研究了不同参数组合下SVM模型的性能,然后采用遗传算法(Genetic Algorithms, GA)寻找模型相关的最优参数取值,并将其代入SVM预测模型中,得到了GA-SVM负荷预测模型,利用此模型进行负荷预测,从而提高了预测结果的精确性;文献[5]采用蚁群优化算法来寻求支持向量机模型的最优参数组合,与正交法、遗传算法等算法相比,该方法在参数寻优方面可以快速地进行全局搜索;文献[6]则采用粒子群算法(Particle Swarm Optimization, PSO),方便快速地寻求SVM模型的较优相关参数的取值,提出了基于PSO-SVM模型的负荷预测方法.
结合相关文献的研究成果,本文提出了一种基于双种群粒子群(Double Population Particle Swarm Optimization, DP-PSO)优化LS-SVM的预测模型,采用基于DP-PSO优化算法寻求LS-SVM模型相关的最优参数取值,然后将训练好的LS-SVM模型用于负荷预测,从而提高了模型的训练速度和预测精度.最后,将该预测模型应用到浙江省某市的短期负荷预测中,与经典的SVM相比,精度有了一定提高.
1 最小二乘支持向量机支持向量机算法引入核方法,将输入样本空间映射到高维度的特征空间,然后利用线性方法解决非线性问题[7].作为标准支持向量机的一个扩充,最小二乘支持向量机(LS-SVM)[8]将其求解从非线性优化问题转换成求解线性方程组,把不等式约束转化为等式约束,从而可以简化计算.
在回归问题中,对于样本集D={(x1, y1), (x2, y2), …,(xm, ym)}, yi∈R引入一个非线性映射φ(x)把n维输入和1维输出样本集D从原始样本空间映射到高维度的特征空间,决策函数的形式为
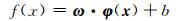 (1)
(1)
式中:ω为权重向量;φ(x)为将x映射后的特征向量;b为阈值.
由结构风险最小化原理[9],引入松弛变量ξi,LSSVM可形式化为下式所述的二次规划问题:
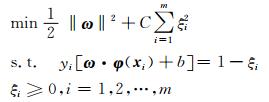 (2)
(2)
其中,C > 0为惩罚参数.
构造拉格朗日函数可得
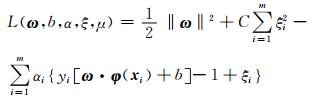 (3)
(3)
其中,μi≥0, αi≥0.
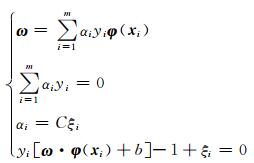 (4)
(4)
对于i=1, 2, …, m,消去式(4)中的ω、ξ得到如下线性方程组:
 (5)
(5)
根据希尔伯特-施密特(Hilbert-Schmidt)原理,引入满足摩西(Mercer)条件[12]的核函数:
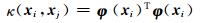 (6)
(6)
引入核方法,并考虑特征映射的形式,则得到最终的决策函数为
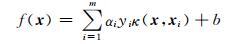 (7)
(7)
常用的核函数及其参数有以下几种,此外还可以根据核函数的构造原理对下列核函数进行组合得到新的核函数.
1) 线性核
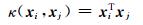 (8)
(8)
2) 多项式核
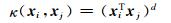 (9)
(9)
其中,d≥0为多项式次数.
3) 高斯核
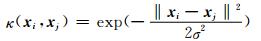 (10)
(10)
其中,σ>0为核函数宽度.
4) 拉普拉斯核
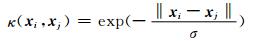 (11)
(11)
其中,σ>0.
5) Sigmoid核
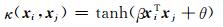 (12)
(12)
其中,tanh为双曲线正切函数.
对于复杂的预测问题,由于数据的来源不一,其组成也可能是异构数据集,这就造成数据分布的复杂性,如果只是选择单一核函数SVM模型,有可能无法取得满意的预测性能.
对于式(8)~(12)所述的常用核函数,按照它们对回归预测问题影响的情况可划分为全局性及局部性的核函数[13].全局性核函数的典型代表是多项式核函数,它的突出特点是泛化性能比较强,能很好地提取样本数据的全局性,但不足之处在于学习能力相对较弱.高斯核函数作为局部核函数的典型代表之一,对一定距离内的样本具有很好的学习能力,不足之处在于其泛化能力相对较差.因此,综合考虑二者的优缺点,将上述2种核函数按照一定的权重进行组合,构成最终的核函数,从而可以提高模型的综合性能.
根据上述分析,设最终的混合核函数中高斯核κG的权重系数为a,多项式核κP的权重系数为1-a,则组合之后的最终混合核函数为
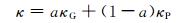 (13)
(13)
在进行上述分析与处理之后,本文所采用的LSSVM需要选取的模型参数有4个,即正则化常数C、高斯核宽度σ、多项式次数d和最终混合核函数组合权重a.其中C决定了训练误差的大小和泛化能力的强弱;σ和a反映了训练样本数据的分布特性.这几个参数直接影响着模型的预测能力和算法效率,通常是采用交叉验证或梯度下降法等对多个参数组合的比较来确定最优的参数组合.然而,实际经验表明,这些方法人为因素较多、盲目性较大、效率偏低.对于寻求模型相关参数最佳取值的问题,粒子群算法不但具有快速求解的能力,并且可以进行全局性搜索.本文拟通过DP-PSO算法寻求LS-SVM模型相关参数的最优取值.
2 粒子群算法1) 标准粒子群算法
粒子群优化算法(PSO)引入群智能算法的思想,兼备进化算法的优点,具有优良的优化及搜索能力.
粒子群算法借助适应度函数将个体粒子移动到更好的区间.它将种群中个体视作一个既没有质量又没有大小的质点,并在搜索空间中不断运动,然后参考个体和种群当前的运动轨迹,动态地调整粒子的运动速度.
在标准PSO算法中,粒子在搜索空间之中按照下式不断对其速度和位置进行更新[14]:
 (14)
(14)
式中:ω为权重;c1和c2为加速因子;r1、r2为在区间[0, 1]中均匀分布的任意数;pij为当前粒子本身飞行过的最好位置;gj为粒子所对应的整个种群的最好位置;xt=(x1, x2, …, xn)与vt=(v1, v2, …, vn)为时刻t的位置与速度.
2) 基于双种群的粒子群优化算法
PSO算法每次迭代过程中,粒子都依据全局最优值来更新自己,这样就造成了粒子趋于同一化,粒子的多样性迅速消失,从而造成算法的早熟;而且PSO算法对计算中的信息利用率不足,这样容易造成运算后期收敛比较慢,影响算法的效率.为解决上述标准PSO算法的缺陷,采用具有全局搜索性能与局部搜索性能俱佳的双种群粒子群算法(DP-PSO)[15],并采用具有动态加速因子的方法,可以克服上述缺点,提高算法的运算效果.
为了提高种群的多样性,采用双种群协同进化的粒子群优化算法,将种群分为局部寻优和全局寻优的2个种群.具体方法为:将具有s个粒子的粒子群分为2个子群,即具有局部寻优性能的子群Q1以及具有全局寻优性能的子群Q2,Q1和Q2分别由s1和s2个粒子组成,s=s1+s2.2个子群按照不同的进化方式,子群Q1具有快速收敛的进化方程;子群Q2的进化方式则具有全局搜索特点;相应的加速因子则应用反正切调整的方式.具体的进化方程如下:
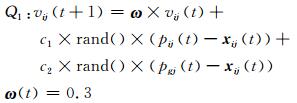 (15)
(15)
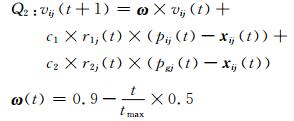 (16)
(16)
其中,rand()为在[0, 1]中分布均匀的任意数.
子群Q1的作用是围绕最优位置在小范围内进行快速搜索(局部寻优),因为较小的权重使粒子能够获得很好的局部搜索能力,因此可以在较小的区间内小范围寻优并加快收敛的速度;子群Q2的任务则是围绕着最好位置在大范围内搜索(全局寻优),当子群Q2的粒子搜寻到新的全局性最好位置,经个体粒子间信息交流,指导子群Q1到达新的最好位置附近进行局部搜索.通过子群分工协作,不仅使种群的多样性有所增加,而且也进一步优化了PSO算法的运算效率.
加速因子c1和c2分别代表将粒子推向局部最优和全局最优位置的统计加速项的权重.通过分析加速因子对DP-PSO算法的影响,利用反正切函数动态调整c1和c2的策略,可以在全局与局部搜索性能方面取得更好的平衡性,c1、c2的取值公式分别为
 (17)
(17)
式中:c1start和c2start分别是c1和c2的初值;c1end和c2end分别是c1和c2的终值;Tmax为算法的最大迭代次数;e为调节系数,控制曲线的衰减,一般取值为0~10;l=arctan(20-e)+arctan e.
3 基于DPPSO-LSSVM预测模型的建立采用K-折交叉验证对训练样本集进行交叉验证,取均方误差作为适应度函数,可很好地避免过拟合,降低模型对特定样本的依赖.
采用DP-PSO算法,寻求本文所提出的混合核函数LSSVM的较优参数取值组合,得到最终的混合核函数DPPSO-LSSVM的负荷预测模型,并用其进行实际电网日平均负荷预测的流程如下.
第1步 搜集相关数据,进行数据处理与归一化.对于缺失数据,如果数据缺失规模不大,可采取线性插值的方法,否则采用相似日的数据来进行填充;对于异常数据,分别采用水平处理或垂直处理.进行了上述处理之后,采用线性映射的方式将相关数据映射到[0, 1]范围内,线性映射的公式为下式:
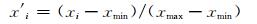 (18)
(18)
对于工作日类型的数据,周二至周日取值0.8,周六取0.4,周日取0.3,周一取0.7.然后划分学习样本与测试样本.
第2步 对粒子群(C、σ、ε、a)进行初始化,并给出惯性权重ω的取值范围、种群s及子群s1、s2的数量、最大迭代次数Tmax等,在搜索空间中随机产生粒子的初始位置和速度.
第3步 建立本文所提出的混合核函数LS-SVM的预测模型,并按照下式计算每个粒子的适应度值:
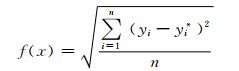 (19)
(19)
式中:yi是测试样本集中的第i个样本的实际负荷值;yi*是第i个样本的预测负荷值;i=1, 2, …, n为相应的样本数.
第4步 按照式(15)~(17)对种群中个体粒子的速度和位置进行更新.
第5步 判断适应度值是否满足要求或者是否达到最大迭代次数,如满足条件,将每个粒子当前位置及种群中所有粒子所经历的最好位置进行比较,如果这个粒子的位置最优,则将其设置为当前的最好的LS-SVM参数取值,否则,最好位置不变.
第6步 返回第4步,直到达到迭代次数Tmax或满足实际情况对误差所提出的相应要求.
第7步 对LS-SVM模型进行求解,将通过DP-PSO算法所寻找到的最优参数取值和阈值b的取值代入式(7),得到最终的回归函数,利用此函数即可进行负荷预测.
4 算例分析现选取中国浙江某市实际电网2009年2月14日至3月26日的历史负荷数据、温度数据、湿度数据以及工作日类型作为训练样本,用本文所提出的DPPSO-LSSVM模型来预测同年3月27日至3月31日的日平均负荷.
在本算例中,设定正则化常数C的取值范围为[0.1,100],高斯核宽度σ取值范围为[0.1,10],多项式次数d的取值范围为[0, 4];取迭代次数Tmax= 200,种群数量s=30,各子群数量分别为s1=10, s2=20, 加速因子调节系数e=6,惯性权重系数ω的取值范围为[0.4,0.9],学习因子c1start=2.75, c1end=1.25,c2start=0.5,c1end=2.25.取LS-SVM的均方根误差作为适应度函数,并采用5折交叉验证.
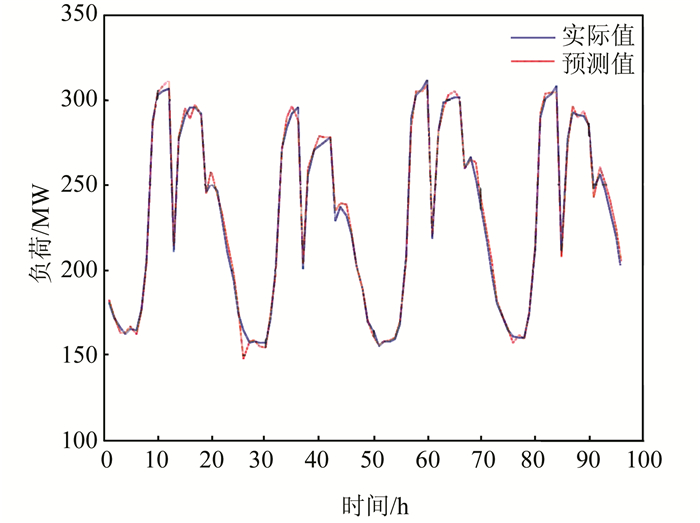
图 1给出了采用DPPSO-LSSVM模型进行负荷预测所得到的4个工作日的时点负荷预测值与实际值对比.从中可以直观地看到,负荷预测曲线与实际负荷曲线基本重合,这说明本算法不仅对负荷值的预测精确高;在负荷曲线中,预测曲线与实际曲线在相同的时点出现“峰-谷”,并且在每个工作日的13:00左右出现了大幅度的下降(对应于人们午间的休息时间),说明该负荷预测方法可以准确地预测负荷变化的趋势.
|
| 图 1 负荷的实际值与预测值曲线对比 Figure 1 Comparison of load curve between the actual and predicted values |
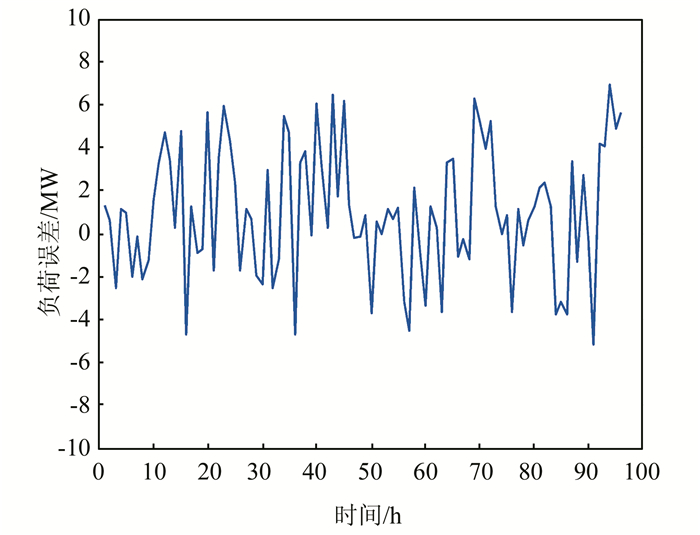
图 2给出了采用DPPSO-LSSVM预测模型的预测结果的误差曲线图.从中可以看出,除少数几个时点预测误差相对较大之外,其他绝大部分时点的预测误差都很小,在0附近波动,预测结果良好.
|
| 图 2 负荷预测结果的误差曲线 Figure 2 Error of the load curve of forecasting results |
为测试本文所述方法在负荷预测中的预测效果,分别采用时间序列模型、RBF作为核函数的单一核函数LS-SVM模型(LS-SVM)、神经网络模型、标准PSO优化的LS-SVM模型(PSO-LSSVM)、双种群粒子群优化的混合核函数LS-SVM模型(DPPSO-LSSVM),结合上述实际电网分别进行日平均负荷预测.表 1给出了使用这几种方法预测的日平均负荷的绝对误差与4个工作日的平均误差,仿真结果表明,本文提出的DPPSO-LSSVM预测模型可有效提高预测精度.
| % | |||||
| 模型 | 绝对误差 | 平均误差 | |||
| 3月28日 | 3月29日 | 3月30日 | 3月31日 | ||
| 时间序列 | 2.73 | 2.76 | 3.18 | 3.08 | 2.94 |
| SVM | 2.72 | 1.83 | 1.63 | 2.25 | 2.11 |
| PSO-LSSVM | 1.17 | 1.26 | 1.69 | 1.43 | 1.39 |
| 神经网络 | 1.01 | 1.62 | 1.65 | 1.15 | 1.36 |
| DPPSO-LSSVM | 1.15 | 1.22 | 1.69 | 1.22 | 1.22 |
在实际应用中,影响负荷预测的因素众多、关系复杂,且各因素之间的相关性具有较大的不确定性.本文采用DP-PSO优化算法来搜索混合核函数LSSVM的最优参数组合,从而克服了采用人工方式对LSSVM模型进行参数取值的局限性.最后,结合实际电网经过仿真计算,结果表明,使用该方法进行负荷预测在预测精度上有了较大的提高,具有较高的实际价值.
| [1] |
刘孝杰, 苏小林, 阎晓霞, 等. 面向主动响应和售电市场的主动配电系统负荷预测[J].
电力系统及其自动化学报, 2017, 29(2): 121–127.
Liu Xiaojie, Su Xiaolin, Yan Xiaoxia, et al. Load forecast of active distribution system based on active response and electricity market[J]. Proceedings of the CSU-EPSA, 2017, 29(2): 121–127. DOI:10.3969/j.issn.1003-8930.2017.02.020 |
| [2] |
王建国, 张文兴.
支持向量机——建模及其智能优化[M]. 北京: 清华大学出版社, 2015.
Wang Jianguo, Zhang Wenxing. Support Vector Machine-Modeling and Optimization[M]. Beijing: Tsinghua University Press, 2015. |
| [3] |
康重庆, 夏清, 张伯明. 电力系统负荷预测研究综述与发展方向的探讨[J].
电力系统自动化, 2004, 28(17): 1–9.
Kang Chongqing, Xia Qing, Zhang Boming. Review and prospect of power system load forecasting[J]. Automation of Electriec Power Systems, 2004, 28(17): 1–9. DOI:10.3321/j.issn:1000-1026.2004.17.001 |
| [4] |
吴景龙, 杨淑霞, 刘承水. 基于混合遗传算法的支持向量机短期负荷预测方法[J].
中南大学学报, 2008, 40(1): 180–184.
Wu Jinglong, Yang Shuxia, Liu Chengshui. Parameter selection for support vectormachines based on genetic algorithms to short-term power load forecasting[J]. Journal of Central South University, 2008, 40(1): 180–184. |
| [5] |
刘春波, 王鲜芳, 潘丰. 基于蚁群优化算法的支持向量机参数选择及仿真[J].
中南大学学报:自然科学版, 2008, 39(6): 1309–1313.
Liu Chunbo, Wang Xianfang, Pan Feng. Parameters selection and simulation of support vector machines based on ant colony optimization algorithm[J]. Journal of Central South University: Natural Science Edition, 2008, 39(6): 1309–1313. |
| [6] |
曾勍炜, 徐知海, 吴键. 基于改进粒子群优化和支持向量机的电力负荷预测[J].
微电子学与计算机, 2011, 28(1): 147–149, 153.
Zeng Qingwei, Xu Zhihai, Wu Jian. Forecasting of electricity load based on particle swarm optimization and support vector machine[J]. Microelectronics & Computer, 2011, 28(1): 147–149, 153. |
| [7] |
周志华.
机器学习[M]. 北京: 清华大学出版社, 2016.
Zhou Zhihua. Machine Learning[M]. Beijing: Tsinghua University Press, 2016. |
| [8] | Gestel T V, Suykens J A K, Baesens B, et al. Benchmarking least squares support vector machine classifiers[J]. Machine Learning, 2004, 54(1): 5–32. |
| [9] | Vapnik V, Chervoknenkis A Y. Theory of pattern recognition[M]. Moscow: Nauka, 1974. |
| [10] | Burges C. Geometry and invariance in kernel based methods[C]//Advanced in Kernel Methods-Support Vector Learning, Cambridge, MA: MIT Press, 1998: 640-646. http://dl.acm.org/citation.cfm?id=299100 |
| [11] | Shevade S K, Keerthi S S, Bhattacharyya C, et al. Improvements to the SMO algorithms for SVM regression[J]. IEEE Transactions on Neural Networks, 2000, 11(5): 1188–1193. DOI:10.1109/72.870050 |
| [12] | Burges C J C. A tutorial on support vector machines for pattern recognition[J]. Data Mining and Knowledge Discovery, 1998, 2(2): 121–167. DOI:10.1023/A:1009715923555 |
| [13] |
李希鹏.基于混合核函数支持向量机的文本分类研究[D].青岛: 中国海洋大学, 2012.
Li Xipeng.Research on text classification based on support vector machine with mixture of kernels[D]. Qingdao: Ocean University of China, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10423-1012504708.htm |
| [14] |
彭宇, 彭喜元, 刘兆庆. 微粒群算法参数效能的统计分析[J].
电子学报, 2004, 32(2): 209–213.
Peng Yu, Peng Xiyuan, Liu Zhaoqing. Statistic analysis on parameter efficiency of particle swarm optimization[J]. Acta Electronica Sinica, 2004, 32(2): 209–213. DOI:10.3321/j.issn:0372-2112.2004.02.008 |
| [15] | Wang Jianguo, Hang Zhijie, Hang Wenxing. Support vector machine based on double-population particle swarm optimization[J]. Journal of Convergence Information Technology, 2013, 8(8): 898–905. DOI:10.4156/jcit |
 2018, Vol. 51
2018, Vol. 51




