文章信息
- 黄顺杰, 方华亮
- HUANG Shunjie, FANG Hualiang
- 实时需求响应的主从博弈模型与算法研究
- Research on master-slave game model and algorithm for real-time demand response
- 武汉大学学报(工学版), 2019, 52(2): 151-156
- Engineering Journal of Wuhan University, 2019, 52(2): 151-156
- http://dx.doi.org/10.14188/j.1671-8844.2019-02-008
-
文章历史
- 收稿日期: 2017-06-15
新时期的电网发展强调充分利用广泛的数据收集和开放的信息共享系统,灵活调度需求侧资源,鼓励引导用户优化传统用电形式并积极参与电网运行调度,调整用电行为以实现电网侧的削峰填谷[1-3].需求响应是智能电网框架下重要的互动资源,智能家电在负荷侧已有较大范围应用,已有研究表明智能家电可以短时响应系统的调控需求[4].
目前,文献[5-10]针对智能家电参与需求响应展开研究.文献[5-8]基于实时电价,合理分析实时电价下用户的用电响应行为并加以引导.文献[9-10]侧重于建立兼顾家庭用电的经济性和舒适性的调度优化模型,对家庭能源系统进行优化控制.文献[11-12]以家庭微电网为研究目标,综合考虑光伏、储能、智能家电等设备,实现家庭微电网的优化运行.但是上述文献没有考虑到需求响应过程中,电网与用户的互动存在先后性及多利益主体的决策问题.文献[13]指出博弈论可以解决现代电力系统中的多决策主体优化问题,Stackelberg博弈理论(即主从博弈)中的领导者和跟随者可以很好地描述参与需求响应主体的关系,主从博弈理论在电网调度中应用较少,文献[14]针对电动汽车负荷,提出一种未来智能小区代理商的定价及车主购电策略,文献[15]提出一种将分时上网电价和风储系统作为不同地位决策者进行动态博弈优化的主从模型.
本文以家庭能量管理中心和智能家电分别为领导者和跟随者建立主从博弈模型,领导者以虚拟价格为策略,跟随者以自身电能需求为策略,在搭建的虚拟电能交易过程中进行博弈.根据本文所建立的博弈模型,采用逆向归纳法,得出博弈平衡点,并通过数学解析证明其唯一性,将其转化为一个凸优化问题在Matlab中进行仿真求解,验证模型和算法的有效性,能够实现对设备的最优负荷控制.
1 博弈模型博弈论用于研究决策主体的行为相互作用时的决策和均衡问题,本文选择的主从博弈双方是指家庭能量管理单元(energy management center,EMC)与智能家电(smart household,SH),如空调(air condition,AC)、电灯(light)、电动汽车(electrical vehicles,EV)和智能洗衣机(washing machine,WM)等.领导者(EMC)和跟随者(SH)并非同时作出决策,而是领导者做出决策后跟随者作出最优回应,最后领导者根据跟随者可能的决策而对自身决策作出修正.EMC从电网接收实时电价(real-time price,RTP),并负责管理智能家电实现最优负荷控制策略.
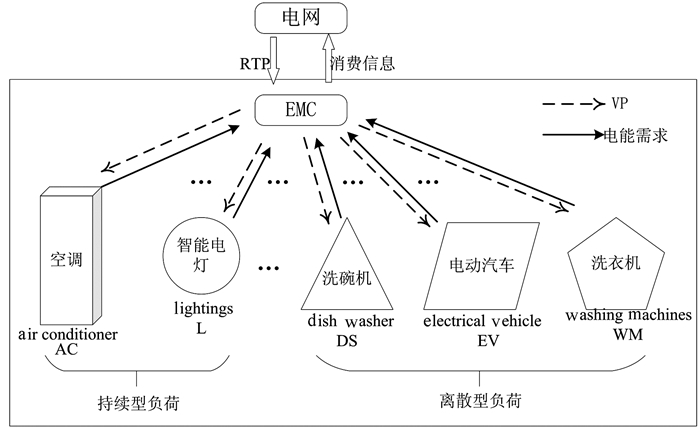
搭建如图 1所示的虚拟电力交易过程,图中所示虚拟价格(virtual price,VP)概念,与现实电价完全不同,没有实际的物理意义,仅存在于本文的博弈过程中,表征EMC的决策通过修改VP达到控制SH的目的.在本文中,领导者即EMC,其策略为一系列虚拟价格VP;跟随者即SH,其策略为家电电能需求.分别建立领导者和追随者的效用函数,通过量化,领导者“卖电”收入最大化,而追随者根据电力需求选择“买电成本”最小.在博弈平衡点,博弈双方能够各自获得最优效用.
|
| 图 1 虚拟电能交易框架 Fig. 1 Virtual energy trading framework |
对智能家居用电的不满意度建模,不满意度函数φi(xi)应该是一个对xi不断递减的函数,电能需求的平均水平用mi表示,如果xi小于mi(设备不满意当前能源需求),不满意度成本增加.如果xi大于mi,不满意度为负,表征设备的能源需求得到满足.随着xi继续增加,负函数值下降缓慢,设备的满意度水平饱和(不能无限满意).当xi等于mi,函数值为零,表明设备不需要能源供应.为满足以上条件,构建如下式所示的不满意度函数:
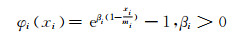 (1)
(1)
式中:βi表征设备运行优先考虑因素,其值越小,在能源供应中优先级越高,其值越大,在能源供应中的优先级越低.实际上,与人们日常生活密切相关的设备的βi通常较小.跟随者智能家电集合i=[1, 2, …, N],x表示跟随者策略.
跟随者效用函数由两部分组成,购电成本cixi和不满意度成本φi(xi).其效用函数应是EMC的策略ci和设备的电能需求xi的函数:
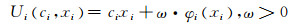 (2)
(2)
式中:Ui(ci, xi)表示跟随者i的效用函数;ω是一个权重系数,表征给定时间内电力供应满意度的重要性.一天中每个时期(负荷高峰、低估)的ω不同,ω越大表示用户更关注改善满意度(即减少不满意度成本).
在跟随者模型中,每个智能家电需要对领导者的策略作出最优响应,即自身购电成本和不满意度成本最低,优化目标、约束条件和跟随者策略集如下式所示:
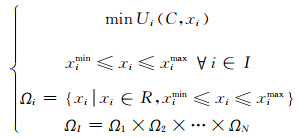 (3)
(3)
式中:Ωi表示跟随者i可能采取的策略集合;ΩI表示所有跟随者的策略集合.
1.1.2 离散型负荷在以前的连续型用电设备模型中,xi表征设备的能源需求,这并不适用于离散型用电设备,本文作出以下修改.对于离散型用电设备,用xi表示其状态决策变量,即xi=[0 1],表征设备的运行或停止,而用xinom表示设备运行时的能源需求,为一固定值.对应地,离散型设备存在一个阈值来确定设备以后的动作,用τi代替mi,其中0≤τi≤1(在本文的仿真计算中τi取一极限值1,体现对离散负荷的绝对控制).作出如上改进,则离散型负荷的数学模型与连续型负荷相似,分析连续型模型的方法亦可用于离散型负荷,如下式所示:
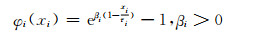 (4)
(4)
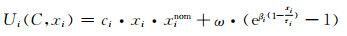 (5)
(5)
领导者(EMC)的策略集C即面向N个跟随者的一系列的虚拟价格,与EMC接收到的RTP存在如下关系:
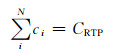 (6)
(6)
领导者的效用函数指的是收益,应该最大化.领导者效用函数应是领导者策略C与跟随者总策略X的函数:
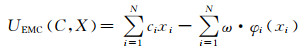 (7)
(7)
式中:跟随者策略集合X=[x1, x2, …, xN];领导者策略集合C=[c1, c2, …, cN].
领导者的优化目标、约束条件和策略集如下式所示:
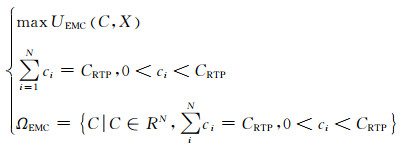 (8)
(8)
推导步骤如下:
1) 领导者公布虚拟价格:C=[c1, c2, …, cN];
2)跟随者i对C作出响应,根据公式(3)从Ωi选取最优响应策略为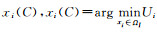
3) 基于步骤2中跟随者们的策略X*,领导者根据公式(7)从ΩEMC中更新策略为C*,C*= 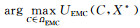
4) 重复步骤1~3,获得解决方案,即最终的博弈平衡点,即
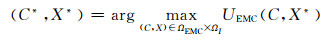 (9)
(9)
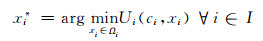 (10)
(10)
如前所述的博弈过程,正向求取涉及到反复博弈,步骤繁琐,本文采用逆向归纳法,博弈参与者在决策时“向前展望,向后推理”,即首先仔细思考自己的决策可能引起的所有后续反应,以及后续反应的后续反应,直至博弈结束;然后从最后一步开始,逐步倒推,以此找出自己在每一步的最优选择.
根据逆向归纳原理,首先基于公式(10)找到每个设备的最优回应策略,跟随者效用函数连续可微.在领导者策略C已知情况下,可以对其效用函数求一阶导数即为最优策略:
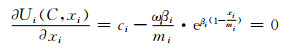 (11)
(11)
即
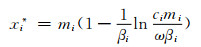 (12)
(12)
对公式(2)求二阶导数:
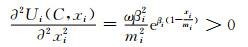 (13)
(13)
由高等数学定理可知,当某点的一阶导数值为0、二阶导数值大于0时,该点取函数极小值,即式(12)是跟随者i的最优响应策略.
领导者基于跟随者对C的最优回应X*,根据优化问题(9)对自身策略作出修正:
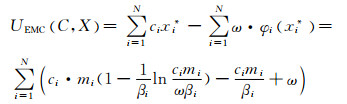 (14)
(14)
将式(12)进行等价变形:
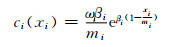 (15)
(15)
式(15)为一递减函数,结合式(8),ci满足以下条件:
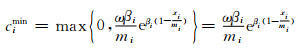 (16)
(16)
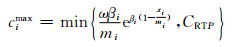 (17)
(17)
由于权重系数ω已知,博弈过程中可根据式(16)和式(17)对式(8)中的虚拟价格约束进行修正,从而得到:
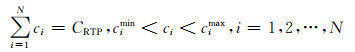 (18)
(18)
领导者效用最优问题(14)可等效转化为
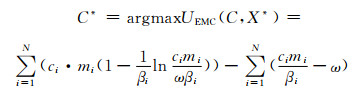 (19)
(19)
展开式(19),并对其求二阶导数,得到海森矩阵:
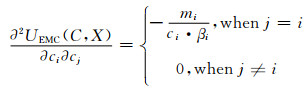 (20)
(20)
经分析,海森矩阵对角线元素为负,非对角线元素为0,海森矩阵严格负定,UEMC(C, X)优化问题严格非凸,优化问题(19)是一个标准的凸优化问题,可用凸优化理论求解,其存在唯一最优解C,领导者最优策略唯一且确定,通过式(12)确定跟随者的最优解,即得到最终的博弈平衡点.
以上分析证明,所建立的数学模型存在解析解,领导者和跟随者的策略集非空且为凸集,存在唯一的博弈平衡点.因此,本文的优化问题可采用逆向归纳法,减少了迭代计算,提高了算法运行效率并减少了运算时间.在本文的博弈优化问题中,领导者EMC获得最大化的虚拟收益,而跟随者的智能设备使得用电费用最小化.由此,通过“虚拟价格VP”这一虚拟量,得到智能设备的最优负荷控制,完成需求响应.
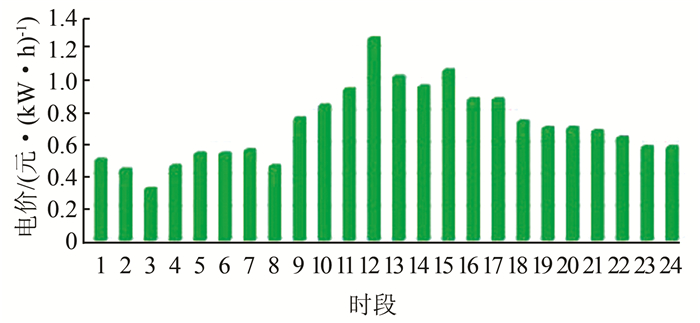
3 仿真计算智能家居中含连续型和离散型的用电设备,连续型设备包含2个智能空调和2个智能电灯,能够通过调温和调光控制自身的用电功率,用户根据设备所在区域(客厅、卧室等)对智能家居的运行有不同的要求.例如,优先保证卧室的温度适宜,那么处于卧室的电器则具有更高的优先级,其不满意度指数βi被赋予一个较小值.离散型设备包含洗衣机和电动汽车,发挥削峰填谷作用,仅考虑在谷荷时的用电行为,并设置较大的βi.具体设置如表 1所示.离散型设备中,WM的运行时间被限定在19:00-22:00,并且不可中断.而电动汽车的充电时段不受限制,可中断.针对不满意成本,不满意度权重在一天中应是有所变化的,将不满意度权重的取值分为3个时期,峰荷时权重最小,表征此时设备相比谷、平时段的电能需求更小,以降低购电费用,从而适应用户需求,降低其不满意度成本,本文设置ω峰=0.07,ω平=0.1,ω谷=0.18.图 2为本文模拟仿真计算所用的实时电价RTP.
| 设备 | 连续型 | 离散型 | |||||
| AC1 | AC2 | L1 | L2 | WM | EV | ||
| βi | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | |
| 功率/kW | 1.5~3.0 | 1.5~3.0 | 0.8~1.8 | 0.8~1.8 | 1.3 | 1.4 | |
| 运行时间 | 0:00-24:00 | 0:00-24:00 | 0:00-24:00 | 0:00-24:00 | 19:00-22:00 | - | |
|
| 图 2 模拟实时电价 Fig. 2 Simulated real-time electricity prices |
基于上述设置,在Matlab中凸优化工具箱进行仿真计算,验证本文所提模型和算法,得到领导者和跟随者的博弈平衡点决策,仿真输出结果如图 3~6所示.
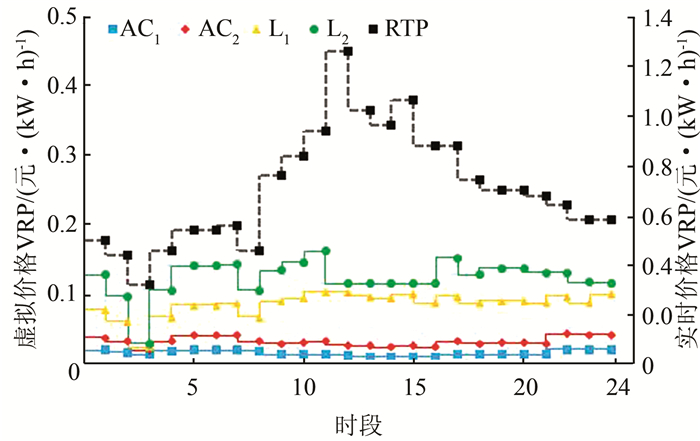
|
| 图 3 连续型负荷VP Fig. 3 VP of continuous load |
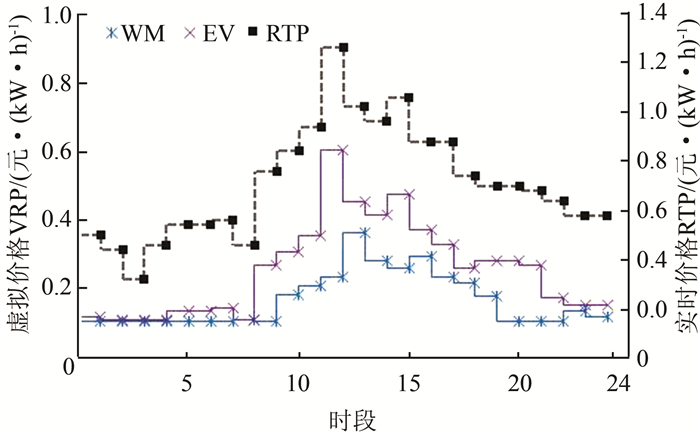
|
| 图 4 离散型负荷VP Fig. 4 VP of discrete load |
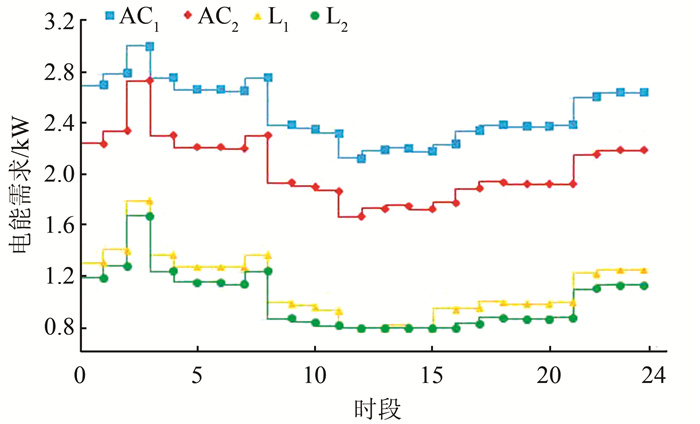
|
| 图 5 连续型负荷需求 Fig. 5 Continuous load demand |
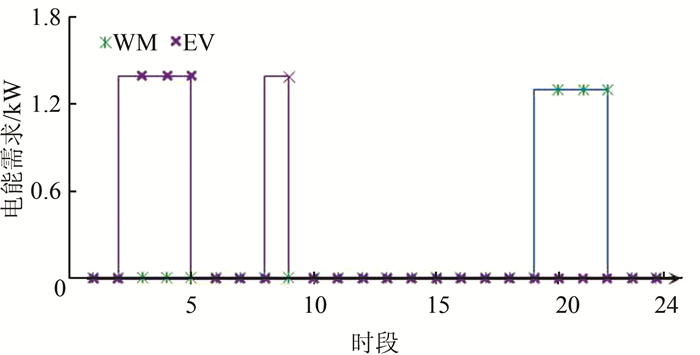
|
| 图 6 离散型负荷需求 Fig. 6 Discrete load demand |
图 3和图 4分别显示每个设备的VP优化结果,每个时刻内所有设备的VP总和等于该时刻的实时电价RTP.如图 3所示,较低优先级(即较大βi)的设备所分配的VP较大,如AC2的VP大于AC1,这因为AC1的用电优先级更高(即较小的βi),这是表示在电能一定的情况下,优先满足AC1的电能需求.在L1和L2的比较中也可反映供电优先级.对比图 3和图 4可知,离散型设备的供电优先级较低,同一时刻离散型设备被分配较大的VP,以便控制它们的运行.洗衣机WM是不可中断的离散型设备,在图 4中显示从19:00-22:00时段内VP不变,在这一时段内,即使RTP变小,由于WM工作时间被确定,其VP仍会增大.
图 5和图 6分别显示连续型设备和离散型设备的最优电能需求,反映其最优负荷控制,每小时的电能需求时刻变化,对应实时电价和虚拟价格的变化.总体趋势表现为削峰填谷,在峰荷时设备电能需求少,而在谷荷时电能需求增大,以降低电费.AC1的电能需求总是高于AC2,这一点在图 3中的虚拟价格中也有反映,高优先级的设备能够消耗更多的电能.以12:00这一时刻为例,智能电灯L保持最低消耗,而AC能够工作于高功率.在WM工作时段,即使RTP下降,EMC为保证突然加入的WM设备正常工作,AC的电能需求不能进一步增加.观察对比16:00和17:00两个时刻,实时电价相同,但是17:00的能源需求普遍高于16:00,这是因为不满意度权重ω发生突变,设备为降低不满意度成本而增加电能消耗.
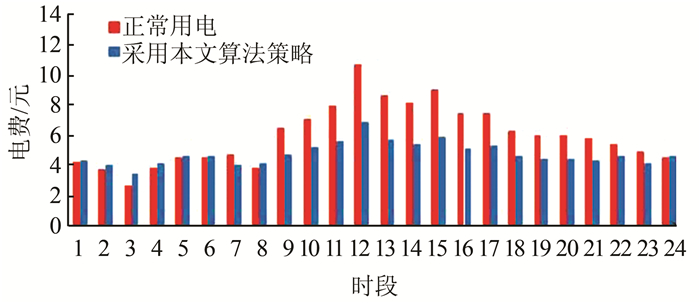
计算家庭的正常日运行成本,每个智能家电均运行在平均水平,AC和L运行在功率中间点,而离散型设备EV和WM可以在任意时间请求并消耗电能.与本文所提算法模型作比较,如图 7所示.优化前该家庭日运行成本达到144.22元,而采用本文优化方法后,可降为114.65元,降幅达到20.5%,有效降低了家电的运行成本.
|
| 图 7 购电费用 Fig. 7 Costs of power purchase |
本文研究智能家电的需求响应行为,建立主从博弈模型,家庭能量管理中心和智能家电分别作为领导者和跟随者,“虚拟价格”和电能需求分别为领导者策略和跟随者策略,引入虚拟价格VP这一概念应用于博弈过程,体现双方的策略互动性.根据所建模型,逆向归纳并证明博弈平衡点,结果表明本文所提模型和算法能够对用电设备进行最优控制,降低用户电费成本,达到自身经济最优.在未来,对用电设备的βi需要进一步调查分析,综合考虑家庭微网中的设备如光伏、储能等装置,深入研究博弈论在家庭需求响应中的应用.
| [1] |
张新昌, 周逢权. 智能电网引领智能家居及能源消费革新[J]. 电力系统保护与控制, 2014, 42(5): 59-67. Zhang Xinchang, Zhou Fengquan. Smart grid leads the journey to innovative smart home and energy consumption patterns[J]. Power System Protection and Control, 2014, 42(5): 59-67. |
| [2] |
高媛, 孙军平, 范闻博, 等. 用户侧需求响应系统试验技术研究[J]. 电气应用, 2013, 3(17): 40-45. Gao Yuan, Sun Junping, Fan Wenbo, et al. The research of the user side demand response system test technology[J]. Electric Technology, 2013, 3(17): 40-45. |
| [3] |
赵雪霖, 何光宇, 杨文轩, 等. 智能用电网络的设计与初步实现[J]. 电工电能新技术, 2014, 3(10): 52-57. Zhao Xuelin, He Guangyu, Yang Wenxuan, et al. Design and initial implementation of smart electric appliance network[J]. Advanced Technology of Electrical Engineering and Energy, 2014, 3(10): 52-57. DOI:10.3969/j.issn.1003-3076.2014.10.011 |
| [4] |
汤奕, 邓克愚, 孙华东, 等. 智能家电参与低频减载协调配合方案研究[J]. 电网技术, 2013, 37(10): 2861-2867. Tang Yi, Deng Keyu, Sun Huadong, et al. Research on coordination scheme for smart household appliances participating under frequency load shedding[J]. Power System Technology, 2013, 37(10): 2861-2867. |
| [5] |
阮冰洁, 杨强, 颜文俊. 计及实时电价的柔性负荷系统需求侧响应机制研究[J]. 机电工程, 2015, 32(6): 857-862. Ruan Bingjie, Yang Qiang, Yan Wenjun. Demand response under real-time price for domestic energy system[J]. Journal of Mechanical & Electrical Engineering, 2015, 32(6): 857-862. |
| [6] |
黄海新, 邓丽, 文峰, 等. 基于实时电价的用户用电响应行为研究[J]. 电力建设, 2016, 37(2): 63-68. Huang Haixin, Deng Li, Wen Feng, et al. Customer response behavior based on real-time pricing[J]. Electric Power Construction, 2016, 37(2): 63-68. DOI:10.3969/j.issn.1000-7229.2016.02.009 |
| [7] |
Li X H, Hong S H. User-expected price-based demand response algorithm for a home-to-grid system[J]. Energy, 2014, 64: 437-449. DOI:10.1016/j.energy.2013.11.049 |
| [8] |
Ding Y M, Hong S H, Li X H. A demand response energy management scheme for industrial facilities in smart grid[J]. IEEE Trans.Ind. Informat., 2014, 10(4): 2257-2269. DOI:10.1109/TII.2014.2330995 |
| [9] |
王丹, 范孟华, 贾宏杰. 考虑用户舒适约束的家居温控负荷需求响应和能效电厂建模[J]. 中国电机工程学报, 2014, 34(13): 2071-2077. Wang Dan, Fan Menghua, Jia Hongjie. User comfort constraint demand response for residential thermostatically-controlled loads and efficient power plant modeling[J]. Proceedings of the CSEE, 2014, 34(13): 2071-2077. |
| [10] |
王春梅, 李杨, 王旭东, 等. 计及用户舒适性的家庭智能用电调度优化[J]. 电网与清洁能源, 2016, 32(4): 58-62. Wang Chunmei, Li Yang, Wang Xudong, et al. Optimal scheduling for smart home power consumption considering user's comfort[J]. Power System and Clean Energy, 2016, 32(4): 58-62. DOI:10.3969/j.issn.1674-3814.2016.04.010 |
| [11] |
汤庆峰, 张建华, 樊玮, 等. 考虑电价激励的家居型微电网的优化运行[J]. 电器与能效管理技术, 2014, 10: 37-43. Tang Qingfeng, Zhang Jianhua, Fan Wei, et al. Optimal operation of residential micro-grid based on price incentive[J]. Appliances and Management Technology of Energy Efficiency, 2014, 10: 37-43. |
| [12] |
阳小丹, 李杨. 家庭用电响应模式研究[J]. 电力系统保护与控制, 2014, 42(12): 51-56. Yang Xiaodan, Li Yang. Research on household electricity response mode[J]. Power System Protection and Control, 2014, 42(12): 51-56. DOI:10.7667/j.issn.1674-3415.2014.12.009 |
| [13] |
卢强, 陈来军, 梅生伟. 博弈论在电力系统中典型应用及若干展望[J]. 中国电机工程学报, 2014, 34(29): 5009-5017. Lu Qiang, Chen Laijun, Mei Shengwei. Typical Applications and Prospects of Game Theory in Power System[J]. Proceedings of the CSEE, 2014, 34(29): 5009-5017. |
| [14] |
魏韡, 陈玥, 刘锋, 等. 基于主从博弈的智能小区代理商定价策略及电动汽车充电管理[J]. 电网技术, 2015, 39(4): 939-945. Wei Wei, Chen Yue, Liu Feng, et al. Stackelberg game based retailer pricing scheme and EV charging management in smart residential area[J]. Power System Technology, 2015, 39(4): 939-945. |
| [15] |
栗然, 党磊, 董哲, 等. 分时电价与风储联合调度协调优化的主从博弈模型[J]. 电网技术, 2015, 39(11): 3247-3253. Li Ran, Dang Lei, Dong Zhe, et al. Coordinated optimization of time-of-use price and dispatching model combining wind power and energy storage under guidance of master-slave game[J]. Power System Technology, 2015, 39(11): 3247-3253. |
 2019, Vol. 52
2019, Vol. 52




