武汉大学学报(工学版)   2016, Vol. 49 Issue (3): 335-340

文章信息

陈浩, 洪林, 梅超, 赖永明, 曾子悦
CHEN Hao, HONG Lin, MEI Chao, LAI Yongming, ZENG Ziyue
基于D8算法的分布式城市雨洪模拟
Distributed simulation of urban storm water based on D8 algorithm
武汉大学学报(工学版), 2016, 49(3): 335-340
Engineering Journal of Wuhan University, 2016, 49(3): 335-340
http://dx.doi.org/10.14188/j.1671-8844.2016-03-003

文章历史

收稿日期: 2015-12-15
 Abstract              PDF               Figures               Tables
引用本文 0
陈浩, 洪林, 梅超, 赖永明, 曾子悦. 基于D8算法的分布式城市雨洪模拟[J]. 武汉大学学报(工学版), 2016, 49(3): 335-340.
CHEN Hao, HONG Lin, MEI Chao, LAI Yongming, ZENG Ziyue. Distributed simulation of urban storm water based on D8 algorithm[J]. Engineering Journal of Wuhan University, 2016, 49(3): 335-340.
基于D8算法的分布式城市雨洪模拟
陈浩1,2, 洪林1, 梅超1, 赖永明1,3, 曾子悦1,4     
1. 武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072;
 2. 中国电建集团昆明勘测设计研究院有限公司，云南 昆明 650033;
 3. 广西水利电力职业技术学院，广西 南宁 530023;
 4. 清华大学水利工程系，北京 100084
收稿日期: 2015-12-15
作者简介: 陈浩（1990-），男，硕士研究生，研究方向为灌排工程，E-mail：whuchenhao@126.com.
通讯作者: 洪林（1963-），女，教授，博士，主要从事农田水利水环境研究，E-mail：lhong@whu.edu.cn
基金项目: 水利部公益性行业科研专项经费项目（编号:201501013）；国家自然科学基金项目（编号:91547205）.
摘要: 为了有效地控制城市雨洪，选取武汉市汤逊湖流域作为研究区，建立一个基于D8算法的分布式城市雨洪模型，实现对城市暴雨积水动态模拟.通过对产汇流和管网排水过程进行简化,建立了流域雨洪模拟模型,并分别利用该流域2013年7月5-7日和2010年7月11-13日降雨径流资料进行模型率定及验证.与实测资料对比，模型率定期的积水总量相对误差为5.4%，典型地段积水深度相对误差均值为9.5%，绝对误差均值为18.9 mm，均方根误差(RMSE)为20.0 mm；验证期的典型地段积水深度相对误差均值为14.9%，RMSE为49.3 mm.模拟结果表明：基于D8算法的分布式城市雨洪模型能够较好地模拟城市雨洪过程，可以进一步用于未来条件下城市雨洪情景分析，为城市雨洪控制提供决策依据.
关键词： 城市雨洪     地理信息系统（GIS）技术     分布式模拟     积水动态     D8算法    
Distributed simulation of urban storm water based on D8 algorithm
CHEN Hao1,2, HONG Lin1, MEI Chao1, LAI Yongming1,3, ZENG Ziyue1,4     
1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;
 2. HydroChina Kunming Engineering Corporation Limited, Kunming 650033, China;
 3. Guangxi Hydraulic and Electric Power Technique College, Nanning 530023, China;
 4. Department of Hydraulic Engineering, Tsinghua University, Beijing 100084, China
Abstract: In order to effectively control urban storm water, the Tangxun Lake basin in Wuhan City is selected as a study area to establish a distributed urban storm water simulation model, which is based on D8 algorithm for realization of urban storm water dynamic simulation. Urban storm water simulation model of the basin is built through simplifying the processes of runoff generation, routing and drainage of pipe network; and the model is calibrated and verified using rainfall-runoff data in the basin in July 5-7, 2013 and July 11-13, 2010. Compared with measured data, the relative error of the total drainage volume is 5.4%;the averaged relative error of the maximum inundation depth in typical points is 9.5%; the averaged absolute error is 18.9 mm; and the root mean squared error (RMSE) is 20.0 mm in the calibration period; in the verification period, the averaged relative error of the maximum inundation depth in typical points is 14.9%; and the RMSE is 49.3 mm. The simulation results show that the distributed urban storm water model based on D8 algorithm can be used to simulate urban storm water process satisfactorily, and can provide decision support for urban storm water control in the future through scenario analyses.
Key words: urban storm water     geographic information system(GIS) technique     distributed simulation     inundation dynamics     D8 algorithm    

随着城市化进程的加快与全球气候变化，城市水文特性发生显著变化，城市地区遭受突发性强暴雨洪水的几率大增[1~2].而我国大多数城市的排涝标准相对较低，排水系统建设严重滞后，再加上城市经济类型的多元化和资产的高度密集性，使得城市雨洪灾害损失日益严重[3].

为了控制雨洪灾害，欧美等发达国家和地区从20世纪50年代便开始研究将流域水文模型应用到城市水文中，70年代早期相继开发出了城市雨洪仿真模型，并加以应用[4~5].20世纪90年代以来，随着GIS技术的迅速发展，雨洪灾害风险分析中越来越多地引进GIS技术和空间分析技术，用以有效地更新信息和提高模型模拟计算的能力[6~8].为了尽可能减少雨洪灾害损失，本文选取武汉市汤逊湖流域作为研究对象，进行基于D8算法的城市雨洪模型研究，为城市雨洪灾害控制提供理论依据.

1 分布式雨洪模型 1.1 建模思路及假设

在DEM基础上将城市湖泊流域栅格化[9]，形成533 015个30 m×30 m的网格，建立分布式雨洪模拟模型.为了简化计算过程，本模型有以下几个假设：1) 同一栅格内降雨均匀，且每个栅格内部地面高程、水深、流速一致；2) 考虑到研究区为平原湖区，地形波动幅度较小，在一个较短的时间段(1 min)内，坡面汇流简化为明渠均匀流，且不考虑水流波动影响.

1.2 产汇流简化模型 1.2.1 产流计算

流域0~t时段的产流计算可以用下式表示[10]：

${{R}_{S}}(t)=\int\limits_{0}^{t}{idt-\int\limits_{0}^{t}{{{i}_{n}}dt-\int\limits_{0}^{t}{edt-\int\limits_{0}^{t}{{{s}_{d}}dt-\int\limits_{0}^{t}{fdt}}}}}$    (1)

式中：Rs(t)指在0~t时段产生的地表径流深;i是降雨强度;in是植被截留率;e是蒸发率;sd是填洼率;f是下渗率.

在以上损失中，下渗对城市径流形成过程起决定性作用.为简化计算，本模型仅考虑下渗因素.因此，地面产流过程可简化为

${{R}_{S}}(t)=\int\limits_{0}^{t}{idt-\int\limits_{0}^{t}{fdt}}$    (2)

对上式进行微分：

$\frac{d{{R}_{S}}(t)}{dt}={{r}_{s}}(t)=i(t)-f(t)$    (3)

由式(3)可知，只有当i>f时才会有径流产生.下渗水量采用分段法计算，当雨强较小时，根据下渗和降雨的关系，将下渗水量简化为降雨量与固定系数的乘积；当雨强较大时，采用经验入渗模型——霍顿模型进行计算.

霍顿模型主要描述下渗率随时间变化的过程，认为当降雨持续进行时，下渗率逐渐减小，下渗过程是一个下渗速率不断衰减的过程，衰减的速度与时间成正比.模型可反映土壤入渗能力随时间变化情况，参数少，适用于土壤质地相同区域产流计算.霍顿公式为

${{f}_{t}}={{f}_{c}}+({{f}_{0}}-{{f}_{c}})\times {{e}^{-\beta t}}$    (4)

式中:ft为t时刻的土壤下渗率，mm/h；f0为土壤初始下渗率，mm/h；fc为稳定下渗率，mm/h；β为下渗衰减系数，与土壤物理性质有关，h-1；t为时间，h.其中f0、fc和β为常数，称为霍顿入渗参数，应根据实测入渗资料或利用研究区的土壤分布图获取各栅格的土壤类型后确定.

1.2.2 汇流计算

城市地面产生径流后，各单元径流在出口断面汇集的过程称为汇流.本文采用基于D8算法的简化的水文水动力学模型进行汇流计算.降雨和邻区水量流入使得栅格水量增加，为正；排水、下渗和流向邻区水量使得栅格水量减少，为负.按照每个最小的时间间隔Δt，以栅格为计算单元进行水流的方向、流速和水深的计算，且每隔一段时间输出一次计算结果.模拟的总时间长度T根据降雨后总的排水所需要的时间而定.

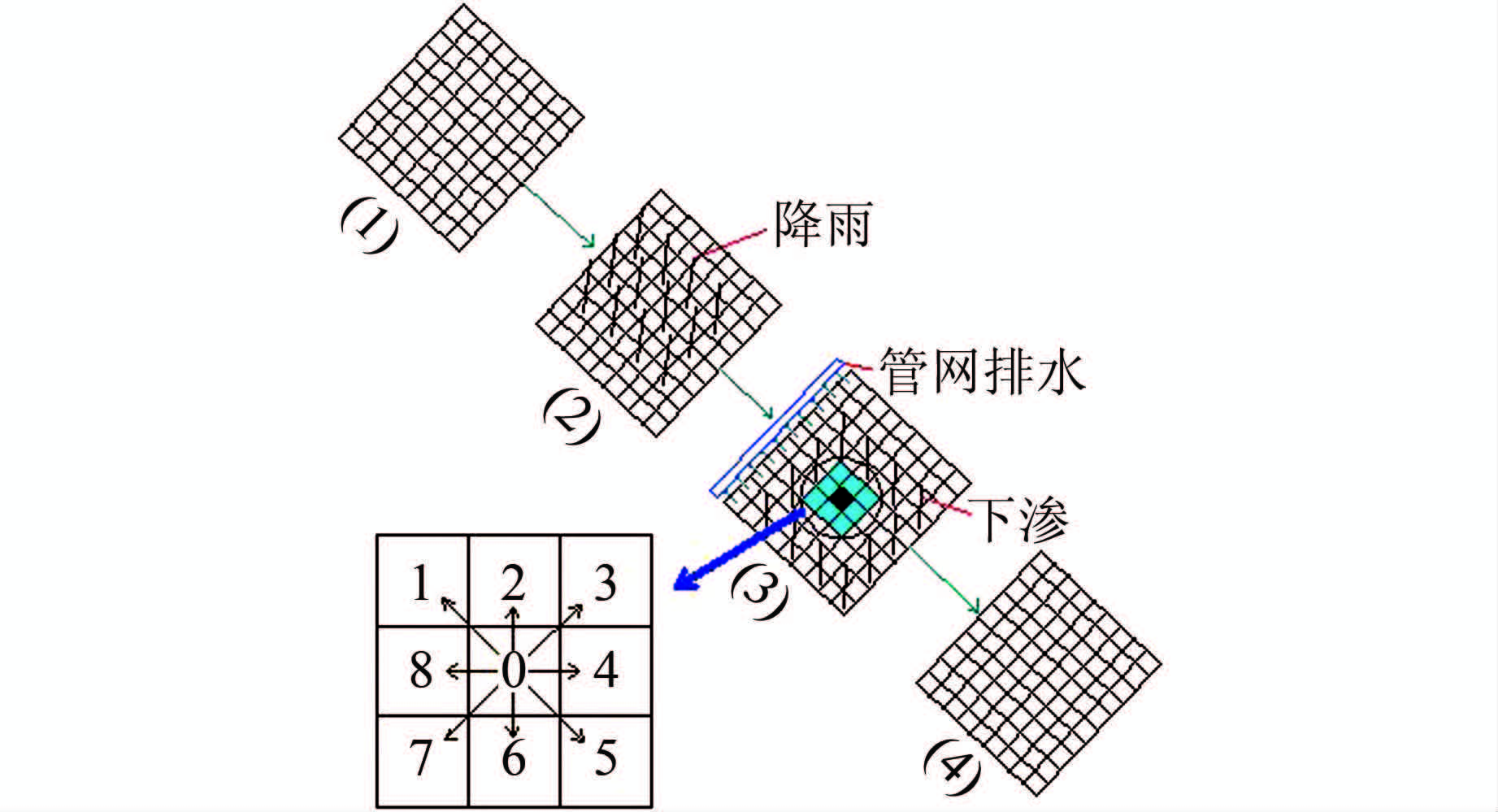
简化的汇流计算过程详见图 1.图 1中(1)~(4)代表一个计算时段Δt内的4个模拟阶段，分别是：(1) 本时段计算初始状态，前一时段计算末状态；(2) 本时段降雨计算；(3) 本时段降雨入渗、排水及径流计算；(4) 本时段计算结束状态，下一时段计算初状态.

图 1 模拟过程示意图 Figure 1 Diagram of simulation process
图选项
1.2.3 管网排水计算简化模型

城市排水系统可以抽象地认为是由节点和排水管道构成的网络，其中节点包括检查井、集水池、出水口等水力设施.除管道的排水能力以外，管道的空间布局对于排水能力影响也很大.

随着城市化的加快，区域管网系统会变得越来越复杂，排水模拟的难度也随之增加.本模型采用简化的排水系数计算法，将非水域排水区管网排水能力概化为栅格单元的排水系数pout，排水系数pout和径流深R直接相关.因此，管网Δt时段排水量wout=pout×R.根据各栅格排水能力及前期排水情况，pout在0~max(pout)之间取值，max(pout)为栅格最大排水能力.非承泄区的pout随着降雨时间递减，承泄区的pout=0.

1.2.4 确定水流流向

水流方向是指水流离开网格时的指向，它决定着地表径流的方向及网格单元间流量的分配，是基于DEM的分布式水文模型汇流演算的基础.本研究采用D8算法进行水流方向的提取，并进行交换水量和水深计算，具有计算简单、效率高、对地形适应性强且已集成到GIS软件中的优点[11~12].

D8算法确定的水流方向有如下特点：1) 流向是间隔45°的8个可能的格网方向之一；2) 单流向，即可以有多个上游单元而只有一个下游单元.并采用最陡坡度法确定中心栅格水流最终流动方向[13]，在3×3网格单元中，设中心栅格编码为0，其水流流出方向指向其相邻8个格网中的i，左上角起按顺时针方向i分别为1-2-3-4-5-6-7-8(见图 1).最大坡度Si为

${S_i}{\text{ = }}\mathop {\max }\limits_{i = 1,2, \cdots ,8} \frac{{\left( {{Z_0} + {h_0}} \right) - \left( {{Z_i} + {h_i}} \right)}}{d}$    (5)

式中：Z0、Zi分别为中心栅格和周围栅格中心点地面高程;h0、hi分别为中心栅格和周围栅格中心点水深;d为中心栅格中心点与相邻8个栅格中心点距离，当i位于坐标轴X、Y轴方向时，d=1，当i位于对角线方向时，d=2.

当Si≤0时，则赋以中心栅格编码0，表明此栅格水流不流出；当Si>0时，且只有一个取值时，则流向赋以对应坡度最大相邻栅格编码号；当Si>0时，且有一个以上取值时，则按照图 1所示顺时针方向赋以流向编码号，同时根据水位最低确定水流方向.

1.2.5 确定流速及水深

考虑到栅格细分及城市短距离地表汇流特点，将每个栅格的水流简化为明渠均匀流，采用曼宁公式计算坡面水流流速v[14~15]：

$v={{n}^{-1}}\times {{R}^{2/3}}\times \sqrt{{{S}_{i}}}$    (6)

式中：n是曼宁系数;R是水力半径，对于栅格而言，水力半径R即为网格单元水深.

为了防止出现急流紊动情况，根据弗洛德数判定流态，给速度限定一个阈值，即$\max \upsilon =\sqrt{g\times h}$，g为重力加速度，h为水深.

在计算出流速后，交换水量Δw可以根据计算时间步长Δt和水流截面面积A得出：

$\Delta \omega =\upsilon \times \Delta t\times A$    (7)

根据水量平衡可以得到Δt时段水深变化：

$\Delta h=P-{{\omega }_{\text{out}}}-F-\Delta \omega $    (8)

式中：P为中心栅格Δt时段降雨量；F为时段Δt下渗量；Δw为中心栅格与周围栅格交换水量，流出水量为正，流入为负.

进一步计算得到下一时刻栅格水深h2=h1+Δh，此处h1和h2分别为时段前和时段后的水深.

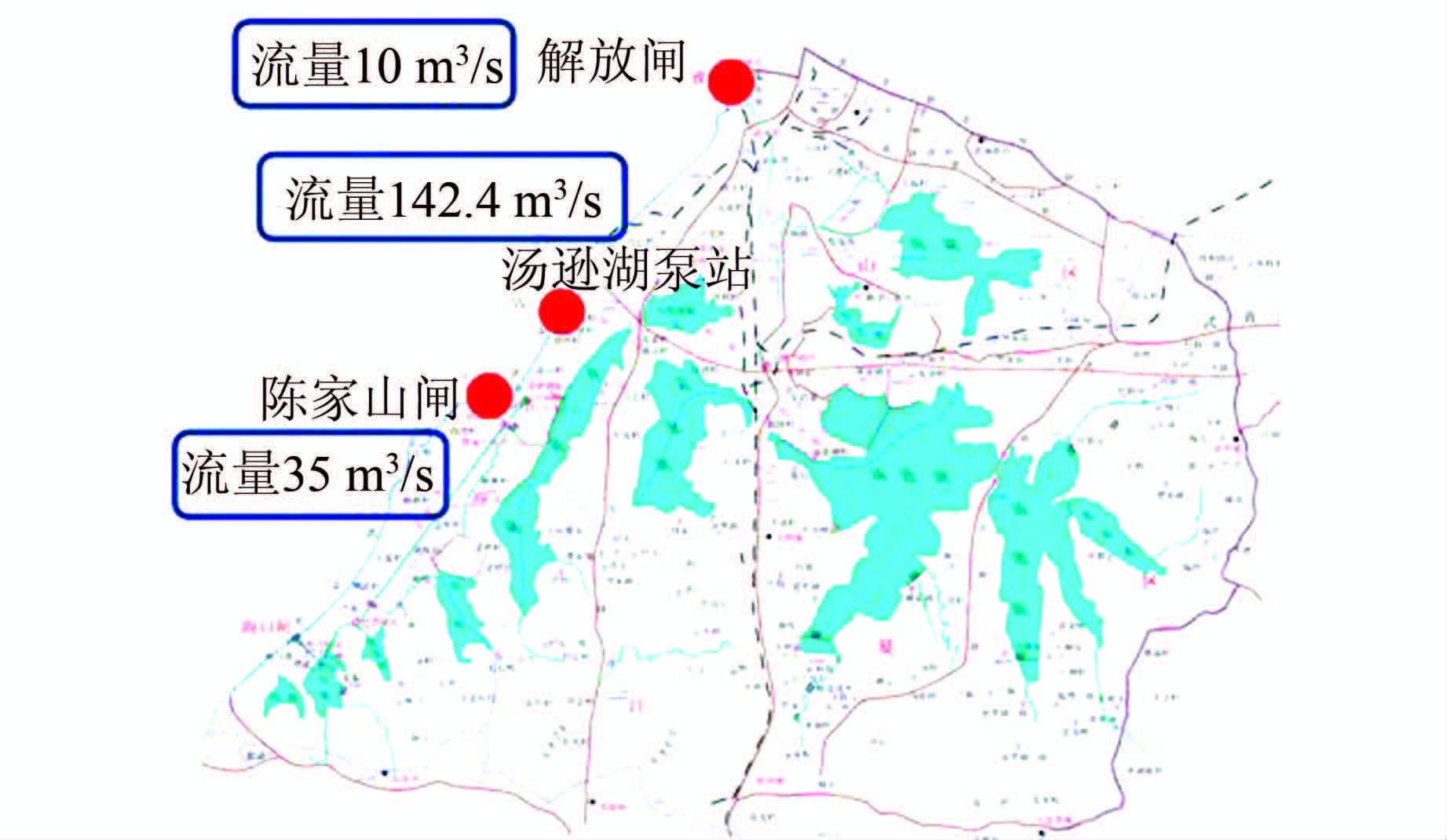
2 研究区概况及基本资料 2.1 研究区概况

汤逊湖位于武汉市东南部，流域面积为479.71 km2，其中水域面积为61.38 km2.流域中心位于东经114°26′52″，北纬30°26′30″.该流域为剥蚀堆积平原区，高程25~45 m(Ⅲ级阶地)，地形波状起伏，垅岗与坳沟相间分布.属亚热带湿润季风气候区，雨量充沛，雨热同季.流域多年平均降雨量为1 327.0 mm，最大年降雨量为2 105.3 mm，最小年降雨量为575.9 mm.降水主要集中在汛期(4-10月)，雨量占全年的73.6%.6-7月为梅雨季节，雨强大、历时长、笼罩面积广，易形成城市内涝.汛期的雨水入湖调蓄，外江水位较高时由汤逊湖泵站抽排入江、较低时由解放闸和陈家山闸自排入江.图 2为汤逊湖流域水系及排水工程概况.流域土地利用现状如表 1所示，土地利用分布如图 3所示.

图 2 汤逊湖流域水系及排水工程概况 Figure 2 River and drainage systems in Tangxun Lake basin
图选项
表 1 流域土地利用现状、霍顿入渗参数及曼宁系数 Table 1 Horton infiltration parameters and Manning coefficient n of different land uses
编号 土地利用类型 面积/km2 f0/(mm·h-1) fc/(mm·h-1) β/min-1 n
1 耕地 186.03 280 10 1.6 0.035
2 林地 51.49 670 15 1.4 0.120
3 草地 16.40 670 20 1.4 0.030
4 灌木林地 30.06 210 5 2.0 0.100
5 水域 121.88 210 5 2.0 0.022
6 建筑用地 40.43 0 0 0 0.013
7 裸土地 19.36 0 0 0 0.025
8 不可识别区 4.35 210 5 2.0 0.022
表选项
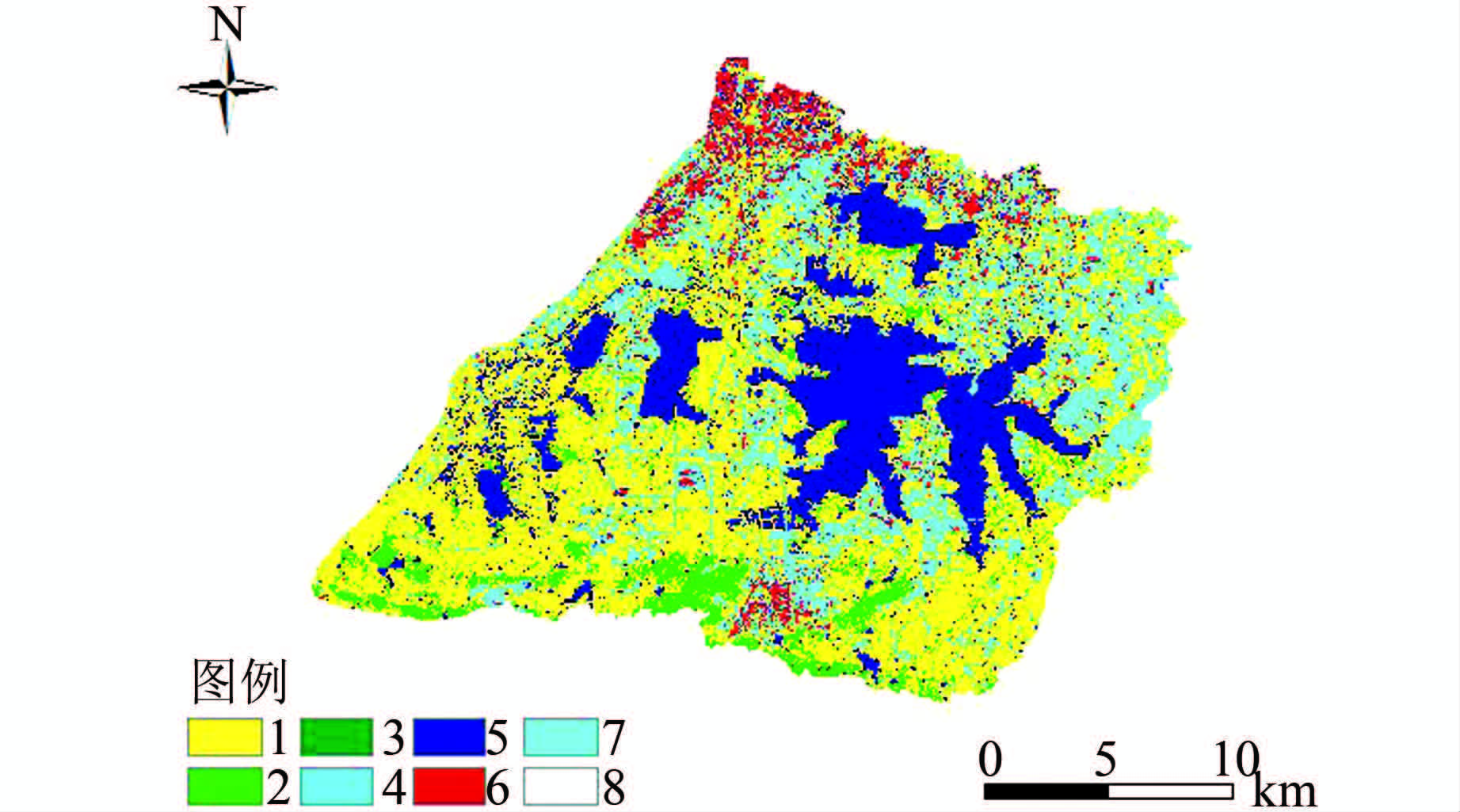
图 3 汤逊湖流域土地利用类型图 Figure 3 Land uses in Tangxun Lake basin
图选项
2.2 数据及参数获取

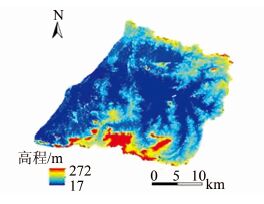
1) 数字地面高程(DEM).本研究流域高程数据来源于ASTER GDEM，空间分辨率为30 m，垂直精度2 m，水平精度3 m.利用ARCGIS10.0的水文分析模块对原始DEM进行预处理，将洼地和小平地修正为斜坡.填洼后的流域地面数字高程如图 4所示.

图 4 填洼后的犇犈犕 Figure 4 DEMafter depression modification
图选项

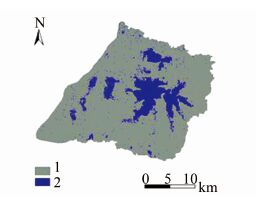
2) 排水区域标记.基于上述无洼地的DEM进行湖泊的提取.为了便于程序对数据的识别，定义排水区和承泄区栅格属性值bj：排水区j赋值1，承泄区j赋值2.如图 5所示.

图 5 排水区和承泄区标记 Figure 5 Code of drainage area and receiver area
图选项

3) 栅格排水能力.流域雨污分开，结构复杂.为简化计算，将非水域排水区栅格管网排水能力用maxpout表示，各栅格maxpout大小通过率定确定.

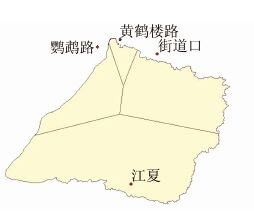
4) 降雨.汤逊湖流域及其周边地区有4个国家自动降雨监测站(鹦鹉路站、黄鹤楼站、街道口站以及江夏站)，根据站址和流域范围，利用泰森多边形划分降雨区域，如图 6所示.在同一区域降雨过程相同，并对4个站所辖区域分别进行标记和赋值.

图 6 雨量站分布 Figure 6 Layout of rainfall gauges
图选项

5) 霍顿入渗模型参数及曼宁系数n.根据流域土壤性质，确定不同土地类型的霍顿模型参数f0、fc、β；通过查阅资料，确定流域内不同土地利用的曼宁系数n，如表 1所示.

2.3 模型的建立与求解

应用上述模型理论和参数，初步建立城市流域分布式水文模型，并加以率定和验证.模型运行前，需要向模型输入9个数据库文件，其中栅格数据文件8个(地面高程、降雨区域标记、排水区域标记、排水最大排水能力系数、霍顿参数(f0、fc及β)、曼宁系数n等数据dat格式文件)以及1个txt格式的雨量信息文件.利用Visual Fortran进行编程，并进行调试；将上述数据文件导入程序进行模型运算，输出txt格式的数据文件后，由ArcGIS进行后期处理，得到流域各栅格各时段积水过程模拟结果.

3 模型的率定

选取典型暴雨(2013年7月5-7日)作为模型的率定期，总模拟历时T为96 h，率定期暴雨停止时流域积水水量统计如表 2所示.

表 2 率定期降雨停止时刻流域水量统计表 Table 2 Total volume in basin when rainfall stopped in calibration period

分段
序号		 水深/m 象元数/
(30 m·30 m)		 面积/km2 流域水量/
万m3
1 0~0.005 342889 308.6001 145.11
2 0.005~0.050 32864 29.5776 133.14
3 0.05~0.1 48006 43.2054 367.39
4 0.1~0.5 37780 34.0020 1530.70
5 0.5~1.0 2405 2.1645 184.07
6 1.0~2.0 46343 41.7087 7719.97
7 2.0~3.0 21006 18.9054 5465.30
8 3.0~5.0 1708 1.5372 598.06
9 >5.0 14 0.0126 7.26
总计 533015 479.7135 16151.00
表选项

由于汛期流域排水区降雨产流先进入湖泊调蓄，然后由汤逊湖泵站抽排入江，表 2中的流域总水量扣除湖泊原有水量即为率定期流域降雨产生的积水水量.模型模拟时将湖水深设为1.85 m，利用ArcGIS软件的重分类功能统计出水域面积为61.383 0 km2，故湖泊原有水量为11 355.86万m3.表 2计算出的流域总水量减去湖泊原有水量则为2013年7月5-7日暴雨产生的流域积水水量：V1=16 151.00-11 355.86=4 795.14(万m3) .另外，据泵站运行记录可知： 2013年7月5-7日汤逊湖泵站累计排水量为5 068.01万m3.由此可得：模型率定期模拟结果的积水总量相对误差：Δ=(V2－V1)/V2×100%=5.4%.

选取流域易积水的7个典型地段，根据经纬度坐标确定典型地段位于栅格中的行列数，输出模拟期间最大积水水深，进行误差分析，结果如表 3.

表 3 率定期典型地段积水深度误差分析 Table 3 Error analysis of maximum inundation depths in calibration period
编号 地名 最大积水水深/mm 绝对误差/mm 相对误差/%
计算值 实测值
1 雄楚大道石牌岭路口 370.4 350 20.4 5.8
2 雄楚大道图书城门口 364.4 350 14.4 4.1
3 卓豹路教师小区 230.8 250 -19.2 -7.7
4 卓豹路保利华都路段 79.7 110 -30.3 -27.5
5 出版城路金地格林城 272.2 260 12.2 4.7
6 民族大道新竹路路口 334.7 360 -25.3 -7.0
7 白沙洲大道三桥下桥处 99.5 110 -10.5 -9.5
误差均值 18.9 9.5
剔除最大最小误差后的均值 18.3 6.9
表选项

从表 3可知，率定期典型地段积水深度绝对误差均值为18.9 mm，均方根误差RMSE为20.0 mm，相对误差均值为9.5%，剔除最大、最小误差后的相对误差均值为6.9%.各积水点的积水成因大致为持续暴雨、排水能力偏低、地势低洼、内湖水位顶托等，符合这些积水点的降雨、地形和下垫面特征.其中“卓豹路保利华都路段”积水水深相对误差较大，可能是因为积水范围较小，最大受淹处的栅格坐标不易确定，使得最大积水水深输出位置与实测受淹处有偏离.

模型模拟结果表明，率定期降雨产流总量以及典型地段最大积水水深模拟误差较小，与实际状况较为吻合，参数设置较为合理.

4 模型的验证

选取2010年7月11-13日作为验证期进行雨洪模拟，并与实测积水过程相比较，模拟总历时T同样为96 h.由于验证期和率定期时间相隔较短，期间流域土地利用和管网建设变化不大.因此，模型的参数设定不变，仅雨量资料不同，其余数据与模型率定期相同.验证期各典型地段最大积水水深计算值、实测值及误差分析如表 4所示.

表 4 验证期典型地段积水深度误差分析 Table 4 Error analysis of maximum inundation depths in verification period
编号 地名 最大积水水深/mm 绝对误差/mm 相对误差/%
计算值 实测值
1 雄楚大道石牌岭路口 578.5 500 78.5 15.7
2 雄楚大道图书城门口 533.5 500 33.5 6.7
3 卓豹路教师小区 274.4 300 -25.6 8.5
4 卓豹路保利华都路段 97.4 130 -32.6 25.1
5 出版城路金地格林城 389.1 330 59.1 17.9
6 民族大道新竹路路口 442.5 500 -57.5 11.5
7 白沙洲大道三桥下桥处 145.6 180 -34.4 19.1
误差均值 45.9 14.9
剔除最大最小误差后的均值 37.6 14.5
表选项

由表 4可知，验证期典型地段总体上积水深度相对误差均值为14.9%，绝对误差均值为45.9 mm，RMSE为49.3 mm.误差在合理范围内，说明模拟结果可靠.与率定期原因相同，出现“卓豹路保利华都路段”积水水深相对误差较大.

比较表 3和表 4可知，验证期典型地段最大积水水深的计算值和实测值均大于率定期.分析其原因为：率定期3 d暴雨为268.0 mm，验证期3 d暴雨为313.5 mm.经频率计算，率定期3 d暴雨重现期为11.8 a，验证期3 d暴雨重现期为17.4 a.再加上汤逊湖泵站排水能力有限，所以得出上述验证期模拟和实测的流域典型地段最大积水深度大于率定期的结果，符合实际情况.

5 结论

本文通过对降雨径流过程进行简化，建立了基于D8算法的城市分布式雨洪模型.率定期与验证期模型运行结果表明：通过对产汇流及管网排水过程进行简化，基于D8算法的城市雨洪模型可以有效地模拟城市湖泊流域雨洪积水过程.

利用所建立的模型进行不同水平年不同重现期暴雨雨洪情景分析，可以进一步研究雨洪影响机制及风险分析，为城市雨洪灾害控制提供决策依据.

参考文献
[1] 胡伟贤, 何文华, 黄国如, 等. 城市雨洪模拟技术研究进展[J]. 水科学进展, 2010, 21(1): 137–144.
Hu Weixian, He Wenhua, Huang Guoru, et al. Review of urban storm water simulation techniques[J]. Advances in Water Science, 2010, 21(1): 137–144.
[2] 谈广鸣, 胡铁松. 变化环境下的涝渍灾害研究进展[J]. 武汉大学学报(工学版), 2009, 42(5): 565–571.
Tan Guangming, Hu Tiesong. New research advances of waterlogging disasters under climate change and human activities[J]. Engineering Journal of Wuhan University, 2009, 42(5): 565–571.
[3] 孙艳伟, 魏晓妹, PomeroyC A. 低影响发展的雨洪资源调控措施研究现状与展望[J]. 水科学进展, 2011, 22(2): 287–293.
Sun Yanwei, Wei Xiaomei, Pomeroy C A. Review of current research and future directions of low impact development practices for storm water[J]. Advances in Water Science, 2011, 22(2): 287–293.
[4] Barco J, Wong K M, Stenstrom M K. Automatic calibration of the US EPA SWMM model for a large urban catchment[J]. Journal of Hydraulic Engineering, 2008, 134(4): 466–474. DOI:10.1061/(ASCE)0733-9429(2008)134:4(466)
[5] Shahapure S S, Eldho T I, Rao E P. Flood simulation in an urban catchment of Navi Mumbai City with detention pond and tidal effects using FEM, GIS and remote sensing[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2011, 137(6): 286–299. DOI:10.1061/(ASCE)WW.1943-5460.0000093
[6] 解以扬, 李大鸣, 李培彦, 等. 城市暴雨内涝数学模型的研究与应用[J]. 水科学进展, 2005, 16(3): 384–390.
Xie Yiyang, Li Daming, Li Peiyan, et al. Research and application of the mathematical model for urban rainstorm water logging[J]. Advances in Water Science, 2005, 16(3): 384–390.
[7] Chen Y R, Yeh C H, Yu B. Integrated application of the analytic hierarchy process and the geographic information system for flood risk assessment and flood plain management in Taiwan[J]. Natural Hazards, 2011, 59(3): 1261–1276. DOI:10.1007/s11069-011-9831-7
[8] Qi H, Altinakar M S. A GIS-based decision support system for integrated flood management under uncertainty with two dimensional numerical simulations[J]. Environmental Modeling & Software, 2011, 26(6): 817–821.
[9] 刘学军, 卢华兴, 卞璐, 等. 基于DEM的河网提取算法的比较[J]. 水利学报, 2006, 37(9): 1134–1141.
Liu Xuejun, Lu Huaxing, Bian Lu, et al. Comparison of algorithms for extracting drainage network from grid-based digital elevation model[J]. Journal of Hydraulic Engineering, 2006, 37(9): 1134–1141.
[10] 黄膺翰, 周青. 基于霍顿下渗能力曲线的流域产流计算研究[J]. 人民长江, 2014, 45(5): 16–18.
Huang Yinghan, Zhou Qing. Calculation of basin runoff yield based on Horton infiltration capacity curve[J]. Yangtze River, 2014, 45(5): 16–18.
[11] O’Callaghan J F, Mark D M. The extraction of drainage networks from digital elevation data[J]. Computer Vision, Graphics and Image Processing, 1984, 28: 323–344. DOI:10.1016/S0734-189X(84)80011-0
[12] Tarboton D G. A new method for the determination of flow directions and upslope areas in grid digital elevation models[J]. Water Resources Research, 1997, 33(2): 309–319. DOI:10.1029/96WR03137
[13] Hickey R J. Slope angle and slope length solution for GIS[J]. Cartography, 2000, 39(1): 1–8.
[14] 张罗号. 明渠水流阻力研究现状分析[J]. 水利学报, 2012, 43(10): 1154–1162.
Zhang Luohao. Analysis of the present situation of open channels roughness[J]. Journal of Hydraulic Engineering, 2012, 43(10): 1154–1162.
[15] 赵振国, 黄春花. 明渠均匀流研究[J]. 水利学报, 2013, 44(12): 1482–1487.
Zhao Zhenguo, Huang Chunhua. Study on the uniform flow in open channel[J]. Journal of Hydraulic Engineering, 2013, 44(12): 1482–1487.