武汉大学学报(工学版)   2016, Vol. 49 Issue (1): 9-15

文章信息

魏文礼, 蔡亚希, 刘玉玲
WEI Wenli, CAI Yaxi, LIU Yuling
温差对辐流式沉淀池水力特性影响的数值模拟
Numerical simulation of influence of temperature difference on hydraulic characteristics in radial flow sedimentation tank
武汉大学学报(工学版), 2016, 49(1): 9-15
Engineering Journal of Wuhan University, 2016, 49(1): 9-15
http://dx.doi.org/10.14188/j.1671-8844.2016-01-002

文章历史

收稿日期: 2015-05-21
 Abstract              PDF               Figures               Tables
引用本文 0
魏文礼, 蔡亚希, 刘玉玲. 温差对辐流式沉淀池水力特性影响的数值模拟[J]. 武汉大学学报(工学版), 2016, 49(1): 9-15.
WEI Wenli, CAI Yaxi, LIU Yuling. Numerical simulation of influence of temperature difference on hydraulic characteristics in radial flow sedimentation tank[J]. Engineering Journal of Wuhan University, 2016, 49(1): 9-15.
温差对辐流式沉淀池水力特性影响的数值模拟
魏文礼, 蔡亚希, 刘玉玲     
西安理工大学水利水电学院,陕西 西安 710048
收稿日期: 2015-05-21
作者简介: 魏文礼(1965-)，男，教授，博士，主要从事环境水力学、水污染控制理论与技术研究, E-mail:wei_wenli@126.com.
基金项目: 国家自然科学基金(编号:51578452,51178391)；陕西省西北旱区生态水利工程重点实验室开放基金(编号:106-221223)；中央财政支持地方高校发展专项资金特色重点学科项目资助(编号:106-00X101).
摘要: 在同时考虑进水与池内水的污泥质量浓度差异及不同季节进水与池内水的温度差异的条件下，对城市污水处理厂中广泛应用的辐流式二沉池内的异重流现象进行数值模拟，重点研究冬夏季温差导致的异重流对池内流场、速度场及浓度场的影响，为提高沉淀池污水处理效率提供理论支持.选取Mixture模型和Realizable k-ε 湍流模型，设初始时刻池内充满水，进水为含一定质量浓度污泥的污水(污泥密度为1 051 kg/m3，污水密度为1 000.35 kg/m3)，并通过设置池内水与进水的不同温差，对沉淀池内冬季与夏季不同时刻各工况下异重流的演变规律进行数值模拟.结果表明：由于温度不同导致水流密度变化，使得夏季低温水进入池内产生下异重流，而冬季高温水进入时产生上异重流；冬夏季由温差导致的异重流的存在，均使沉淀池内产生较大的回流区，夏季沉淀池内形成较大的逆时针旋流，而冬季则在池中部形成逆时针旋流，池后部形成较大的顺时针旋流，异重流导致的旋流作用对沉淀池内水流流态及污水处理效率的影响不容忽视.
关键词： 辐流式沉淀池     温度     异重流     数值模拟    
Numerical simulation of influence of temperature difference on hydraulic characteristics in radial flow sedimentation tank
WEI Wenli, CAI Yaxi, LIU Yuling     
Faculty of Water Resources and Hydroelectrio Engineering, Xi’an University of Technology, Xi’an 710048, China
Abstract: Considering the sludge concentration difference and the temperature difference between the inflow water and the water in pool in different seasons, the radial flow sedimentation tank is numerically simulated especially, the influence of temperature difference on the flow field, velocity field and sludge concentration distribution of density current in the radial flow sedimentation tank is studied in summer and in winter, to improve the efficiency of wastewater treatment. The mixture model with the realizable k-ε model is used to simulate the property of density current by setting the different temperature differences between the inflow water and the water in the tank in summer and in winter. In initial time the sedimentation tank is filled with water and the inflow water is sewage which contains certain sediment mass concentration (sediment density is 1 051 kg/m3, sewage density is 1 000.35 kg/m3).The results show that: water density changes with temperature difference, which makes the low temperature inflow water to strengthen the gravity flow in the bottom in summer;while the high temperature inflow water produces the gravity flow on the top in winter；the larger recirculation region in sedimentation tank is produced by the density current of temperature difference in summer and in winter;the counterclockwise vortex obviously forms in summer;while in winter the counterclockwise vortex forms in the middle of the tank and large clockwise vortex forms at the back of the tank, which influences the water flow property and the efficiency of wastewater treatment in the sedimentation tank.
Key words: radial sedimentation tank     temperature     density current     numerical simulation    

沉淀池是污水处理过程中一种重要的处理构筑物，辐流式沉淀池由于其排泥性能好、出水水质高、用地面积少，在现代污水处理厂被广泛应用.国内外研究者大多采用计算流体力学(CFD)技术来模拟辐流式二沉池的运行情况[1, 2]，刘玉玲[3]等采用两相流混合模型，选取RNG k-ε湍流模型封闭两相流时均方程，对辐流式二沉池液固两相流力学特性进行三维数值模拟.刘跃[4]等选取Mixture模型和RNG k-ε两方程紊流模型对平流式沉淀池内的异重流现象进行数值模拟，研究异重流对池内流场及污泥沉降规律的影响.秦博[5]通过在辐流式沉淀池内设置斜管，对辐流式斜管沉淀池处理生活污水进行实验研究，掌握了斜管沉淀池的构造功能及沉淀原理.汪强林[6]等对合肥市望塘污水处理厂辐流式二沉池集水渠附近的流速及沿池径方向SS指标进行监测，结果表明辐流式二沉池的水面上SS浓度最低的位置在距离池壁3.0~4.0 m处，沉淀池内存在明显的异重流.金光[7]等对可以实现混凝沉淀的新型辐流式沉淀池进行数值模拟研究，结果表明，在传统辐流式沉淀池内增设强化扰流和改变水流方向的反应罩和导流板，可以使辐流式沉淀池内部流场紊流度明显增强；侯小能[8]采用多相流模型对辐流式沉淀池内流场、悬浮物浓度场进行模拟，经分析认为不同粒径的颗粒可设置为不同的相，据此实现了对沉淀池的三相流数值模拟；李博[9]等采用二维 k-ε紊流模型，在清水状态下对二沉池内的温差异重流现象进行数值模拟.王晓玲[10]等结合高雷诺数k-ε模型，在考虑池形结构变化的条件下，对辐流式二沉池三维流态及悬浮物分布进行模拟研究.

异重流的形成是影响二沉池水力特性的主要因素，形成异重流的主要原因包括沉淀池内污泥质量浓度差异和温度差异.本研究采用Mixture模型和Realizablek-ε湍流模型，在同时考虑进水与池内水的污泥质量浓度差异及不同季节进水与池内水的温度差异的条件下，对辐流式沉淀池内异重流的演变规律进行三维数值模拟研究，模拟结果可以为辐流式沉淀池设计、运行提供参考.

1 数学模型 1.1 连续方程

混合模型是一种简单的多相流模型，可以用于模拟各相间以不同速度运动的流动，也可以用于模拟速度相同的具有强耦合的均匀多相流，同时也可以用于模拟非牛顿流体的黏度.该模型是通过求解混合相的连续性方程、动量方程及能量方程来模拟多相流动.

混合模型连续性方程的表达式为[11, 12]

$\frac{\partial }{\partial t}({{\rho }_{m}})+\nabla \cdot ({{\rho }_{m}}{{v}_{m}})=\dot{m}$    (1)

式中：ρm表示混合密度，ρm=∑nk=1αkρk；∇为哈密顿算子；vm表示质量平均速度，${{v}_{m}}=\frac{{{\sum }^{n}}_{k=1}{{\alpha }_{k}}{{\rho }_{k}}{{v}_{k}}}{{{\rho }_{m}}}$；αk表示第k相的体积分数；ρk为第k相的密度；vk为第k相的质量平均速度；n为项数；为用户定义的质量源的质量传递.

1.2 动量方程

将所有相的动量方程综合可得到混合模型的动量方程表达式：

$\begin{align} & \frac{\partial }{\partial t}\left( {{\rho }_{m}}{{v}_{m}} \right)+\nabla \cdot \left( {{\rho }_{m}}{{v}_{m}}{{v}_{m}} \right)=-\nabla p+\nabla \cdot [{{\mu }_{m}}(\nabla {{v}_{m}}+\nabla {{v}^{T}}_{m})]+{{\rho }_{m}}g+F+ \\ & \nabla \cdot (\sum\limits_{k=1}^{n}{{{\alpha }_{k}}{{\rho }_{k}}{{v}_{dr,k}}{{v}_{dr,k}}})~ \\ \end{align}$    (2)

式中：P为压力；μm为混合黏度；g为重力加速度；F为体积力；vdr,k为第二相k的漂移速度，vdr,k=vk－vm.

1.3 第二相p的体积分数方程

第二相p的体积分数方程为

$\frac{\partial }{\partial t}({{\alpha }_{p}}{{\rho }_{p}})+\nabla \cdot ({{\alpha }_{p}}{{\rho }_{p}}{{v}_{m}})=-\nabla \cdot ({{\alpha }_{p}}{{\rho }_{p}}{{v}_{dr,p}})$    (3)

式中：αp表示第p相的体积分数；ρp为第p相的密度；vdr,p为第p相的漂移速度.

1.4 能量方程

将密度定义为温度的函数，引入能量方程计算温度场，考虑水流由温差引起的密度变化.混合模型的能量方程表达形式为

$\frac{\partial }{\partial t}\sum\limits_{k=1}^{n}{({{\alpha }_{k}}{{\rho }_{k}}{{E}_{k}})}+\nabla \cdot \sum\limits_{k=1}^{n}{({{\alpha }_{k}}{{v}_{k}}}({{\rho }_{k}}{{E}_{k}}+p))=\nabla \cdot ({{k}_{eff}}\nabla T)+{{S}_{E}}~$    (4)

其中，keff是有效导热系数，计算表达式为

keff=∑αk(kk+kt)

kt是湍流热传导系数；式(4)右侧第1项表示由于传导而造成的能量输移；SE包括了所有体积热源；可压缩相Ek的表达式为Ek=hk－p/ρk+v2k/2；不可压缩相Ek的表达式为Ek=hk，这里hk代表第k相的焓值.

1.5 Realizable k-ε湍流模型

Realizable k-ε模型与其他k-ε模型相比适合的流动类型更加广泛，在计算有旋的均匀剪切流、平面混合流、圆形射流、管道内充分发展流动等方面均取得了与实验数据比较一致的结果.其湍动动能k方程及湍动能耗散率ε方程可表示为[13, 14]

$\frac{\partial \left( {{\rho }_{m}}k \right)}{\partial t}+\frac{\partial \left( {{\rho }_{m}}k{{u}_{i}} \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left( \frac{{{\mu }_{m}}}{{{\sigma }_{k}}}\frac{\partial k}{\partial {{x}_{j}}} \right)+{{G}_{k}}-{{\rho }_{m}}\varepsilon $    (5)
$\frac{\partial ({{\rho }_{m}}\varepsilon )}{\partial t}+\frac{\partial \left( {{\rho }_{m}}\varepsilon {{u}_{i}} \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left( \frac{{{\mu }_{m}}}{{{\sigma }_{\varepsilon }}}\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right)+{{\rho }_{m}}{{C}_{1}}E\varepsilon -{{\rho }_{m}}{{C}_{2}}\frac{{{\varepsilon }^{2}}}{k+\sqrt{v\varepsilon }}$    (6)

式(5)为湍动动能k方程，式(6)为湍动动能耗散率ε方程.式中：ui为i方向的速度分量；xi和xj分别为i方向和j方向的坐标分量；Gk为由平均速度梯度引起的紊动动能；经验系数的取值及各系数的计算公式如下：

$\begin{align} & {{\sigma }_{k}}=1.0,{{\sigma }_{\varepsilon }}=1.2{{C}_{2}}=1.9,{{C}_{1}}=max\left( 0.43,\frac{\eta }{\eta +5} \right) \\ & \eta ={{(2{{E}_{ij}},{{E}_{ij}})}^{1/2}},{{E}_{ij}}=\frac{1}{2}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right) \\ & {{C}_{\mu }}=\frac{1}{{{A}_{0}}+{{A}_{s}}{{U}^{*}}k/\varepsilon }{{A}_{0}}=4.0,{{A}_{s}}=\sqrt{6}cos\phi \\ & \phi =\frac{1}{3}co{{s}^{-1}}\left( \sqrt{6}W \right),W=\frac{{{E}_{ij}}{{E}_{jk}}{{E}_{ki}}}{{{({{E}_{ij}}{{E}_{ij}})}^{1/2}}} \\ & {{U}^{*}}=\sqrt{{{E}_{ij}}{{E}_{ij}}+{{\Omega }_{ij}}{{\Omega }_{ij}}}{{{\tilde{\Omega }}}_{ij}}={{\Omega }_{ij}}-2{{\varepsilon }_{ijk}}{{\omega }_{k}}{{\Omega }_{i,j}}{{=}_{ij}}+2{{\varepsilon }_{ijk}}{{\omega }_{k}} \\ \end{align}$

混合流体的紊动黏度μm的计算公式为

$~{{\mu }_{m}}={{\rho }_{m}}{{C}_{\mu }}\frac{{{k}^{2}}}{\varepsilon }~$    (7)

式中：k为混合流体的紊动动能；ε为混合流体紊动动能耗散率；Cμ为常数，其值为0.09.

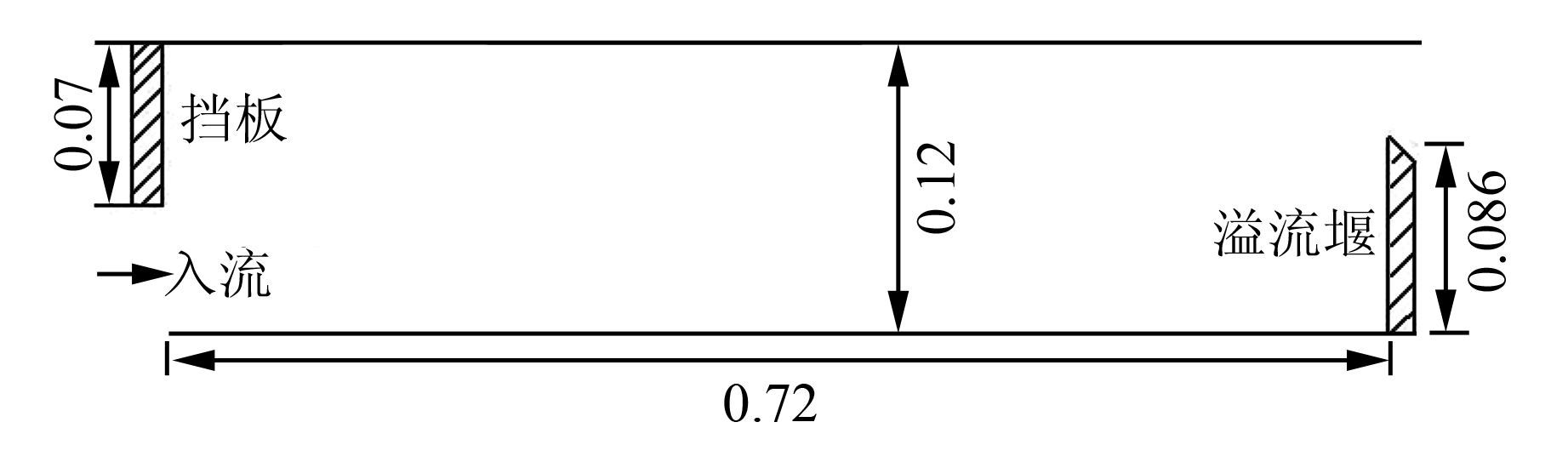
2 模型验证

选取文献[15]中矩形沉淀池内水流的分布实验结果作为验证实例.这里对该沉淀池进行简化，忽略污泥斗和挡板位置的影响.模型尺寸如图 1所示.

图 1 模型尺寸图(单位：m) Figure 1 Model size (unit:m)
图选项

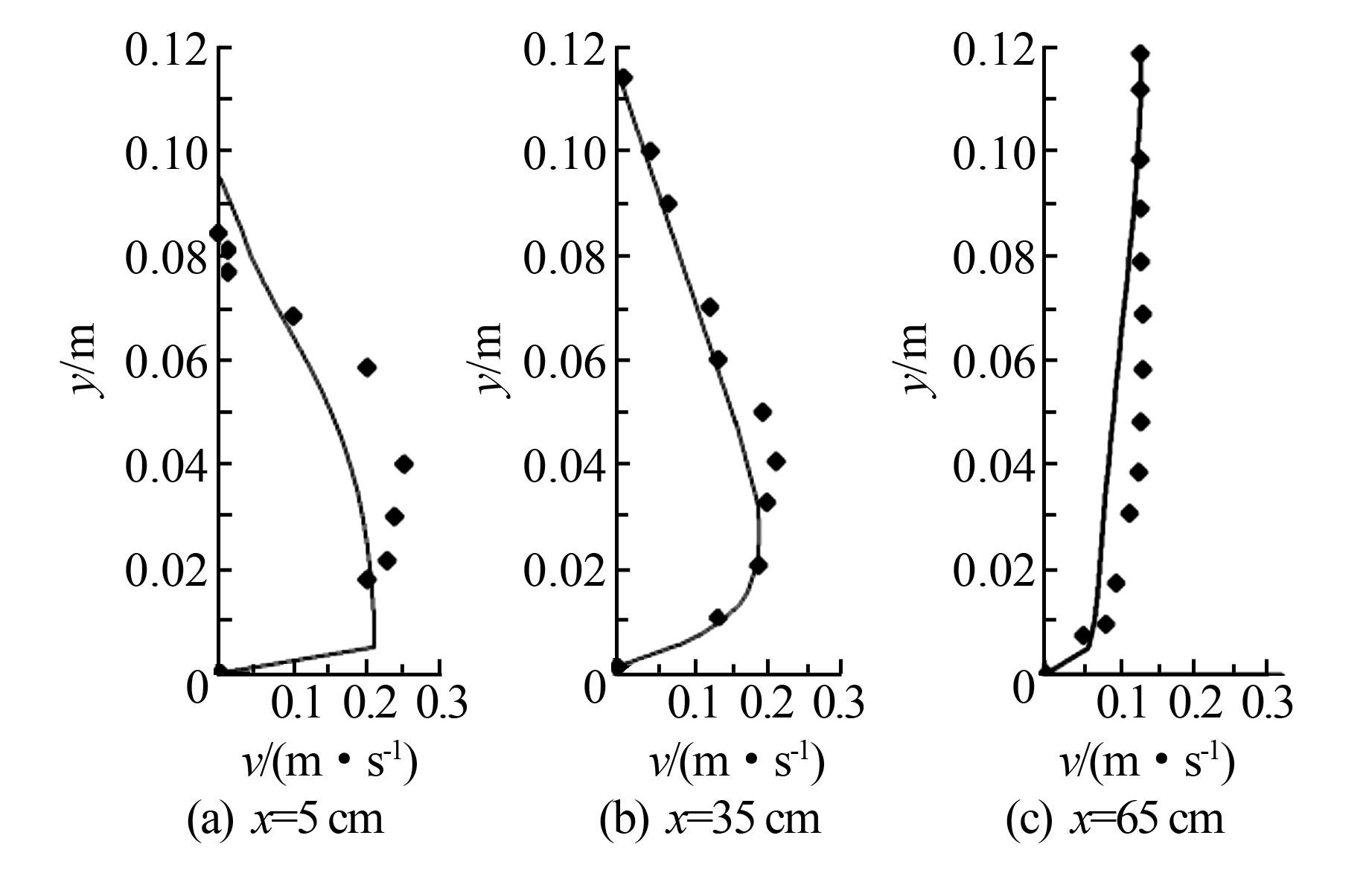
图 2是矩形沉淀池内各断面模拟的速度值与实测值的对比图.由图 2可知,各个断面流速的模拟值和文献[15]的实测值基本吻合，从而验证了Mixture模型和Realizable k-ε湍流模型模拟沉淀池固液两相流的有效性.

图 2 各断面模拟的速度值与实验值对比图 Figure 2 Comparisons of simulation velocity values and the experimental values
图选项
3 数值模拟及结果分析 3.1 计算区域

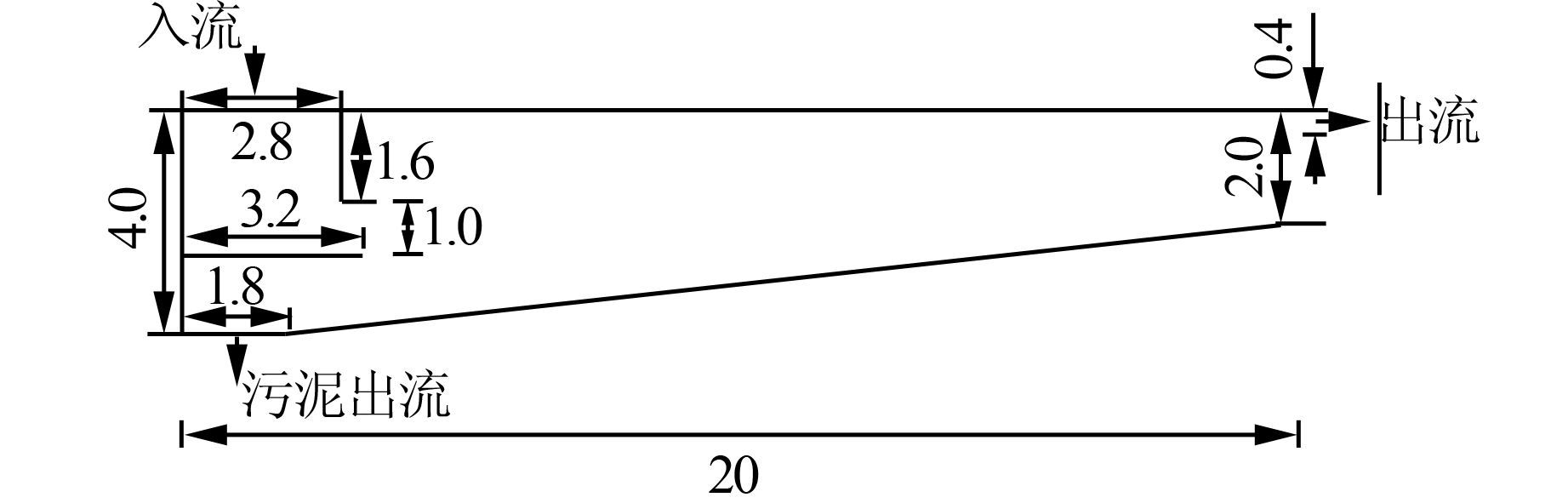
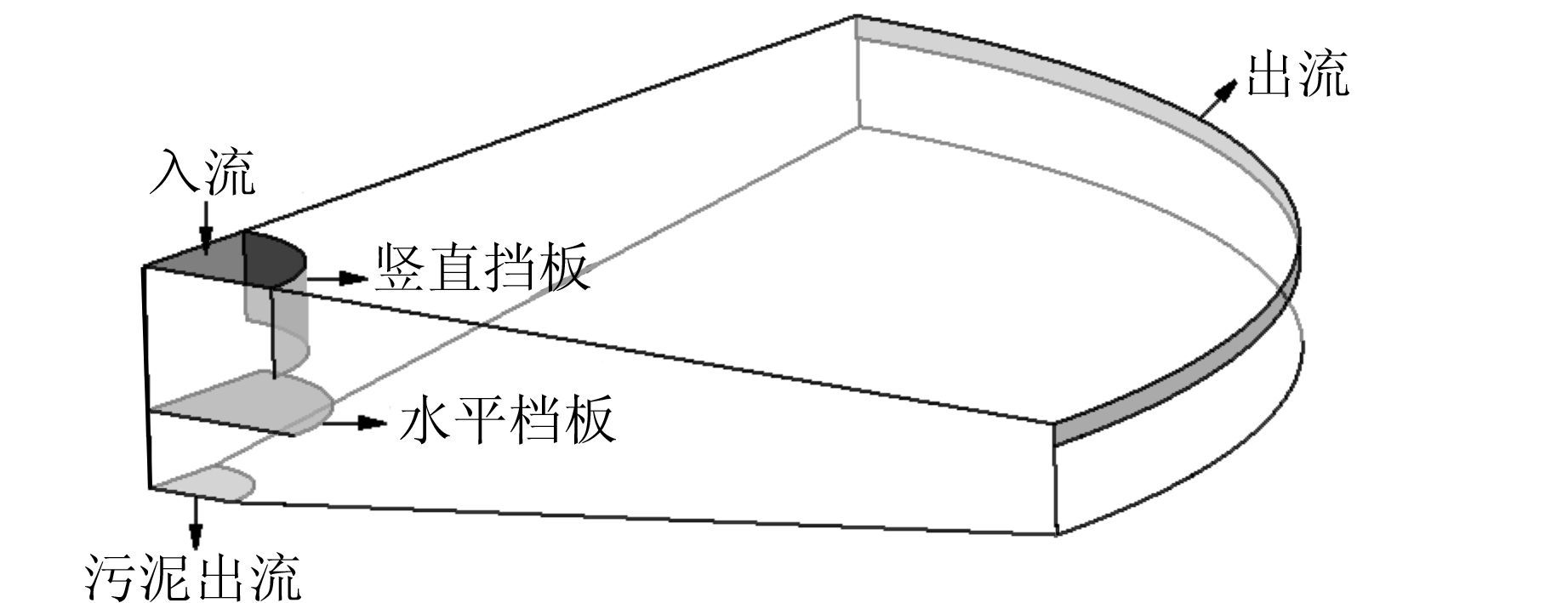
研究所用的辐流式二沉池中心深4.0 m，周边深2.0 m，泥斗设在池中央，池底向中心倾斜，1块垂直挡板用于把入流引向池底，1块水平挡板用于防止进水和污泥回流之间的短流.该辐流式沉淀池平面尺寸如图 3所示，由于二沉池模型为轴对称体，因此取1/4区域进行计算，如图 4所示.

图 3 沉淀池模型尺寸图(单位：m) Figure 3 Model size of sedimentation tank (unit:m)
图选项
图 4 沉淀池三维计算区域图 Figure 4 Three-dimensional computational region of sedimentation tank
图选项
3.2 网格划分

初始计算网格由GAMBIT软件生成，网格划分采用了非结构化网格，网格总单元数为123 996个.计算网格如图 5所示.

图 5 沉淀池三维计算网格图 Figure 5 Three-dimensional computational mesh of sedimentation tank
图选项
3.3 边界条件

设计算初始时刻池内充满水，进水为含一定质量浓度污泥的污水(污泥密度为1 051 kg/m3，污水密度为1 000.35 kg/m3)，并设置池内水与进水的不同温差(夏季池内水温为25 ℃，冬季池内水温为8 ℃，进水温度均为18 ℃).将密度定义为温度的函数，引入能量方程，考虑水流由温差引起的密度变化.边界条件设置：进口边界定义为速度进口，入流速度v=0.015 m/s，温度为18 ℃；出水口及泥沙出口均采用自由出流；沉淀池固体壁面(包括挡板)上的边界条件按“壁面函数”法给定，即符合流速在壁面上的不分离和无滑移条件；自由水面按“刚盖”假定给出边界条件.模型的离散采用有限体积法，速度与压力耦合方程组求解时使用半隐式SIMPLE算法[14].

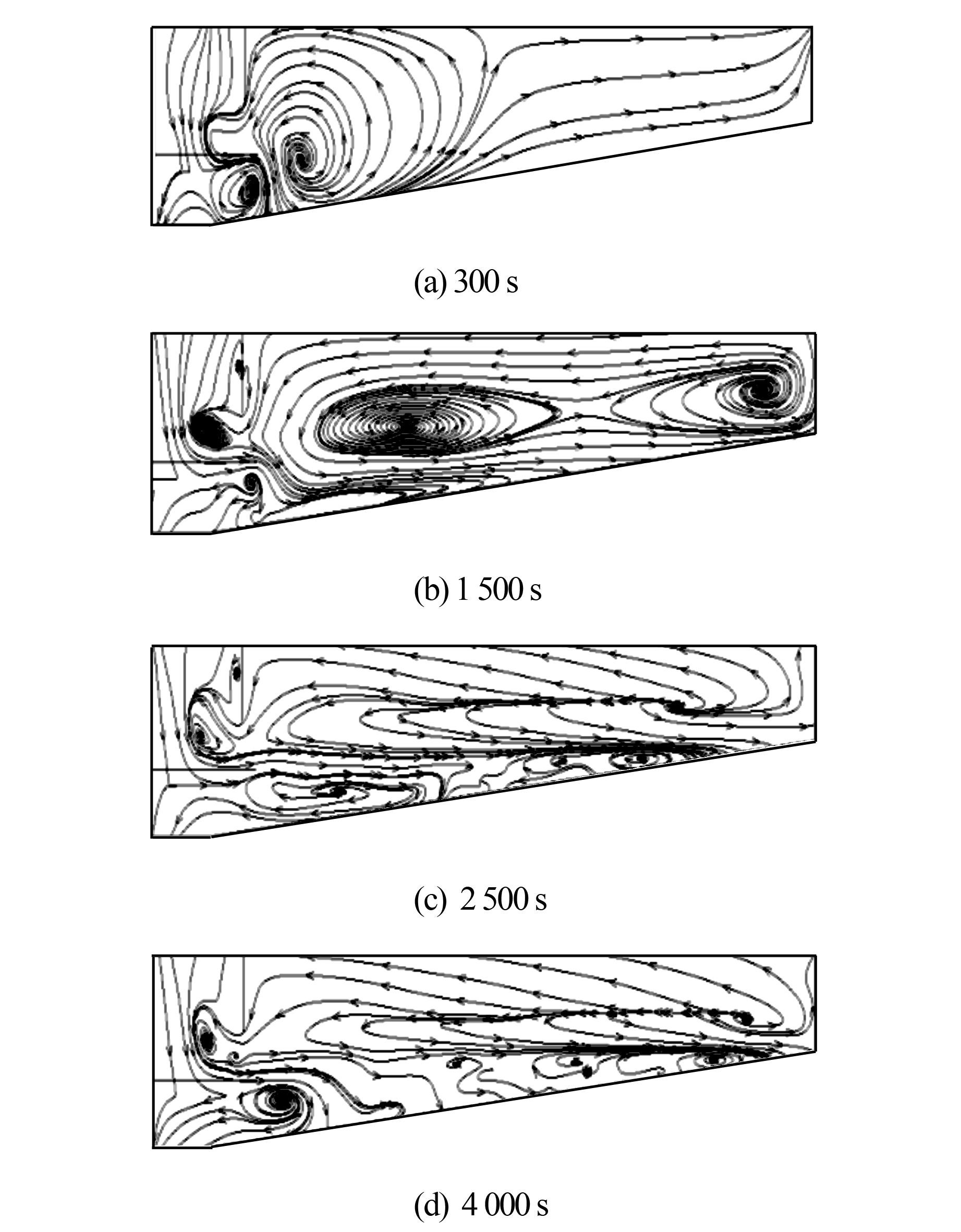
3.4 冬夏季不同时刻流场结构分析

图 6为夏季不同时刻池内水流的流场结构分布.通过池内流线的变化，反映出异重流对池内流态的影响.由图 6(a)、(b)可知：夏季低温水进入形成下异重流，入流一部分紧贴边壁向泥沙出口处运动，另一部分在竖直挡板后形成由池底至池表面的逆时针旋流.图 6(b)中随着计算时间的增加，逆时针旋流的中心后移，影响范围逐渐扩大，整个池内受到旋流的影响形成自池底至池表面的逆时针旋流.由图 6(c)、(d)可知，随着时间的推移，沉淀池中后部逆时针旋流作用逐渐减弱，能量递减，池内流态趋于稳定，泥沙出口后方仍然受到低能量旋流的影响,形成较小的回流区.

图 6 夏季不同时刻流线分布图 Figure 6 Streamlines distribution under different time in summer
图选项

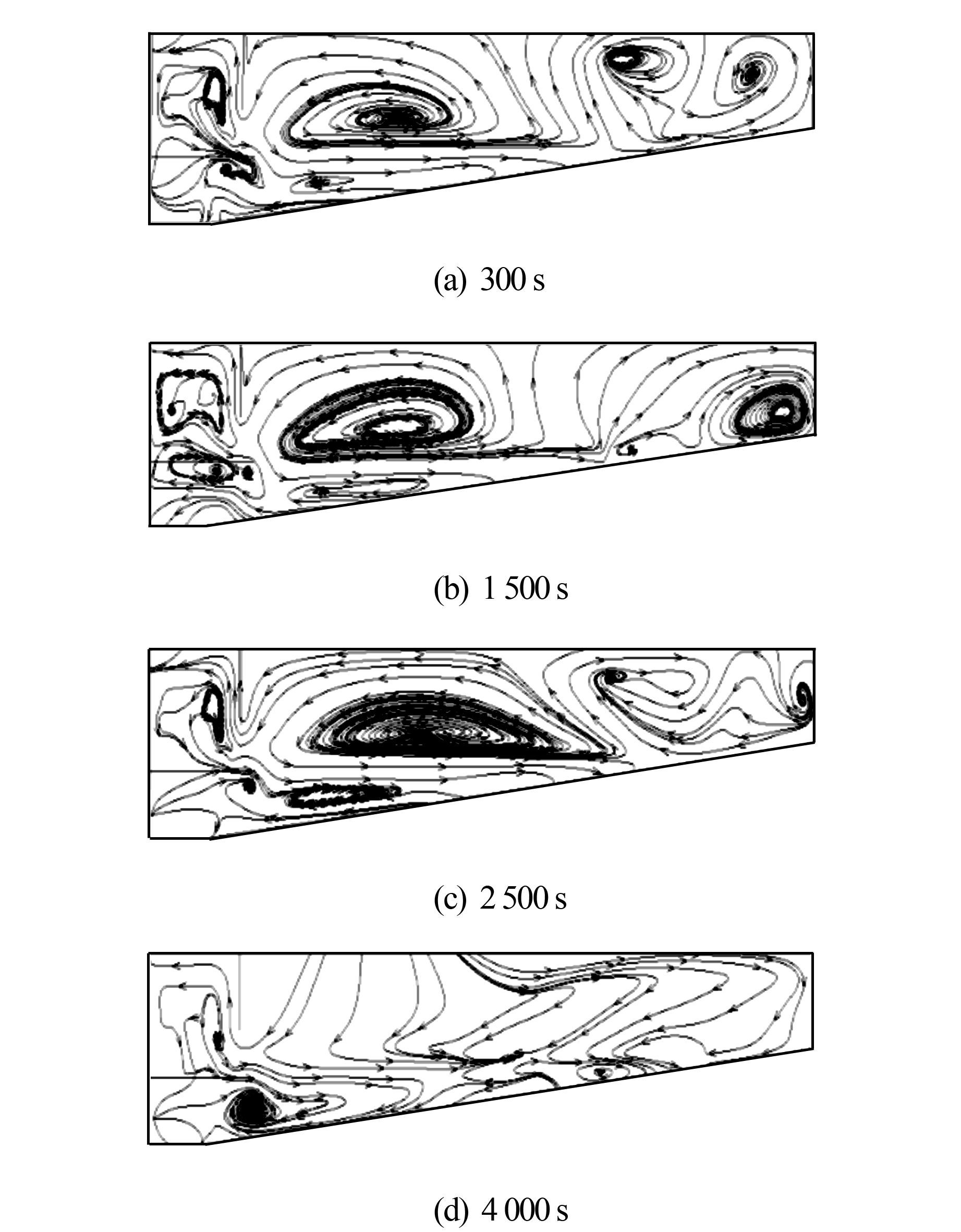
图 7为冬季不同时刻池内水流的流线分布，由图可见与夏季不同，冬季高温水进入形成上异重流.由于水流密度受到温度的影响，温度越高密度越小，因此高温水进入池内先沿池表面流动，随后再由表面向下流动，形成明显的上异重流.由图 7(a)-(c)可以看到，上异重流导致沉淀池中部形成较大的逆时针旋流，而在沉淀池的后部形成顺时针旋流.由图 7(d)可知，随着计算时间的延长，旋流作用减弱，除泥沙出口后方仍然受到低能量旋流的影响形成较小的回流区外，池内流态趋于稳定.

图 7 冬季不同时刻流线分布图 Figure 7 Streamlines distribution of different time in winter
图选项
3.5 冬夏季不同时刻流速分布云图分析

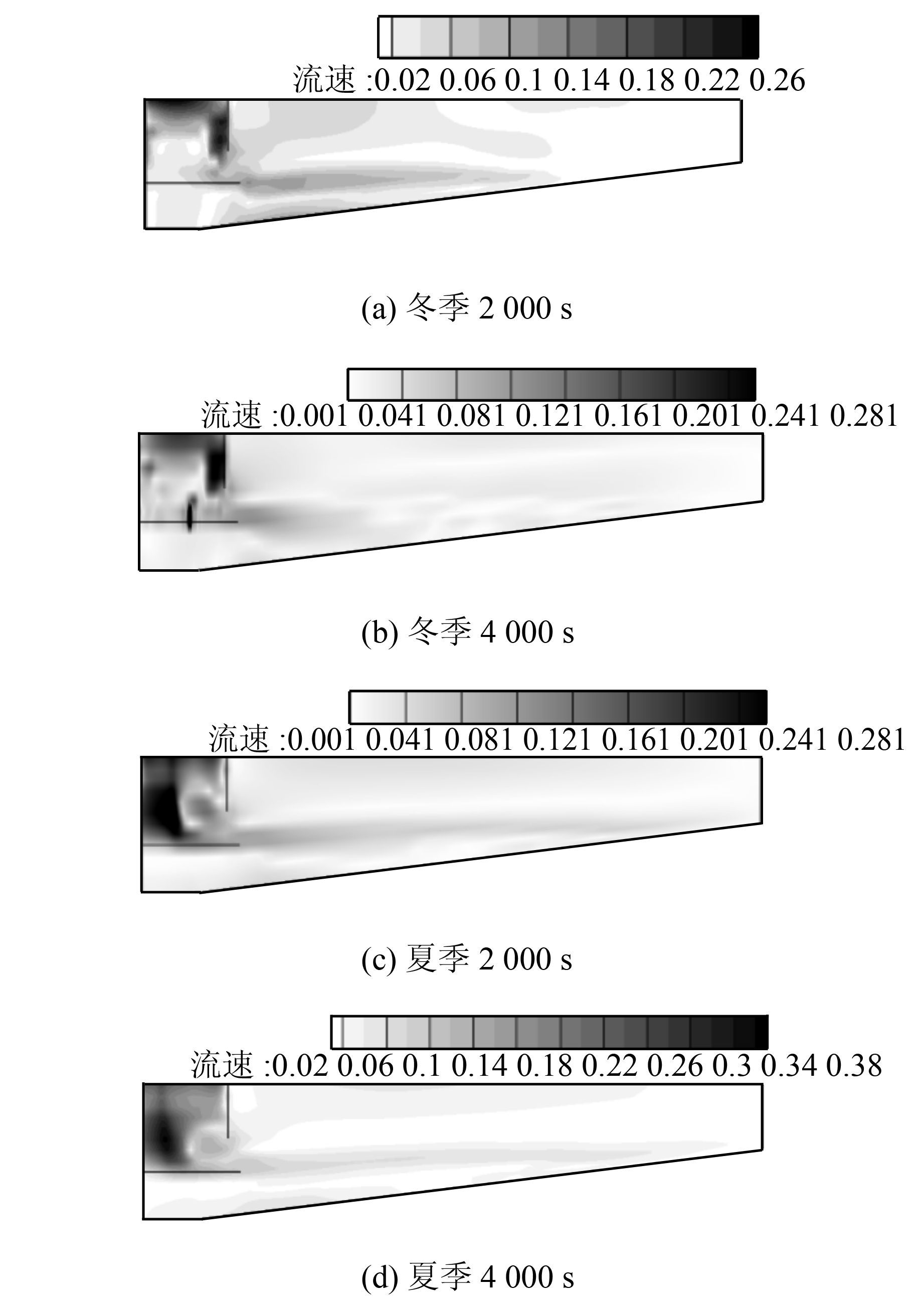
图 8为冬夏季不同时刻池内流速云图分布，从图 8(a)、(b)可以看出，冬季高温水进入沉淀池后，由于高温水的密度比低温水小，因此受到浮力的作用大于重力的作用，使得高温水流浮于沉淀池表面，如图所示表现为进水口表面流速大于底部流速，形成明显的上异重流.图 8(c)、(d)为夏季不同时刻池内的流速分布，从图中可以看出，夏季低温水进入沉淀池后，水流直接下潜，并没有向池内扩散和混合，而是一直向下推进直至水平挡板附近才有了明显的扩散和混合现象，如图所示表现为进水口下部流速大于表面流速，形成了明显的下异重流.

图 8 冬夏季不同时刻流速分布云图(单位：m/s) Figure 8 Velocity contour of different time in summer and winter (unit:m/s)
图选项
3.6 速度分布分析

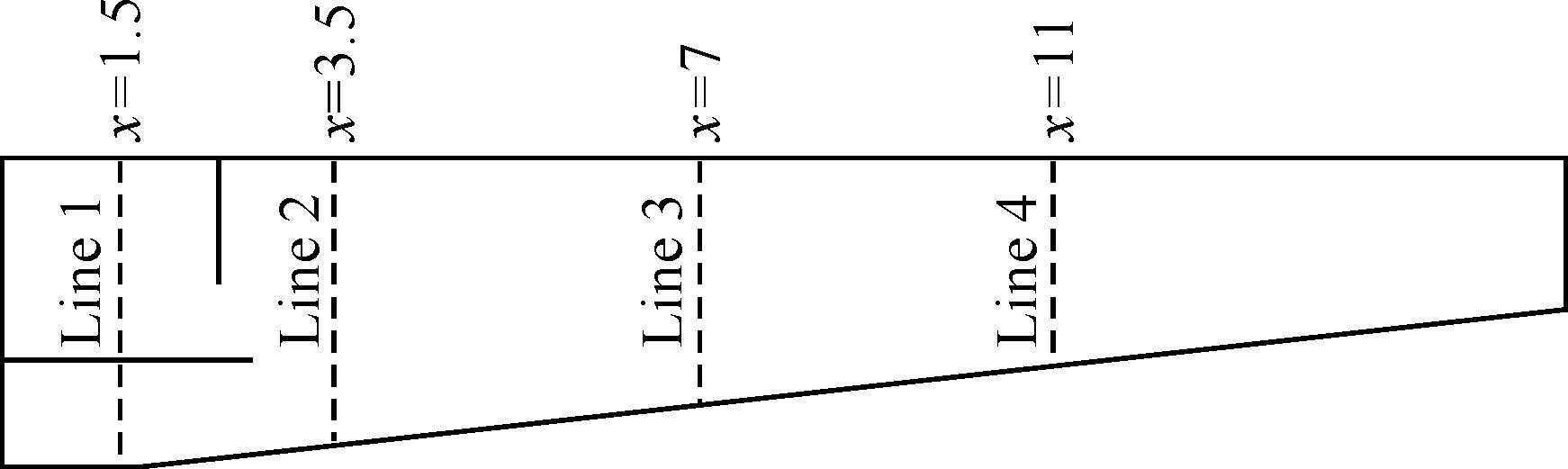
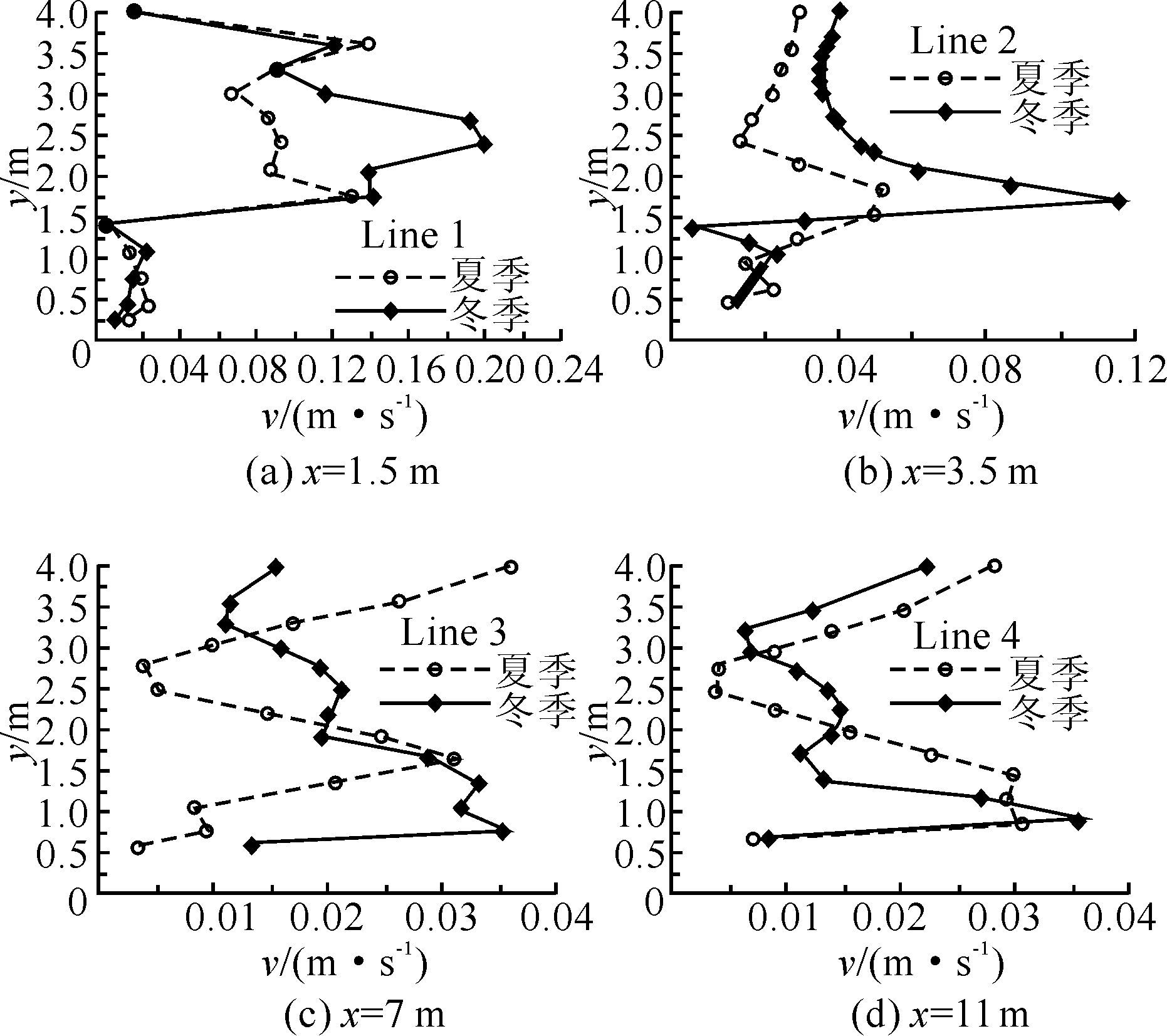
温度对沉淀池内流速沿水深方向的分布有着重要影响.为能更加直观地观察和分析沉淀池内水流流速分布受温度差的影响，取计算时间为4 000 s时距入口处x=1.5、3.5、7、11 m处共4条测线上流速沿水深方向的分布.图 9为沉淀池流速测线布设图，图 10为冬夏季各测线上的流速分布.

图 9 沉淀池流速测线布设图(单位：m) Figure 9 Diagram of measuring lines for velocity distribution in sedimentation tank (unit:m)
图选项
图 10 速度分布图 Figure 10 Velocity distributions
图选项

图 10为沉淀池内各测线沿y方向速度分布图.图 10(a)是接近沉淀池左边壁处的流速分布，从图中可以看出,由于冬季形成上异重流，使得池内中上部流速大于夏季流速.图 10(b)是竖直挡板后池内沿y方向的流速分布，由于冬季形成上异重流夏季形成下异重流，因此图中冬夏季流速曲线表现为在池上部冬季池内流速大于夏季，而池下部夏季池内流速大于冬季.由于冬夏季产生的异重流现象均会使池中部产生自下向上的逆时针旋流，使得下层异重流及上层回流的流速都变大，因此图中冬夏季流速曲线均呈上升趋势.除此之外，由图 10(c)、(d)可知，由于异重流导致池内中后部产生旋流，下异重流使得池内中后部整体形成自下向上的逆时针旋流，随着回流区域逐渐扩大，下层异重流及上层回流的流速都会变大，这也正如图 10(c)、(d)中表现的夏季流速曲线在池顶部流速增大.上异重流在池内中部形成自下向上的逆时针旋流，但在池后部形成自上向下的顺时针旋流，因此图 10(c)中冬季流速曲线在池中下部速度大于夏季，而池上部流速小于夏季.冬夏季在泥沙出口处由于污泥沉积，导致流速曲线在接近泥沙出口处流速均出现减小的趋势，见图 10(d).

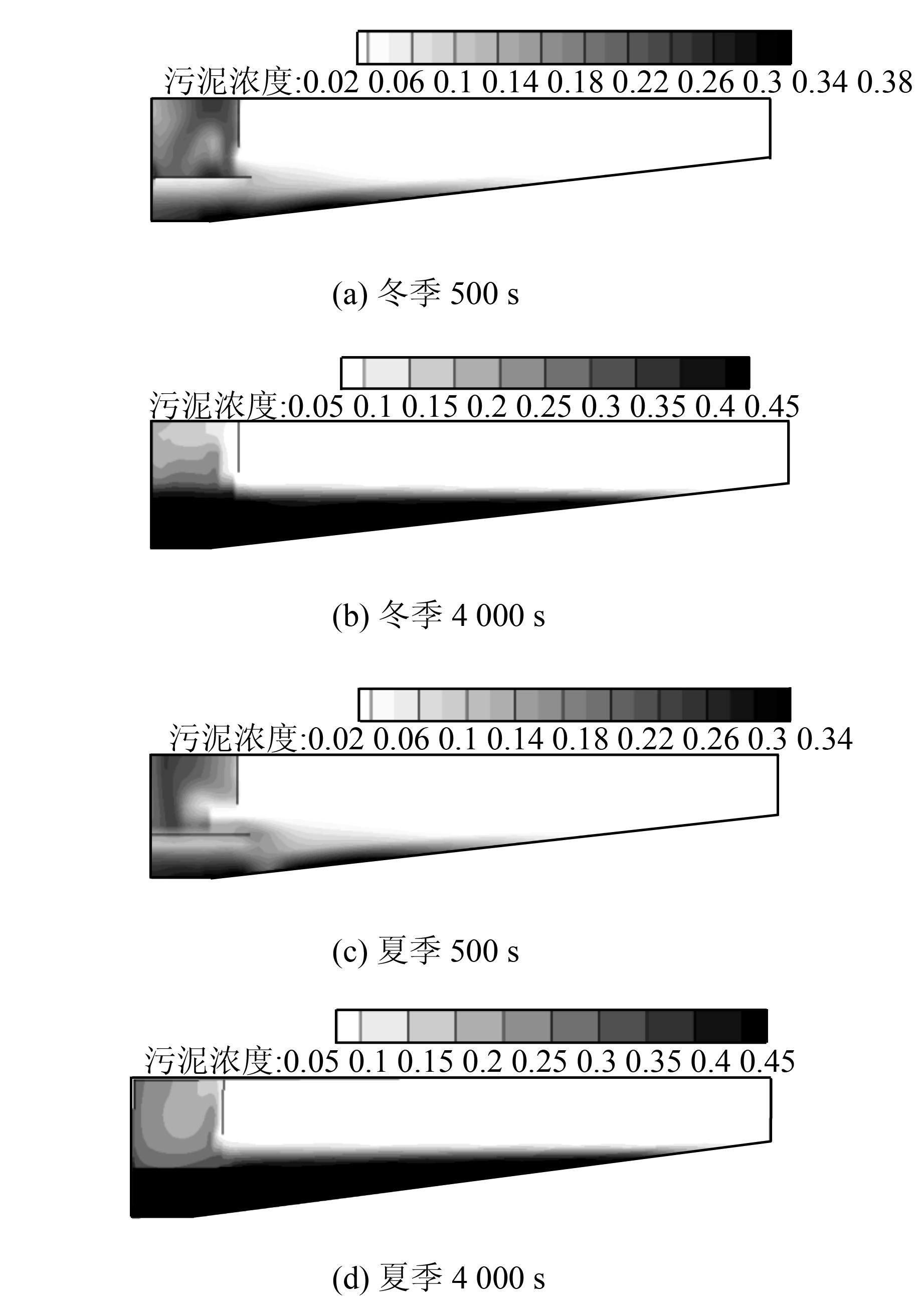
3.7 浓度分布分析

图 11为冬夏季不同时刻沉淀池内污泥浓度分布，由图 11(a)沉淀池运行500 s时冬季池内的污泥质量浓度分布可以看出，高温水进入池内后，在进水口附近形成上异重流现象，污泥受到浮力作用大于重力作用，因此在池子表面运动，使得池子表面的污泥浓度较大，随着水流前进过程中能量的交换，导致浮力减弱，污泥开始下沉；在图 11(b)中，污泥质量浓度的分布出现正常的分层现象，异重流的影响逐渐减弱.由图 11(c)、(d)夏季污泥浓度分布可知，低温水流入沉淀池后，水流直接下潜，池子表面的污泥浓度较小，形成典型的下异重流现象.

图 11 冬夏季不同时刻污泥浓度分布图 Figure 11 Sludge concentration of different time in summer and winter
图选项

夏季池内产生的下异重流现象使得进水直接下潜，促进了进水中颗粒的沉淀，这是异重流有利的一面.下异重流使池内产生自下向上的逆时针旋流，在出口位置，旋流会导致部分未经过沉淀作用的进水直接从出口排出，这将严重影响沉淀池的出水水质.冬季产生的上异重流现象使得进水受到的浮力作用大于重力作用，污泥浮于池子表面，不利于颗粒的沉淀.因此，异重流的存在会使沉淀池的处理效率大幅下降，入流所产生的异重流对二沉池的影响不容忽视.

4 结论

研究选取Mixture模型和Realizable k-ε湍流模型在同时考虑进水与池内水的污泥质量浓度差异及不同季节进水与池内水温度差异的条件下，对辐流式二沉池内的异重流现象进行数值模拟，重点研究冬夏季温差导致的异重流对池内流场、速度场及浓度场的影响，并得出以下主要结论：

1) 冬夏季沉淀池进水温度与池内水温的差异，均会使沉淀池产生异重流现象.这是由于水流的温度差异会导致密度差异，夏季进水温度较池内水温低，使得进水的水流密度大于池内水密度，易产生下异重流现象，而冬季进水温度高于池内水温，则产生上异重流现象.

2) 流场的分析结果表明，温差导致的异重流现象使辐流式沉淀池内存在明显的回流区，夏季沉淀池中后部形成较大的逆时针旋流；冬季沉淀池中部形成逆时针旋流，而池后部则形成顺时针旋流.回流区的存在影响了沉淀池内的水流流态，对提高沉淀池污水处理效率不利.

3) 沉淀池内流速及污泥浓度分布的分析结果表明，冬季形成的上异重流现象使得进水口表面流速较大，污泥受到的浮力作用大于重力作用，使得池子表面的污泥浓度也较大；夏季低温水流入沉淀池后，水流直接下潜，进水口下部流速大于表面流速，使得池子表面的污泥浓度较小，形成典型的下异重流现象.

4) Mixture模型和Realizable k-ε湍流模型是研究温度对辐流式沉淀池水力特性影响的有效方法，模拟结果对实际工程中提高辐流式沉淀池的污水处理效率具有一定的指导意义.

参考文献
[1] 刘玉玲, 张沛, 魏文礼. 辐流式沉淀池液固两相流力学特性二维数值模拟[J]. 武汉大学学报(工学版), 2013, 46(4): 410–412.
Liu Yuling, Zhang Pei, Wei Wenli. Two-dimensional numerical simulation of properties of liquid-solid two-phase flow in a circular secondary clarifier[J]. Engineering Journal of Wuhan University, 2013, 46(4): 410–412.
[2] Fan Long, Xu Nong, Ke Xiyong. Numerical simulation of secondary sedimentation tank for urban wastewater[J]. Journal of the Chinese Institute of chemical Engineers, 2007, 38(6): 425–433.
[3] 刘玉玲, 张沛, 魏文礼, 等. 辐流式沉淀池液固两相流力学特性三维数值模拟[J]. 水资源与水工程学报, 2013, 24(4): 25–27.
Liu Yuling, Zhang Pei, Wei Wenli, et al. Numerical simulation of mechanical property of solid-liquid two-phase turbulent flow in a secondary sedimentation tank of radial flow[J]. Journal of Water Resources & Water Engineering, 2013, 24(4): 25–27.
[4] 刘跃, 谭立新. 平流二沉池中计及温差影响的异重流数值模拟[J]. 西北农林科技大学学报(自然科学版), 2013, 41(9): 1–8.
Liu Yue, Tan Lixin. Numerical simulation of gravity flow in rectangular sedimentation tanks with the consideration of temperature difference[J]. Journal of Northwest A & F University (Natural Science Edition), 2013, 41(9): 1–8.
[5] 秦博. 辐流式斜管沉淀池处理生活污水的实验研究[J]. 环境科学与管理, 2012, 37(4): 82–85.
Qin Bo. Research on domestic wastewater treatment with radial flow inclined tube settling tank[J]. Environmental Science and Management, 2012, 37(4): 82–85.
[6] 汪强林, 汤利华, 李玲霞. 双侧堰辐流式二沉池出水存在的问题及其机制分析[J]. 工业用水与废水, 2012, 43(2): 53–56.
Wang Qianglin, Tang Lihua, Li Lingxia. Existing problems of double side-weir radial flow secondary sedimentation tank and mechanism analysis thereof[J]. Industrial Water & Wastewater, 2012, 43(2): 53–56.
[7] 金光, 张保生, 张菊, 等. 实现辐流式沉淀池混凝沉淀的数值模拟研究[J]. 人民黄河, 2011, 33(5): 41–45.
Jin Guang, Zhang Baosheng, Zhang ju, et al. Realization of radial flow sedimentation tank coagulation precipitation numerical simulation research[J]. Yellow River, 2011, 33(5): 41–45.
[8] 侯小能. 沉淀池的三相流数值模拟[J]. 山西建筑, 2011, 37(23): 124–125.
Hou Xiaoneng. Three-phase numerical simulation in a sedimentation tank[J]. Shanxi Architecture, 2011, 37(23): 124–125.
[9] 李博, 谭立新, 胡钟林. 平流二次沉淀池中温差异重流的数值模拟[J]. 水力发电学报, 2010, 29(1): 37–43.
Li Bo, Tan Lixin, Hu Zhonglin. Numerical simulation of gravity flow caused by temperature difference in rectangular sedimentation tank[J]. Journal of Hydroelectric Engineering, 2010, 29(1): 37–43.
[10] 王晓玲, 曹月波, 张明星, 等. 辐流式沉淀池固液两相流三维数值模拟[J]. 工程力学, 2009, 26(6): 243–249.
Wang Xiaoling, Cao Yuebo, Zhang Mingxing, et al. Three-dimensional simulation of solid-liquid two-phase flow in a circular secondary clarifier[J]. Engineering Mechanics, 2009, 26(6): 243–249.
[11] 戴会超, 槐文信, 吴玉林, 等. 水利水电工程水流精细模拟理论与应用[M]. 北京: 科学技术出版社, 2006.
Dai Huichao, Huai Wenxin, Wu Yulin, et al. Theories and Applications of Flow Refined Simulation for Hydraulic and Hydropower Engineering[M]. Beijing: Science and Technology Press, 2006.
[12] 谭立新, 李博, 李尔康. 平流二次沉淀池中温差对异重流影响的数值模拟研究[J]. 西安理工大学学报, 2013, 29(2): 182–187.
Tan Lixin, Li Bo, Li Erkang. Numerical simulation of the effect of temperature difference on gravity flow in rectangular secondary setting tanks[J]. Journal of Xi’an University of Technology, 2013, 29(2): 182–187.
[13] 王磊磊, 许光明, 陈俊, 等. 超大型周进周出式沉淀池优化设计中的水力性能数值模拟[J]. 河海大学学报(自然科学版), 2012, 40(2): 168–172.
Wang Leilei, Xu Guangming, Chen Jun, et al. Numerical simulation of hydraulic performance of optimally designed super sedimentation tank with peripheral inflow and peripheral effluent[J]. Journal of Hohai University (Natural Sciences), 2012, 40(2): 168–172.
[14] 魏文礼, 戴会超. 紊流模型理论及工程应用[M]. 西安: 陕西科学技术出版社, 2006.
Wei Wenli, Dai Huichao. Turbulence Model Theory and Engineering Applications[M]. Xi’an: Shaanxi Science and Technology Press, 2006.
[15] Imam E, McCrquodale J A, Bewtra J K. Numerical modelling of sedimentation tank[J]. Journal of Hydraulic Engineering, 1983, 109(12): 1740–1754. DOI:10.1061/(ASCE)0733-9429(1983)109:12(1740)