武汉大学学报(工学版)   2016, Vol. 49 Issue (2): 274-278

文章信息

莫小宝, 胡雪蛟
MO Xiaobao, HU Huejiao
含多组分不凝气体蒸汽冷凝的热扩散模型
Thermal diffusion model for vapor condensation with multicomponent non-condensable gases
武汉大学学报(工学版), 2016, 49(2): 274-278
Engineering Journal of Wuhan University, 2016, 49(2): 274-278
http://dx.doi.org/10.14188/j.1671-8844.2016-02-020

文章历史

收稿日期: 2015-06-23
 Abstract              PDF               Figures               Tables
引用本文 0
莫小宝, 胡雪蛟. 含多组分不凝气体蒸汽冷凝的热扩散模型[J]. 武汉大学学报(工学版), 2016, 49(2): 274-278.
MO Xiaobao, HU Huejiao. Thermal diffusion model for vapor condensation with multicomponent non-condensable gases[J]. Engineering Journal of Wuhan University, 2016, 49(2): 274-278.
含多组分不凝气体蒸汽冷凝的热扩散模型
莫小宝1,2, 胡雪蛟1,2     
1. 武汉大学 动力与机械学院，湖北 武汉 430072;
 2. 水力机械过渡过程教育部重点实验室，湖北 武汉 430072
收稿日期: 2015-06-23
作者简介: 胡雪蛟（1975-），男，教授，博士生导师，主要从事传热传质及热物性光学测量研究，E-mail: xjhu@whu.edu.cn.
基金项目: 国家重点基础研究发展计划项目（973计划）（编号：2014CB239203）;国家自然科学基金项目（编号：50906064）;教育部博士点基金项目（编号：20100141110022）.
摘要: 提出了考虑热扩散的非等温扩散层模型，根据提出的模型模拟计算了蒸汽冷凝过程中存在N2和H2情况下扩散层中各组分的变化情况，N2和H2在主流区的摩尔分数分别为0.2和0.1。模拟结果表明：分子量较大的N2在界面附近大量聚集，而分子量较小的H2则分布较为均匀，因此N2对凝结过程中热质传递的影响更为显著。在不同温度梯度下，扩散层中H2的浓度变化要大于N2，这是由于H2的热扩散因子要大于N2。最后，利用新的热扩散层模型计算了包含空气的冷凝过程中总的换热系数，并同已有实验结果进行了对比，新模型比传统扩散层模型更加吻合。
关键词： 凝结     热质传递     不凝气体     多组分     热扩散    
Thermal diffusion model for vapor condensation with multicomponent non-condensable gases
MO Xiaobao1,2, HU Huejiao1,2     
1. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China;
 2. Key Laboratory of Hydraulic Transients, Ministry of Education, Wuhan 430072, China
Abstract: A new non-isothermal model considering the accompanied thermal diffusion across the diffusion layer was proposed. An analogy calculation for component variations in the diffusion layer in the presence of N2 and H2 was performed based on the proposed model. The mole fraction of N2 and H2 in the bulk is 0.2 and 0.1, respectively. The results show that N2, the heavier component, accumulates close to the condensing surface and H2, the lighter component, is relatively uniformly distributed. Therefore, the heavier component may have bigger impact on vapor condensation. The variations of H2 are more obvious than N2 in the diffusion layer under different temperature gradient since the thermal diffusion factor of H2 is larger than N2. The total heat transfer coefficients of condensation with air are calculated using the proposed model and compared with experimental data, improved agreement is obtained over the traditional diffusion layer model.
Key words: Condensation     Heat and mass transfer     Non-condensable gases     Multicomponent     Thermal diffusion    

凝结是一种复杂的气液相变传质过程，在自然界和工程领域普遍存在，如海水淡化[1]、热管理[2]和热力发电站[3]等.自努塞尔于1916年提出了纯净蒸汽凝结模型后，许多学者对蒸汽的凝结进行了研

究[4, 5].但这些研究都是在纯蒸汽的条件下展开的，实际情况是纯蒸汽中往往可能会存少量不凝气体.相关研究表明[6]，即使少量不凝气体的存在也会恶化冷凝过程中的热质传递.Colburn等最先采用滞

膜模型(stagnant film model)对蒸汽-空气的混合物进行了理论分析[7].在该模型中，总的凝结热阻包括液膜热阻和气体边界层热阻.在空气存在的情况下，气体边界层的热阻会显著增加.由于该模型较复杂，存在多次迭代，不适合于工程应用.Peterson等在滞膜模型的基础上进行简化得出了扩散层模型(diffusion layer model)[8].Peterson提出了有效凝结热导系数的概念，与气液界面温度弱耦合，数值计算时，可以实现快速收敛.正是这些优点，使该模型广泛应用于核反应堆的热工水利计算[9, 10].Peterson将该模型扩展到了存在多组分不凝气体的凝结过程中，讨论了氢气和空气混合在蒸汽中时，扩散层的传热传质状况[11]，但利用扩散层模型计算的结果有时与实验结果相差40%~70%.因此，许多学者都对该模型进行了修正.Brouwers等在考虑了抽吸和雾化的影响后，在扩散层模型中增加了修正因子，以便得到更为精确的结果[12].另外考虑到液面波动的影响，Peterson等在模型中增加了大小为1.2的液膜波动因子来进行修正[8].另外，Liao等人认为Peterson的扩散层模型是基于摩尔分数来推导的，忽略了分子之间质量的差异，当分子质量相差较大时，计算结果会存在较大误差，因此，提出基于质量分数的形式来推导扩散层模型会更精确[13].虽然许多学者都对简单的扩散层模型进行了修正，但这些修正都没有考虑到热扩散对扩散层的影响，而凝结过程恰恰是伴随着显著热交换的复杂传热传质过程.本文基于Maxwell-Stefan方程推导了扩散层中各组分在温度梯度影响下质量传递情况.新模型的预测结果能够更好地与实验测量结果吻合.

1 热扩散层模型

Peterson在扩散层模型中提出了有效凝结导热系数[11]：

${{k}_{c}}=\frac{1}{\phi }\frac{h_{\text{fg}}^{'}{{h}_{\text{fg}}}P{{}_{\text{eff}}}M_{\text{v}}^{2}}{{{R}^{2}}{{T}^{3}}}$    (1)

其中：P为压力；Deff为有效质量扩散系数；Mv为冷凝蒸汽的分子量；R为气体常数；T为主流区温度Tb和气液界面温度Ti的算术平均值；系数φc为

$\phi =\frac{\ln \left[ (1-{{x}_{\text{gb}}})/(1-{{x}_{\text{gi}}}) \right]}{\ln ({{x}_{\text{gi}}}/{{x}_{\text{gb}}})}$    (2)

其中：xgb为主流区不凝气体的浓度；xgi为气液界面处不凝气体的浓度.

在有效凝结导热系数中一个重要的参数就是有效质量扩散系数Deff，根据Wilke建议[14]，Deff可以表示为

${{D}_{\text{eff}}}=\frac{{{x}_{\text{g},\text{ave}}}}{\sum\limits_{j=1}^{n}{({{x}_{j,\text{ave}}}/{{D}_{j,v}})}}$    (3)

其中：Dj,v为蒸汽与不凝气体之间的质量扩散系数，xg,ave和xj,ave分别可以表示为

${{x}_{\text{g},\text{ave}}}=\frac{{{x}_{\text{g,b}}}-{{x}_{\text{g,i}}}}{\ln ({{x}_{\text{g,b}}}/{{x}_{\text{g,i}}})}$    (4)
${{x}_{j,\text{ave}}}=\frac{{{x}_{j,\text{b}}}-{{x}_{j,\text{i}}}}{\ln ({{x}_{j,\text{b}}}/{{x}_{j,\text{i}}})}$    (5)

其中：xg,b和xg,i分别为主流区和界面处不凝气体总的摩尔分数，由下式给出:

${{x}_{\text{g,b}}}=\sum\limits_{j=1}^{n}{{{x}_{j,\text{b}}}}$    (6)
${{x}_{\text{g,i}}}=\sum\limits_{j=1}^{n}{{{x}_{j,\text{i}}}=1-\frac{{{P}_{\text{v}}}({{T}_{\text{i}}})}{P}}$    (7)

从式(3)~(7)可以看出，计算有效扩散系数Deff和系数φ需要知道主流区和界面处各组分的摩尔分数.

在凝结过程中，明显存在着一定的温度梯度，从而引起组分的扩散.温度梯度和浓度梯度的双重影响会使凝结中各组分在新的状态下达到平衡.根据Maxwell-Stefan方程有

$-\frac{d\ln {{x}_{j}}}{dy}\text{=}\sum\limits_{k\ne j}{\frac{1}{{{D}_{jk}}}{{x}_{k}}(u_{j}^{T}-u_{k}^{T})}$    (8)

其中，ujT定义为[15]

$u_{j}^{T}={{u}_{j}}+\frac{D_{jk}^{T}}{{{\rho }_{j}}}\frac{\nabla T}{T}$    (9)

其中:DjkT为二元热扩散系数(binary thermal diffusion coefficient)，可以表示为[16]

$D_{jk}^{T}=\frac{{{c}^{2}}}{\rho }{{M}_{j}}{{M}_{k}}{{D}_{jk}}{{k}_{T}}$    (10)

其中:kT为热扩散比(thermal diffusion ratio).另外引进热扩散因子(thermal diffusion factor)αjkT，其跟热扩散比之间的关系为kT=αjkTxjxk.将kT代入式(10)得

$D_{jk}^{T}\text{=}\alpha _{jk}^{T}{{D}_{jk}}\rho {{\omega }_{j}}{{\omega }_{k}}$    (11)

其中:ωj=ρj/ρ和ωk=ρk/ρ分别为组分j和k的质量分数，αjkT的求解见参考文献[17]，再将上式代入式(9)得

$u_{j}^{T}={{u}_{j}}+\alpha _{jk}^{T}{{D}_{jk}}{{\omega }_{k}}\frac{\nabla T}{T}$    (12)

质量扩散系数一般由下式计算[18]：

$\begin{align} & {{D}_{jk}}= \\ & 3.16\times {{10}^{-8}}\frac{{{T}^{1.75}}}{P(V_{j}^{1/3}+V_{k}^{1/3})}\left( \frac{1}{{{M}_{j}}}+\frac{1}{{{M}_{k}}} \right)1/2 \\ \end{align}$    (13)

其中:Vj和Vk分别为组分j和k的摩尔体积，一般可由查表或者根据实际气体状态方程计算得到，Mj和Mk分别为组分j和k的分子量.

当考虑某一不凝气体j在混合气体中扩散时，将上式中的冷凝蒸汽v和其他不凝气体k分开来表示

$\begin{align} & -\frac{\text{d}\ln {{x}_{j}}}{\text{d}y}\text{=}\frac{1}{{{}_{jv}}}{{x}_{v}}(u_{j}^{T}-u_{v}^{T})+ \\ & \sum\limits_{k\ne j}^{n-1}{\frac{1}{{{D}_{jk}}}{{x}_{k}}(u_{j}^{T}-u_{k}^{T})} \\ \end{align}$    (14)

其中:Djk为不凝气体之间的质量扩散系数，将式(12)代入上式得

$\begin{align} & -\frac{\text{d}\ln {{x}_{j}}}{\text{d}y}\text{=}\frac{1}{{{D}_{jv}}}{{x}_{v}}\left[ {{u}_{j}}+\alpha _{jv}^{T}{{D}_{jv}}{{\omega }_{v}}\frac{\nabla T}{T}- \right. \\ & \left. ({{u}_{v}}+\alpha _{vj}^{T}{{D}_{vj}}{{\omega }_{j}}\frac{\nabla T}{T}) \right]+\sum\limits_{k\ne j}^{n-1}{\frac{1}{{{D}_{jk}}}{{x}_{k}}\left[ {{u}_{j}}+ \right.} \\ & \left. \alpha _{jk}^{T}{{D}_{jk}}{{\omega }_{k}}\frac{\nabla T}{T}-({{u}_{k}}+\alpha _{kj}^{T}{{D}_{kj}}{{\omega }_{j}}\frac{\nabla T}{T}) \right] \\ \end{align}$    (15)

又因为稳态时，不凝气体速度为0，同时根据热扩散因子αjkT+αkjT=0和扩散系数Djk=Dkj的关系，上式可以表达为

$\begin{align} & -\frac{\text{d}\ln {{x}_{j}}}{\text{d}y}\text{=}-\frac{1}{{{D}_{jv}}}{{x}_{v}}{{u}_{v}}\text{+}{{x}_{v}}\left[ \alpha _{jv}^{T}({{\omega }_{j}}+{{\omega }_{v}})\frac{\nabla T}{T} \right]+ \\ & \sum\limits_{k\ne j}^{n-1}{{{x}_{k}}\left[ \alpha _{jk}^{T}({{\omega }_{j}}+{{\omega }_{k}})\frac{\nabla T}{T} \right]} \\ \end{align}$    (16)

将冷凝蒸汽的摩尔通量Nv=cxvuv=c$\tilde{u}$j代入上式得

$\begin{align} & {{N}_{v}}=c{{{\tilde{u}}}_{j}}=c{{D}_{jv}}\left[ \frac{\text{d}\ln {{x}_{j}}}{\text{d}y}\text{+}{{x}_{v}}\alpha _{jv}^{T}({{\omega }_{j}}+{{\omega }_{v}})\frac{\nabla T}{T}+ \right. \\ & \left. \sum\limits_{k\ne j}^{n-1}{{{x}_{k}}\alpha _{jk}^{T}({{\omega }_{j}}+{{\omega }_{k}})\frac{\nabla T}{T}} \right] \\ \end{align}$    (17)

从上式中可以发现，在计算冷凝蒸汽的摩尔通量时，增加了温度梯度对通量的影响.对于一维扩散，由质量守恒得

$\frac{\text{d}{{N}_{v}}}{\text{d}y}=0$    (18)

在边界层内，总压不变，温度的变化对摩尔浓度c的影响可以忽略不计，因此式(18)又可以表达为

$\frac{\text{d}{{N}_{v}}}{\text{d}y}\text{=}\frac{\text{d}(c{{{\tilde{u}}}_{j}})}{\text{d}y}=c\frac{\text{d}{{{\tilde{u}}}_{j}}}{\text{d}y}+{{\tilde{u}}_{j}}\frac{\text{d}c}{\text{d}y}=\frac{\text{d}{{{\tilde{u}}}_{j}}}{\text{d}y}=0$    (19)

上式可以积分得

$\ln {{x}_{j}}=\ln {{x}_{j,b}}+{{c}_{1}}(y-\delta )+{{k}_{T}}\ln \frac{T}{{{T}_{b}}}$    (20)

其中：c1为常数；${{k}_{T}}={{x}_{v}}\alpha _{jv}^{T}({{\omega }_{j}}+{{\omega }_{v}})+\sum\limits_{k\ne j}^{n-1}{{{x}_{k}}\alpha _{jk}^{T}({{\omega }_{j}}+{{\omega }_{k}})}$，为混合物的热扩散比.

N种不凝气体就有N个形如式(20)的方程，具有相同的表达形式.在主流区各组分摩尔分数为已知，而在界面处冷凝蒸汽与不凝气体的摩尔分数之间的关系可以表示为式(7).根据已知条件，可以发现在界面处给出的信息不足，从式(20)中也可以看出，其中存在一未知系数待求解，因此需要额外的方程来增加约束条件：

${{\tilde{u}}_{j}}={{\tilde{u}}_{k}}$    (21)
2 应用实例及分析

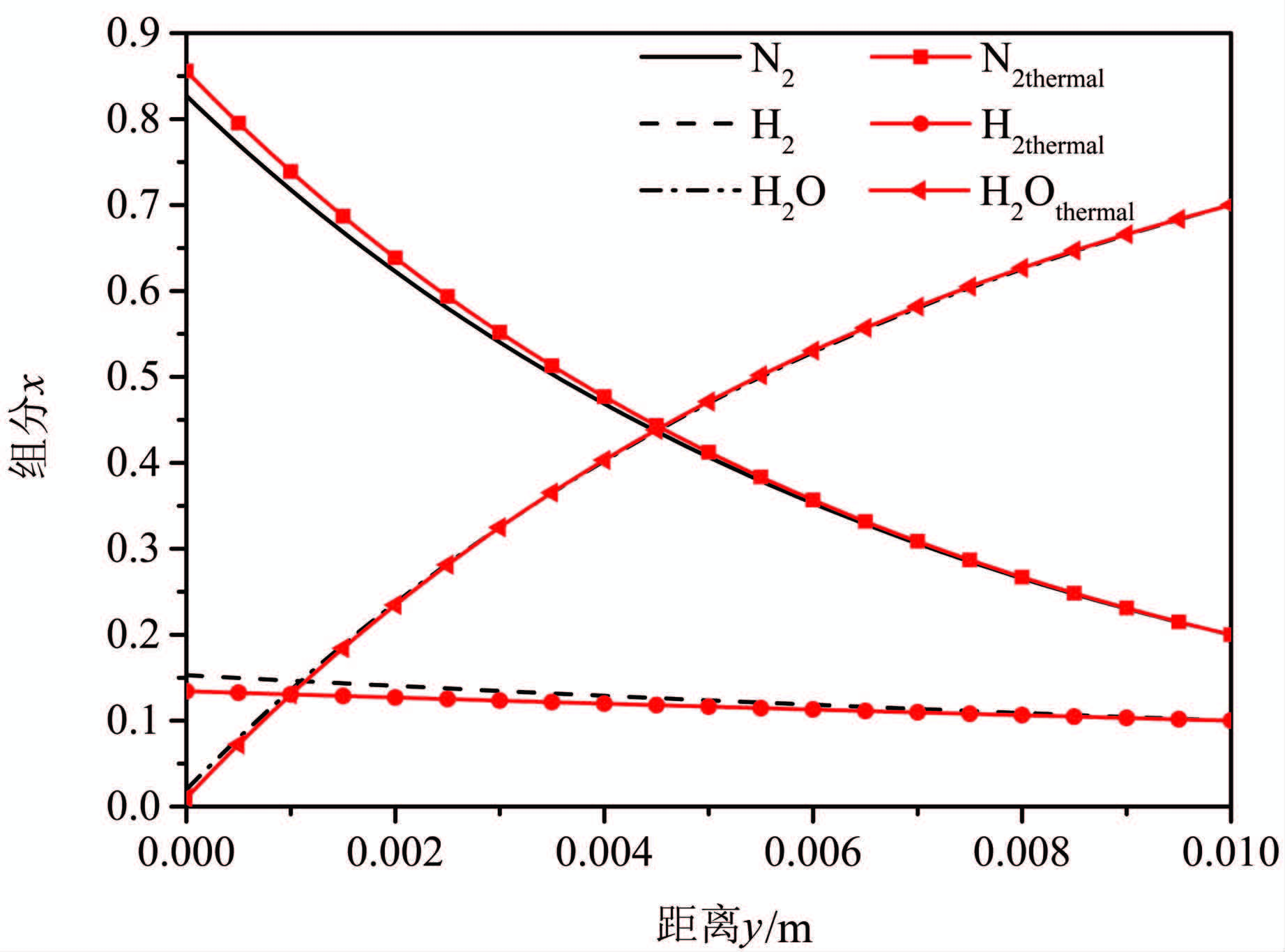
本文以表 1所给出的参数为例计算边界层中各组分的浓度分布，计算结果如图 1所示.结果显示，考虑热扩散与否，组分浓度分布趋势一致.不凝气体N2在界面附近大量聚集，浓度远远高于H2，从而对凝结的影响也远比H2要大.这主要是因为N2的分子量较大，扩散系数较小，聚集在界面处的气体不能快速扩散到主流区，而H2则由于分子量较小，扩散系数较大，分布情况与之相反.这为我们考虑不凝气体对凝结的影响提供了新的思路.同时N2和H2是由壁面附近向主流区扩散，阻碍水蒸气从主流区向壁面扩散.另外也可以看出，温度梯度对组分浓度的分布存在着一定的影响，特别是在冷凝界面处：考虑温度梯度时，N2的浓度要比未考虑时的高出3.5%，相反H2的浓度则要比未考虑时的低出12.2%.这是由于在温度梯度的作用下，分子量较大的N2向冷端运动，而分子量较小的H2则向热端运动，从而导致在冷凝界面附近处N2的浓度升高，H2的浓度则会降低.

表 1 扩散层浓度分布计算初始参数 Table 1 Initial parameters for calculation of diffusion layer
参数值
主流区xN2,b0 0.2
主流区xH2,b0 0.1
主流区温度Tb/K 373.15
气液界面处温度Ti/K 281.15
壁面处xv,i 0.02
扩散层厚度δ/m 0.01
总压P/atm 1
传质系数DN2-H2O/(m2·s-1) 3.094×10-5
传质系数DH2-H2O/(m2·s-1) 1.034×10-4
表选项
图 1 考虑温度梯度和未考虑温度梯度情况下组 Figure 1 Distribution of components in diffusion layer
图选项

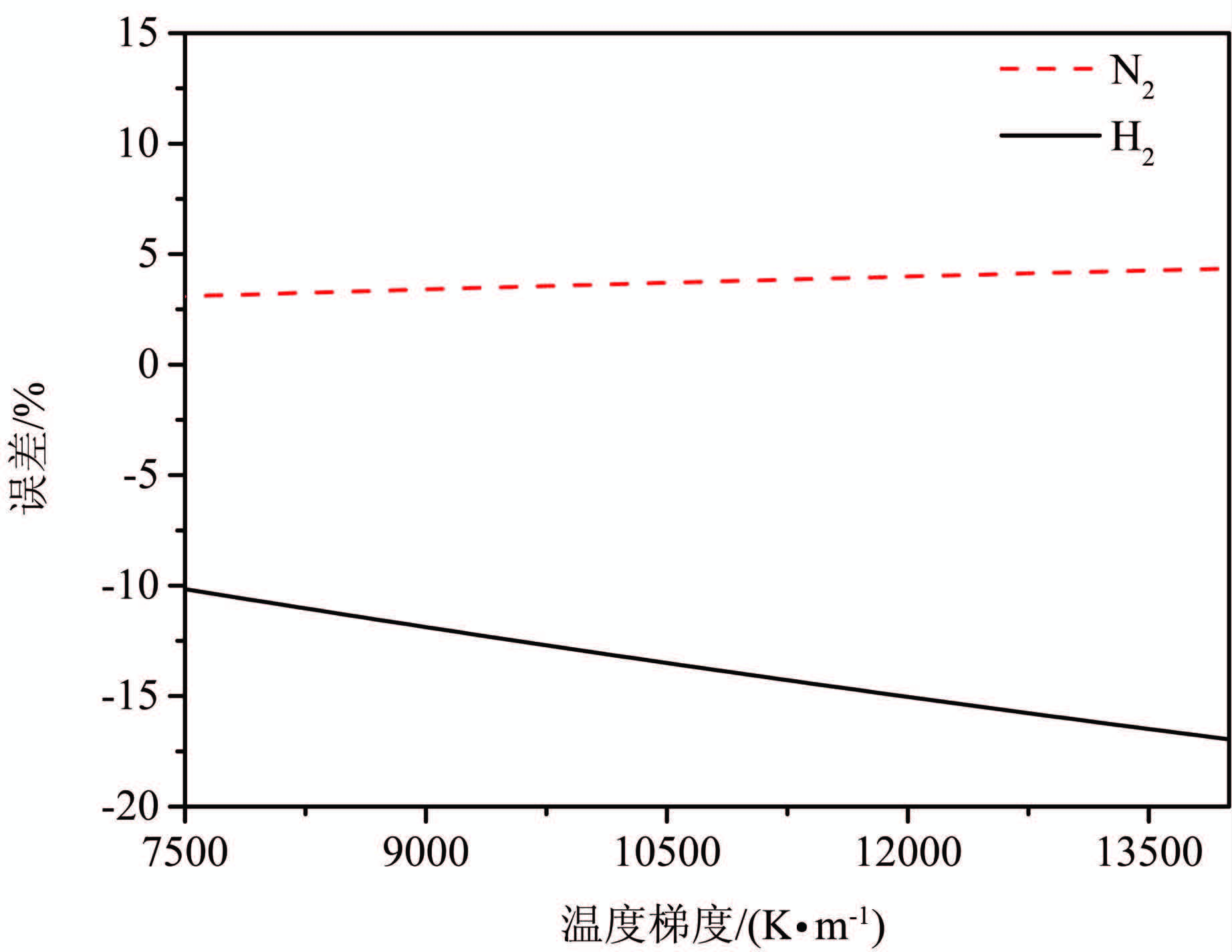
图 2给出了不同温度梯度下，N2和H2摩尔分数与未考虑热扩散时相比的误差变化情况.其中H2的变化要大于N2，因为H2的热扩散因子要大于N2.随着温度梯度的增大，热扩散的影响也越来越明显.同时由于在界面处不凝气体的重新分布，水蒸气在界面处的含量进一步降低，使相应饱和温度下降，减小凝结传质动力，削弱凝结过程.

图 2 组分浓度误差在界面处随温度梯度变化情况 Figure 2 Temperature gradient dependence of concentration error at condensing surface
图选项
3 扩散层传热

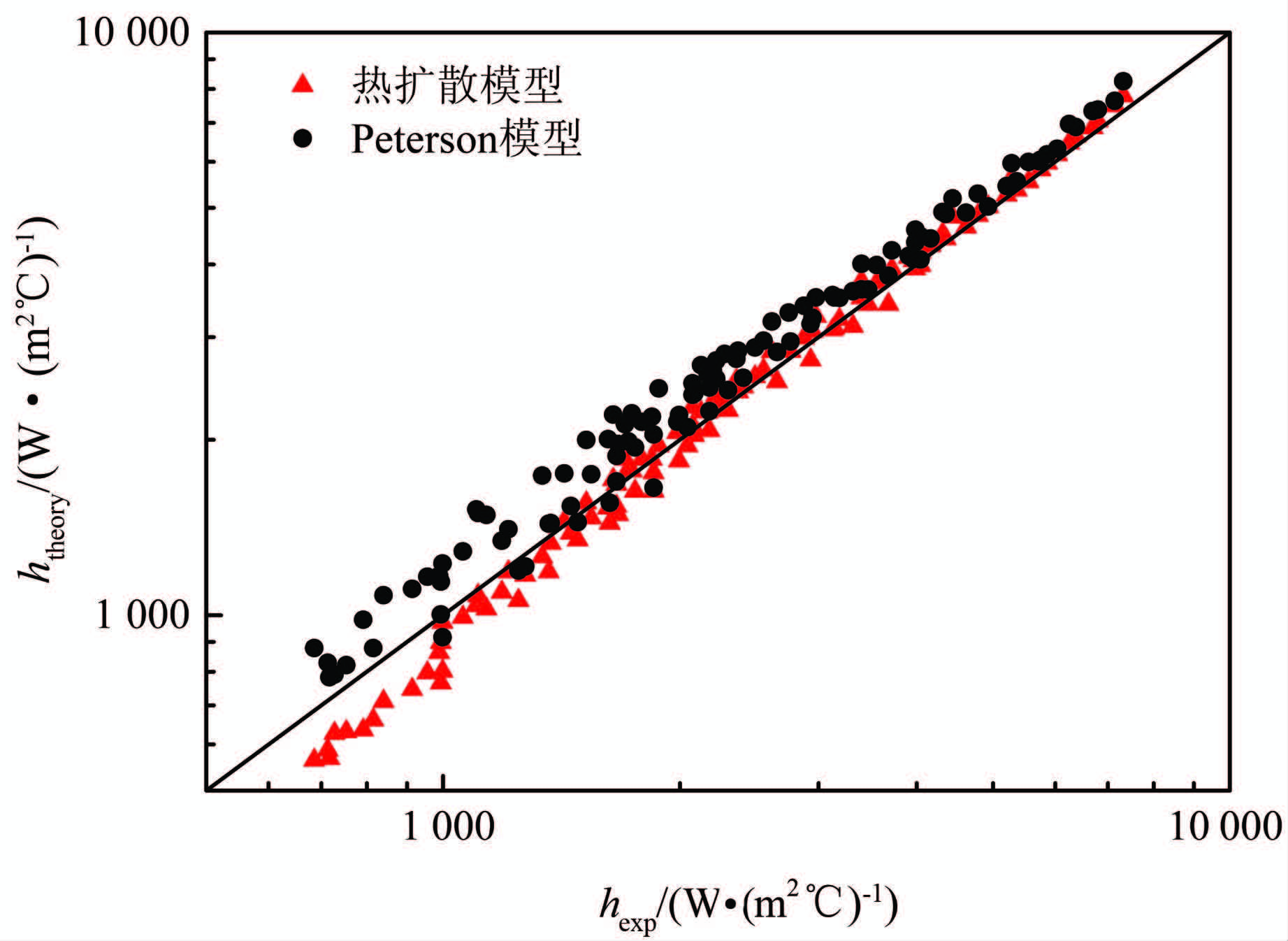
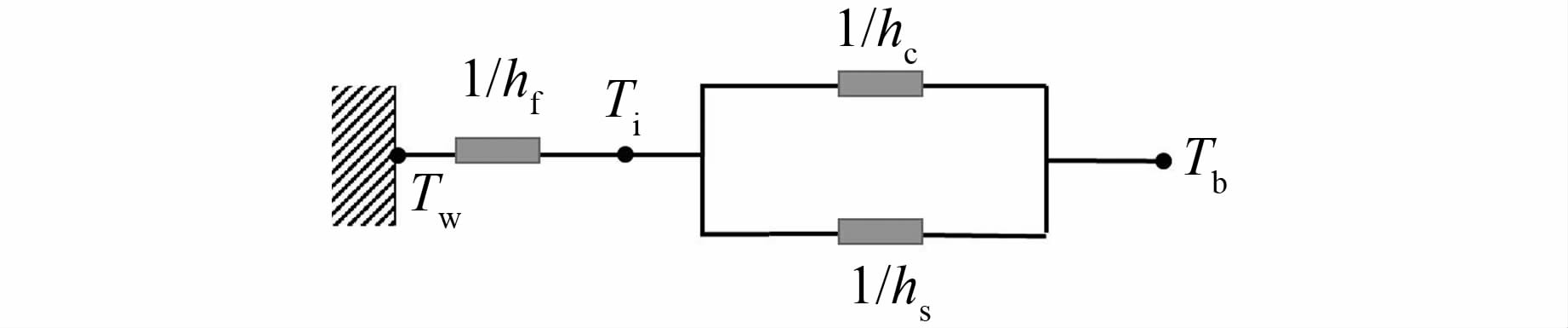
为了验证本文热扩散层模型的正确性，将模型的计算结果同文献[19]的实验结果进行了对比，如图 3所示.文献[19]中测量了蒸汽混合空气在强制对流情况下总的换热系数.在理论计算中，空气的主要成分选取了N2和O2进行计算.凝结过程的热阻系统如图 4所示，整个换热过程包括纯对流换热hs、水蒸汽在壁面凝结释放的潜热hc和液膜导热hf3个部分.于是，总换热系数可由下式计算：

$\frac{1}{{{h}_{\text{t}}}}=\frac{1}{{{h}_{\text{c}}}+{{h}_{\text{s}}}}+\frac{1}{{{h}_{\text{f}}}}=\frac{L}{Sh\cdot {{k}_{\text{c}}}+Nu\cdot {{k}_{\text{s}}}}+\frac{{{\delta }_{\text{f}}}}{{{k}_{\text{f}}}}$    (22)
图 3 理论计算与实验总换热系数对比 Figure 3 Comparison of theoretical and experimental total heat transfer coefficients
图选项

其中：L为特征长度；Sh和Nu分别为舍伍德数和努塞尔数；kc为扩散层模型中定义的有效凝结导热系数，由式(1)计算得到；δf为液膜厚度；kf为液膜的导热系数；ks为扩散层的显热导热系数，由下式计算：

${{k}_{\text{s}}}=\frac{1}{\frac{{{x}_{v,\text{ave}}}}{{{k}_{v}}}+\sum\limits_{j=1}^{n}{\frac{{{x}_{j,\text{ave}}}}{{{k}_{j}}}}}$    (23)

理论结果与实验结果之间的标准差按照下式计算：

$\text{std}=\sqrt{\sum\limits_{j=1}^{N}{\left( \frac{{{h}_{theory}}}{{{h}_{exp}}}-1 \right)}_{j}^{2}/\left( N-1 \right)}$    (24)

其中：N为实验数据点个数.计算得到的标准差为9%，实验结果与理论计算吻合较好，而Peterson的扩散层模型结果与实验结果标准差为14%，这表明热扩散层模型更好地预测了凝结过程总的换热系数.从图 3中可以看到，当换热系数较小时(h＜1 000 W/(m2℃))，理论与实际测量结果相差较大，这主要是由于换热区域较小的区域主要存在于下流区，液膜厚度较大，并且容易产生波纹，能够在垂直于液面的方面产生流动，从而加强换热.因此，此时应当考虑波纹对传热的影响，加入适当的修正系数.

图 4 含不凝气体冷凝过程热阻系统示意图 Figure 4 Schematic illustration of thermal resistance of condensation with noncondensable gases
图选项
4 结论

本文提出了考虑热扩散的含多组分不凝气体的蒸汽冷凝扩散层模型，利用Maxwell-Stefan方程推导了扩散层的组分分布.发现N2在气液界面处聚集程度较高，而H2的聚集程度则明显偏小.这主要是因为N2的质量扩散系数小于H2的质量扩散系数，通过对流作用聚集到界面处的H2能够很快地扩散到主流蒸汽区中，而N2则只能聚集在界面处.在考虑温度梯度时，气液界面处N2浓度要高3.5%，而H2浓度要低12.2%.这是由于在温度梯度的作用下，分子量较大的物质朝冷端运动，而分子量较小的物质朝热端运动造成的.

本文利用新的热扩散层模型计算了凝结过程总的换热系数，并将结果同Kuhn的实验结果进行了对比，结果表明，基于热扩散的扩散层模型能够准确预测凝结换热系数，标准误差在9%以内，优于Peterson的扩散层模型.

参考文献
[1] Khawaji A D, Kutubkhanah I K, Wie J. Advances in seawater desalination technologies[J]. Desalination, 2008, 221(1): 47–69.
[2] Mudawar I. Assessment of high-heat-flux thermal management schemes[J]. Components and Packaging Technologies, IEEE Transactions on, 2001, 24(2): 122–141. DOI:10.1109/6144.926375
[3] Beér J M. High efficiency electric power generation: The environmental role[J]. Progress in Energy and Combustion Science, 2007, 33(2): 107–134. DOI:10.1016/j.pecs.2006.08.002
[4] Dobran F, Thorsen R S. Forced flow laminar filmwise condensation of a pure saturated vapor in a vertical tube[J]. International Journal of Heat and Mass Transfer, 1980, 23(2): 161–177. DOI:10.1016/0017-9310(80)90194-5
[5] Lilburne G M, Wood D G. Condensation inside a vertical tube: heat transfer[C]// Proc. 7th Int. Conf., 1982.
[6] 刘泉, 杨渐志, 顾海林, 等. 不凝性气体对竖直平板对流冷凝的影响[J]. 中国科学技术大学学报, 2015, 45(5): 397–403.
Liu Quan, Yang Jianzhi, Gu hailin. Effect of non-condensable gas on convective condensation on a short vertical plate[J]. Journal of University of Science and Technology of China, 2015, 45(5): 397–403.
[7] Colburn A P, Hougen O A. Design of cooler condensers for mixtures of vapors with noncondensing gases[J]. Industrial & Engineering Chemistry, 1934, 26(11): 1178–1182.
[8] Peterson P F, Schrock V E, Kageyama T. Diffusion layer theory for turbulent vapor condensation with noncondensable gases[J]. Journal of Heat Transfer, 1993, 115(4): 998–1003. DOI:10.1115/1.2911397
[9] Herranz L E, Anderson M H, Corradini M L. A diffusion layer model for steam condensation within the AP600 containment[J]. Nuclear Engineering and Design, 1998, 183(1): 133–150.
[10] Herranz L E, Muńoz-Cobo J L, Verdu G. Heat transfer modeling in the vertical tubes of the passive containment cooling system of the simplified boiling water reactor[J]. Nuclear Engineering and Design, 1997, 178(1): 29–44. DOI:10.1016/S0029-5493(97)00178-7
[11] Peterson P F. Diffusion layer modeling for condensation with multicomponent noncondensable gases[J]. Journal of Heat Transfer, 2000, 122(4): 716–720. DOI:10.1115/1.1318215
[12] Brouwers H. Effect of fog formation on turbulent vapor condensation with noncondensable gases[J]. Journal of Heat Transfer, 1996, 118(1): 243–245. DOI:10.1115/1.2824052
[13] Liao Y, Vierow K. A generalized diffusion layer model for condensation of vapor with noncondensable gases[J]. Journal of Heat Transfer, 2007, 129(8): 988–994. DOI:10.1115/1.2728907
[14] Wilke C R. Diffusional properties of multicomponent gases[J]. Chemical Engineering Progress, 1950, 46(2): 95–104.
[15] Krishna R, Wesselingh J A. The Maxwell-Stefan approach to mass transfer[J]. Chemical Engineering Science, 1997, 52(6): 861–911. DOI:10.1016/S0009-2509(96)00458-7
[16] Kleijn C R, Hoogendoorn C J. A study of 2-and 3-D transport phenomena in horizontal chemical vapor deposition reactors[J]. Chemical Engineering Science, 1991, 46(1): 321–334. DOI:10.1016/0009-2509(91)80141-K
[17] Shashkov A G, Zolotukhina A F, Fokin L R. Generalization and calculation of the thermal diffusion factor of binary hydrogen-containing gaseous mixtures[J]. Journal of Engineering Physics and Thermophysics, 2011, 84(1): 39–48. DOI:10.1007/s10891-011-0454-3
[18] Wesselingh J A, Krishna R. Mass transfer in multicomponent mixtures[M]. 2000.
[19] Kuhn S Z, Schrock V E, Peterson P F. An investigation of condensation from steam-gas mixtures flowing downward inside a vertical tube[J]. Nuclear Engineering and Design, 1997, 177(1): 53–69.