文章信息
- 姜有泉, 黄良, 王波, 赵立进, 吕黔苏, 杨涛, 吴建蓉
- JIANG Youquan, HUANG Liang, WANG Bo, ZHAO Lijin, LU Qiansu, YANG Tao, WU Jianrong
- 基于DGA和深度置信网络的变压器内部故障诊断
- Transformer internal fault diagnosis based on DGA and deep belief network
- 武汉大学学报(工学版), 2017, 50(5): 749-753
- Engineering Journal of Wuhan University, 2017, 50(5): 749-753
- http://dx.doi.org/10.14188/j.1671-8844.2017-05-018
-
文章历史
- 收稿日期: 2017-05-19
2. 武汉大学电气工程学院,湖北 武汉 430072
2. School of Electrical Engineering, Wuhan University, Wuhan 430072, China
电力变压器是电力系统重要的电气设备,长期运行的变压器在电、热作用下,其内部的绝缘材料会逐步发生老化和分解,产生可溶解的氧气、氢气和烃类气体[1, 2].由于变压器油中溶解气体可以反映变压器内部绝缘老化、电弧放电等常见故障,溶解气体分析(dissolved gases analysis,DGA)技术[3, 4]已成为应用广泛的诊断变压器潜伏性故障的检测手段.
DGA技术主要包括:1)以油中特征气体组分含量为特征量的故障诊断;2)以油中特征气体组分比值为特征量的故障诊断方法[5].前者依据故障点产生气体特征随故障类型、故障能量及绝缘材料不同而不同,可以反映热分解本质;但由于涉及同一种气体特征可能包含不同类型的故障,因此难以准确判断故障类型.后者主要包括三比值法、改良三比值法和罗杰斯三比值法,从5种特征气体中选用2种溶解溶度和扩散系数相近的气体组分组成比值对,反映气体组分的相对浓度与温度间的相互依赖关系及变化规律[6].该方法基于典型事故统计分析得到推荐编码组合,实际应用中常出现“超码”或“缺码”问题,无法准确进行变压器故障定位,限制了DGA的使用条件和应用范围[7].
随着人工智能的发展,如BP深度网络、支持向量机[8, 9]等机器学习算法被广泛应用于电气设备的故障诊断.但是,该类人工智能方法存在一定问题.如BP神经网络在训练过程中容易陷入局部最优,故障样本的数量对故障诊断精度也有较大影响[10];支持向量机虽然可以在少样本下学习数据特征,但对于多类型故障和部分信息缺失时的识别准确率有待提高[11].近年来,深度学习越来越得到重视,与传统的机器学习算法相比,深度学习可以自动提取特征,发现复杂数据结构中的样本特征,其多隐含层结构能够将复杂特征信息通过函数表达,适合对电力设备进行精确的模式识别和诊断.
因此,本文提出基于DGA技术和深度学习的电力变压器故障诊断方法,利用深度置信网络的特征提取,构建多隐含层的深度学习模型,采用无监督特征学习方法,实现在少样本情况下的变压器故障的高精度识别.算例表明,所提的深度置信网络提高了电力变压器故障诊断的准确率.
1 深度置信网络算法分析变压器油中溶解气体的成分、比例代表不同类型的故障,但是,支持向量机等监督学习算法的精度有待提高.分析实际的变压器油溶解气体数据可知,部分监测数据缺少样本“标签”,导致监督学习算法无法发挥作用[12].针对样本的实际模式识别任务和样本特点,本文提出基于深度学习中的深度置信网络,利用无监督特征学习算法对油溶解气体数据进行特征选择和学习,其本质上可以看作是在高维空间中对离群对象挖掘的问题.
深度置信网络是具有多层隐元的深度学习模型,可看作由多层简单学习模型按特定的组合方式形成的复合模型.
1.1 深度置信网络模型深度置信网络在训练过程中需要学习联合概率分布,联合概率在机器学习领域中表示对象的生成模型.2006年有学者提出了深度置信网络的模型,它是多个受限玻尔兹曼机重叠在一起和一个BP神经网络构成的深度结构,其训练过程主要包括2个方面:1)利用受限玻尔兹曼机结构训练,筛选数据特征信息;2)将各层受限玻尔兹曼机连接,在最后一层将受限玻尔兹曼机的输出作为BP神经网络的输入,并利用数据进行监督训练,构成整个深度结构.
深度置信网络对原始信息进行逐步提取,实现具体到抽象的转换,最终得到更加便于分类的特征向量作为神经网络得到的输入,同时,在特征提取过程中需要被剔除的错误信息由于多层受限玻尔兹曼机组成的深度结构被弱化.深度置信网络模型克服了传统神经网络在深度结构增加时训练时间长、易陷入局部最优、大数据处理慢的缺点,具有明显的优势.
1.2 受限玻尔兹曼机在训练的过程中,深度置信网络采用了逐层无监督的方法来学习参数.受限玻尔兹曼机是由可见层和隐含层组成的两层的玻尔兹曼机器,在同一层上的单元之间没有连接.通过执行无监督学习算法,可以提取特征来压缩高维数据到低维数据.可见层的每个单元与隐藏层的单元具有对称加权连接.换句话说,单元之间的耦合是双向的.
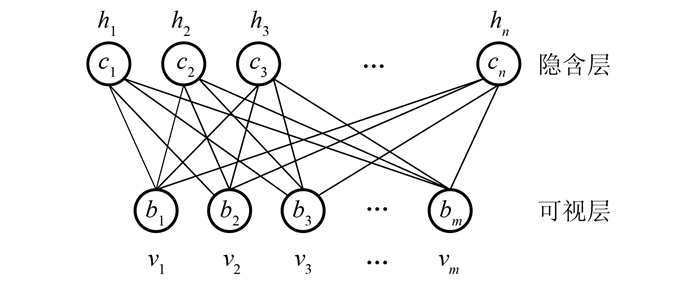
受限玻尔兹曼机仅层与层之间的单元互联,假设有m个可视层单元,n个隐含层单元,可视层和隐含层的偏置分别为bi(i=1, 2, …, m)、cj(j=1, 2, …, n),Wij为第i个可视层单元与第j个隐含层单元的连接权重,vi和hj分别为可视层和隐含层的状态.图 1为受限玻尔兹曼模型示意图.
|
| 图 1 受限玻尔兹曼机模型 Figure 1 Limited Boltzmann model |
玻尔兹曼机的训练目标,是令训练得到的参数θ={Wij, bi, cj}拟合输入数据的误差最小.受限玻尔兹曼机的能量和联合概率的定义分别如下:
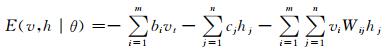 (1)
(1)
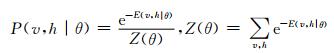 (2)
(2)
式中:e-E(v, h|θ)称为势函数;Z(θ)为配分函数.第n个受限玻尔兹曼机模型训练在第n-1个受限玻尔兹曼机模型训练后进行,输入来自于第n-1个受限玻尔兹曼机模型的输出,同时它的输出作为第n+1个模型的输入.
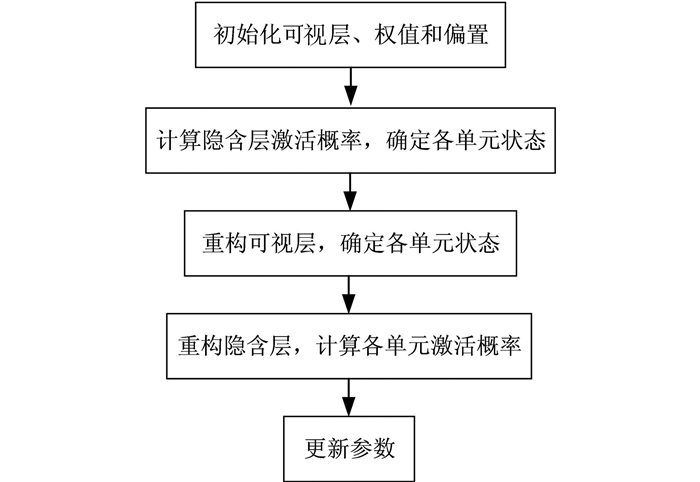
1.3 对比歧化算法传统受限玻尔兹曼机采用吉布斯采样得到对数似然函数关于未知参数梯度的近似,采样步数较大,因此效率不高,难以实现深度置信网络的快速学习与训练,本文采用了对比歧化算法(Contrastive Divergence,CD)[13].对比歧化算法训练过程如图 2所示.
|
| 图 2 对比歧化算法训练过程 Figure 2 Contracting disambiguation algorithm training process |
可视层和隐含层的激活概率可按照下式计算:
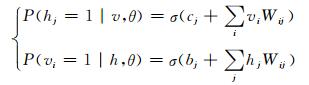 (3)
(3)
其中:σ(·)为sigmoid激活函数.
2 深度置信网络模型建立 2.1 故障气体分析油中溶解气体分析(dissolved gas-in-oil analysis,DGA)是有效的判断油浸式电力变压器早期故障的方法.
变压器油主要由烃类组成,当设备发生故障时, 如发热、放电等,变压器油中某些烃类物质的C-H、H-C键断裂,同时产生不稳定的氢原子和碳氢自由基,这些氢原子和自由基通过化学反应生成氢气和低分子烃类气体,如甲烷、乙烷、乙烯、乙炔等.变压器设备中的固体绝缘材料的分解也会产生这些气体.
变压器故障主要包括过热、放电和受潮等.由于变压器制造工艺的提高,密封性越来越好,受潮发生的概率降低,故障主要是过热和放电.
根据气体检测成分,变压器油中溶解气体在线监测可分为单组分和多组分在线监测.单组分气体在线监测主要检测H2等某一特征气体或可燃气体的总含量,可提供的气体组分信息有限,只适合在现场做初步的故障分析,而多组分气体能够为变压器故障检测提供更加完整的气体信息,具有更加广阔的发展前景.
2.2 数据分析深度学习的一大优势是避免了繁琐的数据预处理过程,可以直接从高维数据中自动学习样本特征,挖掘数据中隐含的价值.本文以某变压器的油溶解气体数据(包括氢气、甲烷、乙烷、乙烯、乙炔、总烃、一氧化碳和二氧化碳的体积分数(单位:μL/L))为输入,并根据变压器油溶解气体数据可确定变压器5种工况:正常、低能放电、中温放电、电弧放电和高温放电[14],利用油溶解气体的三比值法,推算出变压器故障.基于油溶解气体组分的三比值诊断方法如表 1所示.深度学习避免了传统方法需要将样本数据离散化编码形成决策表,直接将历史数据和对应的运行工况用于训练和测试模型.表 2为部分故障样本数据,若变压器正常运行则各气体含量均为0.
| 故障类型 | 体积分数比 | ||
| C2H2/C2H4 | CH4/H2 | C2H4/C2H6 | |
| 正常 | < 0.1 | 0.1~1.0 | < 1.0 |
| 低能放电 | >0.1 | 0.1~1.0 | >1.0 |
| 中温放电 | < 0.1 | >1.0 | 1.0~3.0 |
| 电弧放电 | 0.1~3.0 | 0.1~1.0 | >3.0 |
| 高温放电 | < 0.1 | >1.0 | >3.0 |
| 日期 | 体积分数/10-6 | |||||||
| H2 | CH4 | C2H6 | C2H4 | C2H2 | CmHn | CO | CO2 | |
| 3.12 | 4.82 | 18.9 | 3.84 | 21.0 | 0 | 43.74 | 930 | 3009 |
| 3.13 | 5.00 | 20.6 | 3.88 | 19.2 | 0 | 43.68 | 985 | 2866 |
| 3.14 | 4.84 | 18.6 | 4.06 | 20.7 | 0 | 43.36 | 942 | 3077 |
| 3.15 | 5.34 | 20.4 | 3.67 | 21.7 | 0 | 45.77 | 980 | 2937 |
| 3.16 | 4.97 | 20.9 | 4.35 | 21.1 | 0 | 46.35 | 929 | 2922 |
| 3.17 | 4.80 | 18.2 | 3.72 | 18.9 | 0 | 40.82 | 901 | 2932 |
| 3.18 | 5.19 | 21.9 | 4.03 | 21.2 | 0 | 47.13 | 1003 | 2994 |
本文从实际监测数据中选取1 908条样本,其中训练样本1 300条,测试样本608条,对训练和故障样本分别归一化处理.
每个时间采集点的样本均有8维,因此本文将每层的玻尔兹曼的可视层单元个数设置为8,隐含层单元设置为30[15],模型的层数分别为1、3、5,模型的输出节点有5个,分别代表运行的5种工况.激活函数选择sigmoid函数,学习率alpha=1,最大遍历次数为5,batchsize=5,momentum=0.
3 实例分析在确定深度置信网络输入、输出和隐含层节点后,输入同样的变压器训练样本,分别用深度置信网络和支持向量机对其进行训练,取最好的一次训练结果表征模型识别精度.表 3为深度置信网络3种结构训练和测试结果,表 4为深度置信网络与支持向量机和BP神经网络对比.
| 模型层数 | 训练误差/% | 测试误差/% |
| 1 | 0.103 3 | 0.099 6 |
| 3 | 53.384 0 | 53.384 5 |
| 5 | 46.665 4 | 46.615 4 |
| 模型 | 误差样本个数 | 误差率/% |
| 深度置信网络 | 1 | 0.099 6 |
| 支持向量机 | 13 | 2.138 2 |
| BP神经网络 | 17 | 2.796 1 |
由表 3可知,深度置信网络模型的不同会导致训练和测试精度显著区别.单层的受限玻尔兹曼机(可视作特殊的深度置信网络)的识别误差仅为0.996%,远优于3层和5层的模型识别误差,原因在于实际样本数据每条记录仅为8维,每个隐含层单元所学习到的特征数量有限,当玻尔兹曼机层数仅为1层时就足以完成特征学习的任务,提取故障样本对应的气体组分特征.本文的深度置信网络均采用快速歧化算法,当玻尔兹曼机层数为3、5或者更多时,误差会随特征传播至下一层的模型,误差的积累导致输出分类结果受到极大影响,不能满足变压器故障诊断的要求.
同时本文还建立支持向量机模型和BP神经网络,使用相同的训练和测试样本进行多类型故障识别.前文提及,样本中存在数据缺失的问题,因此BP神经网络的识别误差要高于深度置信网络;从仿真实例中看出,支持向量机在多分类识别任务的精度与深度置信网络仍存在较大差距.
4 结论本文根据变压器故障诊断实时性和高精度的要求,针对传统DGA诊断技术和人工智能技术遇到的瓶颈,提出利用深度学习故障进行诊断,并采用快速歧化算法优化参数调整和加快训练速度.仿真结果表明,本文所提出的基于深度学习的变压器故障诊断方法的诊断精度要比传统的学习模型如支持向量机和BP神经网络训练精度高、收敛速度快,提高了变压器诊断的准确性.同时网络测试表明,单层的深度置信网络识别精度要比多层网络高,可见深度学习模型并非层数越多越好.如何根据实际数据选择合适的模型结构和初始化参数,提高诊断精度是下一步研究的重点.
| [1] |
武中利. 电力变压器故障诊断方法研究[D]. 北京: 华北电力大学, 2013.
Wu Zhongli. Research on fault diagnosing methods for power transformers[D]. Beijing: North China Electric Power University, 2013. http://www.cqvip.com/QK/72150X/201605/epub1000000210597.html |
| [2] |
杨廷方. 变压器在线监测与故障诊断新技术的研究[D]. 武汉: 华中科技大学, 2008.
Yang Tingfang. Study on new techniques of online monitoring and fault diagnosis for power transformer[D]. Wuhan: Huazhong University of Science and Technology, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D065693 |
| [3] |
张庆磊. 基于油中气体分析和局部放电检测的变压器故障诊断技术研究[D]. 南京: 南京理工大学, 2014.
Zhang Qinglei. Study on power transformer fault diagnosis technology based on DGA and partial discharge detection[D]. Nanjing: Nanjing University of Science & Technology, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2521528 |
| [4] |
彭宁云. 基于DGA技术的变压器故障智能诊断系统研究[D]. 武汉: 武汉大学, 2004.
Peng Ningyun. Research on an intellectual fault diagnosis system for power transformer based on dissolved gas analysis technology[D]. Wuhan: Wuhan University, 2004. http://www.cnki.com.cn/Article/CJFDTOTAL-BYQZ200210013.htm |
| [5] |
赵峰, 李硕. 基于DGA和改进型灰关联度模型的牵引变压器故障诊断[J].
高压电器, 2015(1): 41–45.
Zhao Feng, Li Shuo. Fault diagnosis for traction transformer based on DGA and improved grey correlation analysis model[J]. High Voltage Apparatus, 2015(1): 41–45. |
| [6] |
罗建波. 基于DGA的电力变压器故障诊断技术研究[D]. 杭州: 浙江大学, 2005.
Luo Jianbo. Research on fault diagnosis technology of power transformer based on DGA[D]. Hangzhou: Zhejiang University, 2005. |
| [7] |
郭创新, 朱承治, 张琳, 等. 应用多分类多核学习支持向量机的变压器故障诊断方法[J].
中国电机工程学报, 2010(13): 128–134.
Guo Chuangxin, Zhu Chengzhi, Zhang Lin, et al. A fault diagnosis method for power transformer based on multiclass multiple-kernel learning support vector machine[J]. Proceedings of the CSEE, 2010(13): 128–134. |
| [8] |
郑蕊蕊, 赵继印, 赵婷婷, 等. 基于遗传支持向量机和灰色人工免疫算法的电力变压器故障诊断[J].
中国电机工程学报, 2011(7): 56–63.
Zheng Ruirui, Zhao Jiyin, Zhao Tingting, et al. Power transformer fault diagnosis based on genetic support vector machine and gray artificial immune algorithm[J]. Proceedings of the CSEE, 2011(7): 56–63. |
| [9] |
公茂法, 张言攀, 柳岩妮, 等. 基于BP网络算法优化模糊Petri网的电力变压器故障诊断[J].
电力系统保护与控制, 2015(3): 113–117.
Gong Maofa, Zhang Yanpan, Liu Yanni, et al. Fault diagnosis of power transformers based on back propagation algorithm evolving fuzzy Petri nets[J]. Power System Protection and Control, 2015(3): 113–117. DOI:10.7667/j.issn.1674-3415.2015.03.017 |
| [10] |
赵文清, 李庆良, 王德文. 基于多模型的变压器故障组合诊断研究[J].
高电压技术, 2013, 39(2): 302–309.
Zhao Wenqing, Li Qingliang, Wang Dewen. Combination diagonosis for transformer faults bares on multi-model[J]. High Voltage Engineering, 2013, 39(2): 302–309. |
| [11] |
朱永利, 尹金良. 组合核相关向量机在电力变压器故障诊断中的应用研究[J].
中国电机工程学报, 2013(22): 68–74.
Zhu Yongli, Yin Jinliang. Study on application of multi-kernel learning relevance vector machines in fault diagnosis of power transformers[J]. Proceedings of the CSEE, 2013(22): 68–74. |
| [12] |
刘伟峰, 韩崇昭, 石勇. 修正Gibbs采样的有限混合模型无监督学习算法[J].
西安交通大学学报, 2009(2): 15–19.
Liu Weifeng, Han Chongzhao, Shi Yong. Unsupervised learning for finite mixture models via modified gibbs sampling[J]. Journal of Xi'an Jiaotong University, 2009(2): 15–19. DOI:10.7652/xjtuxb200902004 |
| [13] | Hinton G E. Learning multiple layers of representation[J]. Trends in Cognitive Sciences, 2007, 11(10): 428–434. DOI:10.1016/j.tics.2007.09.004 |
| [14] |
程声烽, 程小华, 杨露. 基于改进粒子群算法的小波神经网络在变压器故障诊断中的应用[J].
电力系统保护与控制, 2014(19): 37–42.
Cheng Shengfeng, Cheng Xiaohua, Yang Lu. Application of wavelet neural network with improved particle swarm optimization algorithm in power transformer fault diagnosis[J]. Power System Protection and Control, 2014(19): 37–42. DOI:10.7667/j.issn.1674-3415.2014.19.006 |
| [15] | Hinton G, Osindero S, Teh Y. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527–1554. DOI:10.1162/neco.2006.18.7.1527 |
 2017, Vol. 50
2017, Vol. 50



