文章信息
- 刘明顺, 赵立进, 黄良, 林成, 苏华英, 龙志君, 刘阳, 张思颖, 张晓伟
- LIU Mingshun, ZHAO Lijin, HUANG Liang, LIN Cheng, SU Huaying, LONG Zhijun, LIU Yang, ZHANG Siying, ZHANG Xiaowei
- 基于模糊综合评价的电网风险评估分级
- Power grid risks assessment and classification based on fuzzy comprehensive evaluation
- 武汉大学学报(工学版), 2017, 50(5): 733-737
- Engineering Journal of Wuhan University, 2017, 50(5): 733-737
- http://dx.doi.org/10.14188/j.1671-8844.2017-05-015
-
文章历史
- 收稿日期: 2017-05-17
2. 贵州电网有限责任公司电力科学研究院,贵州 贵阳 550002;
3. 武汉大学电气工程学院,湖北 武汉 430072
2. Guizhou Electric Power Research Institute, Guizhou Power Grid Co., Ltd., Guiyang 550002, China;
3. School of Electrical Engineering, Wuhan University, Wuhan 430072, China
近些年来,我国一直坚持建设坚强智能电网的发展规划[1],随着特高压输电和大电网互联趋势的持续发展,电网建设卓有成效,电网性能也愈发“坚强”.但与此同时,随着电网结构复杂程度的增加,一旦出现系统故障将会带来更加严重的后果[2, 3].传统的N-1准则仅从事故后果出发,且结果往往过于保守[4],因此迫切需要量化电网安全性指标,对当前电网运行风险进行评估分级.
风险是事故发生的可能性与后果严重程度的综合性度量[5],国内外在电网风险评估领域做了大量研究[6].文献[7, 8]基于风险理论,分别对低电压的稳态风险及对频率偏移、功角稳定裕度等暂态风险进行评估,并通过模糊推理将各指标综合加权.文献[9]从元件角度出发,考虑停运概率及停运可能对系统产生的影响.文献[10]以线路过载指标来量化系统中级联故障的风险.电压和潮流问题均可通过负荷削减使得系统恢复到正常工况从而得到解决,因而在对发输电电力系统可靠性评估中,切负荷量常作为重要的量化指标.文献[11]建立了基于直流潮流的负荷削减线性规划模型,在运行时间上具备优势,但计算精度有待提高.文献[12]基于交流潮流的负荷非线性规划模型计算各系统事故状态下的最优负荷削减量.上述文献从不同角度对电网风险进行量化评估,而风险的描述往往是笼统、模糊的.而风险等级科学合理的划分可以给运行调度人员直观的信息从而更好地辨识当前电网的风险情况,因此在风险评估的基础上实现科学合理的电网风险分级亟待进一步研究.
本文首先基于内点法中的路径跟踪法建立最优负荷削减模型,结合模糊数学隶属度函数以切负荷量来量化事故后果的严重度,并按照最大隶属度原则对事故后果进行分级,随后应用模糊C均值聚类对事故发生的概率进行分级,最后基于模糊综合评价法建立电网风险的模糊评价向量,从而实现对当前电网状态进行风险评估及等级划分.
1 最优负荷削减量模型内点法[13]是求解最优潮流模型的有效算法,按照目标函数信息确定搜索方向,常用于线性规划、二次规划和非线性规划问题.内点法中的路径跟随法具有收敛速度快、鲁棒性强、对初值的选择不敏感,且迭代次数与系统规模或控制变量的数目关系不大等优点,因而广泛应用于电力系统中.
本文以最优潮流算法为基础建立如下数学模型:
 (1)
(1)
式中:PGi、QGi表示发电机的有功出力和无功出力;PDi、QDi表示负荷的有功功率和无功功率;Pi、Qi表示节点的有功功率和无功功率;Ci表示节点的负荷削减量;Vi表示节点的电压幅值;Sij表示线路i-j的视在功率;NLd表示系统输电线路数.
该数学模型以发电机节点有功出力PG、无功出力QG和节点负荷PD为控制变量,得到基于交流潮流最优负荷削减量的非线性优化模型.
2 电网风险的模糊分级方法 2.1 失负荷严重度数学模型当系统元件发生强迫停运时,可能会导致部分节点电压出现越限或支路潮流过载的情况,此时往往采取切负荷措施使系统满足安全运行工况,系统失负荷量表征了当前系统风险情况,基于此本文定义失负荷严重度SC为
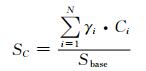 (2)
(2)
式中:γi为第i个被切除负荷的重要度因子;Ci为第i个节点的负荷削减量;Sbase为系统容量基准值;N为节点负荷数量.
对电力系统失负荷等级进行模糊划分,即划分为4类,分别表示为Ⅰ、Ⅱ、Ⅲ和Ⅳ,失负荷隶属度函数如图 1所示,横坐标代表失负荷严重度,纵坐标代表所属的隶属度函数值.
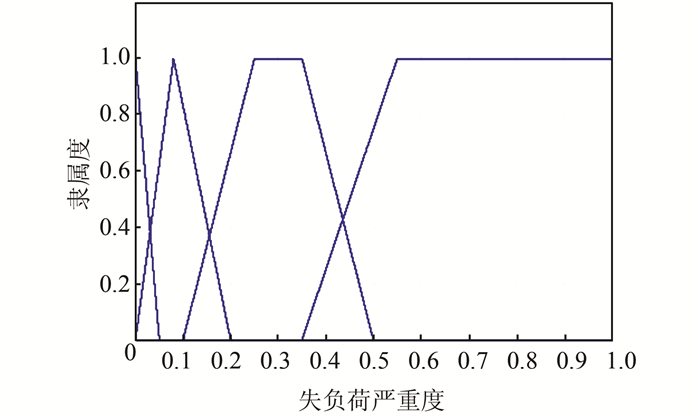
|
| 图 1 失负荷严重度隶属度函数 Figure 1 Overload severity membership function |
历史数据统计发现,电力系统元件发生故障的数学模型可用泊松分布描述[14],即:
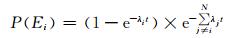 (3)
(3)
式中:λi表示第i个电气设备的强迫停运率;t为停运时间;N为总电气设备数量.
2.3 模糊C均值聚类分析模糊C均值聚类算法(FCM)由Bezdek提出,该算法随机选取初始聚类中心,通过搜索目标函数达到最小值,调整聚类中心及隶属度,经多次迭代收敛后根据隶属度大小确定样本所属类别.与K-means聚类相比,该聚类算法能够实现柔性的模糊划分,应用广泛,本文采用该方法实现对元件故障率的分级.
将系统元件故障概率集合P={p1, p2, …, pn}进行模糊聚类分析.令uik表示第k个样本xk属于第i类的隶属度,数据集隶属度之和为1,即满足约束条件: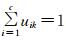
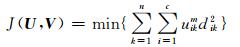 (4)
(4)
式中:目标函数值J(U, V)表示各类中的样本与聚类中心的加权平方距离和;U=(uik)c×n,为隶属度矩阵;dik=||xk-vi||;vi=(vi1, vi2, …, vip)(i=1, 2, …,c),为各类的聚类中心.模糊C均值聚类的目标是求出U和V使J(U, V)为最小值,其具体步骤为:
1) 确定聚类数目c,幂指数m,以及初始的隶属度矩阵U(0)=(uik(0)),其中m为模糊度,一般可取为2,U(0)为均匀分布在[0, 1]上的一系列的随机数.
2) 用l表示迭代步数,第l步的聚类中心表示为
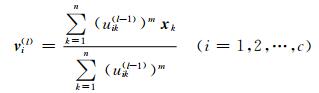 (5)
(5)
3) 修正隶属度矩阵U(l),并计算目标函数值J(l).
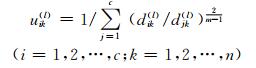 (6)
(6)
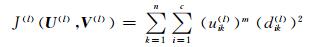 (7)
(7)
式中,dik(l)=||xk-vi(l)||.
4) 确定终止迭代的隶属度容限εu>0,当满足条件max{|uik(l)-uik(l-1)|} < εu时,终止迭代,否则令l=l+1,再转到步骤2).
通过上述迭代步骤后,即可求得当目标函数J(U, V)取得最小值时的聚类中心V以及最终的隶属度矩阵U,进而实现模糊聚类划分.
2.4 模糊综合评价风险分级风险是对事故发生概率与后果严重程度的综合性度量,针对上文中元件故障概率模糊划分和失负荷严重度分级,基于模糊综合评价对电网风险建立评估分级模型.电网风险的模糊评价向量矩阵R可由下式计算:
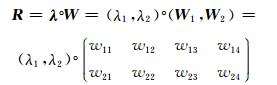 (8)
(8)
式中:λ为权重向量矩阵;λ1为故障概率权重,λ2为失负荷严重度指标权重,可采用客观赋值法的熵权法进行权重赋值,其中λ1+λ2=1;符号°为模糊合成算子,取为加权平均型M(·, ⊕);W表示故障概率与失负荷严重度组成的模糊评价向量矩阵.
3 电网风险分级方法流程根据上文建立的最优负荷削减及电网风险模糊综合评价模型,对电网风险进行分级,流程图如图 2所示.
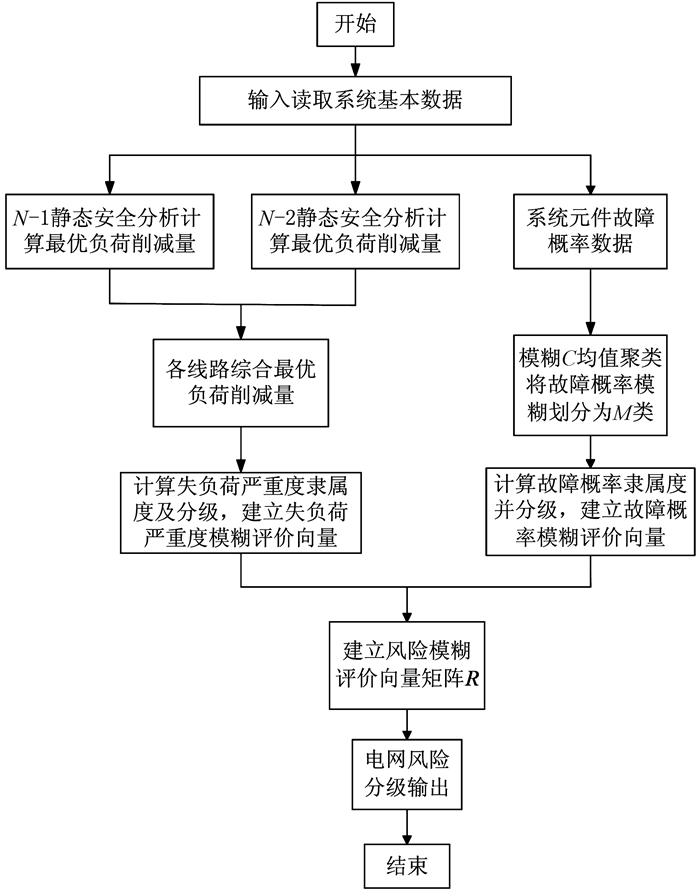
|
| 图 2 电网风险分级方法流程 Figure 2 Flowchart of power grid risk classification method |
具体步骤如下:
1) 读取系统的基本数据,包括技术数据、约束条件、线路故障数据等.
2) 根据内点法计算N-1和N-2的最优负荷削减量.
3) 按下式计算各条线路的综合最优负荷削减量:
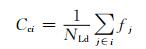 (9)
(9)
式中:Cci表示支路i故障后的综合最优负荷削减量;f表示N-1和N-2的最优负荷削减量;NLd表示总支路数.
4) 计算各支路的故障概率Pi.
5) 根据失负荷严重度隶属度函数及模糊聚类隶属度矩阵得到模糊评价向量矩阵.
6) 基于模糊综合评价法,将权重向量λ与故障概率及失负荷严重度所组成向量W进行模糊合成,得到电网风险模糊评价向量R.
7) 根据最大隶属度原则进行电网风险分级并输出.
4 算例分析以IEEE-RTS79可靠性测试系统[15]为例进行仿真计算,该系统包含32台发电机、38条支路,其中包括5台变压器和33条输电线路,系统机组总装机容量为3 405 MW,总负荷为2 850 MW,共有138 kV和230 kV两个电压等级.图 3为算例系统网架接线图.
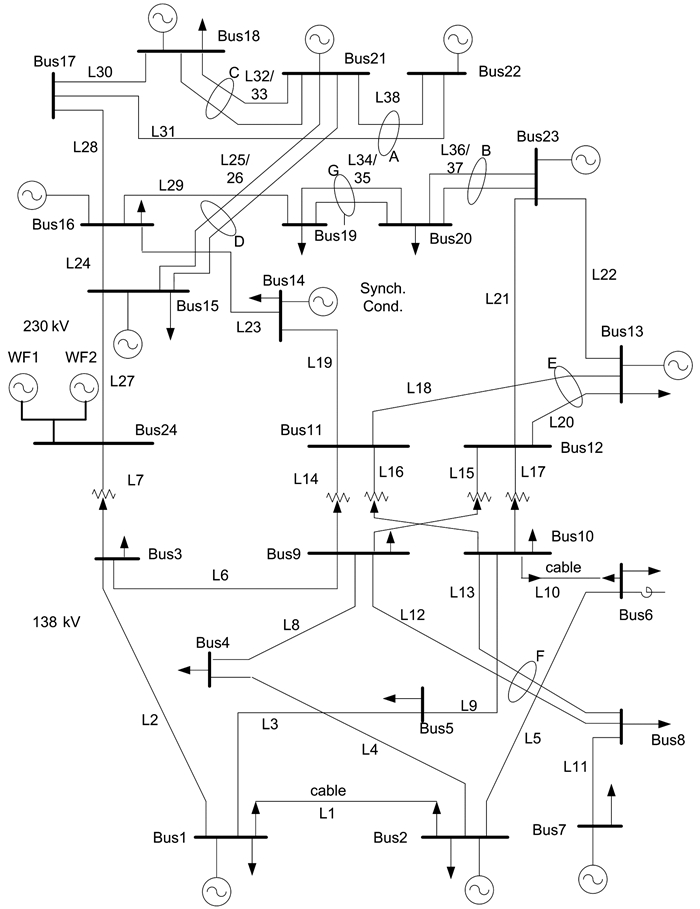
|
| 图 3 IEEE-RTS79可靠性测试系统 Figure 3 IEEE-RTS79 reliability test system |
本文通过模糊C均值聚类将系统元件故障概率模糊划分为4个等级,表 1为分级结果.
| 故障概率等级 | 支路编号 |
| Ⅰ | 1, 3, 4, 6, 8, 9, 11, 19, 23, 24, 28, 29, 30, 32, 33, 34, 35, 36, 37 |
| Ⅱ | 2, 5, 12, 13, 18, 20, 21, 22, 25, 26, 27, 31, 38 |
| Ⅲ | 10 |
| Ⅳ | 7, 14, 15, 16, 17 |
从表 1可以看出,大部分支路的出现故障概率的级别为Ⅰ和Ⅱ级,只有支路10故障概率等级为Ⅲ级,系统中的变压器支路7、14、15、16、17出现故障的概率相对较高,属于Ⅳ级.
在对故障概率分级后,再计算各事故下恢复系统正常水平所切除的负荷量,并按照失负荷隶属度函数得到严重度分级,通过模糊综合评价模型输出当前事故状态下的电网风险级别,表 2给出了部分分级结果.
| 校核初始线路 | 故障概率级别 | 严重度级别 | 风险级别 |
| 10(6-10) | Ⅲ | Ⅳ | Ⅳ |
| 27(15-24) | Ⅱ | Ⅲ | Ⅲ |
| 7(3-24) | Ⅳ | Ⅱ | Ⅱ |
| 17(10-12) | Ⅳ | Ⅱ | Ⅱ |
| 14(9-11) | Ⅳ | Ⅱ | Ⅱ |
| 15(9-12) | Ⅳ | Ⅱ | Ⅱ |
| 16(10-11) | Ⅳ | Ⅰ | Ⅰ |
根据表 2电网风险分级结果可以看出,当支路10发生故障时导致的当前电网风险最高,风险等级为Ⅳ级,支路27发生故障时导致的当前电网风险次之,为Ⅲ级,因此可将支路10和27视为系统关键线路,在电网安全中占有重要地位.变压器支路7、14、15、16和17故障概率为Ⅳ级,但由于该支路发生故障后失负荷量较小,对系统造成的严重度较低,因此电网风险为Ⅱ级和Ⅰ级;而支路10和27故障概率没有达到最高级别,但一旦发生事故,其造成的后果相对严重,电网风险级别升高;二者比较可以发现,支路10故障概率及后果严重度比支路27均高一级,因此电网风险等级为最高.综上可以看出,本文方法综合度量了事故概率与后果严重度,能够很好地实现系统关键线路的辨识及电网风险等级的划分.
从表 3可以看出,系统在正常工况下运行时,通过支路5和支路10向节点6输送有功,支路10的负载率已达到86.11%,已存在潜在的过载风险;当支路10出现故障后,潮流发生转移,支路5为提供节点6有功及无功的唯一路径,其负载率达到88.59%,造成该支路存在潜在过载风险;节点6由发出无功变为吸收无功,无功流向发生变化,表现为电压跌落现象,电压为0.904 2,出现低电压风险.因此从运行指标也可以看出支路10的关键程度,支路10一旦故障将造成较高的电网风险.
| 运行指标 | 正常运行 | 支路10故障 |
| 支路5潮流 | 0.478 5-0.344 7j | 1.472 8+0.484 2j |
| 支路10潮流 | 0.896 6-1.211 2j | - |
| 支路5负载率/% | 33.70 | 88.59 |
| 支路10负载率/% | 86.11 | - |
| 节点6电压 | 1.075 8 | 0.904 2 |
| 注:支路5有功潮流方向为由2→6,支路10有功潮流方向为10→6. | ||
图 4给出支路10故障的部分最严重的N-2事故组合的负荷削减量,可以看出支路10和1的故障组合需要切除较大负荷量(8.59 MW)才能维持系统在安全范围内稳定运行,即该事故组合造成后果相对严重.因此一旦支路10出现故障,应对图 4中所示后果相对严重的部分支路重点关注,采取相应预防措施来减少损失.
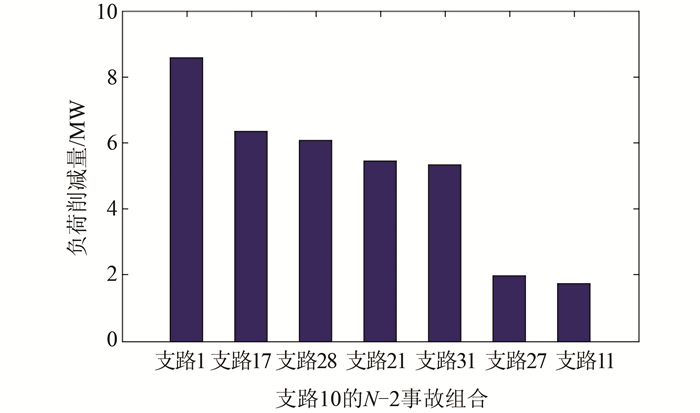
|
| 图 4 支路10的N-2事故组合 Figure 4 N-2 accident combination of branch 10 |
本文基于内点法建立了最优负荷削减量模型,计算N-1/N-2各事故状态下的失负荷量,并按照隶属度函数对失负荷严重度进行分级,得到如下结论:
1) 该模型通过模糊聚类将各事故发生的概率模糊分级,并将其与失负荷严重度构成电网风险模糊评价向量.
2) 该模型基于模糊综合评价法和最大隶属度原则实现了电网风险评估及风险分级.
3) 该模型能够辨识出对电网造成高风险的故障支路,为系统安全预警及制定差异化运维策略提供了有效参考.
| [1] |
李兴源, 魏巍, 王渝红, 等. 坚强智能电网发展技术的研究[J].
电力系统保护与控制, 2009, 37(17): 1–7.
Li Xinyuan, Wei Wei, Wang Yuhong, et al. Study on the development and technology of strong smart grid[J]. Power System Protection & Control, 2009, 37(17): 1–7. |
| [2] |
汤涌, 卜广全, 易俊. 印度"7.30"、"7.31"大停电事故分析及启示[J].
中国电机工程学报, 2012, 32(25): 167–174.
Tang Yong, Bu Guangquan, Yi Yun. Analysis and lessons of the blackout in Indian Power Grid on July 30 and 31, 2012[J]. Proceedings of the CSEE, 2012, 32(25): 167–174. |
| [3] | Yamashita K, Li J, Zhang P, et al. Analysis and control of major blackouts events[C]//Power Systems Conference and Exposition, 2007, 31(1): 1-3. |
| [4] |
陈为化, 江全元, 曹一家, 等. 电力系统电压崩溃的风险评估[J].
电网技术, 2005, 29(19): 36–41.
Chen Weihua, Jiang Quanyuan, Cao Yijia, et al. Risk assessment of voltage collapse in power system[J]. Power System Technology, 2005, 29(19): 36–41. |
| [5] | GIGRE Task Force 38.03.12. Power system security assessment, a position paper[J]. Elctra, 1997, 175: 49–77. |
| [6] | Mahadev P M, Christie R D. Envisioning power system data: vulnerability and severity representations for static security assessment[J]. IEEE Transactions on Power Systems, 1994, 9(4): 1915–1920. DOI:10.1109/59.331450 |
| [7] |
刘新东, 江全元, 曹一家, 等. 基于风险理论和模糊推理的电力系统暂态安全风险评估[J].
电力自动化设备, 2009, 29(2): 15–20.
Liu Xindong, Jiang Quanyuan, Cao Yijia, et al. Transient security risk assessment of power system based on risk theory and fuzzy reasoning[J]. Electric Power Automation Equipment, 2009, 29(2): 15–20. |
| [8] |
陈为化, 江全元, 曹一家, 等. 基于风险理论和模糊推理的电压脆弱性评估[J].
中国电机工程学报, 2005, 25(24): 20–25.
Chen Weihua, Jiang Quanyuan, Cao Yijia, et al. Voltage vulnerability assessment based on risk theory and fuzzy reasoning[J]. Proceedings of the CSEE, 2005, 25(24): 20–25. DOI:10.3321/j.issn:0258-8013.2005.24.004 |
| [9] |
张毅明, 张忠会, 姚峰, 等. 基于风险理论的电力系统元件风险评估[J].
电力系统保护与控制, 2013, 41(23): 73–78.
Zhang Yiming, Zhang Zhonghui, Yao Feng, et al. Risk assessment of power system components based on the risk theory[J]. Power System Protection & Control, 2013, 41(23): 73–78. DOI:10.7667/j.issn.1674-3415.2013.23.012 |
| [10] |
周彦衡, 吴俊勇, 张广韬, 等. 考虑级联故障的电力系统脆弱性评估[J].
电网技术, 2013, 37(2): 444–449.
Zhou Yangheng, Wu Junyong, Zhang Guangtao, et al. Assessment on power system vulnerability considering cascading failure[J]. Power System Technology, 2013, 37(2): 444–449. |
| [11] |
荣雅君, 马秀蕊, 杨伟, 等. 发输电系统可靠性分析中最优切负荷模型[J].
电工电能新技术, 2015, 34(7): 58–62.
Rong Yajun, Ma Xiurui, Yang Wei. Model of optimal load shedding program for reliability assessment of composite generation and transmission system[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(7): 58–62. |
| [12] |
赵渊, 周家启. 发输电组合系统可靠性评估的最优负荷削减模型研究[J].
电网技术, 2004, 28(10): 34–37.
Zhao Yuan, Zhou Jiaqi. Analysis of optimal load shedding model in reliability evaluation of composite generation and transmission system[J]. Power System Technology, 2004, 28(10): 34–37. DOI:10.3321/j.issn:1000-3673.2004.10.008 |
| [13] |
钟世霞, 袁荣湘. 内点法在电力系统中的应用述评[J].
高电压技术, 2005, 31(12): 76–79.
Zhong Shixia, Yuan Rongxiang. An application of interior point method in optimization of power systems[J]. High Voltage Engineering, 2005, 31(12): 76–79. DOI:10.3969/j.issn.1003-6520.2005.12.027 |
| [14] | Hua Wan, McCalley J D, Vittal V, et al. Risk based voltage security assessment[J]. IEEE Transactions on Power Systems, 2000, 15(4): 1247–1254. DOI:10.1109/59.898097 |
| [15] | IEEE APM Subcommittee. IEEE reliability test system[J]. IEEE Transactions on Power Apparatus and Systems, 1979, PAS-98(6): 2047–2054. DOI:10.1109/TPAS.1979.319398 |
 2017, Vol. 50
2017, Vol. 50




