文章信息
- 陈东斌, 陈益峰, 洪佳敏, 王敏, 唐文嘉
- CHEN Dongbin, CHEN Yifeng, HONG Jiamin, WANG Min, TANG Wenjia
- 丹巴水电站长引水隧洞涌水量预测
- Water inflow predictions of Danba water diversion tunnel
- 武汉大学学报(工学版), 2017, 50(2): 193-199, 206
- Engineering Journal of Wuhan University, 2017, 50(2): 193-199, 206
- http://dx.doi.org/10.14188/j.1671-8844.2017-02-006
-
文章历史
- 收稿日期: 2016-01-30
2. 武汉大学水工岩石力学教育部重点实验室,湖北 武汉 430072;
3. 浙江省水利河口研究院,浙江 杭州 310020
2. Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering of Ministry of Education, Wuhan University, Wuhan 430072, China;
3. Zhejiang Institute of Hydraulics and Estuary, Hangzhou 310020, China
我国西南地区河谷深切、岸坡陡峻、地质环境复杂,在水电、交通等领域涉及大量的深埋长隧洞工程.由于深埋长隧洞在克服高山峡谷地形障碍、缩短空间距离及改善陆路交通工程运行质量等方面具有不可替代的作用,深埋长引水隧洞的修建越来越受到重视.在复杂地质条件下,深埋长隧洞的建设将面临一系列的工程地质问题,而涌水问题便是其中最突出的一种[1, 2].
通过对水文地质特征的概化和分析,研究人员提出了一系列涌水量预测方法,其中,Goodman[3]、大岛洋志和Tani[4]等公式得到了广泛的认可.国内学者王建宇[5]建立的公式考虑了衬砌与灌浆结构渗透系数对涌水量的影响.基于工程经验,诸如我国铁路勘测规范、佐藤邦明、落合敏郎、科斯嘉科夫等经验方法[6]也被提出并得到了应用.随着计算机技术的发展,数值模拟法、回归分析法、模糊数学模型法、灰色系统理论法、人工神经网络法和时间序列分析等[7, 8]也相继提出,并在工程中得到应用.
本文以丹巴长引水隧洞为例,通过对区域水文地质特征的调查与分析,深入研究了区域地下水的分布规律.基于地勘资料及引水系统布局,建立了30.6 km范围的工程区有限元模型,进而对天然渗流场进行了反演分析,并对施工期及运行期隧洞沿线涌水量分布特征进行了数值模拟.与解析法预测结果的对比分析表明,有限元分析结果具有较好的代表性和可靠性,可为工程建设提供一定参考.
1 涌水量预测方法目前,常用的隧道涌水预测方法大致可划分为确定性预测方法和非确定性预测方法2类.确定性方法主要包括解析法、数值模拟法和水均衡法.非确定性方法包括水文地质比拟法、回归分析法、模糊数学模型、灰色系统理论、BP人工神经网络以及时间序列分析等.但是,由于涌水量预测的不确定性,这些方法均有不同的适用条件.其中,解析法、数值模拟法、水均衡法均可依据工程区地质条件,在工程实施前对隧道的涌水量进行预测分析[9].
2.1 水均衡法水均衡法包括大气降雨入渗系数法和地下水径流深度法等.对于降雨入渗法,隧洞涌水量的预测公式为
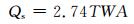 (1)
(1)
对于地下径流深度法,隧洞涌水量预测公式为
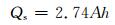 (2)
(2)
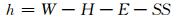 (3)
(3)
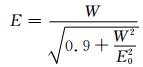 (4)
(4)
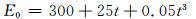 (5)
(5)
式中:Qs为隧道通过含水体地段的涌水量,m3/d;T为降水入渗系数;W为年降水量,mm;A为隧道集水面积,km2;h为年地下径流深度,mm;H为年地表径流深度,mm;E为年蒸发蒸散量,mm;SS为地表滞水深度,mm;t为流域年平均气温,℃.
1.2 数值模拟法数值模拟法有效克服了解析法对地质条件和边界条件考虑的不足,适用于具有复杂地质特征和边界条件的隧洞涌水预测问题.王媛[10]、任旭华[11]、许国安[12]等均采用有限元方法对隧洞涌水量进行了成功的预测.而有限元数值模拟中的重点就在于渗流场的精确模拟问题,其中涉及渗流溢出边界和渗流自由面的确定,主要包括剩余流量法、节点虚流量法等直觉化方法以及理论基础更严密的变分不等式方法.本文采用Signorini型变分不等式和自适应罚函数相结合的方法[13-15],实现对天然渗流场的模拟和隧洞涌水量的预测分析.
1.3 解析法解析法主要是基于稳定水流的前提,采用数学解析方法结合给定的边界条件和初始条件,通过地下水稳定渗流方程进行求解分析.一般基于如下假定:1) 围岩为均质、各向同性材料;2) 洞室形状为圆形;3) 不考虑渗流场与应力场的耦合作用;4) 大多不考虑实际工程中的衬砌灌浆结构.因此,解析模型预测结果与工程实际涌水量往往存在偏差,但由于推导严谨,在参数取值较为合理的情况下可为工程涌水量预测提供参考.
根据实际情况,涌水量的预测包括初期最大涌水量q0、经常涌水量qs和递减涌水量qt 3个不同阶段涌水量的预测.由于递减涌水量随时间变化,本文仅对最大涌水量与经常涌水量进行计算分析.计算模型如图 1所示,常用计算公式见表 1.
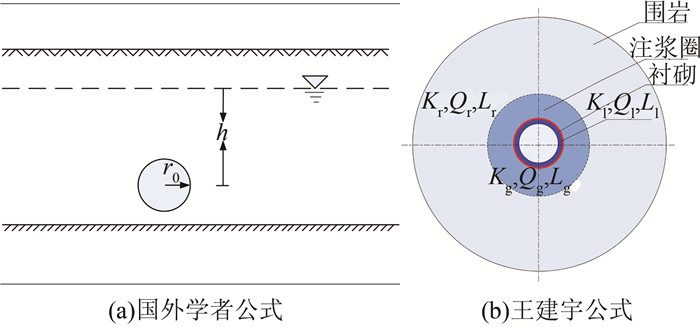
|
| 图 1 解析模型示意图 Figure 1 Schematic diagrams of empirical formulas |
| 涌水量 | 方法 | 公式 | 备注 |
| 初期最大涌水量 | 大岛洋志公式 | 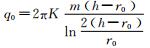 |
K为岩体渗透系数,m/d; m为转换系数,一般取0.86; h为静水位至洞底距离,m; r0为隧道半径,m; 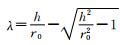 ; ;Kr为围岩渗透系数,m/d; Kg为注浆圈渗透系数,m/d; Kl为衬砌渗透系数,m/d; rl为衬砌外半径,m; rg为注浆圈半径,m; R为隧道涌水影响半径, 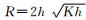 ; ;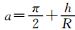 . . |
| 铁路勘测规范 | q0=0.025 5+1.922 4Kh | ||
| Goodman公式 | 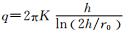 |
||
| M.El.Tani公式 | 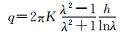 |
||
| 王建宇公式 | 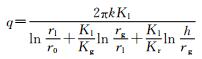 |
||
| 经常涌水量 | 铁路勘测规范 | qs=Kh(0.676-0.06K) | |
| 佐藤邦明公式 | qs=q0-0.584XKr0 | ||
| 落合敏郎公式 | 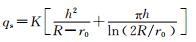 |
||
| 科斯嘉科夫公式 | 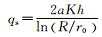 |
丹巴水电站位于大渡河上游四川省甘孜藏族自治州丹巴县境内,为大渡河干流22级梯级开发中的第8级梯级电站.引水系统布置在大渡河左岸山体中,为2洞4机布置,由进水口、引水隧洞、调压室群和压力管道等建筑物组成.引水系统平均总长约17.4 km,其中2条引水隧洞长度分别为16.52、16.67 km.隧洞轴线布置如图 2所示.

|
| 图 2 长引水隧洞平面布置图 Figure 2 Layout of Danba long diversion tunnel |
丹巴水电站引水系统位于大渡河左岸,以剥蚀中-高山地貌为主.区内山高谷深,地势险峻,隧洞沿线山体雄厚,地面高程为2 200~3 000 m,主要山脉展布方向与区域构造线走向基本相近.区内大渡河大致呈SN流向,沿线发育近东西向深切沟谷,主要为燕耳岩沟、德罗沟及根巴沟.
区域沿线地质构造比较复杂,以规模不等的褶皱和断裂构造为主.沿线中前部未见规模较大区域性断裂通过,后部主要发育F12、F13和F14断裂,均为NW走向,与引水隧洞交角一般为40°~60°.节理裂隙中等发育,局部较发育,总体透水性差,地下水活动微弱.
工程区主要由志留系茂县群Smx4和Smx5地层组成,为一套深变质岩组成,产状变化大,一般为N20°~60°W,NE∠50°~75°.地表低洼处或平缓台地及坡脚处多分布第4系(Q4)松散堆积物.其中,第4岩组(Smx4)主要为云母石英片岩、长英质变粒岩夹少量片麻岩组成,岩相与厚度变化大;第5岩组(Smx5)主要由石英岩、变粒岩与云母石英片岩、石英云母片岩组成;第4系堆积物以崩坡积、冲洪积物为主.隧洞轴线地质分布如图 3所示.

|
| 图 3 隧洞轴线地质剖面图 Figure 3 Geological profile along the tunnel |
大渡河是工程区的干流水系,地表水资源较为丰富,其中,燕耳岩沟、德罗沟、根巴沟中常年有水且流量较大;其余冲沟中流量较小,时有断流情况发生.
工程区地下水主要有基岩裂隙水和孔隙水2大类,其补给来源主要是大气降水与冰雪融水,水量大小受季节性影响较明显,向低洼处或沟谷排泄,最终汇入大渡河.
区域岩体完整,地表排水通畅,岩溶发育程度微弱.沿线第4系覆盖层较薄,降水入渗条件差,且多被沟谷排泄,孔隙水发育不良.地下水主要为基岩裂隙水,富集于浅表部风化、卸荷岩体中的断层和节理裂隙中,有一定的埋深,贮量不丰,活动性较弱.
3 有限元模型与计算 3.1 有限元模型通过对区域工程地质、水文地质进行分析,本文建立了长达30.6 km的区域地下水有限元分析模型,准确反映了研究区域内的地形地貌情况、地层岩性、地质构造特征和水文地质特征.为了准确模拟天然渗流场的边界条件,以河流与分水岭作为有限元模型的边界.模型以进水口为坐标原点O,以大渡河水流方向为X轴正方向,以垂直大渡河并指向山体左岸方向为Y轴正方向,以竖直向上为Z轴正方向.模型共划分有限元单元593 631个,节点132 091个,最低高程为1 200 m,最高高程为4 806 m,有限元模型如图 4所示.采用稳定渗流有限元方法进行计算.
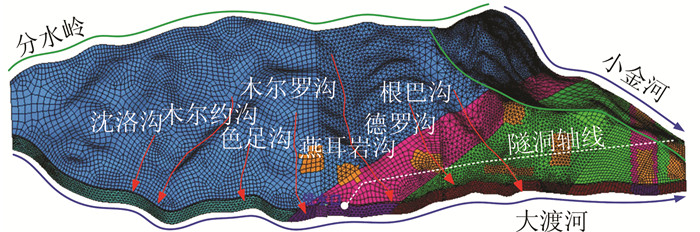
|
| 图 4 有限元模型图 Figure 4 Finite element mesh |
根据钻孔压水试验结果,并结合工程类比经验,各类岩体渗透系数取值如表 2所示.
| cm/s | ||||||||
| 介质 | 大理岩 | 石英变粒岩 | 石英云母片岩 | 断层 | 覆盖层 | |||
| 卸荷带 | 微风化 | 卸荷带 | 微风化 | 卸荷带 | 微风化 | |||
| 渗透系数 | 1.0×10-3 | 5.0×10-5 | 8.0×10-4 | 3.0×10-5 | 5.0×10-4 | 8.0×10-6 | 2.0×10-3 | 8.0×10-3 |
区域模型大渡河边界淹没区取定水头边界,水头值为大渡河常年平均水位;小金河边界淹没区取定水头边界,水头值为小金河常年平均水位;模型分水岭取定水头边界,水头值取反演的地下水位;模型底部边界取隔水边界;其余边界取为潜在溢出边界.其中,选取施工期与运行期,即隧洞中无内水压与内水压为1 996 m,分别作为初期最大涌水量和经常涌水量的隧洞边界条件设定.
3.2 计算结果分析 3.2.1 区域天然渗流场反演依据工程地质及水文地质条件,充分利用引水隧洞沿线钻孔、冲沟径流,大渡河、小金河水位等水文地质资料,作为地下渗流的参考控制条件,对工程区天然渗流场进行整体反演分析.通过对区域分水岭地下水位埋深进行试算,使冲沟、长观测孔反演水位与实际水文地质情况相符,确定出区域天然渗流场分布.
区域水文地质模型的主要分水岭如图 5所示.模型分水岭可大致分为AB段、BC段、CD段、BE段.通过对分水岭地下水位埋深进行试算,最终确定出AB、BC、CD、BE段的地下水位埋深分别为280、220、180、200 m.
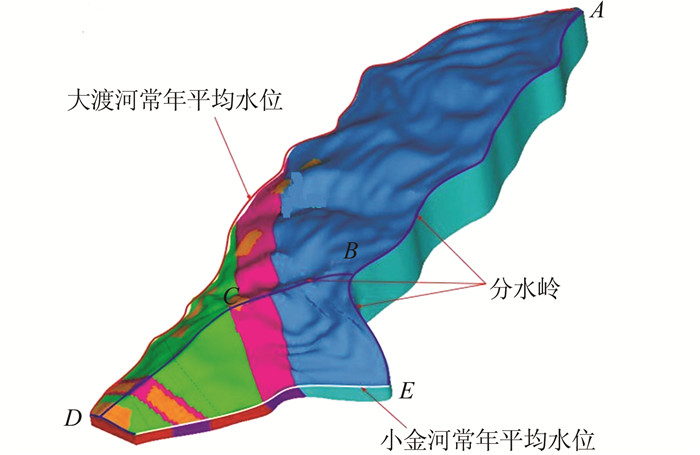
|
| 图 5 分水岭范围图 Figure 5 Scope of watershed |
将数值计算结果与水文地质控制条件进行对比分析,对研究区域天然渗流场的反演结果进行评价.地表冲沟径流特征对比见图 6,渗流计算结果显示,在主要冲沟处均有水溢出,反演出的地表冲沟径流特征与实际情况吻合很好.
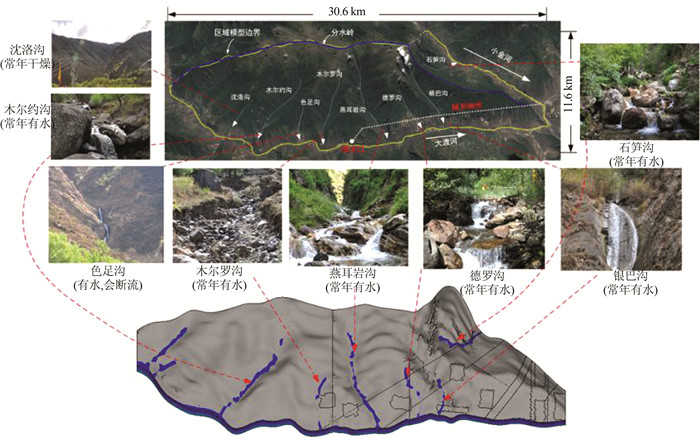
|
| 图 6 地表冲沟径流特征对比 Figure 6 Comparison of characteristics of gully runoff |
长观测孔水位对比分析结果如表 3所示,反演水位值与长观测孔实测水位值吻合很好,最大误差不超过2.445%.虽然BK111钻孔处实测水位与计算水位相差49.71 m,但根据实地调查,进水口处洞室干燥,地下水位埋深较大.如果完全按照BK111钻孔水位进行反演,得到的地下水位将偏高,与实际不符.因此,在反演过程中,以BK110钻孔水位为主,同时兼顾BK111钻孔水位情况.综合分析可知,区域天然渗流场反演结果符合实际.
| 编号 | 实测水位/m | 计算水位/m | 误差/m | 误差百分比/% |
| BK110 | 1 964.53 | 1 963.18 | 1.35 | 0.007 |
| BK111 | 2 033.43 | 2 083.14 | 49.71 | 2.445 |
依据反演出的天然渗流场,对模型进行有限元分析,计算得到运行期隧洞总涌水量,并与水均衡法计算结果进行对比分析,结果见表 4.其中,水均衡法中的计算参数根据实测水文地质资料与勘察规范得到,取值见表 5.年地表径流深度与地表滞水深度可忽略不计.
| m3/d | |||
| 计算方法 | 有限元 | 降雨入渗法 | 地下径流深度法 |
| 涌水量 | 132 875 | 87 169 | 78 548 |
| 降雨量/mm | 积水面积/km2 | 降雨入渗系数 | 平均气温/℃ |
| 616.3 | 258.1 | 0.2 | 14.3 |
通过表中对比结果可以得到,3种计算方法总涌水量略有差异.其中,相对于有限元模拟结果,降雨入渗法计算结果最相近.地下径流深度法由于无法定量估算冰雪融水部分,因此计算结果差异略大.而降雨入渗法由于降雨入渗系数的人为选定,致使计算结果有偏差.综上所述,水均衡法由于公式假定较简单,准确性不足,计算结果略有偏差,但基本能反映总涌水量的预测情况,具有一定的参考性.
3.2.3 单宽涌水量对比分析为进行详细对比分析,本文同时对单宽涌水量进行计算.分别选取隧洞沿线主要冲沟处、岩性变化处以及典型地势处作为典型断面进行分析,各断面分布位置如图 7所示.隧洞沿线最大涌水量与经常涌水量有限元计算结果见图 8.

|
| 图 7 典型断面位置分布图 Figure 7 Profile section along the tunnel |
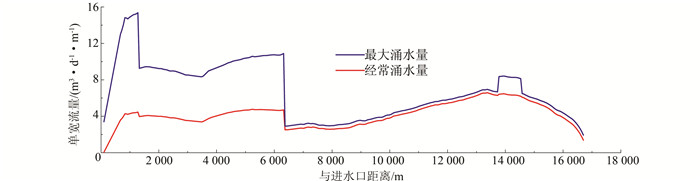
|
| 图 8 隧洞沿线涌水量有限元计算结果图 Figure 8 Calculated discharge of finite element method along the tunnel |
由图中可以看出,石英变粒岩区域的隧洞沿线涌水量比石英云母片岩区域要大.其原因是石英云母片岩裂隙不发育,裂隙连通性较弱,渗透系数较小.
依据各断面水文地质参数,得到初期最大涌水量与经常涌水量解析解,并与数值模拟结果进行对比,结果见表 6、7.
| m3/(s·m) | ||||||
| 断面 | 理论解析 | 有限元数值模拟 | 经验解析 | |||
| Goodman | M EI Tani | 王建宇 | 大岛洋志 | 铁路规范 | ||
| A | 10.55 | 10.54 | 14.86 | 10.4 | 9.56 | 13.08 |
| B | 11.21 | 11.21 | 15.12 | 11.3 | 9.93 | 16.23 |
| C | 9.45 | 9.44 | 13.67 | 10.6 | 8.34 | 13.09 |
| D | 12.47 | 12.46 | 17.11 | 11.9 | 11.32 | 18.52 |
| E | 3.58 | 3.58 | 2.43 | 3.3 | 3.12 | 5.44 |
| F | 3.81 | 3.81 | 2.55 | 3.6 | 3.29 | 58.87 |
| G | 5.50 | 5.50 | 3.71 | 4.7 | 4.85 | 9.20 |
| H | 8.15 | 8.15 | 5.76 | 9.9 | 7.06 | 14.76 |
| I | 7.72 | 7.72 | 5.51 | 7.3 | 6.66 | 13.83 |
| m3/(s·m) | |||||
| 断面 | 经验解析 | 有限元数值模拟 | |||
| 铁路规范 | 佐藤邦明 | 落合敏郎 | 科斯嘉科夫 | ||
| A | 4.57 | 7.07 | 5.00 | 4.78 | 3.36 |
| B | 5.69 | 8.44 | 5.51 | 5.07 | 4.06 |
| C | 4.58 | 6.92 | 4.74 | 4.37 | 3.75 |
| D | 6.49 | 9.52 | 6.06 | 5.57 | 4.41 |
| E | 1.90 | 2.76 | 2.27 | 1.93 | 2.51 |
| F | 2.06 | 2.96 | 2.39 | 2.03 | 2.58 |
| G | 3.22 | 4.41 | 3.25 | 2.76 | 3.56 |
| H | 5.18 | 6.69 | 4.54 | 3.88 | 6.27 |
| I | 4.85 | 6.32 | 4.33 | 3.70 | 5.73 |
从最大涌水量结果对比可以看出,不同计算方法各断面涌水量分布规律相同.但由于计算模型的简化以及经验性,经验解析法与有限元计算结果相差较大.而理论解析法由于假定条件与实际工程地质条件较吻合,计算结果与有限元结果较为相近.其中,Tani公式结果最为接近.从经常涌水量对比结果可以得到,经验解析公式与有限元计算结果略有不同.尽管几种经验公式统计参数与依据不同,但结果相差不大.其中,铁路规范经验公式依据我国隧洞工程资料统计,与有限元结果最为相近.
综上所述,通过区域有限元模型隧洞涌水量的计算分析,并与经验公式、理论公式方法对比,结果表明有限元计算结果具有一定的可比性,说明隧道涌水量的有限元预测是可信的.
4 结论本文通过对丹巴左岸长引水隧洞的水文地质资料进行研究,建立了相应的有限元模型,并对区域天然渗流场进行反演分析,采用多种预测方法对隧洞涌水量进行对比分析.
1) 依据区域工程地质及水文地质条件,通过对边界水位的试算分析,天然渗流场反演结果能良好反映工程区的实际情况.
2) 由于石英云母片岩裂隙不发育,连通性较弱,渗透系数较小, 因此隧洞沿线单宽涌水量在石英变粒岩区域较大.
3) 通过有限元数值模拟与解析法进行隧道单宽涌水量预测对比,结果吻合较好,表明有限元方法具有一定的可比性和可信度.
| [1] |
房倩, 张顶立, 黄明琦. 基于连续介质模型的海底隧道渗流问题分析[J].
岩石力学与工程学报, 2007, 26(Supp.2): 3776–3783.
Fang Qian, Zhang Dingli, Huang Mingqi. Analysis of seepage problem induced by subsea tunnel excavation based on continuum medium model[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Supp.2): 3776–3783. |
| [2] |
杨会军, 王梦恕. 深埋长大隧道渗流数值模拟[J].
岩石力学与工程学报, 2006, 25(3): 511–519.
Yang Huijun, Wang Mengshu. Numerical simulation of seepage in deep-buried long and big tunnels[J]. Chinese Journal of rock Mechanics and Engineering, 2006, 25(3): 511–519. |
| [3] | Goodman R E, Moye D G, Van Schalkwyk A, et al. Ground Water Inflows During Tunnel Driving[M]. College of Engineering, University of California, 1964. |
| [4] | El Tani M. Circular tunnel in a semi-infinite aquifer[J]. Tunnelling and Underground Space Technology, 2003, 18(1): 49–55. DOI:10.1016/S0886-7798(02)00102-5 |
| [5] |
王建宇. 再谈隧道衬砌水压力[J].
现代隧道技术, 2003, 40(3): 5–10.
Wang Jianyu. Once more on hydraulic pressure upon lining[J]. Modern Tunnelling Technology, 2003, 40(3): 5–10. |
| [6] |
邓百洪, 方建勤. 隧道涌水预测方法的研究[J].
公路交通技术, 2005(3): 161–163.
Deng Baihong, Fang Jianqin. Study on forecast method for water gush of tunnels[J]. Technology of Highway and Transport, 2005(3): 161–163. |
| [7] |
黄涛, 杨立中. 渗流与应力耦合环境下裂隙围岩隧道涌水量的预测研究[J].
铁道学报, 1999, 21(6): 75–80.
Huang Tao, Yang Lizhong. A prediction study of water-gush yield in fractured tunnels under coupling between seepage and stress[J]. Journal of the China Railway Society, 1999, 21(6): 75–80. |
| [8] |
朱大力, 李秋枫. 预测隧道涌水量的方法[J].
工程勘察, 2000(4): 18–22, 32.
Zhu Dali, Li Qiufeng. Methods to predict discharge rate of tunnel[J]. Geotechnical Investigation and Surveying, 2000(4): 18–22, 32. |
| [9] |
王建秀, 朱合华, 叶为民. 隧道涌水量的预测及其工程应用[J].
岩石力学与工程学报, 2004, 23(7): 1150–1153.
Wang Jianxiu, Zhu Hehua, Ye Weimin. Forward and inverse analyses of water flow into tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(7): 1150–1153. |
| [10] |
王媛, 秦峰, 李冬田. 南水北调西线工程区地下径流模数、岩体透水性及隧洞突、涌水量预测[J].
岩石力学与工程学报, 2005, 24(20): 3673–3678.
Wang Yuan, Qin Feng, Li Dongtian. Groundwater runoff modulus, rock permeability and prediction of water inflow and inrush of tunnel in West Route of South-to-North Water Transfer Project[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(20): 3673–3678. DOI:10.3321/j.issn:1000-6915.2005.20.011 |
| [11] |
任旭华, 束加庆, 单治钢, 等. 锦屏二级水电站隧洞群施工期地下水运移、影响及控制研究[J].
岩石力学与工程学报, 2009, 28(Supp.1): 2891–2897.
Ren Xuhua, Shu Jiaqing, Shan Zhigang, et al. Research on groundwater transport, influence and control in tunnel group of Jinping Ⅱ hydropower station during construction[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Supp.1): 2891–2897. |
| [12] |
许国安, 邵宇. 锦屏二级水电站引水隧洞三维渗流分析[J].
长江科学院院报, 2009, 26(Supp.1): 18–22.
Xu Guoan, Shao Yu. Three-dimensional seepage analysis of diversion tunnel of Jinping Ⅱ hydropower station[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(Supp.1): 18–22. |
| [13] | Chen Y F, Zhou C B, Zheng H. A numerical solution to seepage problems with complex drainage system[J]. Computers and Geotechnics, 2008, 35(3): 383–393. DOI:10.1016/j.compgeo.2007.08.005 |
| [14] |
陈益峰, 周创兵, 毛新莹, 等. 水布垭地下厂房围岩渗控效应数值模拟与评价[J].
岩石力学与工程学报, 2010, 29(2): 308–318.
Chen Yifeng, Zhou Chuangbing, Mao Xinying, et al. Numerical simulation and assessment of seepage control effects on surrounding rocks of underground powerhouse in Shuibuya hydropower project[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(2): 308–318. |
| [15] | Chen Yifeng, Hu Ran, Zhou Chuangbing, et al. A new classification of seepage control mechanisms in geotechnical engineering[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2010, 2(3): 209–222. DOI:10.3724/SP.J.1235.2010.00209 |
 2017, Vol. 50
2017, Vol. 50




