文章信息
- 池寅, 时豫川, 吴海洋, 卢秋如
- CHI Yin, SHI Yuchuan, WU Haiyang, LU Qiuru
- 砂质海床中船锚运动全过程数值模拟
- Numerical simulation of whole movement process of an anchor in sandy seabed
- 武汉大学学报(工学版), 2017, 50(6): 807-814
- Engineering Journal of Wuhan University, 2017, 50(6): 807-814
- http://dx.doi.org/10.14188/j.1671-8844.2017-06-002
-
文章历史
- 收稿日期: 2017-06-14
2. 中国电力工程顾问集团中南电力设计院有限公司, 湖北 武汉 430071
2. Central Southern China Electric Power Design Institute Co., Ltd., China Power Engineering Consulting Group, Wuhan 430071, China
近年来,随着我国岛屿间电力网络的不断完善、国际间信息传输交流的逐渐增多,我国海底电缆的数量日益增加.然而电缆事故也随之增多,船锚抛锚和拖锚所造成的损害就是最主要的原因之一[1].
船锚在海床土体中的最大贯入深度是海底电缆保护工程的主要控制因素,不少学者[2-4]对抛锚情况下的船锚贯入深度进行了研究,结果表明海床土体基质对贯入深度具有显著影响.随着计算机技术的发展,数值仿真已成为研究船锚在海床土体中运动过程的主要手段之一.常用的仿真计算方法有有限元法(FEM)[5]和任意拉格朗日-欧拉法[2, 3]等,研究结果表明数值仿真具有较高的效率和精确度.但目前的数值仿真主要针对抛锚情况下船锚的最大贯入深度进行研究,而抛锚和拖锚是2个不同的运动过程,因此,研究船锚的抛锚和拖锚运动全过程对确立海底电缆安全埋深具有实际的工程意义.
本文利用ANSYS/LS-DYNA软件,采用SPH和FEM耦合法对船锚在砂质海床土体中的抛锚和拖锚运动全过程进行了计算仿真,分析了不同砂质海床土体和拖曳速度对船锚贯入深度与拖曳力的影响规律.此研究可为海底电缆的安全性定量分析提供理论研究基础,也可为海底电缆防护工程的设计和评估提供依据.
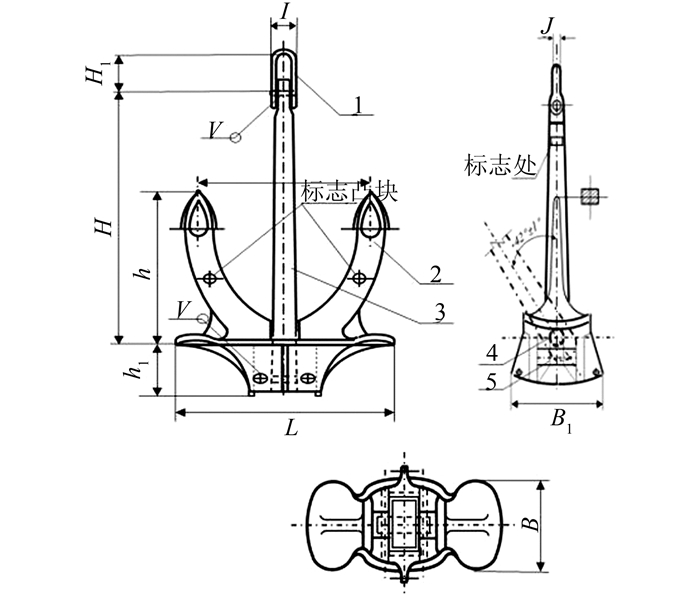
1 计算模型描述 1.1 几何模型 1.1.1 船锚采用A型霍尔锚(图 1)进行建模分析.参考国家标准《霍尔锚》(GB/T546-1997)[6]的规定,选用3种不同尺寸的霍尔锚,质量分别为1 020、1 590、2 100 kg.相关几何参数列于表 1.采用FEM法建立霍尔锚模型,模型形状不规则且网格数量大,故采用自由网格划分的方法,如图 2所示.
|
| 图 1 A型霍尔锚尺寸 Figure 1 Dimensions of A-type Hall anchor |

|
| 图 2 霍尔锚三维有限元模型 Figure 2 Three-dimensional FEM model of Hall anchor |
| 霍尔锚 | 重量/kg | H/mm | h/mm | h1/mm | L/mm | L1/mm | B/mm | B1/mm | H1/mm | I/mm | J/mm |
| Anchor-1 | 1 020 | 1 645 | 891 | 195 | 1 268 | 891 | 492 | 584 | 255 | 200 | 60 |
| Anchor-2 | 1 590 | 1 906 | 1 035 | 226 | 1 475 | 1 035 | 571 | 677 | 310 | 236 | 68 |
| Anchor-3 | 2 100 | 2 093 | 1 136 | 249 | 1 614 | 1 136 | 628 | 743 | 340 | 256 | 74 |
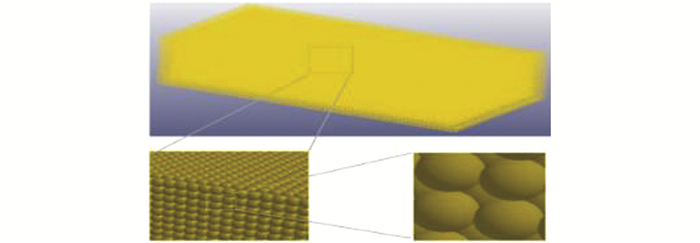
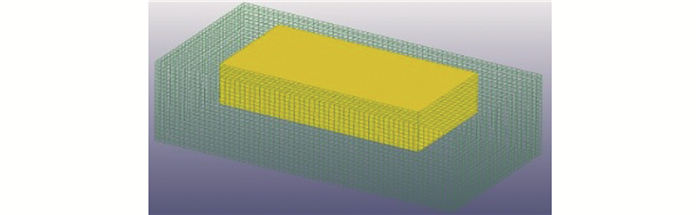
由于抛锚及拖锚是2个非常复杂的运动过程,涉及大变形、非线性和弹塑性等问题,是高度非线性力学耦合问题.而SPH法是一种无网格Lagrangian粒子法,其计算精度不受物质变形程度的影响,能够求解大变形以及高应变率问题[7].因此,在建立土体模型时,采用SPH法将变形较大的土体处理成SPH粒子(图 3),可避免由于土体大变形而导致的网格畸变问题和土体在外荷载作用下的微观破坏行为.对应力较小区域采用FEM法建模,考虑到海床土体模型形状为长方体,可实现均匀的网格划分,故采用延伸网格划分的方法(图 4).两部分海床土体通过接触算法进行连接.SPH和FEM耦合法能最大限度地发挥2种算法的优势,既能保证计算精度又能提高计算效率.综合考虑船锚贯入海床土体的实际工作参数及仿真效率,建立的砂质海床土体FEM-SPH耦合几何模型为长12 m、宽6 m、高4 m的长方体(其中, SPH模型尺寸为8 m×4 m×2 m).
|
| 图 3 砂质海床土体SPH模型 Figure 3 SPH model of sandy seabed soil |
|
| 图 4 砂质海床土体FEM-SPH耦合模型 Figure 4 FEM-SPH coupling model of sandy seabed soil |
定义船锚材料模型为MAT_RIGID,材料参数为密度ρ=7.85 g/cm3,弹性模量E=210 GPa,泊松比v=0.3.
1.2.2 海床土体海床土体分别为松散细砂、中密细砂、密实细砂、中密粗砂及中密粉土5种海床土质材料,材料的相关物理与力学参数根据调研资料以及试验得到,列于表 2.定义材料模型为MAT_FHWA_SOIL土体本构模型.土体处于动荷载作用下且涉及运动和大变形问题,因此假定弹性阶段弹性模量与压缩模量一致,即E=Es.根据Trautmann和Kulhawy等[8],对砂质海床土体取泊松比v=0.3.为模拟孔隙水压力的作用,定义体积模量是关于无孔隙体积模量、孔隙度及饱和度的函数:
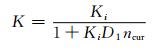 (1)
(1)
| 土质 | 含水率/% | 湿密度 /(g·cm-3) |
干密度 /(g·cm-3) |
土粒比重 | 孔隙比 | 饱和度 /% |
压缩模 量/MPa |
内聚力 /kPa |
内摩擦角 /(°) |
| 细砂(松) | 26.08 | 1.89 | 1.51 | 2.64 | 0.76 | 92.44 | 5.5 | 5 | 25 |
| 细砂(中) | 25.01 | 1.91 | 1.53 | 2.64 | 0.733 | 90.33 | 13.3 | 8 | 30 |
| 细砂(密) | 24.11 | 1.88 | 1.52 | 2.62 | 0.733 | 93 | 15.3 | 10 | 35 |
| 粗砂(中) | 21.3 | 1.91 | 1.57 | 2.64 | 0.677 | 83 | 11.4 | 15 | 30 |
| 粉土(中) | 32.2 | 1.88 | 1.42 | 2.7 | 0.903 | 96.5 | 5.5 | 15 | 15 |
式中:Ki为固结土体的体积模量;ncur为孔隙率;D1为控制孔隙坍塌前土体刚度的材料常数.采用Abbo等[9]提出的修正Mohr-Coulomb屈服准则,屈服面F为
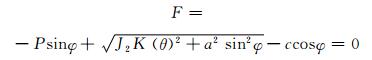 (2)
(2)
式中,参数a用来表征修正后的Mohr-Coulomb屈服面与标准的Mohr-Coulomb屈服面之间的拟合程度.当值为0时,上式即为标准的Mohr-Coulomb屈服面.参数a应接近于0,但需始终满足:
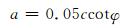 (3)
(3)
将标准Mohr-Coulomb屈服面的偏平面形状函数K改为Klisinski[10, 11]所使用的函数:
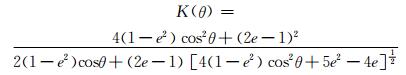 (4)
(4)
其中,cos3θ=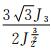
为反映土体的应变硬化特性,定义内摩擦角是关于有效塑性应变的函数.为模拟应变软化特性,模型采用Ju[12]提出的连续损伤算法.最终确定出5种不同砂质海床土体材料的本构参数,列于表 3~5.
| 土质 | 断裂应变 | 土密度/(g·cm-3) | 输出变量 | 比重 | 水密度/(g·cm-3) | 粘性系数 | 粘性系数 | 迭代次数 |
| 细砂(松) | 0.8 | 1.89 | 3 | 2.64 | 1 | 1.1 | 0 | 10 |
| 细砂(中) | 0.8 | 1.91 | 3 | 2.64 | 1 | 1.1 | 0 | 10 |
| 细砂(密) | 0.8 | 1.88 | 3 | 2.62 | 1 | 1.1 | 0 | 10 |
| 粗砂(中) | 0.8 | 1.91 | 3 | 2.63 | 1 | 1.1 | 0 | 10 |
| 粉土(中) | 0.8 | 1.88 | 3 | 2.70 | 1 | 1.1 | 0 | 10 |
| 土质 | 体积模量/MPa | 剪切模量/MPa | 摩擦角/rad | DP修正 | 内聚力/MPa | 偏心系数 | 应变强化(AN) | 应变强化(ET) |
| 细砂(松) | 4.5 | 2.1 | 0.436 | 1×10-4 | 0.005 | 0.7 | 0 | 0 |
| 细砂(中) | 11.1 | 5.1 | 0.523 | 1×10-4 | 0.008 | 0.7 | 0 | 0 |
| 细砂(密) | 12.7 | 5.8 | 0.611 | 1×10-4 | 0.01 | 0.7 | 0 | 0 |
| 粗砂(中) | 9.5 | 4.3 | 0.366 | 1×10-4 | 0.015 | 0.7 | 0 | 0 |
| 粉土(中) | 4.5 | 2.1 | 0.523 | 1×10-4 | 0.015 | 0.7 | 0 | 0 |
| 土质 | 孔隙率mc | 孔隙水应 力系数 |
考虑孔隙 压力的K |
有效压力 系数 |
最小内摩 擦角/rad |
初始损伤 体积应变 |
孔隙能 (断裂能) |
损伤单元 删除阀值 |
| 细砂(松) | 0.261 | 1 | 0.036 | 5 | 0 | 0.002 5 | 5 | 0.9 |
| 细砂(中) | 0.250 | 1 | 0.088 | 5 | 0 | 0.002 5 | 5 | 0.9 |
| 细砂(密) | 0.241 | 1 | 0.102 | 5 | 0 | 0.002 5 | 5 | 0.9 |
| 粗砂(中) | 0.213 | 1 | 0.076 | 5 | 0 | 0.002 5 | 5 | 0.9 |
| 粉土(中) | 0.322 | 1 | 0.036 | 5 | 0 | 0.002 5 | 5 | 0.9 |
对船锚采用速度边界,既能够反映出锚链力随拖曳过程的变化,又能真实反映船锚的实际运动情况.接触土体前,船锚有一个落体速度,并在贯入土体中一定深度后达到平衡状态,而该状态与船锚几何尺寸及质量有关.根据实际情况,设定船锚接触土体时的竖向速度分别是:Anchor-1(1 020 kg)为2.9 m/s、Anchor-2(1 590 kg)为3.15 m/s、Anchor-3(2 100 kg)为3.3 m/s.船锚以0.2 m/s的速度进行水平刚体位移(忽略冲击及速度效应).海床土体模型采用无反射边界条件用以模拟无限远场的影响.
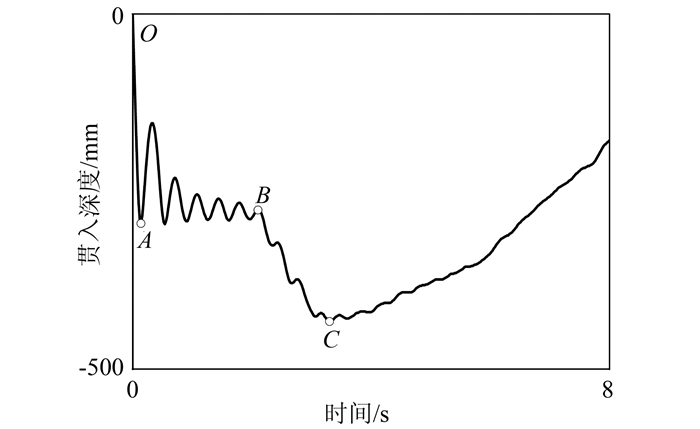
2 数值模拟结果及分析 2.1 船锚抛锚与拖锚运动全过程根据船锚贯入深度-时程曲线(图 5)将船锚抛锚与拖锚运动全过程分为4个阶段:
|
| 图 5 船锚贯入深度-时程曲线 Figure 5 Penetration depth-time curve of an anchor |
1) OA段,船锚以稳定的竖向初始速度与海床表面接触并贯入一定深度.
2) AB段,船锚开始被拖曳、上下波动,直至稳定状态.
3) BC段,船锚继续贯入,土体不断被开挖直到船锚贯入深度达到最大.
4) C后,随海床土体的堆积,船锚所受阻力在C点达到最大,船锚开始被抬升,致使贯入深度不断减小.
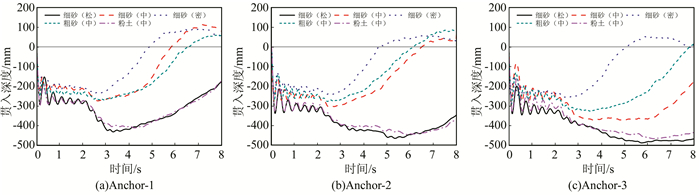
2.2 影响因素分析 2.2.1 海床土质图 6、7分别为5种砂质海床土体条件下的贯入深度-时程曲线和拖曳力-时程曲线对比图.由图可知:细砂土质海床的最大贯入深度随密实度的增加而逐渐减小.由于土体刚度随密实度的增加而增大,在达到使船锚被土体托起的堆积应变能时,密实细砂的变形更小,即表现为最大贯入深度的减小.中密粉土与松散细砂2种海床土体拥有完全相同的材料常数(均为K=4.5 MPa,G=2.1 MPa),使得二者的船锚贯入深度-时程曲线形式相近.但与松散细砂土体相比,中密粉土土体的孔隙水体积分数较大(为32.2%),在孔隙水压力的作用下,孔隙坍塌时材料的硬化速度更快,从而导致其最大贯入深度较小.中密粗砂与中密细砂2种海床土体的弹性常数相近,使得船锚运动初期二者的贯入深度-时程曲线和拖曳力-时程曲线相近.与中密细砂土体相比,中密粗砂土体内摩擦角小而内聚力大,在相同压力条件下,压力较小时粗砂抗剪强度较细砂大,而压力较大时粗砂抗剪强度较细砂小,即显示出拖曳前期材料更“硬”而拖曳后期材料变“软”的现象.随着锚重的增加,压力较大的条件下,这一现象更明显.
|
| 图 6 不同砂质海床土体条件下的船锚贯入深度-时程曲线对比图 Figure 6 Comparison of penetration depths of Hall anchors under different sandy seabed soils |
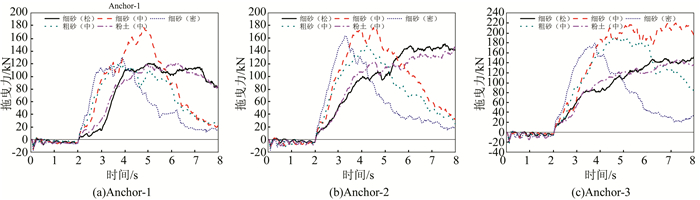
|
| 图 7 不同砂质海床土体条件下的拖曳力-时程曲线对比图 Figure 7 Comparison of dragging forces under different sandy seabed soils |
因此,对于不同砂质海床土体,其船锚运动轨迹受到土体剪切模量、孔隙率、内聚力、内摩擦角等多个因素的影响.分别分析这4个因素对最大贯入深度和峰值拖曳力的影响.
1) 剪切模量的影响
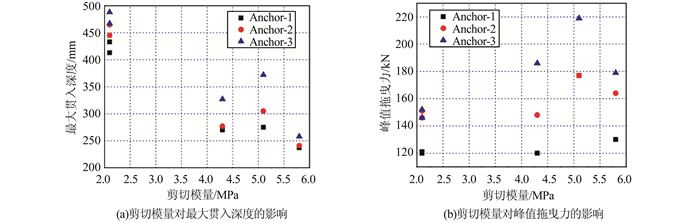
由图 8可得,对于所有船锚,随着砂质海床土体剪切模量的逐渐增大,其对应的最大贯入深度近似呈线性下降趋势.密实细砂海床土体的剪切模量最大从而具有最大的抗剪强度,但其最大贯入深度最小致使土体剪切面最小.在2个因素的影响下,其峰值拖曳力并非最大,在图中表现为峰值拖曳力先增大后减小.
|
| 图 8 剪切模量的影响 Figure 8 Effects of shear modulus |
2) 内聚力与内摩擦角的影响
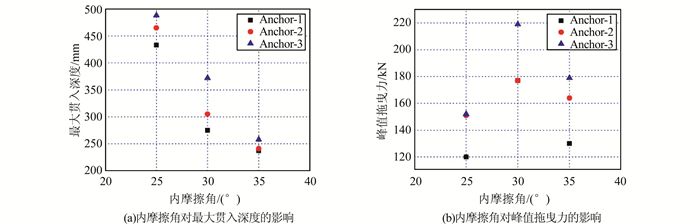
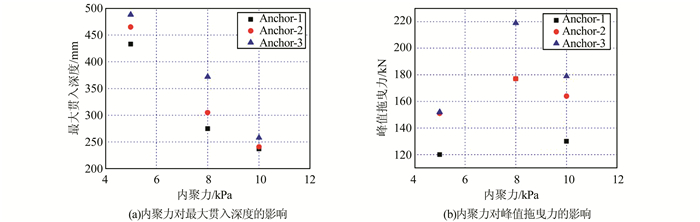
内聚力与内摩擦角是土体不排水抗剪强度的2个重要指标.两者数值越大,则土体不排水抗剪强度越大.对3种细砂土质海床土体(内聚力和内摩擦角随密实度的增加而增大)对应的船锚最大贯入深度及峰值拖曳力进行对比分析(图 9、10), 可得船锚的最大贯入深度随内聚力和内摩擦角的增大而逐渐减小,且呈现线性下降的趋势.同样在最大抗剪强度和最小剪切面2个因素的综合影响下,密实细砂海床土体的峰值拖曳力在3种土体中并未达到最大,表现为图中峰值拖曳力先增大后减小.
|
| 图 9 内摩擦角的影响 Figure 9 Effects of internal friction angle |
|
| 图 10 内聚力的影响 Figure 10 Effects of cohesion |
3) 孔隙率的影响
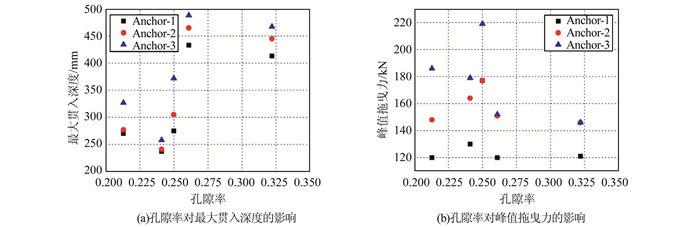
孔隙率对最大贯入深度有一定影响,如图 11所示.在一定范围内(0.24~0.26)孔隙率越大,其最大贯入深度也越大.而当孔隙率从0.26增加到0.32时,其最大贯入深度时并没有明显变化.此外,孔隙率的变化对峰值拖曳力影响较小.
|
| 图 11 孔隙率的影响 Figure 11 Effects of porosity |
表 6为不同砂质海床土体条件下船锚的最大贯入深度及峰值拖曳力的模拟值.可见峰值拖曳力均在220 kN以下.若船只在行进的过程中保持一定马力并匀速行驶,且锚链的最大破断力大于220 kN,则在砂质土体海床条件下,该霍尔型船锚无法锚住船只,最大贯入深度即为本文模拟结果.若锚链的最大破断力小于峰值拖曳力,则最大贯入深度为破断力出现时所对应的船锚贯入深度.
| 海床土质 | Anchor-1 | Anchor-2 | Anchor-3 | |||
| 最大贯入深度/mm | 峰值拖曳力/kN | 最大贯入深度/mm | 峰值拖曳力/kN | 最大贯入深度/mm | 峰值拖曳力/kN | |
| 细砂(松散) | 433 | 120 | 465 | 151 | 488 | 152 |
| 细砂(中密) | 275 | 177 | 305 | 177 | 372 | 219 |
| 细砂(密实) | 237 | 130 | 241 | 164 | 258 | 179 |
| 粗砂(中密) | 270 | 120 | 277 | 148 | 327 | 186 |
| 粉土(中密) | 413 | 121 | 445 | 146 | 467 | 146 |
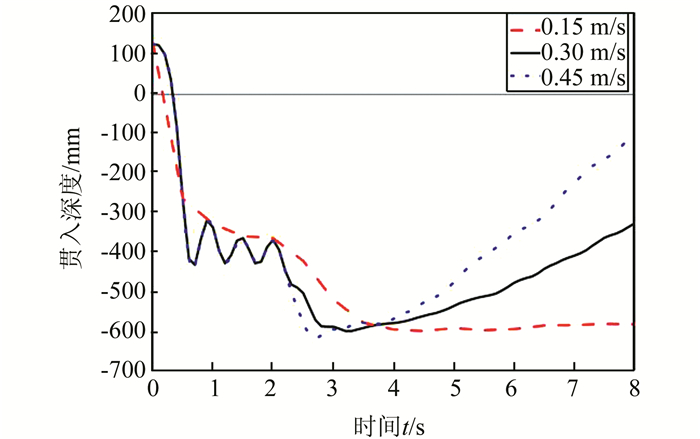
在拖曳速度对贯入深度与拖曳力的影响分析中,采用松散细砂海床土体和质量为3 060 kg的船锚,将拖曳速度分别设定为0.15、0.3、0.45 m/s,得到3种拖曳速度下的船锚贯入深度-时程曲线(图 12)和拖曳力-时程曲线(图 13).由图 12、13可得:
|
| 图 12 不同拖曳速度下的贯入深度-时程曲线 Figure 12 Penetration depth-time curves under different dragging velocities |
|
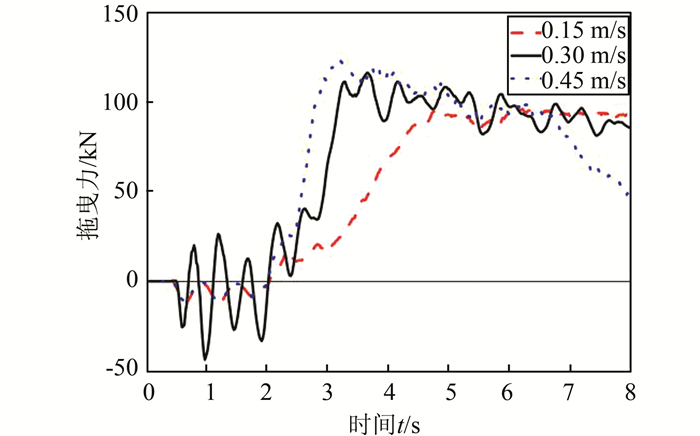
| 图 13 不同拖曳速度下的拖曳力-时程曲线 Figure 13 Dragging force-time curves under different dragging velocities |
1) 随着拖曳速度的提升,贯入深度-时程曲线达到峰值后的斜率逐渐增大,即船锚贯入深度减小速率加快,此外,拖曳力-时程曲线达到峰值前的斜率也逐渐增大,即拖曳力增大速率加快.分析原因是由于应变率效应,土体屈服应力值随拖曳速度的提升而增大,使得船锚所受堆积土体的阻力增大.
2) 拖曳速度的提升缩短了船锚达到最大贯入深度的时间,但对船锚最大贯入深度数值的影响不明显.随着速度从0.15 m/s至0.45 m/s,增至3倍后,其对应的最大贯入深度仅仅从598 mm变化为614 mm,增幅仅为2%.峰值拖曳力受拖曳速度的影响较大.当拖曳速度为0.3、0.45 m/s时,峰值拖曳力分别较速度为0.15 m/s时提高约20%和28%.因此,在实际工程中,若船锚锚链有足够的强度,不考虑其被拉断的可能性时,对最大贯入深度的预测可忽略船锚拖曳速度的影响.
2.3 数值模型的可靠性验证将本文砂质土体抛锚贯入深度模拟值与文献中砂质土体抛锚贯入深度的试验值和理论计算值进行对比,如表 7所示.
| 参考 文献 |
锚 重 /t |
触底 速度 /(m·s-1) |
贯入深度 试验值砂 土/m |
贯入深度计算值/m | ||
| 砂(松 散) |
砂(中 密) |
砂(密 实) |
||||
| [13] | 0.50 | 9 | 0.05 | 0.5 | 0.4 | 0.3 |
| 1.00 | 9 | 0.45 | 0.7 | 0.5 | 0.4 | |
| 1.50 | 9 | 0.75 | 0.8 | 0.7 | 0.5 | |
| 1.75 | 9 | 0.25 | 0.8 | 0.7 | 0.5 | |
| 3.40 | 9 | 0.34 | 1.0 | 0.8 | 0.7 | |
| 本文 | 1.02 | 2.90 | 0.295 | 0.231 | 0.220 | |
| 1.59 | 3.15 | 0.338 | 0.273 | 0.248 | ||
| 2.10 | 3.30 | 0.34 | 0.271 | 0.256 | ||
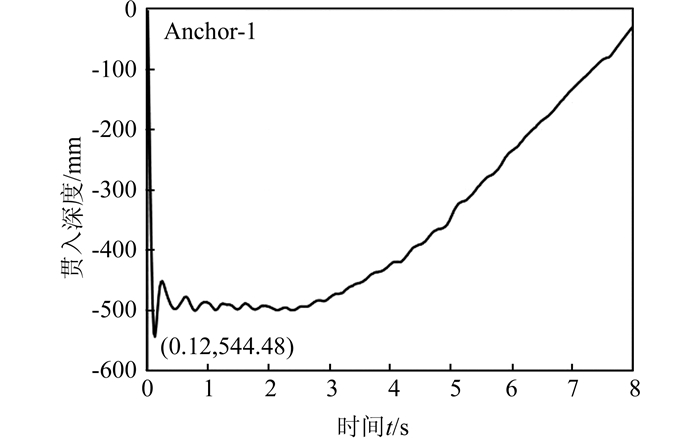
由表 7可知,参考文献[13]在船锚锚重为1.0 t、抛锚触底速度为9 m/s时,船锚贯入砂质土体的深度试验值为0.45 m,计算值针对松散砂、中密砂、密实砂分别为0.7、0.5、0.4 m.而本文的1.02 t船锚,贯入深度模拟值仅分别为0.295、0.231、0.220 m.分析原因是:抛锚触底速度相比参考文献小很多,若保持其他因素不变,将落锚触底速度提高,则贯入深度会显著提升.图 14为船锚质量为1.02 t、船锚触底速度为6.9 m/s、海床土质为松散细砂时的抛锚及拖锚贯入深度-时程曲线.由图可知,船锚触底速度为6.9 m/s时,其抛锚贯入深度的模拟值达到了0.544 m,与实际情况接近.若船锚触底速度设置为9 m/s时,最大贯入深度模拟值可达0.66 m,与参考文献[13]计算值吻合较好.上述对比分析证明本文建立的船锚与砂质海床土体的三维数值模型是可靠的.
|
| 图 14 触底速度为6.9 m/s时的抛锚及拖锚贯入深度-时程曲线 Figure 14 Penetration depth-time curve with bottoming velocity of 6.9 m/s |
1) 利用ANSYS/LS-DYNA软件,采用SPH和FEM耦合法对船锚在砂质海床土体中的运动全过程进行数值模拟,根据贯入深度-时程曲线,可将船锚运动的物理过程分为4个阶段.
2) 船锚的贯入深度与拖曳力受到土体剪切模量、内聚力、摩擦角和孔隙率等多个因素的影响.最大贯入深度分别随着土体材料剪切模量、内聚力、摩擦角的增大而逐渐减小,且近似呈线性变化.峰值拖曳力除密实砂土由于最大贯入深度小从而导致峰值拖曳力较小外,其余皆随剪切模量、内聚力、摩擦角的增大而逐渐增大.此外,孔隙率对最大贯入深度也有一定影响,在一定范围内孔隙率越大,其最大贯入深度也越大,但其对峰值拖曳力的影响较小.
3) 拖曳速度对船锚最大贯入深度的影响不明显.但随拖曳速度的提升,峰值拖曳力的提高幅度较大.当拖曳速度为0.3、0.45 m/s时,峰值拖曳力分别较速度为0.15 m/s时提高约20%和28%.在实际工程中,若船锚锚链有足够的强度,对最大贯入深度的预测可忽略船锚拖曳速度的影响.
4) 通过对比本文砂质土体抛锚贯入深度模拟值与文献中的试验值和理论计算值,证明了数值模型的可靠性.
| [1] |
张国光. 海底电缆安全及其施工埋设技术研究[J].
海洋技术, 1992(1): 64–73.
Zhang Guoguang. Research on safety and construction technology of submarine cable[J]. Ocean Technology, 1992(1): 64–73. |
| [2] |
王彦多. 法向承力锚的初始入土深度研究[D]. 天津: 天津大学, 2008.
Wang Yanduo. Study on initial embedment depth of normal bearing anchor[D]. Tianjin: Tianjin University, 2008. http://d.wanfangdata.com.cn/Thesis/Y1519594 |
| [3] |
马红旗. 鱼雷锚初始贯入海床深度的研究[D]. 天津: 天津大学, 2010.
Ma Hongqi. Study on the initial penetration depth of torpedo anchor[D]. Tianjin: Tianjin University, 2010. http://d.wanfangdata.com.cn/Thesis_Y1925213.aspx |
| [4] |
张磊. 基于船舶应急抛锚的海底管道埋深及保护研究[D]. 武汉: 武汉理工大学, 2013.
Zhang Lei. Study on buried depth and protection of submarine pipeline based on ship emergency anchoring[D]. Wuhan: Wuhan University of Technology, 2013. http://d.wanfangdata.com.cn/Thesis/Y2363293 |
| [5] |
张鹏杨, 王瑛剑, 柯超, 等. 基于ABAQUS的船舶抛锚贯入深度的分析[J].
光纤与电缆及其应用技术, 2016(4): 32–35.
Zhang Pengyang, Wang Yingjian, Ke Chao, et al. Analysis of anchoring penetration depth based on ABAQUS[J]. Optical Fiber & Electric Cable and Their Applications, 2016(4): 32–35. |
| [6] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T546-1997霍尔锚[S]. 北京: 中国标准出版社, 1997.
General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. GB/T546-1997 Hall Anchor [S]. Beijing: Standards Press of China, 1997. |
| [7] | Johnson G R, Stryk R A, Beissel S R. SPH for high velocity impact computations[J]. Comput Methods Appl Mech Engrg, 1996(139): 347–373. |
| [8] | Trautmann C H, Kulhawy F H. A computer program for compress and uplift foundation analysis and design[R]. Electrical Power and Research Institute, 1987. |
| [9] | Abbo A J, Sloan S W. A smooth hyperbolic approximation to the Mohr-Coulomb yield criterion[J]. Computers and Structures, 1995, 54(3): 427–551. DOI:10.1016/0045-7949(94)00339-5 |
| [10] | Klisinski M. Degradation and plastic deformation of concrete[D]. Polish: Polish Academy of Sciences, 1984. |
| [11] | Klisinski M, Mroz Z. Description of inelastic deformation and degradation of concrete[J]. International Journal of Solids and Structures, 1988, 24(4): 391–416. DOI:10.1016/0020-7683(88)90070-4 |
| [12] | Ju J W. Energy-based coupled elastoplastic damage models at finite strains[J]. Journal of Engineering Mechanics, 1989, 115(11): 2507–2525. DOI:10.1061/(ASCE)0733-9399(1989)115:11(2507) |
| [13] |
宣凯. 抛锚作业对海底管线损害研究[D]. 大连: 大连海事大学, 2012.
Xuan Kai. The study on anchoring damage to subsea pipelines [D]. Dalian: Dalian Maritime University, 2012. http://d.wanfangdata.com.cn/Thesis/Y2089498 |
 2017, Vol. 50
2017, Vol. 50




