文章信息
- 赵通, 邱志斌, 阮江军
- ZHAO Tong, QIU Zhibing, RUAN Jiangjun
- 计及损耗及成本的110 kV电缆尺寸多变量最优化
- Multiobjective optimization of 110 kV cable sizes considering cable loss and cost
- 武汉大学学报(工学版), 2018, 51(11): 980-986
- Engineering Journal of Wuhan University, 2018, 51(11): 980-986
- http://dx.doi.org/10.14188/j.1671-8844.2018-11-007
-
文章历史
- 收稿日期: 2017-12-20
电缆是电力系统中不可或缺的设备,因而电缆的优化设计是整个电力系统优化的重要部分.本文使用遗传算法多目标优化方法[1-3]对电缆的损耗和成本进行了同时优化,为电缆设计和施工、电力系统经济运行提供参考.
1 电缆损耗及计算选取电力系统中常见的110 kV高压电力电缆作为研究对象,为了研究方便,设定其形式为常用的单芯电缆,结构如图 1所示.同时限定电缆的工作状态为额定工作状态,即:加载110 kV交流电压,并令每相通有1 164 A的电流.为研究方便,此处仅考虑三相水平敷设的埋地电缆,敷设方式见图 1,其中s为每两相间隔距离.

|
| 图 1 110 kV电缆结构及敷设方式图 Fig. 1 Structure and arrangement scheme of 110 kV cable 1-芯线;2-内半导电屏蔽层;3-绝缘层;4-外半导电屏蔽层;5-阻水层;6-金属护层;7-沥青层;8-PVC外皮;9-半导电涂层 |
电缆的电能损耗越小、输电效率越高,下面首先建立损耗计算模型.电缆的电能损耗包括芯线、绝缘、金属护层和铠装层的损耗[4-5].
1.1 芯线损耗根据交流电阻发热公式,电缆的芯线损耗可以表示为
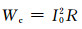 (1)
(1)
其中:I0为芯线电流; R为最高温度下导体的交流电阻.
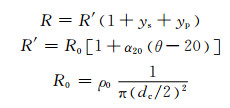
其中:R′为最高工作温度下导体的直流电阻;ys为趋肤效应系数;yp为邻近效应系数;R0为20 ℃时的单位长度直流电阻; ρ0=0.017 241 Ω·mm2/m, 为20 ℃时铜的电阻率; dc为导体直径, mm; α20=3.93×10-3, 为20 ℃时材料的温度系数,可在IEC-60287[6]的附表 1中查看;根据国家标准GB/T 11017.1-2014[7],最高工作温度为θ=90 ℃.
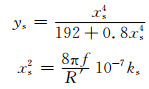
其中:f=50 Hz,为电缆工作频率;ks的值通过IEC-60287的附表 2可以查询.对于3根单芯电缆水平敷设,邻近效应系数:
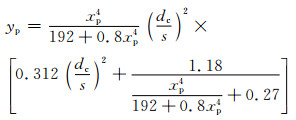 (2)
(2)
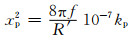
可以看出,趋肤效应和邻近效应的影响相对较小,芯线损耗主要由芯线的直径决定.电缆芯线直径越大,则芯线单位长度上的损耗功率越小.
1.2 绝缘损耗根据介质损耗公式,电缆的绝缘损耗可表示为
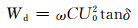 (3)
(3)
其中:ω=2πf; C为单位长度电缆电容; tanδ为介质损耗因数,在IEC-60287的附表 3中可查到.若为圆形导体则电容为
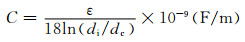
其中:ε为绝缘材料的介电系数; di为绝缘层直径, mm; dc为导体直径(如果有半导电屏蔽层则包含屏蔽层), mm.
1.3 金属护层损耗电缆的金属护层及铠装层损耗可由下式决定:
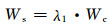 (4)
(4)
其中:Ws为单位长度护层有功功率损耗;λ1为金属护层损耗占芯线损耗的比值,即λ1=Ws/Wc.λ1包括环流损耗λ′1及涡流损耗λ″1,即λ1=λ′1+λ″1.
对于金属护层双端接地的情形,λ″1=0,只考虑环流损耗.针对3根电缆平行敷设,环流损耗按照下式计算:
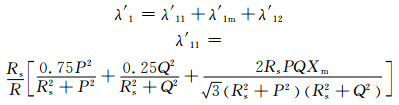 (5)
(5)
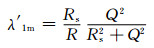 (6)
(6)
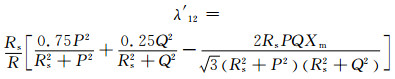 (7)
(7)
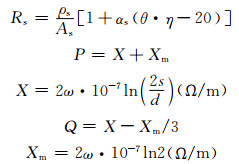
其中:λ′11及λ′12为两边两根电缆金属护层损耗;λ′1m为中间一根电缆金属护层损耗;Rs为护层单位长度电阻;ρs为金属护层电导率;As为金属护层截面积;αs为电阻温度系数;θ为导体工作温度;η为金属护层温度对导体温度的比例系数,一般取为0.75;s为两电缆芯线轴线间的距离; d= ds+dsemi2 /2, 为金属护套的平均直径.
对于金属护层交叉互联接地的情形, λ′1=0,只考虑涡流损耗.针对3根电缆平行敷设,金属护层交叉互联接地,根据IEC-60287提供的计算公式,涡流损耗为
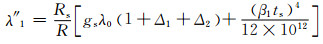 (8)
(8)
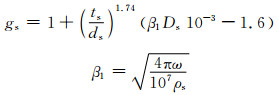
其中:ρs=0.028 264 Ω·m, 是金属护层材料(铝)工作温度下的电阻率; ts是金属护层厚度.对于水平敷设的3根单芯电缆,有:
对中间电缆:
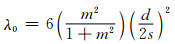 (9)
(9)
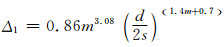 (10)
(10)
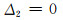 (11)
(11)
对外侧电缆相位超前侧:
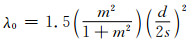 (12)
(12)
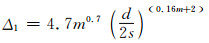 (13)
(13)
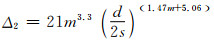 (14)
(14)
对外侧电缆相位滞后侧:
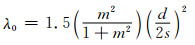 (15)
(15)
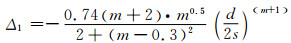 (16)
(16)
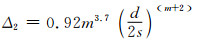 (17)
(17)
其中: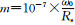
此例中110 kV电缆金属护层由皱纹铝套制成,其外部无铠装,故无铠装损耗.
1.4 损耗计算现选取一市场常见尺寸的110 kV单芯电缆YJLW02 64/110 1×630.电缆芯线为紧压绞合圆形导体,损耗计算时近似为圆形导体.电缆尺寸及计算所用参数如下:芯线(铜绞线)直径为30 mm;内半导体屏蔽层厚度为1 mm;XLPE绝缘层厚度为16.5 mm;外半导体屏蔽层厚度为1 mm;金属护层(皱纹铝套)厚度为2 mm;外护套(PVC)厚度为4.5 mm;电缆芯线标称截面积为630 mm2;芯线电流(三相相同)为1 164 A;绝缘层介质损耗因数为0.005;各相电缆轴心距离为150 mm.以3根电缆水平敷设、金属护层交叉互联接地、电缆芯线不交叉换位排布方式,按照以上公式计算,得出3种损耗分别为(3根电缆的总和):芯线损耗137.5 W/m,绝缘损耗3.9 W/m,金属护套损耗19.7 W/m;换算为每根电缆单位长度损耗为47.1 W/m.而以3根电缆水平敷设、金属护层两端接地、电缆芯线不交叉换位排布方式,按照以上公式计算,得出3种损耗分别为(3根电缆的总和):芯线损耗137.5 W/m,绝缘损耗3.9 W/m,金属护套损耗607.6 W/m;换算为每根电缆单位长度损耗为249.7 W/m.
由于金属护层为铠装,故没有铠装损耗.该型号电缆所涉及的其他部分(阻水层、半导电屏蔽层、沥青、外皮半导电涂料)厚度与损耗关系不大且其厚度有专门的设计考虑[8]不宜变动,故假定半导电屏蔽层厚度为固定值1 mm,其他部分厚度看做0.
由损耗计算结果可见芯线损耗和金属护套损耗占总损耗的绝大部分,而绝缘损耗相对微小,故以下分析仅考虑芯线损耗和金属护套损耗.
2 电缆材料成本根据电缆的型材,电缆单位长度的重量为各材料重量之和:
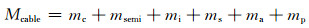 (18)
(18)
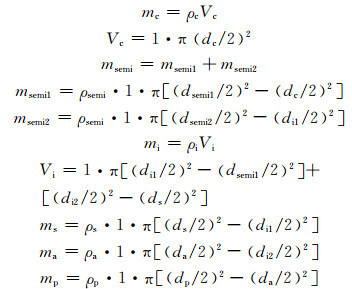
其中:mc为铜芯线质量;Vc为单位长度铜芯线体积(芯线为紧压绞合圆形导体,成本计算时近似为圆形导体);msemi为内外半导体屏蔽层重量之和;msemi1为内半导体屏蔽层重量;msemi2为外半导体屏蔽层重量;ρsemi为半导体材料密度;dsemi1为内半导体层外半径;dsemi2为外半导体层外半径;di1为内绝缘层外半径;mi为绝缘层质量; ρi为绝缘材料密度; Vi为内外两层绝缘层体积之和; ms为金属护层质量; ρs为金属护层材料密度;ma为铠装质量; ρs为金属护层材料密度;mp为PVC外皮质量; ρp为PVC材料密度.为研究方便起见,此处半导电屏蔽层的厚度定为定值tsemi=1 mm.
本文计算时所用材料的单位质量价格及材料密度参数列于表 1.
| 材料名称 | 密度/(g·cm-3) | 价格/(元·t-1) |
| 电解铜 | 8.9 | 29 000 |
| 半导电塑料 | 1.15 | 37 000 |
| 聚乙烯基料 | 0.95 | 9 200 |
| 电解铝 | 2.7 | 24 000 |
| 聚氯乙烯树脂 | 1.2 | 5 150 |
根据表 1数据,由下式可粗略计算单位长度电缆的材料成本:
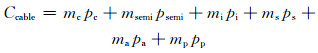 (19)
(19)
式中:pc、psemi、pi、ps、pa、pp分别为铜芯、半导体屏蔽层、绝缘体、金属护层、铠装层、PVC外皮材料质量单价.
为简单起见,计算忽略了材料损耗、生产加工成本,仅考虑了主要原材料成本.原材料成本中忽略了阻水层、沥青、外半导体涂层材料的成本.
3 电缆尺寸优化此处仍针对电压等级为110 kV的单芯电缆YJLW02 64/110 1×630,敷设方式为三相水平敷设,工作电压为110 kV,芯线电流为1 164 A,频率为工频50 Hz.根据国家标准GB/T 3956-2008[9],芯线电阻应不大于0.028 6 Ω/km,换算为芯线直径应不小于27.7 mm.
为了兼顾电缆的能效以及尺寸,可采用多对象最优化的方法(multiobjective optimization),将电缆损耗(Wcable)和电缆成本(Ccable)2项目标函数同时进行优化,在给定的限定条件下,最小化电缆损耗,同时最小化电缆成本.此例中的2个目标函数为
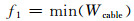 (20)
(20)
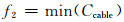 (21)
(21)
此优化问题变量繁多,因此多目标最优化是行之有效的方法.
多目标优化的计算方法包括最速下降法、共轭梯度法、鲍威尔法、罚函数法等,20世纪70年代以来,还出现了使用遗传算法进行优化的方法.由于遗传算法具有随机性强、搜索范围广等优点[1, 10],被广泛应用和研究,并形成了成熟的计算理论.本文采用基于Pareto集合的遗传算法多目标优化方法对电缆设计问题进行计算.
基于Pareto集合的遗传算法多目标优化的步骤为[11]:
1) 在给定的搜索空间内使用随机生成方法产生最初种群的坐标,并设置子代计数t=0.
2) 计算新生成种群的坐标处的目标函数值.
3) 将新生成的种群坐标和已有的种群坐标合并,筛选出非支配解进入繁殖过程.如果最小种群数量未达到,则在筛选剩下的坐标中选取其中的非支配解,直到最小种群数量达到为止.
4) 在步骤3挑选出的种群里随机选择一定数量的坐标作为亲代,根据遗传算法参数产生子代坐标.所产生的子代坐标中超出搜索空间范围的个体被抛弃.
5) 计算新生成的子代坐标处的目标函数值,在停止计算的条件还未达到时,返回步骤3,并使子代计数t=t+1.
根据上文模型,可以提取变量dc、di、ds、s和2个目标函数f1=min(Wcable)、f2=min(Ccable),通过遗传算法多目标最优化方法进行优化.遗传算法中的控制变量选取将影响结果的离散性及计算速度.本文计算所用控制变量列于表 2.
| 参数名称 | 值 | 含义 |
| 初始种群大小 | 300 | 开始计算时的起始种群个体数量 |
| Pareto占比 | 0.35 | 筛选一代种群进入Pareto集合的比例 |
| 基因置换率 | 0.8 | 繁殖时基因置换的比例 |
| 精英数量 | 2 | 不被淘汰直接进入下一代的个体数量 |
针对所涉及的4个变量,需要根据国家标准[7]及相关限制进行限定:
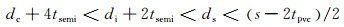 (22)
(22)
金属护层最小标称厚度为2 mm,则
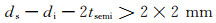 (23)
(23)
绝缘层最小标称厚度为16.5 mm,则
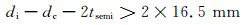 (24)
(24)
同时变量的取值范围需要根据国家标准及电缆适合安装的尺寸上限进行限定:27.7 mm < dc < 50mm;40 mm < di < 80 mm;46 mm < ds < 100 mm;100 mm < s < 1 000 mm.
根据上述参数及限制,依照上文建立的目标函数,根据2种不同的电缆接地方式,得出的Pareto集合图如图 2.图中同时标出了一种常见尺寸110 kV电缆所处的坐标(图中标记为Sample),该尺寸列于表 2中.

|
| 图 2 电缆损耗-成本多目标优化Pareto集合 Fig. 2 Cable loss-cost multiobjective optimized Pareto set |
由图 2可见,最优的结果分布于一条连续的曲线上,损耗功率为63~320 W/m(或23~56 W/m),电缆材料成本为210~560元/m(或210~540元/m).而所选取的一种常见尺寸的电缆均处于Pareto集合上端,即劣于最优解集.该常见尺寸110 kV电缆的尺寸参数、损耗、成本与2种优化尺寸电缆的对应参数对比,如表 3、4.表中cc、ci、cs、csemi、cp分别为铜芯、绝缘层、金属护层、半导体屏蔽层、PVC外皮层材料单位成本;Ws11、Ws1m、Ws12分别表示相位超前侧、中间、相位滞后侧电缆单位长度的金属护层损耗.
| 参数 | 常见 | 优化1 | 优化2 |
| dc/mm | 30.0 | 27.7 | 27.7 |
| di/mm | 63.0 | 60.7 | 60.8 |
| ds/mm | 69.0 | 67.3 | 71.1 |
| s/mm | 150.0 | 146.8 | 169.3 |
| cc/(元·m-1) | 182.4 | 155.6 | 155.8 |
| ci/(元·m-1) | 19.2 | 18.3 | 18.3 |
| cs(元·m-1) | 27.3 | 30.3 | 56.7 |
| csemi/(元·m-1) | 12.7 | 12.0 | 12.1 |
| cp/(元·m-1) | 6.4 | 6.3 | 6.6 |
| Wc/(W·m-1) | 137.4 | 157.8 | 157.3 |
| Ws11/(W·m-1) | 267.2 | 254.8 | 161.1 |
| Ws1m/(W·m-1) | 161.9 | 162.1 | 131.0 |
| Ws12/(W·m-1) | 178.5 | 171.6 | 123.8 |
| Wcable/(W·m-1) | 248.3 | 248.8 | 191.1 |
| Ccable/(元·m-1) | 248.0 | 222.5 | 249.5 |
| 参数 | 常见 | 优化1 | 优化2 |
| dc/mm | 30.0 | 29.5 | 29.9 |
| di/mm | 63.0 | 62.8 | 63.9 |
| ds/mm | 69.0 | 68.8 | 70.0 |
| s/mm | 150.0 | 310.6 | 320.1 |
| cc/(元·m-1) | 182.4 | 176.6 | 181.2 |
| ci/(元·m-1) | 19.2 | 19.2 | 20.0 |
| cs/(元·m-1) | 27.3 | 27.6 | 27.9 |
| csemi/(元·m-1) | 12.7 | 12.6 | 12.8 |
| cp/(元·m-1) | 6.4 | 6.4 | 6.5 |
| Wc/(W·m-1) | 45.8 | 46.9 | 45.8 |
| Ws11/(W·m-1) | 3.6 | 0.8 | 0.8 |
| Ws1m/(W·m-1) | 13.1 | 3.0 | 3.0 |
| Ws12/(W·m-1) | 3.0 | 0.7 | 0.7 |
| Wcable/(W·m-1) | 47.1 | 47.1 | 46.1 |
| Ccable/(元·m-1) | 248.0 | 242.4 | 248.4 |
由表 3、4可见,对于交叉互联接地电缆,优化尺寸仅略微好于常见尺寸;而对于两端接地电缆,优化尺寸较明显好于常见尺寸,也即优化后的尺寸能够较好地降低环流损耗较大时的电缆成本.实际电缆使用中,高压110 kV电缆多采用交叉互联接地方式,双端接地情况不会出现.实际中由于电缆分段长度不均、三相负载不平衡等情况,会出现一定大小的环流.此优化方法对于含有一定环流的交叉互联接地电缆亦具有现实意义.
电缆每相之间的间距s也是变量之一,而此间距在电缆设计时通常并没有考虑.故厂家生产电缆时,可与电缆使用方沟通,根据电缆的实际敷设要求、节能要求来综合考虑,决定最终生产尺寸,亦即定制化生产.
由于电缆一经安装通常将投入运行10年以上,从广义的成本角度,其运行中的电能损耗成本也应考虑到成本计算中.严格而言,电缆的使用年限也和其绝缘老化速度有关,且电缆退役后回收亦能收回部分成本,同时购买成本还应计入通货膨胀因素等[12].现为研究方便起见,按照每度发电价格0.2元的成本,以10年为固定使用期限,回收价格按照原材料(铜、铝)售价的70%考虑,考察单一目标广义成本优化问题,则广义成本C′cable可定义为
 (25)
(25)
其中:y=10×365×24 h, 为使用10年所含小时数;pe=0.2/1 000元/ W·h,为每瓦时电能发电成本;C′cable为算入电能损耗后的广义成本.下面放开电缆尺寸的上限(即芯线、绝缘层、金属护层的直径最大值),应用多变量条件最值的线性逼近法可求出使得广义成本最小的最优解.此最优解的电缆尺寸、各部分损耗及成本连同之前的3组电缆相关数据如表 5、6所示.
| 参数 | 常见 | 优化1 | 优化2 | 最优解 |
| dc/mm | 30.0 | 27.7 | 27.7 | 55.0 |
| di/mm | 63.0 | 60.7 | 60.8 | 88.0 |
| ds/mm | 69.0 | 67.3 | 71.1 | 148.7 |
| s/mm | 150.0 | 146.8 | 169.3 | 950 |
| Wcable/(元·m-1) | 248.3 | 248.8 | 191.1 | 31.8 |
| Ccable/(元·m-1) | 248.0 | 222.5 | 249.5 | 1 387.6 |
| C′cable/(元·m-1) | 4 452.3 | 4 450.5 | 3 448.6 | 1 017.2 |
| 注:由于s≥950 mm后广义成本值随s的变化极小,可忽略,故可认为950 mm是最优解的s值. | ||||
| 参数 | 常见 | 优化1 | 优化2 | 最优解 |
| dc/mm | 30.0 | 29.5 | 29.9 | 54.5 |
| di/mm | 63.0 | 62.8 | 63.9 | 87.5 |
| ds/mm | 69.0 | 68.8 | 70.0 | 93.5 |
| s/mm | 150.0 | 310.6 | 320.1 | 1 000.0 |
| Wcable/(元·m-1) | 47.1 | 47.1 | 46.1 | 19.6 |
| Ccable/(元·m-1) | 248.0 | 242.4 | 248.4 | 696.7 |
| C′cable/(元·m-1) | 925.6 | 925.3 | 909.6 | 592.9 |
由比较的结果可知,考虑了广义成本之后所得出的最优电缆方案,在2种接地方式下,相对于常见110 kV电缆而言,在10年使用寿命内分别节省3 435和333元/m,约节省了77%和36%的广义成本.最优方案的电缆总直径比常见电缆大约80和25 mm.最优化方案需要电缆的敷设宽度达到s=950 mm和s=1 000 mm以上,这一点在工程上会额外增加敷设成本和难度.在实际110 kV电缆安装中,由于接地方式通常为带一定三相不平衡的交叉互联接地(电缆分3段交叉互联,每个交叉互联大单元双端接地),所以所节约的成本应在以上2个结果之间,且主要偏向三相平衡交叉互联接地的结果.
固定变量s为定值300 mm,仅针对与电缆制造尺寸相关的3个变量dc、di、ds进行分析.由于变量已经减少到3个,在求出最优解的同时,可以画出以dc、di、ds为坐标轴的三维广义成本分布图,见图 3.图 3(a)中,表示数据值的实心圆的半径设定为10/ 0.001×C′cable 2,图 3(b)中,圆的半径设定为1/ 0.001×C′cable 2,因此广义成本越低,圆的半径越大.根据线性逼近法可求得在s=300 mm时,广义成本最优尺寸分别为:dc=54.7 mm, di=89.7 mm, ds=149.7 mm(两端接地); dc=53.4 mm, di= 88.4 mm, ds=94.4 mm(交叉互联接地).其10年广义成本分别为1 024.5元/m(两端接地)和612.4元/m(交叉互联接地).由于电缆相间敷设距离s受到电缆沟开挖宽度、已建成电缆沟槽宽度、拓宽改造成本的限制,实际中s的距离通常达不到上述最优化方案给出的长度,故根据有限的s设计电缆尺寸是更加切实的做法.

|
| 图 3 固定s下电缆广义成本分布图 Fig. 3 Distribution of generalized cost of cable with fixed s |
电缆芯线、护层流过电流,由于芯线、护层电阻的作用会产生热量,使得电缆温度升高.温度过高时会加速电缆绝缘老化.而本文优化后电缆产生的热量低于常见尺寸电缆,在保护电缆绝缘方面更具优势.
4 结论应用遗传算法多目标优化方法,计及电缆的损耗、材料成本及电能损耗成本,本文考察了电力系统高压电缆的尺寸最优化问题,结果显示,在满足国家标准的范围内,市场常见的110 kV电缆距离低损耗、低成本的最优解集仍有一定的距离,仍具有改进空间,可以通过适当修改尺寸将损耗和成本同时降低.分析电缆尺寸优化问题时不仅应考虑电缆材料和制造成本,同时还应考虑计及电缆生命周期中的运行损耗成本的“广义成本”.本文也给出了简单假设下“广义成本”最低的110 kV电缆尺寸,以供参考.本文主要价值在于,指出了电缆存在损耗和成本可优化的问题,并举例进行计算.在全球定制化生产的趋势下,根据电缆实际敷设情况最优化地生产相应电缆,可以进一步达到节能降耗的目标.
| [1] |
郑金华. 多目标进化算法及其应用[M]. 北京: 科学出版社, 2007. Zheng Jinhua. Multi-objective Evolutionary Algorithms and Applications[M]. Beijing: Science Press, 2007. |
| [2] |
张葛祥, 金炜东, 胡来招. 多变量系统中多参数多目标满意优化研究[J]. 信息与控制, 2003, 32(6): 481-485. Zhang Gexiang, Jin Weidong, Hu Laizhao. Multi-parameter multi-objective optimization research in multi-variable system[J]. Information and Control, 2003, 32(6): 481-485. DOI:10.3969/j.issn.1002-0411.2003.06.001 |
| [3] |
杨洪山, 汤晶, 陈家训. 应用神经网络和遗传算法实现多变量离散系统优化[J]. 计算机仿真, 2005, 22(12): 118-120. Yang Hongshan, Tang Jin, Chen Jiaxun. Applying neural network and genetic algorithm to discrete multi-variable system optimization[J]. Computer Simulation, 2005, 22(12): 118-120. DOI:10.3969/j.issn.1006-9348.2005.12.035 |
| [4] |
梁永春, 柴进爱, 李彦明, 等. 有限元法计算交联电缆涡流损耗[J]. 高电压技术, 2007, 33(9): 196-199. Liang Yongchun, Chai Jin'ai, Li Yanming, et al. Finite element method applied to crosslinked transmission cable eddy current loss[J]. High Voltage Technology, 2007, 33(9): 196-199. DOI:10.3969/j.issn.1003-6520.2007.09.044 |
| [5] |
刘英. 高压电缆金属护套及铠装结构的损耗计算[J]. 电线电缆, 2013(2): 1-3, 20. Liu Ying. High voltage cable insulating shield and metal sheath loss calculation[J]. Wires and Cables, 2013(2): 1-3, 20. DOI:10.3969/j.issn.1672-6901.2013.02.001 |
| [6] |
IEC60287-1-1(2006.12), Part 1-1: Current Rating Equations (100% Load Factor) and Calculation of Losses-General[S].
|
| [7] |
GB/T11017.1-2014额定电压110 kV(Um=126 kV)交联聚乙烯绝缘电力电缆及其附件[S]. GB/T11017.1-2014 110 kV Crosslinked Polyethylene Insulated Power Cable and Accessories[S]. |
| [8] |
鄢薇, 甄建, 薛志刚. 可交联PE电缆用半导电屏蔽料开发现状[J]. 合成树脂及塑料, 2012(4): 75-79. Yan Wei, Zhen Jian, Xue Zhigang. Crosslinked PE cable insulating material development status review[J]. Synthesized Resin and Plastic, 2012(4): 75-79. DOI:10.3969/j.issn.1002-1396.2012.04.020 |
| [9] |
GB/T3956-2008/IEC 60228: 2004电缆的导体[S]. GB/T3956-2008/IEC 60228: 2004 Conductor of Cables[S]. |
| [10] |
Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. |
| [11] |
Coelho L, Mariani V, Guerra F, et al. Multiobjective optimization of transformer design using a chaotic evolutionary approach[J]. IEEE Transactions on Magnetics, 2014, 50(2): 669-672. DOI:10.1109/TMAG.2013.2285704 |
| [12] |
刘刚, 曹京荥, 陆莹, 等. 以全寿命周期成本为判据的近海风电场高压海底电缆选型标准[J]. 高电压技术, 2015, 41(8): 2674-2680. Liu Gang, Cao Jingxing, Lu Ying, et al. Life-cycle cost based near-sea wind power plant underwater cable selection criteria[J]. High Voltage Technology, 2015, 41(8): 2674-2680. |
 2018, Vol. 51
2018, Vol. 51




