文章信息
- 刘志勇, 刘富峰, 柳卓, 梁兴, 刘梅清
- LIU Zhiyong, LIU Fufeng, LIU Zhuo, LIANG Xing, LIU Meiqing
- “V”形输水管道爆管过渡过程分析与事故控制策略优化
- Pipe bursting transients analysis and accident control strategy optimization for a water delivery pipeline with V-shaped longitudinal profile
- 武汉大学学报(工学版), 2019, 52(8): 659-665
- Engineering Journal of Wuhan University, 2019, 52(8): 659-665
- http://dx.doi.org/10.14188/j.1671-8844.2019-08-001
-
文章历史
- 收稿日期: 2019-03-13
2. 中工武大设计研究有限公司,湖北 武汉 430079;
3. 南昌工程学院,江西 南昌 330099
2. CAMCE WHU Design & Research Co., Ltd., Wuhan 430079, China;
3. Nanchang Institute of Technology, Nanchang 330099, China
水锤是管道输水系统由一种稳定状态过渡到另一种稳定状态的暂态水力现象,众多学者对此进行了研究[1-7].工程实践中,尽管大多数管道输水系统均在设计阶段进行了水锤计算和防护措施设计,但爆管事故仍时有发生,有些甚至发生在稳定运行状态.究其原因,除了水锤防护措施不够完善外,还包括[8]:1)自然因素,如地震、洪水等.2)人为因素,如在管线上方进行大型机械土方开挖.3)管体制作因素,如PCCP管(prestressed concrete cylinder pipe, PCCP)外层保护砂浆出现裂缝,导致预应力钢丝受地下水腐蚀出现断裂;玻璃钢夹砂管由于纤维层含有杂质颗粒、管道材质不均匀导致管道存在薄弱部位等.4)管道施工因素,如管体承插口橡胶密封不严,管线基础施工不稳定等.常规的水锤分析一般都是在假定管道完整的条件下,计算出管道中可能出现的最大、最小水锤压力,为管道承压能力和水锤防护措施的选择提供依据,对爆管水力过渡过程的研究相对较少[9],部分学者对基于水力分析的爆管诊断方法进行了研究[10-14].
对于具有“V”形纵剖面布置的输水管线,由于管线中部与上下游两端存在较大高差且坡度较陡,当管线中部低点因外部因素发生较大面积的破裂时,大量流体将从爆管处流出,在管线中诱发剧烈的水力过渡过程.一方面,爆管外泄流量将远大于管线的正常输水流量,可能对周围的正常生产和生活秩序造成影响,甚至威胁到生命和财产安全;另一方面,管线中的流速可能超过隔断阀操作所允许的极限流速,导致隔断阀不能及时关闭,事故无法得到及时控制;另外,如果隔断阀的关闭规律不合理,有可能因关阀出现2次爆管,使事故进一步扩大.因此,对“V”形输水管道重点部位的爆管水力过渡过程分析应给予足够的重视.本文基于瞬变流基本理论,结合工程实例,对不同爆管位置、爆管面积、爆管历时条件下的爆管水力过渡过程进行了数值模拟,在此基础上,提出了隔断阀关闭规律的优化模型和求解方法,研究了关闭滞后时间对爆管控制效果的影响,为工程实例提出了科学合理的爆管事故处理预案.
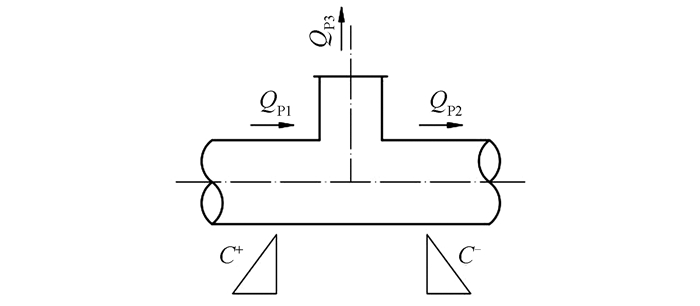
1 数学模型 1.1 爆管边界条件发生爆管时,主管内的流体从爆管点外泄,其水锤计算的边界条件可概化为图 1所示.根据水锤基本理论[2],其数学模型建立如下:
|
| 图 1 爆管点边界条件概化图 Fig. 1 Boundary condition of pipe bursting point |
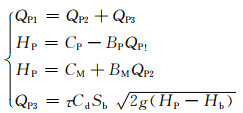 (1)
(1)
式中:QP1、QP2、QP3分别为爆管点上游瞬态流量、下游瞬态流量、外泄瞬态流量;HP为爆管点主管瞬态测压管水头;τ为水力开度;Cd为流量系数;Sb为爆管面积;Hb为爆管点管外测压管水头,其与爆管点高程和管道覆土厚度有关;CP、BP、CM、BM为常数,与管径、水锤波速、爆管点上、下游前一时刻的流量和压力相关.
1.2 隔断阀关闭规律优化模型发生爆管后,最直接的事故控制手段就是关闭爆管点上下游的隔断阀.隔断阀关闭速度越快,外泄流量越小,但可能会因隔断阀的关闭产生新的水锤压力.因此,应对爆管点上、下游隔断阀的关闭规律进行优化.
1.2.1 决策变量上、下游隔断阀采用具有两阶段关闭功能的液控蝶阀或球阀时,决策变量有8个.分别是:上游阀门的快关时间T11、快关角度θ11、慢关时间T12、慢关角度θ12;下游阀门的快关时间T21、快关角度θ21、慢关时间T22、慢关角度θ22.
1.2.2 目标函数控制外泄流量和过阀流速、防止隔断阀关闭过程中的2次水锤是爆管事故处理应注意的2个方面.因此,目标函数可表示为
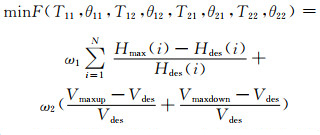 (2)
(2)
式中:i为计算节点编号;N为计算节点总个数;Hmax(i)为节点最大水锤压力;Hdes(i)为节点设计承压;Vmaxup、Vmaxdown分别为上、下游阀最大过阀流速;Vdes为阀门的最大允许流速;ω1、ω1为权重系数.当Hmax(i) < Hdes(i)时,令Hmax(i)-Hdes(i)=0;当Vmaxup < Vdes时,令Vmaxup-Vdes=0;当Vmaxdown < Vdes时,令Vmaxdown-Vdes=0.
1.2.3 约束条件约束条件包括系统约束、决策变量上下限约束.
1) 系统约束:瞬变流的基本方程、各过流元件的边界条件、爆管点的边界条件、液柱分离模型等.
2) 决策变量上下限约束:各决策变量的取值必须在阀门所允许的范围内,关阀总时长应在阀门允许的范围内,阀门快关速度应大于慢关速度.
1.2.4 基于免疫粒子群算法的优化模型求解采用免疫粒子群算法(IAPSO)[15, 16]对前述优化模型进行求解,具体步骤包括:①随机产生符合约束条件的粒子母群,并随机分配粒子速度向量;计算粒子母群中各粒子所对应的适应度值.②根据适应度值记录各粒子的历史最佳位置和对应的适应度值,并记录粒子母群的历史最佳位置和对应的适应度值.③对粒子母群参数进行动态调整,更新各粒子的位置和速度,产生新一代种群;判断是否满足约束条件,不满足条件的用随机产生的新粒子替代,并计算相应适应度值.④根据适应度值的优劣,将粒子母群分为克隆变异、疫苗接种和优胜劣汰三部分;利用克隆变异算子、疫苗接种算子和优胜劣汰算子生成新的粒子群,根据适应度值和约束条件,更新或保留原母群中的粒子,形成新的粒子群.⑤判断是否满足收敛条件,若满足,输出结果;若不满足,转向第②步,重新计算,直到满足收敛条件.
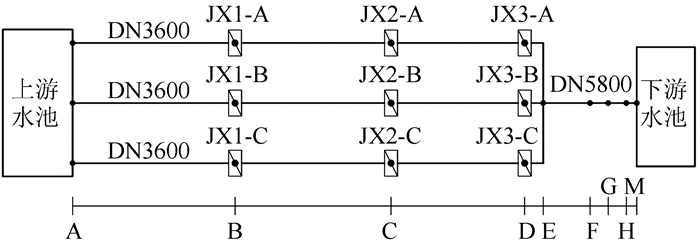
2 爆管过渡过程的影响因素分析 2.1 工程概况东北地区某重力流输水系统布置如图 2所示.设计输水流量42 m3/s;上、下游水池水位分别为225.68、214.49 m;管线全长36 km,其中AE段由3条DN3600的管道(A、B、C线)并联组成,在E点汇流后经1条DN5800的管道(隧洞)流入下游水池,各管段的参数如表 1所示.受地形限制,管线纵剖面呈“V”形布置,如图 3所示,管线最低点的管中心高程为130.23 m,比下游出水池水位低84.26 m.考虑到检修和事故控制的需要,在B、C和D点分别设置了3处隔断阀,将管线中的PCCP管(AD段)划分为9个爆管控制单元(每条并联管各3个).
|
| 图 2 输水系统布置示意图 Fig. 2 Sketch of water delivery system layout |
| 管段名称 | 起止桩号 | 管长/m | 管径/mm | 管材 | 并联安装根数 |
| AB | 0+000~9+596 | 9 596 | 3 600 | PCCP | 3 |
| BC | 9+596~19+722 | 10 126 | 3 600 | PCCP | 3 |
| CD | 19+722~30+065 | 10 343 | 3 600 | PCCP | 3 |
| DE | 30+065~30+146 | 81 | 3 600 | 钢管 | 3 |
| EF | 30+146~33+526 | 3 380 | 5 800 | 隧洞 | 1 |
| FG | 33+526~34+689 | 1 163 | 5 800 | 钢管 | 1 |
| GH | 34+689~35+764 | 1 075 | 5 800 | 隧洞 | 1 |
| HM | 35+764~36+009 | 245 | 5 800 | 钢管 | 1 |
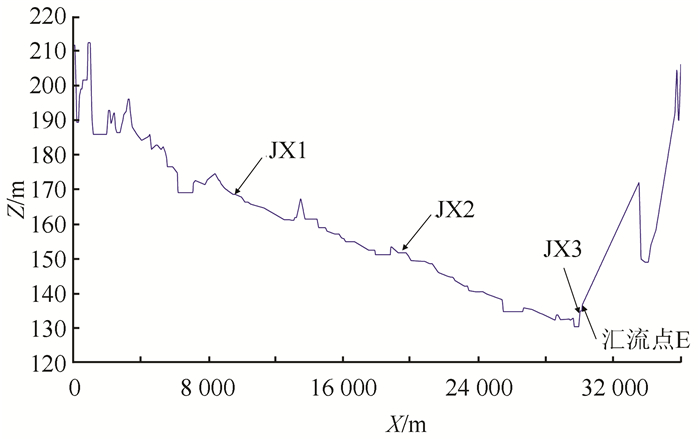
|
| 图 3 输水管线纵剖面图 Fig. 3 Longitudinal profile of water delivery pipeline |
理论上,受管体制作和安装因素的影响,爆管在任何位置都可能发生,且爆管面积、爆管历时(爆管发生到爆管面积最大的时间)均具有不确定性.以下以CD段(隔断阀JX2和JX3之间的管段)中的A线发生爆管时为例,对该输水系统的爆管水力过渡过程进行计算分析.
2.2 爆管位置的影响假定图 2中CD段的A线不同位置发生全断面面积的瞬间爆管,隔断阀不动作时,爆管点最大外泄流量Qmax和爆管点上、下游隔断阀(JX2-A和JX3-A)最大过阀流速Vmaxup、Vmaxdown随爆管点桩号Xb和高程Zb变化的情况如表 2和图 4所示.
| Xb/m | Zb/m | Vmaxup/(m·s-1) | Vmaxdown/(m·s-1) | Qmax /(m3·s-1) |
| 19+920 | 150.29 | 4.69 | 5.89 | 107.00 |
| 21+920 | 145.36 | 4.58 | 6.75 | 115.05 |
| 23+920 | 140.33 | 4.55 | 7.95 | 126.89 |
| 25+920 | 134.58 | 4.44 | 9.75 | 144.32 |
| 27+920 | 133.63 | 4.16 | 12.59 | 169.60 |
| 29+920 | 130.23 | 3.71 | 19.98 | 236.12 |
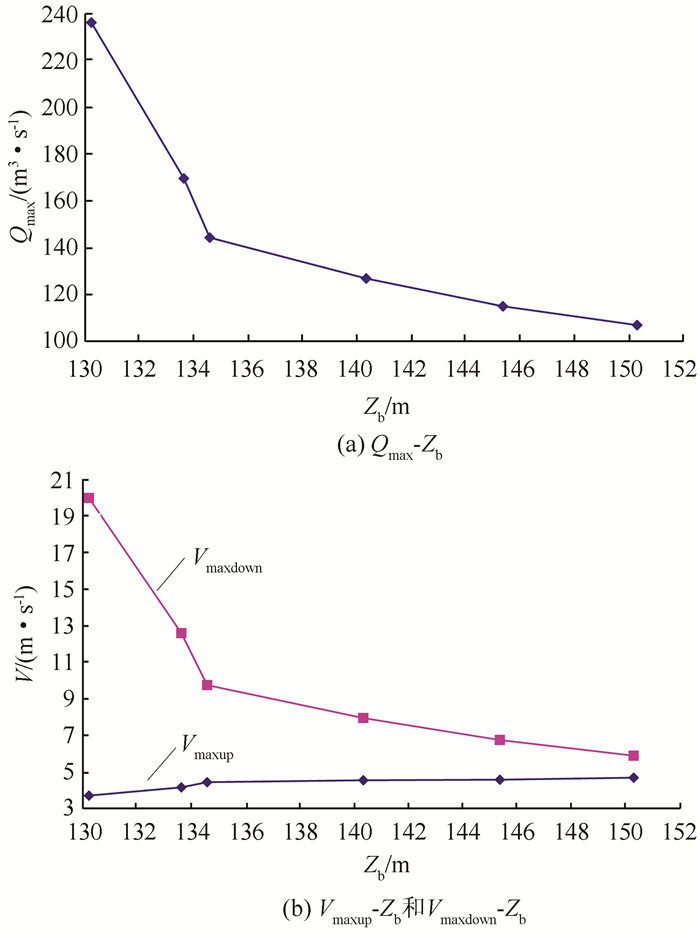
|
| 图 4 最大外泄流量和最大过阀流速随爆管位置的变化 Fig. 4 Change of maximum values of escaping flow and flow velocity across valves for different pipe-bursting positions |
由于爆管点和上下游水池之间的落差分别达到95.45、84.26 m,当管线最低点发生全断面爆管时,因爆管点离下游水池较上游水池近,一方面,下游水池的水通过汇流点(E点)和下游阀JX3-A向爆管点外泄,另一方面,上游水池的水既通过A线和上游阀JX2-A向爆管点外泄,同时也通过B线和C线经E点和下游阀JX3-A向爆管点外泄.因此,从表 2和图 4可以看出:①爆管点高程越低,爆管点的最大外泄流量越大.当管线最低点发生全断面爆管时,爆管点的最大外泄流量达到236.12 m3/s,远大于管线的正常输水流量.②爆管点高程越低,爆管点离下游越近,下游阀JX3-A的最大反向流速越大,受下游顶托,上游阀JX2-A的最大正向流速越小,且JX3-A的最大反向流速大于JX2-A的正向流速.当管线最低点发生全断面爆管时,JX3-A的最大反向流速达到19.98 m/s,高于隔断阀操作所允许的极限流速15 m/s,该阀门无法关闭.
2.3 爆管面积的影响假定图 2中CD段的A线最低处发生不同爆管面积Sb(按主管过流面积的百分比计)的瞬间爆管,隔断阀不动作时,爆管点最大外泄流量Qmax、上下游隔断阀(JX2-A和JX3-A)最大过阀流速Vmaxup和Vmaxdown、管线AE段中A、B线最大水锤压力HAmax和HBmax随爆管面积Sb变化的情况如图 5所示.
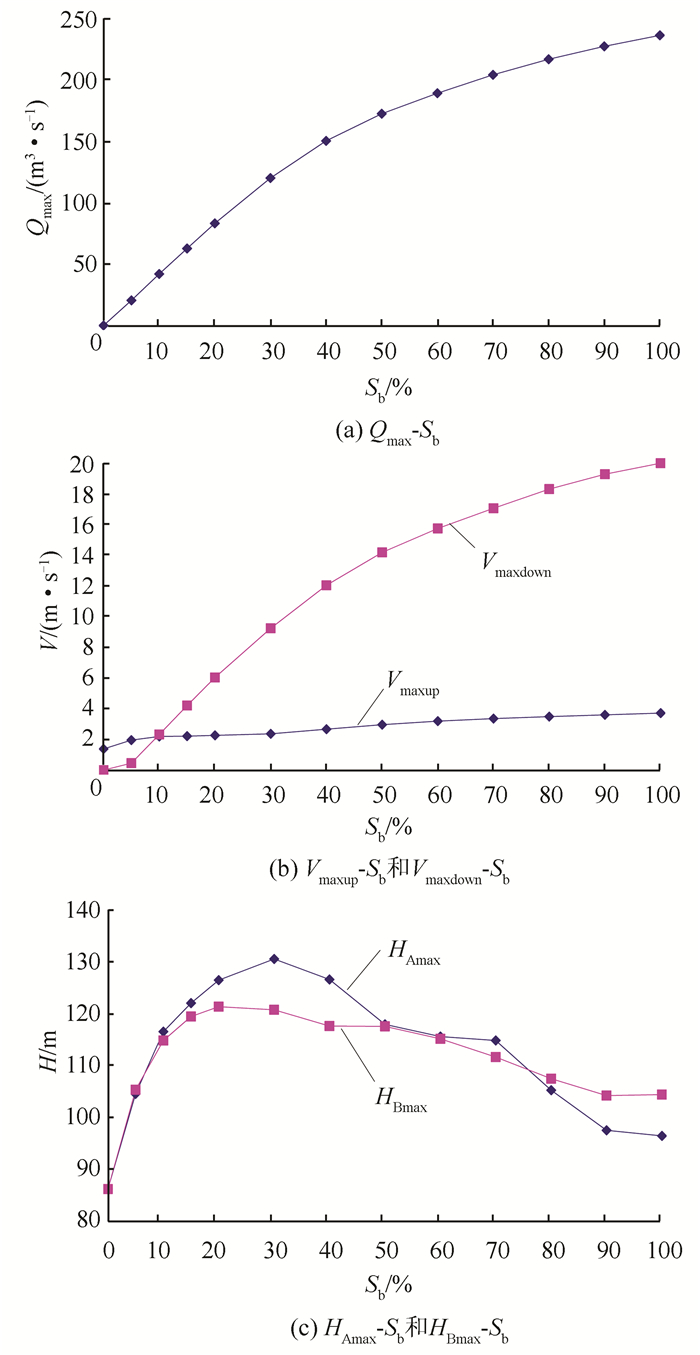
|
| 图 5 最大外泄流量、最大过阀流速和最大水锤压力随爆管面积的变化 Fig. 5 Change of maximum values of escaping flow, flow velocity across valves and water hammer pressure for different pipe-bursting areas |
从图 5可以看出:①爆管点最大外泄流量Qmax随爆管面积Sb的增大而增大.②上下游隔断阀的最大过阀流速Vmaxup和Vmaxdown随Sb的增大而增大,且由于下游水池和上游B、C线中的水均通过下游阀外泄,Vmaxdown增大更快.③随着Sb的增大,A、B线中的最大水锤压力HAmax和HBmax呈现“先增大、后减小”的趋势,这是因为:发生爆管后,爆管点产生的降压波分别向上下游传播,到达上下游水池后反射为升压波,由于爆管点距下游水池较近,若Sb较小,从下游水池首先反射回的升压波可以穿过爆管点,与从上游反射回的升压波在某点相遇,出现升压波的叠加,形成较大的压力升高;当Sb增大到一定值后,从下游水池反射回的升压波在爆管点得到释放,其向上游传播形成的叠加效应减小或消失.因此,爆管点既是水锤发生的根源,又对从上下游水池反射回的升压波具有释放作用.
2.4 爆管历时的影响假定CD段的A线最低处发生全断面面积爆管,隔断阀不动作时,不同爆管历时tb(爆管过程经历的时间)条件下的水力过渡过程计算结果如表 3所示.
| tb /s | Vmaxup/(m·s-1) | Vmaxdown/(m·s-1) | Qmax/(m3·s-1) | HAmax/m | HBmax/m |
| 0 | 3.71 | 19.98 | 236.12 | 96.49 | 104.44 |
| 0.5 | 3.71 | 19.98 | 236.12 | 96.21 | 103.80 |
| 1 | 3.71 | 19.96 | 236.06 | 95.66 | 103.22 |
| 2 | 3.71 | 19.95 | 235.74 | 95.40 | 102.55 |
| 5 | 3.70 | 19.93 | 235.22 | 95.10 | 102.10 |
从表 3可以看出:爆管历时tb越长,管线中的流速变化越缓,因此,管线中的最大水锤压力随着爆管历时的延长而减小.但由于爆管历时一般很短,当tb < 5 s时,其对水锤压力的影响不显著,上下隔断阀的最大过阀流速和爆管点最大外泄流量随爆管历时的变化也很小.
3 爆管事故控制策略优化 3.1 无滞后时间条件下的隔断阀关闭规律优化假定发生爆管后,上下游的隔断阀立即开始关闭.由于隔断阀的阻力系数在大开度时随开度的变化不大,在小开度时随开度的减小增大较快,因此,隔断阀的两阶段关闭比线性关闭更有利于控制爆管点上游阀的最大正向流速和下游阀的最大反向流速,且关闭越快,过阀流速越小,外泄流量越小.对爆管点上游来说,关闭隔断阀产生的正压波可与爆管产生的负压波相互抵消,因此,合理的两阶段关闭比线性关闭产生的水锤压力小;对爆管点下游来说,关闭隔断阀产生的负压波与爆管产生的负压波相互叠加,因此,隔断阀关闭越快,负压波传播至下游水池后反射回的正压波越大,产生的水锤压力也越大.
对图 2所示系统,根据阀门技术资料,隔断阀所允许的最快关闭总时长为600 s,最慢关闭总时长为900 s,可两阶段关闭,最快关闭速率为30 s/70°.采用前述隔断阀关闭规律的优化模型和求解方法,计算得到当CD段的A线在隔断阀JX2和JX3之间爆管时,上游隔断阀JX2的关闭规律为30 s/70°、570 s/20°,下游隔断阀JX3的关闭规律为30 s/32°、570 s/58°.
图 6为该条件下的爆管水力过渡过程计算结果.图中:HGL为初始测压管水头线;HAmin、HBmin分别为A、B线中的最小水锤压力,Vup和Vdown分别为上下游隔断阀过阀流速,其余符号意义同前.从图 6可以看出,隔断阀的最大过阀流速和管线最大水锤压力均可控制在允许范围内.
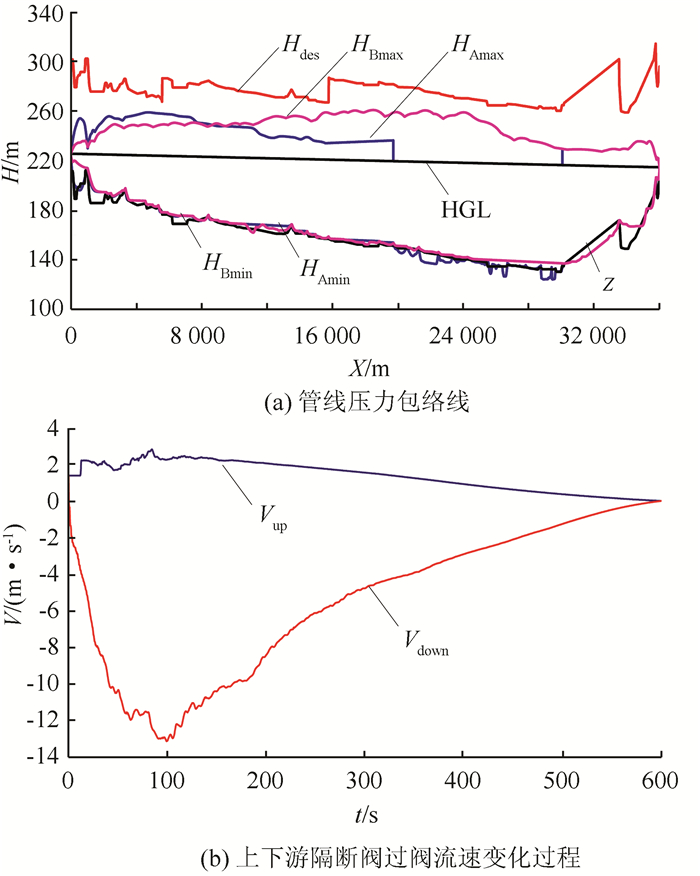
|
| 图 6 无滞后时间条件下的爆管水力过渡过程计算结果(隔断阀两阶段关闭) Fig. 6 Transients calculation results for case of two-phase closing valve under no lag-time condition |
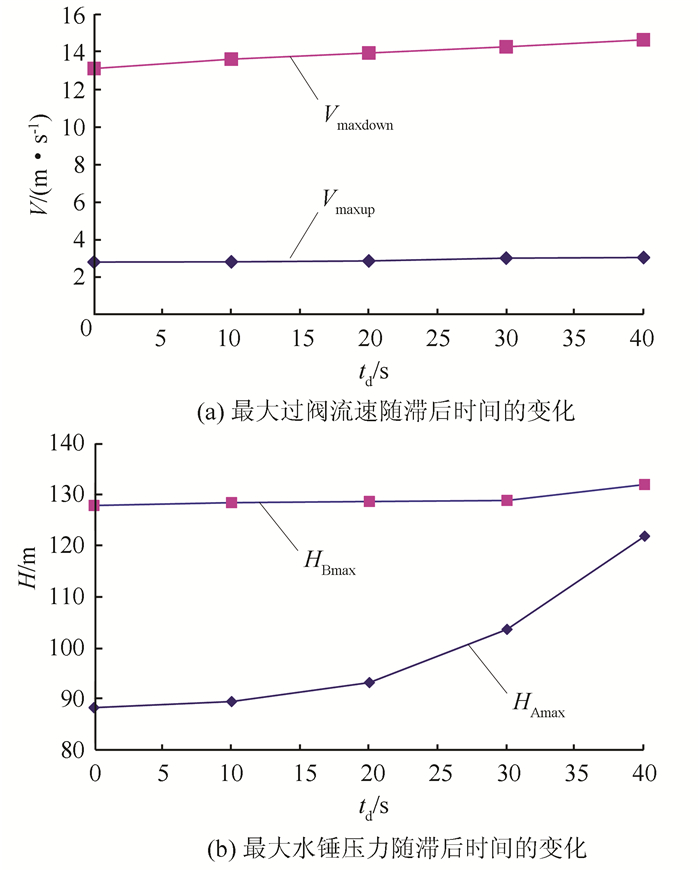
发生爆管后,需要一定的时间判断发生爆管的管段,然后操作相应的隔断阀.对于安装有爆管诊断程序的输水系统,隔断阀开始关闭滞后于爆管发生的时间td决定于以下4个因素:①爆管产生的压力和流量突变信号到达传感器的最不利时间t1,取决于爆管点和传感器之间的距离和水锤波速;②传感器采集信号后传输至数据库的时间t2;③管道爆管诊断程序读取数据、执行程序、反馈结果、发送阀门操作指令的时间t3;④考虑爆管发生时刻和爆管诊断程序运行时刻差异的冗余时间t4.对于图 2所示的系统,不同滞后时间条件下的过渡过程计算结果如图 7所示.
|
| 图 7 隔断阀不同关闭滞后时间下的过渡过程计算结果 Fig. 7 Transients calculation results under different valve-closure lag-time conditions |
从图 7可以看出,隔断阀关闭滞后时间越长,过阀流速越大;对图 2中的A线来说,滞后时间越长,隔断阀关闭时的正向流速越大,水锤压力也越大;对图 2中的B线来说,由于爆管点距下游水池很近,水流很快开始倒流,滞后时间对最大水锤压力的影响较小.
根据上述分析,滞后时间td越短,隔断阀动作越及时,越有利于爆管事故的控制.因此,应尽可能从上述4个方面去缩短td.
4 结论1)“V”形重力流输水管道低点爆管时,外泄流量将远大于正常输水流量.因此,宜根据重点部位爆管水力过渡过程的分析计算,确定隔断阀的关闭程序.
2) 爆管位置、爆管面积和爆管历时具有不确定性.爆管位置越低和爆管面积越大,外泄流量越大;爆管点既是水锤源,又具有泄压作用,最大水锤压力随爆管面积的增大呈现“先增大、后减小”趋势;由于爆管历时一般很短,其对水锤压力的影响不显著.
3) 控制外泄流量,防止隔断阀关闭过快造成2次水锤是爆管事故处理应注意的2个方面,两者相互矛盾.本文提出了以上下游隔断阀关阀序律参数为决策变量、以管线水锤压力和上下游隔断阀过阀流速最小为目标函数的爆管调控优化模型,并采用免疫粒子群算法求解.工程实例应用表明:该模型可以在保证管道安全的前提下,尽快关闭阀门,减小爆管损失.
4) 隔断阀动作滞后时间对爆管事故控制有较大影响.爆管发现越早,隔断阀动作越早,事故控制越有效.因此,重要的管道输水系统宜建设爆管诊断系统,以尽量缩短隔断阀动作滞后时间.
| [1] |
Chaudhry M H. Applied Hydraulic Transients[M]. Third Edition. Springer New York Heidelberg Dordrecht London, 2014.
|
| [2] |
Wylie E B, Streeter V L, Suo Liseng. Fluid Transient in Systems[M]. Prentice Hall, Englewood Cliffs, New Jersey, 1993.
|
| [3] |
Wang Chao, Yang Jiandong. Water hammer simulation using explicit-implicit coupling methods[J]. Journal of Hydraulic Engineering, 2015, 141(4): 04014086. DOI:10.1061/(ASCE)HY.1943-7900.0000979 |
| [4] |
Wu Dazhuan, Yang Shuai, Wu Peng, et al. MOC-CFD coupled approach for the analysis of the fluid dynamic interaction between water hammer and pump[J]. Journal of Hydraulic Engineering, 2015, 141(6): 06015003. DOI:10.1061/(ASCE)HY.1943-7900.0001008 |
| [5] |
杨开林. 长距离输水水力控制的研究进展与前沿科学问题[J]. 水利学报, 2016, 47(3): 424-435. Yang Kailin. Review and frontier scientific issues of hydraulic control for long distance water diversion[J]. Journal of Hydraulic Engineering, 2016, 47(3): 424-435. |
| [6] |
王焰康, 张健, 何城. 长距离重力流输水工程的关阀方案优化[J]. 人民黄河, 2017, 39(5): 131-134. Wang Yankang, Zhang Jian, He Cheng. Valve closing plan optimization of long distance gravity flow water supply project[J]. Yellow River, 2017, 39(5): 131-134. DOI:10.3969/j.issn.1000-1379.2017.05.031 |
| [7] |
刘亚萌, 蒋劲, 李婷, 等. 基于多目标粒子群算法的停泵水锤防护优化[J]. 中国农村水利水电, 2017(6): 162-167. Liu Yameng, Jiang Jin, Li Ting, et al. Optimization of water hammer protection based on multi-objective particle swarm optimization algorithm[J]. China Rural Water and Hydropower, 2017(6): 162-167. DOI:10.3969/j.issn.1007-2284.2017.06.034 |
| [8] |
金鑫. PCCP输水管线爆管隐患分析及预防措施[J]. 水利建设与管理, 2016(6): 51-54. Jin Xin. Analysis on PCCP water pipeline explosion hazard and preventive measures[J]. Water Conservancy Construction and Management, 2016(6): 51-54. |
| [9] |
胡建永, 张健, 陈胜. 大型多支线供水工程的爆管水力过渡过程分析[J]. 水电能源科学, 2014, 32(1): 73-76. Hu Jianyong, Zhang Jian, Chen Sheng. Hydraulic transient process analysis of pipe burst in large-scale and multi-branch water supply project[J]. Water Resources and Power, 2014, 32(1): 73-76. |
| [10] |
Romano M, Kapelan Z, Savic D A. Evolutionary algorithm and expectation maximization strategies for improved detection of pipe bursts and other events in water distribution systems[J]. Journal of Water Resources Planning and Management, 2014, 140(5): 572-584. DOI:10.1061/(ASCE)WR.1943-5452.0000347 |
| [11] |
Qi Zhexian, Zheng Feifei, Guo Danlu, et al. Better understanding of the capacity of pressure sensor systems to detect pipe burst within water distribution networks[J]. Journal of Water Resources Planning and Management, 2018, 144(7): 04018035. DOI:10.1061/(ASCE)WR.1943-5452.0000957 |
| [12] |
Michele Romano, Zoran Kapelan, Dragan A. Automated detection of pipe bursts and other events in water distribution systems[J]. Journal of Water Resources Planning and Management, 2014, 140(4): 457-467. DOI:10.1061/(ASCE)WR.1943-5452.0000339 |
| [13] |
Wang Ronghe, Wang Zhixun, Wang Xiaoxue, et al. Pipe burst risk state assessment and classification based on water hammer analysis for water supply networks[J]. Journal of Water Resources Planning and Management, 2014, 140(6): 04014005. DOI:10.1061/(ASCE)WR.1943-5452.0000404 |
| [14] |
Doosun Kang, Kevin Lansey. Novel approach to detecting pipe bursts in water distribution networks[J]. Journal of Water Resources Planning and Management, 2014, 140(1): 121-127. DOI:10.1061/(ASCE)WR.1943-5452.0000264 |
| [15] |
梁兴, 刘梅清, 刘志勇, 等. 基于混合粒子群算法的梯级泵站优化调度[J]. 武汉大学学报(工学版), 2013, 46(4): 536-539. Liang Xing, Liu Meiqing, Liu Zhiyong, et al. Optimum dispatching of multistage pumping station based on mixed particle swarm optimization[J]. Engineering Journal of Wuhan University, 2013, 46(4): 536-539. |
| [16] |
张晓, 范虹, 张莉, 等. 融入免疫思想的改进型粒子群优化算法[J]. 陕西师范大学学报(自然科学版), 2017, 45(3): 17-23. Zhang Xiao, Fan Hong, Zhang Li, et al. An improved particle swarm optimization algorithm based on immune system[J]. Journal of Shaanxi Normal University (Natural Science Edition), 2017, 45(3): 17-23. |
 2019, Vol. 52
2019, Vol. 52



