文章信息
- 周博, 汪华斌, 江彬, 周宇, 徐一鸣
- ZHOU Bo, WANG Huabing, JIANG Bing, ZHOU Yu, XU Yiming
- 基于FEM和滑移线场理论的高填路堤稳定性分析
- Stability analysis of high-filled embankment based on FEM and slip line field theory
- 武汉大学学报(工学版), 2018, 51(12): 1072-1079
- Engineering Journal of Wuhan University, 2018, 51(12): 1072-1079
- http://dx.doi.org/10.14188/j.1671-8844.2018-12-005
-
文章历史
- 收稿日期: 2017-05-25
2. 广东长大公路工程有限公司,广东 广州 510000
2. Guangdong Provincial ChangDa Highway Engineering Co. Ltd, Guangzhou 510000, China
随着高填路堤的大量出现,已建山区公路中,受土层参数、填料强度参数、外荷降雨、路堤斜坡坡度、路堤台阶高度等因素影响,产生了许多高填路堤失稳破坏的现象.《公路路基设计规范》(JTG F10-2006)和公路路基施工技术规范(JTG F10-2006)未明确定义高填路堤的概念,对路堤地基的容许承载力也未做出明确的要求[1, 2].因而,在实际科学研究中,对于强度指标和安全系数的选取等方面存在一定的随意性,导致高填路堤的稳定性问题变得十分突出,成为了建筑行业、科研院所等单位需要解决的难题之一.高填路堤会产生多种多样的破坏形式,不仅会影响公路的正常运营,而且会引发交通安全事故,对人民群众的生命财产安全产生巨大威胁.因此,对高填路堤的稳定性进行研究具有重要的科学意义和工程实际价值.
目前,路堤的稳定性研究有多种分析方法[3],最常用的有3种:极限平衡法、极限分析法和滑移线法.滑移线法假设土体为理想刚塑性体,强度包络线为直线,根据平衡方程、屈服条件和应力边界条件求解塑性区的应力与位移分布,求得极限荷载[4].滑移线法能够考虑一般的弹塑性模型,不需要对模型做过多的简化,并可以获得比较真实的应力与位移分布,得到临界滑动面和最小安全系数.因此,滑移线方法为高填路堤稳定性分析提供了可能.
Cox于1962年最早运用滑移线法,研究了在基底光滑情况下地基的承载力问题[5].近20年来,滑移线法在求解地基承载力的问题上得到了广泛的研究和发展.肖大平等[6]揭示了无量纲参数与承载力系数之间的相互关系,在考虑有重土的情况下,将滑移线法的精确数值解,拟合为实用的解析式表达地基的极限承载力.Cheng等[7]运用滑移线法,研究了在地震荷载作用情况下的地基承载力问题.Martin[8]运用滑移线法,得到了刚性条形基础情况下地基承载力的解答.Gui等[9]运用滑移线法,证明并且估算了浅层楔锥形桩的地基承载力.Liu等[10]基于滑移线场理论,得到了轴对称分层回填主动土压力.Gao等[11]运用滑移线法,对黏性土管道的极限承载力进行了求解.李丽民等[12]基于潜在滑移线场理论,得到了地基潜在滑移线求解方法,提出了地基承载力的安全分析方法.然而,国内外的相关研究中基于滑移线场理论的山区高填路基的稳定性研究却鲜有发现.
因此,本文将系统建立基于滑移线场理论的山区高填路堤的稳定性分析方法,并在该理论体系中详细考虑土体的弹塑性区和流动法则对坡体稳定性的影响,试图为山区高填路堤的稳定性评价建立一个全新的研究体系,服务于高填路堤的设计和优化.
1 滑移线场理论基于滑移线场理论研究高填路堤稳定性,需要阐明滑移线场理论及其在路堤稳定性分析中的应用.目前滑移线场理论包含经典滑移线场理论和潜在滑移线场理论.经典的滑移线场理论适用于塑性区,潜在的滑移线场理论适用于弹性区,利用两者可以分析全域的稳定性问题.滑移线场理论关系到屈服准则、边界条件、流动法则、剪胀角等的选取问题.因此,本章拟从经典滑移线场理论、潜在滑移线场理论以及滑移线场理论在路堤稳定性分析中的应用等3个方面来进行阐述.
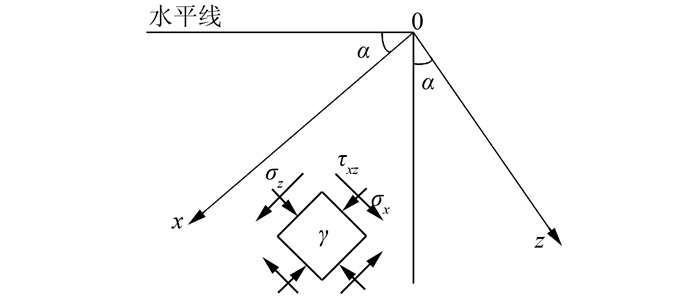
1.1 经典的滑移线场理论 1.1.1 平面问题基本方程假定土体材料为理想刚塑性体,并且服从Mohr-Coulomb屈服准则,土体在自重和外部荷载作用条件下,塑性区域发生塑性流动,对于平面塑性流动问题,如图 1所示.
|
| 图 1 平面单元的应力 Fig. 1 Stress tensors of the plane element |
平衡方程为
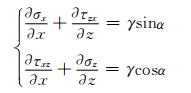 (1)
(1)
式中:σx为平行于x坐标轴的正应力;σz为平行于z坐标轴的正应力;τxz为剪应力,其中前一角标表示与它作用微面的法线方向平行的坐标轴,后一角标表示与作用方向平行的坐标轴,τxz=τzx;γ为土体重度;α为水平线和x轴的夹角.
土体屈服条件为
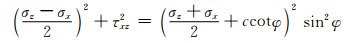 (2)
(2)
式中:φ为土体的内摩擦角;c为土体的黏聚力.
式(1)、(2)构成了滑移线场理论的应力基本方程.理论上,只要知道应力边界条件,就能够求得3个未知的应力分量σx, σz, τxz.然而由于确定边界条件和数学解析上的困难,解析解的获得会比较困难,但是应用滑移线场理论却可以获得近似解.
1.1.2 滑移线场的基本概念在塑性力学的基础上,建立了土力学中的滑移线场理论.经典塑性力学中假定:1)材料为理想刚塑性体;2)连续小变形;3)体积不可压缩;4)服从关联流动法则;5)满足Mises或Tresca屈服条件.对于流动法则的选取,一般而言,金属材料服从相关联流动法则,而岩土材料服从非关联流动法则,能够比较真实地反映理想塑性岩土体的状态.因为岩土材料为摩擦型材料,需考虑体积应变和剪胀性,同时由于岩土材料的拉伸强度和压缩强度相差比较大,不适用于Mises或Tresca屈服准则,所以需使用符合岩土类摩擦体的屈服条件,例如Mohr-Coulomb屈服条件.
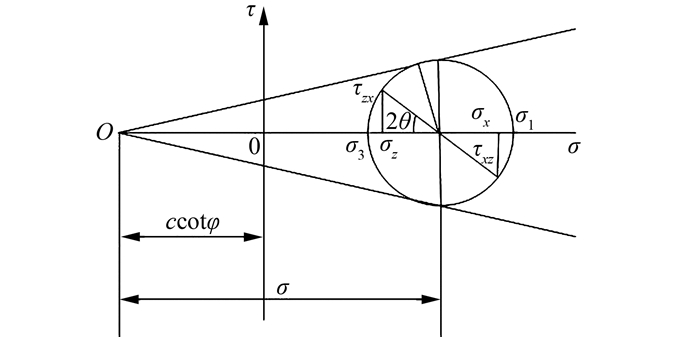
在塑性平面应变问题中,当土体屈服时,平面上每一点将出现1对剪切破坏面,其与最大主应力σ1的夹角为μ=π/4-φ/2.如图 2所示,3个应力分量σx, σz, τxz可分别表示为
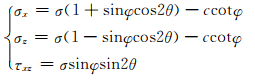 (3)
(3)
|
| 图 2 以σ, θ为自变量表达的应力分量 Fig. 2 Stress components expressed by independent variables σ, θ |
式中:σ=(τz+τx)/2+ccotφ,为平均法向正应力;θ为最大主应力σ1与x轴的夹角.
在平面应变问题中,每一点都存在2个正交的主应力,将每一点的主应力方向按照一定的顺序连贯地相连起来即是主应力迹线.当土体处在塑性屈服状态时,任意一点都有1对剪切破坏面,也就是α线和β线,将每一点的剪切破坏面连贯地相连起来便可得到2族曲线,即滑移线(或滑动线).滑移线上任意一点的切线也就是该点的滑动面方向,滑移线和主应力迹线如图 3所示.
|
| 图 3 滑移线和主应力迹线 Fig. 3 Slip lines and principal stress traces |
滑移线的物理概念是:在塑性变形区域内,最大切应力等于材料屈服切应力的轨迹线,达到塑性流动的区域,滑移线处处密集,称为滑移线场.
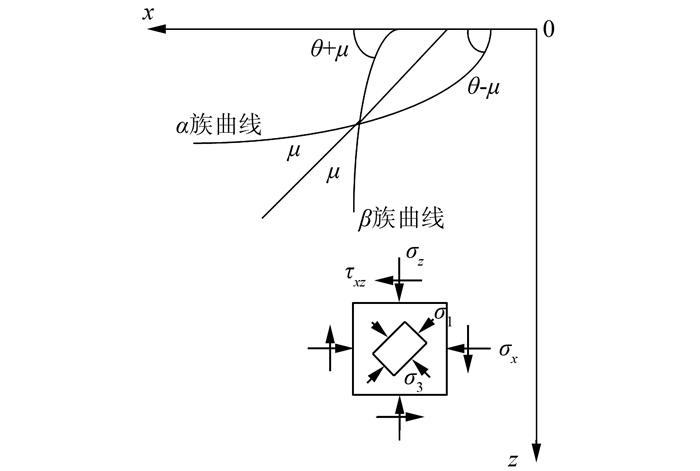
为了方便叙述,约定:以最大主应力σ1方向的迹线为基准线,顺时针方向与基线成锐角的称为α线,逆时针方向与基准线成锐角的称为β线.α线和β线的微分方程式为
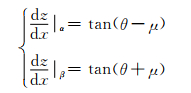 (4)
(4)
式中:μ为剪破面与最大主应力σ1的夹角,μ=π/4-φ/2.
如果应力场不同,则主应力迹线不同,滑移线场也不同.反之假如确定了滑移线场,则主应力迹线和应力场也随之确定.因此,问题可以归结为求解土体处于屈服状态下的滑移线场.
1.2 潜在的滑移线场理论 1.2.1 弹性区域中的滑移线场经典的滑移线场理论,只适用于塑性区域,而路堤较多部分仍处于弹性工作状态下,因而有必要对经典的滑移线场概念进行合理拓展,延伸至弹性区域.当材料处于弹性区域时,岩土中的某点并未产生破坏,但任意点上必然存在2个互相交叉的最危险滑动面,把每个点对应的最危险滑动面连接起来,可以获得2族曲线,即潜在滑移线.潜在滑移线场的微分方程与经典的滑移线场微分方程类似,而潜在滑移线与最大主应力σ1方向的夹角并不相同.
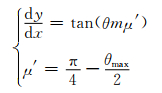 (5)
(5)
式中:μ′为潜在滑移线与最大主应力σ1方向的夹角;θmax为该点的最大应力偏角:
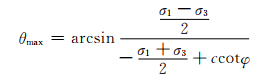
当θmax=φ,该点处于强度极限;当θmax<φ,该点处于弹性状态.
1.2.2 考虑非关联流动法则的滑移线场经典的滑移线场理论认为岩土材料服从关联流动法则,夸大了剪胀角的作用,可能会高估路堤的稳定性.Kabilamany等通过大量的实验和现场观测表明,真实土体的内摩擦角比剪胀角大很多[13].Davis发现剪胀角不等于内摩擦角时,应力特征线与速度滑移线不可能重合,也就是说滑移线方程不满足式(4)[14].此时滑移线上的正应力σ*和剪应力τ*具有类似于Mohr-Coulomb准则的关系:
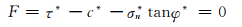 (6)
(6)
式(6)中的c*、φ*和Mohr-Coulomb准则中的c和φ意义相似,具有如下关系:
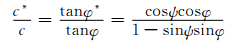 (7)
(7)
式中:ψ为材料的剪胀角.
因此,对于岩土类材料应采用非关联流动法则来构造滑移线场.
1.2.3 潜在滑移线的求解搜索经典的滑移线是潜在滑移线的一种特例,为了方便叙述,把潜在滑移线与经典滑移线统称为滑移线.弹塑性有限元法可以兼顾考虑弹塑性区、应力应变关系、几何方程等,能够全面地反应滑动面的形状、趋势与范围.通过得到的弹塑性有限元应力结果,求得每一点的主应力方向θ与μ′值后,应用式(5)通过数值积分方法求得潜在滑移线.
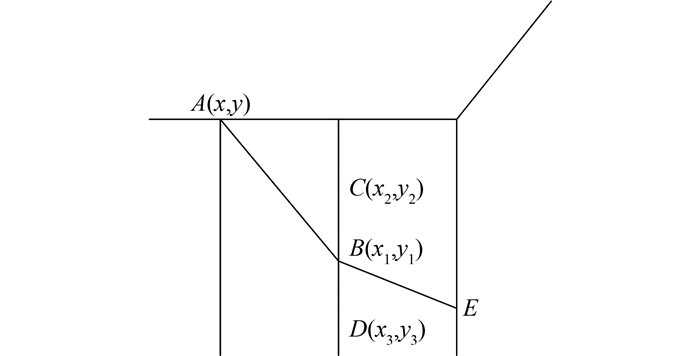
1.2.4 搜索确定临界滑动面各离散点排列规则如图 4所示,从出口点A(x, y)出发,以方向φ作一条直线和经过相邻近一竖列离散点的直线相交于B(x1, y1)点,B点可以是给定的离散点,也可以不是给定的离散点,但它必定在2个离散点之间.
|
| 图 4 追踪示意图 Fig. 4 Tracing diagram |
设这2个离散点为C(x2, y2)和D(x3, y3), 方向分别为φ2和φ3,通过插值法得出B的滑移线方向φ1为
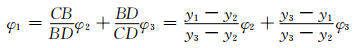 (8)
(8)
按照同样的方法,追踪得到E点的值, 不断地搜索下去,即可获得一条连续的曲线,通过选取不同的出发点,搜索一定的步长,可以获得许多曲线,构成潜在滑动面.当出现了2条滑移线相交的情况时,需要加密步长,重复搜索.由于边界处容易产生奇异点,得到的单元应力异常,会出现滑移线方向不正确或者滑移线突然出现明显的拐折点现象,此时需要通过增大网格单元重新计算,或者选择远离坡顶和坡面的地方作为滑移线的起点.
滑动面上任意一点的正应力和剪应力也可按照同样的插值方法计算得到,便可求得每条滑移线对应的安全系数.安全系数按下式计算:
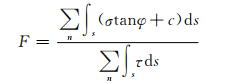 (9)
(9)
式中:n为滑移线跨越的搜索路径的段数;σ和τ为滑移线上的正应力和剪应力.
在塑性区域中材料强度参数按式(7)求解,在弹性区域中按照实际值选取.由滑移线场理论可知,有限元结果可得到许许多多的滑移线,临界滑动面即是其中算得的安全系数最小的一条.
1.3 路堤稳定性分析的滑移线场解法 1.3.1 应力场的滑移线方程路堤属于塑性平面应变问题,在路堤下土体中取一微分单元体,仅考虑重力,z坐标向下为正,应力以压为正,满足Mohr-Coulomb屈服准则,得到如下应力平衡微分方程:
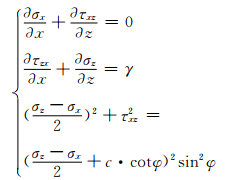 (10)
(10)
Mohr-Coulomb准则中的3个应力分量为
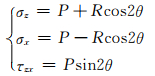 (11)
(11)
式中:P为平均应力,P=(τz-τx)/2;R为极限应力圆半径,R=Psinφ+c·cosφ.
将式(11)代入式(10)中得
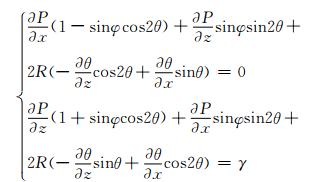 (12)
(12)
根据式(12)求出P和θ,依据屈服条件求出σx,σz和τzx,再结合边界条件求解出极限荷载.
伴随式(12)有2族实特征线,其微分方程为
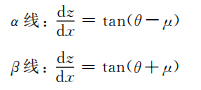 (13)
(13)
取与滑移线与α和β相重合的曲线坐标系统(Sα,Sβ).依据方向导数定义,沿滑移线Sα和Sβ的方向导数为
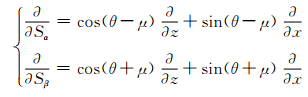 (14)
(14)
由此可得
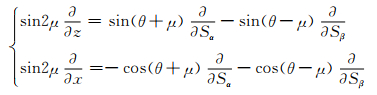 (15)
(15)
将式(15)代入式(14)可得
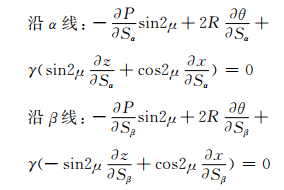 (16)
(16)
式(16)反映了P和θ沿α和β族滑移线的变化规律,通过它便可求得滑移线场分布与极限荷载.然而,由于方程组为非线性偏微分方程组,直接积分有困难,需借用数值方法求解.
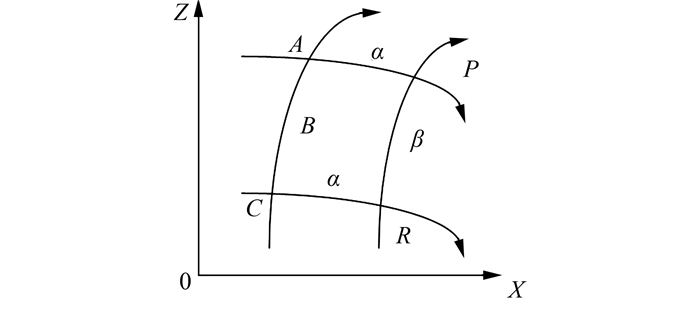
1.3.2 滑移线场数值解如图 5所示算法示意图,已知A点和B点的P和θ值,α线过A点,β线过B点,α线与β线相交于P点,求其xP,zP,PP和θP值.
|
| 图 5 算法示意图 Fig. 5 Diagram of thealgorithm |
联立式(13)和式(16)求P点的xP和zP,运用差分法求P点的PP和θP.应力方程(16)的差分形式为
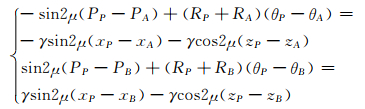 (17)
(17)
滑移线方程(13)的差分形式为
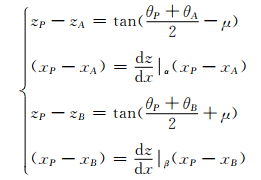 (18)
(18)
式(17)、(18)均为非线性方程组,运用迭代法求解,可求得xP,zP,PP和θP值.
本章从经典滑移线场理论、潜在滑移线场理论、路堤稳定性分析中的滑移线场解法等3个方面进行论述.阐述的主要结论如下:
1) 经典的滑移线场理论不考虑岩土的变形过程,只对破坏后的状态进行研究,只适用于塑性区域,一般难以考虑复杂的地质情况和边界条件.潜在滑移线场理论是经典滑移线场理论的合理拓展,适用于弹塑性区域.弹塑性有限元法可以考虑岩土材料的非线性、几何非线性、各种不同的边界条件、边界面和模拟实际的荷载历程.由于路堤较多部分仍处于弹性工作状态下,基于潜在滑移线场理论,对有限元的应力场进行后处理,生成潜在滑移线和算得最小安全系数,可以判断路堤的稳定性,确定临界滑动面.
2) 岩土材料不适用于Mises或Tresca屈服准则,需使用符合岩土类摩擦体的屈服条件,例如Mohr-Coulomb屈服条件.经典的滑移线场理论认为岩土材料服从关联流动法则,夸大了剪胀角的作用.然而岩土材料不服从关联流动法则,应该采用非关联流动法则,岩土材料的剪胀角应取ψ=φ/2,而非现在使用的ψ=0,才能够比较真实地反映理想塑性岩土体的状态.
1.3.3 路堤稳定性分析方法本节主要研究在不同台阶高度、不同斜坡坡度、不同换填土参数情况下,高填路堤稳定性的一般规律.路堤是一个典型的平面应变问题,利用大型有限元软件Abaqus进行有限元分析,计算中采用的是平面应变有限元法,有限元模拟主要包括3个分析步:第1步是地应力平衡,第2步是路堤自重加载,第3步是路面车辆加载.考虑到模型的对称性,可取一半模型进行数值分析,模型边界条件为:底部限制水平和垂直方向的位移;侧面限制水平位移.采用4节点单元对模型网格进行划分,同时允许少量的3节点单元进行过渡,共计约有61 428个单元和62 127个节点.
Abaqus是大型通用有限元软件,可以解决许多的复杂非线性问题和动力问题.虽然如此,Abaqus的后处理能力仍不能满足本文的要求,因此需要做进一步的人工处理.
本文中,假设材料的剪胀角ψ=φ/2,采用非关联流动法则,符合Mohr-Coulomb屈服准则,利用大型有限元软件Abaqus得到临界状态的应力场,将Abaqus计算所得结果导出到Excel,采用强大的科学计算软件Matlab结合滑移线场理论进行编程求解,得到滑移线场和每一条滑移线对应的安全系数,其中安全系数最小的即是临界滑动面,以此发现滑移线场的分布和变化趋势.搜索确定临界滑动面的步骤总结为
1) 通过工地现场调研,获取工程地质条件与相关工程勘察资料.
2) 根据设计资料的相关参数,作出典型断面剖面图.
3) 建立理想弹塑性模型,采用有限元软件Abaqus得到临界状态的应力场.
4) 将Abaqus计算所得结果导出到Excel,利用Matlab软件结合滑移线场理论进行编程求解,绘制滑移线和确定其相对应的安全系数,确定临界滑动面.
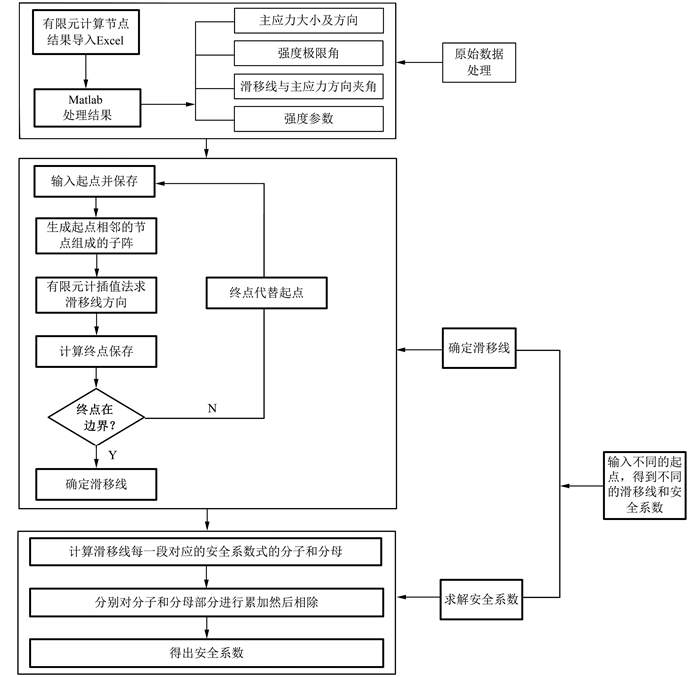
具体的编程求解过程示意图如图 6所示.
|
| 图 6 编程求解过程示意图 Fig. 6 Diagram of programming solving process |
在建广佛肇高速公路肇庆段,路段起始于肇庆市高新技术开发区,往西经四会、端州、德庆、封开等城市,全线大约长180 km,设计时速100 km/h,其主线存在大量高填路堤路段.本文选取山间洼地高填典型断面K89+360为研究对象,其位于广佛肇高速公路C标段,为山区高速公路,人为建设活动少,植被也少,沿线特殊性岩土有膨胀土和高液限土等.
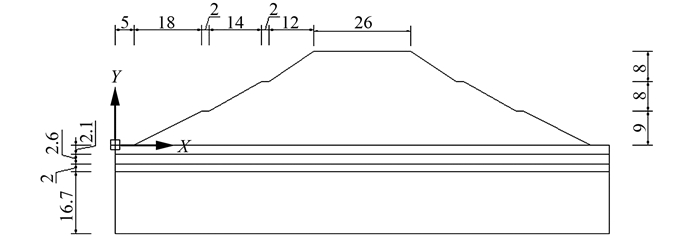
考虑路堤顶部分布19 kPa的车辆静荷载,路堤填土高25 m,路面宽26 m,平台宽度均为2 m,基底分布4层不同性质的土层,从上至下第1层为粉质黏土(堆积成因),第2层为粉质黏土(残积成因),第3层为全风化花岗岩,第4层为强风化花岗岩.换填前的模型剖面示意图如图 7所示,根据工程地质勘察报告,换填前的土层分布和力学参数见表 1.换填后的模型建立在换填前基础上,将第1层粉质黏土(堆积成因)2.1 m换填为2.1 m强风化岩;将第2层粉质黏土(残积成因)上层的1 m换填为1 m片石,下层的1.6 m粉质黏土(残积成因)保持不变.因此,从上至下分布5个土层,第1层为强风化岩,第2层为片石,第3层为粉质黏土(残积成因),第4层为全风化花岗岩,第5层为强风化花岗岩.换填后的土层和力学参数见表 2.
|
| 图 7 换填前模型剖面示意图(单位:m) Fig. 7 Subgrade model section before filling (unit:m) |
| 参数 | H /m | Es /MPa | ν | γ /(kN·m-3) | c /kPa | φ /(°) |
| 粉质黏土(堆积) | 2.1 | 7.5 | 0.22 | 18 | 16 | 18 |
| 粉质黏土(残积) | 2.6 | 8.5 | 0.25 | 18 | 16 | 18 |
| 全风化花岗岩 | 2 | 12 | 0.30 | 20 | 25 | 25 |
| 强风化花岗岩 | 16.7 | 15 | 0.30 | 21 | 28 | 28 |
| 参数 | H /m | Es /MPa | ν | γ /(kN·m-3) | c /kPa | φ /(°) |
| 强风化岩 | 2.1 | 9 | 0.23 | 18 | 20 | 22 |
| 片石 | 1.0 | 10.0 | 0.23 | 20 | 25 | 28 |
| 粉质黏土 | 1.6 | 8.5 | 0.25 | 18 | 16 | 18 |
| 全风化花岗岩 | 2 | 12 | 0.30 | 20 | 25 | 25 |
| 强风化花岗岩 | 16.7 | 15 | 0.30 | 21 | 28 | 28 |
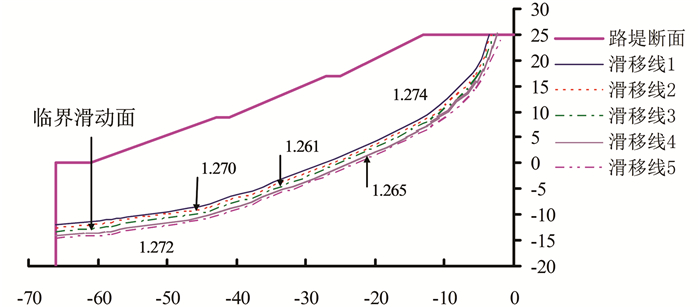
通过第1章基于滑移线场理论的路堤对于换填前后的模型提取了17组数据,即17组滑移线,通过对17组数据进行分析和绘制,同时为了图形的清晰和方便观图,选取了其中5条有代表性的滑移线进行绘制(图 8、9),标出了各条滑移线对应的安全系数,安全系数采用式(9)计算.
|
| 图 8 换填前滑移线场和临界滑动面(单位:m) Fig. 8 Slip line filed and critical slip surface before filling (unit:m) |
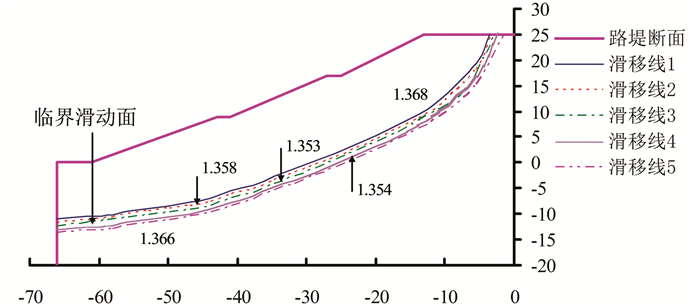
|
| 图 9 换填后滑移线场和临界滑动面(单位:m) Fig. 9 Slip line filed and critical slip surface after filling (unit:m) |
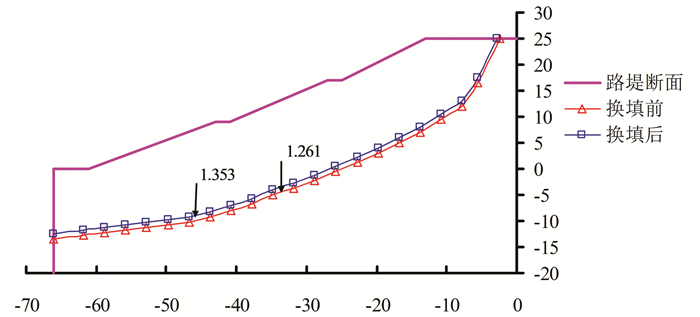
从图 8、9对比可以看出,换填后路堤的最小安全系数显著变大,由原来的1.261变化为1.353.为了更进一步反映临界滑动面的变化趋势,绘制换填前后临界滑动面的变化如图 10所示.
|
| 图 10 换填前后临界滑动面变化(单位:m) Fig. 10 Difference of critical slip surfaces before and after filling (unit:m) |
从图 10可以看出,换填后最小安全系数变大,临界滑动面逐渐上移,滑动土体体积逐渐减小,潜在滑动面切入软土层的深度变小.总体而言,换填后的安全系数为1.353,大于换填前的安全系数1.261,大于工程规范规定的安全系数1.200,也大于高填方路堤工点说明中规定的安全系数1.300.说明换填后稳定性得到了较大提高,能够保证路堤的安全稳定性.也可以证明本文提出的基于滑移场理论的高填路堤的稳定性分析方法的有效性.
3 结论本文基于滑移线场理论建立了对高填路堤稳定性的分析框架,并对有限元的应力场进行后处理,生成潜在滑移线,算得最小安全系数,可以判断路堤的稳定性,确定临界滑动面.在计算过程中详细考虑了土体的弹塑性区和流动法则对坡体稳定性的影响.通过对广佛肇高速公路的高填典型断面K89+360的实例进行研究分析发现2个主要结论:
1) 基于滑移线场理论建立的路堤稳定性分析方法可以有效地计算出边坡的安全系数和临界滑动面.
2) 本文的计算实例中,高填路堤在换填后最小安全系数变大,临界滑动面逐渐上移,滑动土体体积逐渐减小,潜在滑动面切入软土层的深度变小.
| [1] |
中交第二公路勘察设计研究院. JTG F10-2015公路路基设计规范[S].北京: 人民交通出版社, 2015. The Second Highway Survey and Design Research Institute. JTG D30-2015 Highway Roadbed Design Specification[S]. Beijing: The People Traffic Press, 2015. |
| [2] |
中交第一公路工程局有限公司. JTG F10-2006公路路基施工技术规范[S].北京: 人民交通出版社, 2006. China Road Engineering Bureau Co. LTD..JTG F10-2006 Technical Specification for Construction of Highway Subgrade[S]. Beijing: The People Traffic Press, 2006. |
| [3] |
朱大勇.土体稳定性分析方法——临界滑动场法[D].南京: 工程兵工程学院, 1999. Zhu Dayong. A method for soil stability analysis[D]. Nanjing: Nanjing Engineering Institute, 1999. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb200001031 |
| [4] |
陈飞.基于ABAQUS的高土石坝边坡稳定分析研究[D].北京: 北京交通大学, 2011. Chen Fei. Stability analysis of the high earth-rockfill dam slope based on ABAQUS[D]. Beijing: Beijing Jiaotong University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10004-1011101866.htm |
| [5] |
Cox D. Axially-symmetric plastic deformation in soils-Ⅱ. Indentation of ponderable soils[J]. International Journal of Mechanical Sciences, 1962, 4(5): 371-380. DOI:10.1016/S0020-7403(62)80024-1 |
| [6] |
肖大平, 朱维一, 陈环. 滑移线法求解极限承载力问题的一些进展[J]. 岩土工程学报, 1998, 20(4): 28-32. Xiao Daping, Zhu Weiyi, Chen Huan. Progress in slip lines method to solve the bearing capacity problem[J]. Chinses Journal of Geotechnical Engineering, 1998, 20(4): 28-32. |
| [7] |
Cheng M, Au K. Solution of the bearing capacity problem by the slip line method[J]. Canadian Geotechnical Journal, 2005, 42(4): 1232-1241. DOI:10.1139/t05-037 |
| [8] |
Martin C M. Exact bearing capacity calculations using the method of characteristics[C]//Proceedings of International Association for Computer Methods and Advances in Geomechanics. Turin, 2005: 441-450.
|
| [9] |
Gui W, Muhunthan B. Bearing capacity of foundations on sand using the method of slip line[J]. Journal of Marine Science and Technology, 2006, 14(1): 1-14. |
| [10] |
Liu F, Wang J, Zhang L. Axi-symmetric active earth pressure for layered backfills obtained by the slip line method[J]. Journal of Shanghai Jiaotong University (Science), 2008(5): 579-584. |
| [11] |
Gao F P, Zhao B. Slip-line field solution for ultimate bearing capacity of a pipeline on clay soils[J]. Theoretical and Applied Mechanics Letters, 2012, 2(5): 051004. DOI:10.1063/2.1205104 |
| [12] |
李丽民, 张国祥, 肖尚, 等. 基于潜在滑移线理论的地基承载力安全分析方法[J]. 中国安全科学学报, 2013, 23(3): 39-44. Li Limin, Zhang Guoxiang, Xiao Shang, et al. Safety analysis methods of the foundation bearing capacity based on the potential slip line theory[J]. Chinese Journal of Safety Science, 2013, 23(3): 39-44. |
| [13] |
Kabilamany H, Ishihara K. Stress dilatancy and hardening laws for rigid granular model of sand[J]. Soil Dynamics and Earthquake Engineering, 1990, 28(9): 66-77. |
| [14] |
Davis E. Theories of Plasticity and the Failure of Soil Masses Soil Mechanics[M]. London: Butterworth, 1968: 341-380.
|
 2018, Vol. 51
2018, Vol. 51



