乒乓球比赛是以单人或双人的方式进行比赛, 双方运动员均使用球拍交替击球并使球越过或绕过球网装置后触及对方比赛台面, 直至一方运动员击球得分或击球失误, 回合终止[1]。乒乓球比赛属性表明通常即时观察到的是双方运动员互动后的某个比赛片段的结果, 而不是比赛双方技战术实力的完整体现, 说明乒乓球比赛是一个动态变化的互动过程[2]。
在以往的乒乓球比赛分析中, 运用最广泛的分析方法是三段指标评估法, 常用的方法还有人工神经网络模型、数据挖掘、转移矩阵概率以及技术效率评估等。这些方法是以得分率和使用率为基础, 对运动员整场比赛的技战术数据进行分类分析, 从而得出运动员在比赛中技战术的运用或发挥情况。在统计方法中, 大量指标需要人为主观判定, 难免存在误差, 同时忽视运动员状况的起伏。本文基于乒乓球比赛运动员技战术发挥呈动态变化发展的特点, 引入二次移动平均法, 构建乒乓球比赛势态分析模型, 帮助教练员和运动员更加简单、直观地观察与分析优秀运动员整场比赛技战术发挥与发展过程, 快速定位运动员发挥的不同阶段。
1 二次移动平均法及乒乓球比赛势态分析模型 1.1 二次移动平均法简单移动平均法或一次移动平均法将时间数列中的前几项数值计算算术平均值(式1):
| $M{{A}_{\text{forward},k}}\left( n \right)=\frac{1}{k}\sum\limits_{i=0}^{k-1i}{\text{score}\left( n+i \right)}$ | (1) |
式中:MA(n)为第n期的一次移动平均值; k是移动平均值的跨越期, 即拟定的平均移动项数; score(n)为第n期的实际观察值。由于计算所得的平均值必然大于或小于实际观察值(当时间数列呈上升趋势时计算值小于实际观察值, 当呈下降趋势时计算值大于实际观察值), 即存在“滞后”现象。
二次移动平均法是对一次移动平均数再进行第二次移动平均, 再以一次移动平均值和二次移动平均值为基础建立预测模型, 计算预测值的方法:
| $M{{A}_{\text{backward},k}}\left( M{{A}_{\text{forward},k}}\left( n \right) \right)=\frac{1}{k}\sum\limits_{i=0}^{k-1}{M{{A}_{\text{forward},k}}\left( n-j \right)}$ | (2) |
二次移动平均法能够有效改善简单移动平均法滞后偏差, 建立预测目标的线性时间关系数学模型, 求得预测值。它适用于有明显趋势变动现象的时间序列的预测, 同时它还保留了一次移动平均法的优点[3]。
1.2 基于二次移动平均法的乒乓球比赛势态分析模型 1.2.1 比赛观察单位乒乓球比赛开始于一方运动员发球, 一方运动员接发球, 之后双方运动员轮流击球, 直至一方出现失误, 回合终止, 获胜方得1分, 输球方不计分。在一局比赛中, 先得11分方为胜方, 10平后, 先多得2分方为胜方。将每一回合的比赛结果看作是1个观察值, 那么在1场比赛中, 每1个得分或失分、即每一回合就是1个观察单位, 整场比赛的观察值即构成一个新的序列值。运用二次移动平均法对该序列值进行计算, 构建二次移动平均线, 曲线走势即可反映该运动员在比赛中的即时发挥水平[4-6]。
二次移动平均法主要应用于时间序列, 呈现线性趋势变化的预测。乒乓球比赛并非市场现象, 它是由双方运动员激烈对抗后产生的即时结果, 双方的比分均为整数, 比赛结果不属于连续性数据, 且上一回合的发挥对下一回合无任何影响, 故传统的二次移动平均法在乒乓球比赛中并非完全适用, 应结合实际情况进行适当修正。
本文在大量试验的基础上, 选取1和0为计算指标。以一方运动员为观察者, 得分记为1, 失分记为0, 对一场比赛进行统计, 则得到一个新的具有时序特征的观察值序列; 运用二次移动平均法对该序列进行计算, 二次计算所得的值, 将其定义为平均获胜概率。
1.2.2 二次移动平均法移动步长的确定二次移动平均法中步长的选取对结果的平滑作用非常大。如果步长太小, 平均线的波动就很大, 虽然能够反映即时的随机分布势态, 但是过于强烈的随机扰动易使人产生错误的判断。如果步长太长, 模型反映不出即时的随机分布趋势, 因为它与时序中的随机变化的关联太小[7]。
乒乓球的比赛规则为运动员每发两球后交换发球权, 故本文将移动步长定为4, 即每4个回合为1个计算平均值的对象。这样在每4个回合中, 运动员双方都是2次发球和2次接发球, 能够更加客观、公正地发映运动员的水平发挥情况。
此外, 经过验证, 步长选取为4, 从视觉判断与评估比赛发挥水平方面而言也相对合理, 更加符合科研人员的期望。
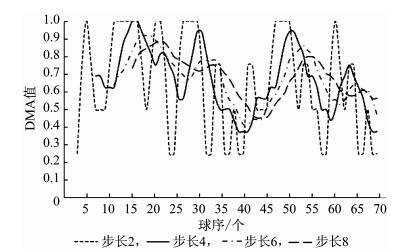
图 1所示为不同步长的移动平均(获胜概率)线, 其横轴表示球序, 纵轴是二次移动平均获胜概率值。从中可以看出:① 步长为2时, 曲线变化过多, 波动较大, 不易评估运动员在比赛中的发挥情况; ② 步长为6和8时, 曲线相对过于平滑, 不能较为完整地反映比赛的即时变化, 且曲线前端数值缺失较多; ③ 当步长选取4时, 正好能够有效地避免过度波动的现象, 既能够做到修匀与平滑, 又可避免与实际的发挥势态相背离。
|
图 1 马龙VS波尔(德国)比赛不同步长的移动平均线走势 Figure 1 The trend of moving line based on different length of Malong VS Boll(DEU) |
本文选取的移动步长为4, 即每4个回合为1次移动平均值的计算对象。① 假定运动员A在某比赛片段中, 4个回合中分别赢1分、输1分, 再赢1分、输1分, 即处于不领先也不落后的平衡势态时, 相对应的计算指标为1、0、1、0, 说明双方运动员竞争比较激烈, 这种势态定义为胶着期; ② 当运动员A在这种平衡状态下, 出现连赢3分时, 说明该运动员发挥非常好, 此时的二次移动平均值为0.625, 这种状态定义为优势期; ③ 当运动员A在平衡状态下, 连输3分时, 说明该运动员发挥比较差, 此时的二次移动平均值为0.375, 这种势态定义为劣势期。据此, 可得出以下势态分析标准(表 1)。
| 表 1 乒乓球比赛势态分析模型评估标准 Table 1 Criteria of momentum analysis model of table tenmis competition |
比赛势态分析模型的应用可分为2个方面:① 根据该模型可以发现运动员在整场比赛中技术状态的起伏过程, 通过长期或多场比赛的观察, 能找到运动员在比赛技战术发挥方面存在的规律性变化特点, 以便教练员在临场指导或训练中对其有针对性地进行调整; ② 分别讨论运动员在优势期、胶着期和劣势期的技战术运用情况与效果, 通过比较与分析, 进一步发现运动员更为细致的技战术特征及运用效果。
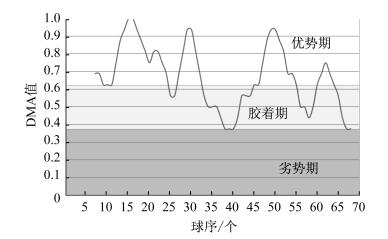
2 案例分析 2.1 单场比赛(马龙VS波尔)势态分析选取2012年男子乒乓球世界杯赛单打半决赛马龙VS波尔(德国)比赛为例, 该场比赛马龙4:0获胜, 4局的比分为11:4、11:3、11:8和11:9, 其整场比赛势态变化过程如图 2所示。
|
图 2 2012年乒乓球世界杯赛男单半决赛马龙VS波尔比赛势态分析模型 Figure 2 Momentum analysis model of Malong VS Boll in Table Tennis World Cup 2012 |
从图 2中的移动平均线可以看出:第1局(0~15球), 马龙发挥得非常好, 从开局到结束, 一直呈上升趋势, 所有的移动平均值均大于或等于0.625;第2局(16~29球), 马龙依旧发挥很好, 由于中局连输2分, 导致曲线下滑, 但整体势态非常好, 拥有绝对优势, 充分说明马龙入赛快, 势头好; 第3局(30~48球), 马龙开局发挥不利, 险些被对手反超, 曲线一度出现下滑趋势, 中局与对手竞争激烈, 后迅速调整, 又逐渐打出高潮, 赢得此局的胜利; 第4局(49~68球), 马龙延续了上一局的优势, 开局便抢占先机, 曲线依旧一直保持在优势期, 直至中局。在与对手的短期胶着后, 马龙又重返主导地位, 尾局虽然一直被对手纠缠, 发挥受阻, 但最终仍赢得比赛。从整场比赛的曲线走势看, 马龙一直占据上风, 优势期占主导, 胶着期次之, 劣势期极少。
2.2 多场比赛(张继科、马龙、许昕)势态分析乒乓球比赛是2名运动员在规定的场地、环境下, 通过激烈对抗, 短时间内决出胜负, 故比赛结果具有一定的偶然性。它不仅受到运动员的近期竞技状态、临场发挥、疲劳程度以及身体状况(伤病)等各种主观因素的影响, 还要受到各种外来因素如场外观众、教练员指导、对手打法类型等的影响。因此, 单场次的技术分析并不能完整地反映该运动员的整体水平, 这就需要将一名运动员的多场比赛或多名运动员的多场比赛根据实际需要, 按照一定的标准叠加分析, 通过定量达到定性分析的目的。
选取张继科、马龙、许昕在2011—2012年所参加的国际比赛各10场(每人胜5场, 负5场, 对手的赛前国际排名均在前23), 通过计算不同运动员在每场比赛中不同比赛势态的出现次数及所占比例, 对每位运动员在近期比赛中的总体发挥做出客观评价。表 2为3位运动员比赛中各种比赛势态所占比例的均值及标准差。
| 表 2 3名运动员各种比赛势态所占的比例 Table 2 The proportion of three players in different momentum status |
通过比较发现, 马龙的优势期出现比例最高(0.427), 其次是张继科(0.311), 许昕最低(0.187), 且有显著性差异(F=4.268, P<0.05)。分析发现, 马龙的优势期所占比例与许昕有显著性差异(P<0.05), 但马龙与张继科无显著性差异(P>0.05), 张继科与许昕也无显著性差异(P>0.05)。许昕在比赛胶着期和劣势期出现比例均高于马龙和张继科, 但无显著性差异(F=3.159, P>0.05;F=1.329, P>0.05)。说明马龙在比赛中具有很多的优势, 张继科次之, 许昕略少。
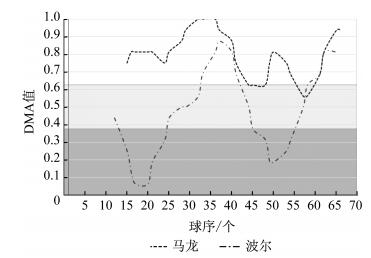
2.3 双方运动员比赛势态分析发球技术是乒乓球技术体系中唯一一项非制约性技术[8], 一个高质量的发球不仅可以直接得分, 还可以为下一拍的进攻创造有利的机会; 因此, 可以发球为基准, 观察双方运动员比赛势态变化的过程。将双方运动员的发球轮单独排列, 即将该场比赛的观察值序列变为2名运动员各自的发球轮序列。根据二次移动平均值算法, 对两列数值进行计算制图, 即可得到双方运动员的发球轮动态模型(以2012年乒乓球世界杯赛男单半决赛马龙VS波尔为例, 图 3)。
|
图 3 马龙与波尔发球轮比赛势态分析模型 Figure 3 Momentum analysis model of Malong VS Boll in service round |
从图 3可以看出, 马龙在整场比赛中, 几乎所有发球轮的移动平均值都高于波尔, 完全占据上风。尤其在前2局, 发球轮的移动平均线一路上升, 与波尔发球轮的差距一直保持在0.3以上, 说明马龙对于发球后的技术衔接及战术运用非常到位, 一直让对手处于被动的地位, 这对整场比赛的胜利起决定性的作用。且在第2局和第4局开局, 接发球技术也运用得非常好。波尔在整场比赛中, 只有在第2局和第3局把握住了发球轮, 第3局的发球轮发挥相对较好, 其余阶段的发球轮均未占太大的优势。
3 模型需进一步解决的问题 3.1 每场比赛缺少前6个回合的平均获胜概率本文二次移动平均法中的移动步长为4, 故只能在有4个观测值的情况下才可以计算移动平均值。在计算一次移动平均值时, 缺失了一场比赛前3个回合的平均值, 在计算二次移动平均值时又缺失了前3个回合的平均值, 共缺失6个; 因此, 该分析模型还不能完整地反映一场比赛的势态变化。
3.2 存在“天花板效应”在本文中, 二次移动平均法的计算指标只有得分和失分, 即1和0。在运动员连赢或连输7个回合后, 二次移动平均值就达到了1或0的极值状态, 即出现“天花板效应”。此后, 无论运动员连赢或连输多少个回合, 获胜概率将一直保持1或0。
4 结束语基于二次移动平均法的乒乓球比赛势态分析模型计算步骤简单, 且能直观、准确、便捷地将双方运动员的比赛过程实时反映出来, 教练员和运动员可以利用该方法解读与掌握整场比赛势态的发展过程; 科研人员也可以运用该模型迅速找出运动员在不同比赛时段(优势期、胶着期、劣势期)的技战术特点, 从而能够更好地指导比赛和训练。目前该方法已在中国乒乓球队有了较广泛的应用基础, 且仅依靠比分进行分析, 适用于多个隔网对抗体育项目的技战术分析应用。
| [1] |
张辉, 戴金彪, 史芙英, 等. 隔网对抗(持拍类)项目技战术特征[J].
上海体育学院学报, 2007, 31(4): 65-69 ( 0) 0)
|
| [2] |
Lames M. Modelling the interaction in game sports-relative phase and moving correlations[J].
Journal of Sports Science & Medicine, 2006, 5(4): 556-560 ( 0) 0)
|
| [3] |
华伯泉. 统计预测中的二次移动平均法[J].
统计研究, 1995(2): 70-73 ( 0) 0)
|
| [4] |
Zhang H, Liu W, Hu J J, et al. Evaluation of elite table tennis players' technique effectiveness[J].
Journal of Sports Sciences, 2013, 31(14): 1526-1534 DOI:10.1080/02640414.2013.792948 ( 0) 0)
|
| [5] |
张辉, 霍赫曼·安德烈亚斯. 乒乓球比赛的数学模拟竞技诊断[J].
上海体育学院学报, 2004, 28(2): 68-72 ( 0) 0)
|
| [6] |
张辉, 霍赫曼·安德烈亚斯. 球类比赛数学模拟竞技诊断的理论与实践——以乒乓球比赛分析为例[J].
体育科技文献通报, 2005, 25(11): 39-44 DOI:10.3969/j.issn.1005-0256.2005.11.053 ( 0) 0)
|
| [7] |
Duan L, Liu S, Lu Q. Study on the determination of the moving step length in moving method of mean[J].
Journal of Beijing University of Technology, 2004, 30(3): 378-381 ( 0) 0)
|
| [8] |
佘竞妍. 乒乓球技术体系的分类及效用研究[D]. 上海: 上海体育学院, 2010: 3-10
( 0) 0)
|
 2017, Vol. 41
2017, Vol. 41


