2. 西南大学 运动与健康虚拟仿真实验中心, 重庆 400715
2. Sports and Health Virtual Simulation Experiment Center, Southwest University, Chongqing 400715, China
过去20年里,加速度计在身体活动测量中的广泛应用促进了身体活动评价的客观量化和推广普及。随着人民生活水平的持续提高与体育强国建设的不断推进,佩戴含有加速度计模块的可穿戴设备成为身体活动监测的重要方式。基于加速度计数据的身体活动评价目前仅停留在描述“整段活动中不同运动强度等级的持续时间”,这已不能满足大众的体育需求。儿童身体活动评价备受学校、家长与社会关注,人们对其视角全面性、细节可视化、过程可追踪的需求越来越高。目前已有不少与ActiGraph计数结果接近的身体活动计数算法开源(如sensormotion库[1]、ActiGraph库[2]、pyActigraphy库[3]等),因此,实现以上现实需求的主要技术问题在于儿童身体活动类型识别的研究成果不尽如人意,这一点也与其他学者达成共识[4]。
21世纪初,识别身体活动类型的研究方法主要以主观观察法和自我报告法为主。主观观察法过于依赖观察者的专业性且大规模测量的成本过高,而自我报告法的客观性也受到很多学者的质疑[5-7]。机器学习方法的广泛应用与加速度计技术的迅速发展使得活动类型的分类研究走向了客观化。目前,使用机器学习方法识别儿童身体活动类型的研究并不多,早期的研究[8-11]主要采用传统机器学习方法(如随机森林、支持向量机、K近邻、隐马尔可夫模型等),通过人工提取时域特征来区分活动类型,这种特征提取方式的分类准确率鲜有突破80%。随后的研究[12-14]提取了更多的时频特征,丰富的特征提取促使身体活动类型识别准确率突破了90%,但这些研究都未构建出通过1组加速度计数据识别多种身体活动类型的模型:有些研究将多种身体活动类型合并后才实现较高的准确率,如Ren等[13]识别19种身体活动的准确率为64.4%,合并为5类身体活动后准确率达到91.7%;有些研究采用2组加速度计数据才实现较高的准确率,如Stewart等[12]采用大腿和后腰2组加速度计数据时,识别6种身体活动类型的准确率为97.3%,当采用1组加速度计数据时准确率下降了26.4%。随着特征提取的不断丰富,模型的时间分辨率也得到了提高,如早期研究的时间分辨率多为1 min[5],之后有研究将模型的时间分辨率提升至10 s[11]、5 s[12],不过对于评价具有短时特征的儿童身体活动而言,模型的时间分辨率仍需改进。
以往研究表明,人工提取特征的机器学习算法很难基于1组加速度计数据实现高准确率、高时间分辨率识别多种儿童身体活动类型,端到端的深度学习算法成为突破身体活动分类问题壁垒的新方法。Jang等[15]的研究便证实了深度学习算法基于1组加速度计数据就可以良好识别10种儿童身体活动类型,其构建的卷积神经网络模型准确率为81.3%,比K近邻、决策树、支持向量机模型的准确率高16%~26%,不过81.3%的分类准确率使其模型在身体活动评价实践中的应用价值仍有局限。
基于身体活动评价的实践需求,本文通过构建高准确率、高时间分辨率的儿童身体活动类型识别模型,证明深度学习算法基于1组加速度计数据识别多种儿童身体活动类型的优越性;通过将模型应用于自主设计的身体活动评价程序,输出身体活动案例的“整段活动以及其中每种活动类型的持续时间、平均计数与不同强度等级占比的数据统计表”“活动类型、强度等级、活动计数在同一时间轴上的对应分布图”,证明身体活动类型识别算法对提高儿童身体活动评价的全面性、直观性、精准性具有重要价值。
1 研究1:儿童身体活动类型识别模型的构建 1.1 数据信息Jang等[15]采集并发布了10种儿童身体活动(跳绳、静止、快跑、慢跑、走下楼梯、走上楼梯、快走、慢走、坐下去、站起来)的公开数据集,该数据采集方案已获得韩国加图立大学(Catholic University of Korea)和首尔圣玛丽医院(Seoul St. Mary's Hospital)的批准。以下就研究数据涉及的研究对象、加速度计设备、数据采集程序、数据预处理、动作任务信息等进行说明。
1.1.1 研究对象研究被试为韩国一所学校和多个体育俱乐部的136名儿童,排除身体与精神疾病者以及采集过程或意外噪声造成的数据无效者,最终获得115名儿童的有效数据,其中75名男孩、40名女孩,年龄在8.5~12.5岁,平均年龄为(10.5±1.1)岁。
1.1.2 数据采集(1)加速度计设备。Jang等[15]在研究中设计了可穿戴加速度计系统,由单片机、三轴加速度传感器、存储芯片、电源单元等组成。设备中只有1个三轴加速度计,没有其他传感器,因此最大限度地减少了传感器信号和电源的使用,同时也提高了便携性。该加速度计范围设置为±4g(g为重力加速度),尺寸为50 mm×30 mm×15 mm,重21 g。电子板外面配有一个带夹子的盒子,可以将其固定在裤子上(图 1)。

|
| 图 1 数据采集系统外观[15] Figure 1 Appearance of devised data acquisition system |
(2) 数据采集程序。要求每个被试完成10个动作,分A、B、C 3组。A组动作包括静止(站立或坐)、坐站交替(包括站起来与坐下去),B组动作包括在平地上的慢走、快走、慢跑、快跑,C组动作包括走上楼梯、走下楼梯、跳绳。为避免练习顺序造成的干扰,将被试随机分成6种组合测试:ABC、ACB、BAC、BCA、CAB、CBA。在执行动作任务时,被试需沿着裤子腰线且在腹部中央和右骨盆之间佩戴加速度计,加速度计的采样频率为45.4 Hz。每种动作任务时间是固定的:静止3 min,坐站交替4 min,跳绳3 min,慢跑、快跑、慢走、快走、走上楼梯、走下楼梯均为2 min。其中,任何动作任务的速度都由被试根据自身感受自行决定,如被试在完成快跑与慢跑2个任务时,只需根据自己的身体感受定义什么速度是快、什么速度是慢,并以此为依据完成动作任务。无论被试完成哪一种动作组合,其每完成一个动作任务都需进行休息,待恢复到安静心率再进行下一个动作任务,休息时间不作严格限制,通常为2~5 min。
1.1.3 数据预处理Jang等[15]在研究中的数据预处理情况如表 1和图 2所示。
| 表 1 数据预处理具体信息[15] Table 1 Data acquisition and data preprocessing |

|
| 图 2 动作任务数据裁剪与数据窗口切片示意[15] Figure 2 Schematic diagram of action task data clipping and data window slicing |
由于此公开数据保存为.mat文件,以元包数组(cell)类型表示,本文使用Python的第三方库H5py将其转换为numpy的数组(array)类型。得到的数据样本共18 357个,各种身体活动类型的样本量在1 000~2 500个,每个样本为128个数据点(约2.8 s),具体情况见表 2、图 3。
| 表 2 数据集动作任务信息 Table 2 Information of the action task in data set |

|
| 图 3 10种儿童身体活动类型原始数据 Figure 3 Raw data display of ten types of physical activity for children |
使用Tensorflow 2.4深度学习框架搭建神经网络;使用Scikitlearn机器学习库计算并输出评估模型的十折交叉验证结果、混淆矩阵、准确率、精准率、召回率、F1分数;使用Matplotlib库输出身体活动原始数据图和混淆矩阵图。
1.2.2 算法设计深度学习技术定义为学习数据表示的多级方法,是机器学习的一个分支领域,是从数据中学习表示的一种新方法,强调从连续的层(layer)中进行学习[16]6。深度学习善于从原始数据中提取抽象的分布式特征表示,而深层神经网络是深度学习的主要形式[17]。本文涉及的卷积神经网络、全连接神经网络、残差卷积神经网络都是深度神经网络中广泛应用的网络结构。
本文设计并对比了全连接神经网络、卷积神经网络、残差卷积神经网络,最终确定了识别准确率最高的残差卷积神经网络作为识别儿童身体活动类型的算法。以下具体陈述神经网络架构与模型训练策略,另外还复述了Jang等[15]搭建的网络模型,作为基线网络供研究者参考对比。
(1)神经网络架构与模型训练策略。本文设计的残差卷积神经网络(图 4),以原始的三轴加速度信号数据片段(数据维度为128×3,大约2.8 s)为输入,最终输出每个片段的预测类别。神经网络架构的特征提取共包含12层,其中9个卷积层、3个全连接层。为加深神经网络架构,采用类似于残差网络的快捷连接(shortcut)[18]设计了7个残差块,每个残差块有1个池化层、1个卷积层,并进行批标准化(BatchNorm)和激活(ReLU)。最终由全连接的Softmax层在10个输出类别上产生分布。

|
| 图 4 残差卷积神经网络架构 Figure 4 Residual convolution neural network architecture 注:Input为输入,Conv1D为一维卷积层,BatchNorm为批标准化,ReLU为激活函数(线性纠正函数),Maxpool1D为一维池化层,Dense为全连接层,Softmax为分类器(归一化指数函数);输出的10个类别分别为慢走(Walk Slow,WS)、快走(Walk Fast,WF)、慢跑(Run Slow,RS)、快跑(Run Fast,RF)、走上楼梯(Stair Up,SU)、走下楼梯(Stair Down,SD)、坐下去(Sit Down,SI)、站起来(Stand Up,ST)、跳绳(Jump Rope,JR)、静止(None,NO)。 |
采用有监督训练模式,使用Adam优化器,默认参数β1=0.9和β2=0.999,将多分类交叉熵(categorical-crossentropy)作为损失函数,数据输入尺寸设置为16,手动调整初始学习速率为0.001以实现最快的收敛,通过早期停止策略(early stopping)监控验证集损失函数(val-loss),参数为10。通过网格搜索找到优化网络结构的最优超参数(表 3),包括卷积滤波器的大小、数量和全连接层节点数量,手动调整残差层数量为7。
| 表 3 残差卷积神经网络超参数的网格搜索结果 Table 3 Grid search results of the hyperparameters of residual convolution neural network |
模型训练中数据集划分是否尽可能实现独立同分布(训练集与测试集中被试不交叉且各分区中的类别比例相等)是评估模型泛化能力的常用方法。Jang等[15]发布的数据集中每个被试每种活动类型的数据都不是完全相等的,为便于在数据集划分时最大限度地实现独立同分布,他们将数据集分为10个部分,每个部分为1种活动类型的数据,由所有被试在该活动类型上的数据按顺序拼接而成。10个部分即为10种活动类型的数据,且每个部分中被试的数量、顺序完全一致。基于数据集的实际情况,本文先将每种活动类型数据平均切成10段并按顺序标注索引,从索引号中随机选取1个数字,将标注该索引号的10种活动类型数据拼接成测试集(1 832个样本),剩余部分数据为训练集(16 525个样本)。为避免单次随机划分数据集造成的模型性能不稳定[16]70,在训练集中进行十折交叉验证,将每种活动类型数据按顺序平均划分成10个分区并标注索引,每次将1个索引相同的分区拼接成验证集用于模型评估,剩余9个分区的数据用于模型训练(训练之前随机打乱),循环10次。如此操作使得训练集与测试集以及十折交叉验证中的数据集(再次划分的训练集与验证集)都最多有2个被试交叉,将被试交叉效应降到最低,同时保证了每个分区中类别的比例相等。
(2)基线神经网络。Jang等[15]以3层卷积神经网络为基线网络(图 5),使用MATLAB搭建神经网络,包括输入层、特征提取层与分类输出层。输入层的数据维度(长度×宽度×通道)为128×1×3,特征提取层包括3个二维卷积层和3个池化层,分类输出层包括2个全连接层,并在Softmax层上产生10个身体活动类别的概率分布。该模型训练为有监督训练,采用随机梯度下降(SGD)优化器,初始学习率为0.003,数据输入尺寸为128,3层卷积滤波器大小分别为7×1、6×1、5×1的矩阵,卷积滤波器数量分别为72、144、108,全连接层节点数量为256,采用早期停止策略[15]。

|
| 图 5 基线网络架构[15] Figure 5 Baseline network architecture 注:Input为输入,Conv2D为二维卷积层,Maxpool2D为二维池化层,ReLU为激活函数(线性纠正函数),Dense为全连接层,Dropout为随机丢失正则化,Softmax为分类器(归一化指数函数);输出的10个类别分别为慢走(Walk Slow,WS)、快走(Walk Fast,WF)、慢跑(Run Slow,RS)、快跑(Run Fast,RF)、走上楼梯(Stair Up,SU)、走下楼梯(Stair Down,SD)、坐下去(Sit Down,SI)、站起来(Stand Up,ST)、跳绳(Jump Rope,JR)、静止(None,NO)。 |
混淆矩阵可表示样本真实属性和输出类别之间的关系,常被用于评估神经网络模型的性能。混淆矩阵的定义[19]如表 4所示。
| 表 4 混淆矩阵的定义 Table 4 The definition of confusion matrix |
根据混淆矩阵中的数据可以得到准确率、精准率、召回率、特异度的公式(表 5)。
| 表 5 准确率、精准率、召回率、特异度的公式与含义 Table 5 Formula and meaning of accuracy, precision, recall and specificity |
由于召回率和精准率常会出现矛盾,这时需要通过F1分数(F1-score)进行综合考量,其公式为:
| $ {{F}_{1}}=TP/[TP+(FN+FP)/2] $ | (1) |
其中,TP(True Positive)是模型把真实值为正类预测为正类的数量,FP(False Positive)是模型把真实值为负类预测为正类的数量,FN(Fasle Negative)是模型把真实值为正类预测为负类的数量,F1分数的取值范围为0~1,其值越接近1代表输出结果越好,越接近0代表输出结果越差。
1.3 研究结果与分析 1.3.1 不同算法识别儿童身体活动类型的准确率对比在识别10种身体活动类型的任务中,Jang等[15]设计的最优算法为二维卷积神经网络模型,准确率为(81.2±0.6)%;本文设计的最优算法为残差卷积神经网络模型,准确率为(91.6±0.4)%,相比前人研究提高了10%左右(表 6)。
| 表 6 不同算法识别10种儿童身体活动类型的准确率对比 Table 6 Comparison of the accuracy of different algorithms for identifying ten types of physical activity |
经过十折交叉验证,残差卷积神经网络模型识别10种身体活动类型的结果如表 7所示。
| 表 7 识别10种身体活动类型的残差卷积神经网络模型评估 Table 7 The evaluation of the model performance on recognizing ten types of physical activity |
残差卷积神经网络模型的识别能力总体上较好(表 7),经过十折交叉验证后平均准确率达到(91.6±0.4)%。除“走上楼梯”和“跳绳”外,其余活动类型识别的精准率与召回率都很高,全部在97%以上,且精准率与召回率不存在矛盾现象。十折交叉验证中的最优模型预测测试集的准确率为92.6%,说明模型的泛化能力较好。
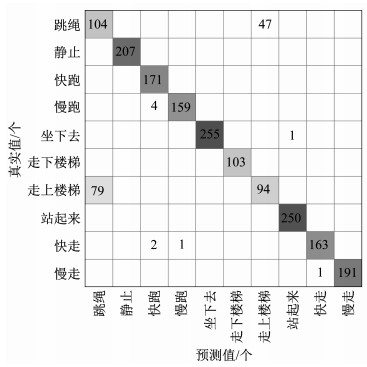
结合混淆矩阵(图 6)来看,“走上楼梯”和“跳绳”识别情况不好的原因是它们之间存在相互混淆。基于此,将这2类身体活动的数据归为1类(跳绳与走上楼梯)后,对9种身体活动类型进行识别,经过十折交叉验证得出结果如表 8和图 7所示。
|
| 图 6 最优模型预测测试集的混淆矩阵(识别10种活动类型) Figure 6 Confusion matrix for optimal model prediction test set (identifying ten types of physical activity) 注:最优模型预测测试集的准确率为92.6%。 |
| 表 8 识别9种身体活动类型的模型评估 Table 8 The evaluation of the model performance on recognizing nine types of physical activity |

|
| 图 7 最优模型预测测试集的混淆矩阵(识别9种活动类型) Figure 7 Confusion matrix for optimal model prediction test set (identifying nine types of physical activity) 注:最优模型预测测试集的准确率为99.3%。 |
残差卷积神经网络模型在识别9种身体活动类型的任务中表现出了优越的性能,经过十折交叉验证得到的平均准确率为(99.3±0.3)%,每个活动类型的F1分数都在0.97以上。然而,模型在识别9种身体活动类型时,对于“快跑”与“慢跑”的识别性能较识别10种身体活动类型时略有逊色。十折交叉验证中的最优模型预测测试集的准确率为99.3%,说明模型的泛化能力较好。
2 研究2:儿童身体活动类型识别模型在身体活动评价中的应用实践应用是人工智能发展的动力,儿童身体活动类型识别模型在身体活动评价中的应用是其价值的重要体现。研究1构建的儿童身体活动类型识别模型具备准确率高、时间分辨率高的特点,研究2将其应用于探讨活动类型、活动时间、活动强度深度融合的身体活动评价方式,以展现身体活动类型识别在身体活动评价中的重要作用。由于现实身体活动案例中很可能包含模型预测分类之外的活动类型,将模型应用于身体活动案例评价之前,须验证模型在识别预测分类之外的活动类型时是否依然保持较高准确率。
因此,研究2包括两部分内容:①评估模型在活动案例中识别活动类型的准确率;②使用自主设计的身体活动评价程序,以1个活动案例为例探讨活动类型识别在身体活动评价中的应用方式。
2.1 研究方法 2.1.1 研究工具运行环境为Python 3.8,使用Tensorflow 2.4深度学习框架运行神经网络,使用Scikitlearn机器学习库计算并输出混淆矩阵及准确率,使用sensormotion库计算身体活动计数,使用Matplotlib库生成身体活动案例图、分类概率阈值与识别准确率的关系曲线图,以及活动类型、强度等级、活动计数的时间分布图。
2.1.2 评估模型在活动案例中识别活动类型准确率的研究方法模型应用于实践须具备识别预测分类之外活动类型的能力,那么将模型应用于身体活动案例评价之前,须验证模型在识别预测分类之外的“其他”活动类型时是否依然保持较高准确率。因此,研究2生成了1 000个包含“其他”活动类型的儿童身体活动案例,并评估模型在1 000个案例识别中的性能,以此判断模型能否应用于身体活动案例的评价。
(1)身体活动案例生成方法。为评估模型在活动案例中识别活动类型的准确率,研究2生成了1 000个儿童身体活动案例,生成案例的数据来源为研究1的测试集,身体活动案例生成的方法与依据如表 9所示。
| 表 9 身体活动案例生成的方法与依据 Table 9 Methods for generating physical activity cases |
(2)“其他”身体活动类型的识别方法。在案例中添加“其他”活动类型来验证模型识别预测分类之外活动类型的能力。在模型识别中,每个样本经过Softmax层都会产生9个分类概率值,即样本被分别预测为跳绳与走上楼梯、静止、快跑、慢跑、走下楼梯、快走、慢走、坐下去、站起来的概率。设置1个分类概率阈值,若最大分类概率小于此值则将样本识别为“其他”活动类型,若最大概率高于此值则将概率值最大的那个类别判定为样本的类别。
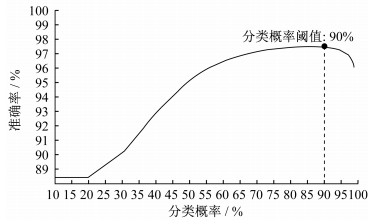
分类概率阈值的探索过程为:首先随机生成1 000个案例(该案例只用于阈值的探索,用于模型评估的1 000个案例另外生成),按照设置的每个分类概率阈值进行尝试,分别得出识别1 000个案例的平均准确率,结果如图 8所示。通过尝试发现分类概率阈值设置为90%时,模型识别跳绳与走上楼梯、静止、快跑、慢跑、走下楼梯、快走、慢走、坐下去、站起来、其他等10种活动类型的准确率最高,达到(97.5±1.4)%,因此将分类概率低于90%的样本识别为“其他”身体活动类型。
|
| 图 8 分类概率阈值与识别准确率的关系 Figure 8 The relationship between the threshold of classification probability and the accuracy of recognition |
(3)提高身体活动类型识别准确率的修正方法。采用窗口滑动方法发现身体活动类型识别错误的位置并予以修正。设置1个大小为5的滑动窗口,滑动步长为1。滑动窗口内的5个样本中,前2个与后2个样本活动类型相同且与中间1个样本活动类型不同时,将中间1个样本的活动类型修正为与前后一致。这种方法可以修正一段相同类型活动(5个样本以上,大约14 s)中的单个错误样本,而无法修正连续多个或出现在一段活动的开头与结尾的错误样本,但考虑到这样的错误很少,无须为了修正它们而放弃程序的高时间分辨率(2.8 s)优势。使用配对样本t检验的方法,检验模型对1 000个案例的识别率在修正前与修正后是否存在差异,以说明修正的必要性,显著性水平设置为P<0.001。
(4)模型评估方法。将研究1构建的儿童身体活动类型识别模型应用于活动案例,需要识别的活动类型比研究1中多一类“其他”类型活动(即模型预测分类之外的活动类型),模型识别准确率会发生变化,因此对模型在活动案例中的识别性能进行了评估。模型评估仍使用Scikitlearn机器学习库计算混淆矩阵并输出准确率,相关原理在研究1的研究方法中已有阐述。
2.1.3 身体活动评价程序设计本文设计的基于身体活动类型识别模型的身体活动评价程序包含3个部分,具体如表 10所示。
| 表 10 身体活动评价程序设计思路 Table 10 Programming of physical activity assessment |
身体活动评价程序最终输出的信息包括:整段活动以及其中每种活动类型的持续时间、平均计数与不同强度等级占比的数据统计表,以及活动类型、强度等级、活动计数在同一时间轴上的对应分布图。这些信息的输出都是基于活动类型的识别结果、活动计数结果、强度等级划分结果计算而得的。以下就完成信息输出涉及的所有计算方法加以说明。
(1)身体活动类型的识别。应用本文构建的残差卷积神经网络模型完成案例中身体活动类型的识别。
(2)活动计数。使用加速度计的活动计数评价身体活动强度已被广泛认可,很多学者通过使用ActiGraph配套软件(Actilife)得到了活动计数结果,而近年来有不少学者也研究并开源了与“ActiGraph Counts”算法结果接近的活动计数算法。本文采用sensormotion库[1]计算活动计数:使用Scipy库进行butter和filtfilt滤波,设置采样间隔(epoch)为1 s;使用sensormotion库的三轴融合计数函数进行运算。
(3)强度等级划分。查阅儿童身体活动强度临界值的相关研究后,选择其中加速度计佩戴在右髋部、采用ActiGraph三轴计数算法(Vector Manitude,VM),且以相同能耗标准划分身体活动强度的研究[21-24]:METs < 1.5为静息状态(Sedentary,SED),1.5≤METs < 3.0为低强度身体活动(Light Physical Activity,LPA),3.0≤METs < 6.0为中强度身体活动(Middle Physical Activity,MPA),6.0≤METs < 9.0为高强度身体活动(Vigorous Physical Activity,VPA),METs≥9.0为超高强度身体活动(Very Vigorous Physical Activity,VVPA)。
如表 11所示,前人[21-24]研究结果之间虽有出入,但这在身体活动强度临界点划分的研究中较为常见[25],目前难以达成共识。Hänggi等[21]与Romanzini等[22]的研究在静息状态临界点划分上有差异,原因是Hänggi等[21]将“站立”归为低强度运动[其研究的多个动作中唯独没有描述“站立”对应的METs,“站立”的每秒活动计数为(3.79±4.20)个],而Romanzini等[22]将“站立”归为静息状态(METs=1.3),事实上,不少研究结果都显示“站立”动作的METs小于1.5,应归为静息状态。
| 表 11 儿童身体活动强度临界值的既往研究结果 Table 11 The previous research results about threshold of physical activity intensity |
由于儿童身体活动的短时特点,有研究[26]发现,高时间分辨率可更准确地分析儿童身体活动案例。Hänggi等[21]的研究虽然符合高分辨率的要求,但其中SED临界值的设置不宜采用。本文选用活动强度区间涵盖较全的朱琳等[24]的研究结果,由于其研究结果缺少静息状态与轻强度的临界点,故选用Romanzini等[22]研究中静息状态下的临界点,并将这些研究结果的单位时间转换为1 s,使活动强度等级划分的时间分辨率更高。因此,本文的强度等级划分标准为:每秒计数SED≤12、12 < LPA≤63、63 < MPA≤103、103 < VPA≤171、VVPA > 171。不过1 s间隔与60 s间隔在强度区分的效度上可能会有差异。
研究2致力于探讨活动类型识别在身体活动评价中的应用方式,划分强度临界点的目的是展示将身体活动类型与活动强度等级相融合的评价方式,因此不再进行能耗预测来验证强度临界点划分的有效程度。
(4)身体活动评价程序输出内容及其计算方法如表 12所示。
| 表 12 身体活动评价程序输出内容及其计算方法 Table 12 The outputs and calculation methods of physical activity evaluation program |
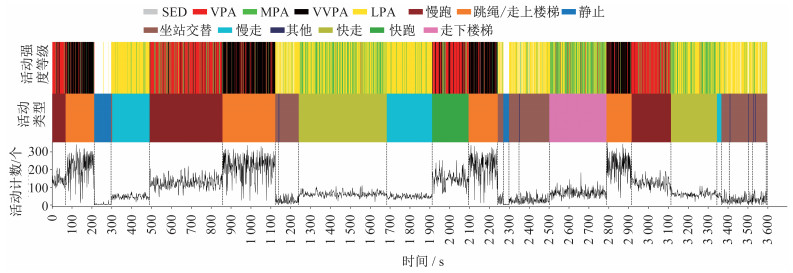
|
| 图 9 整段活动的强度等级、活动类型与活动计数在时间轴上的分布及其对应关系 Figure 9 The distribution and congruent relationship of intensity, type and count on the time axis of the whole activity 注:以上为模型识别后的数据;SED为静息状态,LPA为低强度身体活动,MPA为中强度身体活动,VPA为高强度身体活动,VVPA为超高强度身体活动。 |
为验证模型在识别预测分类之外的活动类型时是否依然保持高准确率,对模型在活动案例中的识别性能进行了评估。评价程序中的自定义规则修正了部分识别错误,因此对修正前后1 000个案例的准确率都进行了计算,修正前后1 000个案例的准确率分布如图 10所示、准确率差异显著性检验结果如表 13所示。

|
| 图 10 修正前后1 000个案例的识别准确率分布 Figure 10 The accuracy distribution of recognizing 1 000 cases before and after correction 注:区间1为准确率≥99.9%,区间2为99.5%≤准确率 < 99.9%,区间3为99.0%≤准确率 < 99.5%,区间4为98.0%≤准确率 < 99.0%,区间5为95.0%≤准确率 < 98.0%,区间6为90.0%≤准确率 < 95.0%。 |
| 表 13 修正前后1 000个案例的准确率差异配对样本t检验结果 Table 13 The paired-sample t test results of recognizing the accuracy of 1 000 cases before and after correction |
修正前的准确率在95.0%~99.0%区间上比较集中,而修正后的准确率主要分布在98.0%~99.9%区间上,尤其是在大于99.5%与小于98.0%的区间上修正前后的准确率差异非常明显。经检验,修正前后的识别准确率有显著差异(P < 0.001),说明修正初次识别结果十分必要。修正后准确率为(99.1±1.0)%,说明模型在识别案例(包含预测分类之外的“其他”活动类型)时也有较好的性能,可以应用于身体活动评价实践。
2.2.2 儿童身体活动类型识别在身体活动评价中的应用方式以往的身体活动评价往往只描述“整段活动中不同运动强度等级的持续时间”,人们难以了解身体活动的活动类型、持续时间、活动强度等多方面信息,更不能直观地看到这些信息在时间轴上的对应关系与变化过程。为解决这些问题,自主设计了身体活动评价程序,在高准确率与高时间分辨率的身体活动类型识别模型基础上,实现了活动类型与活动强度在时间轴上的逐秒对应。研究2将这种活动类型、活动时间、活动强度深度融合的身体活动评价方式通过案例的形式展示出来,希望为身体活动评价的全面化、直观化、精准化提供一种思路。随机抽取1 000个案例中的1个案例,使用身体活动评价程序输出相关结果如图 11所示。

|
| 图 11 身体活动案例 Figure 11 Physical activity cases |
将整段活动以及其中各个活动类型对应的时间、活动强度及强度等级占比进行详细统计(表 14)。图 9直观地展示了活动类型、活动计数、强度等级在以秒为单位的时间轴上的变化过程以及三者精确的对应关系。基于图表输出的结果,可以清晰地看出:活动中有6.1%的静息状态,主要由于活动中存在2 min左右的静止状态以及坐站交替动作中有少部分强度极小的活动;活动中有37.2%的低强度身体活动,主要来自约17 min的慢走与坐站交替动作以及部分强度较低的快走活动;活动中有18.5%的中等强度身体活动,主要来自约11 min的快走和约5 min的走下楼梯中强度相对较高的部分;活动中有18.5%的高强度身体活动,主要来自约10 min的慢跑以及约3 min的快跑中强度相对较高的部分;活动中有19.7%的超高强度身体活动,主要来自约11 min的跳绳/走上楼梯以及快跑中强度最高的部分。从时间轴上看,基于活动类型划分的分段活动时间多为1~4 min,只有静止状态、慢走、“其他”活动存在零星的短时活动,活动强度全程呈现高低交替的特征。
| 表 14 整段活动以及其中每种活动类型的持续时间、平均计数与不同强度等级占比 Table 14 The proportion of duration, average count and different intensity levels in whole and segmented physical activity |
身体活动评价程序输出的结果直观展示了高时间分辨率、高准确率的身体活动类型识别结果在身体活动评价中的重要作用,如展现活动形式的多样性、展示活动过程、精确计算活动时间(分段或整段)、辅助判断活动强度等。而活动类型、活动计数、强度等级的时间序列数据逐秒对应融合并实现可视化,为身体活动评价提供了多模态数据展示评价结果的新思路。
3 讨论研究1证明了端到端的深度学习方法可以高效分类动作相似但强度不同的身体活动类型(快跑、慢跑、快走、慢走),也可以对短时动作“站起来”与“坐下去”进行高效识别,突破了以往识别身体活动类型的局限;对跳绳与走上楼梯、静止、快跑、慢跑、走下楼梯、快走、慢走、坐下去、站起来等9种身体活动类型的识别准确率达到99%以上的优越性能,时间分辨率约为2.8 s,无论是在身体活动类型的数量、准确率以及时间分辨率方面都比以往研究有很大提高,使身体活动类型识别的研究成果可以有充分的条件应用于身体活动评价实践。
研究2验证了模型应用于活动案例(包括模型预测分类之外的活动类型)识别中仍然保持97.7%的准确率,通过自定义规则修正识别错误后模型识别准确率达到99.1%。由于模型满足了高准确率与高时间分辨率的条件,研究2将其应用于自主设计的身体活动评价程序,以1个活动案例为例展示了将活动类型、活动时间、活动强度深度融合的身体活动评价方式。程序通过输出整段活动以及其中每种活动类型的持续时间、平均计数与不同强度等级占比的数据统计表,丰富了对活动类型、持续时间、活动强度对应关系的数据描述;通过输出活动类型、强度等级、活动计数的时间分布图,直观展示了身体活动类型与活动强度在时间轴上的分布及其对应关系。
本文的贡献在于:①构建了高准确率、高时间分辨率的儿童身体活动类型识别模型;②通过自主设计的运用活动类型识别模型的身体活动评价程序,直观展示了视角多方位、细节可视化、过程可追踪的儿童身体活动评价方式。
儿童身体活动类型识别模型的高准确率往往比较受重视,而其高时间分辨率很容易被忽视。事实上,不少研究发现,儿童身体活动存在短时性与间歇性的簇集特征。Bailey等[5]通过主观观察儿童身体活动簇集特征,发现6~10岁儿童中低强度身体活动持续时间的中位数为6 s,高强度身体活动持续时间的中位数为3 s,即使在青少年时期,其身体活动仍然存在短时性、间歇性特征[27-28]。基于此,有研究[20]提出,在儿童身体活动测量中加速度计尽量采用5 s内的采样间隔以将误差最小化;也有研究[26]认为,1 s的采样间隔获取的数据才能真实反映身体活动强度状况;还有研究[29]指出,高分辨率身体活动数据能更准确地发现儿童身体活动与健康之间的关系。很多证据都证明了运用高时间分辨率的数据分析工具才能实现儿童身体活动的准确分析,因此本文设计的神经网络模型以2.8 s的时间分辨率来识别儿童身体活动类型,使其具备了应用于儿童身体活动评价实践的条件。
虽然本文在模型的准确率与时间分辨率方面比前人研究有较大的提高,但仍存在一些不足,如走上楼梯与跳绳动作的混淆问题,本文尝试了时空卷积,仍然没有改善。本文还尝试通过活动计数来区分二者,发现二者在活动计数上并无显著差异(表 15)。Jang等[15]在研究中也提到了同样的问题,认为这可能与儿童在做跳绳动作时会出现双脚交替的情况(而不是一直双脚跳)有关,笔者认同这一观点。此外笔者还认为这跟加速度计的佩戴位置有关,当加速度计佩戴在髋部时采集到的这2种活动数据比较相似,身体活动原始数据(图 3)可以佐证这一观点。未来若要实现跳绳与走上楼梯2种活动类型的区分可能需采集佩戴在其他身体部位(如腕部)的加速度计数据。
| 表 15 跳绳与走上楼梯2种活动类型的活动计数差异检验 Table 15 The variance analysis of the activity counts of Jump Rope and Stair Up |
除了走上楼梯与跳绳动作识别的混淆问题外,涉及的身体活动类型还有待进一步丰富,如增加旋转、投掷、骑车等相对复杂的动作。以往研究[30-31]表明,复杂动作需佩戴多个加速度计才可准确识别,而佩戴多个加速度计的测量方式会增加身体活动测量的经济与运算成本,自然也会增加推广难度,努力实现使用1个加速度计识别多种活动类型是面向实践应用的重要研究方向,也是未来需深入探讨的议题。
4 结论本文构建的残差卷积神经网络模型在区分跳绳/走上楼梯、静止、快跑、慢跑、走下楼梯、快走、慢走、坐下去、站起来等9种儿童身体活动类型时准确率达到99.3%,模型识别活动案例的准确率也达到99.1%,模型时间分辨率为2.8 s。模型的高准确率、高时间分辨率为儿童身体活动类型识别在身体活动评价中发挥重要作用奠定了坚实基础。将模型应用于自主设计的儿童身体活动评价程序,展示了将活动类型、活动时间、活动强度深度融合的身体活动评价方式,为实现儿童身体活动评价的多视角、可视化、可追踪提供了一种新思路。
作者贡献声明:
杨锋:检索文献,提出论文主题,深度学习算法设计与实现,修改论文;
付晓蒙:检索文献,设计论文框架,数据核实与可视化,撰写论文;
张庭然:梳理文献;
罗炯:评估和修改研究方案。
| [1] |
SIMON H O. Sensormotion[EB/OL]. [2021-03-22]. https://pypi.org/project/sensormotion/
(  0) 0)
|
| [2] |
ALEX. Actigraph[EB/OL]. [2021-03-22]. https://bitbucket.org/atpage/actigraph/src/master/
(  0) 0)
|
| [3] |
GREGORY H, MATHILDE R. PyActigraphy[EB/OL]. [2021-03-22]. https://pypi.org/project/pyActigraphy/
(  0) 0)
|
| [4] |
孙建刚, 柯友枝, 洪金涛, 等. 利器还是噱头: 可穿戴设备在身体活动测量中的信效度[J].
上海体育学院学报, 2019, 43(6): 29-38 (  0) 0)
|
| [5] |
BAILEY R C, OLSON J, PEPPER S L, et al. The level and tempo of children's physical activities: An observational study[J].
Medicine and Science in Sports and Exercise, 1995, 27(7): 1033-1041 DOI:10.1249/00005768-199507000-00012 (  0) 0)
|
| [6] |
ADAMO K B, PRINCE S A, TRICCO A C, et al. A comparison of indirect versus direct measures for assessing physical activity in the pediatric population: A systematic review[J].
International Journal of Pediatric Obesity, 2009, 4(1): 2-27 DOI:10.1080/17477160802315010 (  0) 0)
|
| [7] |
AGUILAR-FARIAS N, MIRANDA-MARQUEZ S, TOLEDO-VARGAS M, et al. Comparison between selfreported and accelerometer-derived measurements for classifying children and adolescents as physically active in Chile[J].
Cadernos De Saúde Pública, 2021, 37(2): e00240620 DOI:10.1590/0102-311x00240620 (  0) 0)
|
| [8] |
RUCH N, RUMO M, MADER U. Recognition of activities in children by two uniaxial accelerometers in free-living conditions[J].
European Journal of Applied Physiology, 2011, 111(8): 1917-1927 DOI:10.1007/s00421-011-1828-0 (  0) 0)
|
| [9] |
DE VRIES S I, ENGELS M, GARRE F G. Identification of children's activity type with accelerometer-based neural networks[J].
Medicine and Science in Sports and Exercise, 2011, 43(10): 1994-1999 DOI:10.1249/MSS.0b013e318219d939 (  0) 0)
|
| [10] |
STAUDENMAYER J, POBER D, CROUTER S, et al. An artificial neural network to estimate physical activity energy expenditure and identify physical activity type from an accelerometer[J].
Journal of Applied Physiology, 2009, 107(4): 1300-1307 DOI:10.1152/japplphysiol.00465.2009 (  0) 0)
|
| [11] |
TROST S G, WONG W K, PFEIFFER K A, et al. Artificial neural networks to predict activity type and energy expenditure in youth[J].
Medicine and Science in Sports and Exercise, 2012, 44(9): 1801-1809 DOI:10.1249/MSS.0b013e318258ac11 (  0) 0)
|
| [12] |
STEWART T, NARAYANAN A, HEDAYATRAD L, et al. A dual-accelerometer system for classifying physical activity in children and adults[J].
Medicine and Science in Sports and Exercise, 2018, 50(12): 2595-2602 DOI:10.1249/MSS.0000000000001717 (  0) 0)
|
| [13] |
REN X, DING W, CROUTER S E, et al. Activity recognition and intensity estimation in youth from accelerometer data aided by machine learning[J].
Applied Intelligence, 2016, 45(2): 512-529 DOI:10.1007/s10489-016-0773-3 (  0) 0)
|
| [14] |
ELLIS K, KERR J, GODBOLE S, et al. A random forest classifier for the prediction of energy expenditure and type of physical activity from wrist and hip accelerometers[J].
Physiological Measurement, 2014, 35(11): 2191-2203 DOI:10.1088/0967-3334/35/11/2191 (  0) 0)
|
| [15] |
JANG Y, KIM S, KIM K, et al. Deep learning-based classification with improved time resolution for physical activities of children[J].
PeerJ, 2018, 6: e5764 DOI:10.7717/peerj.5764 (  0) 0)
|
| [16] |
肖莱. Python深度学习[M]. 张亮, 译. 北京: 人民邮电出版社, 2018
(  0) 0)
|
| [17] |
周飞燕, 金林鹏, 董军. 卷积神经网络研究综述[J].
计算机学报, 2017, 40(6): 1229-1251 (  0) 0)
|
| [18] |
HANNUN AY, RAJPURKAR P, HAGHPANAHI M, et al. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network[J].
Nature Medicine, 2019, 25(1): 65-69 DOI:10.1038/s41591-018-0268-3 (  0) 0)
|
| [19] |
彭如香, 杨涛, 孔华锋, 等. 基于CPD-SMOTE的类不平衡数据分类算法研究[J].
计算机应用与软件, 2018, 35(12): 259-262, 268 (  0) 0)
|
| [20] |
MCCLAIN J J, ABRAHAM T L, BRUSSEAU T A, et al. Epoch length and accelerometer outputs in children: Comparison to direct observation[J].
Medicine and Science in Sports and Exercise, 2008, 40(12): 2080-2087 DOI:10.1249/MSS.0b013e3181824d98 (  0) 0)
|
| [21] |
HÄNGGI J M, PHILLIPS L R S, ROWLANDS A V. Validation of the GT3X ActiGraph in children and comparison with the GT1M ActiGraph[J].
Journal of Science and Medicine in Sport, 2013, 16: 40-44 DOI:10.1016/j.jsams.2012.05.012 (  0) 0)
|
| [22] |
ROMANZINI M, PETROSKI E L, OHARA D, et al. Calibration of ActiGraph GT3X, Actical and RT3 accelerometers in adolescents[J].
European Journal of Sport Science, 2014, 14(1): 91-99 DOI:10.1080/17461391.2012.732614 (  0) 0)
|
| [23] |
SANTOS-LOZANO A, SANTIN-MEDIROS F, CARDON G, et al. Actigraph GT3X: validation and determination of physical activity intensity cut points[J].
International Jeurnal of Sports Medicine, 2013, 34: 975-982 DOI:10.1055/s-0033-1337945 (  0) 0)
|
| [24] |
朱琳, 陈佩杰. 应用ROC曲线确定活动计数在青春期少年运动强度诊断中的最佳临界值[J].
体育科学, 2012, 32(11): 70-75 DOI:10.3969/j.issn.1000-677X.2012.11.009 (  0) 0)
|
| [25] |
MIGUELES J H, CADENAS-SANCHEZ C, EKELUND U, et al. Accelerometer data collection and processing criteria to assess physical activity and other outcomes: A systematic review and practical considerations[J].
Sports Medicine, 2017, 47(9): 1821-1845 DOI:10.1007/s40279-017-0716-0 (  0) 0)
|
| [26] |
王超, 陈佩杰, 庄洁, 等. 加速度计以不同采样间隔测量儿童青少年日常体力活动时间的一致性研究[J].
中国运动医学杂志, 2012, 31(9): 759-765, 771 DOI:10.3969/j.issn.1000-6710.2012.09.001 (  0) 0)
|
| [27] |
AIBAR A, BOIS J E, ZARAGOZA J, et al. Do epoch lengths affect adolescents' compliance with physical activity guidelines?[J].
The Journal of Sport Medicine and Physical Fitness, 2014, 54(3): 326-334 (  0) 0)
|
| [28] |
AIBAR A, CHANAL J. Physical education: The effect of epoch lengths on children's physical activity in a structured context[J].
PLoS One, 2015, 10(4): e0121238 DOI:10.1371/journal.pone.0121238 (  0) 0)
|
| [29] |
AADLAND E, NILSEN A K O, ANDERSEN L B, et al. A comparison of analytical approaches to investigate associations for accelerometry-derived physical activity spectra with health and developmental outcomes in children[J].
Journal of Sports Sciences, 2021, 39(4): 430-438 DOI:10.1080/02640414.2020.1824341 (  0) 0)
|
| [30] |
GIL-MARTÍN M, SAN-SEGUNDO R, FERNÁNDEZMARTÍNEZ, et al. Improving physical activity recognition using a new deep learning architecture and post-processing techniques[J].
Engineering Applications of Artificial Intelligence, 2020, 92: 103679 DOI:10.1016/j.engappai.2020.103679 (  0) 0)
|
| [31] |
SORO A, BRUNNER G, TANNER S, et al. Recognition and repetition counting for complex physical exercises with deep learning[J].
Sensors, 2019, 19(3): 714-736 DOI:10.3390/s19030714 (  0) 0)
|
 2021, Vol. 45
2021, Vol. 45

