2. 上海体育学院 中国乒乓球学院,上海 200438
2. China Table Tennis College, Shanghai University of Sport, Shanghai 200438, China
在球类运动中, 相对于棒球、网球、排球、足球, 乒乓球特性鲜明:质量轻(2.7 g)、旋转高(通常3 000 r/min)以及运动速度快(通常5 m·s-1)[1]。由于球体轻, 其自身旋转对运动轨迹影响极大。多数有关乒乓球的研究都是基于乒乓球战术的理论研究, 或者对于球员打法与心理进行分析, 以及对于乒乓球管理、教学进行调查等。乒乓球的运动轨迹受运动速度和旋转速度及方向的影响, 要求球员具有高水平、高精度的预判能力。随着近年乒乓球机器人技术的发展, 乒乓球运动轨迹预测受到许多研究人员的关注。乒乓球运动轨迹预测的准确性在一定程度上决定乒乓球机器人对击球点预测的精确性, 从而影响接球动作。
Nakashima等[1]基于高速摄像机提出一种乒乓球旋转速度和运动速度的评估方法, 并采用动态仿真方法, 对乒乓球转速及速度评估方法进行验证。Liu等[2]基于乒乓球动态模型和碰撞模型, 预测乒乓球击球点, 研究控制乒乓球机器人的手臂球拍运动方法, 仿真求解非线性方程组验证方法的有效性。Nakashima等[3]提出碰撞过程中滚动及滑动摩擦的判断条件, 分析球桌以及球拍的碰撞模型, 并对模型的有效性和准确性进行验证。Kui Ou等[4]采用计算流体力学(Computational Fluid Dyamics, CFD)方法对乒乓球自由轨迹仿真, 计算乒乓球运动轨迹并分析其流场问题, 通过球体和空气的空气动力学耦合仿真求解球体自由运动轨迹以及不同转速对球体运动轨迹的影响。
孙在等[5]在二维平面中建立并求解乒乓球弧圈球运动方程, 表明乒乓球转速对乒乓球轨迹有直接影响, 不同转速的弧圈球轨迹存在明显的差异。杨华等[6]基于ODE(Open Dynamics Engine)交互式可视化仿真环境, 并借鉴网球阻力系数和升力系数, 在三维空间对乒乓球旋转球轨迹进行仿真研究。王奇志等[7]在OpenGL-3D仿真平台中分析乒乓球运动轨迹中的运动学模型以及乒乓球碰撞模型, 改进运动模型并采用最小二乘法曲线拟合求解, 得出乒乓球预测轨迹。杨春卉等[8]基于动量理论和动量矩理论建立乒乓球上、下旋转球碰撞数学模型, 探讨摩擦力对乒乓球碰撞影响; 采用Matlab编程仿真, 并通过实例验证数学模型的有效性及准确性。
无论是近年开展乒乓球机器人研究比较活跃的日本名古屋大学Nakashima教授, 还是国内的一些学者, 在分析乒乓球受力及运动情况时:一方面, 将乒乓球运动中玛格努斯升力系数及阻力系数通常视为常数或采用网球及其他类球体计算公式[5-6], 在球体实际运动过程中, 其玛格努斯升力系数及阻力系数与旋转速度和运动速度有关; 另一方面, 未考虑乒乓球在运动过程中受到空气摩擦阻力及其他力作用, 旋转速度会发生一定的变化, 玛格努斯升力系数及阻力系数也随之变化, 从而导致轨迹预测不准确。
1985年, 美国国家航天航空局(NASA)研究中心空气动力学研究所科研人员研究了除乒乓球之外其他球体(如棒球、网球)的空气动力学特性[8-9]。乒乓球作为我国“国球”, 更应从空气动力学方面对其运动和空气动力学特性进行研究。因此, 本文采用CFD方法无网格算法对乒乓球在不同转速大小方向运动进行仿真计算, 对比分析不同方法对于乒乓球运动轨迹的影响。
1 乒乓球理论基础 1.1 乒乓球及球桌几何参数国际乒联规定比赛使用乒乓球质量为2.7 g以及半径为0.02 m, 并规定恢复系数为0.89~0.92。乒乓球桌尺寸:长2.74 m、宽1.525 m、高0.76 m以及网高0.152 5 m[10-11]。
1.2 乒乓球旋转及玛格努斯效应 1.2.1 乒乓球旋转球乒乓球在运动过程中, 其运动状态各不相同, 运动速度以及旋转速度各不相同, 应了解乒乓球旋转速度大小与方向性。如图 1所示, 乒乓球旋转通常分为左旋、侧旋、上旋、下旋、顺旋以及逆旋, 但在乒乓球运动过程中的旋转通常是以上六大旋转中多种旋转综合作用[12]。
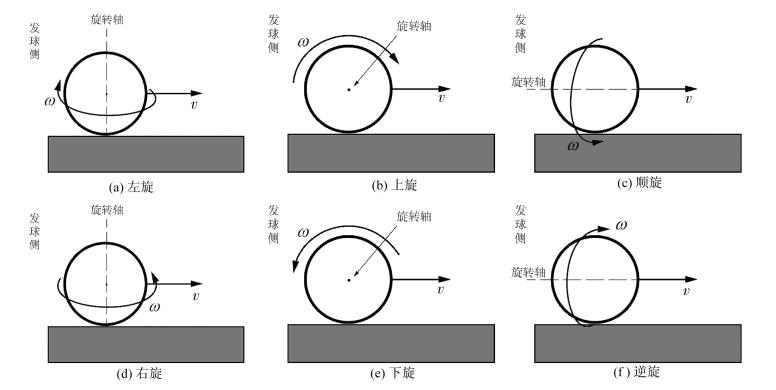
|
图 1 乒乓球六大旋转 Figure 1 Six spins of table tennis 注:v为乒乓球运动速度; ω为乒乓球旋转角速度 |
左右旋:乒乓球绕着通过球心并垂直球桌面的轴旋转的球称作侧旋球, 即左右旋。当以发球员为参考基准, 乒乓球向左旋转称作左旋球, 向右旋转称作右旋球, 如图 1(a)(d)所示。上下旋:乒乓球绕着通过球心垂直运动方向并平行球桌面的轴的旋转, 以发球员为参考基准, 乒乓球绕该轴向前旋转称作上旋球, 绕该轴向后旋转称作下旋球, 如图 1(b)(e)所示。顺逆旋:乒乓球绕着通过球心与球的运动方向平行的轴的旋转, 以发球员作为参考基准, 乒乓球绕轴顺时针旋转称作顺旋球, 绕轴逆时针旋转时称作逆旋球, 如图 1(c)(f)所示。
1.2.2 玛格努斯效应在球体运动中, 乒乓球的旋转球、排球的侧旋球以及足球的“香蕉球”有着相似的形成原理, 即旋转球在运动过程其运动轨道产生弯曲, 这种现象称作玛格努斯效应, 即旋转球在运动过程因旋转受到力的作用使其实际轨迹偏离其原有轨迹的现象, 所受的力称作玛格努斯力。牛顿早在1671年就解释了旋转羽毛球运动轨迹偏离现象。玛格努斯1852年实验研究了旋转圆柱体的玛格努斯效应[13]。
图 2表明, 流体(空气)经过旋转球下方因球体旋转速度方向与流体速度方向相反, 因球体表面黏性作用使得流体速度减少, 在其上方旋转速度方向与流体速度方向相同使得流体速度增大。根据伯努利方程[14]可知:球体下方压力大于上方压力, 从而受到向上的作用力, 该作用力大小以及作用力方向即玛格努斯力大小和方向。
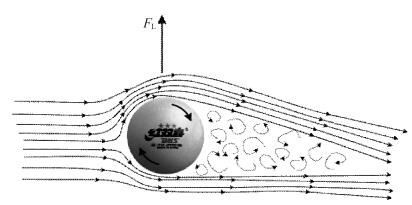
|
图 2 玛格努斯效应示意 Figure 2 Magnus effect |
乒乓球在运动过程中受到重力、浮力、阻力以及玛格努斯力等一系列力的综合作用。重力大小与乒乓球质量有关, 方向为竖直向下。浮力大小与乒乓球体积有关, 作用力方向与重力向反[1]。阻力大小与乒乓球速度有关, 阻力方向与乒乓球运动速度方向相反。玛格努斯力大小与旋转速度以及运动速度大小有关, 其作用力方向与旋转速度和运动速度方向有关。图 3为下旋和侧旋乒乓球在运动中所受的作用力示意。
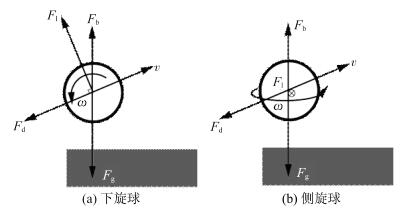
|
图 3 不同旋转乒乓球受力情况 Figure 3 Forces of different spins of table tennis |
无网格方法分为:分子水平仿真, 如Direct Simulation Montecarlo; 宏观层面仿真, 如Vortex Particle Method和Smoothed Particle Hydrodynamics; 基于介观层面上的仿真, 如Lattice Gas Automata和Lattice Boltzmann Method[15]。本文采用基于介观层面的格子Boltzmann方法, 其方法基本思路是以Boltzmann方法为基础, 通过碰撞迁移获得宏观流体的基本信息, 该方法比微观尺度的直接数值模拟节省时间, 比宏观尺度的粒子法具有更高的精度。
2.1 格子Boltzmann方法格子Boltzmann方法(Lattice Boltzmann Method, LBM)是相对新的复杂流体仿真技术, 并吸引了许多研究人员的关注。传统CFD方法是宏观性质上方程守恒(质量、动量以及能量)数值求解, 而LBM是假想流体通过粒子组成, 并且这些粒子在一个离散的格子执行连续的繁殖和碰撞过程。因为这些粒子的性质从而使得LBM比传统CFD方法有着一定的优势, 尤其是在复杂的边界处理、结合微观相互作用以及计算的并行化方面。LBM来源于格子气自动机(Lattice Gas Automata, LGA)方法, 该方法被认为是一个简化的虚拟分子动力学模型, 其空间、时间以及粒子速度都是离散的[16]。LGA在用于流体力学仿真模拟时存在一些缺陷:统计噪声和低雷诺数缩放时格子大小[17-19]。从LGA到LBM的转变主要是通过使用总体平均函数, 即密度分布函数替换格子方向布尔粒子数以除去统计噪声。在LBM发展中一个重要的BGK(Bhatnagar-Gross-Krook)近似简化, LBGK(Lattice Bhatnagar-Gross-Krook)模型的使用使得LBM方法在仿真时更加高效。
2.2 Boltzmann方程及BGK近似 2.2.1 Boltzmann方程Boltzmann方程为:
| $\frac{{\partial f}}{{\partial t}} + \xi \frac{{\partial f}}{{\partial x}} + F\frac{{\partial f}}{{\partial \xi }} = \Omega $ | (1) |
该方程求解是很困难的, 仅在特殊情况下才能求解。Boltzmann求解难点也就是方程等式右边的Ω碰撞项, 该项同时是非线性并且还与分子间的相互作用力存在耦合作用[21]。
2.2.2 BGK近似为简化求解Boltzmann方程, Mohamad等[20-23]进而引入如下方程替代碰撞项, 从而得到Boltzmann方程的BGK近似方程:
| ${\Omega ^{{\rm{BGK}}}} = \frac{1}{\tau }\left( {f_i^{{\rm{eq}}} - {f_i}} \right)$ | (2) |
式中, τ为松弛特性时间(与黏性有关); fieq为局部平衡分布函数。
平衡分布函数为[19]:
| $\begin{array}{l} f_i^{{\rm{eq}}}\left( {r,t} \right) = {\omega _i}\rho \left[ {\frac{{{e_i} \cdot u}}{{c_{\rm{s}}^2}} + \frac{{{{\left( {{e_i} \cdot u} \right)}^2}}}{{2c_{\rm{s}}^4}} - \frac{{{u^2}}}{{2c_{\rm{s}}^2}}} \right] + \\ \quad \quad \quad \quad O\left( {{u^3}} \right) + {\omega _i}\rho \end{array}$ | (3) |
式中:cs为格子声速; u为宏观速度; ωi为权系数; ρ为流体宏观密度; O(u3)为无穷小量。
2.3 格子Boltzmann方程格子Boltzmann方程是Boltzmann方程基于BGK近似在空间、速度以及时间上的离散得来的[22-23]。基于BGK近似的Boltzmann方程在空间、速度以及时间上的离散, 通过数学转换可以得到如下含有外力项的格子Boltzmann方程[20]:
| $\begin{array}{l} {f_i}\left( {r + {e_i}\delta t,t + \delta t} \right) - {f_i}\left( {r,t} \right) = \\ \quad \quad \quad \frac{1}{\tau }\left[ {f_i^{{\rm{eq}}}\left( {r,t} \right) - {f_i}\left( {r,t} \right)} \right] + \delta t{F_i}\left( {r,t} \right) \end{array}$ | (4) |
式中:ei为空间离散量; δt为时间离散步长; Fi(r, t)为外力项。
本文采用简化外力项格子Boltzmann方程, 即在仿真计算时不考虑外力项。简化的格子Boltzmann方程如下所示。
| ${f_i}\left( {r + {e_i}\delta t,t + \delta t} \right) - {f_i}\left( {r,t} \right) = \frac{1}{\tau }\left[ {f_i^{{\rm{eq}}}\left( {r,t} \right) - {f_i}\left( {r,t} \right)} \right]$ | (5) |
根据文献[5]中乒乓球初始参数, 采用计算流体力学方法求解乒乓球运动轨迹并与文献[5]采用运动学方法求解得到的运动轨迹对比。图 4(a)(b)(c)(d)分别为运动轨迹对比及乒乓球各坐标轴方向旋转速度变化曲线对比。球桌长度方向为X轴方向, 宽度方向为Z轴方向, 高度方向为Y轴方向。
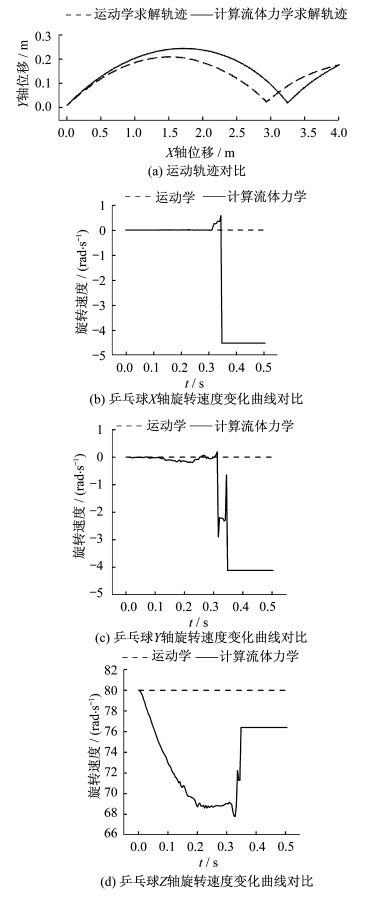
|
图 4 运动学及计算流体力学方法计算结果 Figure 4 The results of methods of kinematics and computational fluid dynamics |
图 4(a)为运动学求解轨迹和计算流体力学求解轨迹对比分析。计算流体力学求解得到的轨迹在Y轴和X轴均大于运动学求解得到的轨迹, 高度方向约高0.05 m, 相对误差约为25%, 长度方向长约0.25 m, 相对误差约为8.5%。文献[5]中简单地考虑乒乓球升力系数为1, 阻力系数为0.44, 相比文献[4]中对于乒乓球静止和旋转时升阻力系数, 文献[5]中对于升阻力系数设置不合理。在图 4(b)(c)(d)中对比了运动学方法和计算流体力学求解过程中乒乓球旋转速度随时间变化曲线, 运动学求解过程中3个方向的旋转速度均为定值, 而在计算流体力学求解中考虑空气阻力作用, 乒乓球在运动过程中受到阻力作用使得旋转速度减小, 在与球桌面发生碰撞各方向的旋转速度均发生一定的变化。综上, 乒乓球运动轨迹的计算流体力学求解比运动学求解更为准确。
3.2 计算流体力学结果分析 3.2.1 条件设置设置计算区域长3 m、宽2 m、高1 m; 对于乒乓球真实环境建模, 乒乓球、球桌以及球网均按照国标所给的几何参数建模以及求解尺度如图 5所示; 外围流场求解尺度为0.1 m, 尾迹加密尺度为12.5 mm, 乒乓球边界求解尺度为6.25 mm, 球桌以及球网表面求解尺度为12.5 mm。仿真计算条件:密度ρ=1.225 kg·m-3, 动力黏度μ=178.94 μPa·s-1, D为乒乓球直径(40 mm); 乒乓球质量为2.7 g, 重力加速度为9.81 m·s-2。乒乓球定义初速度设定:X轴方向分速度为6.2 m·s-1, Y轴方向分速度为1.6 m·s-1。
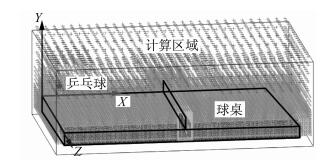
|
图 5 乒乓球、球桌、球网建模及求解尺度 Figure 5 Modeling of ball, table and net |
分别对无旋、下旋、侧旋及上旋乒乓球运动进行仿真, 并对不同旋转速度的乒乓球运动进行仿真(表 1)。
| 表 1 乒乓球旋转方向及对应的旋转速度 Table 1 The rotation direction and speed of table tennis |
由图 6可知, 3种不同旋转速度使得乒乓球轨迹落点距离随着旋转速度越快变得越小。由于旋转速度越快旋转产生的玛格努斯力越大, 轨迹向下偏转越大, 落点越近。下旋球和侧旋球, 旋转速度越快, 所受玛格努斯力越大, 下旋球轨迹越高, 侧旋球轨迹及落点越偏左。
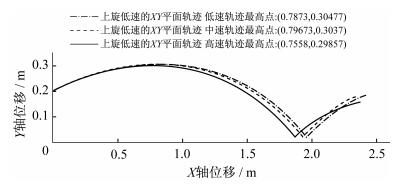
|
图 6 不同旋转速度上旋球XY平面轨迹 Figure 6 The topspin trajectory in different rotation speeds in face of XY |
图 7为分析不同旋转方向在相同运动速度和旋转速度条件下乒乓球运动轨迹。相比于无旋转乒乓球运动轨迹, 下旋、侧旋以及上旋球旋转效应受到向上、向左以及向下的玛格努斯力作用。这种作用力使得下旋球轨迹向上偏转在桌面上无落点, 侧旋球轨迹偏左落点偏左, 但对乒乓球在X轴方向的落点影响不大; 上旋球轨迹向下偏转使得轨迹落点距离变小。
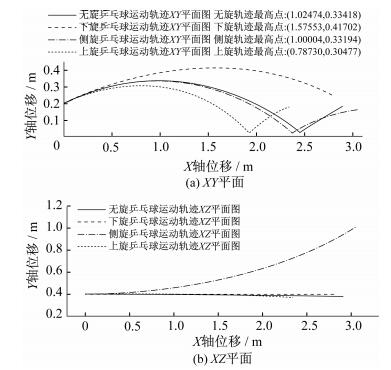
|
图 7 相同旋转速度不同旋转方向的乒乓球运动轨迹 Figure 7 The trajectory of table tennis in the same speed but different rotation directions |
图 8表明, 在乒乓球运动过程中, 在乒乓球后方造成速度最大区域, 对图 9该区域压力最低; 上旋及下旋球相对于无旋球, 乒乓球后高速区域分别向上及向下移动; 在t=0.16 s时可看出, 无旋转乒乓球趋近轨迹最高点, 下旋则处在轨迹上升段, 上旋处在轨迹下降段; 侧旋乒乓球速度流场中高速区域受旋转效应影响发生偏移; 在与桌面发生碰撞即乒乓球落点处, 侧旋球因受侧向旋转作用与其他2种情况下落点速度流场范围小。根据图 9压力流场可知旋转使得乒乓球周围流畅变得更为复杂, 无旋转球的压力流场趋近对称, 而具有旋转的乒乓球压力流场不具有对称性; 高压区处于乒乓球运动前端, 低压区处于球运动尾部。
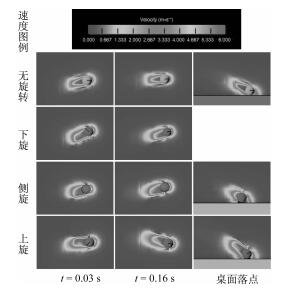
|
图 8 不同旋转方向的乒乓球速度流场 Figure 8 The speed flow fields of table tennis in different rotation directions |

|
图 9 不同旋转方向的乒乓球压力流场 Figure 9 The pressure flow fields of table tennis in different rotation directions |
(1) 对比计算乒乓球运动轨迹的2种方法发现, 相较于运动学求解方法, 计算流体力学计算结果更符合实际。
(2) 分析计算流体力学求解乒乓球运动轨迹可知, 不同旋转方向对乒乓球球轨迹有很大影响:乒乓球在向下旋转时, 乒乓球的旋转产生的玛格努斯力使得轨迹偏高, 轨迹落点超出球桌桌面区域; 乒乓球在向侧旋转时, 乒乓球轨迹向左侧偏转, 轨迹落点亦偏左; 乒乓球在向上旋转时, 乒乓球受到向下的玛格努斯力, 该作用力使得乒乓球轨迹偏低, 落点距离小。旋转速度对乒乓球轨迹亦有很大影响:对于向上旋转的乒乓球, 旋转速度越大, 乒乓球轨迹落点距离越小。
(3) 对乒乓球运动流场分析可知, 相比于无旋转乒乓球, 旋转乒乓球流场较为复杂, 无旋转乒乓球速度及压力流场具有对称性, 旋转乒乓球因受旋转作用其流场不具有对称性。
| [1] |
Nakashima A, Okamoto T, Hayakawa Y.An online estimation of rotational velocity of flying ball via aerodynamics[C]//IFAC World Congress.South Africa:Cape Town, 2014:7176-7181
( 0) 0)
|
| [2] |
Liu C, Hayakawa Y, Nakashima A.Racket control and its experiments for robot playing table tennis[C]//IEEE International Conference on Robotics and Biomimetics.China:Guangzhou, 2012:241-246
( 0) 0)
|
| [3] |
Nakashima A, Kobayashi Y, Ogawa Y, et al.Modeling of rebound phenomenon between ball and tacket tubber with spinning effect[C]//ICCAS-SICE 2009-ICROS-SICE International Joint Conference.Japan:Fukuoka, 2009:2292-2300
( 0) 0)
|
| [4] |
Kui Ou, Patrice C, Antony J.Computational sports aerodynamics of a moving sphere:Simulating a ping pong ball in free flight[C]//Aiaa Applied Aerodynamics Conference.Hawaii:Honolulu, 2011:1-16
( 0) 0)
|
| [5] |
孙在, 余广鑫, 郭美, 等. 乒乓球弧圈球的空气动力学原理及其运动轨迹的仿真分析[J].
体育科学, 2008, 28(4): 69-71 ( 0) 0)
|
| [6] |
杨华, 关志明. 基于ODE的乒乓球运动轨迹仿真研究[J].
计算机仿真, 2011, 28(9): 230-233 ( 0) 0)
|
| [7] |
王奇志, 杨晓晓. 乒乓球轨迹预测的研究与仿真[J].
计算机工程与科学, 2013, 35(2): 164-168 ( 0) 0)
|
| [8] |
杨春卉, 袁志华, 梁振刚. 乒乓球反弹动态特性的仿真研究[J].
计算机仿真, 2014, 31(10): 281-285 DOI:10.3969/j.issn.1006-9348.2014.10.060 ( 0) 0)
|
| [9] |
Mehta R D. Aerodynamics of sports balls[J].
Annual Review of Fluid Mechanics, 1985, 17(1): 151-189 DOI:10.1146/annurev.fl.17.010185.001055 ( 0) 0)
|
| [10] |
The international table tennis federation.ITTF Handbook 2011/2012[EB/OL].[2016-08-07].http://www.ittf.com/ittf_handbook/ittf_hb.html
( 0) 0)
|
| [11] |
The international table tennis federation.ITTF Technical Leaflet T1:The Table[EB/OL].[2016-08-07].http://ittf.com/stories/pictures/T1_The_Table_BoD2013.pdf
( 0) 0)
|
| [12] |
王正伦.
教你打乒乓球[M]. 南京: 江苏科学技术出版社, 2012: 1-163.
( 0) 0)
|
| [13] |
Seifert J. A review of the magnus effect in aeronautics[J].
Progress in Aerospace Sciences, 2012, 55(5): 17-45 ( 0) 0)
|
| [14] |
潘慧炬. 玛格努斯效应的力学模型[J].
浙江体育科学, 1995, 17(3): 16-19 ( 0) 0)
|
| [15] |
刘桂荣.
光滑粒子流体动力学[M]. 长沙: 湖南大学出版社, 2005: 1-148.
( 0) 0)
|
| [16] |
Mcnamara G R, Zanetti G. Use of the boltzmann equation to simulate lattice-gas automata[J].
Physical Review Letters, 1988, 61(20): 2332-2335 DOI:10.1103/PhysRevLett.61.2332 ( 0) 0)
|
| [17] |
Higuera F J, Jiménez J. Boltzmann approach to lattice gas simulations[J].
Europhysics Letters, 1989, 9(7): 663 DOI:10.1209/0295-5075/9/7/009 ( 0) 0)
|
| [18] |
Chen S, Doolen G D. Lattice boltzmann method for fluid flows[J].
Annual Reviews of Fluid Mechanics, 2003, 30(1): 329-364 ( 0) 0)
|
| [19] |
Succi S.
The lattice boltzmann equation:For fluid dynamics and beyond[M]. Oxford: Oxford University Press, 2001: 1-213.
( 0) 0)
|
| [20] |
Mohamad A A.
Lattice boltzmann method:Fundamentals and engineering applications with computer codes[M]. Berlin: Springer, 2011: 1-324.
( 0) 0)
|
| [21] |
He X, Luo L. A Priori derivation of the lattice boltzmann equation[J].
Physical Review E Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics, 1997, 55(6): 6333-6336 ( 0) 0)
|
| [22] |
He X, Luo L S. Theory of the lattice boltzmann method:From the boltzmann equation to the lattice boltzmann equation[J].
Physical Review E:Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 1997, 56(6): 6811-6817 ( 0) 0)
|
| [23] |
Qian Y H, Humieres D, Lallemand P. Lattice BGK models for navier-stokes equation[J].
Europhysics Letters, 1992, 17(6): 479 DOI:10.1209/0295-5075/17/6/001 ( 0) 0)
|
 2017, Vol. 41
2017, Vol. 41


