文章信息
 | 上海财经大学 2015年17卷第4期 |
- 张云, 邓桂丰, 李秀珍
- Zhang Yun, Deng Guifeng, Li Xiuzhen
- 经济新常态下中国产业结构低碳转型与成本测度
- Low-carbon Transition of Chinese Industrial Structure and Cost Measurement under Chinese Economy's New Normal
- 上海财经大学学报, 2015, 17(4): 10-20.
- Low-carbon Transition of Chinese Industrial Structure and Cost Measurement under Chinese Economy's New Normal, 2015, 17(4): 10-20.
-
文章历史
- 收稿日期:2015-01-27

2015第17卷第4期
2.上海立信会计学院 数学与信息学院,上海 201620;
3.上海立信会计学院 经贸学院,上海 201620
2014年12月中央经济工作会议提出要准确把握经济发展新常态,指出我国“环境承载能力已达到或接近上限,必须推动形成绿色低碳循环发展新方式”,这是经济新常态九大特征之一。改变我国传统的粗放式、高能耗的经济发展方式,实现我国经济产业结构低碳化转型,已成为我国经济新常态下实现可持续发展目标的必由之路和重要目标。2009年中国政府公布量化减排目标,即2020年单位国内生产总值的二氧化碳(CO2)排放比2005年下降40%-45%,并作为约束性指标纳入国民经济和社会发展中长期规划。2014年末中美两国发布气候变化联合声明,中国计划2030年左右二氧化碳排放达到峰值,且将努力早日达峰。此次承诺意味着中国工业化和城镇化的碳排放增长“天花板”被量化确定,国家对高能耗、高排放的产业进行调整,必然要限制在可控的、平稳的范围内(邹骥,2014)。我国2008年至2011年增收的中央财政中被节能减排成本抵消掉的部分非常可观(夏炎和范英,2012),因此合理估测我国经济新常态下控制碳排放的宏观经济成本,可以为评估减排方案综合效果、优化产业结构调整以及制定气候谈判策略提供参考。
二、文献述评面对国际减排压力和国内经济转型要求,我国产业结构低碳化已经得到政府和学术界的认可。陈诗一(2012)指出以节能减排、建设资源节约型和环境友好型社会为特征的低碳转型,是中国加快转变经济发展方式的明确路径和重要抓手。产业结构低碳化是中国经济低碳转型的重要路径,有助于实现国内产业升级和提高经济发展水平,就实现减排目标而言是控制碳排放的有效途径(姚宇,2010;张雷等,2011;伍华佳,2012)。还有许多文献通过排放因素分解实证研究,验证了我国产业结构对碳排放的重要影响(Hoekstra和Van den Bergh,2002;Kakali,2004;Guan等,2008;林伯强和蒋竺均,2009;张友国,2010;王锋等,2010;陈诗一,2011;陈永国等,2013)。进入新常态,资源环境的硬约束和刚性压力将逐步强化,在经济增速放缓的背景下,财政收入和企业利润增幅回落,各种矛盾和风险挑战将明显增多(王一鸣,2014),中国产业结构低碳转型紧迫性及控制碳排放的经济成本影响效应不断增强。
关于中国减排成本问题已经得到学术界的关注,王灿等(2005)、中国人民大学能源与气候经济学项目(2009)、刘明磊等(2011)、吴英姿和闻岳春(2013)、姜庆国和穆东(2013)等估测了我国减排宏观经济成本。减排成本是学术界研究减排问题的主要分析工具(Kesicki和Strachan,2011),具体估测方法及函数形式主要有四类。第一类是二次曲线形式表示边际减排成本函数,Ellerman和Decaux(1998)用MIT的EPPA模型模拟回归各国边际减排成本函数,用于分析既定减排目标下全球碳交易结果,Maddison(1995)、Eyckmans等(2001)、Chen(2005)、韩一杰和刘秀丽(2010)、张云和杨来科(2012)等研究均使用二次曲线形式。第二类是利用碳排放影子价格代替边际减排成本,影子价格是“机会成本的货币表现”,常用估计方法有两种:一是参数化方法,包括基于Shephard距离函数的参数方法(Lee,2005)和基于方向距离函数的参数方法(Fare等,2006;陈诗一,2010);二是基于数据包络分析(DEA)的非参数化方法(刘明磊、朱磊和范英,2011;吴英姿和闻岳春,2013)。第三类是构建多目标规划模型测算宏观经济减排成本,相关研究可见Hafkamp和Nijkamp(1980)、Hsu和Chou(2000)、杨浩彦(2000)和Chen(2001)、范英等(2010)、Han和Ahn等(2012)。第四类为利用能源体系内的POLES模型推导幂函数形式的边际减排成本函数(Criqui等,1999;Boehringer和Loeschel,2001;Blanchardi等,2002;Loeschel和Zhang,2002)。已有研究采用不同方法估测了多种形式的减排成本函数,从能源消费、发电成本、增量投资、结构调整等多个角度解析减排经济成本,在理论逻辑和政策建议上指出产业结构低碳转型是我国实现减排目标的主要路径,但关于产业结构低碳化的定量预测还较少。
本文尝试在Hsu和Chou(2000)、唐建荣等(2012)研究基础上构建多目标规划模型,利用妥协规划方法迭代求解产出增长与CO2排放量之间的联动关系,测度分析经济新常态不同产出增长率下产业结构低碳化模拟结果以及控制碳排放的宏观经济成本。尝试改进之处在于:一是依据行业增加值和碳排放构建多目标规划模型,涵盖我国2020年和2015年量化减排目标约束以及一般均衡约束、水资源约束、部门扩张约束、就业约束等影响中国经济增长的主要约束条件;二是以经济新常态下不同产出增长率为基础进行模拟测算,尝试分析限制高碳行业增长情况下我国产业结构低碳优化的可能结果,探索不同产业政策情景模拟下宏观经济成本、就业等情况隐含的政策含义;三是关于碳排放强度测算方法,尝试直接计算能源排放系数和消耗量来测算行业碳排放量,避免一般研究把能源折算成标准煤或归类为固、液、气体三类计算在考察期较长时所产生的误差影响。
三、模型构建与数据来源本文研究对象是经济新常态下中国产业结构低碳转型及其控制碳排放的宏观经济成本,因此把经济增长最大化和CO2排放量最小化作为目标函数构建模型,把一般均衡约束、CO2排放强度约束、水资源约束、充分就业、部门扩张约束等影响我国经济发展和CO2减排的主要决定因素作为约束性指标。
(一) 目标函数新常态经济下,经济增速是“换挡”而不是“失速”,我国经济发展仍需保持合理增长速度,因为发展仍是解决中国一切问题的关键(张占斌,2014),实现经济增长是我国长期以来也是未来较长时期的重要目标。简单采用经济总产出数据存在重复计算的可能性,而且无法反映产业结构等生产效益,本文借鉴唐建荣等(2012)的研究,以各行业增加值总和作为反映经济发展规模的指标,设定经济增长目标是行业增加值总和最大化。为实现2020年单位GDP碳排放量比2005年下降40%-45%的减排目标,中国控制碳排放的理想效果是在一定经济发展条件下二氧化碳排放量最小化。因此,设定两个目标函数:
| $ \max {f_{GDP}}\left( X \right) = {\left( {1 + \alpha } \right)^{ - t}}\sum\limits_{i = 1}^n {{V_{t,i}}{X_{t,i}}} $ | (1) |
| $ \min {f_{C{O_2}}}\left( X \right) = \sum\limits_i^n {{e_i}} {X_{t,i}} $ | (2) |
其中,Xt, i是第i个行业部门在t时期的产出,是决策变量;Vt, i是第i个行业在t时期的增加值系数,即增加值在总产出中所占比重;t是时间,i是行业,α是折现系数;ei是第i个行业的CO2排放强度系数,可定义为各行业部门每万元产出的CO2排放量。
(二) 约束条件1.一般均衡约束条件
从产业生产角度看,一般均衡约束是指每个行业部门的产出和进口之和必须等于最终消费加上其他部门的中间需求,这与许多研究者(Hsu和Chou,2000;范英等,2010;唐建荣等,2012)的设定一致。本文根据美国经济学家Leontief创立投入产出法来推导一般均衡约束表达式,用X表示总产出,A表示直接消耗系数矩阵,F表示最终需求(最终消费),总产出表示为:
| $ X = AX + F,即X = {\left( {I - A} \right)^{ - 1}}F $ | (3) |
公式(3)为涉及对外经济的均衡产出模型,(I-A)-1是里昂惕夫逆矩阵,即与直接消耗系数矩阵A对应的完全需求系数矩阵。开放经济体实际运行时进口商品主要有两种用途:一是直接进入最终消费领域,满足最终需求而被消费掉;二是作为部分中间投入而进入国内生产领域。中国经济属于开放经济体,以中国投入产出表为例构建投入产出模型如下:
| $ X = AX + {F^d} + {F^e} - M $ |
其中,Fd满足国内居民消费、政府消费以及资本形成投资,是国内最终需求;Fe是满足国外需求的商品出口;M是本国从国外的商品进口。用M表示进口系数对角矩阵,最终需求F的表达式为:F=(I-A+M)X。从经济增长要求看,计划求解年份的最优解的最终需求不应该低于2007年的最终需求,得到一般均衡约束为:
| $ F = \left( {I - A + \overline M } \right)X \ge {F_{2007}} = F_{2007}^d + F_{2007}^e $ | (4) |
2.CO2排放强度约束条件
中国公布的具体量化减排目标主要包括:2009年11月25日中国国务院常务会议决定,到2020年中国单位GDP的CO2排放将比2005年下降40%-45%;2011年12月中国国务院会议提出,把积极应对气候变化作为我国经济社会发展的重大战略,在《“十二五”控制温室气体排放工作方案》中明确到2015年全国单位GDP的CO2排放比2010年下降17%。2015年和2020年两个阶段性减排目标,都是以单位GDP的CO2排放降低百分比作为具体量化目标,因此CO2排放强度已成为我国经济社会发展的重要约束条件,本文基于行业分类设定CO2排放强度约束条件:
| $ \left( {\sum\limits_{i = 1}^n {{e_i}} {X_{2005,i}}/\sum\limits_{i = 1}^n {{X_{2005,i}}} - \sum\limits_{i = 1}^n {{e_i}} {X_{2020,i}}/\sum\limits_{i = 1}^n {{X_{2020,i}}} } \right)/\left( {\sum\limits_{i = 1}^n {{e_i}} {X_{2005,i}}/\sum\limits_{i = 1}^n {{X_{2005,i}}} } \right) \ge {R_{2020}} $ | (5) |
| $ \left( {\sum\limits_{i = 1}^n {{e_i}} {X_{2010,i}}/\sum\limits_{i = 1}^n {{X_{2010,i}}} - \sum\limits_{i = 1}^n {{e_i}} {X_{2015,i}}/\sum\limits_{i = 1}^n {{x_{2015,i}}} } \right)/\left( {\sum\limits_{i = 1}^n {{e_i}} {X_{2010,i}}/\sum\limits_{i = 1}^n {{X_{2010,i}}} } \right) \ge {R_{2015}} $ | (6) |
其中,ei是第i个行业的CO2排放强度系数;X2005, i、X2010, i分别表示2005年和2010年第i行业产值,即优化前的各行业产值;R2020和R1995分别表示2020年和2015年单位GDP排放量相比2005年和2010年降低的目标。式(5)和式(6)函数为非线性规划形式,用E2005和E2010分别代表2005年和2010年中国单位GDP的CO2排放量,进行模型转换得到:
| $ \sum\limits_{i = 1}^n {\left[ {{e_i} - \left( {1 - {R_{2020}}} \right){E_{2005}}} \right]{X_{2020,i}}} \le 0 $ | (7) |
| $ \sum\limits_{i = 1}^n {\left[ {{e_i} - \left( {1 - {R_{2015}}} \right){E_{2010}}} \right]{X_{2015,i}}} \le 0 $ | (8) |
3.水资源约束条件
我国淡水资源总量占全球水资源的6%,但人均水资源仅为世界平均水平的1/4、美国的1/5(胡四一,2012),我国还属于干旱缺水严重的国家,未来水资源仍然是制约我国经济发展的重要因素,而且分析发现我国进出口贸易结构还在进一步加剧水资源短缺问题(中国投入产出学会课题组,2007)。我国已经提出全国水资源节约管理目标,2010年《全国水资源综合规划》提出,到2020年我国的年用水总量将努力控制在6700亿立方米以内,并且公布单位产值用水量目标即万元GDP的用水量、万元工业增加值用水量分别降低到120立方米和65立方米,这两个目标值与2008年相比均降低50%左右。2011年1月《中共中央国务院关于加快水利改革发展的决定》又提出建立严格的水资源管理制度以及建立有利于水资源节约和合理配置的水价形成机制,再次明确到2020年量化目标即全国年用水总量控制在6700亿立方米以内。本文以单位GDP取水量降低百分比以及水资源供应上限设定水资源约束条件:
| $ \left( {\sum\limits_{i = 1}^n {{\omega _i}} {X_{2008,i}}/\sum\limits_{i = 1}^n {{X_{2008,i}}} - \sum\limits_{i = 1}^n {{\omega _i}} {X_{2020,i}}/\sum\limits_{i = 1}^n {{X_{2020,i}}} } \right)/\left( {\sum\limits_{i = 1}^n {{\omega _i}} {X_{2008,i}}/\sum\limits_{i = 1}^n {{X_{2008,i}}} } \right) \ge {R_{\omega at}} $ | (9) |
| $ \sum\limits_{i = 1}^n {{\omega _i}} {X_{2020,i}} \le {W_{\max }} $ | (10) |
其中,wi表示第i行业的取水量系数;Rwat表示单位GDP取水量降低目标比例;Wmax表示水资源供应上限。水资源约束条件公式(9)函数为非线性规划形式,用W2008表示优化前单位GDP的取水量,进行模型转换得到:
| $ \sum\limits_{i = 1}^n {\left[ {{\omega _i} - \left( {1 - {R_{\omega at}}} \right){W_{2008}}} \right]{x_{t,i}}} \le 0 $ | (11) |
4.部门扩张约束条件
产业发展具有内在规律性和发展惯性,国家根据发展战略规划和实际运行情况对产业结构和布局进行调整优化。在经济生活中,底线思维适用于防止经济的大起大落或将危机导向最小化,建立较为稳妥可靠、有回旋余地的“最低防线”,避免出现社会秩序混乱和动荡(陈齐芳,2014)。因此为避免经济过大波动,投入产出表行业产值规模短期内限制在一定幅度内变动,得到部门扩张约束:
| $ X_i^{_L} \le {X_i} \le X_i^U $ | (12) |
其中,XiL和XiU分别表示第i部门行业产出的下限和上限。
5.就业约束条件
任何社会发展都首先取决于人力资源配置效率的高低,就业或者失业程度是一国人力资源配置效率高低的首要标志,而且我国保持较高水平的就业率是保证社会稳定的重要前提。从数学模型优化可行解角度看,需要设置最低值即就业底线可以保证模型求解具有现实意义,否则所求得的解具有数学意义上的可行性而缺乏现实可行性。2013年6月我国人力资源和社会保障部部长尹蔚民表示,虽然中国劳动年龄人口的增长开始减速,但是全国就业总量的整体压力不可能马上减轻,到2020年我国就业年龄总人口达到峰值,预计为8.3亿人。本文以就业总人数作为约束条件:
| $ \sum\limits_{i = 1}^n {{j_i}} {X_{2020,i}} \ge {R_{job}} $ | (13) |
其中,ji代表第i行业的就业系数;Rjob代表总就业人数。
6.非负约束条件
投入产出表各行业部门的产出是决策变量,变量的非负约束是决策变量现实意义的要求(唐建荣等,2012),所以得到模型非负约束为:xt, i≥0。
(三) 数据来源与整理计算我国正处在工业化和城镇化进程中,目前我国第二产业绝对主导的产业结构演进,决定了我国单位国内生产总值的能耗过程(张雷等,2011),而能源消耗量对CO2排放又具有决定性作用。姚宇(2010)提出我国产业低碳化是将工业为主导的产业作为基点和抓手,改善我国产业高能耗和经济不可持续发展的态势。本文根据行业代表性和数据可得性选择工业行业作为研究对象。模型所用投入产出表数据来自国家统计局等网站1987年到2007年共9张投入产出表,能源数据来自2006年到2011年的《中国能源统计年鉴》,就业人数等其他数据主要来自中国经济信息网和国研网提供的数据库。根据中国投入产出表与能源统计年鉴,本文对所有工业行业进行对比归类,最后得到统计口径相对清晰和一致、统计数据具有较好延续性的39个行业。一般均衡约束条件中最终需求F是包含39个行业的39×1的矩阵,根据2007年投入产出表数据计算工业行业产出的底限值。关于模型约束条件中的水资源约束,本文设定行业取水量系数主要参考国内研究者宋建军等(2004)、中国投入产出学会课题组(2007)所采用的研究数据。行业产出的下限xiL和上限xiU,通过计算工业行业各年的产值变化数据,确定最大和最小增长率来计算模型约束条件中部门扩张约束。总就业人数约束Rjob是以2007年工业行业产值和就业人数为基准,计算行业的就业系数。另外,根据我国公布的2020年单位GDP的CO2排放降低目标,确定研究考察期为2020年。
关于CO2排放的计算,已有研究方法通常是把消耗的各类能源折算成标准煤或归类为固、液、气体三类,本文为减少折算或归类过程中所产生的误差,直接利用我国各行业所消耗的不同类型能源数量及其排放系数,计算所有工业CO2排放量。《中国能源统计年鉴》中“行业终端能源消费量(实物量)”统计显示,我国各行业所消耗的能源包括18种类型:原煤、洗精煤、其他洗煤、焦碳、焦炉煤气、其他煤气、其他焦化产品、原油、汽油、煤油、柴油、燃料油、液化石油气、炼厂干气、其他石油制品、天然气、热力、电力。本文利用IPCC①计算公式计算中国各能源碳排放系数,计算公式如下:
①联合国政府间气候变化专门委员会(Intergovernmental Panel on Climate Change,IPCC)是世界气象组织(WMO)及联合国环境规划署(UNEP)于1988年联合建立的政府间机构,2006年出具报告《IPCC国家温室气体清单指南》。
| $ {\theta _k} = NC{V_k} \times C{C_k} \times CO{F_k} \times \left( {44/12} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,2,3, \cdots $ |
其中,NCVk表示不同类型能源的平均低位发热量;CCk表示碳排放因子;COFk表示碳氧化因子,IPCC取缺省值为1;44和12分别表示二氧化碳和碳的分子量。
查表获得各能源平均低位发热量,然后计算得到中国18种能源单位标识的碳排放系数(见表 1)。根据39个工业行业消耗的能源类型和数量计算CO2排放量,再利用行业产值数据计算各行业的CO2排放强度系数。根据各行业CO2排放强度系数,计算2005年和2010年行业碳排放强度,再根据减排比例要求测算CO2排放约束条件R2020和R1995。
| 能源类型 | 排放系数 | 单位 |
| 原煤 | 1.8953 | kgCO2/kg |
| 洗精煤 | 2.3881 | kgCO2/kg |
| 其他洗煤 | 0.7581 | kgCO2/kg |
| 焦炭 | 3.0735 | kgCO2/kg |
| 焦炉煤气 | 1.2381 | kgCO2/m3 |
| 其他煤气 | 0.3869 | kgCO2/m3 |
| 其他焦炭产品 | 2.6882 | kgCO2/kg |
| 原油 | 3.0643 | kgCO2/kg |
| 汽油 | 2.9826 | kgCO2/kg |
| 煤油 | 3.0933 | kgCO2/kg |
| 柴油 | 3.1571 | kgCO2/kg |
| 燃料油 | 3.2328 | kgCO2/kg |
| 液化石油气 | 3.1623 | kgCO2/kg |
| 炼厂干气 | 3.3749 | kgCO2/kg |
| 其他石油制品 | 3.0952 | kgCO2/kg |
| 天然气 | 2.1825 | kgCO2/m3 |
| 热力 | 0.1130 | kgCO2/MJ |
| 电力 | 1.1040 | kgCO2/(kW·h) |
| 注:计算中“其他煤气”、“其他焦化产品”和“其他石油制品”的平均低位发热量为平均数。 | ||
本文根据模型目标函数分别求解两个目标函数在约束集下的最优解,即分别求解约束集条件下产出增加值之和最大值fGDP*(X)与CO2排放量最小值f*CO2(X)。在经济新常态运行过程中,各项约束条件下两个目标函数的最优解无法同时实现,优化结果要求尽量接近这两个理想值。本文借鉴范英等(2010)、Han和Ahn(2012)等构建的二维目标空间Sobj,采用妥协规划方法测算中国产出增长与CO2排放关系。以目标函数理想值为基础,在目标空间Sobj中求解约束集条件下两个目标与其理想值的欧几里德距离d最小值,原有多目标规划模型妥协解转化为求解:
| $ \mathop {\min d}\limits_{x \in R} = {\left[ {{\theta _1}{{\left( {{F_{GDP}}\left( X \right) - f_{GDP}^*\left( X \right)} \right)}^2} + {\theta _2}{{\left( {{f_{c{o_2}}}\left( X \right) - f_{C{O_2}}^*\left( X \right)} \right)}^2}} \right]^{1/2}} $ | (14) |
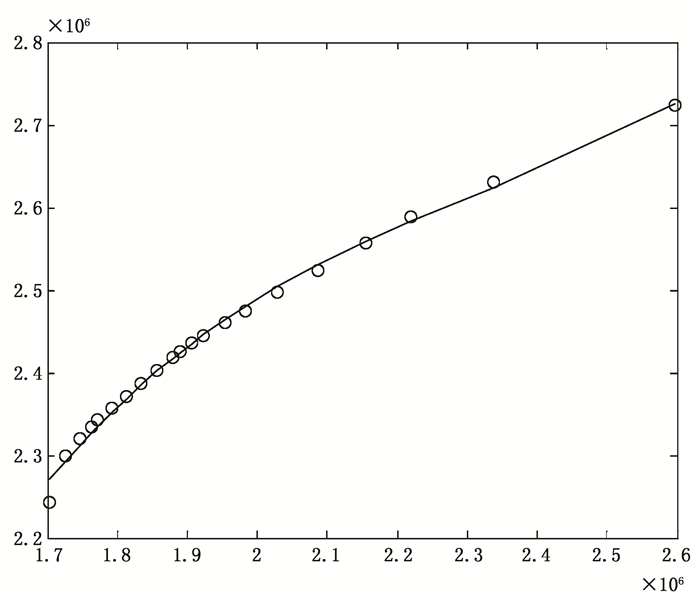
w1=θ1/(θ1+θ2)和w2=θ2/(θ1+θ2)表示行业产出增加值和CO2排放量这两个目标的相对权重,w1+w2=1。改变产出增加值总和与CO2排放量相对权重w1和w2,w1取值由大变小,从1到0,相邻两个值变化量为0.05,相应w2取值从0变为1。通过式(14)计算得到21组非劣解(在目标空间中的相对位置见图 1)。然后把fCO2(X)作为因变量,fGDP(X)作为自变量对非劣解进行拟合,得到在目标空间Sobj中产出增加值与CO2排放量对应关系曲线为:
|
| 图 1 产出与CO2排放关系曲线 |
| $ {f_{c{o_2}}}\left( X \right) = 0.0046f_{GDP}^3\left( X \right) + 0.0214f_{GDP}^2\left( X \right) $ | (15) |
常数项和一次项系数为零,相关系数R2为0.996,F统计量为729.72,对应的p值为1.1102×10-16,拟合效果很好,可以作为产出增加值与CO2排放量之间的联动关系式。
((二)) 经济新常态下不同产出增长率模拟结果与宏观经济成本分析中国经济进入新常态,需要理性对待高速增长转向中高速增长的换挡期,基于经济增长换挡期思维对2005年到2020年设置不同的产出增长率gj,假设为g1=11%、g2=10%、g3=9%、g4=8%、g5=7.5%、g6=7%、g7=6%,计算得到对应的2020年产出增加值fGDP, j,根据式(12)计算相应的CO2排放量fCO2, j。在不同产出增长率下,工业行业不同产值对应着不同的CO2排放量,限制CO2排放总量意味着约束产出、降低产出增长率,显然控制碳排放存在宏观经济成本。测算结果显示,当增长率从11%减少为10%时,宏观经济损失为15.28万亿元,CO2排放量减少73.74亿吨,控制碳排放的平均宏观经济成本为2072.18元/吨CO2;当增长率从10%减少为9%时,宏观经济损失为13.45万亿元,CO2排放量减少56.65亿吨,控制碳排放的平均宏观经济成本为2374.85元/吨CO2;当增长率从9%减少为8%时,宏观经济损失为11.83万亿元,CO2排放量减少43.42亿吨,控制碳排放的平均宏观经济成本为2725.12元/吨CO2;当增长率从8%减少为7.5%时,宏观经济损失为5.36万亿元,CO2排放量减少17.71亿吨,控制碳排放的平均宏观经济成本为3028.98元/吨CO2;当增长率从7.5%减少为7%时,宏观经济损失为5.02万亿元,CO2排放量减少15.48亿吨,控制碳排放的平均宏观经济成本为3247.83元/吨CO2;当增长率从7%减少为6%时,宏观经济损失为9.12万亿元,CO2排放量减少25.32亿吨,控制碳排放的平均宏观经济成本为3602.08元/吨CO2。
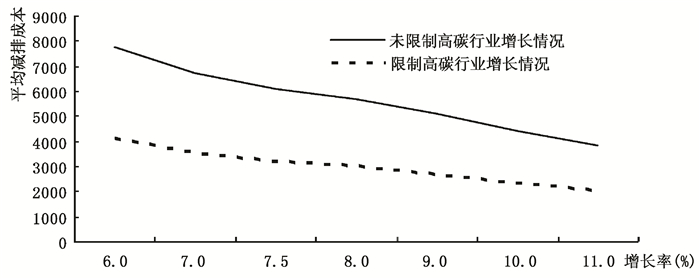
显然,限制CO2排放总量的力度越大,控制碳排放的宏观经济成本代价越大,值得注意的是,产出增长率越大,中国控制碳排放平均宏观经济成本越小。图 2中实线表示不同产出增长率下的平均减排成本,当增长率从11%减小为6%,平均减排成本从2072.18元/吨CO2增长到3602.08元/吨CO2。原因在于,我国公布“到2020年单位国内生产总值的碳排放比2005年下降40%-45%”的减排目标是相对性目标而非绝对性目标,该相对性存在双重含义:一是2020年减排目标是相对于2005年这个基期的排放情况来确定的,二是减排目标的度量指标是排放强度(即排放总量除以产值)而非排放总量。保持较高的经济增长率,虽然可能导致CO2排放总量增加,但只要产值增长比例大于排放总量增长比例,对于降低排放强度、实现既定减排目标来说是有益的,而且有助于推进工业化进程和提高国内就业水平。中国提出的减排目标以单位GDP的CO2排放量作为相对减排指标,是充分考虑了中国作为发展中国家发展仍然是第一要务的国情(陈诗一,2011),保证一定的经济增速是未来很长时间的必由之路。
|
| 图 2 不同增长率下的平均减排成本 |
上述模拟分析结果证实,中国产业结构低碳化是节能减排的有效路径,有助于保证必要的经济增长和充分就业等条件下实现既定减排目标。产业结构低碳化内涵丰富,既包含整体产业组成结构中低碳产业比重上升、高碳产业比重下降,又包含高碳产业的低碳化(范英英,2011),而且产业结构低碳化与高碳化之间具有内在的一致性(孙起生,2010)。本文进一步从产业结构优化升级思路出发,对高碳行业增长率进行限高约束,以估测严控高碳行业增长的可能结果。根据中国工业行业2005年和2010年的CO2排放强度系数进行排序,选择两个计算期排放强度均在1万吨CO2/亿元以上的行业部门作为高碳行业,其中资源能源开采和冶炼行业是主体,包括煤炭开采和洗选业、石油和天然气开采业、石油加工炼焦及核燃料加工业、黑色金属矿采选业、黑色金属冶炼及压延加工业、有色金属矿采选业、有色金属冶炼及压延加工业、非金属矿采选业、非金属矿物制品业、其他采矿业,还包括化学行业以及消耗能源较多的行业,如化学原料及化学制品制造业、化学纤维制造业、纺织业、造纸及纸制品业、橡胶制品业、工艺品及其他制造业、水的生产和供应业、电力热力的生产和供应业等。
本文对高碳行业增长新的约束条件,设定高碳行业年增长率不超过15%,重新计算目标函数在约束集下的最优解,利用妥协规划方法测算经济增长与CO2排放关系,测算不同增长率下控制碳排放的宏观经济成本。结果(见图 2)显示存在与前述不限制高碳行业增长率情景相同的规律,即限制CO2排放总量的力度越大,宏观经济成本的代价越大;产出增长率越大,控制碳排放的平均宏观经济成本越小,比如增长率从11%减小为6%,平均宏观经济成本从3889.77元/吨CO2增长到7789.25元/吨CO2。不同的是,在相同产出增长率下,控制碳排放平均宏观经济成本时与限制高碳行业增长率情景相比不限制高碳行业增长率情景要高,对比数据发现CO2排放强度有较大幅度的下降,实际上在CO2排放强度降低幅度相同的情况下,控制碳排放平均宏观经济成本时与限制高碳行业增长率情景相比不限制高碳行业增长率情景要小。从实现减排目标的角度看,限制高碳行业增长率有助于降低减排平均成本,而且实际测算结果显示在此情景下工业行业总产值和就业人数要略优于不限制高碳行业增长率情景。研究结果隐含说明,发展中国家和地区受其经济发展阶段和产业、能源结构影响,强制性减排的宏观经济成本相对要大,其中经济发展对能源投入及高碳能源消费的依赖,可能导致较大的单位减排宏观经济成本(杨浩彦,2000),这一点对于中国节能减排路径和产业结构优化升级具有重要意义。
五、结论与启示在新常态经济增速换挡期,中国经济必须推动形成绿色低碳循环发展新方式,中国产业结构低碳化是经济低碳转型背景下实现量化减排目标的必然选择。本文构建多目标规划模型利用妥协规划方法迭代求解工业增长与CO2排放量之间的联动关系式,分析经济新常态下不同产出增长率产业结构低碳转型模拟结果及控制碳排放的宏观经济成本。同等规模经济总量的产业结构不同,碳排放总量相差甚远,本文研究证实:通过产业结构低碳优化可以实现我国“2020年单位GDP的二氧化碳排放比2005年下降40%-45%”的减排目标。不同国家或者同一国家在不同时期,所处的经济发展阶段、产业结构演进、能源消费构成以及资源禀赋不同,减排行动所付出的代价存在较大差异。我国控制CO2排放存在明显的宏观经济成本,不同条件下的产业结构优化模拟结果证实,产出增长率越大,中国实现减排目标的平均宏观经济成本越小,原因在于我国排放强度减排目标是相对性指标;而且严控高碳行业增长的结构优化证实,合理调整和优化工业产业结构不仅可以实现较高水平的减排目标,而且可以增加工业产值和就业人数。
基于上述结论,本文提出如下政策建议:(1)我国在经济新常态这个换挡期需要保持一定的经济增长速度,不仅符合我国作为发展中国家的国情,有助于推进工业化和城镇化发展,也有助于降低排放强度、实现既定减排目标。同时,我国需要抓住机遇,通过特定的产业政策和措施对现存产业体系进行直接或间接的调整,实现产业结构低碳化转型升级。我国目前存在着产业结构比例失调、产业关系失衡、产业层次低下、重复建设严重、技术含量低下、空间布局结构不合理等诸多结构性矛盾(孙起生,2010)。为实现经济新常态下经济发展方式的转变,我国产业结构优化不仅需要遵循传统产业结构演进规律,推动产业结构由低到高不断升级发展,同时需要融入低碳经济发展规律,在节约性、持久性和相伴性的生态经济发展要求指引下,实现产业结构低碳转型,这是我国实现可持续发展和应对气候变化的必由之路(郎春雷,2009)。(2)在实现产业结构低碳优化过程中,要及时调整工业结构中高低碳行业间的“数量”比例,还需要注重各个行业的能源效率与碳生产率等“质量”指标,其中最重要的是在转变生产方式和调整产业结构过程中,注重和充分发挥技术创新的作用。面对世界科技创新和产业革命的新一轮浪潮,我国经济增长的动力正逐步发生转换,统计数据显示2013年我国全要素生产率水平是1978年的近3倍,我国经济逐渐转入创新驱动型的新常态经济,需要打造“中国质量”,真正实现增长速度“下台阶”,增长质量“上台阶”(张占斌,2014)。2014年中央经济工作会议在描述经济新常态特征时,提出“基础设施互联互通和一些新技术、新产品、新业态、新商业模式的投资机会大量涌现”,因此我国控制碳排放实现减排目标的路径,需要从产业结构优化层面延伸至技术创新路径。(3)从国际经济地位和气候谈判策略分析,改革开放以来我国产业结构主要位于全球价值链的中低端,比较利益较低(张占斌,2014),经济新常态下产业结构将由中低端向中高端转换,为进一步提升我国产业在全球价值链中的地位和打造“中国效益”,需要在国际气候谈判中争取合理的经济发展所需碳排放空间。控制碳排放的经济成本是影响世界各国实施节能减排政策的重要因素,也是各国参与国际气候谈判和国际碳交易的关键因素。中国可以适时公布控制碳排放的宏观经济成本,这是中国在“共同但有区别的责任”原则下,作为负责任大国主动承担全球气候变化责任、“努力早日达峰”的贡献;而中国在国际气候谈判会议上,除了坚持人均原则、历史责任原则外,也需要注重强调相对原则(如排放强度降低),争取作为发展中国家应该获得的发展排放空间。
| [1] | 陈齐芳. 运用底线思维适应和谋求中国经济发展的新常态[J].企业经济,2014(10). |
| [2] | 陈诗一. 中国碳排放强度的波动下降模式及经济解释[J].世界经济,2011(4). |
| [3] | 陈诗一."低碳转型"会导致经济减速吗?[N].解放日报, 2010-07-26. |
| [4] | 陈诗一. 中国各地区低碳经济转型进程评估[J].经济研究,2012(8). |
| [5] | 陈永国, 褚尚军, 聂锐. 我国产业结构与碳排放强度的演进关系——基于"开口P型曲线"的解释[J].河北经贸大学学报,2013(2). |
| [6] | 范英, 张晓兵, 朱磊. 基于多目标规划的中国二氧化碳减排的宏观经济成本估计[J].气候变化研究进展,2010(2). |
| [7] | 范英英.基于碳排放总量控制的低碳经济发展优化模型研究[D].华北电力大学博士学位论文, 2011. |
| [8] | 韩一杰, 刘秀丽. 中国二氧化碳减排的减排成本测算[J].管理评论,2010(6). |
| [9] | 姜庆国, 穆东. 到2020年中国实现减排目标的减排成本测算[J].北京交通大学学报,2013(1). |
| [10] | 刘明磊, 朱磊, 范英. 我国省级碳排放绩效评价及边际减排成本估计:基于非参数距离函数方法[J].中国软科学,2011(3). |
| [11] | 宋建军, 张庆杰, 刘颖秋. "十一五"时期和2020年我国水资源问题的若干思考[J].经济研究参考,2004(2). |
| [12] | 唐建荣, 张白羽, 陈实. 基于多目标规划的减排路径研究[J].工业技术经济,2012(12). |
| [13] | 王灿, 陈吉宁, 邹骥. 基于CGE模型的CO2减排对中国经济的影响[J].清华大学学报(自然科学版),2005(12). |
| [14] | 王一鸣. 全面认识中国经济新常态[J].求是,2014(22). |
| [15] | 伍华佳. 上海高碳产业低碳化转型路径研究[J].科学发展,2012(5). |
| [16] | 吴英姿, 闻岳春. 中国工业绿色生产率、减排绩效与减排成本[J].科研管理,2013(2). |
| [17] | 夏炎, 范英. 基于减排成本曲线演化的碳减排策略研究[J].中国软科学,2012(3). |
| [18] | 杨浩彦. 台湾地区与能源使用相关的二氧化碳减量成本估计:多目标规划分析法之应用[J].人文及社会科学集刊,2000(3). |
| [19] | 姚宇.我国产业低碳化经济发展研究[D].陕西师范大学博士学位论文, 2010. |
| [20] | 张雷, 李艳梅, 黄园淅, 吴映梅. 中国结构节能减排的潜力分析[J].中国软科学,2011(2). |
| [21] | 张云, 杨来科. 中国工业部门出口贸易、国内CO2排放与影响因素——基于结构分解的跨期对比分析[J].世界经济研究,2012(7). |
| [22] | 中国投入产出学会课题组. 国民经济各部门水资源消耗及用水系数的投入产出分析[J].统计研究,2007(3). |
| [23] | Chen T. Y.. The Impact of Mitigating CO2 Emissions on Taiwan's Economy[J].Energy Economics,2001,23(2):141–151. |
| [24] | Chen W. The Costs of Mitigating Carbon Emissions in China: Findings from China MARKAL-MACRO Modeling[J].Energy Policy,2005,33(7):885–896. |
| [25] | Criqui P., Mima S., Viguier L. Marginal Abatement Cost of CO2 Emission Reductions, Geographical Flexibility and Concrete Ceilings:An Assessment Using the POLES Model[J].Energy Policy,1999,27(10):585–601. |
| [26] | Fare R., Crosskopf S., Weber W. L.. Shadow Prices and Pollution costs in US Agriculture[J].Ecological Economics,2006,56(1):89–103. |
| [27] | Hafkamp W. A., Nijkamp P. An Integrated Interregional Model for Pollution Control[R]. Economic Environmental Energy Interactions Modeling and Policy Analysis, Boston, 1980:149-171. |
| [28] | Han J.H., Ahn Y.C., Lee I. B.. A Multi-objective Optimization Model for Sustainable Electricity Generation and CO2 Mitigation (EGCM) Infrastructure Design Considering Economic Profit and Financial Risk Original Research Article[J]. Applied Energy,2012,95(6):186–195. |
| [29] | Hsu G. J. Y., Chou F. Y. Integrated Planning for Mitigating CO2 Emissions in Taiwan: A Multi-objective Programming Approach[J].Energy Policy,2000,28(8):519–523. |
| [30] | Lee M. The Shadow Price of Substitutable Sulfur in the US Electric Power Plant: A Distance Function Approach[J].Journal of Environmental Management,2005,77(2):104–110. |
| [31] | Maddison D. A Cost-benefit Analysis of Slowing Climate Change[J]. The Centre for Social and Economic Research on the Global Environment Working Paper,1995,23(4):337–346. |
2.School of Mathematics and Information Science, Shanghai Lixin University of Commerce, Shanghai 201620, China;
3.School of Economics and Trade, Shanghai Lixin University of Commerce, Shanghai 201620, China
 2015, Vol. 17
2015, Vol. 17


