2. 中国运载火箭技术研究院研究发展中心,北京 100076
2. China Academy of Launch Vehicle Technology R & D Center, Beijing 100076, China
临近空间距地面20~100 km, 包括大部分平流层区域、整个中间层以及部分电离层区域.按照现有的航空航天技术水平, 这部分空域是航空飞行器能及的最大高度、航天轨道飞行器的最低高度, 对这部分空域的开发研究已经成为国际热点.相比传统的航空空域, 由于较高的轨道, 这部分空域的飞行器隐蔽性更好, 具有更强的突防能力; 相比传统的航天空域, 这部分空域距离地面高度低, 可以节省发射成本, 且具有更好的对地观测能力.研究这部分空域飞行器, 可以将传统的航空和航天空域结合起来, 实现空天一体化, 具有重要的经济价值和军事战略意义.
高超声速飞行器是一种适合于临近空间远程飞行的飞行器, 飞行Mach数大于5,以吸气式发动机或组合发动机为主要动力, 其具体应用形式包括高超声速巡航导弹、高超声速有人/无人飞机、空天飞机和空天导弹等多种飞行器.高超声速飞行器具有快速、隐身、机动强、可防拦截、具有强大破坏力等特征.如今速度是衡量武器系统性能的重要指标, 临近空间高超声速飞行器技术的发展是武器技术发展中的一个重要里程碑.高超声速飞行器将成为未来空天力量对抗中至关重要的武器, 对于未来战争的作战模式、作战过程及战争结局将产生重大影响.
高超声速飞行器总体技术, 将涉及气动布局、气动加热、飞行器结构热防护、热-流-固耦合、高超声速边界层、吸气式推进系统、轻质高强度材料、全球定位等多学科技术问题.而对于气动力和气动热的准确预测研究是开展高超声速飞行器技术研究的重要基础.本文对于高超声速气动力和气动热的研究现状和发展趋势进行了介绍, 系统阐述了其关键技术和研究方法, 对于我国开展高超声速相关研究具有一定的参考意义.
1 高超声速气动力/热工程计算在高超声速飞行器的研制初期, 不可能投入过多的资源进行大量数值仿真和实验研究, 因此发展快捷有效的工程计算方法进行气动力及气动热的计算就显得十分必要.
1.1 气动力工程计算对于高超声速飞行器, 空气黏性主要在比激波层薄很多的边界层内起作用, 而在激波层内, 可以忽略黏性作用.因此, 用无黏流动的分析方法, 可以预测大部分的气动特性, 特别是预测升力和俯仰力矩, 可以取得比较满意的结果.但要更为准确地获得气动力信息, 仍须考虑黏性阻力的影响.下文从无黏气动力的计算方法以及黏性阻力的计算方法对气动力工程计算进行介绍.
1.1.1 无黏气动力计算方法无黏气动力的计算方法包括Newton流模型法、切楔法/切锥法以及Dahlem-Buck法3种常用方法.
(1) Newton流模型
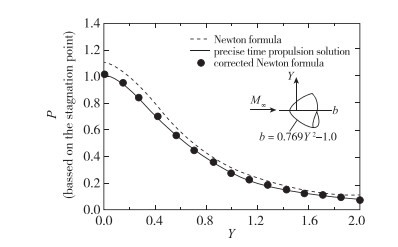
将流体质点的运动看作直线运动的粒子, 流体粒子撞击到物体表面后法向动量完全损失而切向动量保留.在此假设下, 流体作用于物体表面的压力系数只与物面和来流方向的夹角θ有关.原始的Newton压力系数公式适用于Mach数趋近于无穷大的情况, Lees[1]考虑了有限Mach数对Newton公式的影响, 进行了修正. 图 1给出了来流Mach数为8时, Newton公式和Lees修正Newton公式得出的绕椭球体表面压力系数分布与精确时间推进解的对比[2], 可见对于Mach数不太高的钝头体外形绕流问题, Lees修正公式与精确解吻合更好.
(2) 切楔法/切锥法
切楔法/切锥法[3]用于预测二维平面/轴对称体在高超声速流场中的表面压力分布.切楔法/切锥法的基本思想是物面上任意一点的压力等于以当地倾角θ为半楔角/半锥角的平面斜激波/圆锥激波后的压力, 由斜激波关系式/圆锥激波关系式得到.使用切楔法和切锥法须注意物面当地倾角不能大于来流Mach数对应的临界脱体角.因而切楔法/切锥法只适用于具有贴体激波的尖头体外形.
(3) Dahlem-Buck法
Dahlem-Buck法是Newton流模型与切锥法相结合的方法, 在大撞击角时采用修正Newton法, 在小撞击角时采用近似的切锥法.
1.1.2 黏性阻力的计算方法[4]黏性阻力的计算主要指摩擦阻力系数的计算, 对摩阻的工程计算, 是利用平板的研究结果, 把飞行器表面展开成一个“相当平板”.通过将平板的摩阻加入形状修正因子和可压缩性修正因子获得飞行器的摩阻.对于低速情况, 平板摩阻系数为
| $ {{C}_{\text{fp}}}=1.328/\sqrt{R{{e}_{\text{L}}}} $ | (1) |
经过修正, 可以计算高超飞行器摩阻:
| $ {{C}_{\text{f}}}={{C}_{\text{fp}}}\cdot {{\left( 1+0.03{{M}^{2}} \right)}^{-1/3}}\cdot {{\eta }_{\lambda }}\cdot S/{{S}_{\text{ref}}} $ | (2) |
其中, ReL为以飞行器长度计算出的Reynolds数, M为Mach数, η2为形状修正因子, S为飞行器侧面积, Sref为参考平板面积.
1.2 气动热工程计算高超气动热的工程计算方法是基于边界层方程相似解,经过理论分析并进行合理假设推导获得, 或根据实验数据, 通过理论分析形成的半经验方法获得.工程计算方法自提出以来, 因其计算过程简单, 计算效率高, 得到了迅速发展.
1.2.1 零攻角轴对称简单外形飞行器(1) 驻点热流的计算
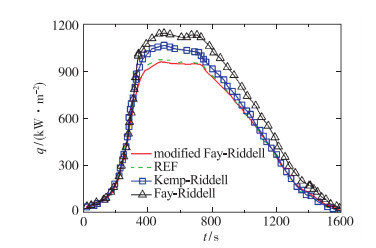
对于飞行器驻点热流的计算, 采用边界层相似解求表面摩阻系数, 层流采用Blasius表面摩阻公式, 湍流采用Schultz-Grunow表面摩阻公式, 并利用Eckert参考焓方法分析高速气流压缩性影响, 及Reynolds比拟关系式计算表面热流密度.广泛采用的Fay-Riddell公式以及考虑了激波效应的Kemp-Riddell公式等均是基于此方法.不同驻点热流计算公式的计算结果对比如图 2所示.
|
| 图 2 不同驻点热流计算公式对比[5] Fig.2 Comparisons of computational results of different stagnation heat transfer formulae[5] |
(2) 非驻点热流的计算
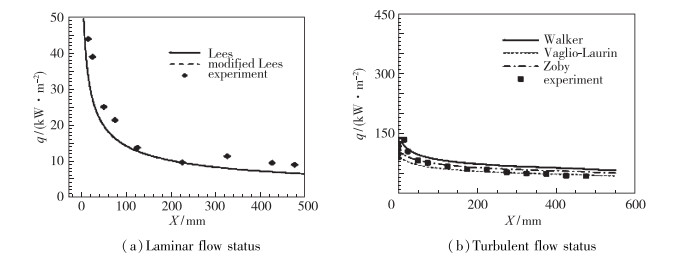
对于非驻点热流计算, 由于流体参数和热力学参数沿物面方向发生变化, 相似解不存在, 因此须引入假设, 即各参数沿物面方向的变化率远小于沿物面法向的变化率.此时速度剖面与法向坐标可以通过一定的变换, 使速度剖面在流向方向相同, 即存在局部相似解, 从而进行计算. Lees[6]根据非驻点局部相似解得到了钝体层流热流密度分布公式, 该公式可以用来预测球头、锥体等部分的热流密度分布, 给出的结果同地面实验数据有良好的一致性. Vaglio-Laurin[7]及Zoby[8]也发展了不同的非驻点湍流热流密度计算公式, 这些计算公式的比较结果如图 3所示.
|
| 图 3 非驻点热流计算与实验比较[5] Fig.3 Comparisons of experiment results and computational results of different formulae for non-stagnation point[5] |
目前飞行器的类型多种多样, 按不同方式可以分为不同的类型, 就气动热研究而言, 飞行器外形可按其身部的宽厚比(飞行器的宽度与厚度之比)划分为小宽厚比飞行器、大宽厚比飞行器等.针对这两种复杂飞行器外形, 有不同的气动热计算方法.
(1) 小宽厚比飞行器计算
小宽厚比飞行器身部大面积区域的工程计算方法主要有轴对称比拟法、等价锥法等.
轴对称比拟法基于小横流假设, 以流线作为一坐标轴, 采用Mager变换[9], 把三维边界层方程简化为准轴对称边界层方程.从而每一条表面流线对应于不同的轴对称等价体, 各个流线间独立, 可用于计算有攻角小宽厚比的飞行器表面热流[10]. DeJarnette等[11]采用此方法建立了一套适用于理想气体和空气平衡气体的计算高超声速流中任意三维钝头体层流、转捩和湍流加热率的方法, 并与实验结果吻合较好.
等价锥法是将有攻角的流动用零攻角等价锥的流动代替, 其等价锥的半锥角是攻角、物面倾角和圆周角的函数, 相当于有攻角物面相对于来流的局部倾角.
(2) 大宽厚比飞行器计算
薄片理论适用于大宽厚比的飞行器.对于大宽厚比外形, 在超声速条件下与展向流动无关.因此, 对此类外形可采用片条理论, 即平行于飞行器的中心线把飞行器切成若干二维的片条, 并假定这些片条之间没有干扰, 把这些二维片条作为二维钝头物体, 计算这些二维物体的表面热流, 最终可获得整个飞行器表面的热流. Adams等[12]采用片条理论对高超声速斜掠柱体, 三角翼等模型的表面压力、表面热流及表面流线流动进行了计算, 并与风洞实验数据进行了比较, 结果吻合较好.
高超声速气动力/热的理论工程计算方法基于现有的基础理论, 进行适当的简化分解, 并依靠一定的工程经验而发展起来的气动力/热快速计算方法, 主要用于高超声速飞行器开发研制前期的气动力/热的粗略计算.因其对物理问题存在简化, 并依赖工程经验, 故在气动力/热的计算准确程度上较差.
2 高超声速气动力/热数值仿真在高超声速飞行器的研究设计中, 数值仿真是获取飞行器气动力/热的重要手段.对于高超声速绕流流场的数值模拟, 现有的大多数数值计算方法在气动力/热的计算中都能够给出令人满意的结果, 可以较好地刻画流场动力学特性.但由于高超声速问题的复杂性, 如高空稀薄流效应、网格/湍流模式的选取以及化学非平衡流效应等, 均会对气动力/热的数值计算造成影响, 因而须对此类问题进行更深入的研究.
2.1 高空稀薄流效应对数值仿真计算的影响高超声速飞行器大气层内飞行一般会经历自由分子流、稀薄过渡流及连续流这3种不同的流动区域. 3种不同的流动区域对于高超声速气动热的数值计算有着重大影响, 针对不同的流动区域有相应的数值仿真算法.
2.1.1 连续流动的气动热数值计算连续流区域的数值模拟是通过求解N-S方程及其各种简化形式来计算飞行器气动力、表面热流密度, 包括求解黏性激波层(VSL)方程, 抛物化N-S方程和全N-S方程等.
2.1.2 稀薄流区的数值模拟稀薄流区域流动不再满足连续性假设, 流体的控制方程为Boltzmann方程, 由于该方程的高度非线性, 传统数值计算方法求解困难.而直接模拟Monte Carlo法(DSMC)基于统计思想, 从微观角度建立气体分子碰撞、迁移和能量交换等过程, 是目前最有能力模拟真实三维高超声速稀薄气体流动的方法.
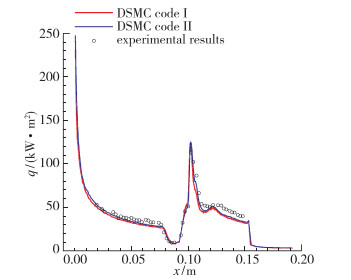
Moss等[13]利用DSMC方法计算了双锥体模型以及中空柱裙模型的高超声速流动状态.计算中考虑了激波边界层干扰、边界层流动分离等重要现象.结果表明计算结果对于网格精度、物理模型参数敏感, 与实验结果吻合较好, 结果如图 4所示.
|
| 图 4 双锥体热流密度DSMC计算与实验数据比较[13] Fig.4 Comparisons of computational results with two different DSMC codes and experiment results for double-cone model[13] |
过渡流区域流动在数值模拟方面极难处理, 由于气体较稀薄, 连续流的N-S方程计算可能局部或全部区域失效, 带来较大误差, 而稀薄流的DSMC方法受网格、时间步长以及仿真分子数等因素限制, 在过渡流区域的计算效率低, 计算量大, 因此并不适用.目前针对这一区域的处理方法主要有如下3种:
(1) 滑移边界条件的CFD算法
过渡流区域的基于N-S方程的CFD数值模拟, 须对壁面边界条件进行修正.此时的边界条件须考虑低密度和热蠕动效应, 采用速度滑移和温度跳跃壁面边界条件.经过滑移边界条件修正的N-S方程数值模拟可以应用于过渡流区域的计算.
(2) 基于Boltzmann方程跨流域高超声速统一算法
基于Boltzmann方程基本理论, 考虑气体分子密度、碰撞频率、热力学效应等作用, 根据微观分子动力学概率统计原理, 推广应用气体运动论离散速度坐标法, 引入最优化方法确定离散速度坐标点, 将单一的气体分子速度分布函数方程化为可用计算流体力学有限差分方法数值求解的双曲型守恒方程, 但此方法计算量较大.
(3) CFD/DSMC耦合算法
将CFD和DSMC方法耦合计算, 发挥各自的优点, 扩展两种算法的使用范围, 使其适合过渡区域流动的计算.这种耦合算法的关键之处在于两种算法之间的数据交换方式, 为了抑制数据交换时产生的统计波动, 发展了多种交换边界处理方法.其中, Schwartzentruber等发展的MPC耦合技术[14]被广泛采用, 该方法可以保证较高的计算精度, 且具有较快的计算速度.
2.2 网格/湍流模式对数值仿真计算影响由于高超声速飞行器壁面流动复杂, 为了对气动力/热进行准确计算, 必须考虑网格对计算的影响, 同时须采用有效的转捩模式和湍流模式.
Alter[15]评估了在高超声速计算中, 结构网格的质量问题以及网格质量对计算结果的影响.认为网格的正交性对准确计算高超声速情况下物面的摩擦阻力很重要, 并定义了一种网格质量评估标准, 1表示最好的网格, 0表示最差的网格, 一般的高超声速计算, 要求网格质量在0.6~0.8之间. Nichols等[16]进一步讨论了高超声速流动中壁面计算问题, 提出了一种适合高超声速流动的湍流壁面函数边界条件, 使得在y+ < 100的范围内, 都能得到较好的壁面压力、摩阻分布. Brown[17]对高超声速流动的湍流模型进行了验证, 考虑物面的压力变化和摩擦阻力变化, 并与实验数据进行比较, 分析表明k-ω SST和k-ω湍流模型能够给出与实验更为接近的结果.阎超等[18]研究了不同计算格式(Roe的FDS格式、Van Leer的FVS格式、AUSM+格式及中心差分格式)对热流计算精度的影响, 认为AUSM+格式对热流计算最为准确.潘沙等[19]讨论了网格形式对热流计算的影响, 结果表明由于壁面温度梯度较大, 热流计算对于壁面法向网格分布极为敏感; 且发现气动热计算的收敛过程比压力和流场收敛慢得多, 即以方程残差和压力收敛作为气动热收敛的依据是不正确的.
综合目前的研究情况, 须根据具体的计算工况以及考察的物理量来决定网格及湍流模式的选取, 才能取得较好的计算效果.
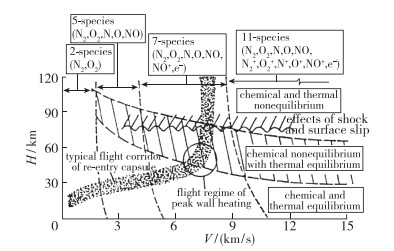
2.3 化学非平衡流效应对数值计算的影响由于高温效应, 高超声速飞行器壁面气体会发生化学反应, 当化学反应时间尺度与流动特征时间尺度相当时, 即处于化学非平衡流动状态, 此时的CFD控制方程须考虑不同的气体化学组分、化学反应模型等. 图 5为Gupta等[20]对一典型的半径为0.305 m的球头驻点区域的热化学状态的分类.
|
| 图 5 球体驻点区域空气热化学状态分区图[20] Fig.5 Flight stagnation region air chemistry for a 0.305 m radius sphere[20] |
Hassan等[21]针对阿波罗返回舱, 开展了考虑化学非平衡效应的气动分析, 研究了化学反应和振动激发对升阻比和配平攻角的影响, 考虑了5组元化学反应模型进行计算(M=27), 并与理想气体和实验结果进行了比较.结果表明考虑化学非平衡效应计算的升阻比系数小于考虑理想气体计算的结果, 并与实验结果吻合较好. Papadopoulos等[22], Prabhu等[23]采用5组元化学非平衡模型对航天飞机不同攻角下俯仰力矩的特征进行了计算研究.结果表明考虑化学非平衡效应, 会推迟俯仰力矩系数的逆转. Bisceglia等[24]也开展了考虑化学非平衡效应的数值模拟研究, 对M=9~26, 高度40~80 km飞行条件的壁面压力分布和摩阻系数进行了比较, 发现压力分布和摩阻系数受到来流Mach数的影响, 并与实验和飞行数据进行对比, 吻合较好.
高超声速气动力/热的数值计算是直接求解流体力学方程, 简化较少, 适合对复杂外形的高超飞行器气动力/热的准确估计.但数值计算处理过程复杂, 对计算机要求高, 耗费大量机时.数值格式、网格划分和湍流模型的选取对气动热数值模拟影响很大, 同时还须考虑稀薄流动效应以及化学非平衡效应对计算结果的影响.
3 高超声速气动力/热实验研究高超声速风洞气动力实验研究对于高超声速飞行器设计和性能评估具有重要的意义.对于高超声速飞行器而言, 工作环境极其特殊, 伴随着高温、高焓、剧烈的化学反应等效应, 再加上其复杂的结构外形, 这对气动性能的数值计算造成了困难.目前高超声速风洞气动实验仍是研究、预测高超声速飞行器气动性能和解决关键气动问题的主要方法[25-26].
3.1 实验研究基础条件及存在问题目前可用于开展高超声速气动力、气动热等各类实验的地面设备主要包括:常规高超声速风洞、脉冲型高超声速风洞(包括激波风洞/炮风洞、高超声速脉冲燃烧风洞、电弧风洞等)以及弹道靶设备等.
现有的常规高超声速风洞, 通常M < 10, 且工作压力及密度均较高, 实验时间相对较长(从s到min量级).但未来临近空间高超声速飞行器飞行速度M > 10, 且飞行环境低密度, 因而须开展对于高Mach数、变密度风洞的设计研究工作, 实现模拟高空、高Mach数飞行的实验条件.
而现有脉冲型高超声速风洞, 虽然模拟M较高, 可达20, 且工作压力及温度(8 000 K)均较高, 但实验时间短(ms量级), 给相关实验数据的测试带来了困难, 因此须开展长时间脉冲高速风洞的设计研究工作.
弹道靶是一种实现气动实验模型在静止气体中自由飞行的空气动力学地面实验设备.实验时, 发射器将模型以一定速度发射到靶室内, 高速图像记录模型的运行轨迹, 然后利用图像处理、参数辨识等技术, 获得模型的气动特性参数, 特别是动导数等动态气动特性系数, 最大Mach数可达15.实验过程中无支架、洞壁干扰, 且靶室内密度可调, 可模拟高焓飞行条件下的真实气体效应以及接近真实飞行的低流动湍流度.但最大缺点是实验时间短、模型尺寸小以及测试精度难于提高, 这些都是弹道靶实验需进一步提高的地方.
3.2 气动力的实验测量风洞天平是高超声速风洞气动力实验研究的核心和关键设备, 风洞天平技术水平的高低, 将直接影响风洞气动力测试结果的准确性和可靠性[27].根据天平测量原理、测量敏感元件的不同, 可以分为应变天平、压电天平和光纤天平等种类.
应变天平在高超声速气动力实验中应用最为广泛, 技术最成熟.但由于高超声速测力环境恶劣, 且往往模型尺寸较小, 因而测力量程小, 这对高超声速测力天平提出了较高要求.目前国内外已经发展出各种内置、外置微量天平, 包含温度修正、动态性能补偿等功能, 如图 6所示[28].
压电天平是利用压电陶瓷或晶体的压电效应进行气动力测量, 压电天平具有刚度高、响应快、结构简单、载荷范围宽和模型适应能力强等特点, 见图 7.国外已有不少学者对此类天平进行了设计、研究, 该类天平已在激波风洞中具有广泛应用[29-31]. Mari-neau[30]的实验结果表明在相同的精度下, 压电天平在频响上比传统应变天平提高350%, 敏度上提高400%.对于升力、阻力系数以及力矩的测量上与CFD数值仿真结果相差在5%以内.
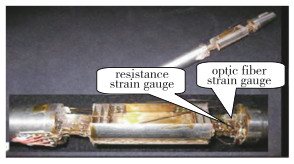
光纤天平是为适应等离子和电磁条件下的空气动力学实验研究而发展起来的一种新型测试天平[32-33].光纤应变天平目前主要有两种类型:一种是基于Fabry-Pérot干涉仪(Fabry-Pérot interferometer)制成, 美国阿诺德工程发展中心(AEDC)对此类天平的设计研制开展了大量工作, 通过与传统应变天平实验对比(如图 8所示), 表明该光纤天平具有更高的精度和抗干扰能力.中国空气动力研究与发展中心(CARDC)根据此原理自主研制了两分量光纤天平原理样机, 如图 9所示, 研究表明此类天平对电磁干扰完全免疫, 对温度变化也不敏感, 故其灵敏度较高、耐腐蚀、抗电磁干扰, 能在高温环境中正常工作.另一种是基于光纤光栅制成, 由光纤光栅反射波长的漂移来感应应变, 沈阳航空航天大学研制了五分量光纤光栅测力天平, 并进行了动校实验, 结果表明该光纤光栅天平与传统应变天平具有相同精度, 但该天平受温度影响较大[34].因此, 基于Fabry-Pérot干涉原理制作的天平更有发展前景, 更适用于高超声速的恶劣实验环境.
3.3 气动热的实验测量由于高超声速飞行器表面极高的温度, 气动热的实验测试难度较大.目前对于气动热的测试, 主要测试结构表面的温度以及热流.
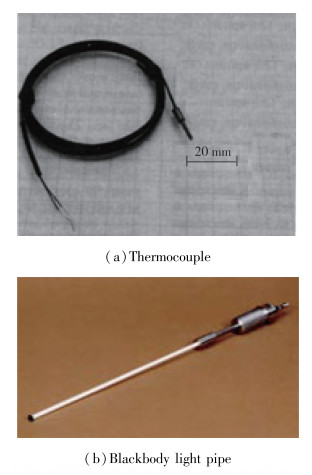
对于结构表面温度测试, 主要采用热电偶.该方法是高温高压恶劣条件下热环境测量的主要手段, 具有响应快、输出大、性能稳定等特点.此外, NASA Dryden研制了黑体光导管温度测试技术, 用于高温复合材料结构温度的精确且可重复性测量.并在黑体校准炉内完成了黑体光导管温度传感器的校准, 在温度范围为800~1 500 ℃之间, 黑体光导管温度传感器与光学高温计之间误差小于1.1 ℃(如图 10所示).黑体光导管具有抗电磁辐射干扰、测试范围宽、耐高温等优点[35].
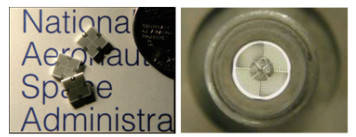
热流测试技术包括点热流测试和大面积热流测试.对于点热流测试, 主要采用电热流传感器, 具有精度高、尺寸小、高频响应等特点. Tao System和Virginia Tech联合研制了新型小尺寸、高频响应热流传感器, 应用于高速航天器热流测试, 如图 11所示. 2002年NASA Glenn提出了在氧化铝基片上研制双面、单面薄膜Wheatstone电桥热流计, 比热电堆型薄膜热流计更容易制造, 且输出信号更大, 如图 12所示.

|
| 图 11 Tao System和Virginia Tech研制的热流计[36] Fig.11 Heat flux meter developed by Tao System and Virginia Tech[36] |
大面积热流测试包括红外热图、温敏漆技术、热色液晶技术等, 它可通过光学测量方法获得模型表面整体的热流分布, 具有空间分辨率好、形象直观的优点, 但其测试精度较低[37-38], 如图 13, 14所示.
4 发展展望对于高超声速气动力/气动热问题的研究是临近空间高超声速武器开发研制的基础保障.对于气动力/热问题已经开展了大量研究, 但仍存在如下问题:
(1) 高超声速气动力的工程计算是一种快捷的气动力计算方法, 传统计算往往忽略摩擦阻力, 只进行无黏阻力计算.原因在于低超声速飞行器(一般指M介于1.2~3.6) 波阻很大而摩阻很小, 在气动力工程计算中注重波阻而忽略摩阻, 即主要采用Newton流模型法进行无黏气动力计算.而对于高超声速飞行器(M > 5), Reynolds数变小, 其摩阻往往不可忽略, 甚至有可能大于波阻, 因而我国未来高超声速武器的气动力工程计算必须考虑摩擦阻力效应.
(2) 由于高温效应, 高超声速飞行器壁面气体会发生化学反应, 对气动力的计算造成影响, 如何开展考虑化学反应的数值计算是重要的研究方向.当化学反应时间尺度与流动特征时间尺度相当时, 即处于化学非平衡流动状态, 此时化学反应效应不能忽略, CFD控制方程须考虑不同的气体化学组分、化学反应模型等, 对控制方程进行补充修正, 从而保证数值求解的准确性.化学反应模型、化学反应组分的选取均是研究热点问题.
(3) 高超声速风洞气动力实验是为高超声速飞行器设计和性能评估提供可靠数据不可或缺的重要技术手段.高超声速风洞测力天平工作条件相对恶劣、天平温度控制要求高, 并可能须要进行电磁隔离, 开展相应的高精度、高灵敏度及抗干扰的天平测力技术研究极其重要.
(4) 常用的气动力/气动热研究方法有理论工程计算、数值仿真以及实验研究3种.理论工程计算对实际问题进行了简化, 并依赖一定的工程经验, 适合简单模型计算, 而复杂的飞行器外形计算结果的精度较差.数值仿真计算直接从理论方程出发, 能准确地计算气动力/气动热, 但数值计算往往计算量较大, 花费大量时间, 因而未来计算研究的发展方向应是将理论工程计算和数值仿真研究相结合, 提高计算精度, 节省计算时间.但对于气动力/热的计算研究, 最终与实际情况有一定的差异, 因而还须进行实验研究, 进而检验计算研究结果的准确性.因此, 临近空间高超声速飞行器气动力/热问题的研究需要理论工程计算、数值仿真和实验研究三者相辅相成, 互补不足, 才能更为有效、准确.
临近空间高超声速飞行器对于应对未来战争、突破导弹防御系统以及对敌方造成威慑力具有重要意义.但我国高超声速问题的研究仍存在一系列的困难, 技术储备、研究基础以及研究条件和能力还比较差.对此, 我国应该借鉴美国等其他国家的发展道路, 吸取其经验教训, 少走弯路, 在此基础上, 结合我国的实际情况, 对我国的能力做出合理的评估, 制定适合我国发展的路线, 这样才能在较短的时间内取得显著的进展.
| [1] |
Lees L. Hypersonic flow[C]. The 5th International Aeronautical Conference, Los Angeles, 1955:241-276. https://link.springer.com/chapter/10.1007/978-1-4615-8624-1_3
|
| [2] |
Anderson J D. Hypersonic and high temperature gas dy-namics[M]. Reston: AIAA, 2000.
|
| [3] |
Gentry A E, Smyth D N, Oliver W R. The mark Ⅳ supersonic-hypersonic arbitratry-body program. volume Ⅱ. program formulation[R]. Technical Report, AFFDL-TR-73-159, 1973. http://oai.dtic.mil/oai/oai?verb=getRecord&metadataPrefix=html&identifier=AD0778444
|
| [4] |
高建力. 高超声速飞行器气动特性估算与分析[D]. 西安: 西北工业大学, 2007. Gao J L. Estimating and analyzing of aerodynamic of hypersonic vehicle[D]. Xi'an:Northwestern Polytechnical University, 2007(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10699-2007057100.htm |
| [5] |
彭治雨, 石义雷, 龚红明, 等. 高超声速气动热预测技术及发展趋势[J]. 航空学报, 2015, 36(1): 325-345. Peng Z Y, Shi Y L, Gong H M, et al. Hypersonic aeroheating prediction technique and its trend of development[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 325-345. (in Chinese) |
| [6] |
Lees L. Laminar heat transfer over blunt-nosed bodies at hypersonic flight speeds[J]. Journal of Jet Propulsion, 1956, 26(4): 259-269. DOI:10.2514/8.6977 |
| [7] |
Vaglio-Laurin R. Turbulent heat transfer on blunt-nosed bodies in two-dimensional and general three-dimensional hypersonic flow[J]. Journal of the Aerospace Sciences, 2012, 27(1): 27-36. |
| [8] |
Zoby E V. Comparisons of free-flight experimental and predicted heating rates for the Space Shuttle[R]. AIAA 1982-0002, 1982. http://arc.aiaa.org/doi/abs/10.2514/6.1982-2
|
| [9] |
Cooke J C, Hall M G. Boundary layers in three dimen-sions[J]. Progress in Aerospace Sciences, 1962, 2(2): 221-282. DOI:10.1016/0376-0421(62)90008-8 |
| [10] |
康宏琳, 阎超, 李亭鹤, 等. 高超声速再入钝头体表面热流计算[J]. 北京航空航天大学学报, 2006, 32(12): 1395-1398. Kang H L, Yan C, Li T H, et al. Numerical study of aeroheating predictions for hypersonic reentry bodies[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(12): 1395-1398. DOI:10.3969/j.issn.1001-5965.2006.12.001 (in Chinese) |
| [11] |
DeJarnette F R, Hamilton H H. Aerodynamic heating on 3-D bodies including the effects of entropy-layer swal-lowing[R]. AIAA 1974-602, 1974.
|
| [12] |
Adams J C, Martindale W R.Hypersonic lifting body windward surface flow-field analysis for high angles of in-cidence[R]. AEDC-TR-73-2, 1973. http://oai.dtic.mil/oai/oai?verb=getRecord&metadataPrefix=html&identifier=AD0756499
|
| [13] |
Moss J N, Bird G A. Direct simulation Monte Carlo simulations of hypersonic flows with shock interactions[J]. AIAA Journal, 2005, 43(12): 2565-2573. DOI:10.2514/1.12532 |
| [14] |
Schwartzentruber T E, Scalabrin L C, Boyd I D. Amodular particle-continuum numerical method for hypersonic non-equilibrium gas flows[J]. Journal of Computational Physics, 2007, 225(1): 1159-1174. DOI:10.1016/j.jcp.2007.01.022 |
| [15] |
Alter S J. A structured-grid quality measure for simulated hypersonic flows[R]. AIAA 2004-0612, 2004. http://arc.aiaa.org/doi/abs/10.2514/6.2004-612
|
| [16] |
Nichols R H, Nelson C C. Wall function boundary conditions including heat transfer and compressibility[J]. AIAA Journal, 2004, 42(6): 1107-1114. DOI:10.2514/1.3539 |
| [17] |
Brown J L. Turbulence model validation for hypersonic flows[R]. AIAA 2002-3308, 2002. http://arc.aiaa.org/doi/abs/10.2514/6.2002-3308
|
| [18] |
阎超, 禹建军, 李君哲. 热流CFD计算中格式和网格效应若干问题研究[J]. 空气动力学学报, 2006, 24(1): 125-130. Yan C, Yu J J, Li J Z. Scheme effect and grid depen-dency in CFD computations of heat transfer[J]. Acta Aerodynamica Sinica, 2006, 24(1): 125-130. (in Chinese) |
| [19] |
潘沙, 冯定华, 丁国昊, 等. 气动热数值模拟中的网格相关性及收敛[J]. 航空学报, 2010, 31(3): 493-499. Pan S, Feng D H, Ding G H, et al. Grid dependency and convergence of hypersonic aerothermal simulation[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(3): 493-499. (in Chinese) |
| [20] |
Gupta R N, Yos J M, Thompson R A, et al. Review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal nonequilibrium calculations to 30000 K[R]. NASA-RP-1232, 1990. http://adsabs.harvard.edu/abs/1989STIN...8921193G
|
| [21] |
Hassan B, Candler G V, Olynik D R. The effect of thermo-chemical nonequilibrium on the aerodynamics of aerobraking vehicles[R]. AIAA 1992-2877, 1992. https://arc.aiaa.org/doi/abs/10.2514/6.1992-2877
|
| [22] |
Papadopoulos P E, Prabhu D, Wright M, et al. CFD simulations in support of shuttle orbiter contingency abort aerodynamic database enhancement[R]. AIAA 2001-3067, 2001. http://arc.aiaa.org/doi/abs/10.2514/6.2001-3067
|
| [23] |
Prabhu D K, Papadopoulos P E, Davies C B, et al. Shuttle orbiter contingency abort aerodynamics. Ⅱ-real-gas effects and high angles of attack[R]. AIAA 2003-1248, 2003. http://arc.aiaa.org/doi/abs/10.2514/6.2003-1248
|
| [24] |
Bisceglia S, Ranuzzi G. Real gas effects on a planetary re-entry capsule[R]. AIAA 2005-3385, 2005. http://arc.aiaa.org/doi/abs/10.2514/6.2005-3385
|
| [25] |
蔡国飙, 徐大军. 高超声速飞行器技术[M]. 北京: 科学出版社, 2012: 1-55. Cai G B, Xu D J. Hypersonic vehicle technology[M]. Beijing: Science Press, 2012: 1-55. (in Chinese) |
| [26] |
唐志共, 杨彦广, 徐翔, 等. 高超声速气动力试验[M]. 北京: 国防工业出版社, 2004: 1-44. Tang Z G, Yang Y G, Xu X, et al. Hypersonic aerodynamic test[M]. Beijing: National Defence Industry Press, 2004: 1-44. (in Chinese) |
| [27] |
贺德馨. 风洞天平[M]. 北京: 国防工业出版社, 2001: 1-38. He D X. Windtunnel balance[M]. Beijing: National Defence Industry Press, 2001: 1-38. (in Chinese) |
| [28] |
唐志共, 许晓斌, 杨彦广, 等. 高超声速风洞气动力试验技术进展[J]. 航空学报, 2015, 36(1): 86-97. Tang Z G, Xu X B, Yang Y G, et al. Research progress on hypersonic wind tunnel aerodynamic testing techniques[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 86-97. (in Chinese) |
| [29] |
Duryea G R, Martin J F. An improved piezo-electricbalance for aerodynamic force measurements[J]. IEEE Transactions on Aerospace and Electronics System, 1968, AES-4(3): 351-359. DOI:10.1109/TAES.1968.5408988 |
| [30] |
Marineau E C. Force measurements in hypervelocity flows with an acceleration compensated piezoelectric balance[J]. Journal of Spacecraft and Rockets, 2011, 48(4): 697-700. DOI:10.2514/1.A32047 |
| [31] |
Jia Z, Gao Y, Ren Z, et al. Research on the characteristics of a piezoelectric balance for the dynamic motion device[J]. International Journal of Industrial and Systems Engineering, 2014, 18(3): 364-381. DOI:10.1504/IJISE.2014.065539 |
| [32] |
ChandraKishore M, Srihari G K, Rudresh C, et al. Aerodynamic load measurements at hypersonic speeds using internally mounted fiber-optic balance system[C]. 21st International Congress on Instrumentation in AerospaceSimulation Facilities, Sendai, 2005:119-122. http://ieeexplore.ieee.org/document/1569912/
|
| [33] |
Vasudevan B. Measurement of skin friction at hypersonic speeds using fiber-optic sensors[R].AIAA 2005-3323, 2005. http://arc.aiaa.org/doi/abs/10.2514/6.2005-3323
|
| [34] |
李勇, 李国文, 杨波. 光纤光栅五分量测力天平及测量方法, CN 101806654 A[P]. 2010. http://www.google.com/patents/CN101806654A?cl=zh
|
| [35] |
Hamlin E, Cruciani E, Pearson P. Blackbody lightpipe temperature sensor development[A].//1999 Research engineering annual report[R]. NASA/TM-2000-209026, 1999.
|
| [36] |
张伟, 张正平, 李海波, 等. 高超声速飞行器结构热试验技术进展[J]. 强度与环境, 2011, 38(1): 1-8. Zhang W, Zhang Z P, Li H B, et al. Progress on thermal test technique of hypersonic vehicle structures[J]. Structure and Environment Engineering, 2011, 38(1): 1-8. (in Chinese) |
| [37] |
周嘉穗, 孔荣宗, 江涛, 等. 激波风洞红外测热试验技术研究[J]. 江汉大学学报(自然科学版), 2010, 38(1): 37-39. Zhou J S, Kong R Z, Jiang T, et al. Infrared thermal test technology study in shock tunnel[J]. Journal of Jianghan University(Natural Sciences), 2010, 38(1): 37-39. (in Chinese) |
| [38] |
周嘉穗, 张扣立, 江涛, 等. 激波风洞温敏热图技术初步试验研究[J]. 实验流体力学, 2013, 27(5): 79-82. Zhou J S, Zhang K L, Jiang T, et al. Preliminary experimental study on temperature sensitive thermography used in shock tunnel[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(5): 79-82. (in Chinese) |