2. 北京航空航天大学航空科学与工程学院国家计算流体力学实验室,北京 100191
2. National Laboratory of Computational Fluid Dynamics, School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China
非定常Euler方程某些问题的解具有自相似特点, 比如一维和二维Riemann问题, 点爆炸问题, 激波反射问题, 激波绕射问题, 以及激波折射问题.利用这种自相似特点, 通过自相似变换将解转化到自相似坐标空间, 可以将原非定常方程转化为定常方程, 称之为自相似Euler方程, 解这种方程的主要好处是可以得到极高分辨率的解.
很多学者在理论上对自相似Euler方程进行了研究[1-4], 但是数值研究较少, 据我们所知, 或许只有Samtaney.在文献[5]中, Samtaney给出了一种自相似Euler方程, 并设计了两种算法求解该方程, 一种是隐式方法, 一种是固定点迭代方法.该自相似Euler方程, 不便于使用目前流行的高分辨率、高精度格式, 这使得这两种方法都具有一定特殊性, 缺乏通用性, 并且略显复杂.作者发现了一种新的简单方法, 无须设计特殊格式, 并且可以得到同样好的解.
本文提出一种新的自相似方法, 主要包含两部分: (1)重写自相似Euler方程, 不同于文献[1, 5]的形式. (2)设计数值方法.通过自相似变换u(x, t)→u(x/t), 原非定常Euler方程初值问题转变为一个定常方程边值问题.为求解该定常方程边值问题, 引入虚拟时间导数项, 并将自相似参数x/t看成局部常数, 这样新方程变回了双曲守恒律形式, 因此可以利用目前已发展成熟的各种高分辨率和高精度格式.
对没有自相似解的问题, 给出了另一种形式的自相似变换, u(x, t)→u(x/t, t), 经过这种变换后方程仍然是非定常的, 原初值问题转化为初边值问题, 这种做法也可以利用自相似解的优点, 并且可以求解不具有自相似性但接近自相似的问题.
本文的基本结构如下:第1节分别给出了一维和多维形式的新自相似Euler方程.第2节给出了新的准自相似Euler方程.第3节分别给出了原Euler方程、自相似Euler方程和准自相似Euler方程的数值方法.这些数值方法都用同一格式, 即2阶熵条件格式.第4节给出了数值计算算例.其中一维、二维Riemann问题, 激波反射问题和激波折射问题, 使用自相似Euler方程进行求解.计算显示, 一维结果几乎等价于精确解, 二维结果也给出了很高的分辨率.一维Shu-Osher问题和双Riemann问题, 使用准自相似Euler方程进行求解, 结果也表现出比原方程更高的分辨率.第5节分析了自相似方法高分辨率的原因, 并在理论和数值上比较了两种形式的自相似方程.
1 自相似Euler方程自相似Euler方程来源于Euler方程的Riemann问题.一维Riemann问题有精确解, 可以用来测试数值方法的优劣.多维Riemann问题, 一般情况下没有精确解.
有些学者对二维Riemann问题进行了理论研究[6], 并按照波出现的种类和个数对解进行了分类. Zhang等[7]指出对多方气体总共有16组不同的Riemann问题; 而Schulz-Rinne[8]证明了其中一种情况是不存在的; Zhang等[9]指出当两条初值的滑移线出现的时候, 根据产生的涡的旋转方向不同还应进行分类.
有些学者对二维Riemann问题进行了数值研究. Schulz-Rinne等[10]使用PPM格式[11]模拟了15种解; 按照文献[9]的分类, Lax等[12]使用正型格式[13]模拟了19种解; Kurganov等[14]使用一种不含Riemann求解器的中心型格式模拟了19种解; Han等[18]使用自适应GRP格式[16-17], 模拟了某些二维Riemann问题, 这些解的类型包含激波与激波相互作用, 涡与涡相互作用, 激波与涡相互作用等, 他们还对比了理论解和数值模拟结果.
1.1 一维自相似Euler方程考虑一维非定常完全气体Euler方程组的Riemann问题
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}_t} + \mathit{\boldsymbol{f}}{{(\mathit{\boldsymbol{u}})}_x} = 0,}&{x{\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} R,t > 0}\\ {\mathit{\boldsymbol{u}}(x,0) = \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_{\rm{L}}},x \le 0\\ {\mathit{\boldsymbol{u}}_{\rm{R}}},x > 0 \end{array} \right.,}&{x{\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} R} \end{array}} \right. $ | (1) |
其中
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}} = \left( {\begin{array}{*{20}{c}} \rho \\ {\rho u}\\ E \end{array}} \right),\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) = \left( {\begin{array}{*{20}{c}} {\rho u}\\ {\rho {u^2} + p(\mathit{\boldsymbol{u}})}\\ {u(E + p(\mathit{\boldsymbol{u}}))} \end{array}} \right)}\\ {p(\mathit{\boldsymbol{u}}) = (\gamma - 1)\left( {E - \frac{{\rho {u^2}}}{2}} \right)} \end{array} $ |
对于Euler方程的Riemann问题, 它的解具有自相似特点, 这种流动称为自相似流动或自模拟流动, 通过坐标变化可以化为定常问题.
引入自相似变换
| $ \bar x = \frac{x}{t} $ |
把u(x, t)变换到u(x/t), 将初值问题(1)变成如下定常边值问题
| $ \left\{ {\begin{array}{*{20}{l}} { - \bar x{\mathit{\boldsymbol{u}}_{\bar x}} + \mathit{\boldsymbol{f}}{{(\mathit{\boldsymbol{u}})}_{\bar x}} = 0,}&{{\lambda _{{\rm{min}}}} \le \bar x \le {\lambda _{{\rm{max}}}}}\\ {\mathit{\boldsymbol{u}}({{\bar x}_{\rm{L}}}) = {\mathit{\boldsymbol{u}}_{\rm{L}}},\mathit{\boldsymbol{u}}({{\bar x}_{\rm{R}}}) = {\mathit{\boldsymbol{u}}_{\rm{R}}}}&{} \end{array}} \right. $ | (2) |
把x看成局部常数(将下式括号内的x冻结, 详见附录A1), 则上式可以改写为
| $ \left\{ {\begin{array}{*{20}{l}} {{{(\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \bar x\mathit{\boldsymbol{u}})}_{\bar x}} = 0,}&{{\lambda _{{\rm{min}}}} \le \bar x \le {\lambda _{{\rm{max}}}}}\\ {\mathit{\boldsymbol{u}}({{\bar x}_{\rm{L}}}) = {\mathit{\boldsymbol{u}}_{\rm{L}}},\mathit{\boldsymbol{u}}({{\bar x}_{\rm{R}}}) = {\mathit{\boldsymbol{u}}_{\rm{R}}}}&{} \end{array}} \right. $ | (3) |
此时方程被改造成了一个定常方程.
注意, 自相似坐标取值范围须满足下式
| $ [{{\bar{x}}_{\text{L}}},{{\bar{x}}_{\text{R}}}]\supset [\text{min}({{\lambda }_{\underset{i,{\mathit{\boldsymbol{u }}}}{\mathop{i}}\,}}({\mathit{\boldsymbol{u }}})),\underset{i,{\mathit{\boldsymbol{u }}}}{\mathop{\text{max}}}\,({{\lambda }_{i}}({\mathit{\boldsymbol{u }}}))] $ |
与原方程(1)对比发现, 对于新方程(3)而言, 通量及其Jacobi矩阵和特征值发生了改变, 左右特征向量保持不变.
新通量, Jacobi矩阵和特征值如下
| $ \begin{array}{l} \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\bar f}}(\mathit{\boldsymbol{u}}) = \mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \bar x\mathit{\boldsymbol{u}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left( {\begin{array}{*{20}{l}} {\rho (u - \bar x)}\\ {\rho u(u - \bar x) + p(\mathit{\boldsymbol{u}})}\\ {(E + p(\mathit{\boldsymbol{u}}))(u - \bar x) + \bar xp(\mathit{\boldsymbol{u}})} \end{array}} \right)} \end{array}\\ \mathit{\boldsymbol{\bar A}}(\mathit{\boldsymbol{u}}) = \mathit{\boldsymbol{\bar f}}{(\mathit{\boldsymbol{u}})_\mathit{\boldsymbol{u}}} = \mathit{\boldsymbol{A}} - \bar x\mathit{\boldsymbol{I}}\\ \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} - \bar x\mathit{\boldsymbol{I}} = \left( {\begin{array}{*{20}{c}} {u - c - \bar x}&{}&{}\\ {}&{u - \bar x}&{}\\ {}&{}&{u + c - \bar x} \end{array}} \right) \end{array} $ | (4) |
方程(3)和(4)就是本文使用的自相似Euler方程.
1.2 与文献中自相似方法的区别对比文献[1, 5]中的自相似方程(记为′有源项′, 方程右端有一源项, 几乎所有其他文献都是此形式), 而我们使用了一种不同形式的方程(3)(记为′无源项′, 方程右端无源项, 自相似参数作为局部常数).需要指出, 我们的处理并没有忽略这个源项, 只是求解方程的一种数值方法.实际上, 原始的自相似方程(2)并没有源项, 只是写成几何守恒形式以后, 才多出来了一个源项.尽管′无源项′和′有源项′自相似方程看起来差别很大, 但理论和计算都表明, 二者其实差别很小.本节给出理论对比, 分析小节中给出计算对比.
为了显示两者的不同, 使用
′无源项′自相似方程为
| $ {(\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over x} \mathit{\boldsymbol{u}})_{\bar x}} = 0 \Leftrightarrow \frac{{\left[ {\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{u}}\left( {\bar x + \frac{{{\rm{d}}\bar x}}{2}} \right)} \right) - \bar x\mathit{\boldsymbol{u}}\left( {\bar x + \frac{{{\rm{d}}\bar x}}{2}} \right)} \right] - \left[ {\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{u}}\left( {\bar x - \frac{{{\rm{d}}\bar x}}{2}} \right)} \right) - \bar x\mathit{\boldsymbol{u}}\left( {\bar x - \frac{{{\rm{d}}\bar x}}{2}} \right)} \right]}}{{{\rm{d}}\bar x}} = 0 $ |
′有源项′自相似方程为
| $ \begin{array}{l} {(\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \bar x\mathit{\boldsymbol{u}})_{\bar x}} + \mathit{\boldsymbol{u}} = 0 \Leftrightarrow \\ \frac{{\left[ {\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{u}}\left( {\bar x + \frac{{{\rm{d}}\bar x}}{2}} \right)} \right) - \left( {\bar x + \frac{{{\rm{d}}\bar x}}{2}} \right)\mathit{\boldsymbol{u}}\left( {\bar x + \frac{{{\rm{d}}\bar x}}{2}} \right)} \right] - \left[ {\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{u}}\left( {\bar x - \frac{{{\rm{d}}\bar x}}{2}} \right)} \right) - \left( {\bar x - \frac{{{\rm{d}}\bar x}}{2}} \right)\mathit{\boldsymbol{u}}\left( {\bar x - \frac{{{\rm{d}}\bar x}}{2}} \right)} \right]}}{{{\rm{d}}\bar x}} + \mathit{\boldsymbol{u}}\left( {\bar x} \right) = 0 \end{array} $ |
可以看出上述两个方程是等价的(都收敛至相同的弱解), 但是离散过程相差一个2阶小量, 利用Taylor展开
| $ \begin{array}{*{20}{l}} {{{(\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \bar x\mathit{\boldsymbol{u}})}_{\bar x}} + \mathit{\boldsymbol{u}} = 0 \Leftrightarrow }\\ {\quad {{(\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over x} \mathit{\boldsymbol{u}})}_{\bar x}} = (\mathit{\boldsymbol{\bar u}} - \mathit{\boldsymbol{u}}) = \frac{{{\mathit{\boldsymbol{u}}_{\bar x\bar x}}{\rm{d}}{{\bar x}^2}}}{8}} \end{array} $ |
其中
| $ \mathit{\boldsymbol{\bar u}}(\bar x) = \frac{1}{2}\left( {\mathit{\boldsymbol{u}}\left( {\bar x - \frac{{{\rm{d}}\bar x}}{2}} \right) + \mathit{\boldsymbol{u}}\left( {\bar x + \frac{{{\rm{d}}\bar x}}{2}} \right)} \right) $ |
同样, 二维情形, 也存在一个2阶小量的差异
| $ \begin{array}{l} {(\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \bar x\mathit{\boldsymbol{u}})_{\bar x}} + {(\mathit{\boldsymbol{g}}(\mathit{\boldsymbol{u}}) - \bar y\mathit{\boldsymbol{u}})_{\bar y}} + 2\mathit{\boldsymbol{u}} = 0\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Updownarrow \\ {(\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over x} \mathit{\boldsymbol{u}})_{\bar x}} + {(\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over y} \mathit{\boldsymbol{u}})_{\bar y}} = 2(\mathit{\boldsymbol{\bar u}} - \mathit{\boldsymbol{u}}) = \\ \frac{{{\mathit{\boldsymbol{u}}_{\bar x\bar x}}{\rm{d}}{{\bar x}^2} + {\mathit{\boldsymbol{u}}_{\bar y\bar y}}{\rm{d}}{{\bar y}^2}}}{8} \end{array} $ |
其中
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\bar u}}(\bar x) = \frac{1}{4}\left( {\mathit{\boldsymbol{u}}\left( {\bar x - \frac{{{\rm{d}}\bar x}}{2},\bar y} \right) + \mathit{\boldsymbol{u}}\left( {\bar x + \frac{{{\rm{d}}\bar x}}{2},\bar y} \right) + } \right.}\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{u}}\left( {\bar x,\bar y - \frac{{{\rm{d}}\bar y}}{2}} \right) + \mathit{\boldsymbol{u}}\left( {\bar x,\bar y + \frac{{{\rm{d}}\bar y}}{2}} \right)} \right)} \end{array} $ |
因此, 从离散意义上讲, ′有源项′自相似方程= ′无源项′自相似方程+2阶黏性小量.
1.3 多维自相似Euler方程考虑通用性我们直接给出三维曲线坐标下Euler方程组, 并使用如下初值问题
| $ \left\{ \begin{array}{l} {{\boldsymbol{u}}_t} + \sum\limits_{e = \xi ,\eta ,\zeta } {{\mathit{\boldsymbol{f}}^e}} {({\boldsymbol{u}})_e} = 0\\ {{{\boldsymbol{u}} = }}\left\{ \begin{array}{l} {{\boldsymbol{u}}_{{\rm{LLL}}}},\xi \ge 0,\eta \ge 0,\zeta \ge 0\\ {{\boldsymbol{u}}_{{\rm{RLL}}}},\xi \ge 0,\eta \ge 0,\zeta \ge 0\\ {{\boldsymbol{u}}_{{\rm{LRL}}}},\xi \ge 0,\eta \ge 0,\zeta \ge 0\\ {{\boldsymbol{u}}_{{\rm{RRL}}}},\xi \ge 0,\eta \ge 0,\zeta \ge 0\\ {{\boldsymbol{u}}_{{\rm{LLR}}}},\xi \ge 0,\eta \ge 0,\zeta \ge 0\\ {{\boldsymbol{u}}_{{\rm{RLR}}}},\xi \ge 0,\eta \ge 0,\zeta \ge 0\\ {{\boldsymbol{u}}_{{\rm{LRR}}}},\xi \ge 0,\eta \ge 0,\zeta \ge 0\\ {{\boldsymbol{u}}_{{\rm{RRR}}}},\xi \ge 0,\eta \ge 0,\zeta \ge 0 \end{array} \right. \end{array} \right. $ | (5) |
上标e表示通量的方向,下标e表示求导,L和R表示左右,LLL,RLL,LRL,RRL,LLR,RLR,LRR,RRR表示三维坐标的8个卦限.其中,
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{u}} = {(\rho ,\rho u,\rho v,\rho w,E)^{\rm{T}}},\\ {\mathit{\boldsymbol{f}}^e}(\mathit{\boldsymbol{u}}) = \left( {\begin{array}{*{20}{c}} {\rho ({e_x}u + {e_y}v + {e_z}w)}\\ {\rho ({e_x}u + {e_y}v + {e_z}w)u + {e_x}p(\mathit{\boldsymbol{u}})}\\ {\rho ({e_x}u + {e_y}v + {e_z}w)v + {e_y}p(\mathit{\boldsymbol{u}})}\\ {\rho ({e_x}u + {e_y}v + {e_z}w)w + {e_z}p(\mathit{\boldsymbol{u}})}\\ {({e_x}u + {e_y}v + {e_z}w)(E + p(\mathit{\boldsymbol{u}}))} \end{array}} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} p(\mathit{\boldsymbol{u}}) = (\gamma - 1)\left( {E - \rho \frac{{{u^2} + {v^2} + {w^2}}}{2}} \right) \end{array} $ | (6) |
对式(5)进行如下自相似变换
| $ \bar x = \frac{x}{t},\bar y = \frac{y}{t},\bar z = \frac{z}{t} $ |
将1.1节自相似的过程直接推广到三维方程为
| $ \left\{ \begin{array}{l} \sum\limits_{e = \xi ,\eta ,\zeta } {({e_{\bar x}}{\rm{f}}(\mathit{\boldsymbol{u}}) + {e_{\bar y}}\mathit{\boldsymbol{g}}(} \mathit{\boldsymbol{u}}) + {e_{\bar z}}\mathit{\boldsymbol{h}}(\mathit{\boldsymbol{u}}) - ({e_{\bar x}}\bar x + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {e_{\bar y}}\bar y + {e_{\bar z}}\bar z)\mathit{\boldsymbol{u}}{)_e} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ \mathit{\boldsymbol{u}}({\xi _{\rm{L}}},{\eta _{\rm{L}}},{\zeta _{\rm{L}}}) = {\mathit{\boldsymbol{u}}_{{\rm{LLL}}}},\mathit{\boldsymbol{u}}({\xi _{\rm{R}}},{\eta _{\rm{L}}},{\zeta _{\rm{L}}}) = {\mathit{\boldsymbol{u}}_{{\rm{RLL}}}}\\ \mathit{\boldsymbol{u}}({\xi _{\rm{L}}},{\eta _{\rm{R}}},{\zeta _{\rm{L}}}) = {\mathit{\boldsymbol{u}}_{{\rm{LRL}}}},\mathit{\boldsymbol{u}}({\xi _{\rm{R}}},{\eta _{\rm{R}}},{\zeta _{\rm{L}}}) = {\mathit{\boldsymbol{u}}_{{\rm{RRL}}}}{\kern 1pt} {\kern 1pt} \\ \mathit{\boldsymbol{u}}({\xi _{\rm{L}}},{\eta _{\rm{L}}},{\zeta _{\rm{R}}}) = {\mathit{\boldsymbol{u}}_{{\rm{LLR}}}},\mathit{\boldsymbol{u}}({\xi _{\rm{R}}},{\eta _{\rm{L}}},{\zeta _{\rm{R}}}) = {\mathit{\boldsymbol{u}}_{{\rm{RLR}}}}\\ \mathit{\boldsymbol{u}}({\xi _{\rm{L}}},{\eta _{\rm{R}}},{\zeta _{\rm{R}}}) = {\mathit{\boldsymbol{u}}_{{\rm{LRR}}}},\mathit{\boldsymbol{u}}({\xi _{\rm{R}}},{\eta _{\rm{R}}},{\zeta _{\rm{R}}}) = {\mathit{\boldsymbol{u}}_{{\rm{RRR}}}} \end{array} \right.\begin{array}{*{20}{c}} {e \in \left( {{e_{\rm{L}}},{e_{\rm{R}}}} \right){\kern 1pt} }\\ {}\\ {}\\ {e = {e_{\rm{L}}},{e_{\rm{R}}}} \end{array} $ | (7) |
其中
| $ \begin{array}{*{20}{c}} {\bar e = {e_{\bar x}}\bar x + {e_{\bar y}}\bar y + {e_{\bar z}}\bar z,{\lambda ^{\bar e,i}}(\mathit{\boldsymbol{u}}) = {\lambda ^{e,i}}(\mathit{\boldsymbol{u}}) - \bar e}\\ {({{\bar e}_{\rm{L}}},{{\bar e}_{\rm{R}}}) \supset (\mathop {{\rm{min}}}\limits_{i,\mathit{\boldsymbol{u}}} {\lambda ^{e,i}}(\mathit{\boldsymbol{u}}),\mathop {{\rm{max}}}\limits_{i,\mathit{\boldsymbol{u}}} {\lambda ^{\bar e,i}}(\mathit{\boldsymbol{u}})),\bar e = \bar x,\bar y,\bar z} \end{array} $ |
注意由(5)到(7)的过程是先把原问题由物理坐标空间(x, y, z)转化到自相似坐标空间
初值问题(5)和边值问题(7)是一维Riemann问题到三维的简单推广, 实际中对不同的初值问题, 对应不同的边值问题, 具体应用时根据不同问题而设定, 在算例部分会有针对性的指出.
2 准自相似Euler方程第1节中介绍的自相似变换法是把解由物理空间变换到自相似坐标空间, 即u(x, t)→u(x), 其中x=x/t, 经过变换后解只与自相似坐标有关, 而与时间无关.原非定常方程的初值问题(1)被转化为一个定常的边值问题(3), 这种做法只适用于解具有自相似特征的问题.下面引入另一种自相似变换, 把解由(x, t)空间变换到(x, t)空间, 即u(x, t)→u(x, t), 经过这种变换原非定常方程(1)仍然是一个非定常方程, 但是除了要满足原来对应的初值条件还要满足相应的边界条件, 这种方法对那些解不具有自相似特点但接近自相似的问题也适用.
对于一维双曲型守恒律方程组的如下初值问题
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}_t} + \mathit{\boldsymbol{f}}{{(\mathit{\boldsymbol{u}})}_x} = 0,}&{t > 0,x{\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\bf{R}}}\\ {\mathit{\boldsymbol{u}}(x,0) = {\mathit{\boldsymbol{u}}_0}(x),}&{t = 0,x{\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\bf{R}}} \end{array}} \right. $ |
采用如下自相似坐标变换
| $ \bar x = \frac{{x - {x_0}}}{{t - {t_0}}} $ |
解由(x, t)空间变换到(x, t)空间, 则初值问题(6)化为如下初边值问题
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}_t} + {{\left( {\frac{{f(\mathit{\boldsymbol{u}}) - \bar x\mathit{\boldsymbol{u}}}}{{t - {t_0}}}} \right)}_{\bar x}} = 0,}&{{\lambda _{{\rm{min}}}} \le \bar x \le {\lambda _{{\rm{max}}}},t > 0}\\ {\mathit{\boldsymbol{u}}(\bar x,0) = {\mathit{\boldsymbol{u}}_0}({x_0} - \bar x{t_0}),}&{{\lambda _{{\rm{min}}}} \le \bar x \le {\lambda _{{\rm{max}}}}}\\ {\mathit{\boldsymbol{u}}|{{\kern 1pt} _{\bar x = {\lambda _{{\rm{min}}}}}} = {\mathit{\boldsymbol{u}}_0}({x_{{\rm{min}}}} + {\lambda _{{\rm{min}}}}t),\mathit{\boldsymbol{u}}|{{\kern 1pt} _{\bar x = {\lambda _{{\rm{max}}}}}} = {\mathit{\boldsymbol{u}}_0}({x_{{\rm{max}}}} + {\lambda _{{\rm{max}}}}t),}&{t > 0} \end{array}} \right. $ | (8) |
其中, λmax是问题的最大特征值, 方程中的x, t-t0看作局部常数
| $ \begin{array}{*{20}{c}} {{t_0} = - \frac{{{x_{{\rm{max}}}} - {x_{{\rm{min}}}}}}{{{\lambda _{{\rm{max}}}} - {\lambda _{{\rm{min}}}}}}}\\ {{x_0} = {x_{{\rm{min}}}} + {\lambda _{{\rm{min}}}}{t_0} = {x_{{\rm{max}}}} + {\lambda _{{\rm{max}}}}{t_0}} \end{array} $ |
如果初值是由两个Riemann组成的, 则xmin, xmax取左右两个间断的位置, 对其他初值取计算区域左右端点即可.
与原方程(1)对比发现, 准自相似方程的通量及其Jacobi矩阵和特征值发生了改变, 左右特征向量保持不变.
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\bar f}}(\mathit{\boldsymbol{u}}) = \frac{{\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \bar x\mathit{\boldsymbol{u}}}}{{t - {t_0}}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{1}{{t - {t_0}}}\left( {\begin{array}{*{20}{l}} {\rho (u - \bar x)}\\ {\rho u(u - \bar x) + p(\mathit{\boldsymbol{u}})}\\ {(E + p(u))(u - \bar x) + \bar xp(\mathit{\boldsymbol{u}})} \end{array}} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\bar A}}(\mathit{\boldsymbol{u}}) = \mathit{\boldsymbol{\bar f}}{(\mathit{\boldsymbol{u}})_\mathit{\boldsymbol{u}}} = \frac{{\mathit{\boldsymbol{A}} - \bar x\mathit{\boldsymbol{I}}}}{{t - {t_0}}}\\ \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }} = \frac{{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} - \bar x\mathit{\boldsymbol{I}}}}{{t - {t_0}}} = \frac{1}{{t - {t_0}}}\left( {\begin{array}{*{20}{c}} {u - c - \bar x}&{}&{}\\ {}&{u - \bar x}&{}\\ {}&{}&{u + c - \bar x} \end{array}} \right) \end{array} $ | (9) |
方程(8)和(9)就是本文使用的准自相似Euler方程.
3 数值方法 3.1 原Euler方程的数值方法原Euler方程(1)的显式守恒型数值格式为
| $ \mathit{\boldsymbol{u}}_j^{n + 1} = \mathit{\boldsymbol{u}}_j^n - \frac{\tau }{h}(\mathit{\boldsymbol{f}}_{j + \frac{1}{2}}^n - \mathit{\boldsymbol{f}}_{j - \frac{1}{2}}^n) $ |
对于数值通量, 本文选择使用2阶熵条件格式[19], 其表达式如下
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{j + \frac{1}{2}}} = {\mathit{\boldsymbol{f}}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right) + {\mathit{\boldsymbol{R}}_{j + \frac{1}{2}}}\left\{ {\frac{{\lambda _{j + \frac{1}{2}}^k}}{2}\left( {\frac{{\mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{L}} + \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{R}}}}{2}} \right) - } \right.}\\ {\left. {\frac{{|\lambda _{j + \frac{1}{2}}^k|}}{2}\left( {\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_{j + 1}^n - \mathit{\boldsymbol{u}}_j^n) + \frac{{\mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{R}} - \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{L}}}}{2}} \right)} \right\}} \end{array} $ |
其中
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{L}} = \varTheta (\mathit{\boldsymbol{L}}_{{j_j} - \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_j^n - \mathit{\boldsymbol{u}}_{j - 1}^n),\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_{j + 1}^n - \mathit{\boldsymbol{u}}_j^n))\left( {1 - \frac{{\lambda _{j + \frac{1}{2}}^k\tau }}{h}} \right)\\ \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{R}} = \varTheta (\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_{j + 1}^n - \mathit{\boldsymbol{u}}_j^n),\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_{j + 2}^n - \mathit{\boldsymbol{u}}_{j + 1}^n))\left( { - 1 - \frac{{\lambda _{j + \frac{1}{2}}^k\tau }}{h}} \right)\\ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}} = \{ L_{j + \frac{1}{2}}^k\} = {\mathit{\boldsymbol{L}}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right),{\mathit{\boldsymbol{R}}_{j + \frac{1}{2}}} = {\mathit{\boldsymbol{R}}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right)}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{j + \frac{1}{2}}} = \{ \lambda _{j + \frac{1}{2}}^k\} = {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right)} \end{array} \end{array} $ |
fE(u), LE(u), RE(u)分别指的是使用熵条件的通量和左右特征向量, Θ是限制器函数, 详见文献[19].
3.2 自相似Euler方程的数值方法1.1节中通过自相似变换后, 发现原非定常方程初值问题(1)转化成了定常方程的边值问题(3), 数值求解问题(3)没有实质性的困难, 引入虚拟时间导数项uθ[20], 式(3)变为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}_\theta } + {{(\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \bar x\mathit{\boldsymbol{u}})}_{\bar x}} = 0,\quad {\lambda _{{\rm{min}}}} \le \bar x \le {\lambda _{{\rm{max}}}}}\\ {\mathit{\boldsymbol{u}}({{\bar x}_{\rm{L}}}) = {\mathit{\boldsymbol{u}}_{\rm{L}}},\mathit{\boldsymbol{u}}({{\bar x}_{\rm{R}}}) = {\mathit{\boldsymbol{u}}_{\rm{R}}}} \end{array}} \right. $ | (10) |
注意, 上式中的θ不是物理时间而是虚拟时间, 这样做的好处是可以使用比较成熟的时间推进法求解, 这里时间推进法其实相当于迭代过程, 可由残差来控制收敛.随着虚拟时间或迭代次数的增加, 当残差收敛时有uθ→0, 这样方程(10)还原到(3).
求解问题(10)无须设计新格式, 现有的守恒律方程的显式或隐式方法(如熵条件格式, 大时间步长格式, 以及分裂隐式方法等)可以直接应用.这里仍然使用显式守恒型数值格式, 数值通量选择2阶熵条件格式, 表达式如下
| $ \begin{array}{l} {\mathit{\boldsymbol{f}}_{j + \frac{1}{2}}} = {\mathit{\boldsymbol{f}}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right) - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over x} }_j}\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{R}}_{j + \frac{1}{2}}}\left\{ {\frac{{\lambda _{j + \frac{1}{2}}^k - {{\bar x}_{j + \frac{1}{2}}}}}{2}\left( {\frac{{\mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{L}} + \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{R}}}}{2}} \right) - \frac{{|\lambda _{j + \frac{1}{2}}^k - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over x} }_j}|}}{2} \cdot } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left( {\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_{j + 1}^n - \mathit{\boldsymbol{u}}_j^n) + \frac{{\mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{R}} - \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{L}}}}{2}} \right)} \right\} \end{array} $ | (11) |
其中
| $ \begin{array}{l} \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{L}} = \varTheta (\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_j^n - \mathit{\boldsymbol{u}}_{j - 1}^n),\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_{j + 1}^n - \mathit{\boldsymbol{u}}_j^n))\left( {1 - \frac{{(\lambda _{j + \frac{1}{2}}^k - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over x} }_j})\tau }}{h}} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{R}} = \varTheta (\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_{j + 1}^n - \mathit{\boldsymbol{u}}_j^n),\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_{j + 2}^n - \mathit{\boldsymbol{u}}_{j + 1}^n)) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( { - 1 - \frac{{(\lambda _{j + \frac{1}{2}}^k - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over x} )\tau }}{h}} \right)\\ {\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}} = \{ \mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k\} = {\mathit{\boldsymbol{L}}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right),{\mathit{\boldsymbol{R}}_{j + \frac{1}{2}}} = {\mathit{\boldsymbol{R}}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{j + \frac{1}{2}}} = \{ \lambda _{j + \frac{1}{2}}^k\} = {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right) \end{array} $ | (12) |
其中,
对比原方程的数值通量发现, 只须将格式中出现的通量和特征值替换为新的通量和特征值, 而新方程和原方程的特征向量是相同的.与求解原方程不同的是, 这里的时间是虚拟时间, 每次推进相当于是一次迭代, 迭代停止的标准由残差来控制.
3.3 多维自相似Euler方程的数值方法将式(10)直接推广到多维问题为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_\theta } + \sum\limits_{e = \xi ,\eta ,\zeta } {({e_{\bar x}}{\rm{f}}(\mathit{\boldsymbol{u}}) + {e_{\bar y}}\mathit{\boldsymbol{g}}(} \mathit{\boldsymbol{u}}) + {e_{\bar z}}\mathit{\boldsymbol{h}}(\mathit{\boldsymbol{u}}) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({e_{\bar x}}\bar x + {e_{\bar y}}\bar y + {e_{\bar z}}\bar z)\mathit{\boldsymbol{u}}{)_e} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ \mathit{\boldsymbol{u}}({\xi _{\rm{L}}},{\eta _{\rm{L}}},{\zeta _{\rm{L}}}) = {\mathit{\boldsymbol{u}}_{{\rm{LLL}}}},\mathit{\boldsymbol{u}}({\xi _{\rm{R}}},{\eta _{\rm{L}}},{\zeta _{\rm{L}}}) = {\mathit{\boldsymbol{u}}_{{\rm{RLL}}}}\\ \mathit{\boldsymbol{u}}({\xi _{\rm{L}}},{\eta _{\rm{R}}},{\zeta _{\rm{L}}}) = {\mathit{\boldsymbol{u}}_{{\rm{LRL}}}},\mathit{\boldsymbol{u}}({\xi _{\rm{R}}},{\eta _{\rm{R}}},{\zeta _{\rm{L}}}) = {\mathit{\boldsymbol{u}}_{{\rm{RRL}}}}{\kern 1pt} {\kern 1pt} \\ \mathit{\boldsymbol{u}}({\xi _{\rm{L}}},{\eta _{\rm{L}}},{\zeta _{\rm{R}}}) = {\mathit{\boldsymbol{u}}_{{\rm{LLR}}}},\mathit{\boldsymbol{u}}({\xi _{\rm{R}}},{\eta _{\rm{L}}},{\zeta _{\rm{R}}}) = {\mathit{\boldsymbol{u}}_{{\rm{RLR}}}}\\ \mathit{\boldsymbol{u}}({\xi _{\rm{L}}},{\eta _{\rm{R}}},{\zeta _{\rm{R}}}) = {\mathit{\boldsymbol{u}}_{{\rm{LRR}}}},\mathit{\boldsymbol{u}}({\xi _{\rm{R}}},{\eta _{\rm{R}}},{\zeta _{\rm{R}}}) = {\mathit{\boldsymbol{u}}_{{\rm{RRR}}}} \end{array} \right.\begin{array}{*{20}{c}} {e \in \left( {{e_{\rm{L}}},{e_{\rm{R}}}} \right){\kern 1pt} }\\ {}\\ {}\\ {e = {e_{\rm{L}}},{e_{\rm{R}}}} \end{array} $ | (13) |
注意, 初值问题(5)和边值问题(7),(13), 只是具有8个常数的特殊情形.对自相似方程, 上述边值问题, 仅给出了8个角点的值, 每条边上完整的边界还须求解各自两端点形成的Riemann问题.一般来讲, n个常数的多维Riemann问题, 对应n点自相似问题.某些自相似问题存在一个反射边界, 可以通过镜像归为上述边界条件.比如, 物面上有n个常数区, 它对应2n个常数区的Riemann问题或2n点的自相似问题.详见算例11中的处理.
使用维数分裂技术[21]数值求解上述方程, 任一方向的求解为
| $ \mathit{\boldsymbol{u}}_\mathit{\boldsymbol{j}}^{n + 1} = \mathit{\boldsymbol{u}}_\mathit{\boldsymbol{j}}^n - \frac{\tau }{h}(\mathit{\boldsymbol{f}}_{\mathit{\boldsymbol{j}} + \frac{1}{2}}^{e,n} - \mathit{\boldsymbol{f}}_{\mathit{\boldsymbol{j}} - \frac{1}{2}}^{e,n}) $ |
注意:下标j, 1, 1/2都是向量, 当e=ξ, j=(i, j, k), 1=(1, 0, 0), 1/2=1/2, 0, 0;当e=η,1=(0, 1, 0), 1/2=0, 1/2, 0;当e=ζ,1=(0, 0, 1), 1/2=0, 0, 1/2
上式写成算子形式为
| $ {\mathit{\boldsymbol{u}}^{n + 1}} = {T_e}({\mathit{\boldsymbol{u}}^n}) $ | (14) |
这样完整的一次求解过程可以写为
| $ {\mathit{\boldsymbol{u}}^{n + 1}} = {T_\xi }{T_\eta }{T_\zeta }({\mathit{\boldsymbol{u}}^n}) $ |
准自相似方程(8)也可以使用守恒型数值格式进行求解, 仍然选择2阶熵条件格式, 表达式如下
| $ \begin{array}{l} {\mathit{\boldsymbol{f}}_{j + \frac{1}{2}}} = \left\{ {{\mathit{\boldsymbol{f}}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right) - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over x} }_j}\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right\}/({t^n} - {t_0}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{R}}_{j + \frac{1}{2}}}\left\{ {\frac{{\lambda _{j + \frac{1}{2}}^k - {{\bar x}_{j + \frac{1}{2}}}}}{{2({t^n} - {t_0})}}\left( {\frac{{\mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{L}} + \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{R}}}}{2}} \right) - \frac{{|\lambda _{j + \frac{1}{2}}^k - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over x} }_j}|}}{{2({t^n} - {t_0})}} \cdot } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left( {\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_{j + 1}^n - \mathit{\boldsymbol{u}}_j^n) + \frac{{\mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{R}} - \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{L}}}}{2}} \right)} \right\} \end{array} $ | (15) |
其中
| $ \begin{array}{l} \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{L}} = \varTheta (\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_j^n - \mathit{\boldsymbol{u}}_{j - 1}^n),\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_{j + 1}^n - \mathit{\boldsymbol{u}}_j^n))\left( {1 - \frac{{(\lambda _{j + \frac{1}{2}}^k - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over x} }_j})\tau }}{h}} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{d}}_{j + \frac{1}{2}}^{\rm{L}} = \varTheta (\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_j^n - \mathit{\boldsymbol{u}}_{j - 1}^n),\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k(\mathit{\boldsymbol{u}}_{j + 1}^n - \mathit{\boldsymbol{u}}_j^n)) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( { - 1 - \frac{{(\lambda _{j + \frac{1}{2}}^k - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over x} }_j})\tau }}{{h({t_n} - {t_0})}}} \right)\\ {\mathit{\boldsymbol{L}}_{j + \frac{1}{2}}} = \{ \mathit{\boldsymbol{L}}_{j + \frac{1}{2}}^k\} = {\mathit{\boldsymbol{L}}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right),{\mathit{\boldsymbol{R}}_{j + \frac{1}{2}}} = {\mathit{\boldsymbol{R}}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{j + \frac{1}{2}}} = \{ \lambda _{j + \frac{1}{2}}^k\} = {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{\rm{E}}}\left( {\frac{{\mathit{\boldsymbol{u}}_j^n + \mathit{\boldsymbol{u}}_{j + 1}^n}}{2}} \right) \end{array} $ | (16) |
对比自相似方程的数值通量式(11)和式(12)和准自相似方程的数值通量式(15),式(16), 可以发现后者只是在通量和特征值中多除以了一个局部常数tn-t0, 其余保持不变.
4 数值计算共给出12个算例:其中一维5个算例(Lax激波管, 反激波, 123问题, Shu-Osher问题, 双Riemann问题), 二维7个算例(5个Riemann问题, 激波楔面反射问题, 激波折射问题).
4.1 一维算例算例1~3是3个激波管问题, 算例4是Shu-Osher问题, 算例5是双Riemann问题.
激波管问题用自相似Euler方程进行求解, 各算例统一使用200点, CFL=1, 残差定义如下
| $ \begin{array}{l} res = \left\| {{\mathit{\boldsymbol{u}}^k} - {\mathit{\boldsymbol{u}}^{k - 1}}} \right\|\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathop {{\rm{max}}}\limits_l \sum\limits_j {\frac{{|({\mathit{\boldsymbol{u}}^{(l)}})_j^k - ({\mathit{\boldsymbol{u}}^{(l)}})_j^{k - 1}|}}{{mu_{{\rm{max}}}^{(l)}}}} \le {10^{ - 6}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{u}} = {({u^{(1)}},{u^{(2)}},{u^{(3)}},{u^{(4)}},{u^{(5)}})^{\rm{T}}} = {(\rho ,p,u,v,w)^{\rm{T}}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{v}} = {(u,v,w)^{\rm{T}}},{\rho _{{\rm{max}}}} = \mathop {{\rm{max}}}\limits_j {\rho _j},{p_{{\rm{max}}}} = \mathop {{\rm{max}}}\limits_j {p_j}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{V}}_{{\rm{max}}}} = \mathop {{\rm{max}}}\limits_j {\left\| {{\mathit{\boldsymbol{v}}_j} - {\mathit{\boldsymbol{v}}_0}} \right\|_1},{\mathit{\boldsymbol{v}}_0} = \frac{1}{m}\sum\limits_j {{\mathit{\boldsymbol{v}}_j}} \end{array} $ |
其中, m是网格数.
Shu-Osher问题, 双Riemann问题用准自相似Euler方程进行求解.
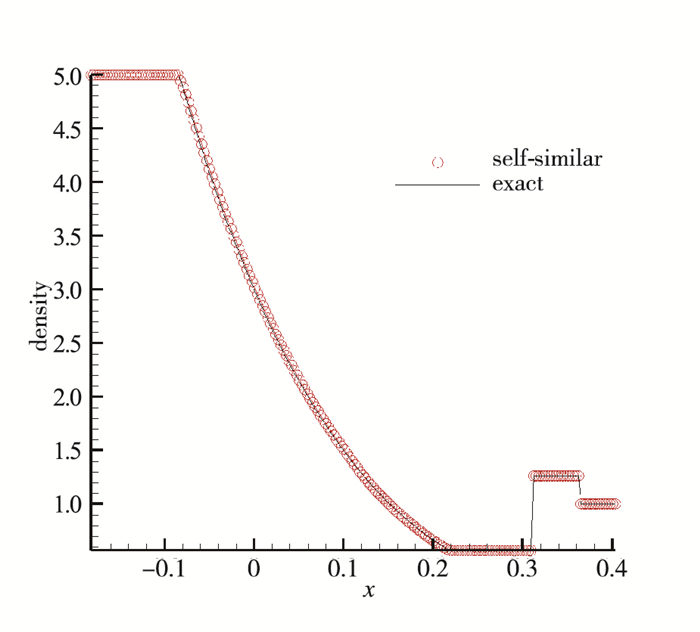
算例1 Lax激波管
| $ \left\{ {\begin{array}{*{20}{l}} {({\rho _{\rm{L}}},{u_{\rm{L}}},{p_{\rm{L}}}) = (0.445,0.698{\kern 1pt} {\kern 1pt} {\kern 1pt} 9,3.527{\kern 1pt} {\kern 1pt} {\kern 1pt} 8)}\\ {({\rho _{\rm{R}}},{u_{\rm{R}}},{p_{\rm{R}}}) = (0.5,0,0.571)} \end{array}} \right. $ |
注:上述数据是Riemann问题的初值, 对自相似方法直接作为边值使用, 下同, 不再赘述.
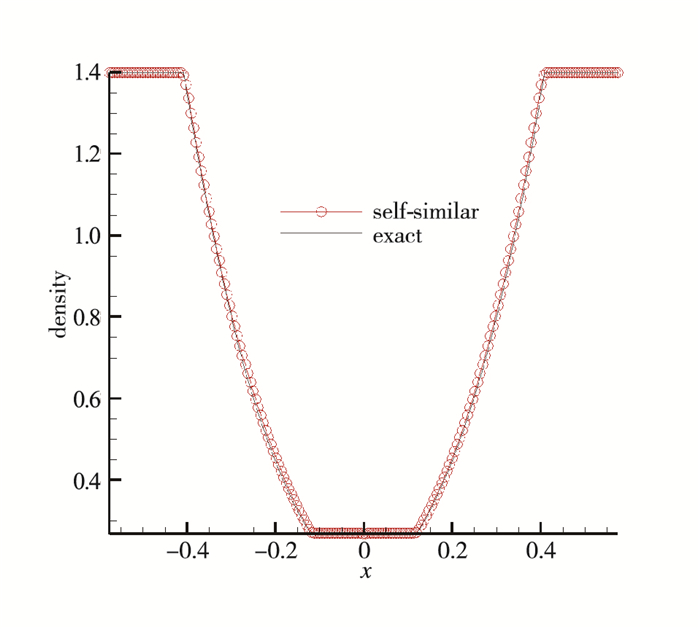
算例2 反激波
| $ \left\{ {\begin{array}{*{20}{l}} {({\rho _{\rm{L}}},{u_{\rm{L}}},{p_{\rm{L}}}) = (5.0,\sqrt {1.4} ,29.0)}\\ {({\rho _{\rm{R}}},{u_{\rm{R}}},{p_{\rm{R}}}) = (1.0,5\sqrt {1.4} ,1.0)} \end{array}} \right. $ |
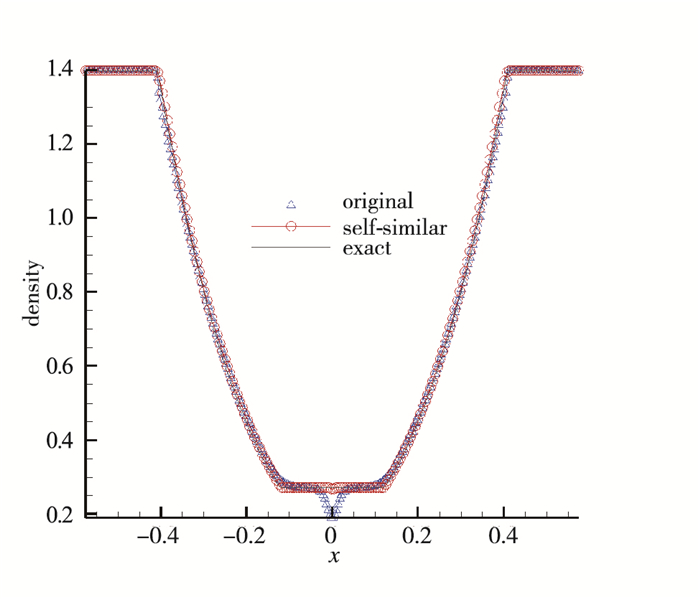
算例3 123问题
| $ \left\{\begin{array}{l} \left(\rho_{\mathrm{L}}, u_{\mathrm{L}}, p_{\mathrm{L}}\right)=(1.4,-1.4,1.0) \\ \left(\rho_{\mathrm{R}}, u_{\mathrm{R}}, p_{\mathrm{R}}\right)=(1.4,1.4,1.0) \end{array}\right. $ |
通过以上数值实验的结果可以发现采用自相似方程的计算结果基本等同于精确解, 如图 1~4所示, 无论在间断处还是光滑区域都保持了精确解的特征, 因此可以说在一定程度上自相似方程的解可以当做精确解使用. 图 4展示的是使用原方程计算123问题出现的“过热现象”, 目前几乎所有格式都存在这个问题, 并且没有一个通用的办法来解决, 但是使用自相似方程求解以后“过热现象”消失了, 如图 3和4所示, 这对探讨过热现象的原因以及解决这个问题给出了有益的启示.

|
| 图 1 Lax激波管问题计算结果 Fig.1 Results of Lax shock tube problem |
|
| 图 2 反激波问题计算结果 Fig.2 Results of inverse shock tube problem |
|
| 图 3 123问题计算结果 Fig.3 Results of 123 problem |
|
| 图 4 123问题计算结果对比 Fig.4 Comparison of the results of 123 problem |
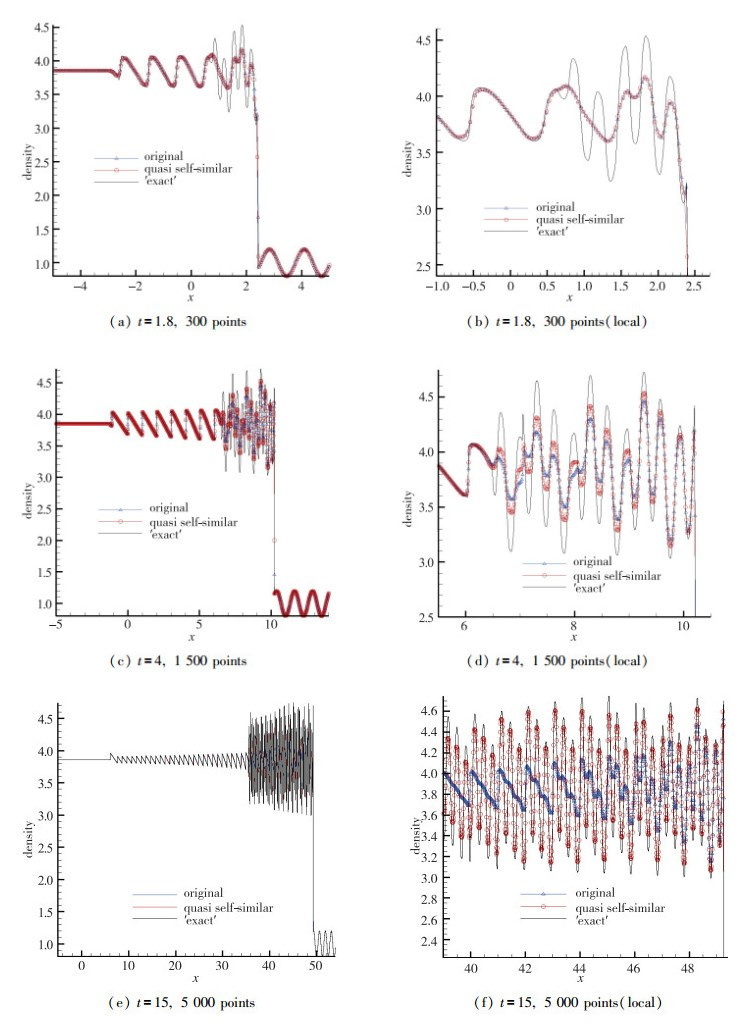
算例4 Shu-Osher问题[22]
| $ {\mathit{\boldsymbol{u}}_0} = \left\{ {\begin{array}{*{20}{l}} {({\rho _{\rm{L}}},{u_{\rm{L}}},{p_{\rm{L}}}) = (3.857,2.629,10.333),x < - 4}\\ {({\rho _{\rm{R}}},{u_{\rm{R}}},{p_{\rm{R}}}) = (1 + 0.2{\rm{sin}}(5x),0,1),x > - 4} \end{array}} \right. $ |
Shu-Osher问题初始流场除了存在一个间断以外, 在一侧还存在密度脉动, 这个问题的解不再具有自相似的特点, 为了利用自相似变换的优点, 可以使用本文提出的准自相似Euler方程进行求解.注意如果计算时间较短, 使用自相似坐标法和普通方程计算的结果差异不大, 但是随着计算时间的增大, 自相似坐标法的优势会逐渐显示出来, 对激波、接触间断, 膨胀波的分辨率都会提高.如图 5(a)(b)所示, 当t=1.8时, 原方程和自相似坐标法的结果几乎一样; 如图 5(c)(d)所示, 当t=4.0时, 自相似坐标法开始体现出优势, 在脉动区域每个极值点处都比原方程计算结果分辨率高, 波形也更准确; 如图 5(e)(f)所示,当t=15时, 自相似坐标法的优势更明显了, 原方程几乎丧失了对脉动的捕捉能力, 但是自相似坐标法还能准确捕捉脉动, 并且极值点精度也较高.注意, 这里′精确解′是指用原方程使用密网格得到的解, t=1.8, 4和15时刻, 所用的点分别为1 000, 10 000, 60 000.
|
| 图 5 Shu-Osher问题计算结果 Fig.5 Results of Shu-Osher problem |
算例5 双Riemann问题
| $ \begin{array}{l} {\mathit{\boldsymbol{u}}_0} = \\ \left\{ {\begin{array}{*{20}{l}} {({\rho _{\rm{L}}},{u_{\rm{L}}},{p_{\rm{L}}}) = (0.445,0.698{\kern 1pt} {\kern 1pt} {\kern 1pt} 9,3.528),x < - 0.4}\\ {({\rho _{\rm{M}}},{u_{\rm{M}}},{p_{\rm{M}}}) = (0.472{\kern 1pt} {\kern 1pt} {\kern 1pt} 5,0.349{\kern 1pt} {\kern 1pt} 45,2.049{\kern 1pt} {\kern 1pt} {\kern 1pt} 5), - 0.4 \le x < 0.4}\\ {({\rho _{\rm{R}}},{u_{\rm{R}}},{p_{\rm{R}}}) = (0.5,0,0.571),x \ge 0.4} \end{array}} \right. \end{array} $ |
本算例由Lax激波管改造而来, 在原来初值间断的基础上再引入中间一个常数区, 构成两个Riemann问题, 中间常数区的各物理量取两侧的算术平均值.该问题的解也不具有自相似的特点, 使用本文提出的自相似坐标法求解.取t=4和t=12两个计算时间, 所用网格分别为800和3 000点. ′精确解′是原方程使用密网格得到的, 分别使用30 000和120 000点.从图 6可以看出, 相比原方程, 准自相似Euler方程给出的解具有更高的分辨率, 800和300 0点几乎可以达到原方程300 00和120 000点的效果, 并且随着计算时间的增加, 这种优势会逐渐扩大.相反随着时间的增加, 原方程分辨率呈下降趋势, 对比图 6(a)(b)可以发现.
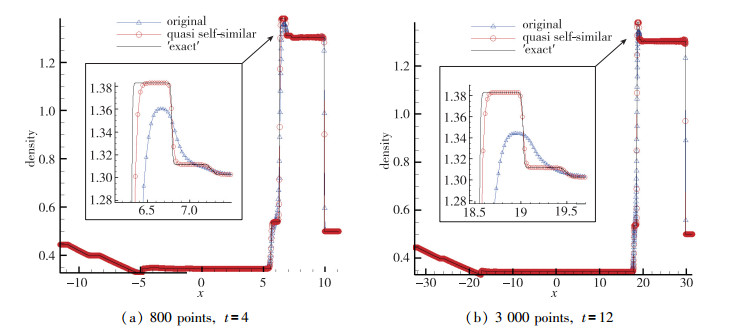
|
| 图 6 双Riemann问题计算结果 Fig.6 Results of double Riemann problem |
算例6~10是二维Riemann问题, 算例11是激波反射问题, 算例12是激波折射+反射问题, 后两个存在物面边界, 镜像后, 也属于Riemann问题.这些解都是自相似, 可以使用自相似方法求解.
相比一维问题, 二维Riemann问题的初值设置要复杂得多.典型的设置是在4个象限都是常数.计算开始后, 这样在交界面处会产生激波、膨胀波、滑移线(接触间断), 并且相互作用.
本文模拟的Riemann问题有4个初值取自文献[14, 16, 18], 均使用自相似Euler方程求解, 网格为400×400.计算停止时的残差设置为10-6, 残差定义见式(17).为区分不同的解, 采用文献[8, 10, 12, 14, 18]中的记号, 即R-膨胀波, S-激波, J-接触间断.
算例6
| $ \begin{array}{*{20}{c}} {}&{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over S} }_{21}}}&{}\\ {{{\vec S}_{32}}}&{}&{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over S} }_{41}}}\\ {}&{{{\vec S}_{34}}}&{} \end{array} $ |
初值为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\begin{array}{*{20}{l}} {{\rho _2}}\\ {{p_2}}\\ {{u_2}}\\ {{v_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.506{\kern 1pt} {\kern 1pt} {\kern 1pt} 5}\\ {0.35}\\ {0.893{\kern 1pt} {\kern 1pt} {\kern 1pt} 9}\\ 0 \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _1}}\\ {{p_1}}\\ {{u_1}}\\ {{v_1}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {1.1}\\ {1.1}\\ 0\\ 0 \end{array}} \right)\\ \left( {\begin{array}{*{20}{l}} {{\rho _3}}\\ {{p_3}}\\ {{u_3}}\\ {{v_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {1.1}\\ {1.1}\\ {0.893{\kern 1pt} {\kern 1pt} {\kern 1pt} 9}\\ {0.893{\kern 1pt} {\kern 1pt} {\kern 1pt} 9} \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _4}}\\ {{p_4}}\\ {{u_4}}\\ {{v_4}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.506{\kern 1pt} {\kern 1pt} {\kern 1pt} 5}\\ {0.35}\\ 0\\ {0.893{\kern 1pt} {\kern 1pt} {\kern 1pt} 9} \end{array}} \right) \end{array} $ |
对自相似Euler方程, 边界条件的确定分两步: (1)设置4个角点的值; (2)在每条边上求解Riemann问题.算例7~11也采用此设置.
算例7
| $ \begin{array}{*{20}{c}} {}&{J_{21}^ - }&{}\\ {J_{32}^ - }&{}&{J_{41}^ - }\\ {}&{J_{34}^ - }&{} \end{array} $ |
初值为
| $ \begin{array}{l} \left( {\begin{array}{*{20}{l}} {{\rho _2}}\\ {{p_2}}\\ {{u_2}}\\ {{v_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 2\\ 1\\ { - 0.75}\\ {0.5} \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _1}}\\ {{p_1}}\\ {{u_1}}\\ {{v_1}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ 1\\ { - 0.75}\\ { - 0.5} \end{array}} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\begin{array}{*{20}{l}} {{\rho _3}}\\ {{p_3}}\\ {{u_3}}\\ {{v_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ 1\\ {0.75}\\ {0.5} \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _4}}\\ {{p_4}}\\ {{u_4}}\\ {{v_4}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 3\\ 1\\ {0.75}\\ { - 0.5} \end{array}} \right) \end{array} $ |
算例8
| $ \begin{array}{*{20}{c}} {}&{J_{21}^ - }&{}\\ {J_{32}^ + }&{}&{J_{41}^ + }\\ {}&{J_{34}^ - }&{} \end{array} $ |
初值为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\begin{array}{*{20}{l}} {{\rho _2}}\\ {{p_2}}\\ {{u_2}}\\ {{v_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.15}\\ {10}\\ {0.5}\\ {0.5} \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _1}}\\ {{p_1}}\\ {{u_1}}\\ {{v_1}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.1}\\ {10}\\ {0.5}\\ { - 0.5} \end{array}} \right)\\ {\kern 1pt} \left( {\begin{array}{*{20}{l}} {{\rho _3}}\\ {{p_3}}\\ {{u_3}}\\ {{v_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.09}\\ {10}\\ { - 0.5}\\ {0.5} \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _4}}\\ {{p_4}}\\ {{u_4}}\\ {{v_4}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.05}\\ {10}\\ { - 0.5}\\ { - 0.5} \end{array}} \right) \end{array} $ |
算例9
| $ \begin{array}{*{20}{c}} {}&{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over S} }_{21}}}&{}\\ {J_{32}^ + }&{}&{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over S} }_{41}}}\\ {}&{J_{34}^ + }&{} \end{array} $ |
初值为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\begin{array}{*{20}{l}} {{\rho _2}}\\ {{p_2}}\\ {{u_2}}\\ {{v_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.531{\kern 1pt} {\kern 1pt} 3}\\ {0.4}\\ {0.827{\kern 1pt} {\kern 1pt} 6}\\ 0 \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _1}}\\ {{p_1}}\\ {{u_1}}\\ {{v_1}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ 1\\ {0.1}\\ 0 \end{array}} \right)\\ {\kern 1pt} \left( {\begin{array}{*{20}{l}} {{\rho _3}}\\ {{p_3}}\\ {{u_3}}\\ {{v_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.8}\\ {0.4}\\ {0.1}\\ 0 \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _4}}\\ {{p_4}}\\ {{u_4}}\\ {{v_4}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.531{\kern 1pt} {\kern 1pt} 3}\\ {0.4}\\ {0.1}\\ {0.727{\kern 1pt} {\kern 1pt} 6} \end{array}} \right) \end{array} $ |
如图 7~10所示, 通过和文献[10, 12, 15]进行对比, 可以发现对每一个初值问题, 我们用自相似方程得到的结果在间断处分辨率更高, 在出现波相互干扰的复杂流动的区域解也更清晰(比如漩涡处的分辨率也更高).另外本文仅采用2阶格式, 限制器也只选择minmod, 而Schulz-Rinne等[10]使用的PPM格式是一个3阶格式, Kurganov等[15]也使用了一个3阶的中心型格式, 并称该格式具有真正的多维性质, Lax等[12]使用的Positive格式在线性退化场中使用了superbee限制器.
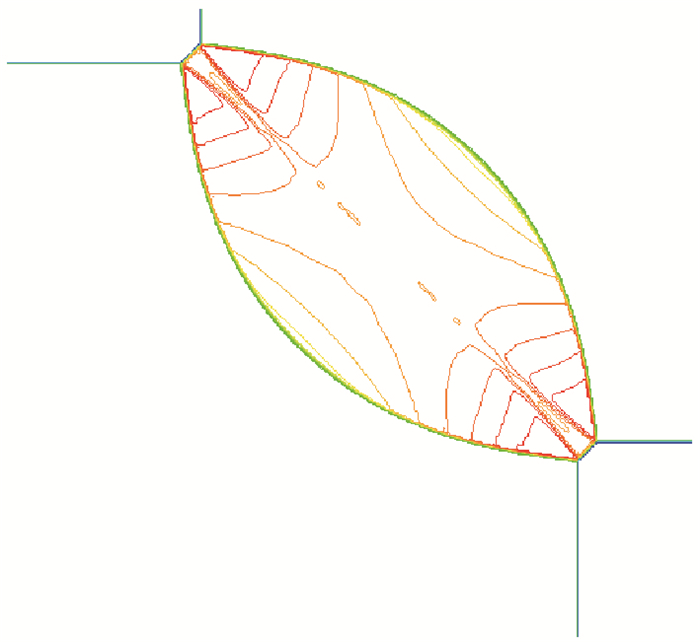
|
| 图 7 算例6密度等值线 Fig.7 Density contour of test 6 |

|
| 图 8 算例7密度等值线 Fig.8 Density contour of test 7 |
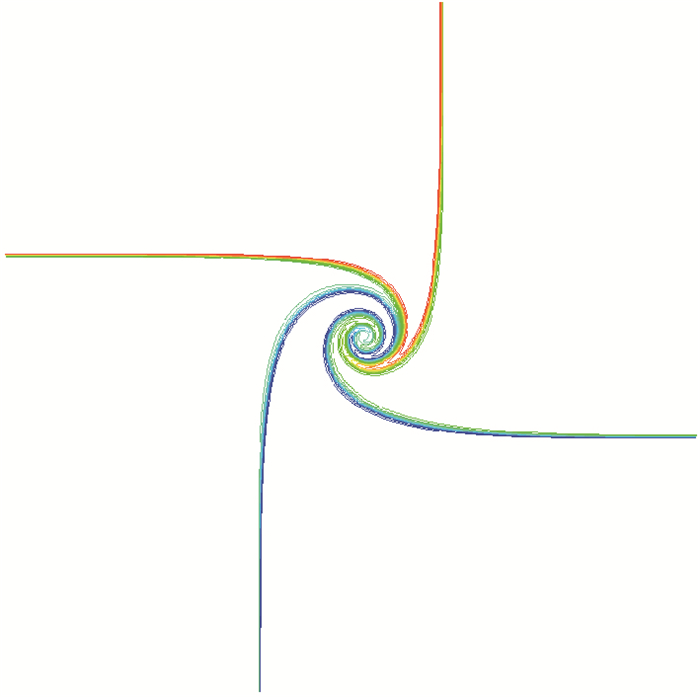
|
| 图 9 算例8密度等值线 Fig.9 Density contour of test 8 |
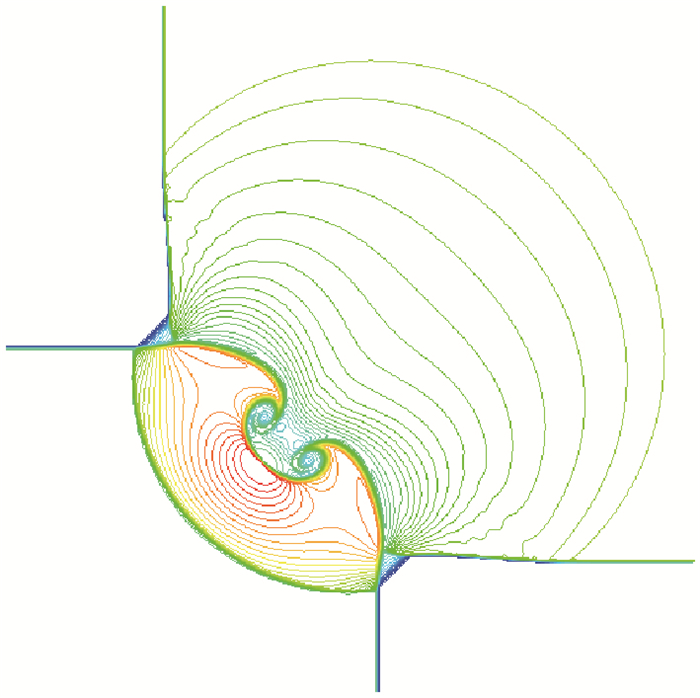
|
| 图 10 算例9密度等值线 Fig.10 Density contour of test 9 |
算例6~9均来自已有文献, 下面构造一个初值.
算例10
| $ \begin{array}{l} \begin{array}{*{20}{c}} {}&{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over S} }_{21}}J_{21}^ - {{\vec S}_{21}}}&{}\\ {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over S} }_{32}}J_{32}^ + {{\vec S}_{32}}}&{}&{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over S} }_{41}}J_{41}^ + {{\vec S}_{41}}}\\ {}&{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over S} }_{34}}J_{34}^ - {{\vec S}_{34}}}&{} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\begin{array}{*{20}{l}} {{\rho _2}}\\ {{p_2}}\\ {{u_2}}\\ {{v_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ 1\\ 3\\ 0 \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _1}}\\ {{p_1}}\\ {{u_1}}\\ {{v_1}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ 1\\ 0\\ 3 \end{array}} \right)\\ {\kern 1pt} \left( {\begin{array}{*{20}{l}} {{\rho _3}}\\ {{p_3}}\\ {{u_3}}\\ {{v_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ 1\\ 0\\ 3 \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _4}}\\ {{p_4}}\\ {{u_4}}\\ {{v_4}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ 1\\ { - 3}\\ 0 \end{array}} \right) \end{array} $ |
使用原Euler方程和自相似Euler方程对上面的初值进行计算, 都使用均匀网格500×500, 计算结果如图 11(a)(b)所示, 从图中可以看出使用自相似方程得到的结果对激波和接触间断的分辨率要高于原方程.
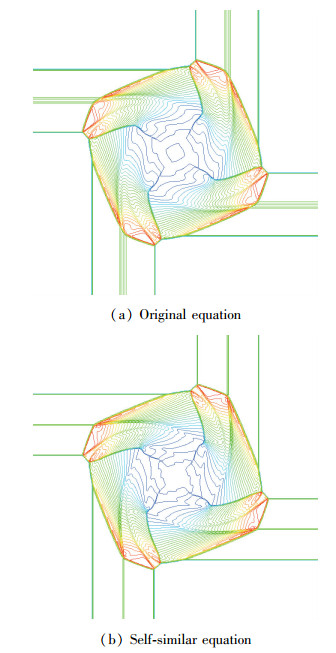
|
| 图 11 算例10密度等值线 Fig.11 Density contour of test 10 |
算例11 激波反射问题
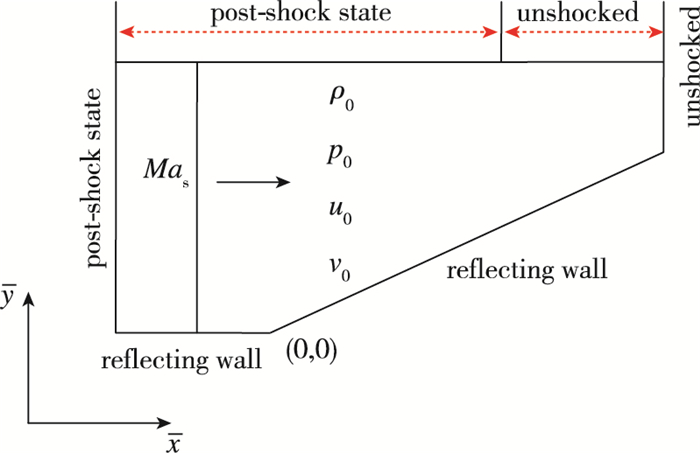
该算例取自文献[23], 初始流场中存在一道从左向右移动的正激波,激波Mach数为Mas, 底部是物面, 物面倾斜段与水平方向的夹角是φ, 如图 12所示.根据激波强度和楔面夹角的不同可以产生多种不同的反射现象, 主要有常规反射, 单Mach反射以及双Mach反射.本算例取激波Mach数Mas=1.7, 夹角φ=25°, 形成一个单Mach反射.
|
| 图 12 激波斜面反射初值和边界设置 Fig.12 Initial data and boundary conditions of shock reflection problem |
该问题的流场具有自相似的特点, 使用自相似方程(13)进行计算, 格式使用2阶熵条件格式.设定波前各参数值为ρ0=1.4, p0=1, u0=v0=0, 激波后的参数值由R-H关系式得到.边界条件的设置如图 12所示, 图示是在自相似坐标空间
| $ \begin{array}{*{20}{l}} {{{\bar x}_{{\rm{min}}}} = {\rm{min}}({u_0} - {c_0},{u_1} - {c_1}),{{\bar x}_{{\rm{max}}}} = {\rm{max}}({u_0} + {c_0},{u_1} + {c_1})}\\ {{{\bar y}_{{\rm{min}}}} = {\rm{min}}({v_0} - {c_0},{v_1} - {c_1}),{{\bar y}_{{\rm{max}}}} = {\rm{max}}({v_0} + {c_0},{v_1} + {c_1})} \end{array} $ |
计算使用的网格数为流向×法向=300×200.实际计算时可以根据问题特点对计算区域适当进行调整, 保证计算区域包括所关心的流场区域即可.
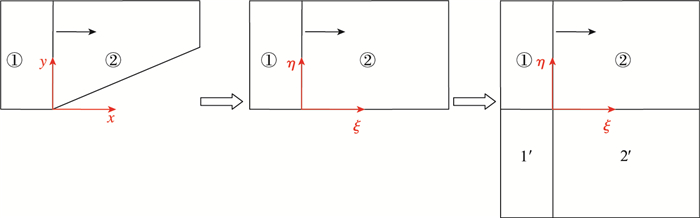
图 13显示了存在物面边界的自相似问题是如何转变为特定Riemann问题的.首先把物理域(x, y)变换到计算域(ξ, η), 然后物面边界就可以通过镜像转化成一个4常数区组成的特殊Riemann问题, 区域1′和2′中的值由镜像条件得到.因此, 大多数自相似问题都可以转化为对应的Riemann问题.实际应用中, 可以直接使用图 12所示的边界条件.
|
| 图 13 Riemann问题中的物面边界 Fig.13 Wall boundary to Riemann problem |
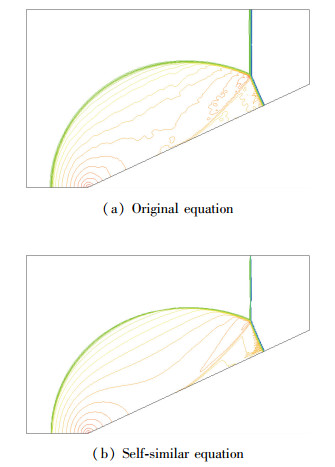
图 14显示的是计算得到的密度等值线, 可以看出明显的单Mach反射流场结构, 存在1个入射激波,1个反射激波, 1根Mach杆以及1条滑移线, 它们交于1个三波点, 使用本文的自相似方程来计算, 正确、清晰地捕捉了这些结构, 与原方程的结果相比较可以看出自相似方程的结果在入射激波、反射激波、Mach杆以及滑移线处的分辨率都更高, 且流场结构更清晰.
|
| 图 14 激波斜面反射的密度图 Fig.14 Density contour of test 11 |
该问题取自文献[5, 24], 初始流场存在一道从左向右移动的正激波, 激波Mach数为Mas=2.02.在激波前有一个气体界面, 该交界面两侧的密度值不同, 其他值都一样, 交界面与垂直方向的夹角α=60°, 底面是一水平物面.交界面左侧各参数值为ρ1=1, p1=1, u1=v1=0, 右侧为ρ2=3, p2=1, u2=v2=0, 激波后的参数值由R-H关系式得到.各边界条件的设置如图 15所示, 图中的u0是指正激波的移动速度.
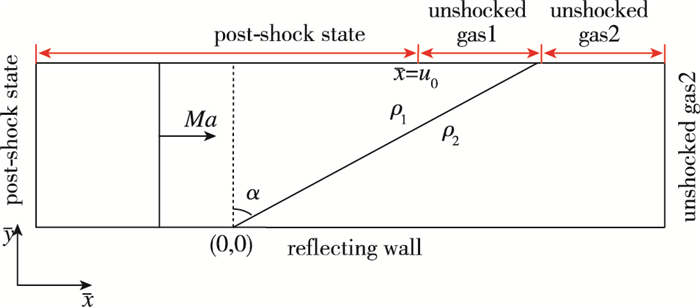
|
| 图 15 激波折射+反射问题初值和边值设置 Fig.15 Initial data and boundary conditions of shock refraction and reflection problem |
计算使用两套网格700×350和1 400×700.在该问题中激波首先在界面上折射, 发生偏折后在物面反射, 产生Mach反射现象, 同时在物面左下角卷起一个涡, 此过程中流场具有自相似的特点.使用原方程和自相似方程进行计算, 计算结果如图 16所示, 与文献[5, 24]的结果吻合很好, 图中所示的界面、入射激波、反射激波、滑移线以及Mach杆的分辨率都很好.
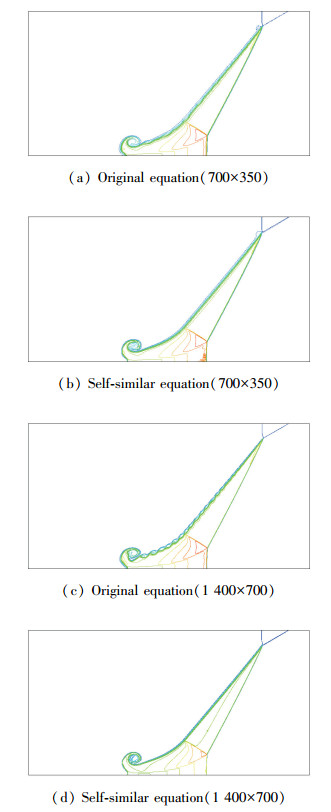
|
| 图 16 算例12密度等值线 Fig.16 Density contour of test 12 |
对比原方程和自相似方程的解, 原方程的解在界面处是不稳定的, 而自相似方程是稳定的, 并具有网格收敛性.我们认为原方程界面处的不稳定可能是由数值扰动造成的, 这可以通过数值黏性来抑制.当网格比较粗时, 数值黏性足够大, 界面是稳定的; 当网格比较密时, 数值黏性不够大, 界面开始变得不稳定.对自相似方程, 数值黏性和数值扰动都较小, 因此分辨率和稳定性都很高.
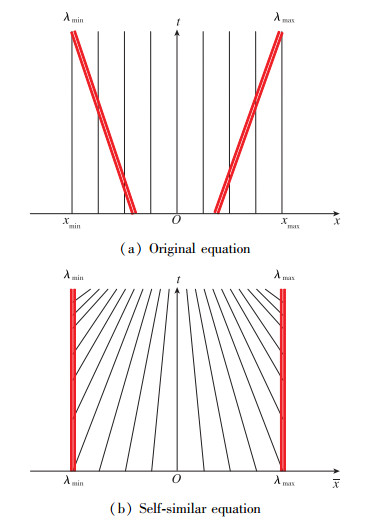
5 分析 5.1 自相似方程高分辨率的原因由第4节的数值计算可以看出, 自相似和准自相似Euler方程的数值解要比原Euler方程的分辨率高.首先, 算法利用解的性质越多, 数值解越精确, 这里利用的是解的自相似性质; 其次, 相比非定常问题, 定常问题更容易得到准确的数值解; 再次, 在使用相同网格的情况下, 自相似方程相当于原方程的网格数随时间增加自动加密, 如图 17所示, 单线为计算实施区域, 两道双线之内为解的变化区, 双线之外为未扰动区, 原方程有一半计算量浪费在未扰动区, 见图 17(a), 而自相似方程的计算完全在扰动区内没有浪费计算量, 从计算实施区域看, 自相似方程相当于随着虚拟时间推进计算被自动加密图,见图 17(b), 单线相当于原方程网格, 这就是后者高分辨率的根本原因.准自相似方法正是基于这个分析而设计的, 见图 18.
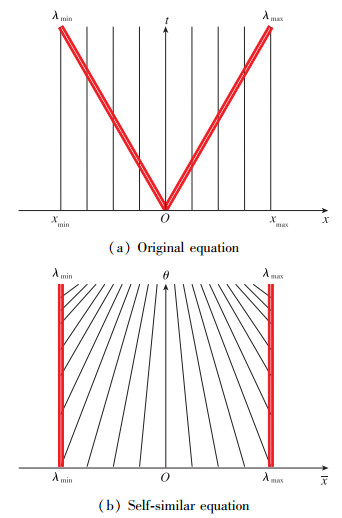
|
| 图 17 自相似问题的原方程和自相似方程计算区域对比 Fig.17 Comparison of computational domains of original and self-similar Euler equations |
|
| 图 18 准自相似问题的原方程和准自相似方程计算区域对比 Fig.18 Comparison of computational domains of original and quasi self-similar Euler equations |
准相似与自相似问题的主要区别是:自相似问题解的变化域是从一点出发的扇形区, 准自相似是从一个区间出发的梯形区.计算初始阶段准自相似方法与自相似方法相差较大, 随着计算时间的增加, 二者差别逐渐消失, 最终达到与自相似方法一样的效果.
5.2 ′无源项′和′有源项′自相似方程的计算对比1.2节已给出了本文自相似方法和文献方法[5]的理论对比, 下面给出二者的计算对比.同1.2节, 本文方法记为′无源项′(no-source), 文献[5]方法记为′有源项′(with-source).
对比1: Sod激波管问题
| $ \left\{ {\begin{array}{*{20}{l}} {({\rho _{\rm{L}}},{u_{\rm{L}}},{p_{\rm{L}}}) = (1,0,1)}\\ {({\rho _{\rm{R}}},{u_{\rm{R}}},{p_{\rm{R}}}) = (0.125,0,0.1)} \end{array}} \right. $ |
从图 19可以看出:在接触间断和激波处, ′无源项′自相似方程解的分辨率要高于′有源项′的.
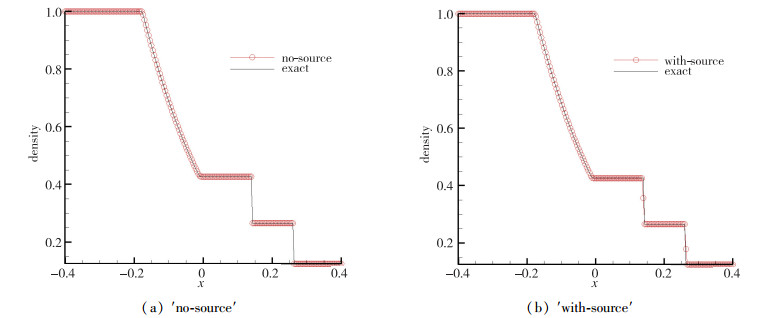
|
| 图 19 ′无源项′和′有源项′计算结果对比 Fig.19 Comparison of the results of ′no-source′ and ′with-source′ |
从图 20可以看出: (a)200点:对′有源项′, 迭代1 000次, 误差收敛, 迭代5 000次, 残差收敛; 对′无源项′, 迭代10 000次, 误差收敛, 迭代40 000次, 残差收敛. (b)400点:对′有源项′, 迭代2 000次, 误差收敛, 迭代10 000次, 残差收敛; 对′无源项′, 迭代5 000次, 误差收敛, 迭代15 000次, 残差收敛. (c) 200点:对′有源项′, 当残差达到10-5时, 误差收敛, 对′无源项′, 当残差达到10-9时, 误差收敛. (d) 400点:对′有源项′, 当残差达到10-7时, 误差收敛, 对′无源项′, 当残差达到10-9时, 误差收敛.详见表 1.
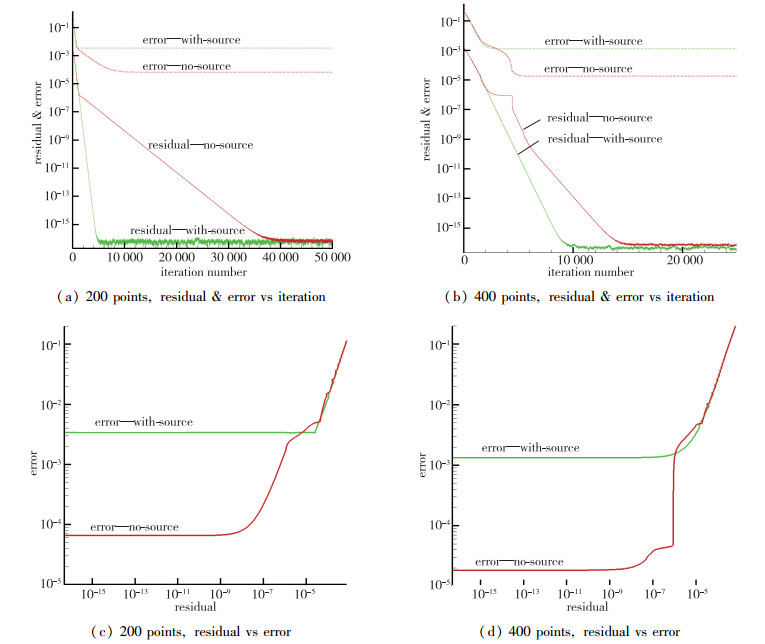
|
| 图 20 ′无源项′和′有源项′残差和误差历史对比 Fig.20 Comparison of residual and error history of ′no-source′ and ′with-source′ |
| 下载CSV 表 1 ′无源项′和′有源项′残差和误差历史对比网格 Tab.1 Comparison of the residual and error history of ′no-source′ and ′with-source′ |
对比2:二维Riemann问题
| $ \begin{array}{*{20}{c}} {}&{J_{21}^ - }&{}\\ {J_{32}^ + }&{}&{J_{41}^ + }\\ {}&{J_{34}^ - }&{} \end{array} $ |
初值
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\begin{array}{*{20}{l}} {{\rho _2}}\\ {{p_2}}\\ {{u_2}}\\ {{v_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 2\\ 1\\ {0.75}\\ {0.5} \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _1}}\\ {{p_1}}\\ {{u_1}}\\ {{v_1}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ 1\\ {0.75}\\ { - 0.5} \end{array}} \right)\\ {\kern 1pt} \left( {\begin{array}{*{20}{l}} {{\rho _3}}\\ {{p_3}}\\ {{u_3}}\\ {{v_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ 1\\ { - 0.75}\\ {0.5} \end{array}} \right),\left( {\begin{array}{*{20}{l}} {{\rho _4}}\\ {{p_4}}\\ {{u_4}}\\ {{v_4}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 3\\ 1\\ { - 0.75}\\ { - 0.5} \end{array}} \right) \end{array} $ |
图 21为流场计算对比. 图 22为密度对比, 由图 22可以看出: (a)网格400×400: ′无源项′和′有源项′的残差收敛速率在10 000步以前是等价的(此时残差=10-7), ′有源项′迭代27 000步后收敛, 残差为10-17, ′无源项′迭代300 000步后收敛, 残差为10-13. (b)网格800×800: ′无源项′和′有源项′的残差收敛速率在28 000步以前是等价的(此时残差=10-8), ′有源项′迭代130 000步后收敛, 残差为10-16, ′无源项′迭代300 000步后收敛, 残差为10-17.详见表 2.
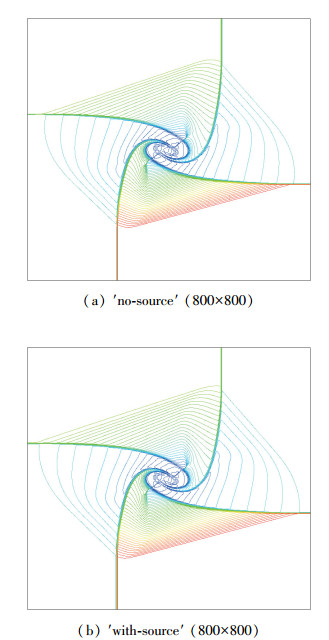
|
| 图 21 ′无源项′和′有源项′密度等值线对比 Fig.21 Comparison of the density contours of ′no-source′ and ′with-source′ |
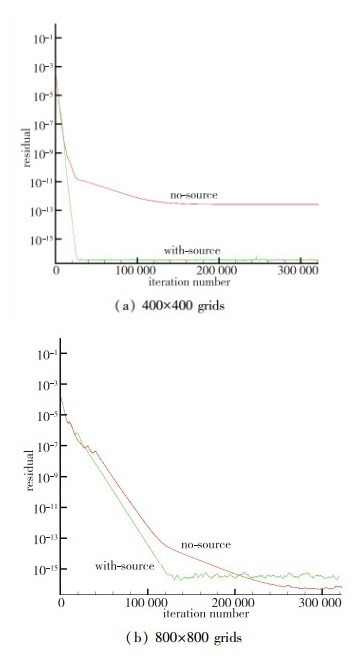
|
| 图 22 ′无源项′和′有源项′残差历史对比 Fig.22 Comparison of the residual history of ′no-source′ and ′with-source′ |
| 下载CSV 表 2 ′无源项′和′有源项′残差历史对比网格 Tab.2 Comparison of the residual history of ′no-source′ and ′with-source′ |
本节通过数值计算对比了′无源项′和′有源项′两种形式的自相似方程.两种形式是等价的, 仅从离散意义进行对比.理论分析表明(见1.2节), 相比′无源项′形式, ′有源项′多出一个2阶黏性小量, 因此′无源项′形式更准确, ′有源项′形式更稳定; 数值解表明, ′无源项′在接触间断和激波处没有过渡点, 而′有源项′有一个过渡点, 因此′无源项′分辨率更高. ′无源项′的误差比′有源项′的小; ′有源项′的残差收敛比′无源项′快; 在相同误差的条件下, ′无源项′和′有源项′的残差是相等的, 表明它们收敛速率相同; 随着网格加密, ′无源项′的残差收敛速率增加, 而′有源项′的残差收敛速率下降, 它们之间的差距变小.
计算表明, 当误差收敛时, 残差的继续下降是没有意义的.所以, 事实就是, ′无源项′和′有源项′的残差收敛速率相等, 而′无源项′更精确.
6 结论本文提出两种数值方法, 即自相似法和准自相似法.通过变换u(x, t)→u(x), 自相似方法把非定常Euler方程的初值问题变为边值问题.通过变换u(x, t)→u(x, t), 准自相似方法把非定常Euler方程的初值问题变为初边值问题.把自相似参数取为局部常数后, 自相似和准自相似Euler方程都是双曲守恒形式, 可以利用各种成熟的守恒律数值方法进行求解.
我们还分析了新方程的特征值, Jacobi和特征向量.用一维和二维Riemann问题, 激波反射问题, 激波折射+反射问题进行了数值实验.一维结果几乎等同于精确解, 二维结果也给出了比原方程更高的分辨率.
总结几点:
(1) 将自相似参数取为局部常数后, 得到一个新的自相似方程, 可以直接使用各种成熟的守恒律方程数值方法, 无须重新设计格式.
(2) 由于利用自相似问题的解具有自相似性这一本质性的特点, 因此求解自相似方程可以得到很高的分辨率, 解的分辨率完全取决于残差的收敛程度, 一维问题可以达到精确解的水平.
(3) 经过自相似变换后, 原非定常Euler方程的初值问题被转化一个定常方程的边值问题, 少了时间自变量t, 问题得到了简化, 因此使用自相似解可以更好地研究自相似问题, 比如二维Riemann问题, 激波反射问题.另外, 由于自相似方程是一个定常方程, 因此它的解具有很好的稳定性和网格收敛性.
(4) 为了利用自相似变换的优点和扩大它的应用范围, 本文提出了自相似坐标法, 把解由u(x, t)变换到u(x, t), 这种做法对于不具有自相似性但接近自相似的问题也适用, 并且也具有自相似变换的优点, 而且随着计算时间的增加优势越明显.
(5)′无源项′和′有源项′两种形式的自相似Euler方程是等价的, ′无源项′分辨率更高一些.
附录A1:自相似变换推导
考虑如下一维完全气体Euler方程
| $ {\mathit{\boldsymbol{u}}_t} + \mathit{\boldsymbol{f}}{(\mathit{\boldsymbol{u}})_x} = 0 $ | (A1.1) |
其中
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}} = {{(\rho ,\rho u,E)}^{\rm{T}}},\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) = {{(\rho u,\rho {u^2} + p,u(E + p))}^{\rm{T}}},}\\ {p = (\gamma - 1)(E - \frac{1}{2}\rho {u^2})} \end{array} $ | (A1.2) |
引入自相似参数x=x/t, 并对(A1.1)作自相似变换
| $ {\mathit{\boldsymbol{u}}_{\bar x}}{{\bar x}_t} + \mathit{\boldsymbol{f}}{(\mathit{\boldsymbol{u}})_{\bar x}}{{\bar x}_x} = 0 $ | (A1.3) |
即
| $ {\mathit{\boldsymbol{u}}_{\bar x}}\left( { - \frac{x}{{{t^2}}}} \right) + \mathit{\boldsymbol{f}}{(\mathit{\boldsymbol{u}})_{\bar x}}\frac{1}{t} = 0 $ | (A1.4) |
即
| $ - \bar x{\mathit{\boldsymbol{u}}_{\bar x}} + \mathit{\boldsymbol{f}}{(\mathit{\boldsymbol{u}})_{\bar x}} = 0 $ | (A1.5) |
将上式x取为局部常数(指u前面的x, 非下标), 重写(A1.5)
| $ {(\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \bar x\mathit{\boldsymbol{u}})_{\bar x}} = 0 $ | (A1.6) |
局部常数x指在微分过程中冻结, 可用下式表达
| $ {(\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}) - \bar x\mathit{\boldsymbol{u}})_{\bar x}} \equiv \frac{{\left[ {\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{u}}\left( {\bar x + \frac{{{\rm{d}}\bar x}}{2}} \right)} \right) - \bar x\mathit{\boldsymbol{u}}\left( {\bar x + \frac{{{\rm{d}}\bar x}}{2}} \right)} \right] - \left[ {\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{u}}\left( {\bar x - \frac{{{\rm{d}}\bar x}}{2}} \right)} \right) - \bar x\mathit{\boldsymbol{u}}\left( {\bar x - \frac{{{\rm{d}}\bar x}}{2}} \right)} \right]}}{{{\rm{d}}\bar x}} $ | (A1.7) |
方程(A1.6)可以很方便地使用各种成熟格式, 易于求解.
附录A2:准自相似变换推导
考虑一维完全气体Euler方程(A1.1).引入如下自相似参数
| $ \bar x = \frac{{x - {x_0}}}{{t - {t_0}}} $ | (A2.1) |
对方程(A1.1)作准自相似变换
| $ {\mathit{\boldsymbol{u}}_t} = {\mathit{\boldsymbol{u}}_t} + {\mathit{\boldsymbol{u}}_{\bar x}}{{\bar x}_t} = {\mathit{\boldsymbol{u}}_t} - {\mathit{\boldsymbol{u}}_{\bar x}}\frac{{x - {x_0}}}{{{{(t - {t_0})}^2}}} = {\mathit{\boldsymbol{u}}_t} - \frac{{\bar x}}{{t - {t_0}}}{\mathit{\boldsymbol{u}}_{\bar x}} $ | (A2.2) |
| $ \mathit{\boldsymbol{f}}{(\mathit{\boldsymbol{u}})_x} = {\mathit{\boldsymbol{f}}_{\bar x}}{{\bar x}_x} = \frac{1}{{t - {t_0}}}{\mathit{\boldsymbol{f}}_{\bar x}} $ | (A2.3) |
其中,第1个符号左侧ut≡∂u(x, t)/∂t, 等号右侧ut≡∂u(x, t)/∂t,下式相同.将(A2.2)和(A2.3)代入(A1.1)
| $ {\mathit{\boldsymbol{u}}_t} + \mathit{\boldsymbol{f}}{(\mathit{\boldsymbol{u}})_x} = {\mathit{\boldsymbol{u}}_t} - \frac{{\bar x}}{{t - {t_0}}}{\mathit{\boldsymbol{u}}_{\bar x}} + \frac{1}{{t - {t_0}}}{\mathit{\boldsymbol{f}}_{\bar x}} = 0 $ | (A2.4) |
取t-t0和x作为局部常数
| $ {\mathit{\boldsymbol{u}}_t} + {\left( {\frac{{\mathit{\boldsymbol{f}} - \bar x\mathit{\boldsymbol{u}}}}{{t - {t_0}}}} \right)_{\bar x}} = 0 $ | (A2.5) |
上式局部常数的意义同(A1.7).
| [1] |
Li J Q, Zheng Y X. Interaction of rarefaction waves of the two-dimensional self-similar Euler equations[J]. Archive for Rational Mechanics and Analysis, 2009, 193(3): 623-657. DOI:10.1007/s00205-008-0140-6 |
| [2] |
Chae D. Unique continuation type theorem for the self-similar Euler equations[J]. Advances in Mathematics, 2015, 283: 143-154. DOI:10.1016/j.aim.2015.06.021 |
| [3] |
Chae D. On the self-similar solutions of the 3D Euler and the related equations[J]. Communications in Mathem-atical Physics, 2011, 305(2): 333-349. DOI:10.1007/s00220-011-1266-1 |
| [4] |
Li J Q. Self-similar solutions of 2-D compressible Euler equations and mixed-type problems, Bulletin of the Institute of Mathematics[J]. Academia Sinica, 2015, 10: 393-421. |
| [5] |
Samtaney R. Computational methods for self-similar solutions of the compressible Euler equations[J]. Journal of Computational Physics, 1997, 132(2): 327-345. |
| [6] |
Li J Q, Zhang T, Yang S L. The two-dimensional Riemann problem in gas dynamics:pitman monographs and surveys in pure and applied mathematics[M]. Harlow: Addison Wesley Longman Ltd., 1998.
|
| [7] |
Zhang T, Zheng Y X. Conjecture on the structure of solutions of the Riemann problem for two-dimensional gas dynamics systems[J]. SIAM Journal on Mathematical Analysis, 1990, 21(3): 593-630. |
| [8] |
Schulz-Rinne C W. Classification of the Riemann problem for two-dimensional gas dynamics[J]. SIAM Journal on Mathematical Analysis, 1993, 24(1): 76-88. |
| [9] |
Chang T, Chen G Q, Yang S L. On the 2-D Riemann problem for the compressible Euler equations Ⅰ. Interaction of shocks and rarefaction waves[J]. Discrete & Continuous Dynamical Systems, 1995, 1(4): 555-584. |
| [10] |
Schulz-Rinne C W, Collins J P, Glaz H M. Numerical solution of the Riemann problem for two-dimensional gas dynamics[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1394-1414. |
| [11] |
Colella P, Woodward P R. The Piecewise Parabolic Method (PPM) for gas-dynamical simulations[J]. Journal of Computational Physics, 1984, 54(1): 174-201. |
| [12] |
Lax P D, Liu X D. Solution of two-dimensional Riemann problems of gas dynamics by positive schemes[J]. SIAM Journal on Scientific Computing, 1998, 19(2): 319-340. |
| [13] |
Liu X D, Lax P D. Positive schemes for solving multi-dimensional hyperbolic systems of conservation laws Ⅱ[J]. Journal of Computational Physics, 2003, 187(2): 428-440. |
| [14] |
Kurganov A, Tadmor E. Solution of two-dimensional Riemann problems for gas dynamics without Riemann problem solvers[J]. Numerical Methods for Partial Differential Equations, 2002, 18(5): 584-608. DOI:10.1002/num.10025 |
| [15] |
Kurganov A, Petrova G. A third-order semi-discrete genuinely multidimensional central scheme for hyperbolic conservation laws and related problems[J]. Numerische Mathematik, 2001, 88(4): 683-729. DOI:10.1007/PL00005455 |
| [16] |
Han E, Li J Q, Tang H Z. An adaptive GRP scheme for compressible fluid flows[J]. Journal of Computational Physics, 2010, 229(5): 1448-1466. |
| [17] |
Li J Q, Zhang Y J. The adaptive GRP scheme for compressible fluid flows over unstructured meshes[J]. Journal of Computational Physics, 2013, 242: 367-386. |
| [18] |
Han E, Li J Q, Tang H Z. Accuracy of the adaptive GRP scheme and the simulation of 2-D Riemann problems for compressible Euler equations[J]. Communications in Computational Physics, 2011, 10(3): 577-609. |
| [19] |
Dong H T, Zhang L D, Lee C H. High order discontinuities decomposition entropy condition schemes for Euler equations[J]. Journal of Computational Fluid Dynamics, 2002, 10(4): 448-457. |
| [20] |
Alonso J, Jameson A. Fully-implicit time-marching aeroelastic solutions[R]. AIAA 94-0056, 1994.
|
| [21] |
Strang G. On the construction and comparison of difference schemes[J]. SIAM Journal on Numerical Analysis, 1968, 5(3): 506-517. |
| [22] |
Shu C W, Osher S. Efficient implementation of essentially non-oscillatory shock-capturing schemes[J]. Journal of Computational Physics, 1988, 77(2): 439-471. |
| [23] |
Toro E F. Riemann solvers and numerical methods for fluid dynamics:a practical introduction[M]. Berlin: Springer, 2009.
|
| [24] |
Samtaney R, Pullin D I. On initial-value and self-similar solutions of the compressible Euler equations[J]. Physics of Fluids, 1996, 8(10): 2650-2655. DOI:10.1063/1.869050 |



