CHAP3D (compatible hydrodynamics analysis program)程序是北京应用物理与计算数学研究所自主研发的通用弹塑性流体力学分析程序, 它基于相容Lagrange动力学数值方法[1-7], 支持非结构的混合网格, 适合于非线性结构的高速碰撞、爆炸以及各种工程问题的数值模拟.由于这些工程问题往往伴随着结构大变形和材料塑性等高度非线性特征, 因此采用并行计算成为必然的选择[8-11].
自从1972年第一台并行计算机ILLIAC-Ⅳ诞生以来, 并行计算机经历了残酷而快速的发展.可以根据并行计算机的硬件系统构成将之区分为:单指令多数据(single-instruction multi-data, SIMD)和多指令多数据(multi-instruction multi-data, MIMD)两类.其中, SIMD针对数据并行, 而MIMD针对多任务并行.
通常的并行计算机大部分基于MIMD平台, 主要形成了对称多处理器(symmetric multi-processor, SMP)共享存储并行机、分布共享存储(distributed shared memory, DSM)并行机、大规模并行机(massively parallel processor, MPP)以及微机机群等4类[12-15].
在这些并行机上, 程序须进行相应的并行化才可以发挥作用.区域分解和处理器间的通信是并行程序的两个最重要部分.一个好的并行程序必须确保处理器用于计算的时间尽可能多, 用于通信的时间尽可能少.这个目标的实现就依赖于并行程序采用的区域分解算法以及依赖此区域分解而建立的通信关系.
区域分解是指在计算之前, 根据计算使用的处理器数目, 将计算区域的有限元网格剖分成相同份数的子网格, 将每一份子网格分配到每个处理器上, 如图 1所示.此区域分解是在计算之前进行, 而且在计算过程中, 每个处理器上的子网格不再变化, 所以被称为“静态区域分解”.在网格的区域分解过程中, 须尽可能将网格均匀地在处理器之间分配, 称为“负载平衡”.如果处理器间的负载不平衡, 可能造成某些处理器在工作, 而另外的处理器在等待的情况, 从而降低并行计算的效率.常用的区域分解工具有METIS[16].
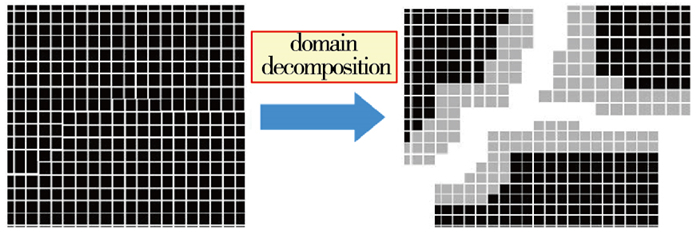
|
| 图 1 区域分解示意图 Fig.1 Sketch of domain decomposition |
在没有接触面的算例计算中, 每个处理器只对其所有的子网格进行计算, 由于节点力以及其他一些物理量的计算与相邻网格相关, 通常须在子网格的边界上搭接来自其他处理器的相邻网格作为保护网格.这个保护网格称为“影像区”, 如图 1的阴影网格所示.
之后, 还须建立处理器之间的通信关系, 用来将每个处理器的计算结果进行传递, 特别是“影像区”网格与节点的物理量传递.消息传递接口(message passing interface, MPI)是目前国际上最流行、可移植性和可扩展性非常好的并行通信设计平台.
当前逐渐成为研究热点的基于图像处理单元(graphic processing unit, GPU)并行的计算机, 则是典型的SIMD结构[11, 14-15].
在Lagrange方法中, 接触算法对相互接触的物质运动界面施加约束以保证接触界面的正确模拟.因此它是Lagrange方法中最重要的部分之一.
大部分的接触算法都基于“接触对”的概念, 即将接触面的两个界面分为主面和从面, 并且考虑主面接触单元或节点与从面接触单元或从点的接触关系.接触算法包含接触搜索算法和接触力耦合计算算法.接触搜索算法是确定物质界面发生接触的时间和位置, 它又可分为全局接触搜索和局部接触搜索两个部分[17, 34].前者的目的是为了寻找可能发生接触的由离散网格构成的接触面单元.后者是确定发生接触的接触面片断、确定接触点.接触力耦合算法是将接触约束条件(界面不可穿透条件、力的相互作用条件等)施加到接触面上.
由于接触问题的非线性, 接触算法成为Lagrange方法中最难处理的部分之一.对于多处理器集群的并行机, 带有大量接触面的工程问题的并行计算, 更是一个巨大的挑战.
挑战的首先一个来源是, 整个计算域在计算初始时刻的“静态区域分解”, 将会把一个完整的接触面分配到不同的处理器上.如图 2所示的上下两块物体叠放的例子, 上块物体下界面与下块物体上界面是一对完整接触面, 假设有3个处理器, 在区域分解后, 这对完整的接触面被分到了不同的处理器上(分别以绿色、红色和蓝色代表).其次, 接触面存在切向滑移, 接触面上相互接触单元在计算中不断变化.
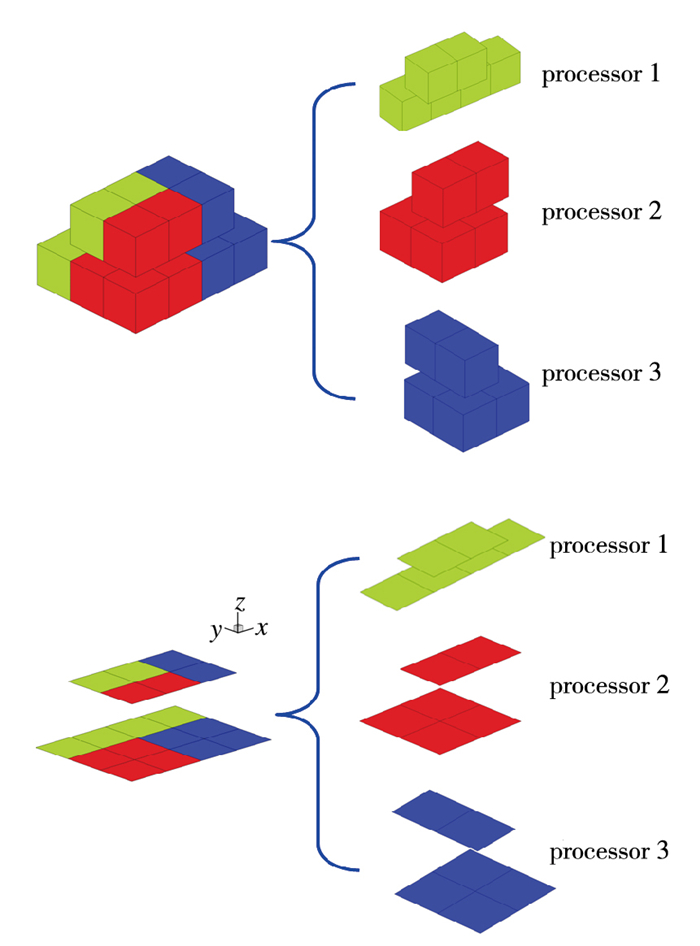
|
| 图 2 区域分解后的接触面 Fig.2 Contact surfaces after domain decomposition |
因此, 每个处理器的接触面计算, 须从其他处理器中寻找与本处理器的单元发生接触的那些单元. Malone等[18-19]提出了一个处理器间的全局接触搜索算法来寻找与本处理器可能接触的单元.在每个时间步, 首先确定本处理器子网格所占据的空间范围, 然后通过全局通信, 得到与本处理器占据空间有相交的其他处理器, 之后将这些处理器上的接触面单元通信到本处理器上, 再进一步进行接触搜索以确定发生接触的单元. Xu等[20]改进了处理器间接触全局搜索算法.
这种并行算法只采用了一次静态的区域分解来同时进行有限元计算和接触面计算.此方法对于接触面的并行计算来说显然是负载不平衡的算法, 因为可能某些处理器上有大量的接触面单元, 而另一些处理器上很少甚至没有接触面单元, 这肯定会造成一些处理器在等待的情况发生.
Dureisseix等[21],Avery等[22-23]和Kozubek等[24]提出另一类的静态区域分解方法, 应用有限元撕裂与连接(finite element tearing and interconnecting,FETI)算法, 将接触面作为区域分解的边界, 如图 3所示, 各个子区域之间的边界, 由Lagrange乘子代表作用力来进行连接.
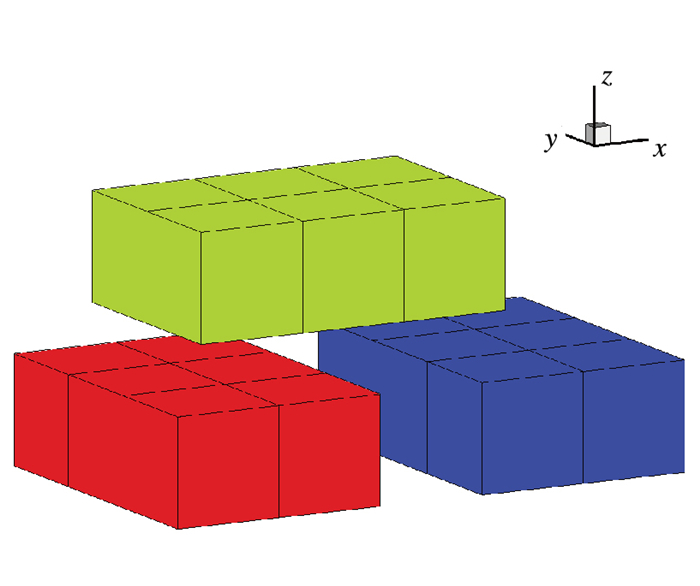
|
| 图 3 FETI方法的区域分解示意图 Fig.3 Sketch of domain decomposition of FETI |
这个方法在并行计算的过程中, 仍然须在处理器间进行接触搜索和接触力(即Lagrange乘子)计算.在接触面的并行计算方面, 仍是一个负载不平衡的算法.
Hallquist等[17]在Dyna3D程序中, 提出了基于桶排序算法[25]的接触面动态区域分解方法来达到接触面并行计算的负载平衡.该方法在初始计算域的静态区域分解之后, 每个计算步内, 首先是通过桶排序算法, 将接触面所占据空间划分为若干个“桶”, 并且将接触面单元依次放入这些“桶”中, 然后再对这些桶进行二次区域分解, 分配到各个处理器上.这种接触面动态二次区域分解的思想, 被广泛应用于接触并行计算中[26-28], 并且采用了多种方法来降低动态区域分解的时间开销. Attaway等[26]采用了坐标递归二分法(recursive coordinate bisection,RCB)来进行接触面动态区域分解, 缩短了二次动态区域分解的时间, 并获得负载平衡的分配结果. Har等[8]提出了智能节点块区域分解方法(node-wise block domain decomposition,NBDD)来进行接触面二次动态区域分解.
二次动态区域分解算法的优点是具有很好的负载平衡.它的缺点是每个计算时间步, 须在不同的处理器间进行接触搜索, 不断重建接触网格连接关系和接触关系, 将会耗费大量的时间在接触面重构和处理器通信上.
自从2008年之后, 基于GPU并行的接触并行算法受到了越来越多的重视[29-31].但是, 基于CPU的并行计算仍然占据了主要的地位, 这是因为GPU并不能脱离CPU单独存在, 而且CPU并行与GPU并行是两种各自具有优缺点的完全不同的架构, 都需要针对性的并行编程.
本文介绍了针对多处理器集群的, 应用于CHAP3D程序中的,基于双重静态区域分解的接触并行算法.这两种接触并行算法都采用METIS进行区域分解, 并且使用MPI构建通信关系.
1 控制方程 1.1 接触约束条件对于接触问题, 考虑两个物体B(α), α=1, 2, 初始时刻占据空间Ω(α)⊂R3, 经过运动后发生接触, 运动的过程分别可以视为两个映射φ(α):φ(α)(X(α), t)=x(α).它们的边界记为Γ(α), 由3部分组成:位移边界Γu(α), 应力边界Γσ(α)和接触边界Γc(α).存在两个初始坐标为X(1)和X(2)的分别位于B(1)和B(2)边界上的点, 经过φ(α)的映射成为同一个点, 即φ(1)(X(1), t)=φ(2)(X(2), t)=x, 如图 4所示.

|
| 图 4 两个物体大变形接触示意图 Fig.4 Notation for large deformation contact between two bodies |
在接触面的法向上应该满足不可穿透条件
| $ \left( {{\mathit{\boldsymbol{x}}_2} - {\mathit{\boldsymbol{x}}_1}} \right) \cdot \mathit{\boldsymbol{n}} \ge 0 $ |
其中,xα, α=1, 2分别表示两个物体上的点, n为接触面上接触点的法向单位矢量.对于φ(2)(Ω(2))的边界上每个点x2, 在φ(1)(Ω(1))上都有一个与之距离最近的点x1, 当x1点已知, 可以定义距离函数(gap function)表述不可穿越条件
| $ {g_{\rm{N}}} = \left\{ {\begin{array}{*{20}{c}} {\left( {{\mathit{\boldsymbol{x}}_2} - {{\mathit{\boldsymbol{\bar x}}}_1}} \right) \cdot {{\mathit{\boldsymbol{\bar n}}}_1}}&{{\rm{if}}\;\;\left( {{\mathit{\boldsymbol{x}}_2} - {{\mathit{\boldsymbol{\bar x}}}_1}} \right) \cdot {{\mathit{\boldsymbol{\bar n}}}_1} < 0}\\ 0&{{\rm{otherwise}}} \end{array}} \right. $ |
其中,下标N表示法向方向.
同时, 在接触区域, 设接触面间的法向作用力为PN, PN必须满足
| $ \left\{ {\begin{array}{*{20}{c}} {{P_{\rm{N}}} < 0,}&{{\rm{if}}\;\;\;\;{g_{\rm{N}}} = 0}\\ {{P_{\rm{N}}} = 0,}&{{\rm{if}}\;\;\;\;{g_{\rm{N}}} > 0} \end{array}} \right. $ | (1) |
因此, 接触约束可以综合表示为
| $ {P_{\rm{N}}} \cdot {g_{\rm{N}}} = 0 $ |
Lagrange计算框架下接触问题的控制方程为
| $ \frac{{{\rm{d}}\rho }}{{{\rm{d}}t}} + \rho \nabla \cdot \mathit{\boldsymbol{\dot u}} = 0 $ |
| $ \rho \cdot \mathit{\boldsymbol{\ddot u}} = \nabla \cdot \mathit{\boldsymbol{\sigma }} + \rho \mathit{\boldsymbol{f}} $ |
| $ \rho \frac{{{\rm{d}}e}}{{{\rm{d}}t}} = \mathit{\boldsymbol{\sigma }}:\nabla \mathit{\boldsymbol{\dot u}} $ |
其中, ρ为密度, u为位移, f为体积力, e为内能, σ为应力张量, 另外还须补充连续介质的本构关系和状态方程.
以α=1, 2表示不同的物体, 那么在当前坐标下, 这两个物体相互接触的控制方程可以写为
| $ 动量方程:{\rho _\alpha } \cdot {\mathit{\boldsymbol{\ddot u}}_\alpha } = \nabla \cdot {\mathit{\boldsymbol{\sigma }}_\alpha } + {\rho _\alpha }{\mathit{\boldsymbol{f}}_\alpha } $ | (2) |
| $ \begin{array}{l} 边界条件:\;\;\;{\mathit{\boldsymbol{u}}_\alpha } = {{\mathit{\boldsymbol{\bar u}}}_\alpha }\;\;\;\;在\;{\mathit{\Gamma }_u}\;上\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{\sigma }}_\alpha } \cdot {\mathit{\boldsymbol{n}}_\alpha } = {{\mathit{\boldsymbol{\bar \sigma }}}_\alpha }\;\;\;\;在\;{\mathit{\Gamma }_\sigma }\;上 \end{array} $ |
| $ \begin{array}{l} 初始条件:\;\;\;{\mathit{\boldsymbol{u}}_\alpha }\left| {_{t = 0}} \right. = {\mathit{\boldsymbol{u}}_{0,\alpha }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\dot u}}}_\alpha }\left| {_{t = 0}} \right. = {{\mathit{\boldsymbol{\dot u}}}_{0,\alpha }} \end{array} $ |
| $ 接触条件:{P_{\rm{N}}} \cdot {g_{\rm{N}}} = 0 $ |
假定有一个向量空间V, 可在其中任取一个测试向量v∈V, 都满足在物体Bα的边界Γu上, v=0, 那么方程(2)描述的接触问题可以写成以下的弱形式
| $ \begin{array}{*{20}{c}} {\sum\limits_{\alpha = 1}^2 {\int_{\varphi \left( {{\mathit{\Omega }_\alpha }} \right)} {\nabla \cdot {\mathit{\boldsymbol{\sigma }}_\alpha } \cdot {\mathit{\boldsymbol{v}}_\alpha }{\rm{d}}V} } + \sum\limits_{\alpha = 1}^2 {\int_{\varphi \left( {{\mathit{\Omega }_\alpha }} \right)} {{\rho _\alpha }\left( {{\mathit{\boldsymbol{f}}_\alpha } - {{\mathit{\boldsymbol{\ddot u}}}_\alpha }} \right) \cdot {\mathit{\boldsymbol{v}}_\alpha }{\rm{d}}V} } + }\\ {\sum\limits_{\alpha = 1}^2 {\int_{{\mathit{\Gamma }_{\alpha ,\sigma }}} {{{\mathit{\boldsymbol{\bar \sigma }}}_\alpha } \cdot {\mathit{\boldsymbol{v}}_\alpha }{\rm{d}}a} } + \sum\limits_{\alpha = 1}^2 {\int_{{\mathit{\Gamma }_{\alpha ,c}}} {{P_{{\rm{N}},\alpha }}{\mathit{\boldsymbol{n}}_\alpha } \cdot {\mathit{\boldsymbol{v}}_\alpha }{\rm{d}}a} } = 0} \end{array} $ | (3) |
考虑到两个相互接触的界面上有PN, 1n1=-PN, 2n2, 式(3)可以演化成
| $ \begin{array}{l} \sum\limits_{\alpha = 1}^2 {\int_{\varphi \left( {{\mathit{\Omega }_\alpha }} \right)} {{\mathit{\boldsymbol{\sigma }}_\alpha } \cdot \left( {\nabla {\mathit{\boldsymbol{v}}_\alpha }} \right){\rm{d}}V} } - \sum\limits_{\alpha = 1}^2 {\int_{\varphi \left( {{\mathit{\Omega }_\alpha }} \right)} {{\rho _\alpha }\left( {{\mathit{\boldsymbol{f}}_\alpha } - {{\mathit{\boldsymbol{\ddot u}}}_\alpha }} \right) \cdot {\mathit{\boldsymbol{v}}_\alpha }{\rm{d}}V} } - \\ \;\;\;\;\sum\limits_{\alpha = 1}^2 {\int_{{\mathit{\Gamma }_{\alpha ,\sigma }}} {{{\mathit{\boldsymbol{\bar \sigma }}}_\alpha } \cdot {\mathit{\boldsymbol{v}}_\alpha }{\rm{d}}a} } - \int_{{\mathit{\Gamma }_{1,{\rm{c}}}}} {{P_{{\rm{N}},1}}{\mathit{\boldsymbol{n}}_1} \cdot \left( {{\mathit{\boldsymbol{v}}_1} - {\mathit{\boldsymbol{v}}_2}} \right){\rm{d}}a} = 0 \end{array} $ | (4) |
一旦接触界面已知, 则式(4)可以写成
| $ \begin{array}{l} \sum\limits_{\alpha = 1}^2 {\left\{ {\int_{{\mathit{\Omega }_\alpha }} {{\mathit{\boldsymbol{\sigma }}_\alpha } \cdot \left( {\nabla {\mathit{\boldsymbol{v}}_\alpha }} \right){\rm{d}}V} - \int_{{\mathit{\Omega }_\alpha }} {{\rho _\alpha }\left( {{\mathit{\boldsymbol{f}}_\alpha } - {{\mathit{\boldsymbol{\ddot u}}}_\alpha }} \right) \cdot {\mathit{\boldsymbol{v}}_\alpha }{\rm{d}}V} } \right\}} - \\ \;\;\;\sum\limits_{\alpha = 1}^2 {\int_{{\mathit{\Gamma }_{\alpha ,\sigma }}} {{{\mathit{\boldsymbol{\bar \sigma }}}_\alpha } \cdot {\mathit{\boldsymbol{v}}_\alpha }{\rm{d}}a} + {C_{\rm{c}}}} = 0 \end{array} $ |
其中,Cc是接触约束的贡献.
1.4 接触算法接触问题弱形式, 描述了接触运动边界的相互作用, 须采用接触算法进行计算.由于接触区域是事先不可知的, 所以接触算法的第一步就是接触搜索, 以确定接触发生的地点.在确定发生接触的区域后, 应用接触算法计算接触作用力, 并将此接触作用力反馈到动量方程的计算中.
1.4.1 接触搜索算法通常将节点在相对接触面上的投影点作为它的接触位置.整个接触搜索过程可以分为两个步骤, 首先是在相对界面上的节点中, 寻找给定节点的最近点, 然后在最近点周围相连的单元面中, 确定节点投影的位置.
搜索节点最近点的过程, 称为全局搜索, 它是一个相对独立的过程, 但是对于三维的、接触面节点数较大的问题, 全局搜索算法就成为接触算法中最耗时的算法, 因此需要有高效的全局搜索算法.最常用的有桶搜索[25]算法, 可以比较高效地寻找到节点的最近点.
确定节点投影单元面的过程, 称为局部搜索[32].设节点A的最近点为a, 其法向为na, 与最近点a相连的其中一个单元面如图 5(a)所示, 定义单元面的外法线方向逆时针旋转, 在旋转的左手边为内侧, 右手边为外侧, 其中,ns为单元面的外法向, vab为沿着外法向逆时针旋转边ab的向量, 同样地vbc, vcd, vda分别为其余三条边的向量.
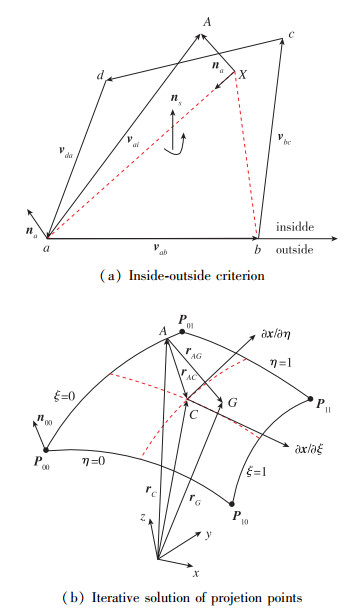
|
| 图 5 接触问题的局部搜索示意图 Fig.5 Local search of the contact |
如果节点A沿着最近点a的法向na投影, 满足下列关系, 则称节点A投影在边ab的内侧
| $ {S_n} = \frac{1}{2}\left( {{\mathit{\boldsymbol{v}}_{aA}} \times {\mathit{\boldsymbol{v}}_{ab}}} \right) \cdot {\mathit{\boldsymbol{n}}_a} \le 0 $ |
如果对于单元面的所有边, 节点A与之构成的三角形沿各条边法向的投影, 都位于边的内侧, 则可以判断为节点A投影在此单元面内[33].
在确定节点A投影在其最近点a的某个单元面内之后, 须在此单元面的曲面片上寻找节点A的投影点.如图 5(b)所示, 节点A坐标为rA, 曲面片形心标记为G, 坐标为rG, 点A在曲面片上的投影点标记C, 坐标为rC, 点A到投影点C的向量rAC, 点A到中心点G的向量rAG.则在参数化的曲面片上, 投影点C处的两个切向与向量rAC正交, 则有以下两个式子成立.
| $ {\left( {\frac{{\partial \mathit{\boldsymbol{r}}}}{{\partial \xi }}} \right)_C} \cdot {\mathit{\boldsymbol{r}}_{AC}} = 0 $ |
| $ {\left( {\frac{{\partial \mathit{\boldsymbol{r}}}}{{\partial \eta }}} \right)_C} \cdot {\mathit{\boldsymbol{r}}_{AC}} = 0 $ |
可以通过Newton-Raphson迭代求解点A在接触片段上的接触点参数坐标(ξC, ηC)[17, 33].
1.4.2 接触力耦合计算方法接触力耦合算法大致可以分成两类:一类是关注接触面之间的作用力, 并且将其作为力的边界条件施加到接触面上, 有Lagrange乘子法、罚函数法、增广Lagrange乘子法等[34]; 另一类是将Wilkins的分配参数的接触耦合算法引入到有限元方法中[35].本文将介绍罚函数法和分配参数法这两种应用于CHAP3D程序中的算法.
(1) 罚函数法
罚函数算法是接触计算中常用的一种算法.此方法中接触面通常分为主面和从面, 之上的节点分别称为主点和从点.经过接触搜索之后, 得到从点在主面上的投影点坐标和法向, 然后计算从点在主面上的穿透深度
| $ {g_n} = \left( {{\mathit{\boldsymbol{r}}_A} - {\mathit{\boldsymbol{r}}_C}} \right) \cdot \mathit{\boldsymbol{n}} $ |
其中, gn为节点的穿透深度, 简称穿深; rA为节点的坐标; rC为投影点坐标; n为投影点的法向.
如果节点的穿深gn < 0, 则对从点施加的惩罚力为
| $ {\mathit{\boldsymbol{f}}_{\rm{s}}} = - k{g_n}\mathit{\boldsymbol{n}},\;\;\;k = \alpha K{A^2}/V $ |
其中, α为缩放系数, 通常取0.1; K为体积模量; A为从点穿透的主面的单元面面积; V为从点穿透的主面的单元体积; n为从点在主面上的投影点的法向.
然后将惩罚力的反向作用力, 通过插值方法施加到从点穿透的主面的顶点上.
| $ \mathit{\boldsymbol{f}}_{\rm{m}}^i = - {\phi _i}\left( {{\xi _C},{\eta _C}} \right) \cdot {\mathit{\boldsymbol{f}}_{\rm{s}}} $ |
其中, ϕi(ξC, ηC)为从点的投影点在主面上的插值形函数.
(2) 分配参数法
在三维分配参数滑移算法中, 通常将两个滑移面分为主面和从面, 其上的节点为主点和从点, 那么根据接触面的法向应力连续条件, 由式(1)可得到接触面相互作用之后主点的加速度[35-36]
| $ \mathit{\boldsymbol{a}} \cdot \mathit{\boldsymbol{n}} = \frac{{\left( {{{\boldsymbol{a}}_{\rm{m}}} \cdot {\boldsymbol{n}} + \frac{{{{\boldsymbol{p}}_s} \cdot {\boldsymbol{n}}}}{{{\rho _{\rm{m}}}}}} \right)}}{{\left( {1 + \frac{{{\rho _s}}}{{{\rho _{\rm{m}}}}}} \right)}} $ | (5) |
其中, a为接触作用之后的主点加速度, n为主点在从面上的接触点的法向, am为主点在接触作用之前的加速度, ρm为主点的质量面密度, ps·n和ρs分别为主点在从面上的接触点的法向压力和质量面密度.
由式(5)可知, 在分配参数滑移算法中, 只要知道主点在从面上投影点的法向压力ps·n和质量面密度ρs, 就可以计算出从面对主点法向加速度的影响.
在得到接触滑移面相互作用后的主点加速度, 由接触面的不可穿透条件, 在分配参数法中, 强制从点的法向速度和法向加速度等于从点在主面上投影点的法向速度和法向加速度, 由此实现接触面的不可穿透条件.
2 基于双重静态区域分解的接触并行算法 2.1 双重静态区域分解双重静态区域分解的基本流程是:
① 初始时刻对计算域进行第1次区域分解;
② 通过处理器间的通信, 重构得到所有接触面的网格拓扑结构关系;
③ 将接触面进行第2次区域分解;
④ 进行时间步的推进计算, 整体计算域的物理量并行计算;
⑤ 接触力并行计算;
⑥ 节点力、加速度、速度更新, 转至第④步.
两次区域分解都在计算的初始时刻进行静态分解, 在后面的时间步推进循环计算中不再变化.
图 2所示的接触问题, 在第①步的整体计算区域分解后, 接触面被分到了3个处理器上, 所以首先要通过处理器间的收集通信操作, 重构接触面结构, 如图 6所示.
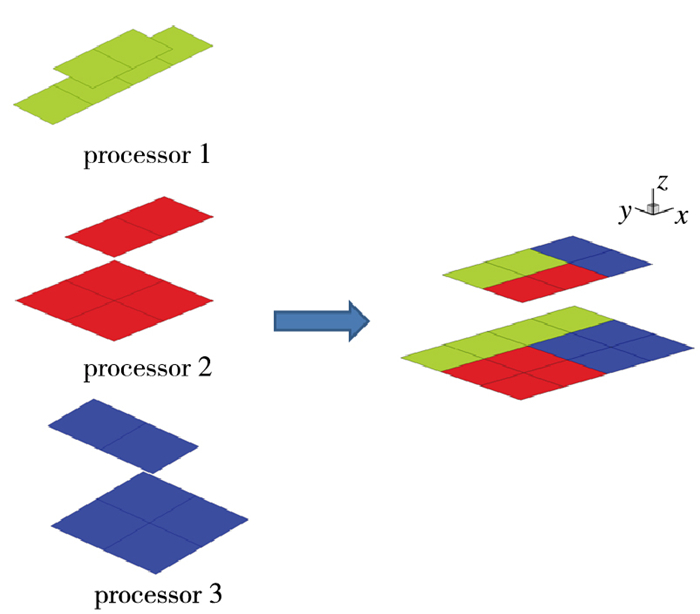
|
| 图 6 接触面的重构 Fig.6 Reconstruction of the contact surfaces |
之后, 进行上述的第③步操作, 在这个步骤中, CHAP3D中采用了两种接触计算区域的分解方法.
2.2 分配完整接触面(distribute whole contact surfaces, DWCS)并行算法(1) 接触面的区域分解
将接触滑移面分配到每个进程上, 无论主体计算过程中滑移面上网格实体在哪个进程上, 将每一对滑移面完整地分配到单一处理器上, 不同处理器完全独立地计算各自拥有的接触滑移面.
因为图 3的例子中只有一对接触面, 所以在接触面区域分解后, 第1个处理器上有完整的接触面, 而在第2, 3个处理器上则没有接触面.
(2) 通信的建立
将整个计算区域进行第1次静态区域分解后, 称之为计算域, 将接触面进行静态区域分解后, 称之为接触域.此并行算法不须建立接触域内各个处理器间的通信, 但是须建立接触域与计算域的消息传递和通信(见图 7).
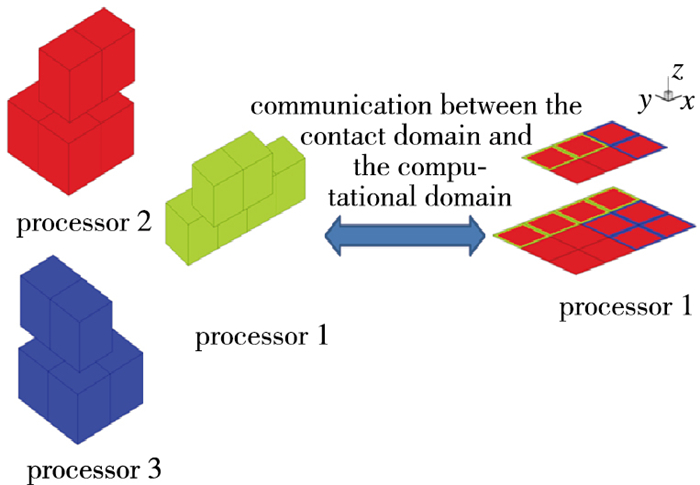
|
| 图 7 DWCS算法中接触域与计算域间的通信 Fig.7 Sketch of the communication between the contact domain and the computational domain in DWCS algorithm |
(3) 接触面的计算
接触面只在第1个处理器上计算, 串行的接触搜索算法和接触力耦合算法不须进行修改就可直接应用.但在同时, 其余处理器将会处于等待的状态, 直至第1个处理器将接触面计算完毕.
在每个时间步的接触计算流程如下:
① 计算域通信物理量到接触域;
② 在有接触面的处理器上(处理器1), 进行接触计算, 其余处理器(处理器2,3)处于等待状态;
③ 将接触计算结果传递回主体计算域.
DWCS方法的优点是简单, 是一个静态的区域分解方法, 只须在计算的开始阶段进行区域即可, 而且串行接触算法不须修改即可用于并行计算.
它的缺点是存在瓶颈问题,如果计算规模不断增加, 但是接触面数量不增加, 接触面计算过程中将会出现大量处理器等待.
2.3 分配主面(distribute master contact surface, DMCS)并行算法 2.3.1 接触面的区域分解DMCS接触并行算法, 在步骤③中将所有接触面的主面作为一个整体进行区域分解, 分配到所有处理器上, 同时根据每个处理器上得到的主面情况, 将相应的完整从面分配到这个处理器上.
图的序号、标题及注释居中放在图的下方.表示数量区域分解后的结果如图 8所示, 设下块物体的上表面为主面, 上块物体的下表面为从面, 那么经过接触面的区域分解之后, 在每个处理器上都有部分主面和完整的从面.
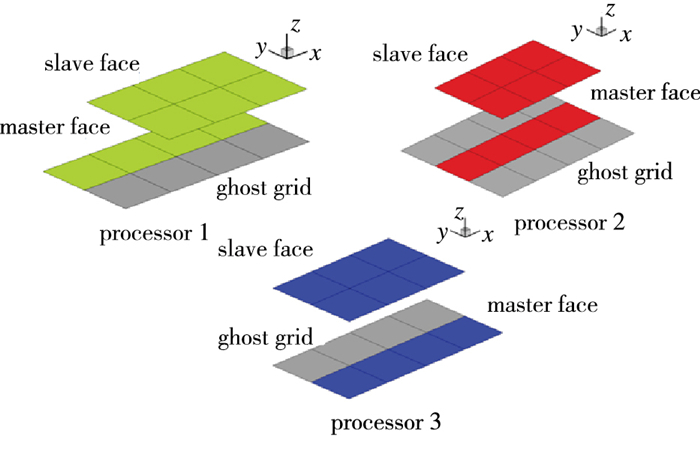
|
| 图 8 DMCS算法中接触面的区域分解 Fig.8 Distribution of the contact surfaces in the DMCS algorithm |
每个进程的主面网格单元, 须在边界上搭接一层邻近单元的影像区, 如图 8的阴影网格所示.此算法须建立接触域内, 处理器之间影像区网格的通信关系.同时还须建立接触域与计算域之间的通信关系(见图 9).
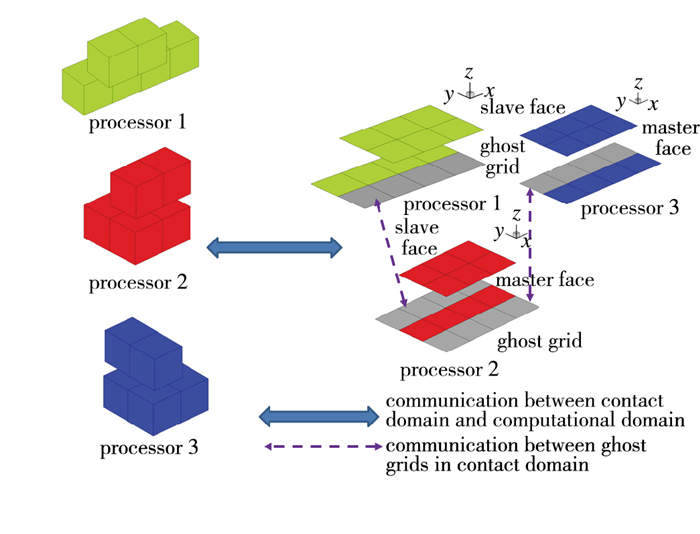
|
| 图 9 DMCS算法中的通信关系 Fig.9 Communications in the DMCS algorithm |
因为每个处理器上有完整的从面, 在单个处理器上, 串行的接触搜索算法可以搜索到所有主点在从面上的接触位置, 并且通过接触耦合算法修正主点的物理量.
而对于从点, 接触搜索算法可以判断出从点是否与进程内的主面单元接触, 还是与影像区内的主面单元相接触, 亦或是落在影像区之外.接触耦合算法对与进程内主面单元接触的从点进行物理量的修正, 其余的从点在本进程内不作处理.
每个时间步的接触计算流程如下:
① 计算域通信物理量到接触域;
② 所有处理器上并行对主面进行接触计算;
③ 接触域内通信主面影像区物理量;
④ 所有进程并行对从面进行接触计算;
⑤ 将接触计算结果传递回主体计算域.
DMCS算法是一个负载平衡的算法, 随着计算规模不断增加, 接触面可以在更多的处理器上完成计算, 减小瓶颈出现的可能.而且DMCS算法接触面区域分解固定, 仍然是一个静态的区域分解方法, 不需要如动态二次区域分解算法一样花费大量的时间进行接触面的动态重构和分解, 通信关系比较简单.
3 数值算例 3.1 平板推平板算例——DMCS算法并行效率的测试设一个问题在串行计算时耗费的时间为Tl, 在n个处理器并行计算时耗费的时间为Tn.为了说明算法的并行效率, 假定问题的计算规模与处理器的数目等比例地增长, 即保持在每个处理器上的网格数为常数, 那么我们定义并行效率为
| $ E = \frac{{{T_l}}}{{{T_n}}} $ |
采用图 2所示的平板推平板的算例, 不断地增加计算的网格数和进程数, 如表 1所示, 来测试并行的效率. 图 10显示随着计算规模的扩大, 能够保持并行的效率, 此并行方法有较好的扩展性.
| 下载CSV 表 1 并行效率的测试, 处理器数与单元数的变化 Tab.1 Number of the processors and elements in the scalability test |
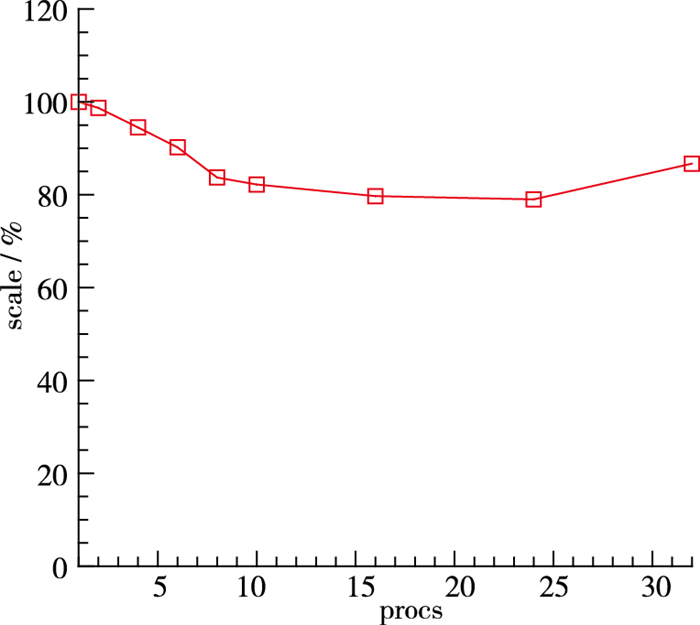
|
| 图 10 DMCS算法的并行效率 Fig.10 Parallel efficiency of the DMCS algorithm |
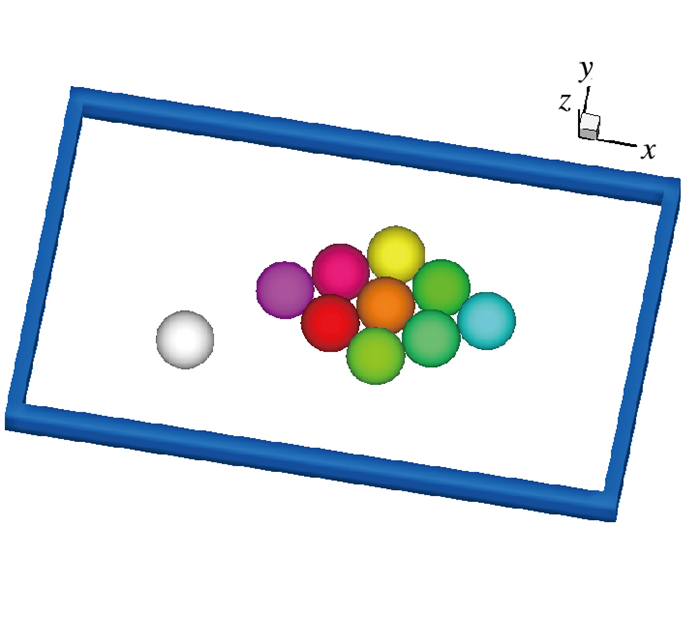
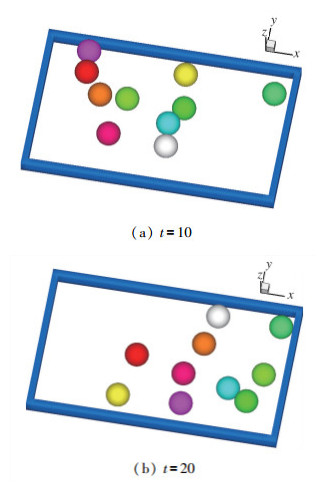
此算例模拟美式桌球碰撞的过程, 如图 11在台球桌内, 摆放有9个彩球, 在彩球的左下方, 一个白色的母球以(5.0, 1.0, 0)的速度击打彩球.算例中有10个球和一个桌边框, 一共存在55对接触面, 计算中采用了DWCS接触并行算法, 使用55个处理器进行并行计算.算例中速度、时间等物理量都经过无量纲化处理. 图 12显示了在t=10时刻和t=20时刻, 各个球运动的状态.结果显示分配完整接触面的并行方法(DWCS)能够正确地将每一对接触面分配到一个进程上, 进行并行计算.
|
| 图 11 九球桌球算例示意图 Fig.11 Sketch of the nine ball billiards |
|
| 图 12 t=10和t=20时刻各球运动的状态 Fig.12 Movements of the balls at t=10 and t=20 |
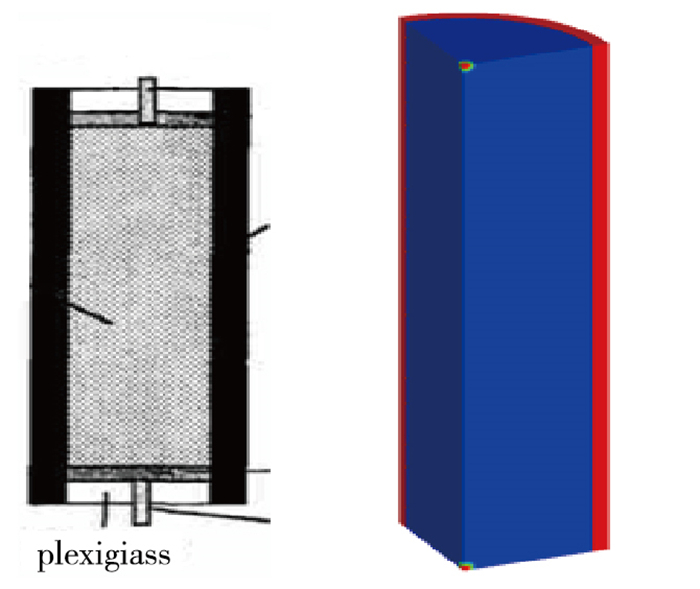
如图 13所示, HR2钢柱壳内填充高能炸药, 两端面中心起爆.采用DMCS并行算法, 使用36个处理器, 采用了网格尺度分别为0.25, 0.4, 0.5 mm的3种网格进行计算.
|
| 图 13 炸药圆筒实验算例示意图 Fig.13 Sketch of the metallic tube expansion induced by inside head on hitting two detonation waves |
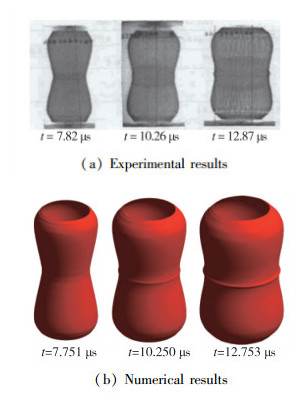
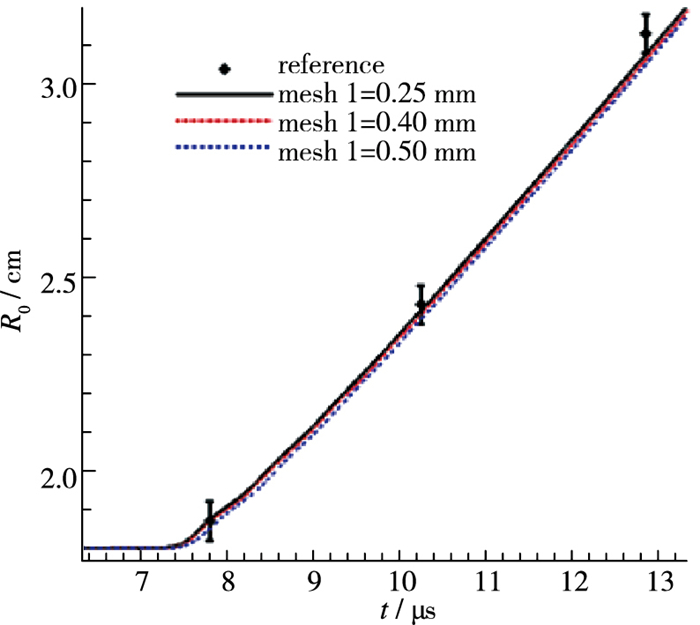
图 14和图 15显示了实验结果与数值模拟结果的对比, 图 14(a)为实验的x光照相, 图 14(b)为数值计算得到的圆筒外形图, 图 15为中间爆轰波对碰区圆筒半径随时间变化的实验结果与数值计算结果的比较.结果显示CHAP3D程序能够很好地模拟炸药圆筒实验, 计算结果与实验结果符合非常好.分配主面的接触并行算法能够正确、高效地并行计算接触问题.
|
| 图 14 炸药圆筒实验结果与数值结果的比较 Fig.14 Comparisons of the numerical results and the experimental results |
|
| 图 15 炸药圆筒中间半径的实验结果与数值结果的比较 Fig.15 Comparisons of the numerical results and the experimental results of the middle radius |
在CHAP3D程序中, 设计了分配完整接触面(DWCS)和分配主面(DMCS)的两种接触并行计算方法. DWCS方法简单, 串行接触算法不须修改即可用于并行计算. DMCS算法是一个负载平衡的算法, 具有很好的可扩展性, 随着接触面规模的扩大能够保持并行的效率.算例结果显示DWCS算法适用于存在有大量接触面的问题, 而DMCS算法能够应对不同类型的大规模接触问题的数值模拟.
| [1] |
Caramana E J, Rousculp C L, Burton D E. A compati-ble, energy and symmetry preserving Lagrangian hydrodynamics algorithm in three-dimensional Cartesian geometry[J]. Journal of Computational Physics, 2000, 157(1): 89-119. |
| [2] |
张树道, 熊俊, 周海兵, 等.拉氏计算方法研究和应用数值模拟软件研制[C].第八届全国爆炸力学学术会议论文集.井冈山: 中国力学学会爆炸力学专业委员会, 2007. Zhang S D, Xiong J, Zhou H B, et al. The study of the Lagrangian numerical algorithm and the development of the numerical application software[C]. The 8th National Conference on Explosion Mechanics, Jinggang Mountain, Jiangxi, 2007(in Chinese). |
| [3] |
Bauer A L, Burton D E, Caramana E J, et al. The internal consistency, stability, and accuracy of the discrete, compatible formulation of Lagrangian hydrodynamics[J]. Journal of Computational Physics, 2006, 218(2): 572-593. |
| [4] |
Barlow A J. A compatible finite element multi-material ALE hydrodynamics algorithm[J]. International Journal for Numerical Methods in Fluids, 2008, 56(8): 953-964. DOI:10.1002/(ISSN)1097-0363 |
| [5] |
Chang C H, Stagg A K. A compatible Lagrangian hydrodynamic scheme for multicomponent flows with mixing[J]. Journal of Computational Physics, 2012, 231(11): 4279-4294. DOI:10.1016/j.jcp.2012.02.005 |
| [6] |
Owen J M, Shashkov M. Arbitrary Lagrangian Eulerian remap treatments consistent with staggered compatible total energy conserving Lagrangian methods[J]. Journal of Computational Physics, 2014, 273: 520-547. DOI:10.1016/j.jcp.2014.05.023 |
| [7] |
Kucharik M, Scovazzi G, Shashkov M, et al. A multi-scale residual-based anti-hourglass control for compatible staggered Lagrangian hydrodynamics[J]. Journal of Computational Physics, 2018, 354: 1-25. DOI:10.1016/j.jcp.2017.10.050 |
| [8] |
Har J, Fulton R E. A parallel finite element procedure for contact-impact problems[J]. Engineering with Computers, 2003, 19(2/3): 67-84. |
| [9] |
Tezuka A, Matsumoto J, Suzuki T, et al. A platform for parallel CFD FEM computations[J]. International Journal of Computational Fluid Dynamics, 2005, 19(3): 235-242. DOI:10.1080/10618560410001683127 |
| [10] |
Kosturski N, Margenov S, Vutov Y. Balancing the communications and computations in parallel FEM simula-tions on unstructured grids[C]. Proceedings of the 9th International Conference on Parallel Processing and Applied Mathematics. Torun, Springer, 2012: 211-220.
|
| [11] |
Pikle N K, Sathe S R, Vyavhare A Y. GPGPU-based parallel computing applied in the FEM using the conju-gate gradient algorithm:a review[J]. Sādhanā, 2018, 43(7): 111. DOI:10.1007/s12046-018-0892-0 |
| [12] |
莫则尧, 袁国兴. 消息传递并行编程环境MPI[M]. 北京: 科学出版社, 2001. Mo Z Y, Yuan G X. MPI:message passing parallel programming environment[M]. Beijing: Science Press, 2001. (in Chinese) |
| [13] |
Mishra B S, Dehuri S. Parallel computing environments:a review[J]. IETE Technical Review, 2011, 28(3): 240-247. DOI:10.4103/0256-4602.81245 |
| [14] |
Gao W J, Kemao Q. Parallel computing in experimental mechanics and optical measurement:a review[J]. Optics and Lasers in Engineering, 2012, 50(4): 608-617. DOI:10.1016/j.optlaseng.2011.06.020 |
| [15] |
Wang T Y, Qian K M. Parallel computing in experimen-tal mechanics and optical measurement:a review (Ⅱ)[J]. Optics and Lasers in Engineering, 2018, 104: 181-191. DOI:10.1016/j.optlaseng.2017.06.002 |
| [16] |
Karypis G. METIS: a software package for partitioning unstructured graphs, partitioning meshes, and computing fill-reducing orderings of sparse matrices[EB/OL]. Version 5.1.0, University of Minnesota, Department of Computer Science. (2013-03-30). https://www.lrz.de/services/software/mathematik/metis/metis_5_0.pdf.
|
| [17] |
Hallquist J O. LS-DYNA theoretical manual R: 9320[EB/OL]. Livermore Software Technology Corporation, Livermore. http://ftp.lstc.com/anonymous/outgoing/jday/manuals/.
|
| [18] |
Malone J G, Johnson N L. A parallel finite element contact/impact algorithm for non-linear explicit transient analysis:part Ⅰ-the search algorithm and contact mecha-nics[J]. International Journal for Numerical Methods in Engineer, 1994, 37(4): 559-590. DOI:10.1002/(ISSN)1097-0207 |
| [19] |
Malone J G, Johnson N L. A parallel finite element contact/impact algorithm for non-linear explicit transient analysis:part Ⅱ-parallel implementation[J]. Interna-tional Journal for Numerical Methods in Engineer, 1994, 37(4): 591-603. DOI:10.1002/(ISSN)1097-0207 |
| [20] |
Xu Z, Accorsi M, Leonard J. Parallel contact algorithms for nonlinear implicit transient analysis[J]. Computa-tional Mechanics, 2004, 34(4): 247-255. |
| [21] |
Dureisseix D, Farhat C. A numerically scalable domain decomposition method for the solution of frictionless contact problems[J]. International Journal for Numerical Methods in Engineer, 2001, 50(12): 2643-2666. DOI:10.1002/(ISSN)1097-0207 |
| [22] |
Avery P, Rebel G, Lesoinne M, et al. A numerically scalable dual-primal substructuring method for the solution of contact problems-part Ⅰ:the frictionless case[J]. Computer methods in Applied Mechanics and Engineering, 2004, 193(23/26): 2403-2426. |
| [23] |
Avery P, Farhat C. The FETI family of domain decomposition methods for inequality-constrained quadratic programming:application to contact problems with confor-ming and nonconforming interfaces[J]. Computer Metho-ds in Applied Mechanics and Engineering, 2009, 198(21/26): 1673-1683. |
| [24] |
Kozubek T, Vondrak V, Menšík M, et al. Total FETI domain decomposition method and its massively parallel implementation[J]. Advances in Engineering Software, 2013, 60-61: 14-22. DOI:10.1016/j.advengsoft.2013.04.001 |
| [25] |
Benson D J, Hallquist J O. A single surface contact algorithm for the post-buckling analysis of shell struc-tures[J]. Computer Methods in Applied Mechanics and Engineering, 1990, 78(2): 141-163. |
| [26] |
Attaway S W, Hendrickson B A, Plimpton S J, et al. A parallel contact detection algorithm for transient solid dynamics simulations using PRONTO3D[J]. Computational Mechanics, 1998, 22(2): 143-159. |
| [27] |
Pierce T, Rodrigue G. A parallel two-sided contact algorithm in ALE3D[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(27/29): 3127-3146. |
| [28] |
Wang F J, Feng Y T, Owen D R. Parallelisation for finite-discrete element analysis in a distributed-memory environment[J]. International Journal of Computational Engineering Science, 2004, 5(1): 1-23. |
| [29] |
Zheng J W, An X H, Huang M S. GPU-based parallel algorithm for particle contact detection and its application in self-compacting concrete flow simulations[J]. Com-puters & Structures, 2012, 112-113: 193-204. |
| [30] |
Melanz D, Fang L N, Jayakumar P, et al. A comparison of numerical methods for solving multibody dynamics problems with frictional contact modeled via differential variational inequalities[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 320: 668-693. DOI:10.1016/j.cma.2017.03.010 |
| [31] |
Cai Y, Cui X Y, Li G Y, et al. A parallel finite element procedure for contact-impact problems using edge-based smooth triangular element and GPU[J]. Computer Physics Communications, 2018, 225: 47-58. DOI:10.1016/j.cpc.2017.12.006 |
| [32] |
姜玉曦, 周海兵, 张树道. 基于三角剖分局部搜索的三维滑移面算法[J]. 北京理工大学学报, 2010, 30(4): 501-504. Jiang Y X, Zhou H B, Zhang S D. Three-dimensional contact algorithm for sliding surface based on triangular subdivision local search[J]. Transactions of Beijing Institute of Technology, 2010, 30(4): 501-504. (in Chinese) |
| [33] |
姜玉曦, 周海兵, 熊俊, 等. 基于双三次曲面片的三维接触面光滑方法[J]. 工程力学, 2016, 33(2): 11-17. Jiang Y X, Zhou H B, Xiong J, et al. A 3D contact smoothing method based on Bi-cubic parametric pat-ches[J]. Engineering Mechanics, 2016, 33(2): 11-17. (in Chinese) |
| [34] |
Wriggers P. Computational contact mechanics[M]. Ber-lin: Springer, 2006.
|
| [35] |
姜玉曦, 周海兵, 熊俊, 等. 三维光滑接触界面上的分配参数滑移面算法[J]. 计算物理, 2015, 32(4): 386-394. Jiang Y X, Zhou H B, Xiong J, et al. A distributed parameter contact algorithm for sliding surfaces on a three-dimensional smoothed contact surface[J]. Chinese Journal of Computational Physics, 2015, 32(4): 386-394. DOI:10.3969/j.issn.1001-246X.2015.04.002 (in Chinese) |
| [36] |
Dawes A S. A three-dimensional contact algorithm for sliding surfaces[J]. International Journal for Numerical Methods in Fluids, 2003, 42(11): 1189-1210. DOI:10.1002/(ISSN)1097-0363 |
| [37] |
张世文, 华劲松, 刘仓理, 等. 金属圆管内爆轰波相互作用效应的数值模拟研究[J]. 爆炸与冲击, 2004, 24(3): 219-225. Zhang S W, Hua J S, Liu C L, et al. A numerical simulation of the metallic tube expansion induced by inside head-on hitting two detonation waves[J]. Explosion and Shock Waves, 2004, 24(3): 219-225. DOI:10.3321/j.issn:1001-1455.2004.03.005 (in Chinese) |



