2. 中国航天空气动力技术研究院,北京 100074
2. China Academy of Aerospace Aerodynamics, Beijing 100074, China
对于可压缩湍流, Euler方程和Navier-Stokes方程的离散格式能否既可捕捉激波又可分辨小尺度波状解是一个长期存在的问题, 具有广泛的应用背景[1-2]. Adams等[3]提出了一个高分辨率激波捕捉格式与类谱紧致有限差分方法的耦合形式.不同于它们的原有形式[4], 通过耦合, 由这些紧致格式的一种迎风组合引入一些适量耗散是必要的.后来, Pirozzoli[5]指出, 适度的耗散能够抑制以不正确的速度传播的高波数波.问题的难点在于确定耗散的大小, 使之足以消除伪高波数波, 又不影响物理上相关的可分辨波数范围.
已经确知的事实是, 有限差分格式的色散误差最大值位于Nyquist截断波数附近, 以致临界分辨的波可传播通过计算域并引起非线性不稳定性或非物理解[6].以Sun等[7]的工作为例, 近些年的相关研究主要集中于控制耗散的必需量, 迄今尚未按照量化准则建立色散和耗散之间的联系.自从Tam等[8]在气动声学上的开创性研究以来, 谱分析[6]已被广泛地引入高阶数值格式构造, 这对于湍流数值模拟更为重要, 必须精确分辨小尺度振幅及相位[9-13].有限差分格式谱分析表明, 数值色散和数值耗散的误差与简单波的传播有关.不同于常规谱分析易于在线性格式上的应用, Pirozzoli[14]针对激波捕捉格式等非线性有限差分格式发展了一种广义谱分析.此外, Sun等[7]认为可在一定程度上分别控制显式线性格式的色散和耗散.
本文旨在揭示数值格式的适度耗散可由色散-耗散条件确定.作为演示验证, 将色散-耗散条件用于减弱以往发展的加权基本无振荡格式WENO-CU6-M2[15]所造成的伪波, 通过数值算例给出该格式的两种直接改进并加以对比确认.
1 色散-耗散条件色散-耗散条件的基本概念可从一维线性对流方程发展而来:
| $ \frac{{\partial u}}{{\partial t}} + c\frac{{\partial u}}{{\partial x}} = 0, \;\;\;\; - \infty < x < + \infty $ | (1) |
初始条件设作单个正弦波u(x, t=0)=eiξx.其中, ξ为波数, c为对流速度, 振幅为单位1[6].方程(1)在空间区域离散为xj=jh, j=1, …, N, 这里h为等分布网格间距.相应地, 网格点上的函数为uj=u(xj).方程(1)的线性半离散形式是一个常微分方程组:
| $ \frac{{\partial {u_j}}}{{\partial t}} = - cu{\prime _j}, \;\;j = 0, \cdots , N, \;\;\;{u_j}\left( {t = 0} \right) = {{\rm{e}}^{{\rm{i}}j\xi h}} $ | (2) |
式中, u'j为xj网格点上的1阶空间导数的有限差分近似:
| $ u{'_j} = \frac{1}{h}\mathop \sum \limits_{l = - q}^r {a_l}{u_{j + l}} $ | (3) |
这里al为满足适当的相容条件的格式系数.采用式(3)的线性格式, 得方程(2)的解析解
| $ {u_j}\left( t \right) = {{\rm{e}}^{{{\tilde \xi }_{\rm{I}}}ct}}{{\rm{e}}^{{\rm{i}}\xi (jh - ct{{\tilde \xi }_{\rm{R}}}/\xi )}} $ | (4) |
式中的修正波数
| $ \begin{array}{l} \tilde \xi \left( \xi \right) = {{\tilde \xi }_{\rm{R}}} + i{{\tilde \xi }_{\rm{I}}} = - \frac{{\rm{i}}}{h}\mathop \sum \limits_{l = - q}^r {a_l}{{\rm{e}}^{{\rm{i}}l\xi h}}\\ \;\;\;\;\;\;\;\; = \frac{1}{h}\mathop \sum \limits_{l = - q}^r {a_l}\left[ {\sin \left( {l\xi h} \right) - {\rm{i}}\cos \left( {l\xi h} \right)} \right] \end{array} $ | (5) |
在xj点将式(4)与方程(1)的精确解对比:
| $ u({x_j}, t) = {{\rm{e}}^{{\rm{i}}\xi (jh - ct)}} $ |
不难看出, 有限差分近似式(3)引入了两类数值误差.数值色散
| $ \nu = \frac{{{\rm{d}}(\xi {c^*}\left( \xi \right))}}{{{\rm{d}}\xi }} = c\frac{{{\rm{d}}{{\tilde \xi }_{\rm{R}}}}}{{{\rm{d}}\xi }} $ |
当波包以不同于精确相速度传输时, 即误差|Δc|=|ν-c|, 就可产生虚假行为.本文提出的色散-耗散条件的核心假设是, 要求伪波的对流特征时间尺度rh/|Δc|与特征衰减时间尺度同量阶:
| $ r\frac{h}{{|\Delta c|}}\sim\frac{1}{\lambda } $ | (6) |
其中, 参数r≥0.该条件意味着, 伪波偏离精确对流波而行进的特征距离是参数r和网格间距h之积的量阶.在该条件下, 由式(6)得
| $ 0 \le \frac{{\left| {\frac{{{\rm{d}}{{\tilde \xi }_{\rm{R}}}}}{{{\rm{d}}\xi }} - 1} \right|}}{{ - {{\tilde \xi }_{\rm{I}}}}} = r $ | (7) |
此即为色散-耗散条件的最终表达式.若离散格式使r偏大, 则伪波可能会污染数值解.这些伪波偏离精确的对流波, 行进相当长距离.另一方面, 若r偏小, 则数值解可能会避免伪波, 但耗散误差将超过所必需的而影响可分辨尺度.由r确定的最优化条件保证了伪波成分的色散和耗散之间的合理平衡.
虽然上述色散-耗散条件出自空间导数的线性有限差分格式及标量对流方程, 但是下节将显示它用于更一般的非线性格式和更复杂的流动问题的可行性.
2 应用借助式(7), 可评估一个给定的有限差分格式是否倾向于产生伪波.另外, 可调控线性格式的系数, 使之满足色散-耗散条件.
2.1 线性格式对于式(3)中的显式线性格式, 条件式(7)给出
| $ r = \frac{{\left| {\mathop \sum \limits_{l = - q}^r {a_l}l\cos \left( {l\xi h} \right) - 1} \right| + \varepsilon }}{{\mathop \sum \limits_{l = - q}^r {a_l}\cos \left( {l\xi h} \right) + \varepsilon }} $ | (8) |
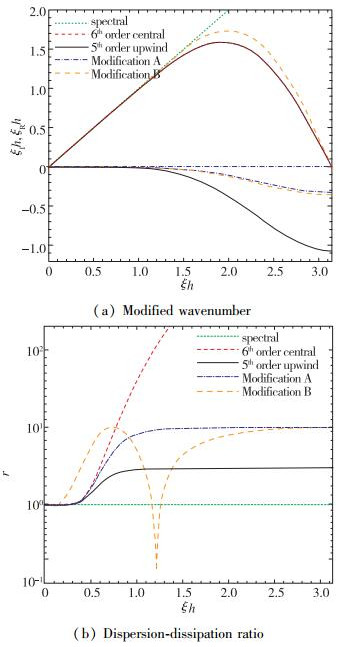
这里ε=10-3以免除数为0. 图 1以修正波数
|
| 图 1 不同线性格式的近似色散关系 Fig.1 Approximate dispersion relations of several linear schemes |
|
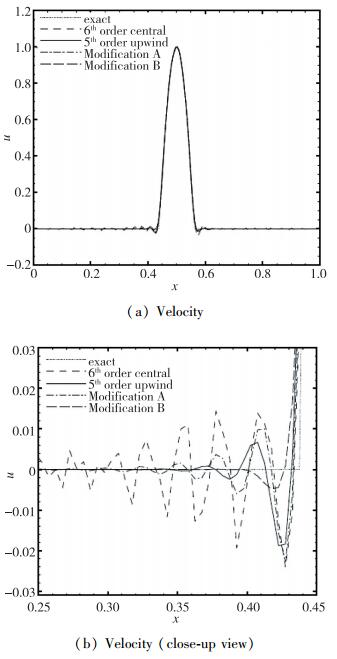
| 图 2 正弦波段对流数值解 Fig.2 Numerical solution of advection of a segment of a sine wave |
给定一个格式的基模, 为了消除伪波, 或者保持色散不变而增加耗散(改进A), 或者同时改进色散和耗散以便满足式(7)的色散-耗散关系式.对于7点基模, 按照式(8)在ξh=π处设置约束r=10, 以此保持色散不变而增加耗散, 则可形成一个5阶线性格式.改进A最终的系数为al= {-13/600, 9/50, -33/40, 1/10, 27/40, -3/25, 7/600}, 如图 1所示, 该改进不改变色散, 但在整个波数范围达到r≤10.对于改进B, 考虑一个4阶格式作为基本格式.为了改善它的色散, 令ξc=1.5/h为临界波数, 在约束|c*-c|≤ 0.015下, 对所有ξ < ξc求解最小化问题:
| $ \min \smallint _0^{\xi h}{{\rm{e}}^{6({\rm{ \mathsf{ π} }} - \varphi )}}|{c^*} - c{|^2}{\rm{d}}\left( {\xi h} \right) $ |
参照文献[7], 它的耗散另行在ξh=π处设置r=10加以限定.改进B最终的系数为al= {-0.032 803, 0.225 61, -0.885 98, 0.110 61, 0.720 07, -0.159 24, 0.021 742}, 如图 1所示, 该改进关于色散获得相当大的改善并在整个波数范围满足r≤10.通过以上改进, 可在较短的距离内从主波面中消除原始的7点6阶中心格式的伪波, 见图 2.
2.2 非线性格式对于非线性格式, 修正波数式(5)可由Pirozzoli[14]提出的近似色散关系式(approximate dispersion relation, ADR)数值估计. ADR仍然满足式(7)定义的色散-耗散条件.作为示例, 考虑WENO-CU6-M2格式[15], 它是一种在光滑流动区为6阶精度的自适应中心-迎风WENO格式.经由非线性自适应加权处理, 该格式在光滑流动区恢复为6阶中心格式, 而在光滑因子检测到的间断处恢复为3阶迎风近似.非线性权为
| $ {\omega _r} = \frac{{{\alpha _r}}}{{\mathop \sum \limits_{r = 0}^3 {\alpha _r}}}, \;\;{\alpha _r} = {d_r}{\left( {{C_q} + \frac{{{\tau _6}}}{{{\beta _{3, r}} + \varepsilon \Delta {x^2}}}\frac{{{\beta _{3, {\rm{ave}}}} + \chi \Delta {x^2}}}{{{\beta _{3, r}} + \chi \Delta {x^2}}}} \right)^q} $ |
其中, 最优化权dr={0.05, 0.45, 0.45, 0.05}, 是一种6阶线性中心格式; 整数q=4, 正常数Cq=103, 且ε=1/χ=10-8.关于WENO方法以及计算β3, r, β3, ave, τ6的细节, 可参见文献[15, 17].
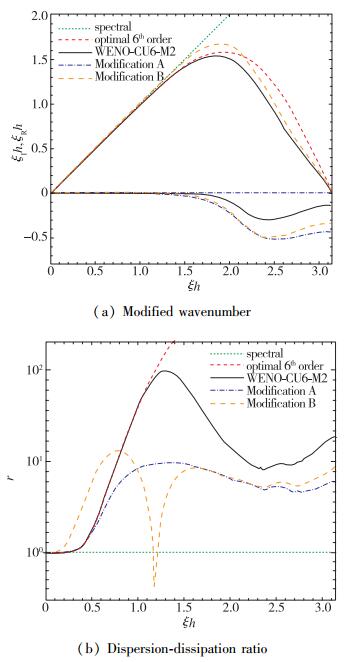
图 3以修正波数
|
| 图 3 不同数值格式的近似色散关系 Fig.3 Approximate dispersion relations of various numerical schemes |
类似于线性格式, WENO-CU6-M2格式可通过改变作为基本优化线性中心格式的色散-耗散特性加以改进.取代6阶线性中心格式, 可按照式(8)在ξh=1.302处设置约束r=10, 构造一个5阶线性格式.改进A最终的最优化权为dr={0.065, 0.495, 0.405, 0.035}, 如图 3所示, 该改进不改变色散, 但在整个波数范围达到r≤10.另一种选择是, 在ξh=π/2处限定r=10对一个4阶线性格式进行约束, 得到WENO-CU6-M2格式的色散-耗散最优化权, 即为改进B.它最终的最优化权为dr= {0.090 45, 0.444 1, 0.392 27, 0.073 18}, 如图 3所示, 该改进获得相当大的色散改善, 并在整个波数范围满足r≤10.
2.3 改进WENO-CU6-M2格式验证现给出两个简单的算例显示WENO-CU6-M2格式会产生伪波, 并且可用上述建议的改进方法减小.一个算例是Sod激波管问题, 另一个算例是Colella等[18]采取的双冲击波干扰问题, 两个问题的参照解选自文献[17]由WENO-5格式在3 200个网格点上得到的高分辨率解.所有计算的CFL(Couran-Friedrichs-Lewy)数均为0.6.
Sod激波管问题的初始条件为
| $ \left( {\rho , u, p} \right) = \left\{ \begin{array}{l} \left( {1, 0.75, 1} \right)\;\;\;\;\;\;\;\;\;\;\;0 < x \le 0.3\\ \left( {0.125, 0, 0.1} \right)\;\;\;\;\;0.3 < x < 1.0 \end{array} \right. $ |
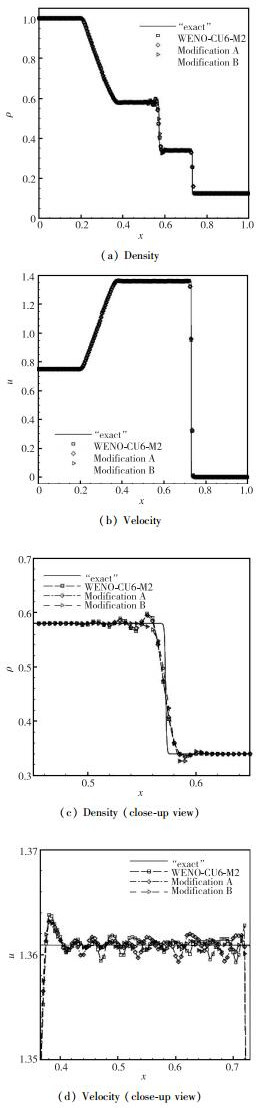
原始WENO-CU6-M2格式及其改进A和改进B的结果以局部Lax-Friedrichs通量在200个网格点上解得, 图 4是t = 0.2时刻的密度和速度曲线及局部放大.原始WENO-CU6-M2格式具有良好的激波捕捉特性(图 4(a)), 但也在x≈0.57的接触间断处产生了微小的振荡(图 4(c)).然而, 其改进格式抑制了这些振荡, 表现为给出的接触间断如原始格式一样锐利. 图 4(b)和图 4(d)的速度曲线也显示了改进A和改进B减小了伪振荡.
|
| 图 4 Sod激波管问题数值解(t = 0.2) Fig.4 Numerical solution of Sod's shock-tube problem at t = 0.2 |
双冲击波干扰问题的初始条件为
| $ \left( {\rho , u, p} \right) = \left\{ \begin{array}{l} \left( {1, 0, 1000} \right)\;\;\;\;0 < x \le 0.1\\ \left( {1, 0, 0.01} \right)\;\;\;\;0.1 < x \le 0.9\\ \left( {1, 0, 100} \right)\;\;\;\;\;0.9 < x < 1.0 \end{array} \right. $ |
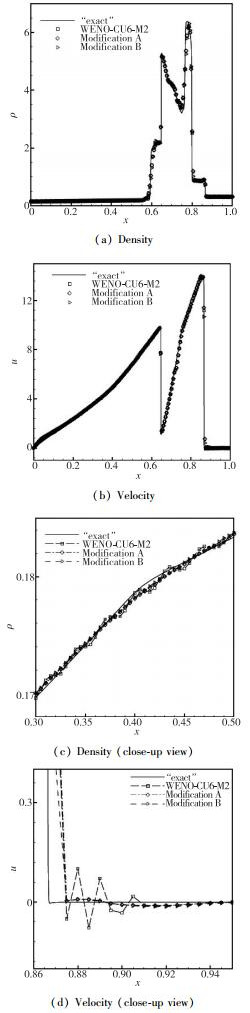
图 5是原始WENO-CU6-M2格式及其改进A和改进B在400个网格点上计算得到的t = 0.038时刻的密度和速度曲线及局部放大.它们在图 5(a)和图 5(b)中初看起来没有差别, 但在图 5(c)和图 5(d)的局部放大图中可观察到, 原始WENO-CU6-M2格式的密度曲线和x≈0.865附近的激波出现了微小的伪波, 而两种改进格式消除了这些伪波.
|
| 图 5 双冲击波干扰问题数值解(t=0.038) Fig.5 Numerical solution of two-blast-wave interaction problem at t=0.038 |
最后, 考虑三维无黏和黏性Taylor-Green涡(Taylor-Green vortex, TGV)问题, 考查改进格式预测转捩到湍流的能力.为此, 改进B选作基本线性格式, 它包含原始WENO-CU6-M2格式参数q, C, 令q=2, C=103. TGV问题的初始条件为
| $ \begin{array}{*{20}{c}} {\rho = 1}\\ {\left( \begin{array}{l} u\\ v\\ w \end{array} \right) = \left( {\begin{array}{*{20}{c}} 0\\ {\rho \cos \left( x \right)\sin \left( y \right)\cos \left( z \right)}\\ {\rho \cos \left( x \right)\cos \left( y \right)\sin \left( z \right)} \end{array}} \right)}\\ {p = \frac{1}{{\gamma M{a^2}}} + \frac{\rho }{{16}}\left[ {\cos \left( {2x} \right) + 2} \right]\left[ {\cos \left( {2y} \right) + \cos \left( {2z} \right) - 2} \right]} \end{array} $ |
其中, γ=1.4, Ma=0.1.计算域取作边长为2π的立方体, 共643个网格点.另外, 在x, y, z三个方向均设周期边界条件.
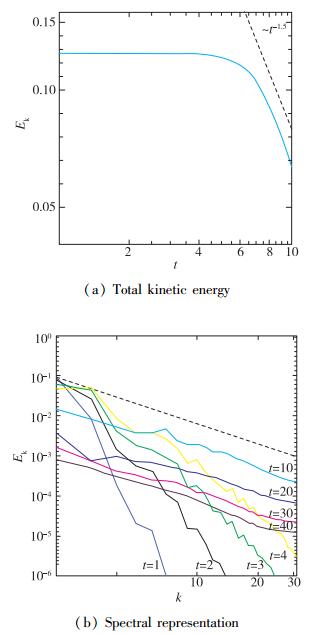
对于无黏情形, 图 6是动能随时间演化的曲线(t≤10)及其不同时刻的谱空间分布(t≤40).在t≈4时刻, 亚网格尺度出现并以其耗散使得动能衰减.改进格式的动能衰减近似以t-1.5幂率, 这类似于原始WENO-CU6-M2格式的动能衰减幂率[15], 仅比Lesieur等[19]发现的值t-1.5略陡, 如图 6(a)中虚线所示. Grinstein等[20]的高分辨率隐式大涡模拟(large eddy simulation, LES)也给出了相似的动能衰减趋势.在t=4和t=10时刻之间, 湍流发展; 在t=10时刻, 充分发展的k-5/3幂率Kolmogorov惯性区已建立, 如图 6(b)中虚线所示.值得注意的是, 数值耗散没有影响计算域内的物理可分辨尺度, Kolmogorov惯性区维持至截断波数.在随后的t=20, 30, 40时刻, 可观察到动能谱的自相似衰减, Kolmogorov谱依然没有受数值格式的明显影响, 继续维持.
|
| 图 6 三维无黏Taylor-Green涡问题动能时间演化及瞬时分布 Fig.6 Temporal evolution and instantaneous distributions of kinetic energy of three-dimensional inviscid Taylor-Green vortex problem |
对于黏性情形, 计算域及网格点不变, 取Re=400, 800, 1 600, 3 000, 这是一组低分辨率数值模拟.将原始WENO-CU6-M2格式的改进B的结果与已有LES模型对比, 如动态Smagorinsky模型和Hickel等[21]的自适应局部反卷积模型(adaptive local deconvolution model, ALDM), 且Brachet等[22]的直接数值模拟(direct numerical simulation, DNS)数据用作参照解.
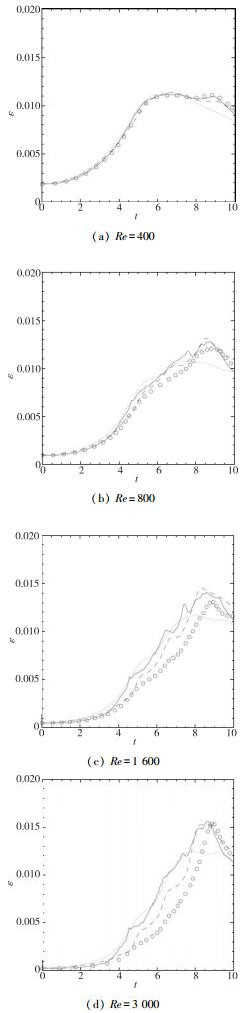
图 7是不同Reynolds数的比耗散率ε(t)=dE/dt随时间演化的曲线, 实线表示改进B解, 点线表示动态Smagorinsky模型解, 虚线表示ALDM解, 而参照解由空心圆符号表示.由图可知, 本文结果与经典动态Smagorinsky模型解相比得到明显改善; 与ALDM解相比, 在较小Reynolds数Re=400, 800条件下给出了相当好的结果, 并且两种方法都复现了Brachet等[22]的比耗散率.在较高Reynolds数Re=1 600, 3 000条件下, 本文结果初期与Brachet等[22]十分吻合, 随后从中期开始趋于高估.不管怎样, 本文结果的峰值与ALDM解非常一致.
|
| 图 7 三维黏性Taylor-Green涡问题不同Reynolds数的比耗散率 Fig.7 Specific dissipation rates of three-dimensional viscous Taylor-Green vortex problem at different Reynolds number |
本文导出了一个色散-耗散条件, 用以确定一个有限差分格式抑制数值解中伪高波数波的最小数值耗散.借助近似色散关系式, 它还可用于非线性格式.线性格式和WENO-CU6-M2格式的算例表明, 该条件可选作更一般网格点上的线性或非线性格式的色散和耗散优化的指导准则.进一步的计算显示, 改进WENO-CU6-M2格式可用来进行简单湍流的低分辨率数值模拟, 较为精确地预测了三维无黏Taylor-Green涡的自相似能量衰减.与三维黏性Taylor-Green涡的DNS数据对比证明, 改进格式的结果明显改善了经典的动态Smagorinsky模型解.
| [1] |
卢炳举, 罗松, 朱珠, 等. 高速射弹入水空泡多相流场数值模拟[J]. 兵器装备工程学报, 2017, 38(12): 242-246. Lu B J, Luo S, Zhu Z, et al. Numerical simulation of multiphase flow field of high velocity projectile entering water[J]. Journal of Ordnance Equipment Engineering, 2017, 38(12): 242-246. DOI:10.11809/scbgxb2017.12.053 (in Chinese) |
| [2] |
程华, 钟华生, 周凌, 等. 脉动风速时程数值模拟[J]. 兵器装备工程学报, 2016, 37(4): 143-148. Cheng H, Zhong H S, Zhou L, et al. Numerical simulation of fluctuating wind velocity time series[J]. Journal of Ordnance Equipment Engineering, 2016, 37(4): 143-148. DOI:10.11809/scbgxb2016.04.035 (in Chinese) |
| [3] |
Adams N A, Shariff K. A high-resolution hybrid compact-ENO scheme for shock-turbulence interaction problems[J]. Journal of Computational Physics, 1996, 127(1): 27-51. |
| [4] |
Lele S K. Compact finite difference schemes with spectral-like resolution[J]. Journal of Computational Physics, 1992, 103(1): 16-42. |
| [5] |
Pirozzoli S. Conservative hybrid compact-WENO schemes for shock-turbulence interaction[J]. Journal of Computational Physics, 2002, 178(1): 81-117. |
| [6] |
Vichnevetsky R, Bowles J B. Fourier analysis of numerical approximations of hyperbolic equations. Studies in applied and numerical mathematics[M]. Philadelphia, PA: Society for Industrial and Applied Mathema-tics, 1982.
|
| [7] |
Sun Z S, Ren Y X, Larricq C, et al. A class of finite difference schemes with low dispersion and controllable dissipation for DNS of compressible turbulence[J]. Journal of Computational Physics, 2011, 230(12): 4616-4635. DOI:10.1016/j.jcp.2011.02.038 |
| [8] |
Tam C K, Webb J C. Dispersion-relation-preserving finite difference schemes for computational acoustics[J]. Journal of Computational Physics, 1993, 107(2): 262-281. |
| [9] |
Weirs V G, Candler G V. Optimization of weighted ENO schemes for DNS of compressible turbulence[C]. Proceedings of 13th Computational Fluid Dynamics Conferen-ce, Fluid Dynamics and Co-located Conferences, Snow-mass Village, CO: AIAA, 1997.
|
| [10] |
Wang Z J, Chen R F. Optimized weighted essentially nonoscillatory schemes for linear waves with discontinuity[J]. Journal of Computational Physics, 2001, 174(1): 381-404. |
| [11] |
Ponziani D, Pirozzoli S, Grasso F. Development of optimized weighted-ENO schemes for multiscale compressible flows[J]. International Journal for Numerical Method in Fluid, 2003, 42(9): 953-977. DOI:10.1002/(ISSN)1097-0363 |
| [12] |
Jiang Z L. On dispersion-controlled principles for non-oscillatory shock-capturing schemes[J]. Acta Mechanica Sinica, 2004, 20(1): 1-15. DOI:10.1007/BF02493566 |
| [13] |
Martín M P, Taylor E M, Wu M, et al. A bandwidth-optimized WENO scheme for the effective direct numerical simulation of compressible turbulence[J]. Journal of Computational Physics, 2006, 220(1): 270-289. |
| [14] |
Pirozzoli S. On the spectral properties of shock-capturing schemes[J]. Journal of Computational Physics, 2006, 219(2): 489-497. |
| [15] |
Hu X Y, Adams N A. Scale separation for implicit large eddy simulation[J]. Journal of Computational Physics, 2011, 230(19): 7240-7249. DOI:10.1016/j.jcp.2011.05.023 |
| [16] |
Colonius T, Lele S K. Computational aeroacoustics:progress on nonlinear problems of sound generation[J]. Progress in Aerospace Sciences, 2004, 40(6): 345-416. DOI:10.1016/j.paerosci.2004.09.001 |
| [17] |
Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. |
| [18] |
Colella P, Woodward P R. The piecewise parabolic method (PPM) for gas-dynamical simulations[J]. Journal of Computational Physics, 1984, 54(1): 174-201. |
| [19] |
Lesieur M, Ossia S. 3D isotropic turbulence at very high Reynolds numbers:EDQNM study[J]. Journal of Turbulence, 2000, 1: N7. DOI:10.1088/1468-5248/1/1/007 |
| [20] |
Grinstein F F, Fureby C. Recent progress on flux-limiting based implicit large eddy simulation[C]. European Conference on Computational Fluid Dynamics, The Nether-land: ECCOMAS CFD, 2006.
|
| [21] |
Hickel S, Adams N A, Domaradzki J A. An adaptive local deconvolution method for implicit LES[J]. Journal of Computational Physics, 2006, 213(1): 413-436. |
| [22] |
Brachet M E, Meiron D, Orszag S, et al. The Taylor-Green vortex and fully developed turbulence[J]. Journal of Statistical Physics, 1984, 34(5/6): 1049-1063. |



