方柱绕流作为一种非常典型的钝体绕流流动, 在航空航天、能源、建筑等领域中广泛存在, 其结构形式简单, 却蕴含了丰富且复杂的流体力学现象, 长久以来一直备受研究者关注.随着实验及数值模拟技术的不断进步, 国内外学者围绕该问题开展了大量工作, 取得了许多进展.
Lyn等[1-2]用实验方法对Reynolds数为21 400的方柱绕流进行了较为细致的测量, 得到了柱体表面、两侧分离区、尾迹区的时均流场、Reynolds应力分布等, 该实验结果在后续的其他研究中作为对照被广泛引用.基于上述数据, Voke[3], Rodi等[4]陆续组织了两次研讨会, 采用大涡模拟方法对Reynolds数为21 400或22 000的方柱绕流进行计算, 分析对比不同研究小组的结果, 发现各小组的数据偏差较大, 没有一个让人完全满意, 计算域尺寸、网格分辨率及边界条件均对计算结果有很大影响, 而来流湍流度、数值格式的耗散等也可能是LES结果与实验数据相偏离的原因.尽管和RANS方法的对比表明LES结果更为可信[5-7], 但对这一较高Reynolds数钝体绕流问题的准确预测显然还面临着诸多挑战. Murakami等[8]和Sohankar等[9]分别评估了几种亚格子模型对Reynolds数22 000的方柱绕流LES结果的影响, 前者发现Lagrange型动力模型的结果与实验数据吻合最好, 后者则认为一方程动力模型最优; Grigoriadis等[10]采用浸没边界方法对同一问题进行大涡模拟, 发现足够的网格分辨率是提高预测精度的关键因素. Minguez等[11], Brun等[12]同时运用实验和LES方法对Reynolds数21 400的方柱绕流进行了更为深入的研究, 探讨了Karman涡街与自由剪切层K-H不稳定性的关系.考虑到过去一些算例存在着网格过于粗糙、计算周期过少及计算域不够大等问题, Trias等[13]采用直接数值模拟方法, 扩大计算域并提高网格分辨率, 增加统计时间, 对Reynolds数22 000的方柱绕流进行了更精细的模拟, 结果与已有数据吻合得很好.
国内研究者对该问题也开展了不少工作, 童兵等[14]对Reynolds数22 000的方柱进行了大涡模拟, 所得气动力和时均速度场与实验结果吻合较好; 邓小兵等[15]采用拟压缩方法结合双时间步求解不可压LES方程模拟同一流动, 通过与实验结果的对比验证了该计算方案的可行性.谢志刚等[16]采用有限体/有限元混合格式、非结构网格和LES方法对Reynolds数22 000的方柱绕流进行了计算, 所得结果都与实验数据符合得较好, 甚至优于前人的密网格结果.张海涛等[17]使用了开源CFD软件OpenFOAM的两种动力模型对Reynolds数22 000的方柱进行计算, 对比发现一方程动力模型的结果与实验数据吻合得更好.唐鹏等[18]运用两种RANS/LES混合方法在粗细两套网格上对同一方柱进行了计算, 发现DES方法的整体表现最优.
DNS方法虽然精确, 但需耗费大量的计算资源, 代价巨大, LES方法对该问题的预测结果还不能令人满意.本文使用自主发展的LES程序, 以远少于DNS的网格对来流Mach数M=0.3, Reynolds数ReD=22 000的孤立方柱绕流进行模拟, 通过与已有实验和DNS数据的比较, 进一步评估LES方法对此类流动的预测能力.
1 数值方法计算工作使用叶建[19-20]发展的大涡模拟程序MPLES, 该程序能够处理任意界面匹配的多块结构化网格, 通过计算域分解和消息传递接口(message passing interface, MPI)实现并行, 具有很高的计算效率. MPLES求解Favre滤波的无量纲化可压缩N-S方程组, 其具体形式如下
| $ \partial \bar{\rho }/\partial t+\partial \left( \bar{\rho }{{{\tilde{u}}}_{j}} \right)/\partial {{x}_{j}}=0 $ | (1) |
| $ \partial \left( \bar{\rho }{{{\tilde{u}}}_{j}} \right)/\partial t+\partial (\bar{\rho }{{{\tilde{u}}}_{i}}{{{\tilde{u}}}_{j}}+\bar{p}{{\delta }_{ij}})/\partial {{x}_{j}}=\partial ({{{\tilde{\sigma }}}_{ij}}-{{\tau }_{ij}})/\partial {{x}_{j}} $ | (2) |
| $ \begin{align} &\partial \left( \bar{\rho }\tilde{E} \right)/\partial t+\partial \left( \bar{\rho }\tilde{E}+\bar{p} \right){{{\tilde{u}}}_{j}}/\partial {{x}_{j}}= \\ &-\partial ({{{\tilde{q}}}_{j}}+{{Q}_{j}}/\left( \gamma - 1 \right)M_{0}^{2})/\partial {{x}_{j}}+\partial {{{\tilde{u}}}_{i}}({{{\tilde{\sigma }}}_{ij}}-{{\tau }_{ij}})/\partial {{x}_{j}} \\ \end{align} $ | (3) |
要封闭上述方程组, 必须对亚格子应力和亚格子热通量进行模化, MPLES采用如下形式的动力涡黏模型:
| $ {{\tau }_{ij}}-{{\delta }_{ij}}{{\tau }_{kk}}/3=-2C\bar{\rho }{{\Delta }^{2}}|\tilde{S}|({{{\tilde{S}}}_{ij}}-{{\delta }_{ij}}{{{\tilde{S}}}_{kk}}/3) $ | (4) |
| $ {{\tau }_{kk}}=2{{C}_{\text{I}}}\bar{\rho }{{\Delta }^{2}}|\tilde{S}{{|}^{2}} $ | (5) |
| $ {{Q}_{j}}=-C{{\Delta }^{2}}\bar{\rho }|\tilde{S}|(\partial \tilde{T}/\partial {{x}_{j}})/P{{r}_{\text{T}}} $ | (6) |
其中的系数CI, C和PrT通过公式动态计算
| $ {{C}_{\text{I}}}=\left\langle {{L}_{kk}} \right\rangle /\left\langle 2{{\Delta }^{2}}\left( \hat{\bar{\rho }}{{\alpha }^{2}}|\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\tilde{S}}{{|}^{2}}-\widehat{\bar{\rho }|\tilde{S}{{|}^{2}}} \right) \right\rangle $ | (7) |
| $ C=\langle ({{L}_{ij}}-{{\delta }_{ij}}{{L}_{kk}}/3){{M}_{ij}}\rangle /\langle {{M}_{kl}}{{M}_{kl}}\rangle $ | (8) |
| $ P{{r}_{\text{T}}}=C\langle {{T}_{k}}{{T}_{k}}\rangle /\langle {{K}_{j}}{{T}_{j}}\rangle $ | (9) |
上述各项的具体含义参见文献[19].将封闭的方程组(1)~(3) 写成积分形式, 采用网格中心的有限体积法离散.对流项使用4阶反对称型的中心格式[21], 黏性项使用2阶中心格式, 时间推进则是3阶3步的紧致Runge-Kutta方法.为消除因对流项中心型格式而在流场中出现的非物理振荡, 还使用11点的显式选择性滤波器对流场变量进行滤波处理[22], 相关细节见文献[20].
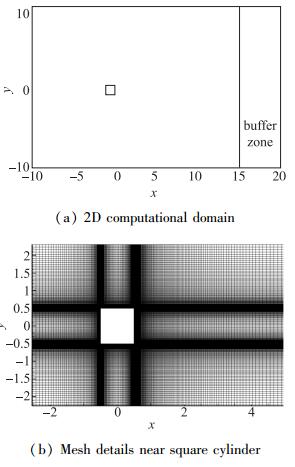
2 算例设计本文所用计算程序主要针对可压缩流动, 为了和实验及数值模拟结果对比, 计算的Reynolds数取22 000, Mach数取0.3.图 1给出了二维计算域及计算网格的示意图, 以方柱中心为坐标原点, x, y分别代表流向和横向, 二维计算域沿展向z拉伸得到三维计算域.以方柱的边长D为参考长度, 结合文献[3-4, 13], 计算域大小设定如下:入口位于x=-10处, 有效计算域出口位于x=15处, 其后有长度为5的缓冲区, 横向计算域高度为20, 展向宽度为π.
|
| 图 1 计算域及计算网格 Fig.1 Computational domain and grids |
计算域沿流向网格单元数为420(包含出口缓冲区的20个单元), 横向为330, 展向为80, 总的网格单元数为1.044×107.柱体附近的网格分布如图 1(b)所示, 壁面每条边长分布80个网格单元, 第1层网格的法向高度为0.003, 通过恰当布置网格点, 可以满足LES方法对网格分辨率的要求.
算例的边界条件设置如下:方柱表面为绝热无滑移壁面, 所有外边界均为远场, 采用特征边界条件处理, 展向则是周期性边界.计算依托国家超算广州中心的天河二号系统完成, 根据实际需要, 本算例使用了188个核心并行, 计算的时间步长取为6.0×10-4, 初场设定为均匀场, 待流场演化足够的时间(2×105步, 无量纲时间120) 后, 初场的影响早已消失, 流动进入统计定常状态, 此后按照每200步输出一个结果的频率输出瞬态流场.本文记录了约1.8×105步的结果, 从中取出15个旋涡脱落周期的数据(约900个瞬态流场)用于统计, 将这些瞬态流场沿时间和展向进行平均, 即可获得时均流场.如无说明, 本文展示的均是无量纲化后的结果.
3 计算结果分析 3.1 统计结果表 1给出了Strouhal数St及阻力系数Cd的对比, 可以看到, 本文计算结果St取0.139, 较多数的实验及DNS结果稍微偏大一些.相比St, 阻力系数的取值为2.17, 与实验及DNS的结果吻合较好.可以看出, 即便对这类统计参数, 要得到完全一致的结果也是非常困难的, 这从一个侧面反映了实现本算例精确预测的难度.
| 下载CSV 表 1 Strouhal数St及阻力系数Cd的对比 Tab.1 Comparisons of St and drag coefficient Cd |
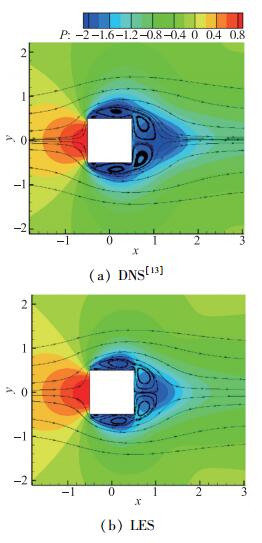
图 2给出了时均流场中柱体附近的压力分布及流线图, 分别为文献[13]的DNS结果及本文LES结果, 尽管没有给出压力的量级, 但显然, 二者在分布上是非常相似的; 从时均流线看, LES与DNS预测的分离区形态及尺寸基本一致.
|
| 图 2 方柱附近压力分布及流线图 Fig.2 Pressure contours and streamlines of time-averaged flow field |
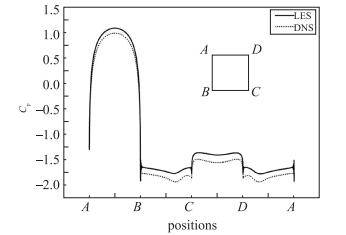
图 3展示了方柱4个表面上压力系数Cp分布的对比, 可以看到, LES与DNS曲线的分布规律完全一致, 但二者的数值存在一些差异, 这种差异应该来源于本文算例取M=0.3, 而DNS是针对不可压流动进行的.
|
| 图 3 方柱表面的Cp分布对比 Fig.3 Comparison of surface pressure coefficient Cp of cylinder |
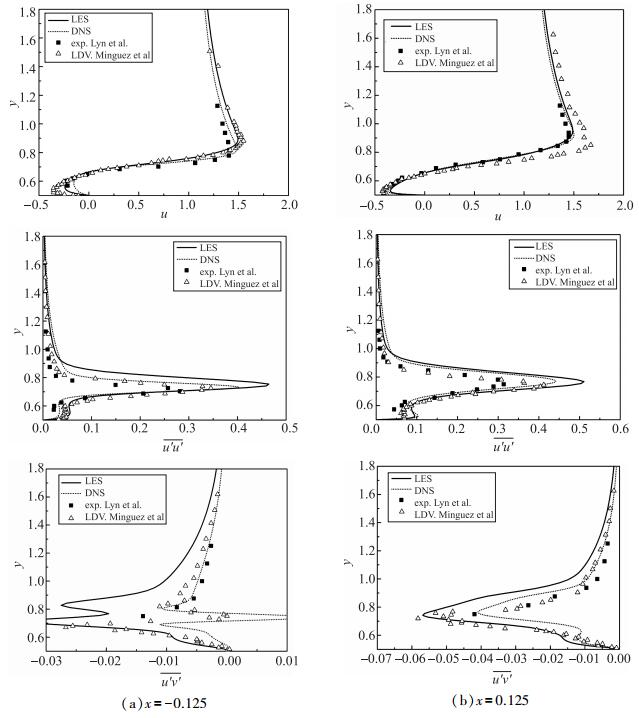
图 4展示了x=-0.125和0.125位置处流向速度u, Reynolds应力分量
|
|
图 4 x=-0.125, 0.125处流向平均速度u, Reynolds应为分量 |
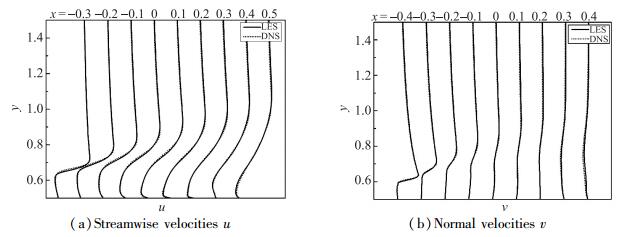
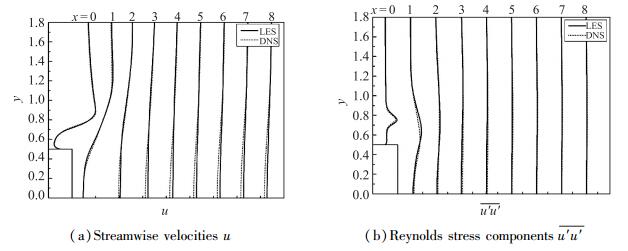
图 5展示了柱体两侧壁面不同位置处的平均速度剖面, 其中实线为LES结果, 短点线为DNS结果.由流向速度u和横向速度v的结果都可以发现, LES与DNS的曲线吻合得很好.图 6展示了方柱尾迹区不同位置处(x=0~8) 的平均速度u及Reynolds应力
|
| 图 5 柱体侧边不同位置的速度剖面 Fig.5 Profiles of time-averaged velocities components at different locations in cylinder side wall region |
|
|
图 6 尾迹区不同位置的速度剖面及Reynolds应力 |
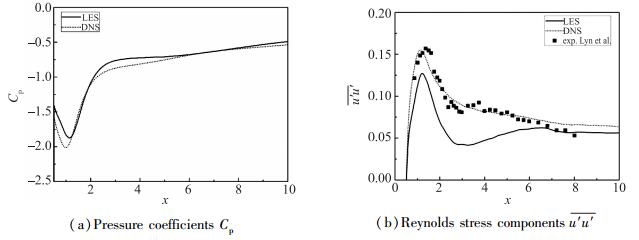
图 7给出了尾迹中心线上压力系数Cp和Reynolds应力
|
|
图 7 尾迹区中心线上压力系数及 |
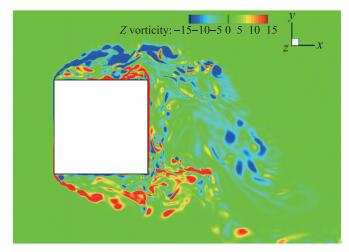
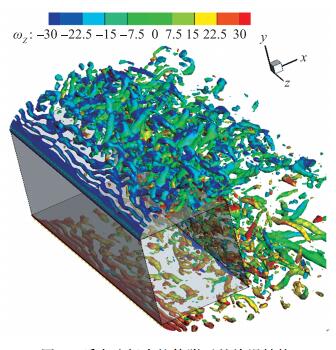
图 8给出了计算所得某一瞬态流场展向截面的涡量云图, 从图中可以看到, 涡量场存在从方柱左侧表面两个角点分离形成的自由剪切层, 剪切层在扰动作用下很快失稳, 产生展向涡结构.图 9给出了同一瞬态流场中的大尺度结构, 旋涡识别采用Q准则, 展向涡量着色, 容易看到, 角点两侧的展向涡继续快速失稳, 从二维演化出复杂的三维结构.图 10为方柱尾迹区的大尺度结构, 通过调小Q值, 从图中可以清楚地观察到Karman涡街的存在, 相邻展向大涡之间有着拉伸的准流向涡结构.
|
| 图 8 瞬态流场的展向涡量云图(取切片z=π/2) Fig.8 Contour of spanwise vorticity of instantaneous flow field (z=π/2 slice) |
|
| 图 9 瞬态流场中柱体附近的旋涡结构(Q准则, Q=100, 展向涡量着色) Fig.9 Vortex structures around the square cylinder of instantaneous flow field (isosurface of Q at Q=100, colored by spanwise vorticity) |

|
| 图 10 瞬态流场中尾迹区的Karman涡街(Q=1, 流向涡量着色) Fig.10 Karman vortex street structures in wake region of instantaneous flow field (isosurface of Q at Q=1, colored by streamwise vorticity) |
采用高精度大涡模拟方法, 对来流Mach数0.3, Reynolds数22 000的孤立方柱绕流进行了计算, 从时均流场、2阶统计量、瞬态流场等角度分析了计算结果, 主要结论如下:
(1) 对于较高Reynolds数下的孤立方柱流动而言, 大涡模拟方法能够以相对很少的计算资源获得与实验和DNS吻合很好的计算结果, 验证了方法的可靠性;
(2) LES的瞬态流场展示了计算条件下方柱绕流分离转捩及尾迹区旋涡交替脱落形成Karman涡街的全过程, 为更细致的流动机理研究提供参考;
(3) LES的预测结果仍然存在尾迹中心流向速度恢复较快的问题, 其原因有待进一步的探讨.
致谢: 本文所有计算工作均在国家超级计算广州中心的天河二号系统上完成, 感谢广州中心提供的超算资源及相关技术支持.| [1] | Lyn D A, Rodi W. The flapping shear layer formed by flow separation from the forward corner of a square cylinder[J]. Journal of Fluid Mechanics, 1994, 267: 353-376. DOI:10.1017/S0022112094001217 |
| [2] | Lyn D A, Einav S, Rodi W, et al. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder[J]. Journal of Fluid Mechanics, 1995, 304: 285-319. DOI:10.1017/S0022112095004435 |
| [3] | Voke P R. Flow past a square cylinder:test case LES2[A]. //Direct and Large-Eddy Simulation Ⅱ[M]. Berlin:Springer Netherlands, 1997:355-373. |
| [4] | Rodi W, Ferziger J H, Breuer M, et al. Status of large eddy simulation:results of a workshop[J]. ASME Journal of Fluids Engineering, 1997, 119(2): 248-262. DOI:10.1115/1.2819128 |
| [5] | Murakami S, Mochida A. On turbulent vortex shedding flow past 2D square cylinder predicted by CFD[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54(94): 191-211. |
| [6] | Rodi W. Comparison of LES and RANS calculations of the flow around bluff bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69: 55-75. |
| [7] | Lübcke H, Schmidt St Rung T, et al. Comparison of LES and RANS in bluff-body flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(14/15): 1471-1485. |
| [8] | Murakami S, Iizuka S, Ooka R. CFD analysis of turbulent flow past square cylinder using dynamic LES[J]. Journal of Fluids and Structures, 1999, 13(7/8): 1097-1112. |
| [9] | Sohankar A, Davidson L, Norberg C. Large eddy simulation of flow past a square cylinder:comparison of different subgrid scale models[J]. ASME Journal of Fluids Engineering, 2000, 122(1): 39-47. DOI:10.1115/1.483224 |
| [10] | Grigoriadis D G, Bartzis J G, Goulas A. LES of the flow past a rectangular cylinder using the immersed boundary concept[J]. International Journal for Numerical Methods in Fluids, 2003, 41(6): 615-632. DOI:10.1002/(ISSN)1097-0363 |
| [11] | Minguez M, Brun C, Pasquetti R, et al. Experimental and high-order LES analysis of the flow in near-wall region of a square cylinder[J]. International Journal of Heat and Fluid Flow, 2011, 32(3): 558-566. DOI:10.1016/j.ijheatfluidflow.2011.03.009 |
| [12] | Brun C, Aubrun S, Goossens T, et al. Coherent structures and their frequency signature in the separated shear layer on the sides of a square cylinder[J]. Flow, Turbulence and Combustion, 2008, 81(1/2): 97-114. |
| [13] | Trias F X, Gorobets A, Oliva A. Turbulent flow around a square cylinder at Reynolds number 22, 000:a DNS study[J]. Computers & Fluids, 2015, 123: 87-98. |
| [14] |
童兵, 祝兵, 周本宽. 方柱绕流的数值模拟[J].
力学季刊, 2002, 23(1): 77-81. Tong B, Zhu B, Zhou B K. Numerical simulation of flow around square cylinder[J]. Chinese Quarterly of Mecha-nics, 2002, 23(1): 77-81. |
| [15] |
邓小兵, 张涵信, 李沁. 三维方柱不可压缩绕流的大涡模拟计算[J].
空气动力学学报, 2008, 26(2): 167-172. Deng X B, Zhang H X, Li Q. Large eddy simulation of 3-dimensional incompressible flow around a square cylinder[J]. Acta Aerodynamica Sinica, 2008, 26(2): 167-172. |
| [16] |
谢志刚, 许春晓, 崔桂香, 等. 方柱绕流大涡模拟[J].
计算物理, 2007, 24(2): 171-180. Xie Z G, Xu C X, Cui G X, et al. Large eddy simulation of flows around a square cylinder[J]. Chinese Journal of Computational Physics, 2007, 24(2): 171-180. |
| [17] |
张海涛, 曹曙阳. 基于动态亚格子模型的方柱绕流大涡模拟[J].
沈阳建筑大学学报(自然科学版), 2013, 29(3): 434-439. Zhang H T, Cao S Y. Large eddy simulation of flow past a square cylinder based on dynamic sub-grid scale models[J]. Journal of Shenyang Jianzhu University (Natural Science), 2013, 29(3): 434-439. |
| [18] |
唐鹏, 韩省思, 叶桃红, 等. 联合RANS/LES方法数值模拟方柱绕流[J].
中国科学技术大学学报, 2010, 40(12): 1287-1292. Tang P, Han X S, Ye T H, et al. Hybrid RANS/LES simulation of flow past a square cylinder[J]. Journal of University of Science and Technology of China, 2010, 40(12): 1287-1292. DOI:10.3969/j.issn.0253-2778.2010.12.013 |
| [19] |
叶建. 非定常环境中叶片边界层时空演化机制的大涡模拟[D]. 北京: 北京航空航天大学, 2008.
Ye J. Large-eddy simulation of blade boundary layer spatio-temporal evolution under unsteady disturbances[D]. Beijing:Beihang University, 2008(in Chinese). |
| [20] |
叶建. 复杂可压缩流动大涡模拟程序的若干改进[D]. 北京: 北京航空航天大学, 2011.
Ye J. Some improvements on the large-eddy simulation solver for complex compressible flows[D]. Beijing:Beihang University, 2011(in Chinese). |
| [21] | Ducros F, Laporte F, Souleres T, et al. High-order fluxes for conservative skew-symmetric-like schemes in structured meshes:application to compressible flows[J]. Journal of Computational Physics, 2000, 161(1): 114-139. DOI:10.1006/jcph.2000.6492 |
| [22] | Berland J, Bogey C, Marsden O, et al. High-order, low dispersive and low dissipative explicit schemes for multiple-scale and boundary problems[J]. Journal of Computational Physics, 2007, 224(2): 637-662. DOI:10.1016/j.jcp.2006.10.017 |



