2. 香港中文大学机械与自动化工程系,中国香港 999077;
3. 阿朴杜拉国王科技大学清洁燃烧研究中心,沙特阿拉伯 23955
2. Department of Mechanical and Automation Engineering, The Chinese University of Hong Kong, Hong Kong 999077, China;
3. Clean Combustion Research Center, King Abdullah University of Science and Technology(KAUST), Saudi Arabia 23955
生物柴油主要包括了甲基酯和乙基酯两大系列[1], 其中乙基酯采用乙醇作为生产原料, 具有绿色环保、安全无毒等优势[2], 因此近年来针对乙基酯燃料燃烧特性的研究逐渐增多.甲酸乙酯(H(CO)OCH2CH3, EF)作为最简单的乙基酯[3], 充分了解其燃烧反应特性有助于增强对其他类型的乙基酯的认识, 因此成为本文的研究目标.
甲酸乙酯的裂解或氧化反应始于单分子分解或者双分子氢提取反应.在裂解方面, Makens等[4]研究了甲酸乙酯在500~700 K温度范围的热解特性, 研究发现甲酸乙酯主要分解生成乙烯和甲酸.随后, Blades开展了流动管实验[5], 进一步对830~903 K温度范围甲酸乙酯的热解特性展开了研究; Balaganesh等[6]也采用激波管实验研究了909~1 258 K范围内的热解特性, 获得了与Makens等[4]一致的结论.最近, Ren等[7-8]进一步开展了激波管热解实验, 结合激光吸收光谱技术, 对甲酸乙酯裂解过程中的H2O, CO和CO2等重要产物进行了测量, 并进行了动力学模拟.
在氧化方面, Osswald等[9]进行了层流平面火焰实验, Westbrook等[10]随后提出了甲酸乙酯的燃烧反应机理. Akih-Kumgeh等[11]通过激波管实验对甲酸乙酯的点火延迟时间进行了测量, 发现已有燃烧反应机理低估了点火延迟时间, 并改进了反应机理以更好预测高温点火延迟时间.最近, Ning等[12]进一步采用激波管对甲酸乙酯的氧化特性进行了研究, 并结合理论计算结果对燃烧反应机理进行了进一步改进.与此同时, Sun等[13]展开了低压火焰实验, 利用真空紫外-同步辐射技术对甲酸乙酯的燃烧产物进行了测量, 并提出了相应的反应机理.
以上研究极大地促进了人们对于甲酸乙酯反应特性的认识, 但目前针对甲酸乙酯反应动力学特性的研究仍有较大的改进空间:其一, 与甲酸乙酯相关的重要反应动力学参数大多采用估计值, 容易带来较大的误差, 因此需要进一步改进或校正; 其二, 已有研究主要集中在单分子反应方面, 而对于双分子反应尤其是氢提取反应速率常数关注较少.特别地, 羟基自由基提取甲酸乙酯的反应速率常数与氧化特性密切相关, 但人们对该反应速率常数尚缺乏准确、统一的认识.目前, 该反应速率常数主要来自于类比估计, 仅有Wu等[14]采用理论计算方法获得了500~2 000 K范围内的速率常数.值得注意的是, Wu等采用了一维内转子近似对非谐效应进行了校正[15].通过分析甲酸乙酯与羟基的反应特征可知, 该类型反应的过渡态存在较强的氢键, 导致其内转动容易与其他自由度发生耦合.因此, 采用一维内转子近似处理该非谐效应容易引起较大的误差.
基于上述考虑, 本文采用了理论计算和实验测量的手段对该反应展开了进一步研究:在理论方面, 采用了最新的多结构-扭转(multi-structure torsion, MS-T)方法[16-17]对内转动耦合问题进行了处理, 并结合传统过渡态理论(transition state theory, TST)获得了200~2 000 K温度范围内的速率常数; 在实验方面, 采用激波管实验测量了900~1 321 K温度范围内的反应速率常数.通过实验测量对理论计算结果进行了验证, 获得了准确、统一的速率常数.
1 方法 1.1 理论计算对于具有紧致过渡态的双分子反应, 其速率常数表达式为
| $ k = \kappa \frac{{{k_{\rm{B}}}T}}{h}\frac{{Q_{{\rm{TS}}}^ + }}{{{Q_{{\rm{react}}}}}}\exp \left( {\frac{{ - \Delta {V^ + }}}{{RT}}} \right) $ |
式中, κ为隧穿系数, kB为Boltzmann常数, h为Planck常数, T为反应温度, QTS+为过渡态配分函数, Qreact为反应物配分函数, ΔV+为反应能垒, R为理想气体常数.其中, 过渡态或者反应物的配分函数均包括了电子、平动、转动、以及振动等4方面贡献, 可以表示为
| $ Q = {Q_{{\rm{elec}}}}{Q_{{\rm{trans}}}}{Q_{{\rm{rot}}}}{Q_{{\rm{vib}}}} $ |
式中, Qelec, Qtrans, Qrot, Qvib分别为电子、平动、转动以及振动配分函数.振动配分函数通常采用谐振近似处理
| $ Q_{{\rm{vib}}}^{{\rm{HO}}} = {\prod\limits_i^n {\left[{1-\exp \left( {\frac{{-hc{\omega _i}}}{{kT}}} \right)} \right]} ^{ - {g_i}}} $ |
式中, c为光速, ωi为第i个振动模式的频率, gi为该振动模式下的简并度.值得注意的是, 在反应过程中的物种通常具有内转动的运动模式, 利用谐振近似处理该运动模式会引入较大误差, 最佳处理办法是将各个内转动模式筛选出来单独采用非谐振模型进行处理, 如简单高效的一维受阻转子模型.然而, 本反应的难点在于由于反应体系含氧原子, 因此极易形成氢键, 导致内转动模式与其他运动模式发生强耦合.运用传统的一维受阻转子模型难以准确描述强耦合下的振动配分函数.鉴于此, 本文采用Zheng等[18]提出的多结构-扭转方法(MS-T)对该配分函数进行校正
| $ F = \frac{{Q_{{\rm{rovib}}}^{{\rm{MS - T}}}}}{{Q_{{\rm{vib}}}^{{\rm{HO}}}}} $ |
式中, F为简谐振动配分函数的校正系数, QrovibMS-T为采用MS-T方法获得的振转配分函数.最后获得了考虑了强耦合非谐效应的速率常数为
| $ {k^{{\rm{MS - T}}}} = \kappa \frac{{{F^{{\rm{TS}}}}}}{{{F^{{\rm{react}}}}}}\frac{{{k_{\rm{B}}}T}}{h}\frac{{Q_{{\rm{TS}}}^ + }}{{{Q_{{\rm{react}}}}}}\exp \left( {\frac{{ - \Delta {V^ + }}}{{RT}}} \right) $ |
另外, 对于能垒为正的反应通道, 其隧穿效应采用了Eckart方法进行处理[19]; 而对于能垒为负的反应通道, 则采用了Wigner方法进行处理[20].
1.2 实验方法本实验所用激波管直径为14.2 cm, 低压段长9 m, 高压段长度可根据实验需求进行更换, 最大长度亦为9 m.反应物甲酸乙酯体积分数为309 ppm (即0.0309%), 采用较低的反应物浓度可以减小反应过程中温度变化, 有助于获得更准确的激光吸收光谱测量.另外, 羟基自由基反应活性极高, 难以稳定存在, 因此采用叔丁基过氧化氢(tert-butyl hydro-peroxide, TBHP)作为羟基的前驱体, 其体积分数为20 ppm(即0.0020%). TBHP具有快速分解、分解产物活性低等特点, 因而被广泛用作高温环境下羟基自由基(OH)的前驱体. EF,TBHP以及氩气(Ar)在混气罐中充分混合后再充入激波管低压段.为保证反应物与浴气充分混合, 其搅拌时间应不低于2 h.在距离低压端部1.5 m处安装了5个PZT压力传感器, 用于监测入射激波速度.激波1区压力(P1)由两个高精度Baratron压力传感器进行测量, 反射激波后温度与压力(T5,P5)根据标准激波关系式直接计算获得.
羟基自由基在波长为306.7 nm处存在较强的吸收峰, 因此在该波长下进行直接吸收测量可获得较高的探测灵敏度.本文通过对波长为613.4 nm的可见光进行倍频处理后获得了波长为306.7 nm的紫外光, 并采用了共模抑制方法来减小光强波动带来的影响(I为吸收后光强,I0为参考光光强,见图 1).最后, 根据Beer-Lambert定律, 确定羟基的浓度.经分析, 本文实验误差主要来自于激波管内反应温度和羟基的吸收系数, 实验测得的羟基浓度的相对不确定度约为±3%.

|
| 图 1 激波管可协调二极管激光吸收光谱测量羟基自由基浓度示意图 Fig.1 Schematic diagram of measuring the hydroxyl radical in shock tube using tunable diode laser absorption spectroscopy(TDLAS) |
最后, 基于Metcalfe等[21]的甲酸乙酯与Pang等[22]的TBHP反应机理, 本文对反应过程中的羟基浓度进行了模拟, 并将模拟所得的羟基浓度与实验测量的浓度曲线进行了对比.通过调整EF+OH的反应速率常数使二者吻合最佳, 此时调整后的EF+OH的速率常数即为实验测量值.经分析, 本文所测反应速率常数的相对误差约为±20%.
2 结果与讨论 2.1 反应势能面根据甲酸乙酯的结构特征(H(CO)OCH2CH3), 其与羟基自由基的反应有如下3个通道:
EF+OH → (CO)OCH2CH3+H2O (Rxn.1)
EF+OH → H(CO)OCHCH3+H2O (Rxn.2)
EF+OH → H(CO)OCH2CH2+H2O (Rxn.3)
获得精确的反应势能面对于反应速率的计算至关重要, 而反应势能面的建立又依赖于理论计算方法及采用的水平.前期研究表明[23], M06-2x/ma-TZVP水平可获得与CCSD(T)-F12a/jun-cc-pVTZ相近的精度, 因此作为本文的首选.为简洁起见, 用TS1,TS2以及TS3分别对应上述3个反应通道所涉及的过渡态; P1, P2, P3分别对应上述通道形成的甲酸乙酯自由基产物.在本研究中, 反应过程中所涉及的过渡态、反应物、产物均采用M06-2x/ma-TZVP方法进行优化和频率计算.对于过渡态, 须保证最终得到的频率中仅存在1个虚频; 同时进行了IRC分析, 确保该过渡态准确连接到所对应的反应物和产物.
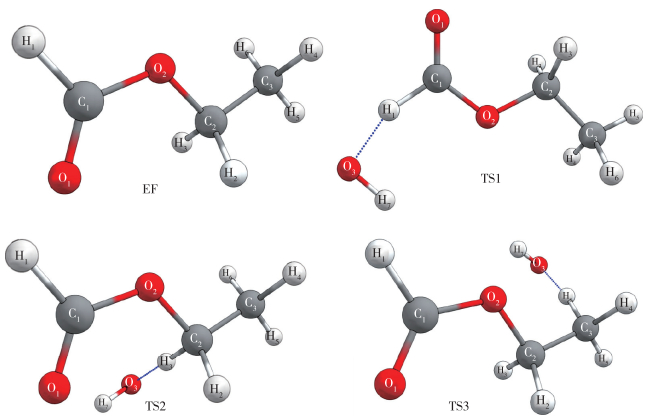
在构建反应势能面的过程中, 首要任务是获得反应物与过渡态的最稳定构象(即能量最低).本文利用MSTor中的ConfGen程序[17]对反应物和3个过渡态进行了构象搜寻.以反应物EF为例, 其分子结构中具有3个内转动模式, 除甲基外, 其余两个内转子分别扭转0°,120°,-120°, 总共获得9个初始构象.随后对此9个构象进行优化, 获得能量最低的构象, 所涉及的结构优化、频率计算等任务采用Gaussian 09完成[24].同理, 针对TS1, TS2和TS3亦采用相同的方式获得其能量最低的构象, 能量最低结构如图 2所示.
|
| 图 2 反应物(EF)及过渡态(TS1, TS2, TS3)的最低能量构象 Fig.2 Lowest-energy conformers of reactant (EF) and the transition states (TS1, TS2, TS3) |
本文对比了基于M06-2x/ma-TZVP水平所得能量最低构象与基于M06/cc-pVTZ水平获得的能量最低构象, 结果表明二者能量最低构象的结构几乎完全一致, 由此可通过上述各构象的单点能构建反应势能面.
表 1给出了两种理论水平下甲酸乙酯与羟基的反应势能面, 其中E1,E2分别为M06-2x/ma-TZVP和CCSD(T)/CBS(D-T)//M062x/cc-pVTZ[14]水平下所得势能面.对于反应势垒而言(过渡态与反应物的能量差), 两种水平下的最大差异为0.4 kcal·mol-1; 对于反应焓变而言(产物与反应物的能量差), 两种水平下的最大差异为1.0 kcal·mol-1.以高水平的CCSD(T)/CSD(D-T)所得势能面为基准, 发现M06-2x/ma-TZVP所得势能面的不确定度均在化学精度(±1.0 cal·mol-1)以内.更为重要的是, 该密度泛函方法计算效率远高于CCSD(T), 而二者之间的精度相近, 所以利用该密度泛函方法有助于准确快速地构建反应势能面.
| 下载CSV 表 1 甲酸乙酯(EF)与羟基(OH)的反应势能面 Tab.1 Potential energy surface of EF and OH |
如前所述, 甲酸乙酯与羟基的反应中涉及氢键形成, 引起各个自由度之间的强耦合.此时采用谐振近似或者一维内转子近似均不足以准确描述其配分函数, 因此须采用MS-T方法处理内转动所致的非谐效应, 以获取振动配分函数的校正系数.在本研究中, 通过ConfGen搜索获得了诸多显著、稳定的构象.具体而言, 在M06-2x/ma-TZVP水平下EF出现了3个稳定构象; TS1,TS2以及TS3分别形成了5,6和11个稳定构象.值得注意的是, 由于羟基对甲酸乙酯中的甲基官能团进行提取破坏了甲基的对称性, 因此导致TS3的构象急剧增多.最后, 采用MSTor程序[17]获得了考虑内转子耦合情况下的非谐校正系数.
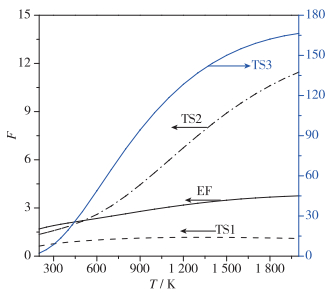
图 3示出了200~2 000 K温度范围内非谐校正系数的变化, 随着温度的升高, TS2和TS3的非谐效应急剧增强.在200 K时, TS2的非谐校正系数约为1.4, 而当温度升至2 000 K, 其非谐校正系数则增至11.5;在200 K时, TS3的非谐校正系数为2.2, 该系数在2 000 K时急剧增大到166.4.相比之下, EF和TS1的非谐校正系数随温度的波动则相对稳定. TS3的非谐效应远远强于其他过渡态的根本原因在于, 羟基提取破坏了甲酸乙酯分子中甲基的对称性, 导致稳定的构象增多.
|
| 图 3 反应物及过渡态的非谐校正系数 Fig.3 Anharmonic correction coefficients of reactant and transition states |
甲酸乙酯氢提取反应所涉及的3个通道中, 均涉及反应前复合物和反应后复合物的生成.在本文所研究的温度范围内, 复合物对最终速率常数产生的影响较小, 因此在速率常数的计算过程中不予考虑.另外, 通道Rxn.2表现出负能垒特性, 这主要是由于其过渡态中出现较强的氢键, 从而形成了较为稳定的7元环结构, 使得过渡态能量降低.
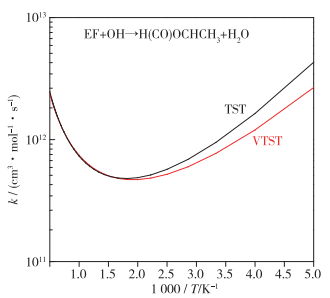
从IRC分析可知, TS1及TS2与反应物之间的能垒较低, 其势能面相对平缓, 该类型则可能存在较为显著的变分效应.为探索变分效应对速率常数的影响, 本文以Rxn.2为例, 分别采用了过渡态理论(TST)以及变分过渡态理论(variational transition state theory, VTST)计算了反应速率常数, 结果如图 4所示.由图 4可知, 在高温区域(>500 K), 采用TST和VTST计算得到的速率常数几乎完全一致; 而在200~500 K之间, 采用VTST获得速率常数较小.随着温度的降低, 二者之间的差异逐渐增大.在200 K时, 采用VTST获得的速率常数仅为TST的62%.实际上, 在低温范围内, 由于变分效应引起的速率常数变化远远小于能垒不确定度所带来的误差.例如, 能垒不确定度为1.0 kcal·mol-1时, 会导致200 K处的速率常数的不确定高达1 200%;在2 000 K时, 其速率常数的不确定度为28%.因此, 在本文所关注的温度范围内, 可以忽略变分效应对速率常数的影响.最后, 本文统一采用TST理论处理上述3个反应通道, 利用KisThelP软件[25]计算了其在200~2 000 K范围内的速率常数.
|
| 图 4 基于过渡态及变分过渡态理论的速率常数对比 Fig.4 Comparison of rate coefficients calculated by TST and VTST method |
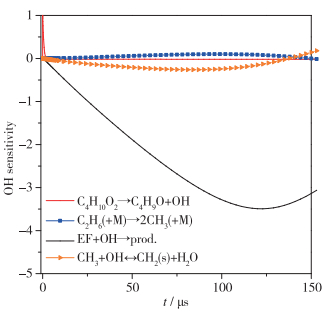
本文利用激波管实验和激光吸收光谱技术测量了900~1 321 K温度范围及1.4~2.0 atm压力范围的速率常数.需注意, 在EF与OH的反应过程中还涉及其他诸多二级反应, 有可能会对实验测量带来干扰.因此, 本文进一步开展了敏感度分析, 考察其他化学反应对OH浓度的影响. 图 5敏感度分析表明, 在EF的整个反应过程中, EF+OH反应对OH的浓度变化起决定性作用, 其他反应对OH浓度的影响几乎可以忽略, 该分析进一步表明本文测量结果的准确可靠性.
|
| 图 5 OH浓度历史的敏感性分析 Fig.5 Sensitivity analysis of OH concentration |
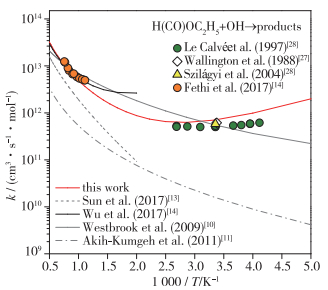
最后, 图 6比较了理论计算所得速率常数与实验测量结果, 在整个温度范围内, 本文计算结果与Westbrook等[10]的估计值与实验测量值吻合较好, 而Sun等[13],Akih-Kumgeh等[11]则低估了反应速率常数.具体地, 在高温范围内(500~2 000 K), 本文的计算结果与激波管实验测量值吻合较好, 同时Westbrook等[10]的估计值、Wu等[14]的理论计算结果均与实验测量值吻合较好.在低温范围内(200~500 K), 从Le Calvé等[26], Wallington等[27]以及Szilágyi等[28]的测量值可以观察到轻微的负温度效应.已有估计值或理论计算结果均未能描述出该现象, 但本文的理论计算结果很好地捕捉到了该负温度效应.尽管在低温范围内, 本文计算结果略高于实验测量值, 但考虑到实验测量以及理论计算的误差, 该结果是合理的、可接受的.
|
| 图 6 反应速率常数的理论计算与实验结果对比 Fig.6 Comparisons of the theoretical and experimental rate coefficients |
本文对甲酸乙酯与羟基自由基反应动力学展开了理论与实验研究, 在理论方面, 采用了M06-2x/ma-TZVP水平快速准确地获得反应势能面, 其精度与CCSD(T)/CBS(D-T)接近.其次, 探讨了由于内转动耦合所引起的非谐效应, 并通过MS-T方法获得了非谐校正系数, 研究了变分效应对速率常数的影响, 最后采用传统过渡态理论获得了200~2 000 K温度范围的速率常数.在实验方面, 通过结合激波管和激光诊断技术, 测量得到了900~1 321 K范围的反应速率常数, 并与前人的低温测量值相结合, 对本文计算结果进行了实验验证, 结果表明本文对甲酸乙酯与羟基反应动力学的理论计算是准确合理的.
致谢 感谢国家自然科学基金(51776179)的资助!| [1] |
Coniglio L, Bennadji H, Glaude P A, et al. Combustion chemical kinetics of biodiesel and related compounds (methyl and ethyl esters):experiments and modeling-Advances and future refinements[J]. Progress in Energy and Combustion Science, 2013, 39(4): 340-382. DOI:10.1016/j.pecs.2013.03.002 |
| [2] |
Yusoff M F, Xu X B, Guo Z. Comparison of fatty acid methyl and ethyl esters as biodiesel base stock:a review on processing and production requirements[J]. Journal of the American Oil Chemists' Society, 2014, 91(4): 525-531. DOI:10.1007/s11746-014-2443-0 |
| [3] |
Lai J Y W, Lin K C, Violi A. Biodiesel combustion:advances in chemical kinetic modeling[J]. Progress in Energy and Combustion Science, 2011, 37(1): 1-14. DOI:10.1016/j.pecs.2010.03.001 |
| [4] |
Makens R F, Eversole W G. Kinetics of the thermal decomposition of ethyl formate[J]. Journal of the American Chemical Society, 1939, 61(11): 3203-3206. DOI:10.1021/ja01266a065 |
| [5] |
Blades A T. The kinetics of the pyrolysis of ethyl and isopropyl formates and acetates[J]. Canadian Journal of Chemistry, 1954, 32(4): 366-372. DOI:10.1139/v54-049 |
| [6] |
Balaganesh M, Sudhakar G, Rajakumar B. Thermal decomposition of ethyl formate behind the reflected shock waves in the temperature range of 909-1258 K[C]. 29th International Symposium on Shock Waves 1, Cham: Springer, 2015: 233-238.
|
| [7] |
Ren W, Dames E, Hyland D, et al. Shock tube study of methanol, methyl formate pyrolysis:CH3OH and CO time-history measurements[J]. Combustion and Flame, 2013, 160(12): 2669-2679. DOI:10.1016/j.combustflame.2013.06.016 |
| [8] |
Ren W, Mitchell Spearrin R, Davidson D F, et al. Experimental and modeling study of the thermal decomposition of C3-C5 ethyl esters behind reflected shock waves[J]. The Journal of Physical Chemistry A, 2014, 118(10): 1785-1798. DOI:10.1021/jp411766b |
| [9] |
Osswald P, Struckmeier U, Kasper T, et al. Isomer-specific fuel destruction pathways in rich flames of methyl acetate and ethyl formate and consequences for the combustion chemistry of esters[J]. The Journal of Physical Chemistry A, 2007, 111(19): 4093-4101. DOI:10.1021/jp068337w |
| [10] |
Westbrook C K, Pitz W J, Westmoreland P R, et al. A detailed chemical kinetic reaction mechanism for oxida-tion of four small alkyl esters in laminar premixed flames[J]. Proceedings of the Combustion Institute, 2009, 32(1): 221-228. DOI:10.1016/j.proci.2008.06.106 |
| [11] |
Akih-Kumgeh B, Bergthorson J M. Experimental and modeling study of trends in the high-temperature ignition of methyl and ethyl esters[J]. Energy & Fuels, 2011, 25(10): 4345-4356. |
| [12] |
Ning H B, Wu J J, Ma L H, et al. Combined ab initio, kinetic modeling, and shock tube study of the thermal decomposition of ethyl formate[J]. The Journal of Physical Chemistry A, 2017, 121(35): 6568-6579. DOI:10.1021/acs.jpca.7b05382 |
| [13] |
Sun W Y, Tao T, Zhang R Z, et al. Experimental and modeling efforts towards a better understanding of the high-temperature combustion kinetics of C3-C5 ethyl esters[J]. Combustion and Flame, 2017, 185: 173-187. DOI:10.1016/j.combustflame.2017.07.013 |
| [14] |
Wu J J, Khaled F, Ning H B, et al. Theoretical and shock tube study of the rate constants for hydrogen abstraction reactions of ethyl formate[J]. The Journal of Physical Chemistry A, 2017, 121(33): 6304-6313. DOI:10.1021/acs.jpca.7b06119 |
| [15] |
Pfaendtner J, Yu X R, Broadbelt L J. The 1-D hindered rotor approximation[J]. Theoretical Chemistry Accounts, 2007, 118(5/6): 881-898. |
| [16] |
Zheng J J, Mielke S L, Clarkson K L, et al. MSTor:a program for calculating partition functions, free energies, enthalpies, entropies, and heat capacities of complex molecules including torsional anharmonicity[J]. Computer Physics Communications, 2012, 183(8): 1803-1812. DOI:10.1016/j.cpc.2012.03.007 |
| [17] |
Zheng J J, Meana-Pañeda R, Truhlar D G. MSTor version 2013:a new version of the computer code for the multi-structural torsional anharmonicity, now with a coupled torsional potential[J]. Computer Physics Communications, 2013, 184(8): 2032-2033. DOI:10.1016/j.cpc.2013.03.011 |
| [18] |
Zheng J J, Yu T, Papajak E, et al. Practical methods for including torsional anharmonicity in thermochemical calculations on complex molecules:the internal-coordinate multi-structural approximation[J]. Physical Chemistry Chemical Physics, 2011, 13(23): 10885-10907. DOI:10.1039/c0cp02644a |
| [19] |
Eckart C. The penetration of a potential barrier by elec-trons[J]. Physical Review, 1930, 35(11): 1303-1309. DOI:10.1103/PhysRev.35.1303 |
| [20] |
Wigner E. On the penetration of potential energy barriers in chemical reactions[J]. Z Phys Chem B, 1932, 19. |
| [21] |
Metcalfe W K, Simmie J M, Curran H J. Ab initio chemical kinetics of methyl formate decomposition:the sim-plest model biodiesel[J]. The Journal of Physical Chemistry A, 2010, 114(17): 5478-5484. DOI:10.1021/jp9120436 |
| [22] |
Pang G A, Hanson R K, Golden D M, et al. High-temperature measurements of the rate constants for reactions of OH with a series of large normal alkanes:n-pentane, n-heptane, and n-nonane[J]. Zeitschrift Für Physi-kalische Chemie, 2011, 225(11/12): 1157-1178. |
| [23] |
Li X Y, You X Q, Law C K, et al. Kinetics and branching fractions of the hydrogen abstraction reaction from methyl butenoates by H atoms[J]. Physical Chemistry Chemical Physics, 2017, 19(25): 16563-16575. DOI:10.1039/C7CP01686G |
| [24] |
Frisch M J, Trucks G W, Schlegel H B, et al. Gaussian 09, revision D.01[R]. 2009.
|
| [25] |
Canneaux S, Bohr F, Henon E. KiSThelP:a program to predict thermodynamic properties and rate constants from quantum chemistry results[J]. Journal of Computational Chemistry, 2014, 35(1): 82-93. |
| [26] |
Le Calvé S, Le Bras G, Mellouki A. Temperature dependence for the rate coefficients of the reactions of the OH radical with a series of formates[J]. The Journal of Physical Chemistry A, 1997, 101(30): 5489-5493. DOI:10.1021/jp970554x |
| [27] |
Wallington T J, Dagaut P, Liu R Z, et al. The gas phase reactions of hydroxyl radicals with a series of esters over the temperature range 240-440 K[J]. International Journal of Chemical Kinetics, 1988, 20(2): 177-186. DOI:10.1002/(ISSN)1097-4601 |
| [28] |
Szilágyi I, Dóbé S, Bérces T, et al. Direct kinetic study of reactions of hydroxyl radicals with alkyl formates[J]. Zeitschrift Für Physikalische Chemie, 2004, 218(4): 479-492. |




