超声速飞行器和周围大气相互作用形成的激波现象, 对于飞行器的气动力和气动热计算非常重要, 是计算流体力学主要研究内容. 1954年Lax提出双曲线守恒律方程弱解理论以后, 建立了自动捕捉激波的格式; 1959年Godunov基于弱解理论构造出物理背景清晰计算稳定的格式, 开创了激波捕捉的新纪元[1].早期这些1阶格式主要限于一维模型方程求解[2], 直到1969年Lax和Wendroff提出了著名的2阶格式Lax-Wendroff格式, 捕捉方法才真正开始在多维问题中应用.之后, MacCormack格式(1969年)Beam-Warming格式(1978年)Jamason格式(1983年)等相继被提出.然而, 在使用过程中发现:高阶捕捉方法在提高流场计算精度和激波分辨率的同时也会在激波附近产生非物理数值振荡, 这极大地限制了高阶捕捉格式的应用.为了解决这些高阶(2阶)格式在激波附近出现非物理振荡的问题, CFD工作者提出了各种各样的解决办法[3]. 1986年, Harten提出TVD格式, 激波捕捉法开始广泛应用于复杂工程领域.随后又先后出现了ENO,WENO,紧致格式等标志性的成果, 在激波的数值求解方面很多问题都貌似得到了解决.但是, Moretti回顾30年来CFD发展历程[4], 尖锐地指出激波捕捉法存在的问题:
(1) 限制器:几乎所有高精度捕捉格式需要构建或选择限制器, 通过降阶来实现计算稳定.阎超[5]比较了6种限制器, 得出的结论是阻尼小的流场“不干净”, 耗散大的激波被“抹平”; Rawat等[6]及Prakash等[7]使用5阶WENO5模拟包含激波的流场, 数值结果表明精度很难超过1阶.
(2) 斜激波:目前没有真正的多维格式, 即使直角网格模拟直线型激波, 如果二者不正交, 计算得到的激波形状也变成沿网格变化的的折线, 激波在网格内夹角不同导致波后参数误差不均, 需要一定网格的空间范围(所谓激波过渡区)后才能大致恢复到均匀流动.尽管旋转格式[8]的采用有利于改善激波捕捉格式对网格方向依赖性, 但是本文后面例证表明, 对于三波点等特殊结构产生的误差无法消除, 影响持续到下游流场出口.
(3) 理论解:基于守恒型Euler方程的弱解理论认为激波为数学间断, 流动参数在此突跃, 理论解表现为多值函数, 但是, 所有激波捕捉法会计算出过渡区, 过渡区内每个网格点流动参数唯一, 与波前波后值比较均不合适, 精度无从谈起.理论上N-S方程存在过渡区, 但在建立方程时采取了热力学局部平衡假设忽略松弛时间的状态方程密度不存在剧烈变化的Stokes假设等, 这些约束条件无法描述激波内部处于热力学非平衡状态的物理机理, 过渡区流场参数是非物理的.
(4) 影响域:按照超声速空气动力学理论, 扰动沿特征线传播过程中保持不变, 理论上过渡区内产生的误差一直保持到下游流场出口, Bonhaus[9]采用精度直到9阶的SUPG捕捉格式模拟在收敛段存在激波的准一维的Laval喷管流动, 计算结果表明整个激波下游流场难以恢复到应有精度.
作为另一种激波计算方法, 激波装配法由来已久. 1966年, Moretti等[10]采用激波装配法模拟超声速钝体绕流场取得很好效果, 在精度和计算效率方面明显优于当时的激波捕捉法, 开创了激波装配法的新阶段, 极大地推动了超声速流动的应用研究.在国内, 直到1991年激波装配法还是模拟黏性流动[11]和复杂外型无黏流场[12]的主要方法.然而, 传统激波装配法需要事先估计激波位置作为计算边界, 流场内部激波相交等复杂结构装配困难, 应用受到极大限制, 研究热情消退, 国内近20年几乎没有报道.
但是, 随着研究问题Mach数的提高, 激波捕捉方法的缺陷也越来越明显.一些CFD工作者开始重新审视激波装配方法, 以此寻求更为理想的解决方案. Rawat等[6]及Prakash等[7]提出了激波阵面追踪法(front-tracking), 将传统激波装配方法和高精度有限差分方法相结合, 避免了由捕捉激波造成的流场精度降阶问题. Paciorri等[13-14]及Bonfiglioli等[15]发展了浮动激波装配法(floating shock-fitting), 在捕捉法流场内嵌入激波, 形成以R-H关系式为边界条件的多块拼接网格, 明显地提高了高超声速流场的计算精度.这些新型激波装配法发挥捕捉法强大的流场模拟能力提供了复杂波系, 装配在背景网格上运动的激波弥补了捕捉法的不足, 解决了内部激波装配难题, 成功模拟了激波相交和Mach反射等复杂波系结构.
刘君等应用动网格技术模拟高超声(Mach数为20) 飞行器多体分离过程, 遇到了常规捕捉法计算动态强激波不稳定难题.为了解决这一问题, 发展了基于非结构动网格的激波装配方法[16], 并且比较了Mach数为6时捕捉法和装配法的计算结果, 完全一致, 初步验证了装配法.随后, 刘君等[17]又在该激波装配方法的基础上模拟了斜激波壁面反射问题.在该算例中, 不但对入射激波进行了装配, 而且对内部反射激波和接触间断进行了装配, 大大地扩展了激波装配方法的应用范围.为了和传统激波装配方法相区别, 将该方法命名为基于非结构变形网格的间断装配法(deforming-grid discontinuity-fitting,DDF).本文采用该方法模拟了激波管非定常流动过程以及激波气泡相互作用问题, 并以此对该方法的基本原理进行说明.
1 基于非结构变形网格技术的间断装配法复杂形状激波初场及间断速度的计算方法后面讨论.首先采用在捕捉格式中经常讨论的一维激波管问题, 来说明算法的基本原理.
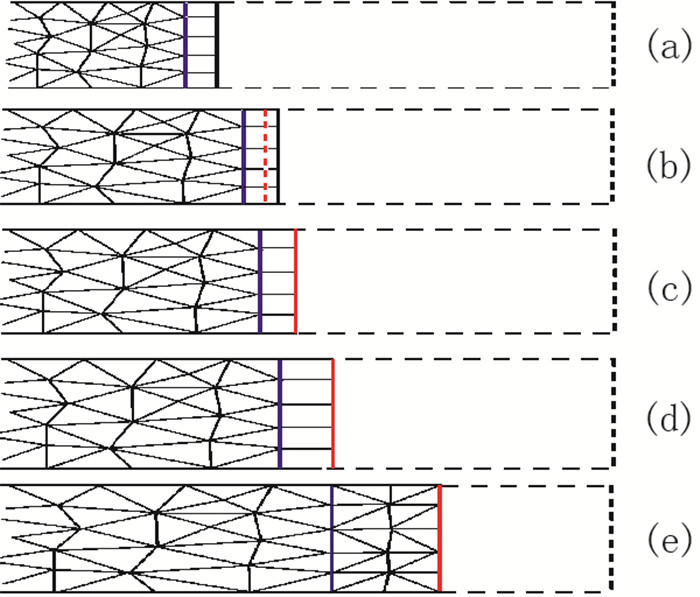
1.1 基本原理图 1(a)是初始状态, 左右侧流动参数构成Riemann问题, 左侧多排网格用于模拟参数连续区域, 右侧只留一排准备装配激波的网格.开始计算后, 根据Riemann分解理论计算得到接触间断(蓝色)和激波(红色)速度, 接触间断运动牵引左侧网格变形, 同时采用捕捉法计算膨胀波的向右传播, 接触间断右侧一排网格单元按照刚体运动, 激波到达第1排网格右边界前, 采用刘君等处理阀门关闭问题时提出的虚拟网格方法处理[18-19], 记录激波在单元中的精确位置, 如图 1(b)所示.接触间断右侧第1排网格单元内虚拟激波到达右侧边界时装配激波, 如图 1(c)所示.由于激波运动速度大于接触间断, 第1排网格单元开始变形, 如图 1(d)所示.随着第1排网格单元不断拉长, 网格质量低于判据标准后进行重构, 如图 1(e)所示.重构后, 对定常流动采用插值得到新网格单元的流动参数, 对非定常流动采用刘君等提出的信息传递算法[20-21]进行新旧网格之间的流场参数传递, 保持时间和空间2阶精度.
|
| 图 1 激波和接触间断的装配 Fig.1 Fitted shock and contact discontinuity |
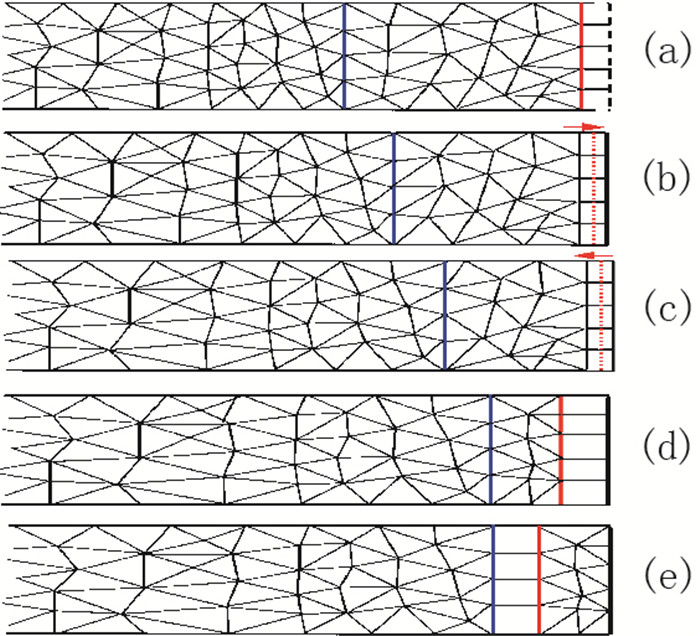
重复变形结合重构过程, 直到激波接近固壁前预设的位置, 激波右侧边界不再运动.在激波和固壁之间增加新的计算区域(第3区), 其内布置一排网格, 如图 2(a)所示.此后, 第12区网格继续变形或重构, 激波在第3区静止网格内部向右虚拟运动, 如图 2(b)所示, 直到固壁反射.根据激波反射理论给出波后流动参数和速度, 反射激波在保持静止的第3区网格内向左虚拟运动, 如图 2(c)所示.当反射激波到达第3区那一排网格的左侧边界, 装配向右运动的激波, 网格在激波运动牵引下变形, 如图 2(d)所示, 直到满足条件进行重构.由于初始接触间断和反射激波相向运动, 不断压缩第2区, 重构使内部网格减少, 直到剩下一排网格, 如图 2(e)所示.此后, 第2区按照接触间断速度刚性运动, 激波在内部虚拟运动.如果接触间断和激波重合, 在局部范围又构成新的Riemann问题, 回到前面图 1的初始状态, 重复以上方法.
|
| 图 2 激波反射和间断相 Fig.2 Shock wave reflection and interaction of discontinuities |
新型激波装配法给出的空间多维算例是定常流动, 初始激波误差随着收敛过程逐步消除, 因此, 处理初始激波很少考虑时间精度.非定常流动的初始激波位置影响整个计算过程, 需要尽量给出准确初场.对于事先位置无法准确描述形状复杂的激波, 本文提出在捕捉法流场中辨识的算法来确定初始激波位置:
(1) 寻找全场密度梯度最大单元, 记为E0, 然后找出该单元顶点周围密度梯度最大的单元, 记为E1;
(2) 增加不属于已经标记过单元到Ei-1格心大于Ei与Ei-1格心距离约束, 找出与Ei单元共点的密度梯度最大的单元, 记为Ei+1, 直到捕捉法计算出区域边界;
(3) 采用Bézier方法进行拟合, 得到用于网格生成的初始激波位置曲线.
图 3给出了捕捉法网格和密度等值线, 采用梯度跟踪算法辨识出来的激波边界曲线, 以及根据边界曲线生成装配法的内部网格.对于装配法网格的初始流场, 边界以外的网格采用信息传递方法或线形插值得到.为了避免捕捉法过渡区内非物理解的影响, 初场边界点两侧参数特殊处理:取边界点对应的捕捉法网格及其相邻网格单元中最大压力作为波后压力值; 对于激波前参数未知的内部激波, 取边界点对应的捕捉法网格及其相邻网格单元中最小压力所在单元参数作为波前流场值.
假设激波左右两侧单元编号为1和2, 激波离散面法向为n, 激波运动速度为ms, 激波运动和波后参数按以下步骤进行确定.
(1)根据单元1和单元2的熵大小确定波前波后.如果单元1的熵小于单元2的熵, 则单元1为波前,单元2为波后; 反之单元1为波后,单元2为波前.记波前参数为UQ, 波后参数为UH, 其中U=[ρ, u, v, w, p]T.
(2) 进行一次坐标变换, 将参数变换到激波坐标系下.沿激波面元法向, 波前速度可以表示为
| ${\mathit{\boldsymbol{V}}_{Qn}} = \left( {{\mathit{\boldsymbol{V}}_Q} \cdot \mathit{\boldsymbol{n}}} \right) \cdot \mathit{\boldsymbol{n}} - {\mathit{\boldsymbol{m}}_s}$ |
其中, VQ为波前运动矢量; VQn为激波坐标系下波前速度矢量, 方向为沿面元法向.
(3) 经过坐标变换后的波前Mach数为
| $ M = \sqrt {1 + \frac{{\gamma + 1}}{{2\gamma }}\left( {\frac{{{p_{\rm{H}}}}}{{{p_{\rm{Q}}}}} - 1} \right)} $ |
其中, γ为比热比, 如没有特殊说明γ=1.4; pQ为激波波前压力; pH为激波波后压力.
(4) 根据确定的波前Mach数, 可以确定经过坐标变换后的沿激波法向的速度为
| $ \mathit{\boldsymbol{W = }}\mu \cdot M \cdot c \cdot \mathit{\boldsymbol{n}} $ |
且
| $ \mathit{\boldsymbol{W = }}{\mathit{\boldsymbol{V}}_{Qn}} $ | (1) |
其中,c为波前单元声速,
(5) 根据式(1) 可以确定激波运动速度:
| $ {\mathit{\boldsymbol{m}}_s} = \left( {{\mathit{\boldsymbol{V}}_Q} \cdot \mathit{\boldsymbol{n}}} \right) \cdot \mathit{\boldsymbol{n}} - \mu \cdot M \cdot c \cdot \mathit{\boldsymbol{n}} $ |
(6) 确定波后参数, 波后压力不变, 波后密度为
| $ {\rho _{\rm{H}}} = {\rho _{12}} \cdot {\rho _Q} $ |
其中, 波后波前密度比
| $ {\rho _{12}} = \frac{{(\gamma + 1){M^2}}}{{(\gamma - 1){M^2} + 2}} $ |
(7) 根据质量守恒方程确定波后速度为
| $ {\mathit{\boldsymbol{V}}_{\rm{H}}} = \underbrace {\mu \cdot M \cdot c \cdot \mathit{\boldsymbol{n}} + {\mathit{\boldsymbol{m}}_s}}_{{\mathit{\boldsymbol{V}}_{\rm{H}}}_n} + \underbrace {{\mathit{\boldsymbol{V}}_Q} - \left( {{\mathit{\boldsymbol{V}}_Q} \cdot \mathit{\boldsymbol{n}}} \right) \cdot \mathit{\boldsymbol{n}}}_{{\mathit{\boldsymbol{V}}_{\rm{H}}}_\tau } $ |
其中,VHτ为波后切向速度.
边界速度就是激波速度: xc=ms, 内点采用下面介绍的非结构动网格技术随动, 不需要像浮动激波装配法和激波阵面追踪法那样复杂的判断。
1.3 接触间断边界算法接触间断可以视为物质界面, 沿着界面法向两侧的速度和压力相等,密度不等.界面追踪法是一种常用的处理间断的方法.在界面追踪法中,通过准确求解Riemann问题得到接触间断两侧的参数.为了提高界面追踪法的性能, Lee等[22]对传统界面追踪法进行了改进.在本文介绍的间断装配方法中, 接触间断边界算法借鉴了之前的界面处理办法.
首先, 接触间断两侧参数沿界面法向构成一个Riemann问题, 通过求解该Riemann问题可以获得两侧流动参数, 分别标记为UL和UR, 其中U=[ρ, u, v, w, p]T.根据特征线理论, 使用Riemann不变量对求得的参数UL和UR进行修正.在这个过程中, 假设计算得到的流动速度是正确的, 这样就可以得到
| $ J = {\overline V _n} + \frac{{2a}}{{\gamma-1}} = {V_{en}} + \frac{{2{a_e}}}{{\gamma-1}} $ | (2) |
其中, Vn=V·n, 下标e表示对应的边界单元.
求解方程(2) 可以得到声速a, 对压力和密度进行修正只需要求解下面的方程:
| $ \begin{array}{l} \left\{ {_{p/{\rho ^\gamma } = {p_e}/\rho _e^\gamma }^{\rho {a^2} = \gamma p}} \right.\\ \;\;\;\;{V_\tau } = {V_{e\tau }} \end{array}$ |
按照上面的步骤逐步求解各个方程, 就可以全部获得接触间断的边界参数.
1.4 变形网格技术和ALE形式的有限体积法装配的激波和接触间断将流场分成多个光滑的子区域.计算过程中间断边界的运动速度按照上一小节算法确定, 牵引内部网格变形.变形网格算法采用弹簧比拟法, 基本原理是将连接网格边视为弹簧, 整个计算区域网格构成弹簧系统, 在弹簧系统内部节点(网格点)列出力的平衡方程组, 边界发生运动或变形后使弹簧网络受到拉伸和挤压, 整个弹簧系统受力发生变化, 通过求解弹簧网络的平衡方程来更新网格节点的位置, 由于求解的力平衡方程组对角占优, 采用Jacobi迭代很快收敛.
变形网格计算基于ALE(arbitrary Lagrange-Euler)有限体积描述下的三维可压缩非定常N-S方程:
| $ \frac{\partial }{{\partial t}}\iiint\limits_\varOmega \mathit{\boldsymbol{Q}}{\rm{d}}V + \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{\partial \varOmega } {\left[ {{\mathit{\boldsymbol{F}}_c}\left( {\mathit{\boldsymbol{Q}},{\mathit{\boldsymbol{x}}_c}} \right) + {\mathit{\boldsymbol{F}}_{\rm{V}}}\left( \mathit{\boldsymbol{Q}} \right)} \right]} \cdot \mathit{\boldsymbol{n}}{\rm{d}}S = 0 $ |
其中,Q和F分别表示守恒变量和流动通量. Ω为控制体,
由于篇幅所限这部分内容不再详述, 请参考刘君等的专著[23].
2 新型间断装配法的验证本文以激波管问题为例着重介绍基于非结构动网格的间断装配方法的原理.在激波管问题模拟中, 发现对于接触间断的计算未达到预计精度.为此模拟激波气泡问题, 分析造成这一问题的原因.
2.1 激波管问题包含非定常激波接触间断膨胀波等结构的Sod激波管问题[24]常被用来验证捕捉法高精度格式的间断分辨率.初始计算条件如下:
| $ (\rho, u, p) = \left\{ {_{(0.125, 0, 0.1)}^{(1, 0, 1)}} \right.\;\;\;\;_{0\; \le x < 1}^{ - 1 \le x < 0} $ |
采用二维非结构网格模拟这一问题, 计算过程参见图 1和图 2.在图 1(a)所示的初始时刻, D左侧有36752个三角形单元40个四边形单元.在图 2(a)所示在固壁反射前, D左侧有59370个三角形单元40个四边形单元.为了进行对比还采用捕捉法对该问题进行模拟, 整个计算域具有73536个三角形单元, 采用的通量计算方法和时间离散格式与装配方法是一样的, 分别是HLLC格式和4步Runge-Kutta格式.
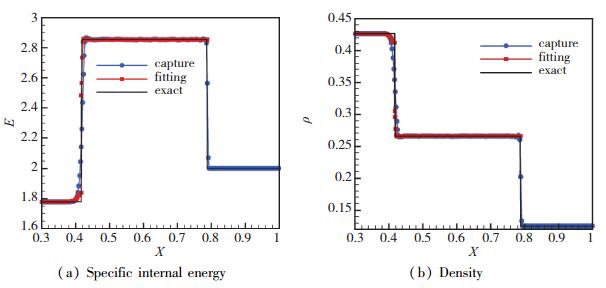
图 4给出了t=0.45时采用间断装配方法和捕捉方法计算得到的数值解和理论解的比较.比较发现:采用本文方法得到的激波位置和理论解几乎一致; 采用本文方法和激波捕捉方法计算得到的接触间断位置大致准确, 但都有一定的过渡区域, 且激波捕捉方法的过渡区要比本文装配方法的过渡区宽.
|
| 图 4 t=0.45时数值解与精确解的比较 Fig.4 Comparisons between numerical solutionds and exact solutions at unit time t=0.45 |
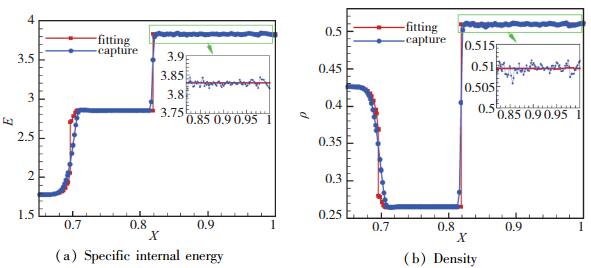
另外, 对激波在右侧壁面发生反射后的过程进行了模拟. 图 5给出了t=0.75时采用间断装配方法和捕捉方法计算得到的结果的对比.可以看出, 由于非结构网格的使用采用捕捉方法计算得到的结果会产生明显的波动, 这些波动破坏了物理上的一维特性, 网格对于结果的影响清晰可见.相对而言, 尽管同样是基于非结构网格,采用装配方法计算得到的结果却很光滑, 网格对结果的影响不是特别明显.
|
| 图 5 t=0.75时装配方法数值解与捕捉方法数值解的比较 Fig.5 omparisons between numerical solutions at unit time t=0.75 |
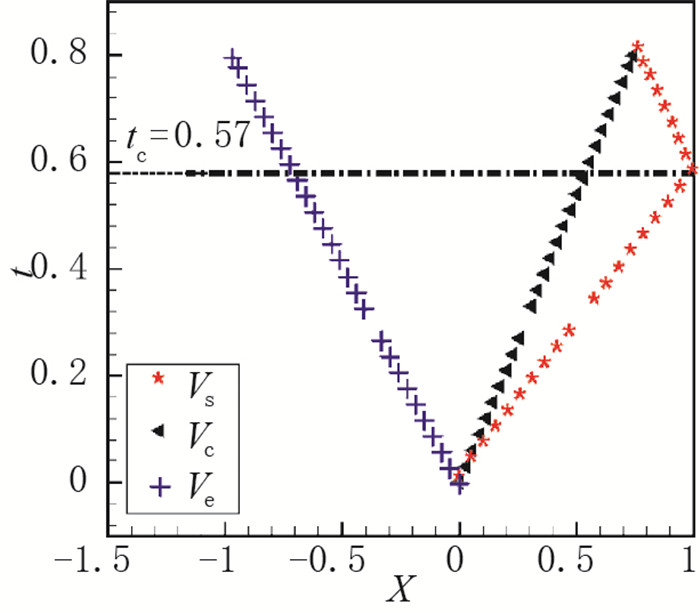
通过分析, 得出结论:采用激波装配方法计算得到的流场能够改善非结构网格的使用带来的不均匀性, 提高流场计算精度; 特别是对于激波的计算能够得到较为理想的计算结果, 有效地保证了空间格式的设计精度.然而还发现, 对于接触间断的计算却差强人意.为了弄清其中的道理, 对一些流动特征速度进行了统计分析, 如图 6所示.图中包含的特征速度分别有:Vs表示激波运动速度, Vc表示接触间断运动速度,Ve表示膨胀波运动速度.从图中可以看出:在t∈(0, 0.57) 范围内, 激波和接触间断匀速向右运动, 膨胀波匀速向左运动, 且激波运动速度大于接触间断运动速度.在t≈0.57时刻, 激波率先达到右侧壁面, 然后在壁面处发生反射, 反射后又匀速向左运动, 直到与接触间断发生相交, 形成一个新的Riemann问题.
|
| 图 6 特征速度 Fig.6 Characteristic velocity |
表 1给出了不同时段特征速度值与理论解的比较, 发现在激波碰撞前, 计算的激波运动速度误差最小, 反射后误差会有所增加, 但仍只有1.4%左右.相比之下, 对于膨胀波的计算(捕捉得到)误差达到3.8%左右.目前常用的Riemann求解方法对膨胀波的考虑很少, 特别是使用非结构网格时往往很难准确计算膨胀波的扇形区域.由于接触间断的计算严格依赖两侧参数, 膨胀波计算产生的误差是否严重影响了接触间断的计算精度, 为了对此进行分析设计了第2个算例, 激波气泡相互作用问题的模拟.
| 下载CSV 表 1 特征速度的比较 Tab.1 Comparisons of characteristic velocity |
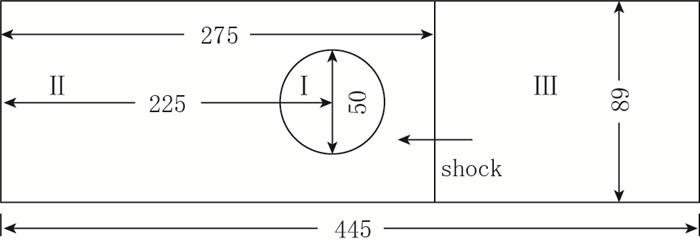
实验由Haas等完成[25], 静止空气中放置圆柱形氦气泡或R22(refrigerant 22) 气泡,在平面运动激波作用下气泡界面发生扭曲变形失稳.由于这个过程中出现激波在流体界面处的透射与反射多组分混合界面扰动的非线性传播等复杂的流动现象, 常用作检验自由界面捕捉类算法的经典算例[26-28].本文采用间断装配方法对气泡界面装配其他区域进行捕捉的方法进行模拟.几何模型和计算区域如图 7所示, 选择运动激波Mach数M=1.22的混合气泡实验条件, 气泡内是氦气和空气的混合气体, 比热比γ=1.648, 气体常数为R=1.578 kJ/(kg·K). I区为气泡内部, II区为激波波前静止空气, III区为激波波后区域. II区的密度和压力分别为ρⅡ=1.225 kg/m3和p=101325 Pa, III区参数由激波关系式得到, I区与II区的温度压力均相等.
|
| 图 7 计算模型(mm) Fig.7 Sketch of computational domain(lengths in millimeters) |
本算例是为了对2.1节问题进行验证, 因此只对流场中的接触间断进行了装配,考察接触间断装配算法的有效性.通过计算观察到:激波向左侧运动, t=35μs时与气泡表面相交, 在气泡表面反射.从激波气泡相交时刻算起, 图 8给出典型时刻的纹影图像, 图中虚线表示了气泡初始的位置.激波的作用使气泡产生变形, 气泡内压力急剧上升, 在气泡内形成一道向左运动的新的激波, 由于氦气中声速比空气高, 这道新的激波的运动速度快于入射激波.在t=52μs时刻, 在轴线处激波即将与气泡下游边界相遇, 而远离轴线处, 激波越过了气泡边界, 同时产生了向气泡内传播的反射激波. t=63μs时刻, 向气泡内传播的反射激波继续向前运动, 并在轴线处相交后互相穿越.到了t=102μs时刻, 气泡内的反射激波与气泡的上游边界相交, 再次产生了两道波系, 一是透过气泡向上游传播的稀疏波, 二是在气泡内产生的反射激波, 这道激波的强度很弱, 以至于在实验照片上都观察不到.

|
| 图 8 不同时刻的纹影图 Fig.8 Schlieren images of bubble at different times |
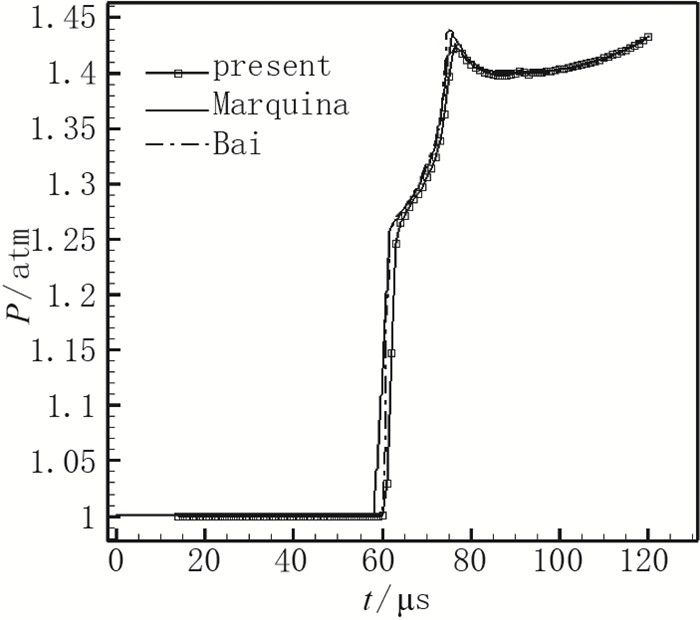
图 9中还给出气泡左侧边界下游3 mm处监测点的压力时程曲线和文献[27-28]计算值的定量比较, 符合很好.与实验进行对比分析可知, 计算结果定性合理, 具有较好的准确性, 从而验证了本文提出的接触间断计算方法.通过本算例的计算, 排除了接触间断装配算法的错误性, 也定性地说明2.1节算例中膨胀波的计算误差对接触间断产生了影响.消除膨胀波捕捉误差对计算结果精度提高会有帮助.
|
| 图 9 压力历程 Fig.9 Pressures profiles at 3 mm downstream the initial bubble position |
本文从激波管问题出发, 对基于非结构动网格间断装配方法原理进行了介绍.在对激波管问题模拟中发现, 非结构网格的使用会破坏物理上的一维特性, 使得计算结果出现不均匀性, 且这种不均匀性会在发生反射后随着激波强度增大而愈加明显.此外, 通过对激波气泡相互作用问题的模拟, 验证了本文中接触间断计算方法的科学性, 同时也定性地说明了采用非结构网格计算膨胀波也会产生较大的误差, 且产生的误差会对接触间断的计算产生影响.
致谢 本文工作是在国家自然科学基金No. 9154117的资助下完成的, 在此表示感谢| [1] |
李松波. 耗散守恒格式理论[M]. 北京: 高等教育出版社, 1997: 1-5. Li S B. The Theory of Dissipative Conservation Scheme[M]. Beijing: Higher Education Press, 1997: 1-5. (in Chinese) |
| [2] |
周毓麟, 李德元. 非定常流体力学数值方法的若干问题[J]. 数学进展, 1981, 10(1): 48-56. Zhou Y L, Li D Y. Some problems of the numerical method for unsteady flow dynamics[J]. Advances in Mathematics, 1981, 10(1): 48-56. (in Chinese) |
| [3] |
张涵信, 沈孟育. 计算流体力学—差分格式原理和应用[M]. 北京: 国防工业出版社, 2003. Zhang H X, Shen M Y. Computational fluid dynamics—theory and application of difference scheme[M]. Beijing: National Defense Industry Press, 2003. (in Chinese) |
| [4] |
Moretti G. Thirty-six years of shock fitting[J]. Computers & Fluids, 2002, 31: 719-723. |
| [5] |
阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006: 123-131. Yan C. Computational fluid dynamics algorithm and its application[M]. Beijing: Beihang University Press, 2006: 123-131. (in Chinese) |
| [6] |
Rawat P S, Zhong X L. On high-order shock-fitting and front-tracking schemes for numerical simulation of shock-disturbance interactions[J]. Journal of Computational Physics, 2010, 229: 6744-6780. DOI:10.1016/j.jcp.2010.05.021 |
| [7] |
Prakash A, Parsons N, Wang X, et al. High-order shock-fitting methods for direct numerical simulation of hypersonic flow with chemical and thermal nonequilibrium[J]. Journal of Computational Physics, 2011, 230(23): 8474-8507. DOI:10.1016/j.jcp.2011.08.001 |
| [8] |
Ren Y X. A robust shock-capturing scheme based on rotated Riemann solvers[J]. Computer & Fluids, 2003, 32: 1379-1403. |
| [9] |
Bonhaus D. A higher accurate finite element method for viscous compressible flows[D]. Blacksburg: Virginia Polytechnic Institute and State University, 1998.
|
| [10] |
Moretti G, Abbett M. A time-dependent computational method for blunt body flows[J]. AIAA Journal, 1966(4): 2136-2141. |
| [11] |
沈清, 高树椿, 张涵信. 钝锥大攻角超声速分离流场的数值模拟[J]. 空气动力学学报, 1991(1): 21-28. Shen Q, Gao S C, Zhang H X. Numerical simulation of supersonic separated flow over blunt cones at high angles of attack[J]. Acta Aerodynamics Sinica, 1991(1): 21-28. (in Chinese) |
| [12] |
叶友达. 航天飞机简化外形的数值模拟[D]. 长沙: 国防科技大学, 1991. Ye Y D. Numerical simulation of simplified shape of space shuttle[D]. Changsha: National University of Defense Technology, 1991(in Chinese). |
| [13] |
Paciorri R, Bonfiglioli A. A shock-fitting technique for 2D unstructured grids[J]. Computers & Fluids, 2009, 38(3): 715-726. |
| [14] |
Paciorri R, Bonfiglioli A. Shock interaction computations on unstructured, two-dimensional grids using a shock-fitting technique[J]. Journal of Computational Physics, 2011, 230(8): 3155-3177. DOI:10.1016/j.jcp.2011.01.018 |
| [15] |
Bonfiglioli A, Grottadaurea M, Paciorri R, et al. An unstructured three-dimensional shock-fitting solver for hypersonic flows[J]. Computers & Fluids, 2013, 73(6): 162-174. |
| [16] |
刘君, 邹东阳, 徐春光. 基于非结构动网格的非定常激波装配法[J]. 空气动力学学报, 2015, 33(1): 10-16. Liu J, Zou D Y, Xu C G. An unsteady shock-fitting technique based on unstructured moving grids[J]. Acta Aerodynamics Sinica, 2015, 33(1): 10-16. (in Chinese) |
| [17] |
刘君, 邹东阳, 董海波. 动态间断装配法模拟斜激波壁面反射[J]. 航空学报, 2016, 37(3): 836-846. Liu J, Zou D Y, Dong H B. A moving discontinuity fitting technique to simulate shock waves impinged on a straight wall[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 836-846. (in Chinese) |
| [18] |
刘君, 徐春光, 张帆. 电磁阀颤振的流固耦合模拟研究[J]. 航空学报, 2014, 35(7): 1922-1930. Liu J, Xu C G, Zhang F. Fluid-structure interaction simulation of the flutter phenomenon in eletromagnetiv valve[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(7): 1922-1930. (in Chinese) |
| [19] |
刘君, 徐春光, 董海波. 基于流固耦合计算方法模拟减压器动态特性[J]. 推进技术, 2014, 35(6): 721-726. Liu J, Xu C G, Dong H B. Numerical analysis of dynamics properties for a pressure relief vavle using a method of fluid and structure interaction[J]. Journal of Propulsion Technology, 2014, 35(6): 721-726. (in Chinese) |
| [20] |
Liu J, Bai X Z, Guo Z, et al. A new method for transferring flow information among meshes[J]. Computational Fluid Dynamics Journal, 2007, 15(4): 509-514. |
| [21] |
刘君, 白晓征, 王巍. 网格之间流场信息传递的高精度方法和验证[J]. 空气动力学学报, 2010, 28(1): 1-6. Liu J, Bai X Z, Wang W. High accurate method for transferring flow information among meshes and its valida-tion[J]. Acta Aerodynamics Sinica, 2010, 28(1): 1-6. (in Chinese) |
| [22] |
Lee T K, Zhong X. Spurious numerical oscillations in simulation of supersonic flows using shock-capturing schemes[J]. AIAA Journal, 1999, 37: 383-394. |
| [23] |
刘君, 白晓征, 郭正. 非结构动网格计算方法[M]. 长沙: 国防科技大学出版社, 2009: 23-98. Liu J, Bai X Z, Guo Z. The computational method of unstructured moving grids[M]. Changsha: National University of Defence Technology Press, 2009: 23-98. (in Chinese) |
| [24] |
Marquina A, Mulet P. Restoration of the contact surface in the HLL-Riemann solver[J]. Shock Waves, 1994, 4: 25-34. DOI:10.1007/BF01414629 |
| [25] |
Haas J F, Sturtevant B. Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities[J]. Journal of Fluid Mechanics, 1987, 181(1): 41-76. |
| [26] |
Quirk J J, Karni S. On the dynamics of a shock-bubble interaction[J]. Journal of Fluid Mechanics, 1996, 318(1): 129-163. |
| [27] |
Marquina A, Mulet P. A flux-split algorithm applied to conservative models for multi-component compressible flows[J]. Journal of Computational Physics, 2003, 185(1): 120-138. DOI:10.1016/S0021-9991(02)00050-5 |
| [28] |
白晓征. 包含运动界面的爆炸流场数值模拟方法及其应用[D]. 长沙: 国防科技大学, 2009. Bai X Z. Numerical simulation method and its application of explosion flow field involving moving interface[D]. Changsha: National University of Defense Technology, 2009(in Chinese). |



