21世纪以来, 湍流数值模拟方法的研究一直受到国内外相关机构的密切关注, 并把与其相关的研究方向列为重大研究计划.例如, 欧盟于2002年、2004年和2009年陆续资助的FLOMANIA研究计划、DESider研究计划以及ATAAC研究计划均涉及了湍流数值模拟方法的研究.在我国, 国家自然科学基金委在“十二五”和“十三五”期间均把与湍流(尤其是可压缩湍流)相关的数值研究列为重点资助的领域.
现阶段, Reynolds平均/大涡模拟(RANS/LES)混合方法属于一类有希望替代RANS方法, 被广泛应用于工程问题的湍流数值模拟方法. RANS/LES混合方法能够兼顾LES和RANS的优点, 即边界层内的湍流应用RANS计算, 分离区则采用LES计算.分离涡模拟(detached eddy simulation, DES)方法属于一类当今比较热门的RANS/LES混合方法, 如Spalart等[1]提出的基于Spalart-Allmaras(SA)一方程模型的DES方法, 以及Strelets[2],Fan等[3]提出的基于两方程SST模型的DES方法等.原始版本的DES方法关于RANS和LES计算区域的划分严重依赖网格尺度, 且RANS和LES计算区域的分界位置模糊, 即DES方法的“灰区”问题[4].如果网格设计不好, “灰区”问题将会导致边界层内的模化应力严重不足, 进而出现网格诱导分离的伪物理现象.为了解决DES方法的“灰区”问题, 人们给出了不同的改进策略, 如DDES方法[5]、IDDES方法[6]以及ZDES方法[7]等.这些改进的方法尽管在某些物理问题上能够减缓边界层内模化应力不足的问题, 给出一些改善的计算结果, 然而仍未从根本上解决“灰区”问题.
为了避开DES方法中的“灰区”问题, 人们通过引入第二长度尺度, 发展了另外一类能够实现RANS和LES混合计算的方法, 即尺度自适应模拟(scale-adaptive simulation, SAS)方法[8-13].在SAS方法中, von Karman长度Lvk被选作第二长度尺度, 该长度尺度由流场信息求解得出. RANS和LES的计算分界通过与Lvk有关的函数进行自适应判断, 减少了由网格设计等非物理因素对RANS和LES计算分区带来的影响, 进而可以减少边界层内的模化应力不足问题.需要说明的是, SAS方法本质上仍旧是一种RANS方法, 然而在分离区可以实现类似LES的计算效果.
从上述分析可以看出, 改进版DES和SAS方法的主要思想是:通过减少或避开网格设计对RANS和LES计算分区的影响, 进而缓和边界层内模化应力不足的问题.人们习惯于单独关注RANS和LES计算的合理分区这一线索, 而未关注这些方法存在的另一个问题, 即如何建立这些方法计算的流场与准确流场或者直接数值模拟(direct numerical simulation, DNS)流场之间的联系.我们知道, LES流场与DNS流场之间的关联, 可以通过对DNS流场进行直接滤波得到.然而, 现有的研究无法给出SAS(或DES)流场与LES流场之间的关联, 这导致了SAS(或DES)流场与DNS流场之间的“失联”. SAS和DES方法均存在RANS和LES计算的分区问题, 而LES方法不存在计算分区问题.若探索出SAS(或DES)方法与LES方法之间的关联机理, 即可建立SAS(或DES)流场与DNS流场之间的联系, 也就可以从根本上消除由SAS(或DES)方法的计算分区引起的边界层内模化应力不足问题.
本文针对SAS和LES方法之间的关联性开展了研究.通过分析SAS和LES控制方程、湍流模式和动态亚格子(SGS)模型以及SAS流场和LES流场的关联性, 旨在从理论上和数值流场上建立二者之间的联系, 为SAS方法的进一步改进提供机理层次上的建议.
1 数值计算方法 1.1 SAS和LES方法的控制方程SAS在本质上仍属于RANS方法, 故采用的控制方程应与RANS相同. RANS和LES采用的控制方程是通过对连续性方程、动量方程和能量方程进行某种平均或者滤波操作而得到.这里, 须作如下说明: (1)平均或者滤波属于数学形式上的操作, 均是隐式操作; (2)系综平均是指针对某物理量进行的时间和统计空间平均, 在RANS方法中常等价于时间平均; (3) Reynolds平均泛指系综平均和Favre平均(也称为密度加权平均), 故由这些平均操作推导出来的Navier-Stokes(N-S)方程为Reynolds平均N-S方程.为了表述的方便, 文中的一些符号作如下说明: 〈·〉和{·}分别记作系综平均操作和Favre平均操作; 顶标“-”和“~”分别记作直接滤波和Favre滤波.对于任意物理量ϕ而言, 则有
| $ \left\{ \phi \right\} = \left\langle {\rho \phi } \right\rangle /\left\langle \rho \right\rangle 和\widetilde \phi = \overline {\rho \phi } /\overline \rho $ |
在直角坐标系下, 经过Favre平均的三维可压缩控制方程可以写成如下的守恒形式:
| $ \frac{{\partial \left\langle \rho \right\rangle }}{{\partial t}} + \frac{{\partial \left( {\left\langle \rho \right\rangle \{ {u_i}\} } \right)}}{{\partial {x_i}}} = 0 $ | (1) |
| $ \begin{align} & \frac{\partial (\left\langle \rho \right\rangle \{{{u}_{i}}\})}{\partial t}+\frac{\partial \left( \left\langle \rho \right\rangle \{{{u}_{i}}\}\{{{u}_{j}}\} \right)}{\partial {{x}_{j}}}=-\frac{\partial \left\langle p \right\rangle }{\partial {{x}_{i}}}+ \\ & \ \ \ \ \ \frac{\partial \left( \{{{\tau }_{ij}}\}+\tau _{ij}^{\bmod } \right)\text{ }}{\partial {{x}_{j}}} \\ \end{align} $ | (2) |
| $ \begin{gathered} \frac{{\partial \left( {\left\langle \rho \right\rangle \{ E\} } \right)}}{{\partial t}} + \frac{{\partial \left[ {\left( {\left\langle \rho \right\rangle \{ E\} + \left\langle p \right\rangle } \right)\{ {u_i}\} } \right]}}{{\partial {x_i}}} = - \hfill \\ \;\;\;\;\;\;\frac{{\partial \left( {\{ {q_i}\} + q_i^{\bmod }} \right)}}{{\partial {x_i}}} + \frac{{\partial \left( {\{ {u_j}\} \{ {\tau _{ij}}\} + \{ {u_j}\} \tau _{ij}^{\bmod }} \right)}}{{\partial {x_i}}} \hfill \\ \end{gathered} $ | (3) |
经过Favre滤波的三维可压缩控制方程则可以写成如下的形式:
| $ \frac{{\partial \bar \rho }}{{\partial t}} + \frac{{\partial (\bar \rho {{\tilde u}_i})}}{{\partial {x_i}}} = 0 $ | (4) |
| $ \frac{{\partial (\bar \rho {{\tilde u}_i})}}{{\partial t}} + \frac{{\partial (\bar \rho {{\tilde u}_i}{{\tilde u}_j})}}{{\partial {x_j}}} = - \frac{{\partial \bar p}}{{\partial {x_i}}} + \frac{{\partial ({{\tilde \tau }_{ij}} + \tau _{ij}^{{\text{SGS}}} + D_{ij}^{{\text{SGS}}})}}{{\partial {x_j}}} $ | (5) |
| $ \begin{gathered} \frac{{\partial (\bar \rho \tilde E)}}{{\partial t}} + \frac{{\partial [(\bar \rho \tilde E + \bar p){{\tilde u}_i}]}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left( { - {{\tilde q}_i} + {{\tilde u}_j}{{\tilde \tau }_{ij}} + } \right. \hfill \\ {\text{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {J_i^{{\text{SGS}}} + \sigma _i^{{\text{SGS}}} - Q_i^{{\text{SGS}}} - H_i^{{\text{SGS}}}} \right) \hfill \\ \end{gathered} $ | (6) |
在方程(1)~(6)中, ρ为密度, ui为速度分量, p为压力, E为总能, 下角标i和j为张量指标.由理想气体状态方程可以建立p和E之间的关系: p=(γ-1)(E-0.5ρuiui). τij和qi分别为黏性应力项和热通量项:
| $ {\tau _{ij}} = \mu \left( {2{S_{ij}} - \frac{2}{3}{\delta _{ij}}{S_{kk}}} \right) $ |
| $ {q_i} = - \frac{\mu }{{(\gamma - 1)Pr}}\frac{{\partial T}}{{\partial {x_i}}} $ |
其中, γ为空气的比热比, μ为分子黏性系数, Pr为层流Prandtl数,
| $ \tau _{ij}^{\bmod } = - \left( {\left\langle {\rho {u_i}{u_j}} \right\rangle - \left\langle \rho \right\rangle \{ {u_i}\} \{ {u_j}\} } \right) $ |
| $ q_i^{\bmod } = \frac{1}{{\gamma - 1}}\left( {\left\langle {\rho {u_i}T} \right\rangle - \left\langle \rho \right\rangle \{ {u_i}\} \{ T\} } \right) $ |
τijSGS, DijSGS, JiSGS, QiSGS, HiSGS和σiSGS为方程(5)和(6)经过Favre滤波后出现的SGS未封闭项:
| $ \tau _{ij}^{{\text{SGS}}} = - \bar \rho (\widetilde {{u_i}{u_j}} - {\tilde u_i}{\tilde u_j}) $ | (7) |
| $ D_{ij}^{{\text{SGS}}} = {\bar \tau _{ij}} - {\tilde \tau _{ij}} $ | (8) |
| $ J_i^{{\text{SGS}}} = - \frac{1}{2}\bar \rho (\widetilde {{u_i}{u_k}{u_k}} - {\tilde u_i}\widetilde {{u_k}{u_k}}) $ | (9) |
| $ Q_i^{{\text{SGS}}} = {\bar q_i} - {\tilde q_i} $ | (10) |
| $ H_i^{{\text{SGS}}} = \frac{1}{{\gamma - 1}}(\bar \rho {\text{ }}\widetilde {{u_i}T} - \bar \rho {\tilde u_i}\tilde T) $ | (11) |
| $ \sigma _i^{{\text{SGS}}} = \overline {{u_j}{\tau _{ij}}} - {\tilde u_j}{\tilde \tau _{ij}} $ | (12) |
方程(2)和(3)中的未封闭项τijmod和qimod可以通过建立湍流涡黏假设进行处理:
| $ \tau _{ij}^{\bmod } = {\mu _{\text{T}}}\left( {2\{ {S_{ij}}\} - \frac{2}{3}{\delta _{ij}}\{ {S_{kk}}\} } \right) $ |
| $ q_i^{\bmod } = - \frac{{{\mu _{\text{T}}}}}{{(\gamma - 1)P{r_{\text{T}}}}}\frac{{\partial \{ T\} }}{{\partial {x_i}}} $ |
其中, μT为湍流黏性系数, 须建立湍流模型进行求解; PrT为湍流Prandtl数, 在RANS或SAS计算中, 常近似取定值0.92.
在本文中, 湍流黏性系数μT由基于SA湍流模型的SAS方法[13]计算得出.原始的SA湍流模型输运方程[14]可以写成如下形式:
| $ \begin{gathered} \frac{{\partial {\nu _{\text{T}}}}}{{\partial t}} + \{ {u_j}\} \frac{{\partial {\nu _{\text{T}}}}}{{\partial {x_j}}} = {C_{{b_1}}}(1 - {f_{{t_2}}})\{ \mathit{\Omega }\} {\nu _{\text{T}}} + \hfill \\ \left[ {{C_{{b_1}}}((1 - {f_{{t_2}}}){f_{{v_2}}} + {f_{{t_2}}})/{\kappa ^2} - {C_{{w_1}}}{f_w}} \right]{\left( {\frac{{{\nu _{\text{T}}}}}{d}} \right)^2} - \hfill \\ \frac{{{C_{{b_2}}}}}{\sigma }{\nu _{\text{T}}}\frac{{{\partial ^2}{\nu _{\text{T}}}}}{{\partial x_j^2}} + \frac{1}{\sigma }\frac{\partial }{{\partial {x_j}}}\left[ {(\nu + (1 + {C_{{b_2}}}){\nu _{\text{T}}})\frac{{\partial {\nu _{\text{T}}}}}{{\partial {x_j}}}} \right] \hfill \\ \end{gathered} $ | (13) |
湍流黏性系数μT按照下面的式子进行计算:
| $ {\mu _{\text{T}}} = \left\langle \rho \right\rangle {\nu _{\text{T}}}{f_{{v_1}}}, {f_{{v_1}}} = \frac{{{\chi ^3}}}{{{\chi ^3} + C_{{v_1}}^3}}, \chi \equiv \frac{{{\nu _{\text{T}}}}}{\nu } $ |
方程(13)中的一些函数具体表达式如下:
| $ {f_{{t_2}}} = {C_{{t_3}}}\exp ( - {C_{{t_4}}}{\chi ^2}), {f_w} = g{\left[ {\frac{{1 + C_{{w_3}}^6}}{{{g^6} + C_{{w_3}}^6}}} \right]^{\frac{1}{6}}}, $ |
| $ g = r + {C_{{w_2}}}({r^6} - r), \;\;\;\;r \equiv \frac{{{\nu _{\text{T}}}}}{{\mathit{\hat \Omega }{\kappa ^2}{d^2}}}, $ |
| $ \mathit{\hat \Omega } = \{ \mathit{\Omega }\} + \frac{{{\nu _{\text{T}}}{f_{{v_2}}}}}{{{\kappa ^2}{d^2}}}, {f_{{v_2}}} = 1 - \frac{\chi }{{1 + \chi {f_{{v_1}}}}} $ |
其中,
| $ {C_{{b_1}}} = 0.1355, \sigma = 2/3, {C_{{b_2}}} = 0.622, \kappa = 0.41, $ |
| $ \;\;\;\;\;{C_{{w_1}}} = \frac{{{C_{{b_1}}}}}{{{\kappa ^2}}} + \frac{{1 + {C_{{b_2}}}}}{\sigma }, {C_{{w_2}}} = 0.3, {C_{{w_3}}} = 2 $ |
| $ \;\;\;\;\;\;\;\;\;\;{C_{{v_1}}} = 7.1, {C_{{t_3}}} = 1.2, {C_{{t_4}}} = 0.5{\text{ }} $ |
为了实现SAS计算, 须在SA湍流模型中引入von Karman长度尺度Lvk, 并把Lvk作为湍流计算的第二长度尺度.在具体操作中, SA模型方程中的壁面距离d求解方式须改为下面的形式:
| $ \hat d = \min (d, {L_{{\text{vk}}}}/\kappa ) $ | (14) |
Lvk按照下面的式子进行计算:
| $ {L_{{\text{vk}}}} = \frac{{\kappa \{ \mathit{\Omega }\} }}{{\sqrt {\frac{{{\partial ^2}\{ {u_k}\} }}{{\partial x_i^2}}\frac{{{\partial ^2}\{ {u_k}\} }}{{\partial x_j^2}}} }} $ |
在公式(7)~(12)描述的6个SGS未封闭项中, σiSGS, DijSGS和QiSGS这3项经常被忽略[15-17], 故仅须对τijSGS, HiSGS和JiSGS进行建模.对于可压缩湍流而言, τijSGS分解成反对称部分τijSGS-δijτkkSGS/3和对称部分τkkSGS进行单独建模[18]:
| $ \tau _{ij}^{{\text{SGS}}} - \frac{1}{3}{\delta _{ij}}\tau _{kk}^{{\text{SGS}}} = 2{C_{\text{R}}}{{\hat \Delta }^2}\bar \rho \tilde S\left( {{{\tilde S}_{ij}} - \frac{1}{3}{\delta _{ij}}{{\tilde S}_{kk}}} \right) = {C_{\text{R}}}{\alpha _{ij}} $ |
| $ \tau _{kk}^{{\text{SGS}}} = - 2{C_{\text{I}}}{{\hat \Delta }^2}\bar \rho {{\tilde S}^2} = - {C_{\text{I}}}\alpha $ |
其中,
| $ {C_{\text{R}}} = \frac{{\left\lceil {{L_{ij}}{M_{ij}}} \right\rceil }}{{\left\lceil {{M_{kl}}{M_{kl}}} \right\rceil }} - \frac{1}{3}\frac{{\left\lceil {{L_{mm}}{M_{nn}}} \right\rceil }}{{\left\lceil {{M_{kl}}{M_{kl}}} \right\rceil }} $ |
| $ {C_{\text{I}}} = \frac{{\left\langle {{L_{kk}}} \right\rangle }}{{\left\langle {\beta - \hat \alpha } \right\rangle }} $ |
下角标m, n, k和l均为张量指标.符号
| $ \widetilde {\widetilde f} = \widehat {\overline {\rho f} }/\widehat {\bar \rho };{L_{ij}} = \widehat {\bar \rho {{\tilde u}_i}{{\tilde u}_j}} - \widehat {\bar \rho }{\widetilde {\widetilde u}_i}{\widetilde {\widetilde u}_j},{M_{ij}} = {\beta _{ij}} - {\hat \alpha _{ij}} $ |
其中, β和βij的数学表达式分别为
| $ \beta = 2{\hat \Delta ^2}\bar \rho \widetilde {\widetilde S},{\beta _{ij}} = - 2{\hat \Delta ^2}\bar \rho \widetilde {\widetilde S}\left( {{{\widetilde {\widetilde S}}_{ij}} - \frac{1}{3}{\delta _{ij}}{{\widetilde {\widetilde S}}_{kk}}} \right) $ |
HiSGS的建模方式如下:
| $ H_i^{{\text{SGS}}} = \frac{1}{{\gamma - 1}}(\bar \rho {\text{ }}\widetilde {{u_i}T} - \bar \rho {{\tilde u}_i}\tilde T) = - \frac{{{\mu _{\text{T}}}}}{{(\gamma - 1)P{r_{\text{T}}}}}\frac{{\partial \tilde T}}{{\partial {x_j}}} $ |
湍流黏性系数μT的计算公式为
| $ P{r_{\text{T}}} = \frac{{{C_{\text{R}}}\left\lceil {{K_j}{K_j}} \right\rceil }}{{\left\lceil {{N_i}{K_i}} \right\rceil }} $ |
Ni和Ki的数学表达式分别为
| $ {N_i} = \widehat {\bar \rho {{\tilde u}_i}\tilde T} - \widehat {\bar \rho }{\widetilde {\widetilde u}_i}\widetilde {\widetilde T} $ |
| $ {K_i} = {{\hat \Delta }^2}\bar \rho \widehat {|\tilde S\frac{{\partial \tilde T}}{{\partial {x_i}}}|} - {{\hat \Delta }^2}\widehat {\bar \rho }|\widetilde {\widetilde S}|\frac{{\partial \widetilde {\widetilde T}}}{{\partial {x_i}}} $ |
JiSGS的建模可以直接简化为下面的形式[23]:
| $ J_i^{{\text{SGS}}} = {{\tilde u}_j}\tau _{ij}^{{\text{SGS}}} $ |
控制方程的求解采用有限体积方法.在可压缩湍流流场中, 激波结构可能会出现.激波的捕捉需要高耗散的格式(如迎风格式), 而湍流的捕捉则需要低耗散的格式(如中心格式).为了同时满足捕捉激波和湍流的离散格式要求, 对流项的离散须谨慎处理.我们曾发展了一类适用于模拟激波和湍流共存流动的数值离散格式, 即中心/迎风混合格式[24].在当前研究中, 对流项的离散采用2阶精度的中心/迎风混合格式, 黏性项的离散则采用2阶精度的中心格式, 时间推进采用2阶精度的近似因子分解方法.
2 SAS和LES方法的关联性理论分析从动态SGS模型的建模过程可以看出, 如果把τijmod和qimod分别对应τijSGS和HiSGS, 不难发现SAS和LES的控制方程在数学形式上是相同的.针对同一个流动物理问题, 求解数学形式是一样的控制方程, 为何会获得不同的结果?SAS和LES方法之间存在什么样的差异?他们之间又存在何种联系?为了解答这些疑问, 下面将从控制方程的数学推导过程以及未封闭项的处理过程进行分析.
2.1 SAS和LES的控制方程关联性分析SAS和LES方法的控制方程可以看作是针对原始的控制方程(即连续性方程、动量方程和能量方程), 采用某种数学积分而得到的. SAS中的系综平均操作可以写成如下的数学积分形式:
| $ \left\langle \phi \right\rangle = \frac{1}{T}\int_t^{t + T} {\phi {\text{d}}t} $ |
事实上, 系综平均操作与局部各向同性的体积平均操作存在等价关系[25], 即
| $ \left\langle \phi \right\rangle = \frac{1}{T}\int_t^{t + T} {\phi {\text{d}}t} = \frac{1}{V}\int_V {\phi {\text{d}}V} $ |
在LES中, 物理量ϕ的滤波可以写成下面的积分形式:
| $ \bar \phi = \int_{ - \infty }^\infty {\phi G{\text{d}}V} $ |
其中, G为滤波函数, 常见有盒式滤波、Gauss滤波和谱截断滤波[26].对于盒式滤波而言, 在滤波体积V中, G=1/V为定值; 在其他位置, G=0.因此, LES中的盒式直接滤波等价于局部体积平均操作:
| $ \bar \phi = \frac{1}{V}\int_V {\phi {\text{d}}V} $ |
系综平均和盒式直接滤波在数学形式上存在一致性.不难理解, Favre平均和Favre滤波在数学形式上也存在一致性.对于Gauss滤波和谱截断滤波而言, 滤波函数G在滤波空间存在变化, 因此滤波操作不等价于局部体积平均操作.为了编程的方便, 人们常选用盒式滤波函数作为LES的滤波操作.
从上面的分析可以看出, 平均操作和盒式滤波操作仅存在名称上的差异, 而数学形式相同.因此, SAS和LES的控制方程在数学形式上具有一致性.在数学形式上, SAS方法采用的控制方程, 既可看作经过Favre平均处理得到, 也可看作经过基于盒式滤波的Favre滤波处理得到.在物理上, 关于SAS的控制方程作如下解释更为合理:在RANS计算区域内, SAS方法的控制方程经过Favre平均处理得到; 在LES计算区域内, SAS方法的控制方程经过基于盒式滤波的Favre滤波处理得到.
虽然SAS和LES的控制方程在数学形式上具有一致性, 但是我们还必须清醒地认识到, SAS控制方程中的未封闭项τijmod和qimod以及LES控制方程中的未封闭项τijSGS和HiSGS, 存在建模的较大差异, 这也是SAS和LES方法计算效果存在差异的关键之处.因此, 湍流建模之间的关联性是SAS和LES两种方法之间建立关联性的核心.
2.2 SAS和LES的湍流建模关联性分析在SA模型的输运方程(13)中, 方程右端的第1项、第2项和其他项分别为源项的产生项SP, 毁灭项SD以及扩散项SC:
| $ {S_{\text{P}}} = {C_{{b_1}}}(1 - {f_{{t_2}}})\{ \mathit{\Omega }\} {\nu _{\text{T}}} $ |
| $ {S_{\text{D}}} = \left[ {{C_{{b_1}}}((1 - {f_{{t_2}}}){f_{{v_2}}} + {f_{{t_2}}})/{\kappa ^2} - {C_{{w_1}}}{f_w}} \right]{\left( {\frac{{{\nu _{\text{T}}}}}{d}} \right)^2} $ |
| $ {S_{\text{C}}} = \frac{1}{\sigma }\frac{\partial }{{\partial {x_j}}}\left[ {(\nu + (1 + {C_{{b_2}}}){\nu _{\text{T}}})\frac{{\partial {\nu _{\text{T}}}}}{{\partial {x_j}}}} \right] - \frac{{{C_{{b_2}}}}}{\sigma }{\nu _{\text{T}}}\frac{{{\partial ^2}{\nu _{\text{T}}}}}{{\partial x_j^2}} $ |
在非定常分离流动区, 可假设源项的产生项SP和毁灭项SD相平衡, 即SP+SD=0.因此, 可以得出源项平衡时的等效湍流黏性系数μTeq的表达式:
| $ \mu _{\text{T}}^{{\text{eq}}} = {C_{\text{S}}}\left\langle \rho \right\rangle {d^2}\{ \mathit{\Omega }\} $ | (15) |
其中,CS为μTeq的Smagorinsky涡黏模型系数:
| $ {C_{\text{S}}} = \frac{{ - {C_{{b_1}}}(1 - {f_{{t_2}}})}}{{{C_{{b_1}}}\left[ {(1 - {f_{{t_2}}}){f_{{v_2}}} + {f_{{t_2}}}} \right]/{\kappa ^2} - {C_{{w_1}}}{f_w}}}{f_{{v_1}}} $ |
由公式(14)和(15)可得出SAS方法在非定常分离流动区的等效湍流黏性系数μTeq :
| $ \mu _{\text{T}}^{{\text{eq}}} = \left\langle \rho \right\rangle {C_{\text{S}}}{\left( {\frac{{{L_{vk}}}}{\kappa }} \right)^2}\{ \mathit{\Omega }\} $ | (16) |
可以看出, 在非定常分离流动区, SAS和LES方法关于湍流黏性系数的计算公式存在如下的相似关联性: (1)模型系数CR和CS之间的相似; (2)长度尺度
圆柱可压缩绕流属于一类典型的流动问题, 它包含了一些常见的流动现象, 如边界层流动、剪切层流动、大范围分离流动、涡脱落以及激波/湍流相互作用等.关于圆柱可压缩绕流的实验方面, 现有的文献可以收集到大量的定量实验数据, 用于数值方法的可靠性验证.本文选取的绕圆柱可压缩湍流的流动参数为:来流Mach数Ma∞为0.55, 基于圆柱直径D的Reynolds数Re为2×105.为了保证计算结果的可靠性验证, 选取了3组来自不同实验的数据, 且实验数据与当前计算参数相近, 见表 1.
| 下载CSV 表 1 用于验证的实验细节 Tab.1 Experimental details for validation |
为了保证对比分析的公正性, SAS和LES的计算参数和边界条件设置均相同.计算网格采用O型网格; 周向、径向和展向的网格数分别为257, 257和81; O型计算域的直径为50 D; 圆柱壁面的最小网格尺度为10-5D. O型计算域的远场边界采用基于当地一维Rieman不变量的无反射边界条件, 圆柱壁面采用无滑移、无穿透的绝热边界条件, 展向采用周期性边界条件.为了便于SAS和LES的对比讨论, 下文中的物理量去掉前文中系综平均或滤波的符号, 并把符号〈·〉t-s记为时间和展向平均.
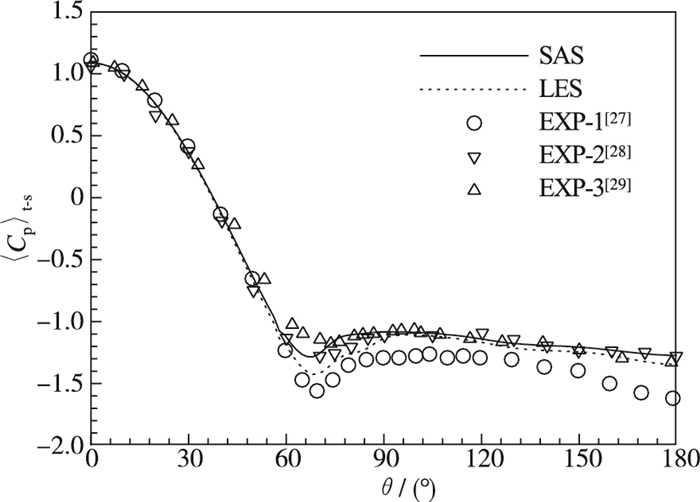
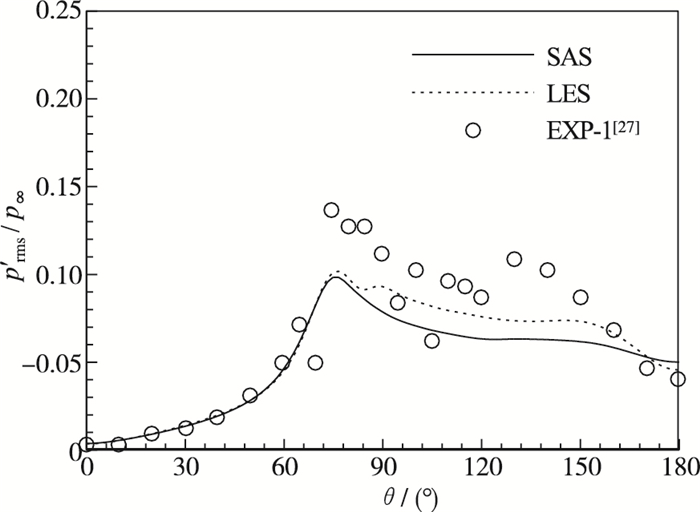
3.2 SAS和LES的定量流场信息对比分析对于圆柱绕流而言, 能够代表其流场的主要流动特征有:圆柱的受力、流场中的速度分布和湍流统计量分布等. 图 1给出了圆柱表面的平均压力系数〈Cp〉t-s分布曲线.这里, θ=0°对应圆柱的迎风滞止点.可以看出SAS预测的圆柱背压略高于LES, 尤其在边界层分离位置较为明显, 这与SAS方法在边界层内仍属于RANS计算有关. SAS和LES预测的边界层分离位置分别为θ ≈75.8°和77.4°, SAS预测的流动分离位置比LES略微靠前.圆柱表面的压力脉动均方根值prms′分布如图 2所示.在边界层流动分离前, SAS和LES预测的prms′值几乎一致.然而在流动分离后, SAS预测的prms′值则略低于LES, 这意味着SAS在边界层内模拟的湍流脉动仍存在略微不足的情况.同时, 这也说明SAS在边界层内的模化应力不足仅对流动分离后的边界层存在明显影响.
|
| 图 1 圆柱表面平均压力系数分布 Fig.1 Distributions of mean pressure coefficient on cylinder surface |
|
| 图 2 圆柱表面压力脉动均方根值分布 Fig.2 Distributions of root-mean-square value of fluctuating pressure on cylinder surface |
图 1和图 2还给出了当前计算结果与实验数据的对比.从图 1的〈Cp〉t-s曲线对比结果可以看出, SAS和LES的计算结果与Gowen等[28]和Macha[29]的实验数据较为接近, 略高于Rodriguez[27]的实验数据.从图 2的prms′曲线对比结果可以看出, 在流动分离前, SAS和LES的计算结果与Rodriguez的实验数据均相符较好; 在分离位置后方, 虽然在某些位置处当前计算略低于Rodriguez的实验数据, 然而整体而言仍存在较好的相符性.事实上, Ma∞=0.5~0.6的圆柱绕流处于阻力上升现象的初始阶段[30-31], 圆柱的表面压力和压力脉动对来流参数的变化较为敏感, 不同的实验存在明显的偏差[32].基于此, 从上面的整体对比结果而言, 当前计算具有较好的可靠性.
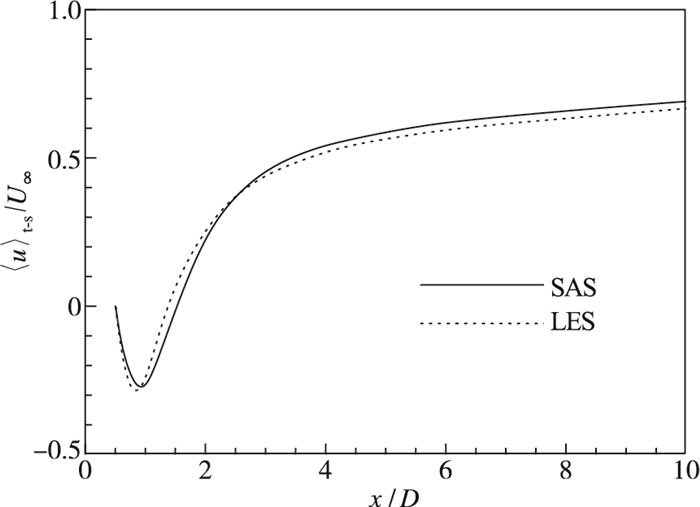
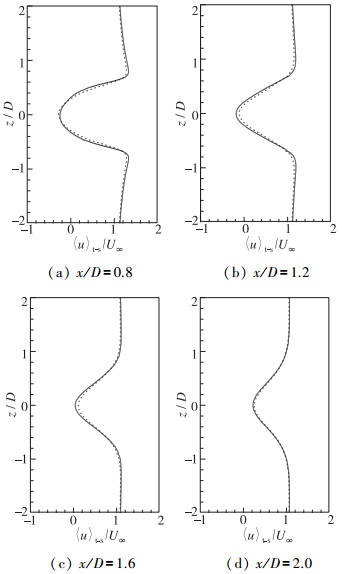
流场中的速度分布能够反映SAS和LES对大尺度流动信息的预测能力. 图 3和图 4分别给出了尾迹中心线上和不同流向位置处的平均流向速度分布, 可以看出SAS和LES预测的大尺度平均流动信息较为接近.我们知道, SAS在边界层内采用RANS计算, 在圆柱的尾迹区内则采用LES计算.通过图 3和图 4的对比结果, 可以看出边界层内的RANS计算并未影响SAS对圆柱尾迹区大尺度平均流动信息的预测.
|
| 图 3 尾迹中心线上的平均流向速度分布 Fig.3 Mean streamwise velocity distributions on centering line in the wake |
|
| 图 4 不同流向位置处的平均流向速度剖面 Fig.4 Profiles of mean streamwise velocities at different streamwise positions |
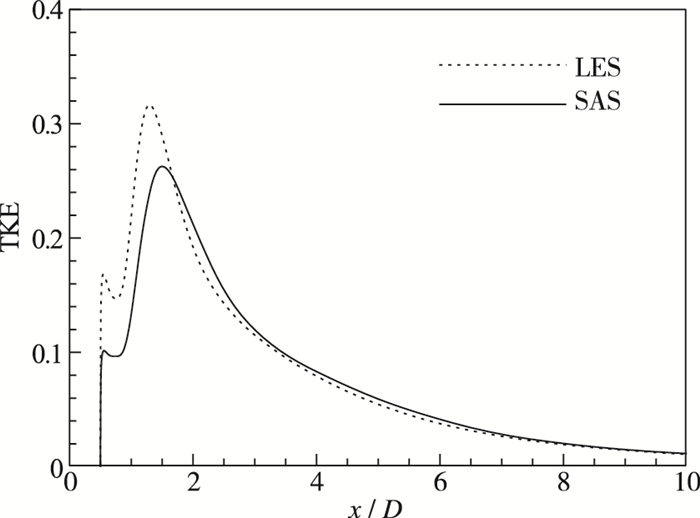
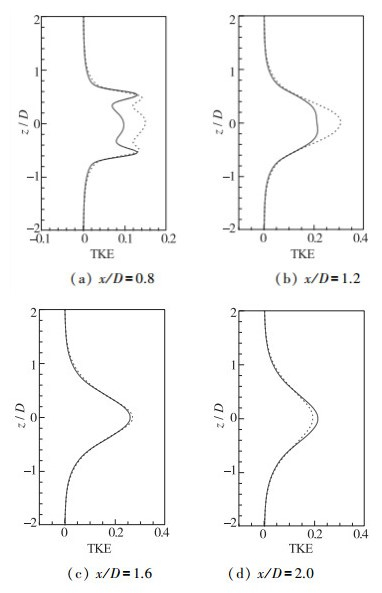
SAS和LES对小尺度湍流脉动信息的预测能力可以通过湍流统计量(如湍动能)的分布来评估. 图 5和图 6分别给出了尾迹中心线上和不同流向位置处的平均湍动能TKE分布.这里, TKE的定义为TKE= 〈ρui′ui′〉t-s/2.从图 5中可以看出, 对于SAS而言, 在x/D<1.6的近尾迹区, 预测的TKE值明显低于LES, 而在x/D>1.6的稍远尾迹区则几乎与LES一致.前面曾经指出, SAS方法仍存在边界层内模化应力不足的问题. 图 5的结果说明SAS方法在边界层内的模化应力不足问题会影响到近尾迹区, 即影响区超过边界层的范围.此外, 通过详细对比不同流向位置处的TKE剖面(见图 6)可以看出, 在x/D=0.8和1.2处, SAS预测的TKE分布仅峰值比LES偏低, 整体变化趋势则几乎与LES一致, 这说明SAS在圆柱近尾迹区的湍流耗散大于LES.在x/D=1.6和2.0处, SAS预测的TKE剖面则几乎与LES一致, 这意味着在圆柱稍远的尾迹区SAS几乎可以完全等效于LES.
|
| 图 5 尾迹中心线上的平均湍动能分布 Fig.5 Mean turbulent kinetic energy distributions on centering line in the wake |
|
| 图 6 不同流向位置处的平均湍动能剖面 Fig.6 Profiles of mean turbulent kinetic energies at different streamwise positions |
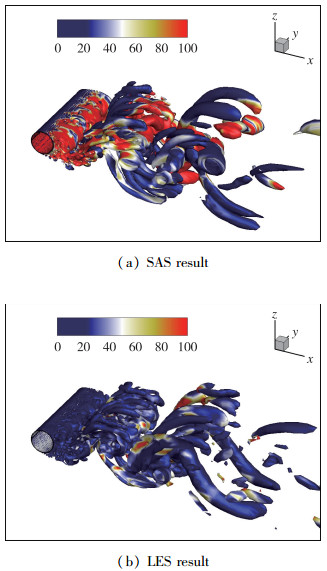
在湍流数值模拟方法中, 湍流黏性系数μT可以反映两方面的内容:一是湍流引起的Reynolds应力值; 二是模拟的湍流黏性耗散大小. 图 7给出了SAS和LES的μT值瞬态分布.这里, 大尺度结构为Q准则描述的涡结构, 云图为μT值.可以看出, 在近尾迹区SAS的μT值明显大于LES, 这说明SAS中的过多RANS湍流模型耗散会明显影响近尾迹流场.在稍远的尾迹区, SAS的μT值仅在某些局部区域高于LES.从大尺度涡结构的分布特征来看, SAS捕捉小尺度涡结构的能力略低于LES, 这与SAS会带来过多的湍流耗散有关.然而, 这些耗散并未明显影响到SAS方法对大尺度涡结构的预测.
|
| 图 7 瞬态的湍流黏性系数μT Fig.7 Instantaneous turbulent viscosity coefficients μT |
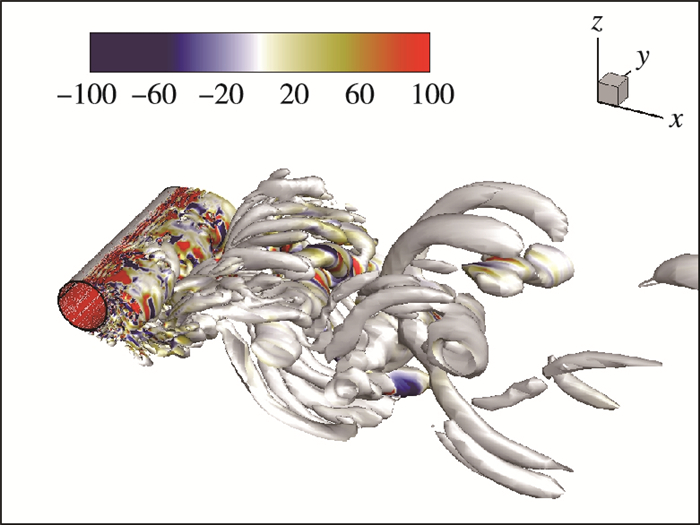
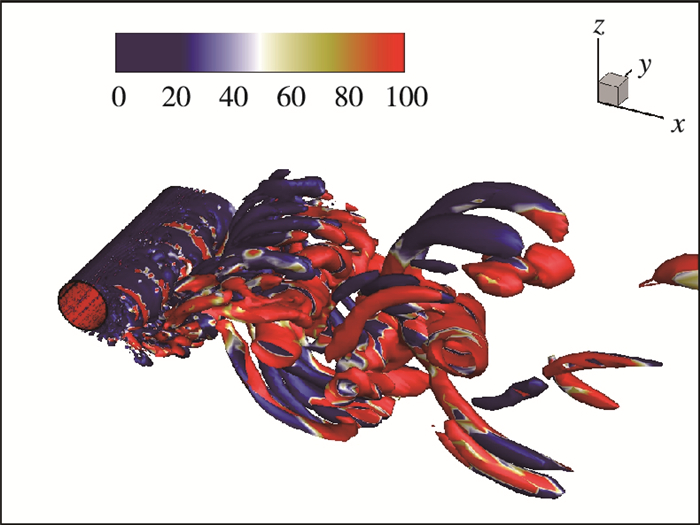
从前面的理论分析知道, SAS的湍流耗散主要来源于SA一方程湍流模型的耗散.在SA模型方程中, 扩散项SC对湍流黏性系数μT起到耗散的作用.为了考察扩散项SC对湍流黏性的影响范围, 图 8给出了圆柱尾迹区的SC值分布.可以看出, SC仅在圆柱近尾迹区存在较大的影响, 而在稍远的尾迹区则影响较小.前文提到, 由SA模型方程的源项平衡假设可以得出SAS在LES计算区域(即圆柱的尾迹区)的等效湍流黏性系数μTeq, 见公式(16). 图 9给出了圆柱尾迹区的μTeq值分布.对比图 7(a)和图 9可以发现, 在稍远的尾迹区, SAS的真实湍流黏性系数μT几乎就是等效湍流黏性系数μTeq.然而, 在近尾迹区, SAS的真实湍流黏性系数μT明显大于等效湍流黏性系数μTeq.这说明在稍远的尾迹区SAS方法几乎完全等效于LES, 而在近尾迹区则更像RANS和LES的混合效果.
|
| 图 8 扩散项SC的瞬态分布 Fig.8 8 Instantaneous distributions of diffusion term SC |
|
| 图 9 等效湍流黏性系数μTeq的瞬态分布 Fig.9 Instantaneous distributions of equivalent turbulent viscosity coefficients μTeq |
本文针对SAS和LES的关联性问题, 采用理论分析和数值模拟相结合的方法进行了详细研究, 并选取来流Mach数0.55, Reynolds数2×105的圆柱可压缩绕流问题作为分析算例.通过理论分析和数值模拟结果的讨论, 得到了如下的一些结论:
(1) 系综平均操作等价于盒式直接滤波操作, SAS和LES的控制方程在数学形式上具有一致性; SAS存在过多的湍流耗散, 主要来源于SA一方程湍流模型方程中的扩散项.
(2) 在圆柱的全流场中, SAS和LES预测的大尺度平均流场信息几乎一致; 在圆柱的近尾迹区, SAS预测的湍流脉动值略低于LES, 而在稍远的尾迹区, SAS预测的湍流脉动值则几乎与LES一致.
(3) SAS在RANS计算区域的过多湍流耗散会影响到圆柱近尾迹区, 而在稍远的尾迹区, SAS的湍流耗散特性几乎能够完全等效于LES.
下一步工作将针对SAS中的过多湍流耗散问题开展研究.通过在RANS计算区域内补充一定的小尺度湍流脉动, 减少由湍流模型方程中的扩散项引起的过多湍流耗散, 进而提高SAS对湍流脉动信息的预测能力.
| [1] |
Spalart P R, Jou W H, Strelets M, et al. Comments on the feasibility of LES for wings and on a hybrid RANS/LES approach[C]. Proceeding of the First AFSOR International Conference on DNS/LES, Rusliton: Grey-den, 1997.
|
| [2] |
Strelets M. Detached eddy simulation of massively separated flows[R]. AIAA 2001-0879, 2001.
|
| [3] |
Fan T C, Tian M, Edwards J R, et al. Validation of a hybrid Reynolds-averaged/large-eddy simulation method for simulating cavity flameholder configurations[R]. AIAA 2001-2929, 2001.
|
| [4] |
Spalart P R. Detached-eddy simulation[J]. Annual Re-view of Fluid Mechanics, 2009, 41(1): 181-202. DOI:10.1146/annurev.fluid.010908.165130 |
| [5] |
Spalart P R, Deck S, Shur M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid de-nsities[J]. Theoretical and Computational Fluid Dyna-mics, 2006, 20(3): 181-195. DOI:10.1007/s00162-006-0015-0 |
| [6] |
Shur M L, Spalart P R, Strelets M K, et al. A hybrid RANS-LES approach with delayed-DES and wall-model-led LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649. DOI:10.1016/j.ijheatfluidflow.2008.07.001 |
| [7] |
Deck S. Numerical simulation of transonic buffet over a supercritical airfoil[J]. AIAA Journal, 2005, 43(7): 1556-1566. DOI:10.2514/1.9885 |
| [8] |
Menter F R, Kuntz M, Bende R. A scale-adaptive simulation model for turbulent flow predictions[R]. AIAA 2003-0767, 2003.
|
| [9] |
Menter F R, Egorov Y. A scale-adaptive simulation model using two-equation models[R]. AIAA 2005-1095, 2005.
|
| [10] |
Egorov Y, Menter F R. Development and application of SST-SAS turbulence model in the DESider project[A]//Advances in Hybrid RANS-LES Modelling[M]. Ber-lin: Springer-Verlag, 2008: 261-270.
|
| [11] |
Menter F R, Egorov Y. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 1: theory and model description[J]. Flow, Turbulence and Combustion, 2010, 85(1): 113-138. DOI:10.1007/s10494-010-9264-5 |
| [12] |
Zhao R, Xu J L, Yan C, et al. Scale-adaptive simulation of flow past wavy cylinders at a subcritical Reynolds number[J]. Acta Mechanica Sinica, 2011, 27(5): 660-667. DOI:10.1007/s10409-011-0490-4 |
| [13] |
Xu C Y, Zhou T, Wang C L, et al. Applications of scale-adaptive simulation technique based on one-equation turbulence model[J]. Applied Mathematics and Mechanics (English Edition), 2015, 36(1): 121-130. DOI:10.1007/s10483-015-1898-9 |
| [14] |
Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flows[R]. AIAA 1992-0439, 1992.
|
| [15] |
Piomelli U. Large-eddy simulation: achievements and challenges[J]. Progress in Aerospace Sciences, 1999, 35(4): 335-362. DOI:10.1016/S0376-0421(98)00014-1 |
| [16] |
Vreman B, Geurts B, Kuerten H. Subgrid-modelling in LES of compressible flow[J]. Applied Scientific Re-search, 1995, 54(3): 191-203. DOI:10.1007/BF00849116 |
| [17] |
Pino Martín M, Piomelli U, Candler G V. Subgrid-scale models for compressible large-eddy simulations[J]. Theoretical and Computational Fluid Dynamics, 2000, 13(5): 361-376. |
| [18] |
Yoshizawa A. Statistical theory for compressible turbulent shear flows, with the application to subgrid modeling[J]. Physics of Fluids, 1986, 29: 2152-2164. DOI:10.1063/1.865552 |
| [19] |
Lilly D K. A proposed modification of the Germano subgrid-scale closure method[J]. Physics of Fluids A, 1992, 4(3): 633-635. DOI:10.1063/1.858280 |
| [20] |
Moin P, Squires K, Cabot W, et al. A dynamic subgrid-scale model for compressible turbulence and scalar tran-sport[J]. Physics of Fluids A, 1991, 3(11): 2746-2757. DOI:10.1063/1.858164 |
| [21] |
Germano M, Piomelli U, Moin P, et al. A dynamic subgrid-scale eddy viscosity model[J]. Physics of Fluids A, 1991, 3(7): 1760-1765. DOI:10.1063/1.857955 |
| [22] |
Fureby C. On subgrid scale modeling in large eddy simulations of compressible fluid flow[J]. Physics of Fluids, 1996, 8(5): 1301-1311. DOI:10.1063/1.868900 |
| [23] |
Knight D, Zhou G, Okong'o N, et al. Compressible large eddy simulation using unstructured grids[R]. AIAA 1998-0535, 1998.
|
| [24] |
Xu C Y, Chen L W, Lu X Y. Large-eddy simulation of the compressible flow past a wavy cylinder[J]. Journal of Fluid Mechanics, 2010, 665: 238-273. DOI:10.1017/S0022112010003927 |
| [25] |
Jiang Z, Xiao Z L, Shi Y P, et al. Constrained large-eddy simulation of wall-bounded compressible turbulent flows[J]. Physics of Fluids, 2013, 25(10): 106102. DOI:10.1063/1.4824393 |
| [26] |
许常悦. 圆柱可压缩绕流及其流动控制的大涡模拟研究[D]. 合肥: 中国科学技术大学, 2009. Xu C Y. Large eddy simulation of the compressible flow past a circular cylinder and its flow control[D]. Hefei: University of Science and Technology of China, 2009(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10358-2009110993.htm |
| [27] |
Rodriguez O. The circular cylinder in subsonic and tr-ansonic flow[J]. AIAA Journal, 1984, 22(12): 1713-1718. DOI:10.2514/3.8842 |
| [28] |
Gowen F E, Perkins E W. Drag of circular cylinders for a wide range of Reynolds numbers and Mach numbers[R]. NACA TN-2960, 1953.
|
| [29] |
Macha J M. Drag of circular cylinders at transonic Mach numbers[J]. Journal of Aircraft, 1977, 14(6): 605-607. DOI:10.2514/3.58828 |
| [30] |
Welsh C J. The drag of finite-length cylinders determined from flight tests at high Reynolds numbers for a Mach number range from 0. 5 to 1. 3[R]. NACA TN-2941, 1953.
|
| [31] |
Xia Z H, Xiao Z L, Shi Y P, et al. Mach number effect of compressible flow around a circular cylinder[J]. AIAA Journal, 2016, 54(6): 2004-2009. DOI:10.2514/1.J054420 |
| [32] |
Ackerman J R, Gostelow J P, Rona A, et al. Measurements of fluctuating pressures on a circular cylinder in subsonic crossflow[J]. AIAA Journal, 2009, 47(9): 2121-2131. DOI:10.2514/1.40954 |



