2. 北京航空航天大学先进航空发动机协同创新中心,北京 100191;
3. 北京航空航天大学中法工程师学院,北京 100191
2. Collaborative Innovation Center of Advanced Aero-Engine, Beihang University, Beijing 100191, China;
3. Ecole Centrale de Pékin, Beihang University, Beijing 100191, China
人类对自然界的认识总是从特殊的简化现象出发, 逐渐拓宽进而寻找更普遍的复杂现象中的规律.随着人类认识自然界的深入, 从简化情形向普遍真实情形的跨越是一个必然的过程.人类对湍流的认识也是如此.对于自然界中普遍存在的流动, “定常”“各向同性”“均衡”等假设都属于特殊简化, 而实际的流动通常是“非定常”“各向异性”“非均衡”的形态.多年来在应用中考虑“非定常”和“各向异性”, 已经在越来越多的问题中被证明是极其重要的.然而, 由于困难性和复杂性, 湍流“非均衡性”这一相当普遍的能量传输特性, 迄今仍是一个较新颖的研究课题, 甚至“非均衡(non-equilibrium)”(注:有的学者也称之为“非平衡”)还未能成为一个被大家熟知的名词, 对非均衡的定义和理解也都尚未统一.经典的Richardson-Kolmogorov能量级串理论已经在大量的实验及数值模拟中得到了验证, 并作为湍流的基础理论, 极大地推动了湍流研究的发展.但是, 近年来在实验及直接数值模拟(direct numerical simulation, DNS)中多次观察到了与Richardson-Kolmogorov能量级串理论不相符的现象, 这种新现象打破了Kolmogorov理论中最重要的均衡假设, 引起了对非均衡湍流的研究热潮.本文即致力于介绍近年来对非均衡湍流的相关研究, 并对未来的研究方向进行了展望.
本文第1部分将简要介绍经典的Richardson-Kolmogorov能量级串理论及其主要推论.第2部分将回顾验证Richardson-Kolmogorov均衡能量级串理论的相关实验和数值模拟结果, 主要采用耗散系数
经典Richardson-Kolmogorov能量级串理论[1-4]在湍流研究中一直被认为是最重要、最基础的理论.该理论做了如下假设: (1)在高Reynolds数湍流场中, 湍流尺度范围很宽广, 且在惯性区内湍流为各向同性的, 并处于均衡状态; (2)在惯性区, 能谱E(k)由耗散律
| $ \mathit{\boldsymbol{\epsilon}} = {C_\mathit{\boldsymbol{\epsilon}}}{\mathcal{U}^3}/{\cal L} $ |
其中,
为了定量描述能量在尺度间的分布及其传输规律, 需要寻找一个可以描述不同空间位置不同尺度能量的量, 2阶结构函数〈|δu|2〉即是一个合适的选择, 其中|δu|2=δuiδui, δui=ui(x+r/2, t)-ui(x-r/2, t)为两点间的速度增量.粗略来说, 〈|δu|2〉代表了尺度
| $ \begin{array}{l} \frac{{{{\rm{D}}^ * }}}{{{\rm{D}}t}}\left\langle {{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle + {\nabla _\mathit{\boldsymbol{r}}}\left\langle {\left( {\delta \mathit{\boldsymbol{u + }}\delta \mathit{\boldsymbol{U}}} \right){{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle = \\ \;\;\;\;{P^ * }{\rm{ + }}{T^ * } + {D^ * } + \mathit{\boldsymbol{v}}\nabla _\mathit{\boldsymbol{r}}^2\left\langle {{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle - 4{\mathit{\boldsymbol{\epsilon}}^ * } \end{array} $ | (1) |
其中, 应用Reynolds分解将速度分解为平均速度和脉动速度, 记为U+u, D*/(Dt)为Lagrange导数算子,定义为
现在考虑高Reynolds数流动,
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left\langle {{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle + \mathit{\boldsymbol{U}}\left( \mathit{\boldsymbol{x}} \right) \cdot {\nabla _x}\left\langle {{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle + {\nabla _\mathit{\boldsymbol{r}}} \cdot \left\langle {\delta \mathit{\boldsymbol{u}}{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle = \\ \;\;\;\;\mathit{\boldsymbol{v}}\nabla _\mathit{\boldsymbol{r}}^2\left\langle {{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle - 4\mathit{\boldsymbol{\epsilon}} \end{array} $ | (2) |
Valente等[9]通过规则格栅实验数据发现在r
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left\langle {{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle \mathit{\boldsymbol{ + U}}\left( \mathit{\boldsymbol{x}} \right) \cdot {\nabla _x}\left\langle {{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle + \\ \;\;\;{\nabla _\mathit{\boldsymbol{r}}} \cdot \left\langle {\delta \mathit{\boldsymbol{u}}{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle = - 4\mathit{\boldsymbol{\epsilon}} \end{array} $ |
Kolmogorov[3]所做的关键假设之一就是湍流的小尺度(
| $ \frac{\partial }{{\partial t}}\left\langle {{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle + \mathit{\boldsymbol{U}}\left( \mathit{\boldsymbol{x}} \right) \cdot {\nabla _x}\left\langle {{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle \approx 0 $ |
均衡能量级串便满足
| $ \int {\mathit{\boldsymbol{\hat r}}} \cdot \left\langle {\delta \mathit{\boldsymbol{u}}{{\left| {\delta \mathit{\boldsymbol{u}}} \right|}^2}} \right\rangle {\rm{d}}\mathit{\Omega } \approx - \frac{{16{\rm{ \mathit{ π} }}}}{3}\mathit{\boldsymbol{\epsilon}}r $ | (3) |
其中, dΩ是r空间的角度微元,
上述推导简单介绍了借助现代数学在推导Richardson-Kolmogorov均衡能量级串中的进展.球面积分的跨尺度能量传输是负的, 说明能量由大尺度向小尺度传输, 结果中能量传输只与耗散率相关, 印证了能量级串的尺度间相似性. Pope[14]指出尺度间的相似性是推出能谱E(k)~
| $ \mathit{\boldsymbol{\epsilon}} = {C_\mathit{\boldsymbol{\epsilon}}}\frac{{{\mathcal{U}^3}}}{{\cal L}} $ | (4) |
其中,
由方程(4)及Taylor尺度的定义, 可以得到
| $ \frac{{\cal L}}{\mathit{\boldsymbol{\lambda }}} \sim {C_\mathit{\boldsymbol{\epsilon}}}\mathit{R}{\mathit{e}_\lambda } $ | (5) |
其中,Reλ≡
上述推导中用到的
上面简要回顾了经典Richardson-Kolmogorov能量级串理论及其主要推论, 它们是支撑半个多世纪以来均衡湍流研究的最主要的理论基础.
2 耗散系数(在Richardson-Kolmogorov能量级串理论建立后很长一段时间内, 由于实验测量手段及数值模拟技术能力水平的限制, 对于耗散系数
对
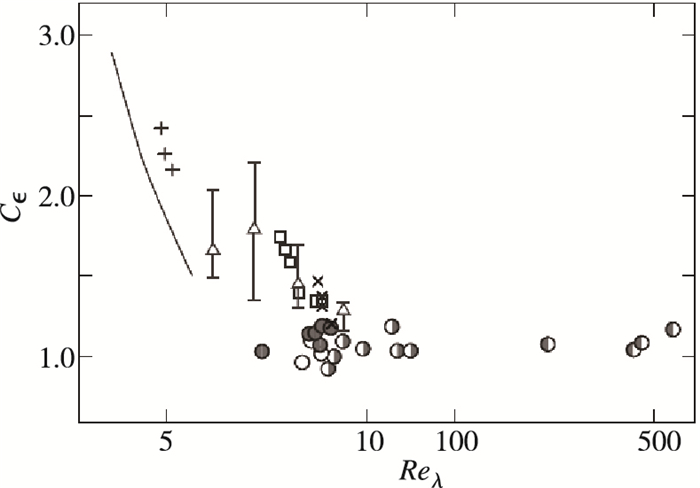
|
|
图 1 多种双平面格栅湍流中耗散系数 |
Antonia等[29]通过量纲分析推导出了自由剪切湍流中
在数值模拟中, Sreenivasan[32]也收集了不同学者的不可压缩均匀各向同性湍流的DNS结果, 并画在同一张
上述众多的实验及DNS数值模拟结果为同一个流动中
Doering等[34]从不可压缩Navier-Stokes方程出发, 推导出了在三维无边界体积力驱动的统计定常周期湍流中耗散率所应满足的条件
| $ \mathit{\boldsymbol{\epsilon}} \le {c_1}\mathit{\boldsymbol{v}}\frac{{{U^2}}}{{{{\cal L}^2}}} + {c_2}\frac{{{U^3}}}{{\cal L}} $ | (6) |
其中, c1与c2是与Reynolds数等参数无关, 仅与大尺度驱动力的形式有关的系数,
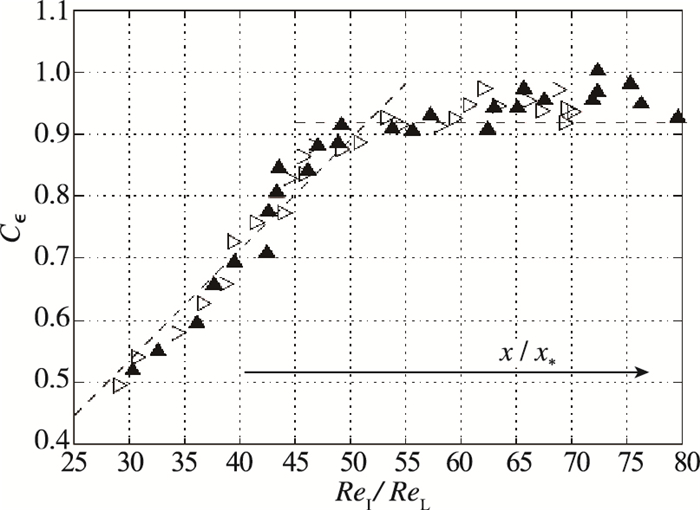
Antonia等[37]在圆柱和垂直平板的尾迹实验中绘制了
Mazellier等[39]利用Liepmann等[40]引入湍流研究的Rice理论建立了
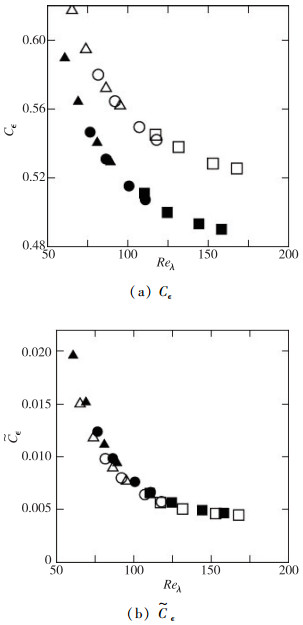
|
|
图 2 存在大尺度驱动的均匀各向同性湍流直接数值模拟中耗散系数 |
Mouri等[43]将公式(4)中代表含能涡特征尺度的
| $ {{\cal L}_{{u^2}}} = \frac{{\int_0^\infty {\left\langle {\left[ {{u^2}\left( {x + r} \right) - \left\langle {{u^2}} \right\rangle } \right]\left[ {{u^2}\left( x \right) - \left\langle {{u^2}} \right\rangle } \right]} \right\rangle {\rm{d}}r} }}{{\left\langle {{{\left( {{u^2} - \left\langle {{u^2}} \right\rangle } \right)}^2}} \right\rangle }} $ |
即基于脉动能量两点相关的长度尺度, 并在格栅湍流、边界层湍流及射流中的17组结果中进行了统计, 发现
Bos等[45]用DNS, LES及湍涡阻尼Markov化准正则(eddy-damping quasi-normal Markovian, ED-QNM)近似方法对衰减湍流及有驱动力的湍流中的
总之, 有很多实验结果认为在一个流动中
虽然由Richardson-Kolmogorov均衡能量级串推导得出的耗散系数
Seoud等[46]最早在Hurst等[47]的3种不同宽度比的方形平面分形格栅实验中发现了不符合
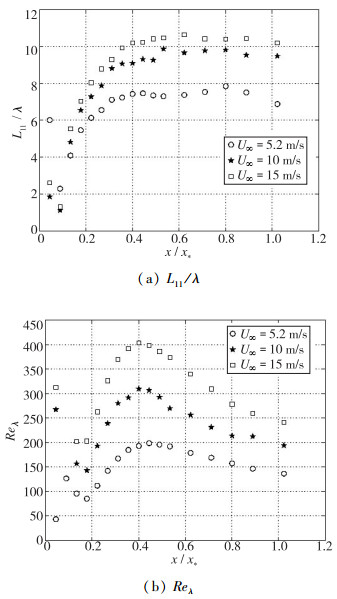
Mazellier等[48]继续研究了上述工作, 在4种不同的方形空间填充平面分形格栅实验中对湍流统计量进行了分析.他们发现在衰减区L11/λ虽然与下游距离及分形格栅几何参数无关, 但是却与入口速度有关, 即与入口Reynolds数ReI有关, 如图 3所示.随着入口Reynolds数ReI的增加, L11/λ趋向于的数值随下游距离变化更小, 意味着
|
| 图 3 分形格栅下游中心线上流向积分尺度L11与Taylor尺度λ的比及Reynolds数Reλ与通过尾迹相关长度尺度x*无量纲化的流向距离x的关系图[48] Fig.3 Ratio of the longitudinal integral length scale L11 to the Taylor microscale λ and Reλ as a function of the streamwise distance from a turbulence-generating fractal square grid along the centerline[48] |
Valente等[51]在规则格栅和分形格栅实验中对两个主要问题进行了研究, 一是验证上文提到的Mazellier等[48]发现的结果, 并进一步发现了L11/λ~ReI1/2的正相关关系(如图 4所示), 由λ的定义得到
|
|
图 4 双平面规则格栅下游耗散系数 |
Valente等[9]对多种分形格栅及规则格栅实验数据利用Kármán-Howarth方程中的各项进行了详细分析, 发现该新耗散律不是流动的非均匀性及各向异性导致的, 也不是在各向异性的条件下不同
在经典自由剪切湍流研究中, 射流尾迹有很强的自相似性, Townsend[20]及George[21]详细介绍了由均衡耗散律
上述研究均是在统计定常的流动中进行的, 而在存在非定常大尺度扰动的流动中同样存在着这种新耗散律. Valente等[56]在周期性均匀各向同性湍流DNS模拟中对存在周期变化的大尺度驱动力的湍流进行了研究.他们用传输谱的过零点波数作为湍动能传输中损失能量与获得能量的分界点.研究发现在传输谱的过零点波数处的湍动能传输率Π与湍动能耗散率
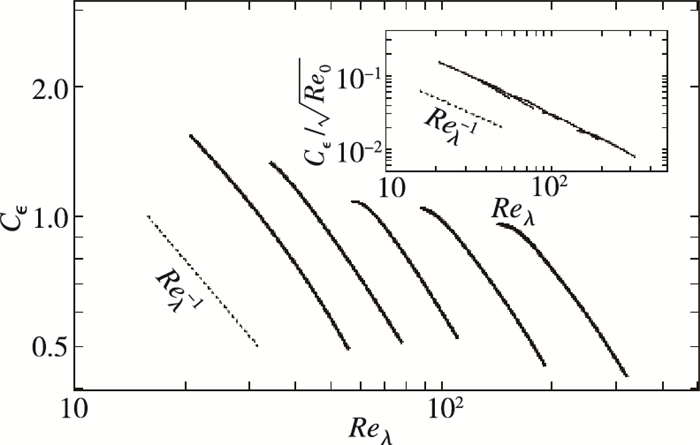
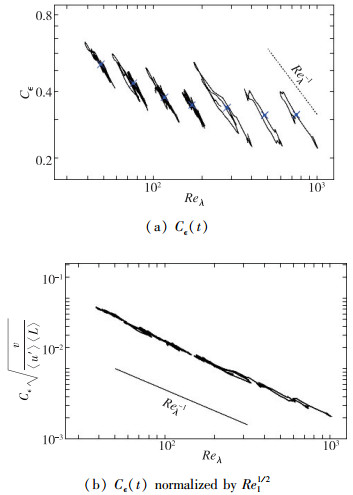
Goto等[57]也在周期性均匀各向同性湍流DNS模拟中对非统计定常的有驱动力的湍流及非统计定常的衰减湍流进行了研究.发现不论是在有驱动力作用的湍流中还是衰减湍流中,
|
|
图 5 周期性均匀各向同性衰减湍流DNS模拟中瞬时耗散系数 |
|
|
图 6 周期性均匀各向同性非定常驱动湍流DNS模拟中瞬时耗散系数 |
Bos等[58]提出了一个简单的理论模型用来描述这种新耗散律.他们提出将能谱、传输谱及耗散率等物理量分解为均衡部分及非均衡部分, 并引入简单的传输模型, 通过推导得到
| $ {C_\mathit{\boldsymbol{\epsilon}}} \sim {\left( {\frac{{\sqrt {\mathit{R}{\mathit{e}_Ⅰ}} }}{{\mathit{R}{\mathit{e}_\lambda }\left( t \right)}}} \right)^{15/14}} $ |
尽管此标度律与前述的标度指数有微小的区别, 但区别并不明显.此理论推导结果也与Valente等[51]的实验及Goto等[57]的DNS模拟结果进行了对比, 得到了很好的一致性.该理论模型本质上是将非均衡部分视为均衡部分的一种类似“谐波”的存在, 从一个崭新的视角对非均衡湍流进行了描述.
综上, 近年来发现在时间/空间非定常湍流中, 在湍流开始衰减时
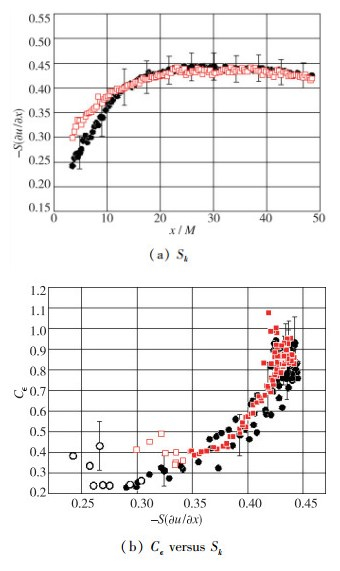
最近三年来, 速度梯度的统计量逐渐被应用到非均衡湍流的研究中来.最早由Isaza等[52]在规则双平面格栅下游对统计量研究时发现流向速度梯度的扭率
|
|
图 7 分形格栅下游流向速度梯度扭率Sk随流向距离变化图及耗散系数 |
为了给Sk的研究更好的理论支持, 我们将全尺度非均衡的概念推广为多尺度非均衡的概念[62]:在惯性区(通常定义为k-5/3的区域)内, 如果大尺度的能量生成与小尺度的能量耗散是统计均衡的, 该流动就被称为谱均衡湍流; 否则被称为谱非均衡湍流.该定义可以被理解为在惯性区内某一尺度处能量正向与反向传输之间的均衡.在此定义下, 可以将Sk推广为可解尺度流向速度梯度扭率Sk<, 即将Sk表达式中的速度改成可解尺度速度, 并提出通过Sk<修正LES亚格子模型的方法.我们在更早的研究中曾提出时间逆湍流的概念[63], 即在充分发展的湍流场中将速度向量u变为-u, 在无黏的条件下, 反转后的湍流将发展回初始状态, 如同时间t变为-t一样; 而在黏性存在时, 该流动为一种简单的谱非均衡流动模型.我们继续应用这个方法将LES中可解尺度的速度分解为谱均衡部分及时间逆湍流部分(时间逆湍流即是我们提出的一种假想的极端的非均衡湍流), 而实际的湍流场为这两种理想模型场的叠加, 通过Sk<来表征流动的非均衡程度, 通过理论推导得到一个简单的LES亚格子模型
根据Bos等[64]推导的Sk与谱空间物理量之间关系, Sk实质上反映了能量传输与耗散的比, 所以其描述非均衡湍流现象的本质与
因此, 实验和理论都发现Sk与
虽然上述Sk的引入已经使得表征湍流非均衡性的物理量的计算变得更加容易, 但不论是
通过Lagrange速度梯度自相关方程对此问题进行了尝试[65].方程写为
| $ \mathit{\Phi }_{_{ijij}}^{'}=\frac{\text{d}\left\langle A_{ij}^{'<}A_{ij}^{'<} \right\rangle }{\text{d}t}\text{=}Q_{_{ijij}}^{'}+\mathit{\Pi }_{_{ijij}}^{'}+V_{_{ijij}}^{'}+\mathit{\Gamma }_{_{ijij}}^{'} $ |
其中, 上标′表示脉动量,
| $ Q_{_{ijij}}^{'}=-2\left\langle A_{ij}^{'<}A_{kj}^{'<}A_{ik}^{'<} \right\rangle $ |
| $ \mathit{\Pi }_{_{ijij}}^{'}=-\frac{2}{\rho }\left\langle A_{ij}^{'<}\frac{{{\partial }^{2}}{{p}^{'<}}}{\partial {{x}_{i}}\partial {{x}_{j}}} \right\rangle $ |
| $ \mathit{V}_{_{ijij}}^{'}=2\left\langle vA_{ij}^{'<}\frac{{{\partial }^{2}}A_{ij}^{'<}}{\partial {{x}_{k}}\partial {{x}_{k}}} \right\rangle $ |
| $ \mathit{\Gamma }_{_{ijij}}^{'}=2\left\langle {{v}_{\mathit{t}}}A_{ij}^{'<}\frac{{{\partial }^{2}}A_{ij}^{'<}}{\partial {{x}_{k}}\partial {{x}_{k}}} \right\rangle $ |
上述4项分别为生成项、压力项、黏性项及亚格子项, νt为亚格子湍流黏性.该物理量为当地统计量, 并且可以应用在非均匀各向异性湍流中.通过Champagne[66]的推导可以得出在均匀各向同性条件下,
| $ \begin{align} & Q_{_{ijij}}^{'}\propto \left\langle A_{11}^{'<}A_{11}^{'<}A_{11}^{'<} \right\rangle =S_{k}^{<}{{\left\langle A_{11}^{'<}A_{11}^{'<} \right\rangle }^{3/2}} \\ & \ \ \ \ \ \ \ \ \ V_{_{ijij}}^{'},\mathit{\Gamma }_{_{ijij}}^{'}\propto \left\langle \frac{\partial A_{11}^{'<}}{\partial {{x}_{1}}}\frac{\partial A_{11}^{'<}}{\partial {{x}_{1}}} \right\rangle \\ \end{align} $ |
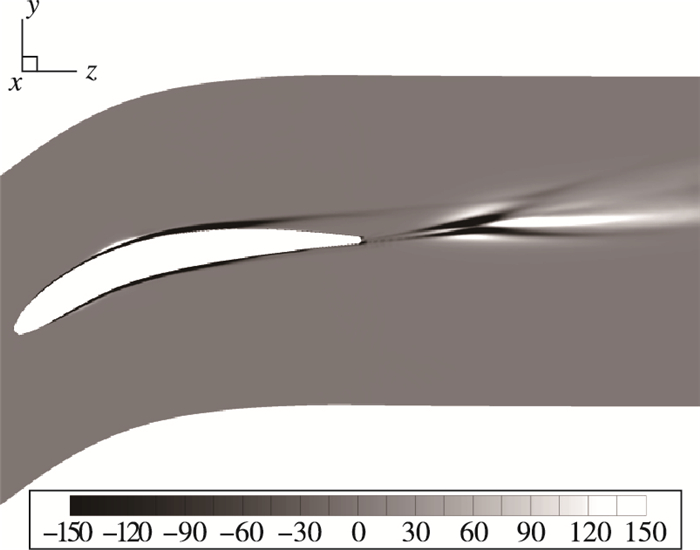
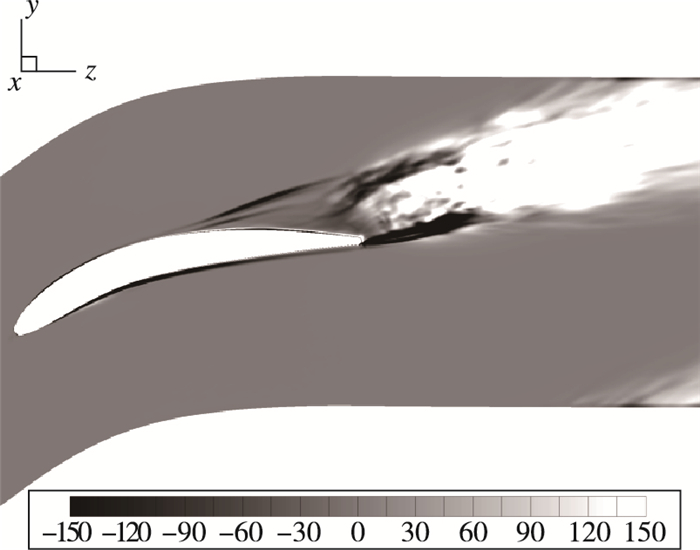
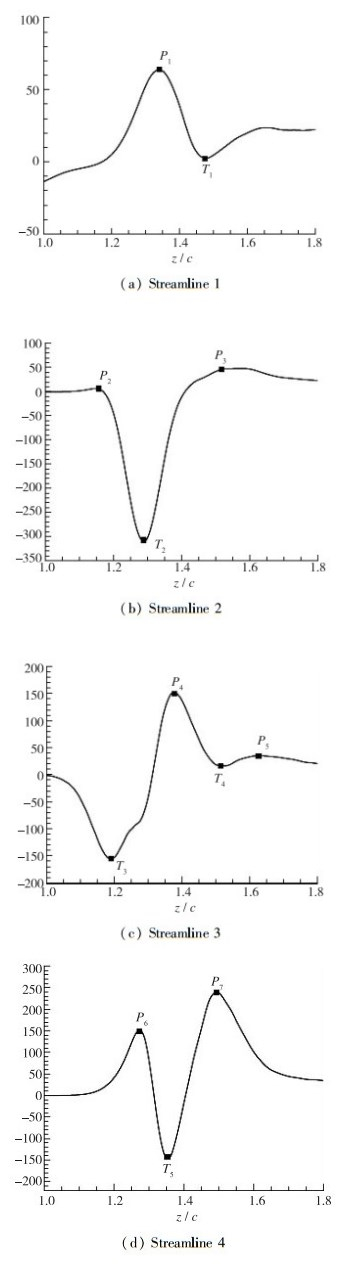
而在均匀的条件下Πijij′=0.我们指出在均匀各向同性的条件下Φijij′实际上反映了Qijij′与Vijij′+Γijij′之间的均衡关系.通过量纲分析, 还可以得到能量传输Qijij′的特征时间远小于耗散Vijij′+Γijij′的特征时间, 这个推论在我们的指定速度分布(prescribed velocity distribution, PVD)叶栅数据中得到了验证.所以假设在Φijij′=0的均衡湍流经历非均衡过程时, Sk<发生改变, 而2阶矩保持不变, 从而导出Φijij′≠0的结果.因此在均匀各向同性湍流中非常数的Sk<与Φijij′≠0是等价的, 在这种条件下
|
| 图 10 50%叶高截面尾迹区沿流线Lagrange速度梯度自相关方程Φijij′变化曲线[65] Fig.10 Non-equilibrium process along streamlines in wake region at 50% span[65] |
在可压缩湍流中可以用同样的方法推导出Φijij′.杨光在其博士论文[68]中对此进行了详细的推导, 但是并未对可压缩湍流中的非均衡性进行深入分析, 目前对于可压缩性及非均衡性之间的相互关系尚不清楚, 有待进行深入研究.事实上, 可压缩湍流与非均衡性之间很可能在统计意义上有某种相似性, 比如我们曾在一个最近的工作[69]中发现它们在同一个速度梯度4阶矩相空间中都具有同样的演化趋势, 且都满足Gauss-RE线性关系.
综上, 基于Lagrange速度梯度自相关方程提出的物理量Φijij′从理论上可以证明在均匀各向同性湍流中与
Richardson-Kolmogorov能量级串理论是湍流中最重要的基础理论, 其一个重要推论是
很多实验结果认为
均衡湍流是一种简化的理想流动, 非均衡湍流才是自然界中更普遍的流动形式.由于从非均衡向均衡过渡的特征时间很短, 非均衡湍流最明显的是那些特征时间极短的流动.比如在典型的航空发动机中, 流动经过压气机单级叶栅的时间量级约为10 ms, 而最大尺度涡的非均衡特征时间却长达150 ms左右[65].这说明在整个压气机中, 非均衡湍流都是主要的流动形式, 因而只有针对非均衡湍流的数值模型才能准确捕捉其真实的流动结构.我们曾经发现角区分离部分具有明显的能量反传, 而螺旋度可以在该流动中表征能量反传这一非均衡现象[70].在此基础上建立了非均衡Spalart-Allmaras(SA)模型, 有效地提高了模拟角区分离的正确性.但此类工作目前仍处于初步阶段, 如何在工程中更准确和合理地考虑非均衡湍流正是未来的主要研究方向.
| [1] |
Richardson L F. Weather prediction by numerical process[M]. Cambridge: Cambridge University Press, 2007.
|
| [2] |
Kolmogorov A N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers[J]. Dokl. Akad. Nauk SSSR, 1941, 30(4): 301-305. |
| [3] |
Kolmogorov A N. On the degeneration of isotropic turbulence in an incompressible viscous fluid[J]. Dokl. Akad. Nauk SSSR, 1941, 31: 319-323. |
| [4] |
Kolmogorov A N. Dissipation of energy in locally isotropic turbulence[J]. Dokl. Akad. Nauk SSSR, 1941, 32(1): 16-18. |
| [5] |
张兆顺. 湍流理论与模拟[M]. 北京: 清华大学出版社, 2015, 80. Zhang Z S. Theory and modeling of turbulence[M]. Beijing: Tsinghua University Press, 2015, 80. (in Chinese) |
| [6] |
Marati N, Casciola C M, Piva R. Energy cascade and spatial fluxes in wall turbulence[J]. Journal of Fluid Mechanics, 2004, 521: 191-215. DOI:10.1017/S0022112004001818 |
| [7] |
Hill R J. Exact second-order structure-function relation-ships[J]. Journal of Fluid Mechanics, 2002, 468: 317-326. |
| [8] |
Danaila L, Krawczynski J F, Thiesset F, et al. Yaglom-like equation in axisymmetric anisotropic turbulence[J]. Physica D: Nonlinear Phenomena, 2012, 241(3): 216-223. DOI:10.1016/j.physd.2011.08.011 |
| [9] |
Valente P C, Vassilicos J C. The energy cascade in grid-generated non-equilibrium decaying turbulence[J]. Phy-sics of Fluids, 2015, 27(4): 045103. DOI:10.1063/1.4916628 |
| [10] |
Laizet S, Vassilicos J C, Cambon C. Interscale energy transfer in decaying turbulence and vorticity-strain-rate dynamics in grid-generated turbulence[J]. Fluid Dyna-mics Research, 2013, 45(6): 061408. DOI:10.1088/0169-5983/45/6/061408 |
| [11] |
Nie Q, Tanveer S. A note on third-order structure functions in turbulence[A]//Proceedings of the Royal Society of London A: Mathematical, Physical and Enginee-ring Sciences[M]. London: The Royal Society, 1999, 455(1985): 1615-1635.
|
| [12] |
Duchon J, Robert R. Inertial energy dissipation for weak solutions of incompressible Euler and Navier-Stokes equations[J]. Nonlinearity, 2000, 13(1): 249-255. DOI:10.1088/0951-7715/13/1/312 |
| [13] |
Eyink G L. Local 4/5-law and energy dissipation anomaly in turbulence[J]. Nonlinearity, 2003, 16(1): 137-145. DOI:10.1088/0951-7715/16/1/309 |
| [14] |
Pope S B. Turbulent flows[M]. Cambridge: Cambridge University Press, 2000.
|
| [15] |
Vassilicos J C. Dissipation in turbulent flows[J]. Annual Review of Fluid Mechanics, 2015, 47: 95-114. DOI:10.1146/annurev-fluid-010814-014637 |
| [16] |
Tennekes H, Lumley J L. First course in turbulence[M]. Cambridge: MIT Press, 1972.
|
| [17] |
Frisch U. Turbulence: the legacy of AN Kolmogorov[M]. Cambridge: Cambridge University Press, 1995.
|
| [18] |
Launder B E, Spalding D B. Mathematical models of turbulence[M]. London: AcademicPress, 1972.
|
| [19] |
Lesieur M, Metais O. New trends in large-eddy simul-ations of turbulence[J]. Annual Review of Fluid Mechanics, 1996, 28(1): 45-82. DOI:10.1146/annurev.fl.28.010196.000401 |
| [20] |
Townsend A A. The structure of turbulent shear flow[M]. Cambridge: Cambridge University Press, 1980.
|
| [21] |
George W K. The self-preservation of turbulent flows and its relation to initial conditions and coherent structures[J]. Advances in Turbulence, 1989, 39-73. |
| [22] |
Batchelor G K. The theory of homogeneous turbulence[M]. Cambridge: Cambridge University Press, 1953.
|
| [23] |
Sreenivasan K R. On the scaling of the turbulence energy dissipation rate[J]. Physics of Fluids, 1984, 27(5): 1048-1051. DOI:10.1063/1.864731 |
| [24] |
Lumley J L. Some comments on turbulence[J]. Physics of Fluids A: Fluid Dynamics, 1992, 4(2): 203-211. DOI:10.1063/1.858347 |
| [25] |
Saffman P G. Lectures on homogeneous turbulence[J]. Topics in Nonlinear Physics, 1968, 485-614. |
| [26] |
Taylor G I. Statistical theory of turbulence[A]//Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences[M]. London: The Royal Society, 1935, 151(873): 421-444.
|
| [27] |
Sreenivasan K R. The energy dissipation in turbulent shear flows[C]. Symposium on Developments in Fluid Dynamics and Aerospace Engineering, Bangalore: Interline, 1995: 159-190.
|
| [28] |
Gad-El-Hak M, Corrsin S. Measurements of the nearly isotropic turbulence behind a uniform jet grid[J]. Journal of Fluid Mechanics, 1974, 62(1): 115-143. DOI:10.1017/S0022112074000607 |
| [29] |
Antonia R A, Satyaprakash B R, Hussain A. Measurements of dissipation rate and some other characteristics of turbulent plane and circular jets[J]. The Physics of Fluids, 1980, 23(4): 695-700. DOI:10.1063/1.863055 |
| [30] |
Douady S, Couder Y, Brachet M E. Direct observation of the intermittency of intense vorticity filaments in turbu-lence[J]. Physical Review Letters, 1991, 67(8): 983-986. DOI:10.1103/PhysRevLett.67.983 |
| [31] |
Cadot O, Couder Y, Daerr A, et al. Energy injection in closed turbulent flows: stirring through boundary layers versus inertial stirring[J]. Physical Review E, 1997, 56: 427-433. DOI:10.1103/PhysRevE.56.427 |
| [32] |
Sreenivasan K R. An update on the energy dissipation rate in isotropic turbulence[J]. Physics of Fluids, 1998, 10(2): 528-529. DOI:10.1063/1.869575 |
| [33] |
Kaneda Y, Ishihara T, Yokokawa M, et al. Energy dissipation rate and energy spectrum in high resolution direct numerical simulations of turbulence in a periodic box[J]. Physics of Fluids, 2003, 15(2): L21-L24. DOI:10.1063/1.1539855 |
| [34] |
Doering C R, Foias C. Energy dissipation in body-forced turbulence[J]. Journal of Fluid Mechanics, 2002, 467: 289-306. |
| [35] |
Rollin B, Dubief Y, Doering C R. Variations on Kolmo-gorov flow: turbulent energy dissipation and mean flow profiles[J]. Journal of Fluid Mechanics, 2011, 670: 204-213. DOI:10.1017/S0022112010006294 |
| [36] |
Doering C R. The 3D Navier-Stokes problem[J]. Annual Review of Fluid Mechanics, 2009, 41: 109-128. DOI:10.1146/annurev.fluid.010908.165218 |
| [37] |
Antonia R A, Pearson B R. Effect of initial conditions on the mean energy dissipation rate and the scaling exponent[J]. Physical Review E, 2000, 62(6): 8086-8090. DOI:10.1103/PhysRevE.62.8086 |
| [38] |
Burattini P, Lavoie P, Antonia R A. On the normalized turbulent energy dissipation rate[J]. Physics of Fluids, 2005, 17(9): 098103. DOI:10.1063/1.2055529 |
| [39] |
Mazellier N, Vassilicos J C. The turbulence dissipation constant is not universal because of its universal dependence on large-scale flow topology[J]. Physics of Fluids, 2008, 20(1): 015101. DOI:10.1063/1.2832778 |
| [40] |
Liepmann H W, Robinson M S. Counting methods and equipment for mean-value measurements in turbulence re-search[J]. NACA Technical Note 3037, National Advi-sory Committee for Aeronautics, 1953. |
| [41] |
Goto S, Vassilicos J C. The dissipation rate coefficient of turbulence is not universal and depends on the internal stagnation point structure[J]. Physics of Fluids, 2009, 21(3): 035104. DOI:10.1063/1.3085721 |
| [42] |
Dallas V, Vassilicos J C, Hewitt G F. Stagnation point von Kármán coefficient[J]. Physical Review E, 2009, 80(4): 046306. DOI:10.1103/PhysRevE.80.046306 |
| [43] |
Mouri H, Hori A, Kawashima Y, et al. Large-scale length that determines the mean rate of energy dissipation in turbulence[J]. Physical Review E, 2012, 86(2): 026309. DOI:10.1103/PhysRevE.86.026309 |
| [44] |
Thiesset F, Antonia R A, Danaila L. Scale-by-scale turbulent energy budget in the intermediate wake of two-dimensional generators[J]. Physics of Fluids, 2013, 25(11): 115105. DOI:10.1063/1.4829763 |
| [45] |
Bos W J T, Shao L, Bertoglio J P. Spectral imbalance and the normalized dissipation rate of turbulence[J]. Physics of Fluids, 2007, 19(4): 045101. DOI:10.1063/1.2714079 |
| [46] |
Seoud R E, Vassilicos J C. Dissipation and decay of fractal-generated turbulence[J]. Physics of Fluids, 2007, 19(10): 105108. DOI:10.1063/1.2795211 |
| [47] |
Hurst D, Vassilicos J C. Scalings and decay of fractal-generated turbulence[J]. Physics of Fluids, 2007, 19(3): 035103. DOI:10.1063/1.2676448 |
| [48] |
Mazellier N, Vassilicos J C. Turbulence without Richardson-Kolmogorov cascade[J]. Physics of Fluids, 2010, 22(7): 075101. DOI:10.1063/1.3453708 |
| [49] |
Nagata K, Sakai Y, Inaba T, et al. Turbulence structure and turbulence kinetic energy transport in multiscale/fractal-generated turbulence[J]. Physics of Fluids, 2013, 25(6): 065102. DOI:10.1063/1.4811402 |
| [50] |
Gomes-Fernandes R, Ganapathisubramani B, Vassilicos J C. Particle image velocimetry study of fractal-generated turbulence[J]. Journal of Fluid Mechanics, 2012, 711: 306-336. DOI:10.1017/jfm.2012.394 |
| [51] |
Valente P C, Vassilicos J C. Universal dissipation scaling for nonequilibrium turbulence[J]. Physical Review Letters, 2012, 108(21): 214503. DOI:10.1103/PhysRevLett.108.214503 |
| [52] |
Isaza J C, Salazar R, Warhaft Z. On grid-generated turbulence in the near-and far field regions[J]. Journal of Fluid Mechanics, 2014, 753: 402-426. DOI:10.1017/jfm.2014.375 |
| [53] |
Hearst R J, Lavoie P. Decay of turbulence generated by a square-fractal-element grid[J]. Journal of Fluid Mechanics, 2014, 741: 567-584. DOI:10.1017/jfm.2013.684 |
| [54] |
Nedić J, Vassilicos J C, Ganapathisubramani B. Axisymmetric turbulent wakes with new nonequilibrium similarity scalings[J]. Physical Review Letters, 2013, 111(14): 144503. DOI:10.1103/PhysRevLett.111.144503 |
| [55] |
Dairay T, Obligado M, Vassilicos J C. Non-equilibrium scaling laws in axisymmetric turbulent wakes[J]. Journal of Fluid Mechanics, 2015, 781: 166-195. DOI:10.1017/jfm.2015.493 |
| [56] |
Valente P C, Onishi R, da Silva C B. Origin of the imbalance between energy cascade and dissipation in turbulence[J]. Physical Review E, 2014, 90(2): 023003. DOI:10.1103/PhysRevE.90.023003 |
| [57] |
Goto S, Vassilicos J C. Energy dissipation and flux laws for unsteady turbulence[J]. Physics Letters A, 2015, 379(16): 1144-1148. |
| [58] |
Bos W J T, Rubinstein R. Dissipation in unsteady turbu-lence[J]. Physical Review Fluids, 2017, 2(2): 022601. DOI:10.1103/PhysRevFluids.2.022601 |
| [59] |
Hearst R J, Lavoie P. Velocity derivative skewness in fractal-generated, non-equilibrium grid turbulence[J]. Physics of Fluids, 2015, 27(7): 071701. DOI:10.1063/1.4926356 |
| [60] |
Ayyalasomayajula S, Warhaft Z. Nonlinear interactions in strained axisymmetric high-Reynolds-number turbulence[J]. Journal of Fluid Mechanics, 2006, 566: 273-307. DOI:10.1017/S0022112006002199 |
| [61] |
Liu F, Lu L P and Fang L. Non-equilibrium turbulent phenomena in transitional channel flows[J]. Journal of Turbulence, Under Review.
|
| [62] |
Fang L, Zhu Y, Liu Y, et al. Spectral non-equilibrium property in homogeneous isotropic turbulence and its implication in subgrid-scale modeling[J]. Physics Letters A, 2015, 379(38): 2331-2336. DOI:10.1016/j.physleta.2015.05.029 |
| [63] |
Fang L, Bos W J T, Shao L, et al. Time reversibility of Navier-Stokes turbulence and its implication for subgrid scale models[J]. Journal of Turbulence, 2012(13): N3. |
| [64] |
Bos W J T, Chevillard L, Scott J F, et al. Reynolds number effect on the velocity increment skewness in isotropic turbulence[J]. Physics of Fluids, 2012, 24(1): 015108. DOI:10.1063/1.3678338 |
| [65] |
Fang L, Zhao H K, Lu L P, et al. Quantitative description of non-equilibrium turbulent phenomena in compressors[J]. Aerospace Science and Technology, Accepted.
|
| [66] |
Champagne F H. The fine-scale structure of the turbulent velocity field[J]. Journal of Fluid Mechanics, 1978, 86(1): 67-108. DOI:10.1017/S0022112078001019 |
| [67] |
Kovasznay L S G. The spectrum of locally isotropic turbulence[J]. Physical Review, 1948, 73(9): 1115. DOI:10.1103/PhysRev.73.1115 |
| [68] |
杨光. 激波/边界层干涉流动及其控制的数值模拟研究[D]. 北京: 北京航空航天大学, 2017. Yang G. Numerical simulation of shock wave/boundary layer interaction flow and its control[D]. Beijing: Beihang University, 2017(in Chinese). |
| [69] |
Fang L, Zhang Y J, Fang J, et al. Relation of the fourth-order statistical invariants of velocity gradient tensor in isotropic turbulence[J]. Physical Review E, 2016, 94(2): 023114. DOI:10.1103/PhysRevE.94.023114 |
| [70] |
Liu Y, Lu L, Fang L, et al. Modification of Spalart-Allmaras model with consideration of turbulence energy backscatter using velocity helicity[J]. Physics Letters A, 2011, 375(24): 2377-2381. DOI:10.1016/j.physleta.2011.05.023 |