2. 北京应用物理与计算数学研究所,北京 100094;
3. 北京大学应用物理与技术研究中心,北京 100871
2. Institute of Applied Physics and Computational Mathematics, Beijing 100094, China;
3. Center for Applied Physics and Technology, Peking University, Beijing 100871, China
Rayleigh-Taylor不稳定性广泛存在于自然现象和工程应用中.从宏观世界到微观世界, Rayleigh-Taylor不稳定性都是重要的科学研究对象.大到超新星爆炸, 小到惯性约束核聚变, 都存在着Rayleigh-Taylor不稳定性的身影.特别地, 在惯性约束核聚变过程中, Rayleigh-Taylor不稳定性会阻碍核聚变效率, 通过外加磁场, 利用Lorentz力抑制Rayleigh-Taylor不稳定性的发展成为了重要的课题. Rayleigh和Taylor分别于1883年[1]和1950年[2]观测和研究了Rayleigh-Taylor不稳定性.在重力场下, 当轻流体(ρl)支撑重流体(ρh)时, 系统处于高势能稳定状态.当轻重流体界面出现微小扰动时, 系统将会向势能最低的状态发展.此时, 系统进入失稳过程, 即Rayleigh-Taylor不稳定性.在重力场作用下, 轻重流体互相混合, 轻流体向上运动形成气泡, 重流体向下运动形成尖钉.自观测到Rayleigh-Taylor不稳定性以来, 众多科学家试图找到气泡和尖钉发展的机理, 得到气泡高度和时间之间的关系.事实上, 普遍研究表明, 在常加速度场g下, 气泡高度的增长过程可分为线性增长阶段、非线性阶段和势流准稳定阶段. Rayleigh-Taylor不稳定性的失稳过程与初始界面处的扰动息息相关[5-8].对微小扰动在空间上做Fourier变换可以得到波数k的频谱[3].对于单模态微小扰动(扰动的模数为单一固定值)而言, 当界面处的扰动十分微小, 即扰动振幅满足h0kk≪1时[9], 气泡高度的变化满足[1-2, 4]
| $ {h_k} = {h_{0k}}\cos h\left( {\mathit{\Gamma }t} \right) $ |
且线性增长率Γ~
| $ A = \frac{{{\rho _{\rm{h}}} - {\rho _1}}}{{{\rho _{\rm{h}}} + {\rho _1}}} $ |
当气泡增长到一定阶段, 气泡高度足够大, 即hk>1/k时[9], 气泡进入非线性增长阶段, 此时气泡高度满足
| $ {h_k} = {\alpha _{\rm{b}}}Ag{t^2} $ |
且气泡和尖钉的发展过程具有自相似性[2].
对于多模态的微小扰动而言, 气泡发展的机理更加复杂.当前学界普遍赞同的气泡发展机制共有两种:融合机制和竞争机制[9-11].多模态扰动由随机波数叠加而成, 其中每一个波数k都对应有波长λ=2π/k.当前研究已经较好地揭示了融合机制.当扰动波长λ远小于系统尺度L时, 气泡之间互相融合形成更大的气泡[12-13].当扰动波长λ和系统尺度L等阶时, 气泡之间存在竞争机制[9, 14].后期混合阶段由大波长气泡之间的竞争主导.气泡竞争机制尚未完全揭开.时至今日, 依旧有众多的科学研究者探索该机制.本文将利用直接数值模拟方法, 计算多模态下的气泡发展过程.
在Rayleigh-Taylor不稳定性的发展过程中, 轻重两种流体开始混合.从理论研究的角度而言组分函数是衡量混合过程的重要物理量.从直接数值模拟的角度, 组分函数是计算气泡和尖钉高度的重要依据.对于混合流体, 其密度
| $ \rho = \frac{m}{V} = \frac{{{m_{\rm{h}}} + {m_1}}}{V} = \frac{{{\rho _{\rm{h}}}{V_{\rm{h}}} + {\rho _1}{V_1}}}{V} = {\rho _i}{f_{{\rm{v}}i}} $ |
其中, ρi为轻重流体的密度, fvi为第i种组分的体积分数, 即单位体积内该种组分所占的体积大小.特别地, 对于重流体而言, 其体积分数可以用下式计算
| $ {f_{{\rm{vh}}}} = \frac{{\rho - {\rho _1}}}{{{\rho _{\rm{h}}} - {\rho _1}}} $ |
同样地, 在单位体积内可以定义第i种组分的质量分数fmi=mi/m.从微观角度而言, 当两种粒子混合处在同一物理空间内时, 粒子整体处于热力学平衡状态, 因此
| $ {f_{{\rm{mh}}}} = \frac{{{m_{\rm{h}}}}}{{{m_{\rm{h}}} + {m_1}}} = \frac{{{\rho _{\rm{h}}}{f_{{\rm{vh}}}}}}{{{\rho _{\rm{h}}}{f_{{\rm{vh}}}} + {\rho _1}\left( {1 - {f_{{\rm{vh}}}}} \right)}} $ |
可以看到, 对于给定的质量分数, 都有唯一对应的体积分数[3].且体积分数剖面和密度剖面具有自相似性.因此, 利用体积分数可以更准确地定义气泡高度和尖钉深度.本文使用h99代替气泡高度, 即重流体体积分数为0.99的高度[3]; 使用h01代替尖钉深度, 即重流体体积分数为0.01的深度[3].本文使用计算流体力学软件CFD2直接输出的组分函数为质量分数, 因而本文探究了二维重流体质量分数剖面的变化过程.
本文的研究内容受到了Boffetta等于2010年对Rayleigh-Taylor不稳定性失稳后期温度剖面研究的启发[15]. Boffetta等从理论的角度出发, 构造了温度扩散方程并给出了温度分布剖面.笔者推测Rayleigh-Taylor不稳定性发展过程中, 组分剖面应当具有相同的性质.通过计算流体力学软件CFD2对二维Rayleigh-Taylor不稳定性进行直接模拟, 本文得到了多模态二维Rayleigh-Taylor不稳定性质量分数剖面的一般规律.
1 数值模拟 1.1 数值模拟方法直接数值模拟(DNS)是目前学界使用最为广泛的模拟方法[16].通常来讲, 数值模拟的网格数与实际物理问题的Reynolds数相关(正相关于Re9/4). Rayleigh-Taylor不稳定性的模拟牵扯到湍流模拟, 即高Reynolds数问题.可见直接数值模拟需要的网格数量十分庞大, 对计算要求十分高.当前计算机发展水平尚不足以支持如此密网格的计算. Youngs指出了隐性大涡流模拟(implicit large eddy simulations, ILESs)可以得到和DNS相当的结果[17].本文模拟Rayleigh-Taylor不稳定性的控制方程为可压缩流体的N-S方程
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{\partial }{{\partial t}}(\rho ) + \nabla \cdot (\rho \boldsymbol{u}) = 0}\\ {\frac{\partial }{{\partial t}}(\rho \boldsymbol{u}) + \nabla \cdot (\rho \boldsymbol{uu}) = - \nabla p + \nabla \cdot \tau + \rho \boldsymbol{g}}\\ {\frac{\partial }{{\partial t}}(\rho e) + \nabla \cdot \left( {\left( {\rho e + p} \right)\boldsymbol{u}} \right) = \nabla \cdot \left( {\boldsymbol{u} \cdot \tau } \right) + \rho \boldsymbol{u} \cdot \boldsymbol{g}} \end{array}} \right. $ |
其中, ρ为流体密度, u为流体速度, e为流体单位质量所携带的总能量, p为压强,
| $ \frac{\partial }{{\partial t}}\left( {\rho {f_{\rm{m}}}} \right) + \nabla \cdot \left( {\rho {f_{\rm{m}}}\mathit{\boldsymbol{u}}} \right) = 0 $ |
此外, 理想气体热力学平衡方程约束了气体能量和压强间的关系
| $ \rho e = p/\left( {\gamma - 1} \right) $ |
γ为气体绝热指数.对于混合之后的流体, 其基本热力学参数的定义遵循等温假设和局部压力假设.
控制方程的数值解使用了3阶Runge-Kutta时间离散格式而对流项则使用了HLL Riemann求解算器和7阶WENO格式[18].
1.2 初始化本文数值模拟的初始化由两个部分组成:界面微小扰动初始化和基本物理量初始化.
本文直接数值模拟过程中, 需要在轻重流体界面添加微小扰动.为了探究多模态下Rayleigh-Taylor不稳定性的发展规律, 本文使用的微小扰动[3]
| $ \mu (x) = \sum\limits_{i = 0}^{1000} {{A_i}} \cos \left( {2{\rm{ \mathsf{ π} }}{k_i}x/L} \right) $ |
其中, Ai为-1×10-5至1×10-5之间的随机数, ki为78至90之间的随机波数, x为横向坐标, L为x方向尺度, 特别地本文取L=10 cm.微小扰动的添加方法主要有两种:密度场的微小扰动和速度场的微小扰动. Dimonte等给出了密度场微小扰动的初始化方案和对流场基本物理量的初始化方案[3].
| $ \rho = {\rho _0}{\left( {1 - \frac{{\gamma - 1}}{\gamma }\frac{{{\rho _0}g\tilde y}}{{{P_0}}}} \right)^{\frac{1}{{\gamma - 1}}}} $ |
| $ p = {P_0}{\left( {1 - \frac{{\gamma - 1}}{\gamma }\frac{{{\rho _0}g\tilde y}}{{{P_0}}}} \right)^{\frac{1}{{\gamma - 1}}}} $ |
| $ {\rho _{\rm{h}}} = 3{\rm{g}}/{\rm{c}}{{\rm{m}}^3} $ |
| $ {\rho _1} = 1{\rm{g}}/{\rm{c}}{{\rm{m}}^3} $ |
| $ \tilde y = y - \mu \left( x \right) $ |
| $ {P_0} = 2{\rm{ \mathsf{ π} }}\left( {{\rho _{\rm{h}}} + {\rho _1}} \right)gL $ |
| $ {\rho _0} = \left\{ {\begin{array}{*{20}{l}} {{\rho _{\rm{h}}},\tilde y > 0}\\ {{\rho _1},\tilde y < 0} \end{array}} \right. $ |
| $ g = 2{\rm{cm}}/{{\rm{s}}^2} $ |
特别地, 通过改变轻重流体的密度便可以改变Rayleigh-Taylor不稳定性的Atwood数, 上述初始化方案给出的A=0.5.
在初始化过程中, 同样需要初始化计算网格.为了简单计算, 本文研究了直角坐标系下的Rayleigh-Taylor不稳定性.为了简化计算, 计算网格为均匀网格.
表 1介绍了3种多模态常加速度场下Rayleigh-Taylor不稳定性数值模拟的物理参数与网格参数.
| 下载CSV 表 1 多模态常加速度场下Rayleigh-Taylor不稳定性数值模拟参数 Tab.1 Simulation parameters of multi-modal Rayleigh-Taylor instability under constant acceleration |
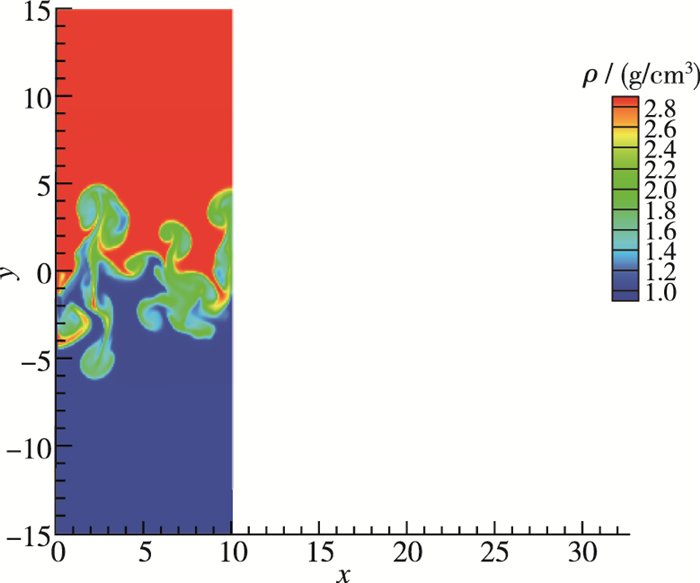
图 1揭示了当A=0.5的情形下Rayleigh-Taylor不稳定性发展到12 s时的密度场.可以看到此时混合已经进入了湍流混合阶段, 轻流体向上发展形成了气泡, 重流体向下发展形成了尖钉.通过计算体积分数, 可以得到不同时刻下气泡高度和尖钉深度随时间的变化规律. 图 1中密度场对应有组分分数场(在CFD2中为质量分数场).组分剖面为组分场的统计性质.对于不同的高度y, 我们可以定义平均组分函数[3]
|
| 图 1 算例2中t=12 s时密度场 Fig.1 Density field of case 2 at t=12 s |
| $ {{\bar f}_{{\rm{v}},{\rm{m}}}}\left( y \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{f_{{\rm{v}},{\rm{m}}}}} \left( {{x_i},y} \right) $ |
其中, N为样本容量.由上述定义, 可以计算平均体积分数剖面, 从而得到气泡高度.本文使用h99代替气泡高度, 即fvh(h99)=0.99.使用h01代替尖钉, 即fvh(h01)=0.01.
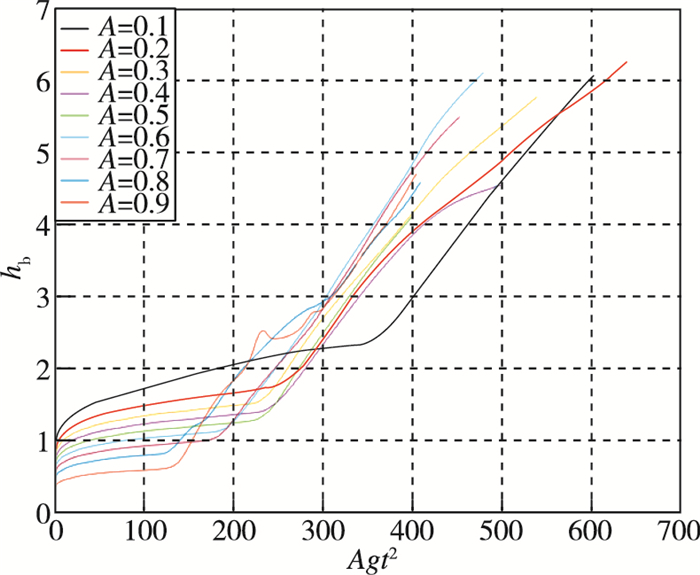
2.2 湍流混合阶段Rayleigh-Taylor不稳定性的湍流混合过程具有自相似性.利用该性质可以将不同时刻下归一化之后的质量分数剖面进行叠加平均, 即对质量分数剖面进行时间方向的平均.由于计算条件的限制, 空间上样本容量往往是十分有限的.但是利用时间方向上的平均可以大大增加样本容量, 使剖面具有更好的统计学性质.然而, Rayleigh-Taylor不稳定性的自相似出现在湍流混合阶段, 因此首先需要确认, 对于不同Atwood数而言, 湍流阶段开始的时间节点.而该结点的判断需要借助气泡高度随时间的变化曲线.
在图 2中可以观测到, 从某一时刻起气泡增长速度突然变快, 气泡高度与Agt2成正比, 即hb~αAgt2.换言之, 在湍流混合阶段, 气泡高度与Agt2之间呈线性关系.而在湍流混合之前, 气泡高度则经历了快速增长的线性增长阶段(气泡高度随时间指数变化).气泡增长的二次律是判断Rayleigh-Taylor不稳定性发展进入湍流混合阶段的重要依据.
|
| 图 2 二维Rayleigh-Taylor不稳定性不同Atwood数下气泡高度随Agt2的变化规律 Fig.2 Evolution of bubble height height with Agt2 for two dimensional Rayleigh-Taylor instability at different Atwood numbers |
对不同的Atwood数, 读取湍流混合阶段的开始时刻ttrans.在该时刻后质量分数剖面呈现自相似性, 可以对其进行时间方向上的平均.
2.3 质量分数剖面的归一化对于任意时刻t>ttrans, CFD2都会直接输出该时刻下的质量分数剖面.一般地来讲, 质量分数的数值被严格限定在0至1之间.特别地, 在气泡上方的未混合重流体区域内质量分数为1.在尖钉下方的未混合轻流体区域内质量分数为0.从而, 通过定义Y=(y-hs)/(hb-hs)可以实现质量分数剖面的归一化.即归一化之后的质量分数函数
| $ {{\tilde f}_{\rm{m}}}\left( Y \right) = {f_{\rm{m}}}\left( {\frac{{y - {h_{\rm{s}}}}}{{{h_{\rm{b}}} - {h_{\rm{s}}}}}} \right) $ |
在Y∈[0, 1]时, 质量分数
经过该归一化之后, 不同时刻下的质量分数剖面都具有了相同的性质, 因而可以对不同时刻下的质量分数曲线进行叠加平均.然而在叠加的过程中, 需要注意到不同时刻下的质量分数剖面归一化之后都具有不同的位置Y, 无法简单地将其直接点对点进行叠加. 3次样条插值可以很好地解决这个问题.对某一时刻下的质量分数曲线做3次样条插值, 可以将该曲线变成定义在0到1之间的均匀坐标的函数.
对每个时刻下的质量分数剖面都做3次样条插值之后, 就可以对其做时间方向上的平均.
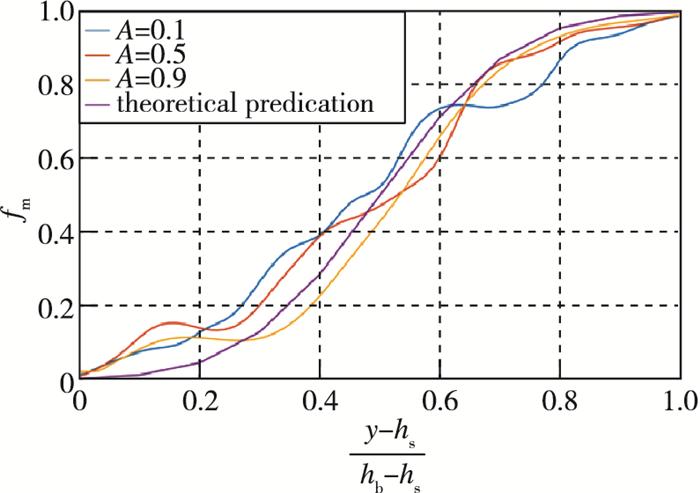
2.4 不同Atwood数下质量分数剖面图 3展示了不同Atwood数下在时间方向平均的归一化质量分数曲线.可以观测到, 无论是在高Atwood数下或是低Atwood数下, 质量分数曲线都有着相同的趋势.事实上, 3条质量分数剖面都可以近似看成分布在同一条曲线两侧, 即
|
| 图 3 不同Atwood数下质量分数剖面 Fig.3 Mass fraction profiles at different Atwood numbers |
| $ {f_{\rm{m}}} \sim \frac{1}{2}{\rm{erf}}\left( {4\left( {Y - \frac{1}{2}} \right)} \right) + \frac{1}{2} $ |
可见, 质量分数剖面并不依赖于Atwood数.且综合上述内容, 可以给出质量分数曲线的一般形式.
| $ {f_{\rm{m}}}\left( {y,t} \right) \sim \frac{1}{2}{\rm{erf}}\left( {4\left( {\frac{{y - {h_{\rm{s}}}(t)}}{{{h_{\rm{b}}}(t) - {h_{\rm{s}}}(t)}} - \frac{1}{2}} \right)} \right) + \frac{1}{2} $ |
通过数值模拟软件CFD2对3种不同Atwood数下的二维Rayleigh-Taylor不稳定性问题做数值模拟, 并将湍流混合阶段的质量分数剖面做时间方向上的平均, 最终得到了3条质量分数剖面.数值模拟的结果表明, 归一化的重流体质量分数剖面不依赖于流体间密度比.也即, 质量分数剖面仅依赖于气泡高度和尖钉深度.因而只要能够预测气泡高度和尖钉深度的变化, 就可以预测整个质量分数剖面的变化规律.但是数值模拟得到的质量分数曲线依旧不是十分光滑.这有可能是二维数值模拟的统计样本容量不够大造成的.下一步研究工作将针对三维Rayleigh-Taylor不稳定性的数值模拟.验证在三维情况下, 二维数值模拟的结果是否依旧成立.通过加大空间上的样本容量, 得到更为光滑的质量分数曲线.探究三维问题中组分剖面的变化规律.
致谢 本文特别感谢中国自然科学基金(91852207, 11801036, 11702029和11602028), NSAF联合基金(U1630247, U1730111和U1830139)以及中国工程物理研究院(ZYYZ1912-12)的大力支持.| [1] |
Rayleigh L. Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density[J]. Proceedings of the London Mathematical Society, 1882, s1-14(1): 170-177. |
| [2] |
Taylor G I. The formation of a blast wave by a very intense explosion I. Theoretical discussion[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1950, 201(1065): 159-174. DOI:10.1098/rspa.1950.0049 |
| [3] |
Dimonte G, Youngs D L, Dimits A, et al. A comparative study of the turbulent Rayleigh-Taylor instability using high-resolution three-dimensional numerical simulations:The Alpha-Group collaboration[J]. Physics of Fluids, 2004, 16(5): 1668-1693. DOI:10.1063/1.1688328 |
| [4] |
Chandrasekhar S. Hydrodynamic and hydromagnetic stability[M]. Oxford: Oxford University Press, 1961.
|
| [5] |
Birkhoff G. Taylor instability and laminar mixing[R]. Report No. LA-1862, 1954.
|
| [6] |
Cherfils C, Mikaelian K O. Simple model for the turbulent mixing width at an ablating surface[J]. Physics of Fluids, 1996, 8(2): 522-535. DOI:10.1063/1.868805 |
| [7] |
Inogamov N A. Turbulent stage of the Rayleigh-Taylor instability[J]. Soviet Technical Physics Letters, 1978, 4(6): 299-300. |
| [8] |
Inogamov N A. Dautray R. Proceedings of the third international workshop phys comp. turbulent mixing[A]. Cesta, France: Commissariat Energie Atomique, 1991.
|
| [9] |
Dimonte G. Dependence of turbulent Rayleigh-Taylor instability on initial perturbations[J]. Physical Review E, 2004, 69(5): 056305. DOI:10.1103/PhysRevE.69.056305 |
| [10] |
Dimonte G, Ramaprabhu P, Youngs D L, et al. Recent advances in the turbulent Rayleigh-Taylor instability[J]. Physics of Plasmas, 2005, 12(5): 056301. DOI:10.1063/1.1871952 |
| [11] |
Youngs D L. The density ratio dependence of self-similar Rayleigh-Taylor mixing[J]. Philosophical Transactions:Mathematical, Physical and Engineering Sciences, 2013, 371(2003): 20120173. DOI:10.1098/rsta.2012.0173 |
| [12] |
Alon U, Hecht J, Ofer D, et al. Power laws and similarity of Rayleigh-Taylor and Richtmyer-Meshkov mixing fronts at all density ratios[J]. Physical Review Letters, 1995, 74(4): 534-536. DOI:10.1103/PhysRevLett.74.534 |
| [13] |
Alon U, Hecht J, Mukamel D, et al. Scale invariant mixing rates of hydrodynamically unstable interfaces[J]. Physical Review Letters, 1994, 72(18): 2867-2870. DOI:10.1103/PhysRevLett.72.2867 |
| [14] |
Ramaprabhu P, Dimonte G, Andrews M J. A numerical study of the influence of initial perturbations on the turbulent Rayleigh Taylor instability[J]. Journal of Fluid Mechanics, 2005, 536: 285-319. DOI:10.1017/S002211200500488X |
| [15] |
Boffetta G, De Lillo F, Musacchio S. Nonlinear diffusion model for Rayleigh-Taylor mixing[J]. Physical Review Letters, 2010, 104(3): 034505. DOI:10.1103/PhysRevLett.104.034505 |
| [16] |
Moin P, Mahesh K. Direct numerical simulation:a tool in turbulence research[J]. Annual Review of Fluid Mechanics, 1998, 30: 539-578. DOI:10.1146/annurev.fluid.30.1.539 |
| [17] |
Youngs D L. Rayleigh-Taylor mixing:direct numerical simulation and implicit large eddy simulation[J]. Physica Scripta, 2017, 92(7): 074006. DOI:10.1088/1402-4896/aa732b |
| [18] |
Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |



