边盖驱动方腔流动是流体动力学研究领域长期关注的问题[1].半个世纪前, Burggraf首先就单边顶盖驱动方腔流动采用解析方法和数值方法确认了低Reynolds数下二维不可压稳态解的存在, 其后该二维稳态解在Pan和Acrivos的流场可视化实验中得到了证实.顶盖驱动方腔流动有着丰富的动力学涡结构, 成为不可压缩流动数值模拟方法的标准算例[2], Ghia等[3]和Schreiber等[4]最早获得了Re < 10 000下的二维稳态数值解, 成为引用最多的方腔流动数值模拟研究工作.在高Reynolds数下可以计算二维稳态数值解之后, 就自然需要考察其三维线性不稳定性[5-6], Ding等[7]最早研究了顶盖驱动方腔流动的三维整体线性稳定性, 发现了在高Reynolds数下顶盖驱动方腔流动会发生三维线性失稳. Theofilis[8]和Albensoeder等[9]则各自独立地发现了比Ding等[7]更低临界Reynolds数的三维失稳模态, 对应的临界Reynolds数为Rec≈782.至此, 单边顶盖驱动方腔流动的稳态解及其稳定性属性已经被深入地研究, 而双侧或四边壁面驱动的方腔流动研究还较为有限. Kuhlmann等[10-11]率先将单边顶盖驱动推广到双侧非相邻的边盖驱动, 即方腔流动由面对面两壁面的平行同向或反向运动驱动.在低Reynolds数下, 这种双侧边盖驱动方腔稳态流动由两个同向或反向旋转的贴近每个运动壁面的主涡构成. Albensoeder等[12]研究了双侧平行壁面同向驱动方腔稳态流动(由两个反向旋转主涡构成)的三维线性稳定性.他们发现当平行驱动壁面相互远离时, 这两个反向主涡趋于相互独立, 失稳机制主要是类似单边顶盖驱动方腔流动的离心不稳定性; 当平行驱动壁面相互靠近时, 两个主涡会发生合并, 流动失稳机制主要是椭圆不稳定性; 当驱动方腔高宽比趋于1时, 发生quadripolar型不稳定性; 进一步当平行驱动壁面非常靠近时, 稳态流动又重新受椭圆不稳定性机制影响. Albensoeder等[13]进一步深入研究了双侧平行壁面反向驱动方腔稳态流动的三维线性稳定性, 得到了类似于同向驱动下的流动失稳机制.
相邻双侧边盖驱动方腔流动(上壁面向右运动和左侧壁面向下运动)首先由Ben-Artzi等[14]对二维不可压缩N-S方程的流函数方程采用一种高阶紧致格式进行了数值模拟研究.他们的模拟结果发现二维稳态基本流关于方腔对角线是对称的, Reynolds数直到1 000这种对称性还是保持的, 而在Re=3 200时这种对称性会被打破, 成为不对称和非定常状态. Wahba[15]对这种双侧驱动方腔流动采用2阶有限差分方法重新进行了数值求解, 获得了一个新的临界Reynolds数Rec≈1 073, 在该临界值之上对称流场发生失稳, 流场将分叉为非对称稳态流场, 这种非对称稳态解直到Re=4 000还存在. Wahba的数值研究是一种动力学分叉研究, 而就本文作者所知关于相邻双侧边盖驱动方腔流动的三维线性稳定性研究还没有开展, 本文将在这方面进行考察研究.在第1节中, 给出相邻双侧边盖驱动方腔流动的稳态二维基本流场和三维线性稳定性方程, 详述相关数值计算方法; 在第2节中, 对相邻双侧边盖驱动方腔流动进行线性稳定性分析, 发现了最不稳定的驻定模态和两对对称行波模态, 同时给出这些失稳模态的时间增长率曲线和中性边界曲线; 在第3节中, 对相邻双侧边盖驱动方腔流动的三维线性整体稳定性进行了简要总结.
1 控制方程和数值方法 1.1 稳态基本流场边盖驱动方腔流动的三维线性整体稳定性研究首先需要获得二维稳态基本流场, 由此在基本流场上叠加三维扰动来开展不稳定分析.通常有两种不同的方法用于二维稳态基本流场的计算:一种是直接数值模拟随时间演化的二维流动控制方程, 直至演化解趋于稳态; 另一种是将控制方程的时间导数取为零, 对稳态方程空间离散后采用Newton迭代方法求解.本文将采用Newton迭代方法求解稳态基本流场, 首先给出无量纲的N-S控制方程如下:
| $ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{\bar v}}}}{{\partial t}} + \left( {\mathit{\boldsymbol{\bar v}} \cdot \nabla } \right)\mathit{\boldsymbol{\bar v}} = \frac{1}{{Re}}{\nabla ^2}\mathit{\boldsymbol{\bar v}} - \nabla \bar p\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\nabla \cdot \mathit{\boldsymbol{\bar v}} = 0 \end{array} $ |
这里, v=(v, w)T为方腔流动的二维速度矢量, 为压力, ∇=(∂y, ∂z)为梯度算子.考虑相邻双侧边盖驱动方腔流动, 即以相同的速度上壁面向右运动和左侧壁面向下运动, 如图 1所示.正方形方腔的高度作为特征长度L, 边盖驱动速度作为特征速度U, 由此可以定义控制方程的Reynolds数为Re=UL/ν, 其中ν为运动黏性系数.
|
| 图 1 相邻双侧边盖驱动方腔流动的二维有限元网格离散(Ny=Nz=16) Fig.1 Triangulation of finite element mesh of two-sided non-facing lid driven cavity flows (Ny=Nz=16) |
稳态控制方程的空间离散采用Taylor-Hood有限元方法, Newton迭代方法用于求解稳态基本流场.低Reynolds数下方腔流动稳态解的计算易于收敛, 然后用低Reynolds数的稳态收敛解作为高Reynolds数的迭代初值, 连续地求解不同Reynolds数下的稳态解.为了稳态控制方程的Taylor-Hood有限元方法快速实现, 可以采用高效集成有限元软件FreeFem++[16], 该软件可以快速而高效地实现方腔流动稳态解的计算.有限元网格节点选择非均匀正交的Chebyshev Gauss配置点, 可以构成一个四边形有限元离散, 如图 1(a)所示.由于FreeFem++是一个三角形有限元软件, 因此可以将每个四边形沿对角线剖分, 形成如图 1(b)所示的三角形有限元离散.为了提高数值模拟的计算精度, 采用Kosloff-Tal-Ezer变换将网格节点更加靠近方腔边界, 节点变换公式如下:
| $ \begin{array}{l} {y_i} = \frac{1}{2}(1 + {\eta _i}), {\eta _i} = \frac{{{{\sin }^{ - 1}}( - {\alpha _0} \cdot \cos ({\rm{ \mathsf{ π} }}i/{N_y}))}}{{{{\sin }^{ - 1}}{\alpha _0}}}, \\ \;\;\;\;i = 0, 1, \cdots , {N_y}\\ {z_j} = \frac{1}{2}(1 + {\zeta _j}), {\zeta _j} = \frac{{{{\sin }^{ - 1}}( - {\alpha _0} \cdot \cos ({\rm{ \mathsf{ π} }}j/{N_z}))}}{{{{\sin }^{ - 1}}{\alpha _0}}}, \\ \;\;\;{\rm{ }}j = 0, 1, \cdots , {N_z} \end{array} $ |
这里, 参数α0可以调节网格节点的拉伸.有限元空间离散后, 就可以通过线性化稳态N-S方程, 在FreeFem++参考手册的帮助下Newton迭代求解相邻双侧边盖驱动方腔流动的稳态解.为了验证编制的FreeFem++程序代码的可靠性, 本文给出了Re=100,500时相邻双侧边盖驱动方腔流动的稳态解, 流线图见图 2.基于双侧边盖运动是关于对角线对称的, 稳态基本流场也是关于对角线对称的, 显然存在一对对称的大主涡以及一对对称的二次涡结构.稳态基本流场的主涡和二次涡结构与Wahba的计算结果[15]在对称性和尺寸大小上相一致, 由此验证了有限元程序计算的可靠性.
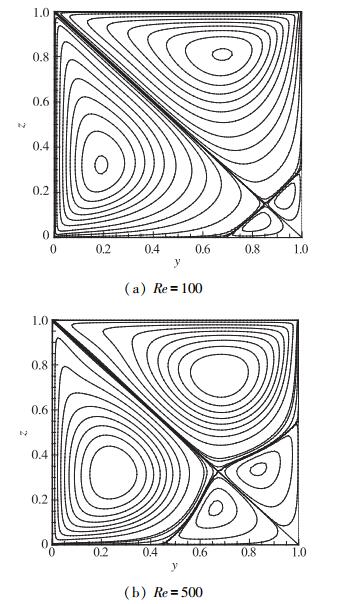
|
| 图 2 相邻双侧边盖驱动方腔流动的二维稳态基本流流线图(Ny=Nz=80) Fig.2 Stream lines of basic steady-state of two-sided non-facing lid driven cavity flow(Ny=Nz=80) |
二维基本流动的三维线性稳定性分析也称为BiGlobal型线性整体稳定性分析[8].假设q(x, y, z, t)=(v, p)T为三维不可压流场的速度场和压力场, 则三维流场可以分解为二维基本稳态流场q=(v, p)T和三维正则模扰动之和, 形式如下
| $ \mathit{\boldsymbol{q}} = \mathit{\boldsymbol{\bar q}} + \varepsilon \mathit{\boldsymbol{\hat q}}\left( {y, z} \right)\exp \left[ {{\rm{i}}\left( {kx - \sigma t} \right)} \right] $ |
这里,
| $ {\rm{i}}k\hat u + {{\rm{D}}_y}\hat v + {{\rm{D}}_z}\hat w = 0 $ |
| $ {\cal L}\hat u - {\rm{i}}k\hat p = - {\rm{i}}\sigma \hat u $ |
| $ ({\cal L} - {{\rm{D}}_y}\bar v)\hat v - ({{\rm{D}}_z}\bar v)\hat w - {{\rm{D}}_y}\hat p = - {\rm{i}}\sigma \hat v $ |
| $ ({\cal L} - {{\rm{D}}_z}\bar w)\hat w - ({{\rm{D}}_y}\bar w)\hat v - {{\rm{D}}_z}\hat p = - {\rm{i}}\sigma \hat w $ |
以及边界条件
各种方腔槽道流动的BiGlobal型线性整体稳定性分析[17-21]通常采用谱配置方法进行空间离散来求解广义特征值问题.然而, 在方腔槽道流动的线性整体稳定性计算[5, 20, 22]中已经揭示了谱配置方法会占用大量内存空间, 所花费的CPU计算时间也非常巨大. Paredes等[22]则证实了Hermanns等[23]的高阶有限差分格式(FD-q格式)将显著优于谱方法: FD-q格式可以基于稀疏矩阵存储技术将花费更小的内存空间, 由此极大地提高了计算效率. FD-q格式是建立在非均匀网格之上的, 可以最小化插值误差, 因此它优于其他著名的高阶有限差分格式, 如DRP格式、SBP格式以及Padé格式.本文广义特征值问题的空间离散采用类似于FD-q格式高阶有限差分格式, 非均匀网格采用的是Kosloff-Tal-Ezer变换的Chebyshev谱配置点, 在每个配置点上采用Welfert的递归过程[24]构造高阶差分矩阵, 该差分矩阵的构造过程已经在Weideman等[25]的MATLAB程序包中实现.
采用高阶有限差分方法空间离散后, 线性稳定性方程就离散成矩阵形式的广义矩阵特征值问题, 形式如下
| $ \mathit{\boldsymbol{A\hat q}} = \sigma \mathit{\boldsymbol{B\hat q}} $ |
这里, A和B为稀疏非对称复数矩阵.如果广义矩阵特征值方程两边同时减去
| $ {\left( {A - \mu \mathit{\boldsymbol{B}}} \right)^{ - 1}}\mathit{\boldsymbol{B\hat q}} = {\left( {\sigma - \mu } \right)^{ - 1}}\mathit{\boldsymbol{\hat q}} $ |
显然, 变换矩阵(A-μB)-1B的最大特征值将对应于原广义矩阵特征值方程中最靠近偏移值μ的特征值, 这个变换过程通常称作shift-and-invert算法[6].标准矩阵特征值问题可以采用隐式重启Arnoldi方法求解最大幅值的特征值, 在MATLAB软件中对应于eigs函数调用.
2 线性整体稳定性分析边盖驱动方腔流动没有流向方向的基本流动, 其时间不稳定模态可以直接从线性稳定性方程找到特定的属性:对于每一个实波数k, 当复数σ=σr+iσi是线性稳定性方程的特征值时, 复数-σ*=-σr+iσi也是线性稳定性方程的另一个特征值(星号表示复共轭).这就意味着对于线性时间不稳定, 要么同时存在两个线性增长率相同而角频率正负号相反的不稳定模态, 称为振荡模态或行波模态, 要么存在的是一个角频率为零的不稳定模态, 称为驻定模态.通过对相邻双侧边盖驱动方腔流动的三维整体线性稳定性方程特征值的计算, 发现最不稳定的时间不稳定模态是驻定的, 同时还发现了另外两对对称行波模态.下面将对它们的线性时间不稳定性分别进行介绍.
2.1 驻定模态对于相邻双侧边盖驱动方腔流动, 首先给出不同Reynolds数下最不稳定驻定模态的线性时间增长率曲线, 如图 3所示.从图中可以容易地看到线性时间增长率随着Reynolds数的增大而增大, 并且最大增长率发生在波数k=2.6附近, 这种不稳定对应于中等波长范围.下沿截断波数随Reynolds数的增大而减小, 上沿截断波数随Reynolds数的增大而增大, 直至在Re=500上方截断波数接近3.9后增长缓慢.截断波数随Reynolds数的变化情况可以更加清楚地从线性时间不稳定的Re-k中性曲线中看出, 如图 4所示.从中性曲线还可以发现此时间不稳定驻定模态存在一个临界Reynolds数Rec=261.5, 对应的临界波数kc=2.64.进一步地, 下沿截断波数减小到零时, 驻定模态中性曲线将与横轴坐标相交于Rec2d=1 061.7, 这将对应于Wahba等[15]发现的二维不稳定性的临界Reynolds数. Wahba经由直接数值模拟方法得到二维临界Reynolds数为1 073, 比我们通过线性稳定性方程的特征值计算得到的临界值稍大.显然, 驻定模态的三维临界Reynolds数远远小于二维临界Reynolds数, 可见相邻双侧边盖驱动方腔流动的三维不稳定性具主导地位.
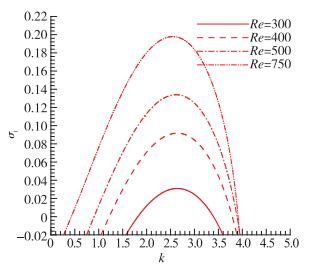
|
| 图 3 相邻双侧边盖驱动方腔流动不同Reynolds数下最不稳定驻定模态的线性时间增长率曲线 Fig.3 Linear temporal growth rates of most unstable stationary mode of the steady two-sided non-facing lid driven cavity flow with different Reynolds numbers |
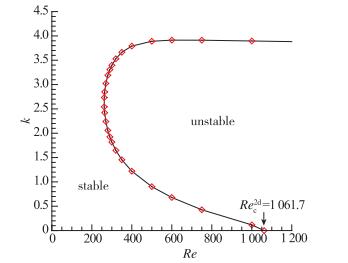
|
| 图 4 相邻双侧边盖驱动方腔流动最不稳定驻定模态的Re-k中性曲线 Fig.4 Neutral curve Re-k of the stationary unstable mode ofsteady two-sided non-facing lid driven cavity flow |
方腔流动在流向x方向上是无限的, 基本流场也没有流向流动, 从而不依赖于坐标x.因此, 方腔流动具有沿x坐标轴的平移不变对称性Tx0, 这一平移对称性通常表示为群变换E(1).基于方形腔体轮廓, 相邻双侧边盖驱动方腔流动还存在额外的对称性:关于对角线的反射对称性Sd, 可以定义成
| $ \begin{array}{l} {S_{\rm{d}}}:\left( {y, z, t} \right) \to \left( {z, y, t} \right), \\ (u, v, w, {\omega _x}) \to (u, - w, - v, - {\omega _x}) \end{array} $ |
这里, ωx为流向涡量.相邻双侧边盖驱动方腔流动对称性同构于E(1)×Z2, 而流动线性失稳是从对称性被打破开始的, 并由此分叉到新的流动状态.最先线性失稳的驻定模态发生在非零的临界波数下, 因此平移不变对称性Tx0被打破.至于关于对角线的反射对称性Sd是否被打破, 需要画出驻定模态在临界点处的特征模态空间结构, 以此来判断Sd是否被打破.首先在临界点处线性增长率为零(σi=0), 如果失稳模态的离散特征向量记为X=Xr+iXi, 那么在临界点处的失稳模态空间结构可以由Re(Xei(kx-σrt))得到, 其中k为实波数, σr为角频率,Re表示实部取值; 然后, 就可以画出驻定不稳定模态在临界点处的流向扰动速度和流向扰动涡量的空间等值面分布, 如图 5所示.
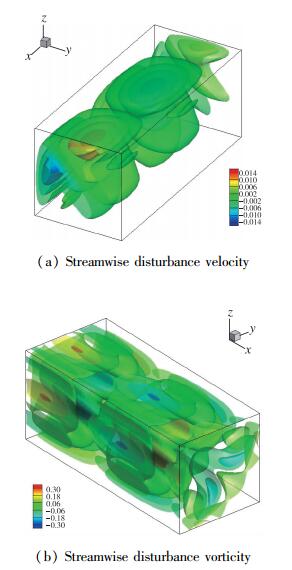
|
| 图 5 相邻双侧边盖驱动方腔流动驻定不稳定模态在临界点处的流向扰动速度和流向扰动涡量的空间等值面分布(Rec=261.5和kc=2.64) Fig.5 Spatial iso-surface of streamwise disturbance velocity and vorticity of the stationary unstable eigenmode at the critical point with Rec=261.5 and kc=2.64 for the steady two-sided non-facing lid driven cavity flow |
从图中可以清楚地看到流向扰动速度关于方腔对角线是反对称的, 而流向扰动涡量关于方腔对角线则是对称的.结合Sd的对称性公式, 流向扰动速度和流向扰动涡量的分布不具有Sd的对称性, 可见流场对称性Sd在驻定模态失稳临界处也被打破了.此外, 从图 5中还可以发现失稳扰动(流向速度和流向涡量)分布在对称的两个主涡区域, 而在对称的二次涡区域没有失稳扰动出现, 可见主涡区域是三维扰动失稳的主要能量来源地, 可以认为三维扰动的失稳机制来源于对称主涡.
2.2 行波模态对于相邻双侧边盖驱动方腔流动, 在Reynolds数小于1 000的范围内, 还可以找到两对线性不稳定行波模态, 每一对模态在不同Reynolds数下的线性时间增长率曲线在图 6(a)和图 7(a)中给出.
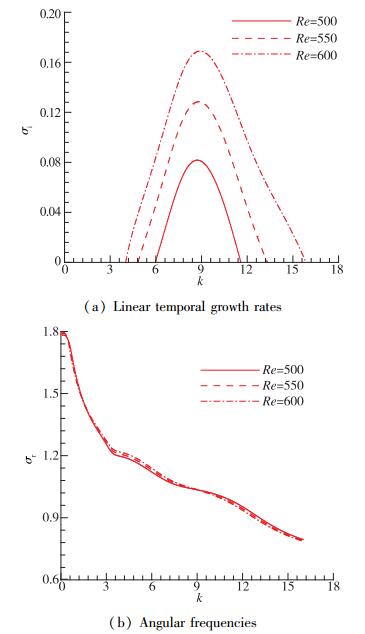
|
| 图 6 相邻双侧边盖驱动方腔流动不同Reynolds数下第1对行波模态的线性时间增长率曲线和角频率曲线 Fig.6 Linear temporal growth rates and angular frequencies of first downstream unstable travelling mode of steady two-sided non-facing lid driven cavity flow with different Reynolds numbers |
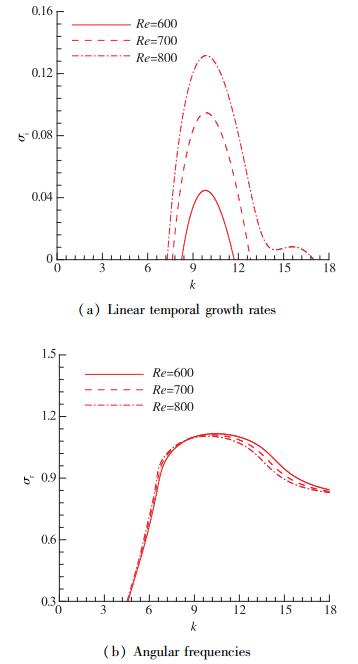
|
| 图 7 相邻双侧边盖驱动方腔流动不同Reynolds数下第2对行波模态的线性时间增长率曲线和角频率曲线 Fig.7 Linear temporal growth rates and angular frequencies of the second pair of unstable travelling mode (positive angular frequency for downstream mode) of the steady two-sided non- facing lid driven cavity flow with different Reynolds numbers |
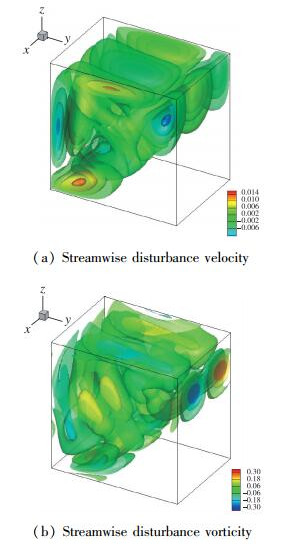
在图中可以清楚地看到不稳定行波模态发生在很大的波数下, 这将对应于短波不稳定; 随着Reynolds数的增大, 不稳定的波数区间也增大, 两对行波模态的最大时间增长率分别发生在k=9和k=10附近.由于每对行波模态的角频率大小相等、符号相反, 在图 6(b)和图 7(b)中只给出了不同Reynolds数下符号为正的角频率曲线(对应向下游传播的行波模态).从角频率曲线中可以看出, Reynolds数的变化对角频率的影响不大.但是, 对于图 6(b)的行波模态, 波数的增加伴随着角频率的减小; 而对于图 7(b)的行波模态, 波数在增加的过程中, 角频率先显著增大, 然后再缓慢减小.进一步地, 两对不稳定行波模态的Re-k中性曲线在图 8中给出.从图中可以容易地得到第1对行波模态的临界Reynolds数为Rec=428.4, 对应的临界波数为kc=8.6;而第2对行波模态的临界Reynolds数为Rec=533.1, 对应的临界波数为kc=9.8.第1对行波模态的上沿截断波数随着Reynolds数的增大而显著增大, 而下沿截断波数随着Reynolds数的增大而减小, 但是减小的趋势变得越来越缓慢.类似地, 可以画出第1对行波不稳定模态在临界点处的流向扰动速度和流向扰动涡量的空间等值面分布, 如图 9所示.
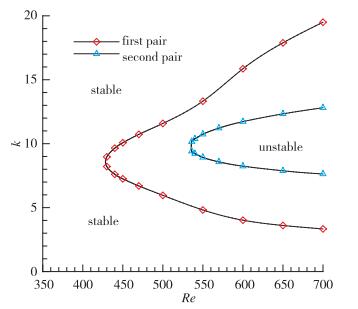
|
| 图 8 相邻双侧边盖驱动方腔流动两对对称行波模态的Re-k中性曲线 Fig.8 Neutral curves Re-k of two pairs of symmetrical travelling unstable modes of steady two-sided non-facing lid driven cavity flow |
|
| 图 9 相邻双侧边盖驱动方腔流动第1对行波模态在临界点处的流向扰动速度和流向扰动涡量的空间等值面分布(Rec=428.4和kc=8.6) Fig.9 Spatial iso-surface of streamwise disturbance velo- city and streamwise disturbance vorticity of the first pair of unstable symmetrical travelling eigenmodes (downstream mode) at the critical points with Rec=428.4 and kc=8.6 for the steady two-sided non-facing lid driven cavity flow |
从图 9中可以清楚地看到流向扰动速度关于方腔对角线是反对称的, 而流向扰动涡量关于方腔对角线则是对称的.因此, 流场对称性Sd在这对行波不稳定模态的临界处也被打破了.同样地, 从图 9中还可以发现失稳扰动(流向速度和流向涡量)分布在对称的两个主涡区域, 而在对称的二次涡区域没有失稳扰动出现.
最后, 如果将驻定模态和两对行波模态的中性曲线放在一起, 尽管最不稳定的模态是驻定模态, 但它的临界点发生在中等波长区域, 并且截断波数随着Reynolds数增大趋于3.9.这样, 对于在x坐标方向受限的情况下, 如果x坐标方向受限尺度小于方腔高度(k>2π), 这时驻定模态无法出现, 而行波模态基于它的短波特征可能会最先失稳.
3 总结本文首先通过稳态二维基本流场的有限元计算和三维线性稳定性方程的广义特征值计算, 研究了相邻双侧边盖驱动方腔流动的三维整体线性稳定性, 发现了一个最不稳定的驻定模态和两对对称行波模态.不稳定驻定模态的临界Reynolds数Rec为261.5, 相应的临界波数kc为2.64.通过画出的驻定模态中性曲线, 可以得到二维不稳定性的临界Reynolds数Rec2d为1 061.7, 比Wahba直接数值模拟得到的临界值稍小.两对不稳定行波模态的临界Reynolds数Rec分别为428.4和533.1, 它们对应于较大临界波数, 因此这两个行波模态是短波不稳定的.最后, 画出不稳定模态在临界点处的流向扰动速度和流向扰动涡量的空间分布, 不仅发现了驻定模态和行波模态在临界点处均打破了稳态系统的Sd对称性, 还发现失稳扰动分布在对称的两个主涡区域, 主涡区域是三维扰动失稳的主要能量来源地.本文尽管揭示了相邻双侧边盖驱动方腔流动的三维整体线性稳定性的一些基本性质, 但是对称主涡三维扰动失稳机制还需进一步研究.
致谢 本项工作得到了国家自然科学基金(11672046, 11771054), 中国工程物理研究院科学发展基金(2015B0201037), 以及计算物理实验室基金的资助.| [1] |
Shankar P N, Deshpande M D. Fluid mechanics in the driven cavity[J]. Annual Review of Fluid Mechanics, 2000, 32: 93-136. DOI:10.1146/annurev.fluid.32.1.93 |
| [2] |
Erturk E. Discussions on driven cavity flow[J]. International Journal for Numerical Methods in Fluids, 2009, 60(3): 275-294. DOI:10.1002/fld.v60:3 |
| [3] |
Ghia U, Ghia K N, Shin C T. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method[J]. Journal of Computational Physics, 1982, 48(3): 387-411. |
| [4] |
Schreiber R, Keller H B. Driven cavity flows by efficient numerical techniques[J]. Journal of Computational Physics, 1983, 49(2): 310-333. DOI:10.1016/0021-9991(83)90129-8 |
| [5] |
Theofilis V. Advances in global linear instability analysis of nonparallel and three-dimensional flows[J]. Progress in Aerospace Sciences, 2003, 39(4): 249-315. DOI:10.1016/S0376-0421(02)00030-1 |
| [6] |
Theofilis V. Global linear instability[J]. Annual Review of Fluid Mechanics, 2011, 43: 319-352. DOI:10.1146/annurev-fluid-122109-160705 |
| [7] |
Ding Y, Kawahara M. Linear stability of incompressible flow using a mixed finite element method[J]. Journal of Computational Physics, 1998, 139(2): 243-273. |
| [8] |
Theofilis V. Globally unstable basic flows in open cavities[R]. AIAA 2000-1995, 2000.
|
| [9] |
Albensoeder S, Kuhlmann H C, Rath H J. Three-dimensional centrifugal-flow instabilities in the lid-driven-cavity problem[J]. Physics of Fluids, 2001, 13(1): 121-135. DOI:10.1063/1.1329908 |
| [10] |
Kuhlmann H C, Wanschura M, Rath H J. Flow in two-sided lid-driven cavities:non-uniqueness, instabilities, and cellular structures[J]. Journal of Fluid Mechanics, 1997, 336: 267-299. DOI:10.1017/S0022112096004727 |
| [11] |
Kuhlmann H C, Wanschura M, Rath H J. Elliptic instability in two-sided lid-driven cavity flow[J]. European Journal of Mechanics-B/Fluids, 1998, 17(4): 561-569. DOI:10.1016/S0997-7546(98)80011-3 |
| [12] |
Albensoeder S, Kuhlmann H C. Three-dimensional instability of two counter-rotating vortices in a rectangular cavity driven by parallel wall motion[J]. European Journal of Mechanics-B/Fluids, 2002, 21(3): 307-316. DOI:10.1016/S0997-7546(02)01188-3 |
| [13] |
Albensoeder S, Kuhlmann H C. Linear stability of rectangular cavity flows driven by anti-parallel motion of two facing walls[J]. Journal of Fluid Mechanics, 2002, 458: 153-180. |
| [14] |
Ben-Artzi M, Croisille J P, Fishelov D, et al. A pure-compact scheme for the streamfunction formulation of Navier-Stokes equations[J]. Journal of Computational Physics, 2005, 205(2): 640-664. |
| [15] |
Wahba E M. Multiplicity of states for two-sided and four-sided lid driven cavity flows[J]. Computers & Fluids, 2009, 38(2): 247-253. |
| [16] |
Pironneau O, Hecht F, Morice J. FreeFem++ v 3.61-1[EB/OL]. (2018-07-12). http://www.freefem.org.
|
| [17] |
Tatsumi T, Yoshimura T. Stability of the laminar flow in a rectangular duct[J]. Journal of Fluid Mechanics, 1990, 212: 437-449. DOI:10.1017/S002211209000204X |
| [18] |
Theofilis V, Duck P W, Owen J. Viscous linear stability analysis of rectangular duct and cavity flows[J]. Journal of Fluid Mechanics, 2004, 505: 249-286. DOI:10.1017/S002211200400850X |
| [19] |
Priede J, Aleksandrova S, Molokov S. Linear stability of Hunt's flow[J]. Journal of Fluid Mechanics, 2010, 649: 115-134. DOI:10.1017/S0022112009993259 |
| [20] |
Hu J, Henry D, Yin X Y, et al. Linear biglobal analysis of Rayleigh-Bénard instabilities in binary fluids with and without throughflow[J]. Journal of Fluid Mechanics, 2012, 713: 216-242. DOI:10.1017/jfm.2012.455 |
| [21] |
Qi T Y, Liu C, Ni M J, et al. The linear stability of Hunt-Rayleigh-Bénard flow[J]. Physics of Fluids, 2017, 29(6): 064103. DOI:10.1063/1.4984842 |
| [22] |
Paredes P, Hermanns M, Le Clainche S, et al. Order 104 speedup in global linear instability analysis using matrix formation[J]. Computer Methods in Applied Mech-anics and Engineering, 2013, 253: 287-304. DOI:10.1016/j.cma.2012.09.014 |
| [23] |
Hermanns M, Hernández J A. Stable high-order finite-difference methods based on non-uniform grid point distri-butions[J]. International Journal for Numerical Methods in Fluids, 2008, 56(3): 233-255. DOI:10.1002/(ISSN)1097-0363 |
| [24] |
Welfert B D. Generation of pseudospectral differentiation matrices I[J]. SIAM Journal on Numerical Analysis, 1997, 34(4): 1640-1657. DOI:10.1137/S0036142993295545 |
| [25] |
Weideman J A C, Reddy S C. A MATLAB differentiation matrix suite[J]. ACM Transactions on Mathematical Software, 2000, 26(4): 465-519. DOI:10.1145/365723.365727 |



