流体力学界面不稳定性对于超燃冲压发动机的混合燃烧、激光驱动惯性约束核聚变(inertial confinement fusion, ICF)及天体物理的超新星爆发有着重要的作用, 而且不稳定性后期非线性演化对于揭示可压缩湍流有着本质重要性.而湍流是一个远未解决的难题, 由于湍流研究的巨大学术价值和广泛的应用范围, 它已成为流体动力学和ICF、航空、航天、化工等领域的重要研究内容, 每年都有大量文章在相关学术会议上交流, 或者学术刊物上发表, 国际上可压缩湍流混合国际研讨会(International Workshop on Physics of Compressible Turbulent Mixing, IWPCTM)是一个集中反映界面不稳定性和湍流研究成果的双年度学术性会议, 国内在《气体物理》上也有较多研究成果.近年来, 高精度多流体界面数值模拟方法发展迅速, 为流体力学界面不稳定性的数值模拟提供了强有力的工具.但对于数值模拟和实验结果的定量比较研究工作还开展得不够深入, 数值模拟方法和程序的验证和确认还很缺乏, 须要进一步研究.
求解Navier-Stokes方程主要包括直接数值模拟(direct numerical simulation, DNS), Reynolds平均数值模拟(Reynolds averaged Navier-Stokes, RANS)和大涡数值模拟(large eddy simulation, LES)3种.大涡数值模拟的基本思想是大尺度脉动进行直接数值模拟计算, 只将小尺度脉动对大尺度的作用做模型假设.在大涡模拟中大部分亚格子模型的假设是基于涡黏性的, 小尺度运动被认为是各向同性的[1-4], 而亚格子尺度的作用则是从大尺度携带能量, 并通过黏性耗散掉[5-6].涡黏模型的最大优点是简单, Smagorinsky模型是参照Reynolds平均模式最早提出的唯象涡黏模型, 至今仍在使用, Smagorinsky模型认为亚格子湍流具有混合长度型的涡黏系数, 混合长度和过滤尺度同一量级, 虽然Smagorinsky模型不能提供小尺度的能量反馈, 但对于预测小尺度能量的产生和耗散是正确的[2].正是由于这些特点, 大涡数值模拟备受关注而取得长足进展.
中国工程物理研究院流体物理研究所在“十五”期间组建界面不稳定性研究团队, 开展了界面不稳定性演化、发展及其诱发界面混合的理论、实验和数值模拟研究工作[7-16], 本文以激波加载初始非均匀气体流场界面不稳定性和界面混合问题研究为代表, 结合相关实验研究工作[17], 重点介绍计算方法和数值模拟能力以及新规律发现和持续深入开展的机理分析.我们在自主研制的二维和三维多介质可压缩黏性流体方法[11, 14](multi-viscosity-fluid piecewise parabolic method, MVPPM)基础上, 通过求解经过Favre滤波后的Navier-Stokes方程, 引入亚格子尺度(subgrid-scale, SGS)模型, 发展了用于可压缩多介质黏性流动的大涡数值模拟方法和程序MVFT[18-26](multi-viscous-flow and turbulence), 运用统计方法分析相关物理量的基本特征[27]. MVFT具有处理多介质、大变形、强冲击等复杂流动等问题的大规模并行计算能力, 适合高精度模拟界面不稳定性及其诱发的界面混合问题.
1 控制方程和计算方法考虑热传导和黏性情况下的大涡模拟控制方程, 采用Descartes坐标系下的Navier-Stokes方程, 经过Favre滤波并略去非线性项后的基本形式为:
| $\begin{align} & \frac{\partial \bar{\rho }}{\partial t}+\frac{\partial \bar{\rho }{{{\tilde{u}}}_{j}}}{\partial {{x}_{j}}}=0 \\ & \frac{\partial \bar{\rho }{{{\tilde{u}}}_{i}}}{\partial t}+\frac{\partial (\bar{\rho }{{{\tilde{u}}}_{j}}{{{\tilde{u}}}_{i}}+\bar{\rho }{{\sigma }_{ij}})}{\partial {{x}_{j}}}=\frac{\partial {{\sigma }_{ij}}}{\partial {{x}_{j}}}-\frac{\partial {{\tau }_{ij}}}{\partial {{x}_{j}}} \\ & \frac{\partial \bar{\rho }\bar{E}}{\partial t}+\frac{\partial (\bar{\rho }{{{\tilde{u}}}_{j}}\bar{E}+\bar{\rho }{{{\tilde{u}}}_{j}})}{\partial {{x}_{j}}}=\frac{\partial ({{{\tilde{u}}}_{i}}({{\sigma }_{ij}}-{{\tau }_{ij}}))}{\partial {{x}_{j}}}-\frac{\partial \left( {{q}_{j}}^{\text{l}}+{{Q}_{j}}^{\text{T}} \right)}{\partial {{x}_{j}}} \\ & \frac{\partial {{{\tilde{Y}}}^{(s)}}}{\partial t}+{{{\tilde{u}}}_{j}}\frac{\partial {{{\tilde{Y}}}^{(s)}}}{\partial {{x}_{j}}}=\frac{\partial }{\partial {{x}_{j}}}\left( \tilde{D}\frac{\partial {{{\tilde{Y}}}^{(s)}}}{\partial {{x}_{j}}} \right)-\frac{\partial {{Q}_{j}}^{Y}}{\partial {{x}_{j}}} \\ & s=1,\text{ }2,\text{ }3,\text{ }\ldots ,\text{ }N-1 \\ \end{align}$ | (1) |
这里i, j分别代表x, y, z这3个方向, 相同的i, j表示求和,
对于多介质混合网格, 采用多流体计算方法, 网格平均物理量定义为各组分介质物理量的体积加权,
| $\begin{matrix} \rho =\sum\limits_{{}}^{N}{{}}{{Y}^{(s)}}{{\rho }^{(s)}} \\ \rho u=\sum\limits_{{}}^{N}{{}}{{Y}^{(s)}}{{\left( \rho u \right)}^{(s)}} \\ \rho E=\sum\limits_{{}}^{N}{{}}\left( {{Y}^{(s)}}{{\left( \rho e \right)}^{(s)}}+\frac{1}{2}{{Y}^{(s)}}{{(\rho {{u}_{i}}^{2})}^{(s)}} \right) \\ \end{matrix}$ |
该公式与状态方程形式密切相关, 对于p=(γ-1) ρe-γπ, 可以直接推导出混合网格中的γ和π, 对于其他形式状态方程则须通过迭代求解.
方程(1) 中σij为Newton流体黏性应力张量,
| ${{\sigma }_{ij}}={{\mu }_{\text{l}}}\left( \frac{\partial {{{\tilde{u}}}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{{\tilde{u}}}_{j}}}{\partial {{x}_{i}}}-\frac{2}{3}{{\delta }_{ij}}\left( \frac{\partial {{{\tilde{u}}}_{k}}}{\partial {{x}_{k}}} \right) \right)$ |
其中, μl为流体动力黏性系数, qjl=-λl∂
在计算方法上采用算子分裂技术, 将公式(1) 中描述的物理过程分解成3个子过程进行计算, 即整个流量计算分解成无黏性流量、黏性流量和热流量3部分计算.对于无黏性流体部分包含对激波、稀疏波以及接触间断的计算和界面处理, 对于黏性流体和热流的计算, 主要考虑有效黏性应力张量和能量流的影响.这样公式(1) 分解成如下两式:
| $\begin{align} & \frac{\partial \bar{\rho }}{\partial t}+\frac{\partial \bar{\rho }{{{\tilde{u}}}_{j}}}{\partial {{x}_{j}}}=0 \\ & \frac{\partial \bar{\rho }{{{\tilde{u}}}_{i}}}{\partial t}+\frac{\partial (\bar{\rho }{{{\tilde{u}}}_{i}}{{{\tilde{u}}}_{j}}+\bar{\rho }{{\delta }_{ij}})}{\partial {{x}_{j}}}=0 \\ & \frac{\partial \bar{\rho }\bar{E}}{\partial t}+\frac{\partial (\bar{\rho }{{{\tilde{u}}}_{j}}\bar{E}+\bar{\rho }{{{\tilde{u}}}_{j}})}{\partial {{x}_{j}}}=0 \\ & \frac{\partial {{{\tilde{Y}}}^{(s)}}}{\partial t}+{{{\tilde{u}}}_{j}}\frac{\partial {{{\tilde{Y}}}^{(s)}}}{\partial {{x}_{j}}}=0,\text{ }s=1,\text{ }2,\text{ }\ldots ,\text{ }N-1 \\ \end{align}$ | (2) |
和
| $\begin{align} & \frac{\partial \bar{\rho }}{\partial t}=0 \\ & \frac{\partial \bar{\rho }{{{\tilde{u}}}_{i}}}{\partial t}=\frac{\partial {{\sigma }_{ij}}}{\partial {{x}_{j}}}-\frac{\partial {{\tau }_{ij}}}{\partial {{x}_{j}}} \\ & \frac{\partial \bar{\rho }\bar{E}}{\partial t}=\frac{\partial ({{\sigma }_{ij}}-{{\tau }_{ij}}){{{\tilde{u}}}_{i}}}{\partial {{x}_{j}}}-\frac{\partial ({{q}_{j}}^{\text{l}}+{{Q}_{j}}^{\text{T}})}{\partial {{x}_{j}}} \\ & \frac{\partial {{{\tilde{Y}}}^{(s)}}}{\partial t}=\frac{\partial }{\partial {{x}_{j}}}\left( \tilde{D}\frac{\partial {{{\tilde{Y}}}^{(s)}}}{\partial {{x}_{j}}} \right)-\frac{\partial {{Q}_{j}}^{Y}}{\partial {{x}_{j}}},\text{ }s=1,\text{ }2,\text{ }\ldots ,\text{ }N-1 \\ \end{align}$ | (3) |
其中, 公式(2) 为可压缩流体Euler方程, 可以采用多介质流体高精度PPM方法进行求解[28].对于公式(3), 含物理黏性和湍流黏性的通量可用2阶空间中心差分计算, 时间推进采用两步Runge-Kutta方法进行求解.由于黏性应力张量和能量流对流场的动量、能量和标量、通量产生影响, 因此不考虑公式(3) 中的第一个方程, 将其写成守恒形式为
| $\frac{\partial \mathit{\boldsymbol{\bar{U}}}}{\partial t}+\frac{\partial \mathit{\boldsymbol{\bar{F}}}}{\partial x}+\frac{\partial \mathit{\boldsymbol{\bar{G}}}}{\partial y}+\frac{\partial \mathit{\boldsymbol{\bar{H}}}}{\partial z}=0$ | (4) |
其中
| $\left\{ \begin{array}{l} \mathit{\boldsymbol{\bar U}} = {(\rho \tilde u,{\rm{ }}\rho \tilde v,{\rm{ }}\rho \tilde w,{\rm{ }}\rho \bar E,{{\tilde Y}^{(s)}})^{\rm{T}}}\\ \mathit{\boldsymbol{\bar F}} = ( - {\sigma _{xx}} + {\tau _{xx}},{\rm{ }} - {\sigma _{xy}} + {\tau _{xy}},{\rm{ }} - {\sigma _{xz}} + {\tau _{xz}},{\rm{ }} - \tilde u({\sigma _{xx}} - {\tau _{xx}}) - \tilde v({\sigma _{xy}} - {\tau _{xy}})\\ - \tilde w({\sigma _{xz}} - {\tau _{xz}}) + {q_x}^{\rm{l}} + {Q_x}^{\rm{T}},{\rm{ }} - \tilde D\frac{{\partial {{\tilde Y}^{(s)}}}}{{\partial x}} + {Q_x}^Y{)^{\rm{T}}}\\ \mathit{\boldsymbol{\bar G}} = ( - {\sigma _{yx}} + {\tau _{yx}},{\rm{ }} - {\sigma _{yy}} + {\tau _{yy}},{\rm{ }} - {\sigma _{yz}} + {\tau _{yz}},{\rm{ }} - \tilde u({\sigma _{yx}} - {\tau _{yx}}) - \tilde v({\sigma _{yy}} - {\tau _{yy}})\\ - \tilde w({\sigma _{yz}} - {\tau _{yz}}) + {q_y}^{\rm{l}} + {Q_y}^{\rm{T}},{\rm{ }} - \tilde D\frac{{\partial {{\tilde Y}^{(s)}}}}{{\partial y}} + {Q_y}^Y{)^{\rm{T}}}\\ \mathit{\boldsymbol{\bar H}} = ( - {\sigma _{zx}} + {\tau _{zx}},{\rm{ }} - {\sigma _{zy}} + {\tau _{zy}},{\rm{ }} - {\sigma _{zz}} + {\tau _{zz}},{\rm{ }} - \tilde u({\sigma _{zx}} - {\tau _{zx}}) - \tilde v({\sigma _{zy}} - {\tau _{zy}})\\ - \tilde w({\sigma _{zz}} - {\tau _{zz}}) + {q_z}^{\rm{l}} + {Q_z}^{\rm{T}},{\rm{ }} - \tilde D\frac{{\partial {{\tilde Y}^{(s)}}}}{{\partial z}} + {Q_z}^Y{)^{\rm{T}}} \end{array} \right.$ | (5) |
其中, u, v, w分别表示x, y, z方向上的速度.在Descartes坐标系下, 可用守恒型有限差分算子将公式(4) 中的空间导数项表示为
| $\begin{matrix} {{L}_{\rm{h}}}(\mathit{\boldsymbol{\bar{U}}}_{i,j,k}^{n})=\frac{\mathit{\boldsymbol{\bar{F}}}_{i-1/2,j,k}^{n}-\mathit{\boldsymbol{\bar{F}}}_{i+1/2,j,k}^{n}}{\Delta x}+ \\ \frac{\mathit{\boldsymbol{\bar{G}}}_{i,j-1/2,k}^{n}-\mathit{\boldsymbol{\bar{G}}}_{i,j+1/2,k}^{^{n}}}{\Delta y}+\frac{\mathit{\boldsymbol{\bar{H}}}_{i,j,k-1/2}^{n}-\mathit{\boldsymbol{\bar{H}}}_{i,j,k+1/2}^{n}}{\Delta z} \\ \end{matrix}$ | (6) |
采用两步Runge-Kutta时间推进方法得到的计算为
| $\left\{ \begin{align} & \mathit{\boldsymbol{\bar{U}}}_{i,j,k}^{(\rm{l})}=\mathit{\boldsymbol{\bar{U}}}_{i,j,k}^{E}+\Delta t{{\mathit{\boldsymbol{L}}}_{\rm{h}}}(\mathit{\boldsymbol{\bar{U}}}_{i,j,k}^{n}) \\ & \mathit{\boldsymbol{U}}_{i,j,k}^{n+1}=\frac{1}{2}\left[ \mathit{\boldsymbol{\bar{U}}}_{i,j,k}^{n}+\mathit{\boldsymbol{\bar{U}}}_{i,j,k}^{(\rm{l})}+\Delta t{{\mathit{\boldsymbol{L}}}_{\rm{h}}}(\mathit{\boldsymbol{\bar{U}}}_{i,j,k}^{(\rm{l})}) \right] \\ \end{align} \right.$ | (7) |
其中, 上标n表示n时刻的量, 上标E表示上文经重映射步后Euler网格上的物理量.
2 不同亚格子尺度模型的比较分析对于涡黏性模型, 认为亚格子湍流具有和分子耗散机理相似的行为, 那么就可以用分子黏性模型和分子扩散模型模拟处理亚格子通量, 本文采用的4种亚格子尺度模型: (1) Smagorinsky模型, (2) Vreman模型, (3) 拉伸涡模型(stretched-vortex model, SVM)模型, (4) 动态Smagorinsky (dynamic Smagorinsky model, DSM)模型.
2.1 亚格子尺度SGS模型 2.1.1 Smagorinsky模型[29]对于Smagorinsky模型, 亚格子黏性系数的表达式为:
| ${{\mu }_{t}}=2C\rho {{\Delta }^{2}}\left| {\bar{S}} \right|$ | (8) |
其中,
| $\begin{matrix} \Delta ={{({{\delta }_{x}}{{\delta }_{y}}{{\delta }_{z}})}^{1/3}} \\ {{\left| {\bar{S}} \right|}^{2}}=2{{{\bar{S}}}_{ij}}{{{\bar{S}}}_{ij}}-\frac{2}{3}{{\left( \Delta \cdot V \right)}^{2}} \\ {{{\bar{S}}}_{ij}}=\frac{1}{2}\left( \frac{\partial {{{\tilde{u}}}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{{\tilde{u}}}_{j}}}{\partial {{x}_{i}}} \right) \\ \end{matrix}$ |
其中, δx, δy, δz为数值计算中三维网格的各个边长, C=CS2, CS为Smagorinsky常数, 对于均匀各向同性湍流CS=0.17, Δ为空间滤波尺度, Sij为可解尺度应变率张量.
2.1.2 Vreman模型[30]对于Vreman模型(VM), 其亚格子黏性系数μt的表达式为:
| ${{\mu }_{\text{t}}}=c\rho \sqrt{\frac{{{B}_{\beta }}}{{{\alpha }_{ij}}{{\alpha }_{ij}}}}$ | (9) |
其中,
| $\begin{matrix} {{\alpha }_{ij}}=\frac{\partial {{{\tilde{u}}}_{j}}}{\partial {{x}_{i}}} \\ {{B}_{\beta }}={{\beta }_{11}}{{\beta }_{22}}-\beta _{12}^{2}+{{\beta }_{11}}{{\beta }_{33}}-\beta _{13}^{2}+{{\beta }_{22}}{{\beta }_{33}}-\beta _{23}^{2} \\ {{\beta }_{ij}}={{\Delta }^{2}}{{\alpha }_{mi}}{{\alpha }_{mj}} \\ \end{matrix}$ |
c为模型常数, 对于各向同性湍流, 有c≈2.5CS2. Vreman模型在高Reynolds数混合层和槽道湍流计算中取CS=0.17, c=0.07.
2.1.3 拉伸涡模型(SVM)[31]对于拉伸涡模型(SVM), 亚格子作用项为:
| $\begin{matrix} {{\tau }_{ij}}=\bar{\rho }\tilde{k}({{\delta }_{ij}}-{{e}_{i}}^{\text{v}}{{e}_{j}}^{\text{v}}) \\ {{Q}_{i}}^{\text{T}}=-\bar{\rho }\frac{{{\Delta }_{\text{c}}}}{2}{{{\tilde{k}}}^{1/2}}({{\delta }_{ij}}-{{e}_{i}}^{\text{v}}{{e}_{j}}^{\text{v}})\frac{\partial ({{{\tilde{c}}}_{\text{p}}}\tilde{T})}{\partial {{x}_{j}}} \\ {{Q}_{i}}^{Y}=-\frac{{{\Delta }_{\text{c}}}}{2}{{{\tilde{k}}}^{1/2}}({{\delta }_{ij}}-{{e}_{i}}^{\text{v}}{{e}_{j}}^{\text{v}})\frac{\partial \tilde{Y}}{\partial {{x}_{j}}} \\ \end{matrix}$ | (10) |
其中,
对于动态模型(DSM), 其亚格子黏性系数μt的表达式为
| ${{u}_{\text{t}}}={{\left( {{C}_{\text{S}}}\Delta \right)}^{2}}\left| {\bar{S}} \right|$ | (11) |
模型系数CS动态确定
| ${{C}_{\text{S}}}=-\frac{1}{2}\frac{<{{L}_{kl}}{{{\bar{S}}}_{kl}}>}{\widetilde{{{{\bar{\Delta }}}^{2}}}<\left| \widetilde{{\bar{S}}} \right|{{{\bar{S}}}_{mn}}{{\widetilde{{\bar{S}}}}_{mn}}>-{{{\bar{\Delta }}}^{2}}<\left| {\bar{S}} \right|{{{\bar{S}}}_{pq}}{{{\bar{S}}}_{pq}}>}$ |
其中, < >表示系综平均,
亚格子湍耗散, 即亚格子应力的功, 表示可解尺度和亚格子尺度之间的能量输运, 定义为[1]
| ${{\varepsilon }_{t}}={{\tau }_{ij}}{{{\bar{S}}}_{ij}}=-{{\mu }_{\text{t}}}{{{\bar{S}}}_{ij}}{{{\bar{S}}}_{ij}}$ | (12) |
如果εt为负, 亚格子尺度从可解尺度携带能量(正传); 如果εt为正, 亚格子尺度向可解尺度反射能量(逆传).基于涡黏性假设的唯象模型如Smago-rinsky模型和Vreman模型, 由于涡黏系数μt总是为正, 即亚格子湍耗散总是为负, 所以此两个涡黏性模型是绝对耗散的.
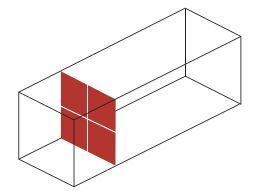
3 亚格子模型模拟比较分析[33] 3.1 计算模型建立以Leinov的二次冲击激波管实验[34]为基础模型, 开展相关数值模拟.计算域为[-10 mm, 80 mm]×[0 mm, 10 mm]×[0 mm, 10 mm], 网格数为576×64×64, 见图 1. Mach数1.2的激波冲击随机扰动air/SF6界面, 扰动振幅0.24 mm, 波长0.4 mm≤λ≤2.8 mm, 初始界面至激波管尾端距离为80 mm.
|
| 图 1 计算模型 Fig.1 Computational model |
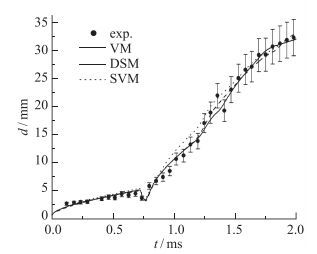
激波冲击air/SF6扰动界面, 斜压效应使激波能量在界面沉积引起扰动增长.透射激波从激波管尾部反射回来再次冲击扰动界面, 压缩使得界面出现短暂的负增长, 并向SF6中反射一束膨胀波, 之后由于能量的二次沉积, 界面又快速增长.膨胀波反射至界面处并相互作用, 同时向SF6中反射一束压缩波.压缩波也会发射回来和界面相互作用, 会再次向SF6中反射一束膨胀波, 如此反复. 图 2对比了界面混合区(turbulent mixing zone, TMZ)宽度的实验结果和数值模拟结果, 吻合较好, 而且采用不同SGS模型计算得到的TMZ宽度相差不是很大.
|
| 图 2 TMZ宽度实验结果和数值模拟比较 Fig.2 TMZ width comprisons between experimental and numerical results |
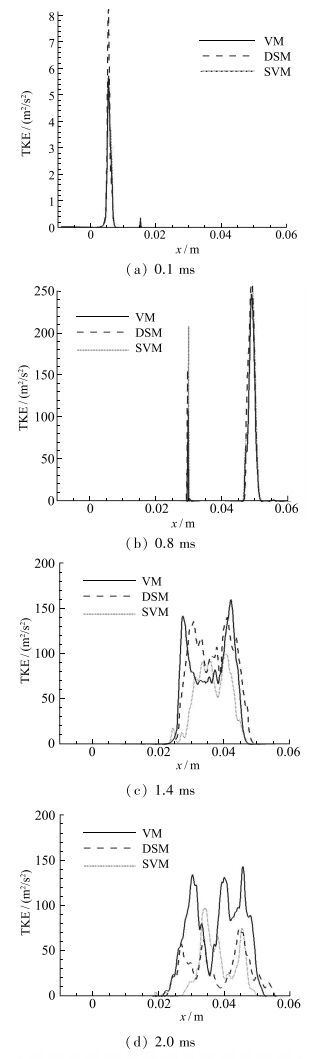
湍动能定义为
|
| 图 3 湍动能流向分布 Fig.3 Distributions of turbulent kinetic energy in streamwise direction for different SGS models at four different times |
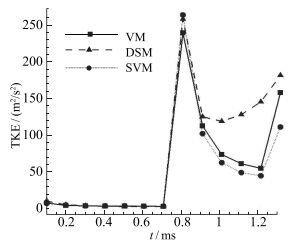
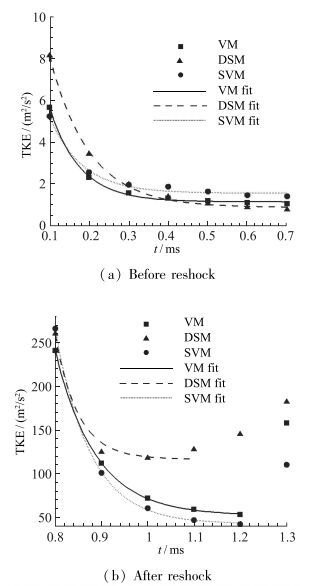
图 4给出了湍动峰值的时间历程, 图 5给出了激波再加载前和激波再加载后湍动能峰值及其按指数衰减规律~e-t/t*拟合的结果, t*为衰减常数.
|
| 图 4 湍动能峰值的时间历程 Fig.4 Time histories of peak values of turbulent kinetic energy for different SGS models |
|
| 图 5 湍动能峰值及其拟合结果 Fig.5 Peak values of turbulent kinetic energies and their fitted results |
从图中看出, 由于初始冲击后界面流动不是完全湍流状态, 所以湍动能大小远不及再冲击后的湍动能, 而再冲击后混合流动已基本发展为完全湍流状态, 且湍动能逐渐哀减, 当受到反射稀疏波的加载后湍动能也相应地增大.在初始冲击后, 采用动态模型计算时, 流场湍动能比Vreman模型和拉伸涡模型的计算结果大.在再冲击之前, 3种模型的计算结果比较接近.但是在反射稀疏波加载前, 采用动态模型计算时, 湍动能比Vreman模型和拉伸涡模型的计算结果大得多, 而且采用动态模型计算时反射稀疏波的加载时间明显提前.在混合区发展后期, 混合区流动早已发展为完全湍流状态, 采用动态模型和拉伸涡模型计算的湍动能比较接近, 但Vreman模型的计算结果偏大, 可能与Vreman模型的绝对耗散性有关, 见图 3(d). 表 1给出了激波再加载前和激波再加载后3种SGS模型计算时湍动能的衰减常数, 可以看出, 在激波再加载前, Vreman模型和拉伸涡模型的结果比较接近, 动态模型结果明显较大; 在激波再加载之后, 同样Vreman模型和拉伸涡模型的结果比较接近, 动态模型结果又明显较小.不同SGS模型计算的激波再加载前后的湍动能衰减常数相比, Vreman模型、拉伸涡模型的差别较小, 动态模型结果差别近1倍.动态模型不适合R-M界面不稳定性这类受脉冲式外力作用下的湍流问题的模拟.
| 下载CSV 表 1 激波再加载前后不同SGS模型计算时湍动能衰减常数 Tab.1 Decay constants of turbulent kinetic energies before and after reshock for different SGS models |
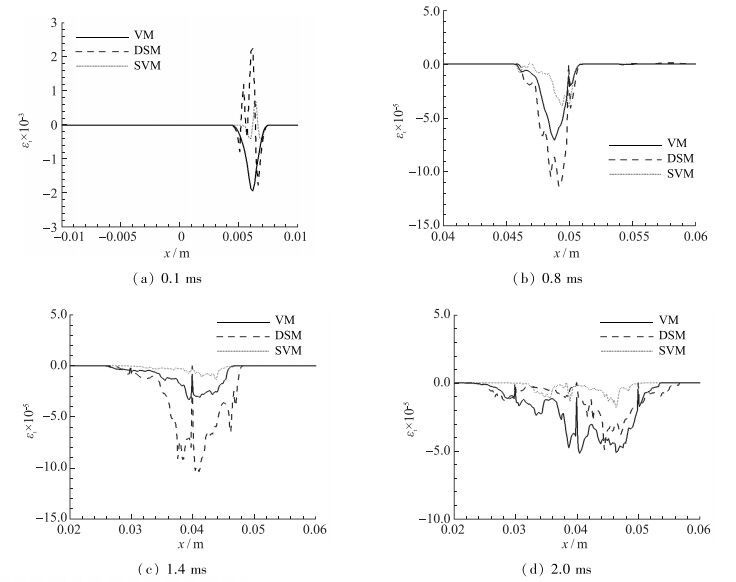
Vreman模型是基于涡黏性假设的唯象模型, 其涡黏系数总为正值, 所以是纯耗散模型, 不能预测湍流输运中的能量逆传.动态模型以Smagorinsky涡黏模型为基础, 通过动态过程来计算涡黏系数, 这样一来涡黏系数为负, 就可以预测能量逆传.拉伸涡模型基于螺旋涡形式的亚格子元素, 这些螺旋涡就是N-S方程的当地近似解, 能够模拟能量逆传. 图 6给出了t=0.1, 0.8, 1.4和2.0 ms这4个时刻流向分布的亚格子湍耗散.可以看出, 在界面流动还未完全发展为湍流状态时, 动态模型和拉伸涡模型均预测到了能量逆传现象, 然而动态模型预测到的逆传能量更大, 范围更广.混合区受到再次冲击后, 湍流强度大大增强, 同时能量逆传也增大, 但动态模型的亚格子湍耗散依然更大, 拉伸涡模型的湍耗散较小.随着湍流的衰减, 湍耗散也逐渐减小, 最后动态模型和Vreman模型的湍耗散基本相当, 而且动态模型也成为了绝对耗散模型, 但是拉伸涡模型预测结果显示依然存在小范围的局部逆传.
|
| 图 6 流向分布的亚格子湍耗散 Fig.6 Distributions of SGS turbulent dissipations in streamwise direction for different SGS models at four different times |
我们选用的实验气体为空气和SF6, 希望对于SF6气体构成的初始非均匀流场, 考虑在空气和SF6气体界面上设置波长相同而振幅不同的两种初始扰动, 目的是观察非均匀流场对扰动发展的影响.通过最简单自然的方法获得非均匀的SF6气体初始流场, 即在激波管的下方开一个直径10 mm的孔流进SF6气体, 在激波管上方开直径10 mm的出孔流出SF6气体, 为了保持SF6气体流场压力恒定, 气体流速非常缓慢, 约为0.417 cm/s, 实验中从SF6气体流入开始持续时间为20 min, 由于SF6气体比重较大, 在气体扩散效应的作用下, 自然形成初始时刻SF6气体非均匀流场, 在激波管下方浓度较高密度较大, 而上方浓度较低密度较小.非均匀流场的初始状态量中压力为恒定1个大气压, 而密度的分布实验难以精确测量, 实验中我们主要测量了入口处和出口处的SF6气体浓度, 须借助于数值模拟工具结合实验现象和实验数据确定非均匀流场的初始密度分布, 再现整个实验过程, 弄清R-M不稳定性中非均匀流场对扰动发展的影响, 这项研究工作对界面不稳定性实验研究中初始条件的设置以及对实验现象和结果的分析均具有重要意义.详细的实验工作参见文献[17].
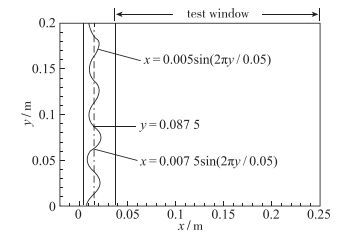
实验激波管宽度为0.2 m, 厚度为0.1 m, air激波Mach数为1.27, air/SF6界面为双模正弦扰动, 波长为0.05 m, 振幅分别为0.005 m和0.007 5 m, 扰动函数定义如下:
| $x=\left\{ \begin{align} & 0.007\text{ }5\sin \left( 2\text{ }\!\!\pi\!\!\text{ }y/0.05 \right)\text{ }\ 0.087\text{ }5<y\le 0.02 \\ & 0.005\sin \left( 2\text{ }\!\!\pi\!\!\text{ }y/0.05 \right)\text{ }\quad 0.0\le y<0.087\text{ }5 \\ \end{align} \right.$ | (13) |
实验中纹影照相的观测窗口大小为0.212 m×0.2 m.初始结构简图如图 7所示, 初始时刻激波阵面位置在x=0.005 56 m处, 扰动平衡位置在x=0.016 m处, 与实验对应的观测窗口在x方向范围为[0.032 8 m, 0.25 m].实验气体物理参数见表 2.
|
| 图 7 计算模型 Fig.7 Computational model |
| 下载CSV 表 2 空气和SF6的物理参数 Tab.2 Properties of air and SF6 gases |
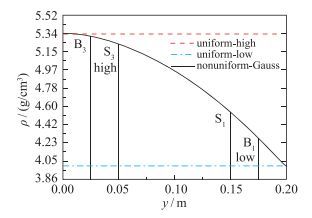
对于非均匀SF6气体初始流场, 沿y方向(垂直激波运动方向) SF6气体的密度运用Gauss函数进行计算: ρ(y)=ρSF6e-((y-yc)2/δ2), 其中yc=0, δ=0.372 9m, 其具体密度分布剖面如图 8.
|
| 图 8 密度为Gauss分布的非均匀流场、高低密度均匀流场中垂直方向密度分布图 Fig.8 Density profiles of nonuniform flows with a Gaussian function and uniform flows in vertical direction |
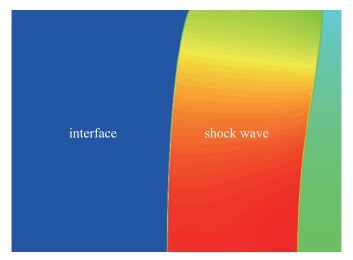
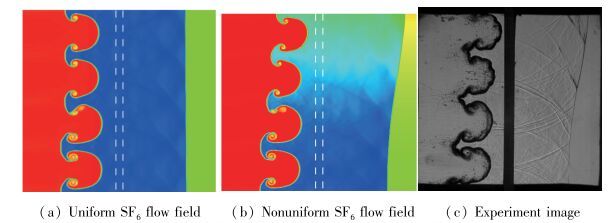
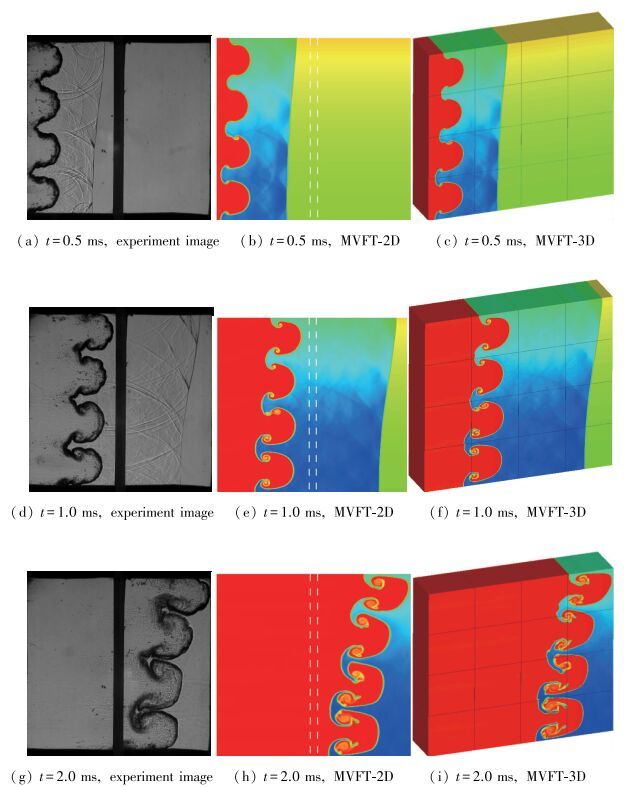
图 9给出了模拟得到的无扰动时1 ms时刻的密度场分布, 可见由于流场中横向密度梯度的存在, 导致了界面和激波的倾斜, 上方激波传播速度较快.实验通过观测窗口获得了t=0.2~2.1 ms每隔0.2 ms的二维流场纹影图, 见图 10(a)~(j)中右侧各图, 图中的黑色柱体为测窗口中间支撑架.考虑SF6气体非均匀性的MVFT-2D计算结果见图 10(a)~(j)中左侧各图, 图中两条白色竖线表示支撑架的位置.二者对比显示, 计算给出的air/SF6界面不稳定性发展形状、位置和斜激波特征等均与实验测试结果一致, 存在的主要差异在于实验纹影图是激波管沿厚度方向上的叠加结果, 而计算仅仅是一个二维截面图.从图 11给出t=1.0 ms时刻两种计算结果与实验图像的比较以及后面扰动发展演化规律可以明显看出, 上面的二维计算忽略了第三个方向的耗散, 其结果可能导致计算偏强.因此采用MVFT-3D进行三维数值模拟, 从图 12给出的二维和三维计算结果以及与实验的比较可见, 两者界面形状和位置几乎完全一致, 流场差异非常小, 可见该实验中流场尚未完全发展至湍流状态.
|
| 图 9 初始非均匀流场中无扰动界面的密度云图(t=1 ms) Fig.9 Density contour images of numerical simulation result in a nonuniform Gaussian function flow without initial perturbation on interface (t=1 ms) |

|
| 图 10 相同时刻MVFT-2D计算和实验纹影图的比较 Fig.10 (Color online) Schlieren photography pictures and numerical simulation results by MVFT-2D at a certain time (sizes of the pictures are ones of the test windows [0.038 m, 0.25 m]×[0.0 m, 0.2 m]) |
|
| 图 11 t=1.0 ms时刻MVFT-2D两种计算结果和实验纹影图的比较 Fig.11 Differences of interface shape, location and shock front at t=1.0 ms in initial uniform and nonuniform flows and experiments |
|
| 图 12 二维和三维计算结果以及与实验的比较 Fig.12 Comparisons of MVFT-2D, MVFT-3D and experimental results at three times |
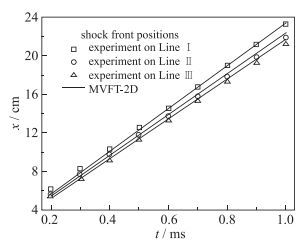
图 13给出气泡和尖钉位置以及3条激波阵面观测线, 其中B1-S1和B3-S3分别对应初始小扰动和大扰动发展后对应的气泡和尖钉位置, 3条激波阵面观测线对应的y坐标值分别为: Line Ⅰ对应17.26 cm, Line Ⅱ对应9.82 cm, Line Ⅲ对应2.78 cm. 图 14给出了3条测试线上不同时刻激波阵面位置的实验和计算结果的比较, 当时间大于1.0 ms以后激波阵面传出测试窗口不再进行比较.从图 14可见, 在LineⅠ上激波阵面位置在0.4 ms以前计算和实验相差约5%, 以后两者几乎完全一致.在Line Ⅱ和Line Ⅲ上激波阵面位置在前期计算和实验几乎完全吻合, 只是到0.8 ms以后两者相差约3%.这种差异可能是由于计算中非均匀初始流场密度分布采用Gauss函数描述, 这仅仅是一个近似而并非完全代替真实非均匀流场, 但这种近似所描述的流场特征与实际情况差异较小, 作为实验结果分析是可以接受的.

|
| 图 13 气泡和尖钉位置以及3条激波阵面观测线 Fig.13 Bubbles and spike locations in test window as well as three shock front line positions |
|
| 图 14 3条测试线上不同时刻激波阵面位置 Fig.14 Shock front locations of experiment and calculated results on three test lines at different times |
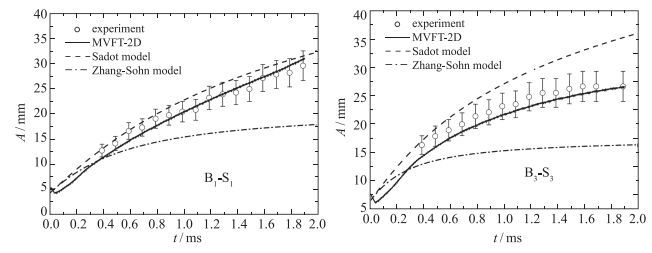
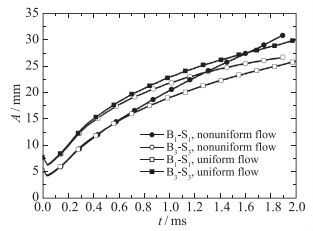
对于初始设置的两种不同振幅的扰动演化发展情况, 图 15给出了B1-S1和B3-S3扰动振幅历程的实验、数值计算以及与Sadot和Zhang-Sohn理论的比较, 其后误差棒为实验值的10%.从图 15可见, 对于大小两种扰动, 数值计算与实验的差别均在实验值的10%范围之内, 而Sadot理论仅在B1-S1中给出的振幅历程与实验和计算接近, Sadot理论对于B3-S3以及Zhang-Sohn理论均远远偏离实验和计算结果.为了分析初始均匀与非均匀流场对界面不稳定性中大小扰动振幅演化发展的影响, 图 16给出了初始均匀与非均匀流场中大小扰动振幅历程的计算比较.从图 16可见, 对于均匀流场, 在t > 0时扰动振幅的发展演化关系是, 初始扰动振幅较大的B3-S3总是大于初始扰动振幅较小的B1-S1.而对于非均匀流场, 在0 < t≤1.3 ms时扰动振幅的发展演化关系是初始扰动振幅较大的B3-S3大于初始扰动振幅较小的B1-S1, 而在t>1.3 ms时则相反, 初始扰动振幅较小的B1-S1大于初始扰动振幅较大的B3-S3.
|
| 图 15 大小扰动振幅历程的理论、实验与数值计算结果比较(其中误差棒为实验值的10%) Fig.15 Perturbation amplitudes history of experiment, numerical computing and comparison to Sadot model and Zhang-Sohn theory, B1-S1 corresponds to small perturbation amplitude, and B3-S3 corresponds to large one (error bars of this visual measurement are equal to ±10%) |
|
| 图 16 均匀与非均匀流场中大小扰动振幅历程计算比较 Fig.16 Perturbation amplitudes history calculations of initial uniform and nonuniform flows in R-M instability |
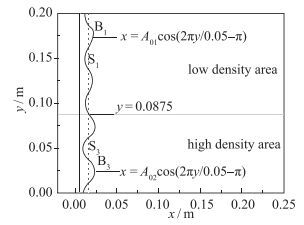
为了进一步探究非均匀流场的界面不稳定性发展机制, 并解释图 16非均匀流场在1.3 ms之后发现的新现象, 我们构造了多组双模态界面进行非均匀流场R-M不稳定性及其混合规律分析.初始计算模型如图 17所示, 计算条件与前面相同.由图 17可知, 界面为双模态的余弦扰动界面, 波长均为0.05 m, 扰动平衡位置在x=0.016 m, B1-S1是界面初始振幅为A01时, 相应波峰和波谷的位置; B3-S3是界面初始振幅为A02时, 相应波峰和波谷的位置.振幅组合如表 3所示, 共6组初始扰动振幅组合.
|
| 图 17 计算模型 Fig.17 Computational model |
| 下载CSV 表 3 振幅组合表 Tab.3 Six groups of initial amplitudes |
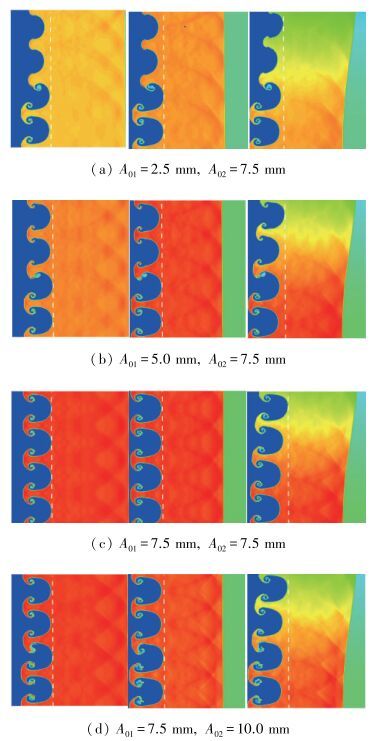
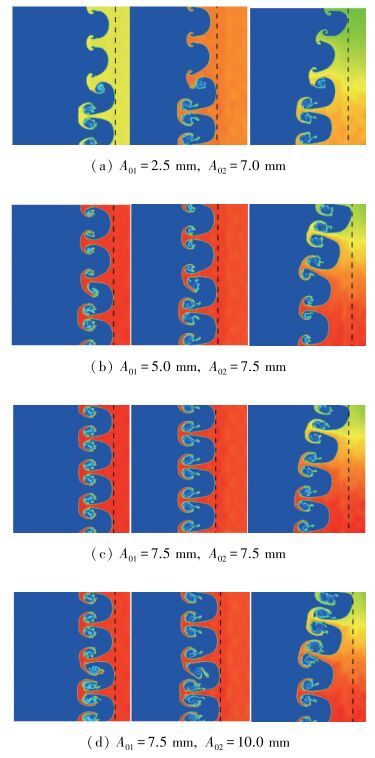
图 18, 19分别对应了1和1.8 ms情况下, 低、高密度均匀流场和非均匀流场的密度云图, 相应行代表了不同的界面振幅组合.通过左、中两列的对比可发现, 不同密度均匀流场的界面演化形态很相似, 尖钉气泡结构基本一致, 初始大振幅的界面演化快于初始小振幅的演化.对于非均匀流场, 其演化规律出现了相反的趋势, 位于非均匀流场低密度区的小振幅界面扰动赶上并超越了非均匀流场高密度区的大振幅界面, 再次说明初始流场的非均匀性对于R-M不稳定性的演化发展也具有重要的作用, 后面我们将从振幅、涡量、环量几个方面进行深入的分析.
|
| 图 18 t=1 ms不同初始振幅组合下的流场密度云图(左列:低密度均匀流场; 中列:高密度均匀流场; 右列:非均匀流场) Fig.18 Density contour images of numerical simulation results at t=1 ms under different groups of initial amplitudes (left column shows low-density uniform flows; middle column high-density uniform flows; and right columnnonuniform Gaussian function flows) |
|
| 图 19 t=1.8 ms不同初始振幅组合下的流场密度云图(左列:低密度均匀流场; 中列:高密度均匀流场; 右列:非均匀流场) Fig.19 Density contour images of numerical simulation result at t=1.8 ms under different groups of initial amplitudes (left column shows low density uniform flows; middle column high-density uniform flows; and right column nonuniform Gaussian function flows) |
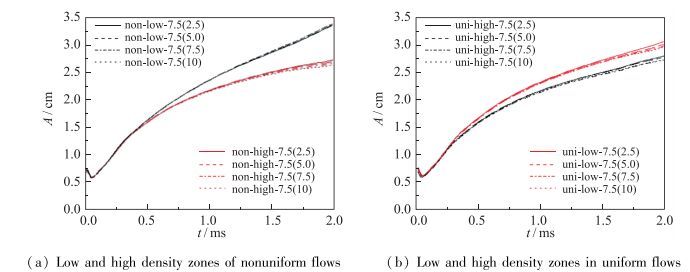
首先讨论双模态界面振幅之间的耦合效应, 图 20所示的是A0=7.5 mm振幅和不同初始振幅组合下, 在3种不同初始流场(高、低密度均匀流场、非均匀流场)中的振幅变化.可以看出, 在均匀和非均匀流场中, 除了界面发展后期振幅有少许的差异, 基本可认为在本研究的时间范围内, 振幅之间的耦合效应很弱, 该效应可以忽略.
|
| 图 20 在4种不同初始流场的振幅扰动增长图 Fig.20 Perturbation amplitudes of A0=7.5 mm initial amplitude with four other initial amplitudes |
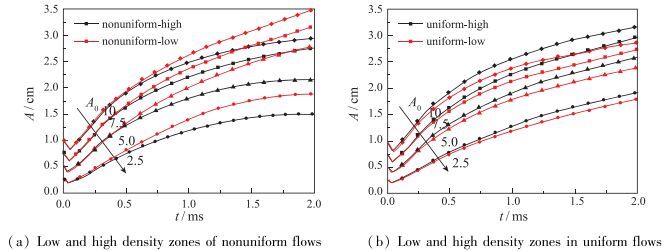
考虑到耦合效应的弱化, 我们进一步研究非均匀性对界面不稳定性的影响, 以及初始非均匀流场中, 初始振幅及密度对界面不稳定性的影响.如图 21所示, 非均匀及均匀流场中, 高、低密度区情况下, 随着初始振幅2.5到10 mm的递增, 相应界面处的振幅变化也逐渐增加.而对于相同初始振幅, 不同密度区域的振幅变化, 与流场的非均匀性息息相关, 非均匀流场中低密度区振幅较大, 界面演化发展更快; 高密度区振幅较小, 界面演化发展更慢.而且图 21(a)定量地显示了非均匀流场低密度区中A0=5, 7.5 mm的界面演化后期赶上了更大初始振幅高密度区的界面发展.这与均匀流场界面不稳定性演化有很大区别, 在均匀流场中, 初始振幅一定情况下, 随着密度增大, Atwood数增加, 界面扰动发展更快.
|
| 图 21 非均匀和均匀流场的高低密度区振幅时间变化图 Fig.21 Perturbation amplitudes of four different initial amplitudes density zones in nonuniform and uniform flows |
R-M不稳定性的发展机理是斜压效应导致的涡量沉积, 下文利用涡量和环量对其现象进行解释.此处选取1 ms时S3, S1位置处的尖钉顶点处涡量值进行分析.随着界面不稳定性演化, 顶点位置不是固定值.考虑到S3, S1顶点位置位于x=0.1 m附近, 为了准确表征气泡顶点处的涡量值, 我们对初始界面波峰Si处上下50格的涡量进行数值平均.
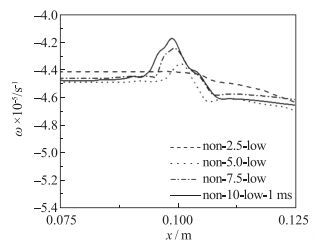
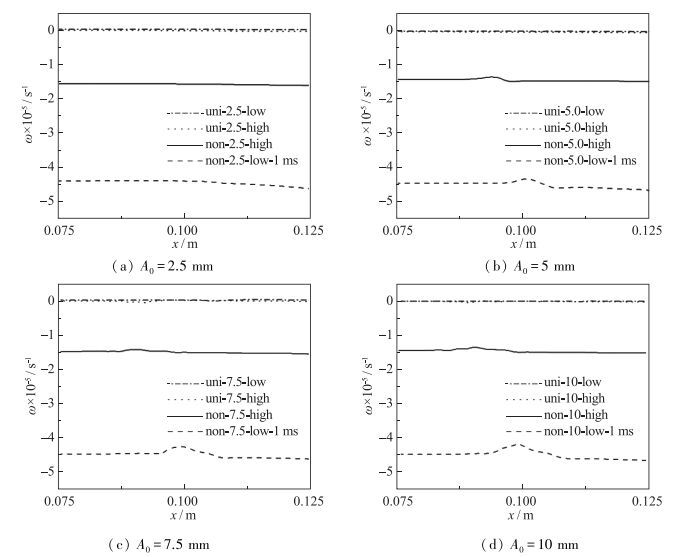
由图 22可知, 在非均匀流场低密度区域内, 初始振幅分别为2.5, 5, 7.5, 10 mm情况下, x=0.1 m处的涡量分别为-4.42×105, -4.35×105, -4.24×105, -4.17×105 s-1.随着初始振幅增加, 涡量数值增加, 与振幅变化趋势吻合.由图 23可知, 在初始振幅一定情况下, 与均匀流场接近于0的涡量值对比, 流场的非均匀性极大地增加了涡量的产生, 非均匀流场低密度区涡量平均增加至4.5×105 s-1, 高密度区平均增加至1.5×105 s-1.对于非均匀流场, 低密度区的涡量值远大于高密度区涡量值.通过密度分布图 8对比可知, 低密度区的密度梯度为-0.112 g/cm4, 高密度区密度梯度为-0.031 g/cm4, 低密度区的密度变化更快, 密度梯度更大, 导致了涡量增加, 进而促使了非均匀流场低密度区R-M不稳定性演化发展更快.
|
| 图 22 t=1 ms, S3非均匀流场低密度区的平均环量 Fig.22 Average vorticities of S3 (spike trough) in low-density zone of nonuniform flows with four different initial amplitudes at t=1 ms |
|
| 图 23 t=1 ms, 不同初始扰动振幅下, 非均匀流场高密度区S3、低密度区S1、均匀流场高低密度区, 波谷处的涡量平均值分布图 Fig.23 Average vorticities of four conditions: the spike trough in low-density zone of nonuniform flows S3, the spike trough in high-density zone of nonuniform flows S1, and the spike trough in low-density uniform flows and high-density uniform flows with four initial amplitudes at t=1 ms |
为了避免尖钉处涡量值的偶然性, 激波所导致的界面上环量沉积也可以量化R-M不稳定性演化的机理.环量Γ是速度矢量沿封闭曲线l的积分, 通过Stokes定理, 可变化为面积A上涡量ω的积分, 利用公式(14) 计算, 其中对于不同振幅区域, 使用相同面积进行积分(其中高密度区[-0.02 m, 0.25 m]×[0.0 m, 0.087 5 m], 低密度区[-0.02 m, 0.25 m]×[0.112 5 m, 0.02 m]).
| $\mathit{\Gamma }\left( t \right) = \oint \mathit{\boldsymbol{v}}{\rm{d}}l = {\smallint _A}\omega \left( {x,{\rm{ }}y,{\rm{ }}t} \right){\rm{d}}A$ | (14) |
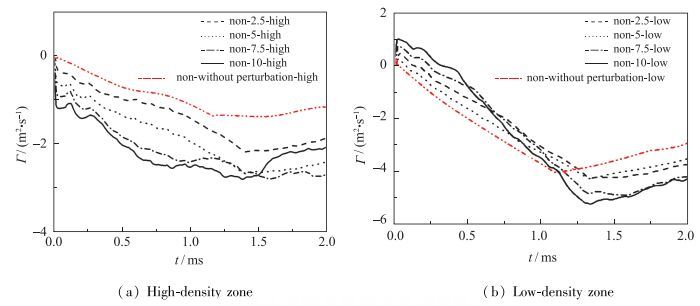
由图 24可知, 初始非均匀流场低密度区域内, 初始振幅分别为2.5, 5, 7.5, 10 mm情况下, t=1 ms时的总环量分别为-3.75, -3.12, -3.20, -3.34, -3.61 m2·s-1.在初始非均匀流场高密度区域内, 初始振幅分别为2.5, 5, 7.5, 10 mm情况下, x=0.1 m处的总环量分别为-1.13, -1.45, -1.95, -2.41, -2.52 m2·s-1.随着初始振幅增加, 总环量值也随之相应增加, 与涡量及振幅变化趋势吻合.同时, 值得注意的是, 对于初始无扰动界面也存在一定量的环量值, 归因于密度梯度的存在, 导致了涡量和环量的沉积.
|
| 图 24 初始扰动振幅为分别为0, 2.5, 5, 7.5, 10 mm情况下, 非均匀流场低密度区、高密度区4/3波长面积内总环量时间图 Fig.24 Total circulations over time with four different initial amplitudes: 0.0, 2.5, 5, 7.5 and 10 mm in low-density zone and high-density zone of nonuniform flows |
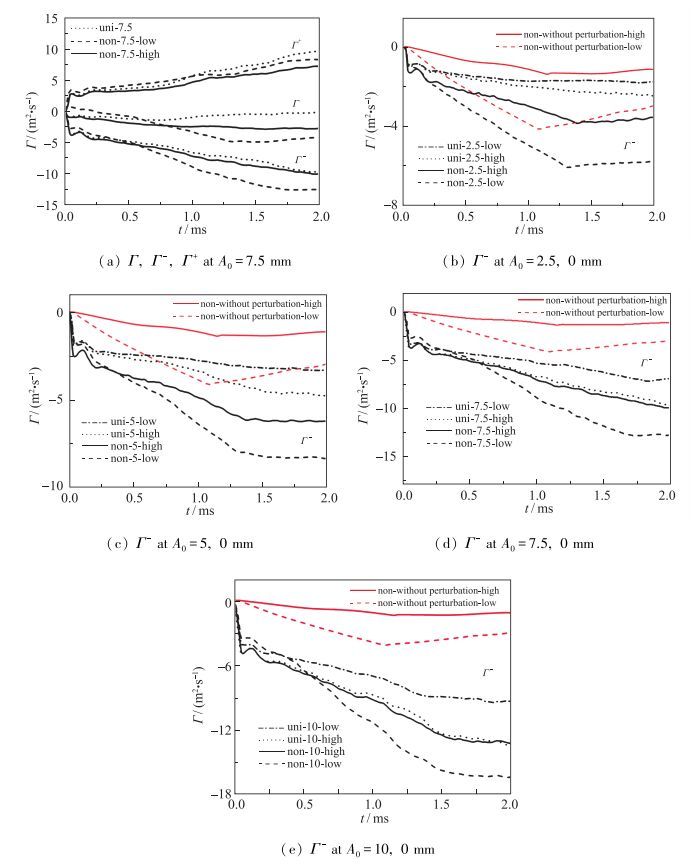
图 25中所示的Γ为总环量, Γ+为正环量, Γ-为负环量.以初始振幅为7.5 mm情况为例, 由图 25(a)可知, 均匀流场正负环量值相近, 总环量接近于0;而对Gauss分布的非均匀流场, 负环量值远大于正环量值, 进而主导了总环量的大小及正负.因此我们通过负环量进行细致的分析.
|
| 图 25 初始振幅为(a)7.5 mm情况下, 非均匀流场高低密度区、高低密度均匀流场区, 4/3波长面积内总环量、正环量、负环量时间图; 初始扰动振幅分别为: (b)2.5 mm, (c)5 mm, (d)7.5 mm, (e)10 mm情况下, 非均匀流场高低密度区、高低密度均匀流场区, 4/3波长面积内负环量时间图 Fig.25 Circulations over time in four conditions: low-density zone of nonuniform flows, high-density zone of nonuniform flows, low-density uniform flows, and high-density uniform flowsunder four initial amplitudes |
1 ms时刻负环量随时间变化如图 25(b)~(e), 并归纳得表 4, 可知当时间为1 ms时, 初始振幅一定情况下, 均匀流场的环量值均小于非均匀流场高、低密度区的环量值, 说明了流场的非均匀性极大地促使了环量产生.在非均匀流场中, 初始振幅一定情况下, 低密度区的负环量值远大于高密度区负环量值, 同涡量变化趋势一致.
| 下载CSV 表 4 t=1 ms时, 初始振幅为2.5, 5, 7.5, 10 mm情况下, 均匀流场高低密度区、非均匀流场高低密度区4/3波长面积内环量对比表 Tab.4 Negative circulations of five initial amplitudes in four flow field at t=1 ms |
通过振幅、涡量和环量分析, 可知流场密度的非均匀性带来了较大密度梯度, 导致了涡量值和环量值的剧增; 在初始非均匀流场中, 振幅大小与涡量值、环量值成正比, 而对于不同密度区域内, 初始振幅一定情况下, 较大的密度变化率促使了涡量和环量的产生, 最终呈现出低密度区大振幅界面扰动增长最快, 高密度区小振幅界面扰动增长最慢的现象.
4.2 反射激波加载两种非均匀流场R-M不稳定性及其混合的数值模拟研究[36]为了探讨初始流场的非均匀性对R-M界面不稳定性混合区的发展演化规律的影响.我们在4.1研究基础上, 通过数值模拟开展激波和反射激波作用下两种初始非均匀流场R-M界面不稳定性混合问题研究, 通过对流场中混合区宽度和涡量、环量的定量分析, 丰富初始条件对界面不稳定性影响的内涵, 获得流场非均匀性对激波反射后较强的非线性阶段界面不稳定性发展、演化规律, 以期对界面不稳定性后期诱发界面混合问题获得更深入的认识.
本数值模拟中, 我们在SF6气体中构造了两种初始非均匀流场, 它们在激波管下端的气体密度均设置为ρSF6, 而激波管上端的气体密度分别设置0.9ρSF6和0.85ρSF6.采用Gauss分布得到SF6气体初始非均匀流场密度分布函数为
| $\rho \left( y \right)={{\rho }_{\text{S}{{\text{F}}_{\text{6}}}}}{{\text{e}}^{-({{\left( y-{{y}_{c}} \right)}^{2}}/{{\delta }^{2}})}}$ | (15) |
其中yc=0, δ1=0.616 2 m, δ2=0.496 1 m.非均匀系数越小, 流场的非均匀性越强.
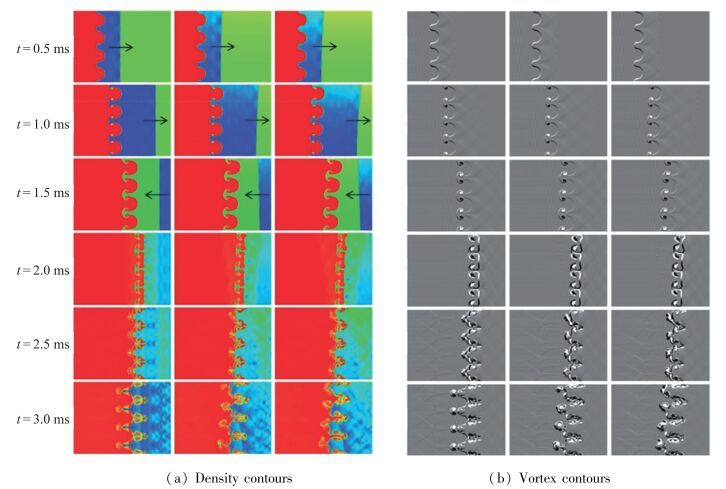
为了对上述两种Gauss分布的初始非均匀流场进行对比分析, 我们也对均匀流场进行了数值模拟.从图 26的比较可以看出, 对于初始均匀流场, 透射激波和反射激波均保持较好的平面性, 激波与正弦扰动界面作用形成R-M不稳定性界面演化发展, 扰动界面在激波反射前后均保持良好的周期性.对于初始非均匀流场, 由于SF6气体存在密度差异, 因此透射激波和反射激波均为斜激波, 导致正弦扰动界面R-M不稳定性演化发展的不均匀性, 但是从计算结果可见, 计算的扰动界面在激波反射前与均匀流场呈现出显著差异, 如t=0.5, 1.0, 1.5 ms时刻的计算结果, 而在激波反射以后这种差异明显减小, 如t=2.0, 2.5, 3.0 ms时刻的计算结果.
|
| 图 26 密度云图和涡量云图(左列:均匀流场, 中列: δ1 Gauss分布的非均匀流场, 右列: δ2 Gauss分布的非均匀流场) Fig.26 Density and vortex contour images of the numerical simulation results by MVFT at certain times (Left column, uniform initial conditions; middle column, δ1 nonuniform Gaussian function; and right column, δ2 nonuniform Gaussian function. Small arrow denotes the direction of propagation of the shock wave fronts before reshock of the interface) |
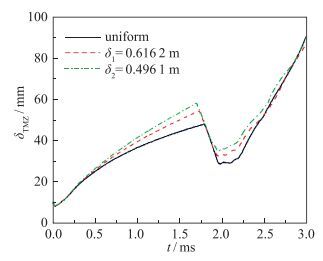
从图 27我们可以看到, 在激波反射前初始非均匀流场中混合区宽度增长快于均匀流场, 非均匀系数δ越小混合区增长越快, 而在激波反射加载以后的流场中三者之间的混合区宽度差异减小.这说明在激波反射前的线性和弱的非线性阶段, 初始流场的非均匀性对界面不稳定性发展和演化影响显著, 经过激波反射加载后界面不稳定性进入到强的非线性阶段, 虽然界面扰动增长加剧, 但是该阶段流场中不稳定性界面扰动幅度较前期更接近于均匀流场, 流场的非均匀性在强的非线性阶段对界面不稳定性影响明显减小.
|
| 图 27 初始均匀流场及Gauss分布δ1和δ2的非均匀流场, 界面不稳定性的混合区域宽度时间变化图 Fig.27 Mixing width history calculations of initial uniform and nonuniform flows in R-M instability |
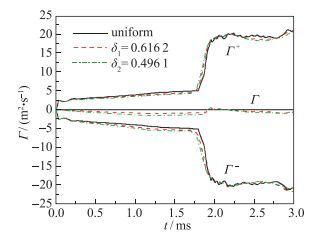
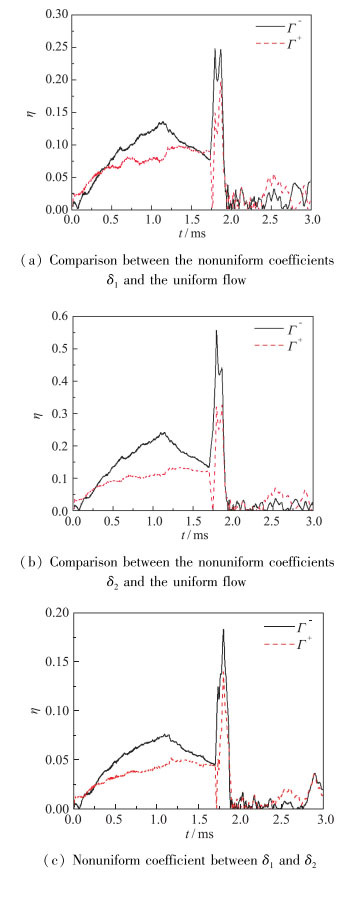
上文给出的混合区宽度演化过程是数值模拟对R-M界面不稳定性混合的一个宏观表征, 为了解释这一现象, 我们需要从导致R-M界面不稳定性的机制上进行分析, 即分析由斜压项产生的涡量及其环量.从图 28的计算结果我们可以看到, 对于初始均匀流场Γ+和Γ-保持了非常好的对称性, 总环量Γ始终为0.而对于初始非均匀流场, 由于扰动增长的非均匀性导致Γ+和Γ-的非对称性, 因此流场中总环量Γ并不保持为0.为了对比分析均匀流场与参数为δ1和δ2两种初始非均匀流场之间的差异, 我们将非均匀流场的Γ+和Γ-与均匀流场对应的Γ+和Γ-的相对误差进行了分析, 见图 29(a)和图 29(b).从图 29 (a)可见, 对于非均匀系数为δ1的流场, 在激波反射前Γ+和Γ-偏离均匀流场的最大值分别为9.8%和13.8%, 在激波反射过渡区达到19.7%和24.8%, 而在激波反射以后则为5.6%和4.8%.从图 29(b)可见, 对于非均匀系数为δ2的流场, 在激波反射前Γ+和Γ-偏离均匀流场的最大值分别为13.6%和24.5%, 在激波反射过渡区达到32.7%和55.7%, 而在激波反射以后则为7.3%和4.0%.从这些数据分析可见, 与均匀流场相比较, 不同的非均匀系数带来的差异主要体现在激波反射前和反射过渡区, 而在激波反射后的差异则明显减小, 平均值约为5%左右.由于流场中环量主要体现在不稳定性界面区域, 因此它直接影响着混合区的发展演化, 激波反射后的流场之间环量差异的减小正是激波反射后初始非均匀流场对界面不稳定性混合影响减小的原因.另外我们还分析了δ1和δ2两种初始非均匀流场之间的差异, 如图 29(c).从图 29(c)可见, 在激波反射前Γ+和Γ-两者差异的最大值分别为5.3%和7.6%, 在激波反射过渡区达到13.9%和18.2%, 而在激波反射以后则为3.6%和3.7%.
|
| 图 28 初始均匀流场及Gauss分布δ1, δ2的非均匀流场, 正负环量、总环量变化图 Fig.28 Positive circulation, negative circulationand total circulation evolutions over time of the flow field of the two elliptic gas cylinders |
|
| 图 29 流场中正负环量之间的相对误差对比图 Fig.29 Relative errors between the flow field in the positive and negative circulations (The reshock times are 1.73, 1.70, and 1.70 ms, respectively, for the three graphs) |
总的来说, 我们可获得的基本结论是, 在激波反射前的线性和弱非线性阶段, 初始流场的非均匀性对R-M界面不稳定性混合区发展和演化影响显著, 经过激波反射加载后界面不稳定性进入强非线性阶段, 虽然界面扰动增长加剧, 但是该阶段流场中R-M界面不稳定性混合区较前期更接近于均匀流场, 也就是说流场的非均匀性在强的非线性阶段对R-M界面不稳定性混合区的影响明显减小.本研究结果进一步表明, 流场的初始条件在R-M界面不稳定性后期对流场中宏观表征量的影响逐渐弱化, 可以推测当完全发展为湍流时流场将可能完全忽略初始条件的影响.
5 结论和展望论文对于激波加载初始非均匀气体流场界面不稳定性和界面混合问题, 根据实验内容构造了一种可能的密度非均匀初始流场分布, 利用MVFT程序, 分析了流场非均匀性、反射冲击和初始扰动对非均匀流场界面不稳定性发展规律的影响及其机制.本研究表明, 在激波反射前的线性和弱的非线性阶段, 初始流场的非均匀性对R-M界面不稳定性混合区发展和演化影响显著, 经过激波反射加载后界面不稳定性进入强的非线性阶段, 但流场的非均匀性在强的非线性阶段对R-M界面不稳定性混合区的影响明显减小, 也就是说流场的初始条件在R-M界面不稳定性后期对流场中宏观表征量的影响逐渐弱化, 可以推测当完全发展为湍流时流场将可能完全忽略初始条件的影响.通过对初始扰动效应的研究, 发现在均匀及非均匀流场中, 密度一定情况下, 初始振幅对界面不稳定性演化规律一致:初始振幅越大, 界面扰动增长越快.但是流场非均匀性极大增加了界面密度梯度, 从而增加了界面各方向速度改变, 导致了不同区域涡量和环量产生差异.在非均匀流场低密度区, 其密度梯度比高密度区密度梯度大, 使得涡量、环量值较大.通过初始振幅和流场非均匀性协同作用, 最终使得低密度区大振幅扰动增长较快, 高密度区小振幅扰动增长较慢.通过这些研究, 我们丰富并拓展了对流体力学相关领域的认识, 为界面不稳定性实验和理论分析提供了依据, 对相关领域的研究具有较重要意义.未来我们将进一步提升实验诊断技术和能力, 尽可能获得定量的混合区流场数据, 为数值模拟方法和程序的确认提供坚实的基础; 并借助于高性能计算平台, 针对R-M不稳定性诱发的界面混合开展精细的直接数值模拟, 深入研究其演化的内在机制和统计规律.
| [1] | Piomelli U, Cabot W H, Moin P, et al. Subgrid-scale backscatter in turbulent and transitional flows[J]. Physics of Fluids A:Fluid Dynamics, 1991, 3(7): 1766-1771. DOI:10.1063/1.857956 |
| [2] | Carati D, Ghosal S, Moin P. On the representation of backscatter in dynamic localization models[J]. Physics of Fluids, 1995, 7(3): 606-616. DOI:10.1063/1.868585 |
| [3] | Leith C E. Stochastic backscatter in a subgrid-scale model:plane shear mixing layer[J]. Physics of Fluids A:Fluid Dynamics, 1990, 2(3): 297-299. DOI:10.1063/1.857779 |
| [4] | Mason P J, Thomson D J. Stochastic backscatter in large-eddy simulations of boundary layers[J]. Journal of Fluid Mechanics, 1992, 242: 51-78. DOI:10.1017/S0022112092002271 |
| [5] | Ghosal S, Lund T S, Moin P, et al. A dynamic localization model for large-eddy simulation of turbulent flows[J]. Journal of Fluid Mechanics, 1995, 286: 229-255. DOI:10.1017/S0022112095000711 |
| [6] | Chasnov J R. Simulation of the Kolmogorov inertial subrange using an improved subgrid model[J]. Physics of Fluids A:Fluid Dynamics, 1991, 3(1): 188-200. DOI:10.1063/1.857878 |
| [7] |
柏劲松, 李平, 陈森华, 等. 内爆加载下果冻内外界面不稳定性数值计算[J].
高压物理学报, 2004, 18(4): 295-301. Bai J S, Li P, Chen S H, et al. Numerical simulation of the instability of the jelly surfaces under the imploding drives[J]. Chinese Journal of High Pressure Physics, 2004, 18(4): 295-301. DOI:10.11858/gywlxb.2004.04.002 |
| [8] |
柏劲松, 李平, 王涛, 等. 可压缩多介质粘性流体的数值计算[J].
爆炸与冲击, 2007, 27(6): 515-521. Bai J S, Li P, Wang T, et al. Computation of compre-ssible multi-viscosity-fluid flows[J]. Explosion and Shock Waves, 2007, 27(6): 515-521. DOI:10.11883/1001-1455(2007)06-0515-07 |
| [9] |
柏劲松, 李平, 谭多望, 等. 界面不稳定性实验的数值研究[J].
力学学报, 2007, 39(6): 741-748. Bai J S, Li P, Tan D W, et al. Numerical study of the interface instability experiment[J]. Chinese Journal of Theoretical Applied Mechanics, 2007, 39(6): 741-748. |
| [10] |
柏劲松, 李平, 邹立勇, 等. 界面不稳定性引起混合过程的二维数值计算[J].
力学学报, 2008, 40(4): 464-472. Bai J S, Li P, Zou L Y, et al. Two-dimensional simulationof the mixing induced by interface instabilities[J]. Chinese Journal of Theoretical Applied Mechanics, 2008, 40(4): 464-472. DOI:10.6052/0459-1879-2008-4-2007-381 |
| [11] | Bai J S, Wang T, Li P, et al. Numerical simulation of the hydrodynamic instability experiments and flow mixing[J]. Science in China Series G:Physics, Mechanics and Astronomy, 2009, 52(12): 2027-2040. DOI:10.1007/s11433-009-0277-9 |
| [12] |
柏劲松, 王涛, 邹立勇, 等. 激波管实验和果冻实验界面不稳定性数值计算[J].
应用力学学报, 2009, 26(3): 418-425. Bai J S, Wang T, Zou L Y, et al. Numerical simulation for shock tube and jelly interface instability experiments[J]. Chinese Journal of Applied Mechanics, 2009, 26(3): 418-425. |
| [13] |
王涛, 柏劲松, 李平, 等. 再冲击载荷作用下流动混合的数值模拟[J].
爆炸与冲击, 2009, 29(3): 243-248. Wang T, Bai J S, Li P, et al. Numerical simulation of flow mixing impacted by reshock[J]. Explosion and Shock Waves, 2009, 29(3): 243-248. DOI:10.11883/1001-1455(2009)03-0243-06 |
| [14] | Wang T, Bai J S, Li P, et al. The numerical study of shock-induced hydrodynamic instability and mixing[J]. Chinese Physics B, 2009, 18(3): 1127-1135. DOI:10.1088/1674-1056/18/3/048 |
| [15] |
王涛, 柏劲松, 李平. 单模态Richtmyer-Meshkov不稳定性数值模拟[J].
计算力学学报, 2012, 29(1): 118-123. Wang T, Bai J S, Li P. Numerical simulations of the single-mode Richtmyer-Meshkov instability[J]. Chinese Journalof Computational Mechanics, 2012, 29(1): 118-123. DOI:10.7511/jslx20121021 |
| [16] |
王涛, 柏劲松, 李平, 等. 单模态RM不稳定性的二维和三维数值计算研究[J].
高压物理学报, 2013, 27(2): 277-286. Wang T, Bai J S, Li P, et al. Two and three dimensional numerical investigations of the single-mode Richtmyer-Meshkov instability[J]. Chinese Journal of High Pressure Physics, 2013, 27(2): 277-286. DOI:10.11858/gywlxb.2013.02.016 |
| [17] |
刘金宏, 谭多望, 柏劲松, 等. 激波管实验研究非均匀流场R-M不稳定性[J].
实验力学, 2012, 27(2): 160-164. Liu J H, Tan D W, Bai J S, et al. Experimental study of Richtmyer-Meshkov instability in nonuniform flow by shock tube[J]. Journal of Experimental Mechanics, 2012, 27(2): 160-164. |
| [18] |
柏劲松, 王涛, 邹立勇, 等. 可压缩多介质粘性流体和湍流的大涡模拟[J].
爆炸与冲击, 2010, 30(3): 262-268. Bai J S, Wang T, Zou L Y, et al. Large eddy simulation for the multi-viscosity-fluid and turbulence[J]. Explosion and Shock Waves, 2010, 30(3): 262-268. DOI:10.11883/1001-1455(2010)03-0262-07 |
| [19] |
柏劲松, 王涛, 李平, 等. 激波反射对扰动界面湍流混合区影响的数值分析[J].
中国科学G辑:物理学力学天文学, 2009, 39(11): 1646-1653. Bai J S, Wang T, Li P, et al. Numerical analyse of the turbulence mixing of re-shocks with a perturbation interface[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2009, 39(11): 1646-1653. |
| [20] | Bai J S, Zou L Y, Wang T, et al. Experimental and numerical study of shock-accelerated elliptic heavy gas cylinders[J]. Physical Review E, 2010, 82(5): 056318 DOI:10.1103/PhysRevE.82.056318 |
| [21] | Bai J S, Wang T, Liu K, et al. Large-eddy simulation of the three-dimensional experiment on Richtmyer-Meshkov instability induced turbulence[J]. International Journal of Astronomy and Astrophysics, 2012, 2(1): 28-36. DOI:10.4236/ijaa.2012.21005 |
| [22] |
柏劲松, 王涛, 刘坤, 等. 柱形和球形壳体内爆界面不稳定性数值分析[J].
应用力学学报, 2012, 29(5): 601-606. Bai J S, Wang T, Li K, et al. Numerical analysis on interface instability of cylindrical and spherical shells under implosive loading[J]. Chinese Journal of Applied Mechanics, 2012, 29(5): 601-606. DOI:10.11776/cjam.29.05.B100 |
| [23] | Li P, Bai J S, Wang T, et al. Large eddy simulation of a shocked gas cylinder instability induced turbulence[J]. Science China Physics, Mechanics and Astronomy, 2010, 53(2): 262-268. DOI:10.1007/s11433-009-0269-9 |
| [24] | Wang T, Bai J S, Li P, et al. Large-eddy simulations of the Richtmyer-Meshkov instability of rectangular interfaces accelerated by shock waves[J]. Science China Physics, Mechanics and Astronomy, 2010, 53(5): 905-914. DOI:10.1007/s11433-010-0099-9 |
| [25] | Wang T, Liu J H, Bai J S, et al. Experimental and numerical investigation of inclined air/SF6 interface instabilityunder shock wave[J]. Applied Mathematics, 2012, 33(1): 37-50. |
| [26] |
王涛, 李平, 柏劲松, 等. 低密度流体界面不稳定性大涡模拟[J].
爆炸与冲击, 2013, 33(5): 487-493. Wang T, Li P, Bai J S, et al. Large-eddy simulation of interface instability of low-density fluids[J]. Explosion and Shock Waves, 2013, 33(5): 487-493. DOI:10.11883/1001-1455(2013)05-0487-07 |
| [27] | Wang T, Bai J S, Li P, et al. Large-eddy simulations of the multi-mode Richtmyer-Meshkov instability and turbulent mixing under reshock[J]. High Energy Density Physics, 2016, 19: 65-75. DOI:10.1016/j.hedp.2016.03.001 |
| [28] | Bai J S, Li P, Zhang Z J, et al. Application of the high-resolution Godunov method to the multi-fluid flow calculations[J]. Chinese Physics, 2004, 13(12): 1992-1998. DOI:10.1088/1009-1963/13/12/003 |
| [29] | Smagorinsky J. General circulation experiments with the primitive equations I. The basic experiment[J]. Monthly Weather Review, 1963, 91(3): 99-164. DOI:10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2 |
| [30] | Vreman A W. An eddy-viscosity subgrid-scale model for turbulent shear flow:Algebraic theory and applications[J]. Physics of Fluids, 2004, 16(10): 3670-3681. DOI:10.1063/1.1785131 |
| [31] | Hill D J, Pantano C, Pullin D I. Large-eddy simulation and multiscale modelling of a Richtmyer-Meshkov instability with reshock[J]. Journal of Fluid Mechanics, 2006, 557: 29-61. DOI:10.1017/S0022112006009475 |
| [32] | Moin P, Squires K, Cabot W, et al. A dynamic subgrid-scale model for compressible turbulence and scalar transport[J]. Physics of Fluids A:Fluid Dynamics, 1991, 3(11): 2746-2757. DOI:10.1063/1.858164 |
| [33] | Wang T, Tao G, Bai J S, et al. Numerical comparative analysis of Richtmyer-Meshkov instability simulated by different SGS models[J]. Canadian Journal of Physics, 2015, 93(5): 519-525. DOI:10.1139/cjp-2014-0099 |
| [34] | Leinov E, Malamud G, Elbaz Y, et al. Experimental and numerical investigation of the Richtmyer-Meshkov instability under re-shock conditions[J]. Journal of Fluid Mechanics, 2009, 626: 449-475. DOI:10.1017/S0022112009005904 |
| [35] | Bai J S, Liu J H, Wang T, et al. Investigation of the Richtmyer-Meshkov instability with double perturbation interface in nonuniform flows[J]. Physical Review E, 2010, 81(5): 056302 DOI:10.1103/PhysRevE.81.056302 |
| [36] | Bai J S, Wang B, Wang T, et al. Numerical simulation of the Richtmyer-Meshkov instability in initially nonuniform flows and mixing with reshock[J]. Physical Review E, 2012, 86(6): 066319 DOI:10.1103/PhysRevE.86.066319 |
| [37] | Xiao J X, Bai J S, Wang T. Numerical study of initial perturbation effects on Richtmyer-Meshkov instability in nonuniform flows[J]. Physical Review E, 2016, 94(1): 013112 DOI:10.1103/PhysRevE.94.013112 |




