2. 中国航天空气动力技术研究院,北京 100074
2. China Academy of Aerospace Aerodynamics, Beijing 100074, China
多介质界面问题的动力学研究作为一门新型的交叉学科, 涉及数学、物理学等各个方向, 在国防、军事、生物医疗等领域中有大量的应用需求, 比如水下爆炸[1]、超声速燃烧[2-3]、高速冲击和穿甲[4]、体外激波碎石[5]等.这里所谓的界面, 是指两种或两种以上不相掺混的介质具有任意拓扑结构的分界面, 或者指自由面.这类问题重点关注不同流体之间的相互作用.从更广泛的意义上讲, 也包括流体和固体的相互作用以及固体间的相互作用.
但是, 目前遇到的物理问题通常非常复杂, 具有大变形、强非线性、多物理过程强耦合等特点, 物质界面的数值模拟是一个很大的挑战, 尤其在界面与激波等高度非线性波系相互作用时更是如此.在极短时间内可能产生各种波系结构的反射、折射等现象, 界面可能会产生严重的变形甚至出现破碎和融合, 产生各种不稳定现象, 同时介质也可能发生相变, 产生蒸发、燃烧等现象.对于固体而言还可能发生弹塑性变形、溶化、汽化等现象.整个过程非常复杂, 对精确模拟多介质界面问题的数值方法提出了很高要求.
有些方法将界面看成有限厚度, 采用混合模型描述界面条件, 如Abgrall[6]提出的γ-模型采用非守恒形式的对流方程来捕捉界面和抑制界面附近非物理振荡.这种思想后来被Shyue[7-9]推广求解各种形式的状态方程, 并模拟激波和界面相互作用[10-11].很多最近发展的方法也来源于Baer等[12]和Saurel等[13]提出的非平衡七方程模型.在两相间压力和速度达到平衡的特征时间为零的假设下, 七方程模型可以简化为五方程模型[14-15].然而, 将界面看成扩散区域可能会导致计算过程中两相流体的非物理混合或产生虚假压力振荡.直到目前不断产生各种技术抑制物质界面的数值扩散或者避免产生数值不稳定[16-21].对于不可压流, 相场(phase field)方法[22]也是一种流行的模拟技术, 近期的发展可以参考Kim[23]的综述性文献.
还有些方法将界面看成零厚度, 由于一种流体只存在于界面的一侧, 界面成为内边界.通常须着重考虑两个方面的问题:一是准确捕获界面位置和拓扑变形, 二是正确定义非线性波与界面相互作用产生的边界条件.
对于第一方面, 界面追踪(front tracking)方法[24]采用低一维的网格来描述界面, 模拟精度高, 能够保持间断的准确和锐利.但该方法难于处理界面拓扑结构的变化, 也难于保持守恒性.近年来提出了相应的处理方法[25-27].水平集(level set, LS)方法[28-29]将表征函数定义为到界面的有向距离, 零等值面就是新时刻的界面位置.该方法可以方便处理复杂的物质界面及其拓扑结构发生变化的情况, 但是不容易保持体积或质量守恒.因此研究人员发展了各种守恒性处理技术应用于不可压多介质流[30]、可压缩多介质流[31-32]和流固耦合[33]等问题.流体体积(volume of fluid, VOF)方法[34-36]通过单元内体积分数来重构界面, 可以实现守恒性, 但是难于计算界面法向和曲率. LS/VOF耦合(CLSVOF)方法[37-38]改善了LS的质量损失和VOF的曲率计算, 但目前主要应用于不可压流体, 而且计算复杂性有待进一步改善.
对于第二方面, 即界面条件的定义可以采用切割网格方法(cut cell method, CCM)[39]或虚拟流体方法(ghost fluid method, GFM)[40].在切割网格方法中, 界面附近的网格切割成两个包含不同流体的子单元.这种方法理论上可以获得非常锐利的界面并实现高精度[41].但在三维问题中的应用较困难, 界面附近网格也可能任意小, 导致计算困难或引起数值不稳定.研究人员发展了相关技术处理界面附近可能产生的极小网格问题[42-43].比较而言, 虚拟流体方法提供了较为简便有效的界面处理方式.通过虚拟流体区域和虚拟流体状态的定义, 避免了切割网格方法中界面附近的小网格问题, 采用常规的单介质数值格式即可求解多介质问题, 不需要较大改动, 而且容易推广至多维.不同虚拟流体方法的区别主要在于如何定义虚拟流体状态[40, 44-48].特别是修正的虚拟流体方法(modified GFM, MGFM)及其变体[45-48], 使用界面附近多介质Riemann问题解定义虚拟流体状态, 能够真实考虑非线性波的相互作用并抑制数值振荡, 可以有效解决各种界面强间断等挑战性难题.结合作者多年来在该领域开展的相关工作, 本文将重点阐述虚拟流体方法的发展历史、理论基础及其在不同领域的应用.
1 虚拟流体方法的基本思想虚拟流体方法的基本思想最早来源于Glimm等[49]基于界面追踪的先驱性工作. 1999年首次被Fedkiw等[40]提出相关概念并应用到可压缩多介质流的计算. 2003年由Liu等[45]引入计算Riemann问题的思路.本节重点回顾算法模拟可压缩多介质流的基本方式.
1.1 问题与方法描述三维可压缩无黏流体用Euler方程表示为
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial y}} + \frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial z}} = 0 $ | (1) |
式中, U=[ρ, ρu, ρv, ρw, E]T, F=[ρu, ρu2+p, ρuv, ρuw, (E+p)u]T, G=[ρv, ρuv, ρv2+p, ρvw, (E+p)v]T, H=[ρw, ρuw, ρvw, ρw2+p, (E+p)w]T分别代表守恒变量和通量. ρ为流体的密度; p为压力; V=(u, v, w)T为流体在x, y和z方向的分速度; E=ρe+ρV2/2是流体的总能量, 其中e为单位质量的内能.略去有关w和z的项, 式(1)变成二维Euler方程.为使方程(1)封闭, 还须补充一个状态方程.具有一般形式的状态方程为
| $ p = p(\rho , e) $ | (2) |
对不同的介质和不同的物理问题具体表现形式不一样.对一般的多介质问题而言, 数学模型就是由Euler方程(1)和不同形式状态方程(2)描述的多种流体组成的含清晰物质界面的问题.
在多介质界面问题的数值模拟中, 物质界面两边流体的状态方程不同, 流体密度可能出现大梯度变化.许多高分辨率格式, 如NND,ENO,WENO,DG等, 如果直接应用于求解该类问题, 界面附近会发生数值不稳定, 出现非物理振荡, 甚至使得计算难以进行.这是由于在更新某一种介质状态时, 跨过界面另一侧的介质状态一般不能直接用来求解数值通量, 必须对紧邻界面网格点的流场量进行修正.在虚拟流体方法中, 物质界面看成内边界.一般每种介质取界面附近3~5个网格点的区域作为虚拟流体区域, 该区域内的流体状态作为内边界条件来定义.这样可以将多介质界面问题转化成多个单介质问题来模拟.每种介质的求解区域包含属于该介质的真实流体区域与虚拟流体区域.原则上, 只要这些虚拟流体状态定义准确, 任何高分辨率计算格式可以直接使用, 不须在界面附近特殊处理.虚拟流体所需最小的网格点数取决于所使用的计算格式, 在实际应用中有可能只有1个或者大于5个.比如, 如果使用1阶Godunov格式对每种介质进行求解, 在界面另一侧就只需要1个虚拟点.在界面附近, 真实流体与虚拟流体共存, 如图 1所示.

|
| 图 1 多介质流动问题中界面附近真实流体与虚拟流体的分布 Fig.1 Distributions of the real fluid and the ghost fluid for multi-medium flows |
对于这个多维问题, 可以在每个计算时间步将式(1)中的速度场投影到界面法向和切向.这样一维多介质初始值Riemann问题可以沿界面法向构造出来
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} = 0, \;\;\;\;\;\;{\left. \mathit{\boldsymbol{U}} \right|_{t = 0}} = \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{U}}_{\rm{L}}}, }&{x < {x_{\rm{I}}}}\\ {{\mathit{\boldsymbol{U}}_{\rm{R}}}, }&{x > {x_{\rm{I}}}} \end{array}} \right. $ | (3) |
式(3)中, U=[ρ, ρu, E]T, F=[ρu, ρu2+p, (E+p)u]T. UL和UR为界面法向上由位于xI处的物质界面分开的两个常值状态.下标I, L和R分别表示界面、左侧和右侧.为了解耦多介质问题(3), 只须在每个时间步对两个带虚拟流体状态的单介质Riemann问题(即GFM Riemann问题[45, 50])单独求解即可.
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} = 0, \;\;\;\;\;{\left. \mathit{\boldsymbol{U}} \right|_{t = 0}} = \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{U}}_{\rm{L}}}, }&{x < {x_{\rm{I}}}}\\ {\mathit{\boldsymbol{U}}_{\rm{R}}^*, }&{x > {x_{\rm{I}}}} \end{array}} \right. $ | (4) |
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} = 0, \;\;\;{\left. \mathit{\boldsymbol{U}} \right|_{t = 0}} = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{U}}_{\rm{L}}^*, }&{x < {x_{\rm{I}}}}\\ {{\mathit{\boldsymbol{U}}_{\rm{R}}}, }&{x > {x_{\rm{I}}}} \end{array}} \right. $ | (5) |
上标*表示虚拟流体.问题(4)的求解区域是从最左边的网格点一直跨过物质界面进入右边介质区的虚拟网格点.问题(5)的求解区域则是从左边的虚拟网格点跨过物质界面一直到最右边的网格点.这种方式可以充分利用各种单介质格式模拟界面问题, 方便编程, 而且容易处理界面的复杂变形.
1.2 虚拟流体方法的代表性版本GFM算法的关键是对虚拟流体状态UR*和UL*定义, 这也是不同GFM版本的主要区别.根据是否使用界面状态定义虚拟流体状态, GFM大体上可以分成基于Riemann解和不基于Riemann解两类算法.原始的GFM(original GFM, OGFM), 作为一种不基于Riemann解的GFM算法, 最初由Fedkiw等[40]在1999年提出.通过水平集方程捕捉运动界面位置后, OGFM提供了界面附近Rankine-Hugoniot跳跃条件的隐式定义方式.为保证压力和速度的连续性, 当地真实流体的压力和速度直接用来定义相应的虚拟流体状态, 虚拟流体的密度通过1阶熵外推得到.为削弱过热现象[51], 通常利用离界面第2层网格点上的熵值进行外推, 如图 2所示.

|
| 图 2 OGFM定义虚拟流体状态的示意图 Fig.2 Illustration of OGFM for defining ghost fluid states |
为了求解刚性更强的气水问题, Fedkiw[44]在2002年提出气水版本的GFM(gas-water version GFM, GWGFM).虚拟流体的压力取为刚性较弱的介质的压力, 速度取为刚性较强的介质的速度, 而保持熵的取法和OGFM一样, 如图 3所示.这样可以较好地模拟气水问题, 但可能不适合刚性不强的气气问题.

|
| 图 3 GWGFM定义虚拟流体状态的示意图 Fig.3 Illustration of GWGFM for defining ghost fluid states |
这两种GFM算法都与问题相关, 根据当地流体变量或由插值来定义虚拟流体状态, 不适用于诸如强激波或高速射流冲击等极端算例[50], 但是其简便性以及容易推广至多维的特点使得这种方法通过结合其他技术得到了一定程度的发展[52-53].而且, 这些方法也被应用于不可压多介质流[30, 54-57]、不可压液体与可压气体耦合[58-59]、化学反应多介质流[60-61]、理想磁流体动力学[62-63]和电动力学[64]等问题的模拟.
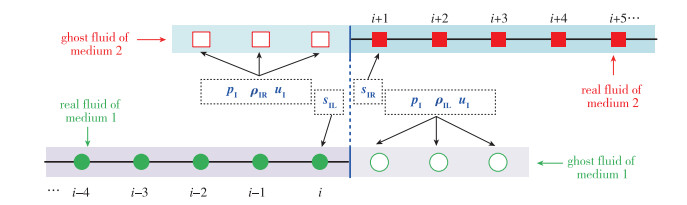
通过对到达界面的波系进行特征分析, Liu等[45]在2003年提出修正的GFM(modified GFM, MGFM).这类方法首先在界面附近近似求解多介质Riemann问题来预测界面状态, 再用得到的预测值定义虚拟流体状态UR*和UL*, 最后对界面附近的真实流体进行必要的等熵修正, 如图 4所示.这样波与物质界面的相互作用和介质性质对界面运动的影响都通过求解一个多介质Riemann问题被充分考虑了.比起OGFM和GWGFM, 这种方法更适合于模拟包含强激波或强间断的挑战性难题[45, 50].
|
| 图 4 MGFM定义虚拟流体状态的示意图 Fig.4 Illustration of MGFM for defining ghost fluid states |
无论是OGFM, GWGFM还是MGFM, 共同点都是如何定义虚拟流体状态.随后, Wang等[47]提出了一种真实的GFM(real GFM, RGFM).作为MGFM的变体, 保持虚拟流体状态UR*和UL*的定义方式与MGFM相同, 并用预测的界面状态重新定义紧邻界面节点的真实流体状态, 如图 5所示. Müller等[65]通过激光诱导空化泡的实验数据验证了这种方法, 并通过对气泡振荡的计算证明比Saurel等[66]的方法更精确.

|
| 图 5 RGFM定义虚拟流体状态的示意图 Fig.5 Illustration of RGFM for defining ghost fluid states |
按照Riemann解的思想, Xu等[48]提出了另一种实用的GFM(practical GFM, PGFM), 也属于MGFM的变体. MGFM须使用3个界面自由度定义虚拟流体状态, 而这种方法只需要1个. PGFM类似于反射边界条件, 仅借助1个界面状态uI就可以计算出虚拟流体速度, 虚拟流体的压力和密度通过镜像对称得到.为抑制界面附近的非物理解, 界面附近和虚拟流体的密度也可以通过某些校正技术[48]获得, 如图 6所示.

|
| 图 6 PGFM定义虚拟流体状态的示意图 Fig.6 Illustration of PGFM for defining ghost fluid states |
这些基于Riemann解的GFM算法具有很好的鲁棒性, 各种大密度比、大压力比的强间断气-气、气-液界面问题已经成功被MGFM或RGFM类算法[50, 65, 67-72]解决.传统的Riemann问题解基于界面压力和速度连续, 如果考虑流体黏性应力、表面张力、相变等影响, 界面压力或速度会发生跳跃, 在定义虚拟流体状态或求解Riemann问题过程中也须将这些因素考虑进去.最近, 基于Riemann解的GFM算法也扩展至模拟不可压流与可压流的耦合[73].
使用基于Riemann解的GFM算法(MGFM,RGFM,PGFM等)在定义虚拟流体状态时, 界面压力、速度和密度等状态不可或缺.采用精确Riemann问题解(exact Riemann problem solver, ERPS)可以避免界面附近的数值耗散或振荡.早些年间, ERPS被用于求解界面状态, 然后在校正步内替换到界面附近的流场变量[74].在GFM框架下, ERPS可以用来计算物质界面的数值通量[75], 或者直接定义虚拟流体状态[26, 69].但是, 完全精确的Riemann解非常复杂, 至今很难推广到二维或者三维.通常须沿界面法向构造多介质ERPS, 类似于一维问题.作为一种近似方法, 隐式近似Riemann问题解(approximate Riemann problem solver, ARPS)广泛用于求解多介质问题, 可以设计成双激波结构[45, 48]或双稀疏波结构[46]的ARPS.隐式ARPS通常包含迭代过程. Fechter等[76]提出了基于线性波形曲线和基于松弛方法的ARPS, 这两种ARPS可以使用更广泛的状态方程形式.对于特殊的刚性气体状态方程[77], Xu等[78]也从双激波结构的ARPS中发展出几种不含迭代过程的显式ARPS.
GFM算法可以看成处理多介质界面条件的一种数值方法, 首先须能够分辨出界面位置, 以及紧邻界面和属于界面内部的节点.大多数情况下采用水平集方法[40, 45-47, 57]捕获物质界面.除此之外, GFM算法也可以与其他界面捕获方法结合, 比如界面追踪方法[52, 59, 70, 79], VOF方法[35]或采用Lagrange坐标系[80].下面简要总结各类GFM算法的一般过程, 更多的细节可以参考文献[40, 44-48].
(1) 更新界面(如利用水平集方法)到下个时间步, 得到新时刻界面位置;
(2) 定义虚拟流体的状态, 然后进行等熵修正或重新定义界面附近的真实流体状态;
(3) 选择合适的单介质高精度格式计算各个流场状态, 将所有流场的解推进到新时刻;
(4) 根据新时刻界面位置获得整个计算域的流场, 然后更新时间步长并进入下次循环.
1.3 多维推广方式多维问题区别于一维问题, 须着重考虑2个或3个速度分量, 而且界面可能发生复杂的拓扑变形.在基于Riemann解的虚拟流体方法中, 首先须确定多介质Riemann问题初始状态的空间位置.对于虚拟流体区域的节点, 比如图 7中的节点P, 存在几种不同的方法确定界面法向上Un, L和Un, R的空间位置.最简单的方法是搜寻界面另一侧真实流体区域的节点P′, 满足P和P′的梯度方向夹角最小[47].或者, 真实流体区域的流场沿界面法向外推到这个节点.这样两种流体状态都位于同一节点P[81].再或者, 两种流体状态的空间位置可以通过插值得到, 如图 7中的节点A和B.通常A和B的距离超过两个网格尺度, 这样在插值中节点P不会提供或提供很小的权重, 在构造Riemann问题时可以避免界面附近误差的影响[45, 69].

|
| 图 7 界面Riemann问题的构造 Fig.7 Construction of the Riemann problem at the interface |
一旦界面附近属于两个不同流体的空间位置确定下来, 可以沿界面法向构造并求解多介质Riemann问题, 然后定义多维问题的虚拟流体状态.一种方法是通过求解
| $ \frac{{\partial {\mathit{\Gamma} _{{\rm{ext}}}}}}{{\partial \tilde t}} \pm \mathit{\boldsymbol{n}} \cdot \nabla {\mathit{\Gamma} _{{\rm{ext}}}} = 0 $ | (6) |
到定常态[40, 47], 将需要外推的变量Γext外推到虚拟流体区域.除去一维问题涉及的变量, 多维问题中Γext还包括界面附近的切向速度.另一种方法是对界面附近虚拟流体区域的每个节点直接定义虚拟流体状态[45, 48, 121].多维问题中, 虚拟流体区域的速度场可以由法向速度分量un·n和切向速度分量Vext-(Vext·n)n构造, 即
| $ \mathit{\boldsymbol{V}}_{{\rm{L}}/{\rm{R}}}^* = {u_n} \cdot \mathit{\boldsymbol{n}} + {\mathit{\boldsymbol{V}}_{{\rm{ext}}}} - \left( {{\mathit{\boldsymbol{V}}_{{\rm{ext}}}} \cdot \mathit{\boldsymbol{n}}} \right)\mathit{\boldsymbol{n}} $ | (7) |
n表示单位法向量.对于基于Riemann解的虚拟流体方法, un为界面法向速度解un, I; 对于非基于Riemann解的虚拟流体方法, un为界面法向上定义的虚拟流体速度. Vext表示外推的速度向量[40, 44, 47, 121].鉴于界面在某些大曲率状态或拓扑变形过程中, 个别虚拟流体节点的界面法向可能很难构造, 或者每个虚拟节点只求解一个Riemann问题的方式可能不会利用足够信息定义界面条件, 界面模拟可能出现计算不准确甚至计算失败.文献[121]给出一种加权平均技术, 充分利用界面周围流场信息定义界面条件, 避免这些情况出现.
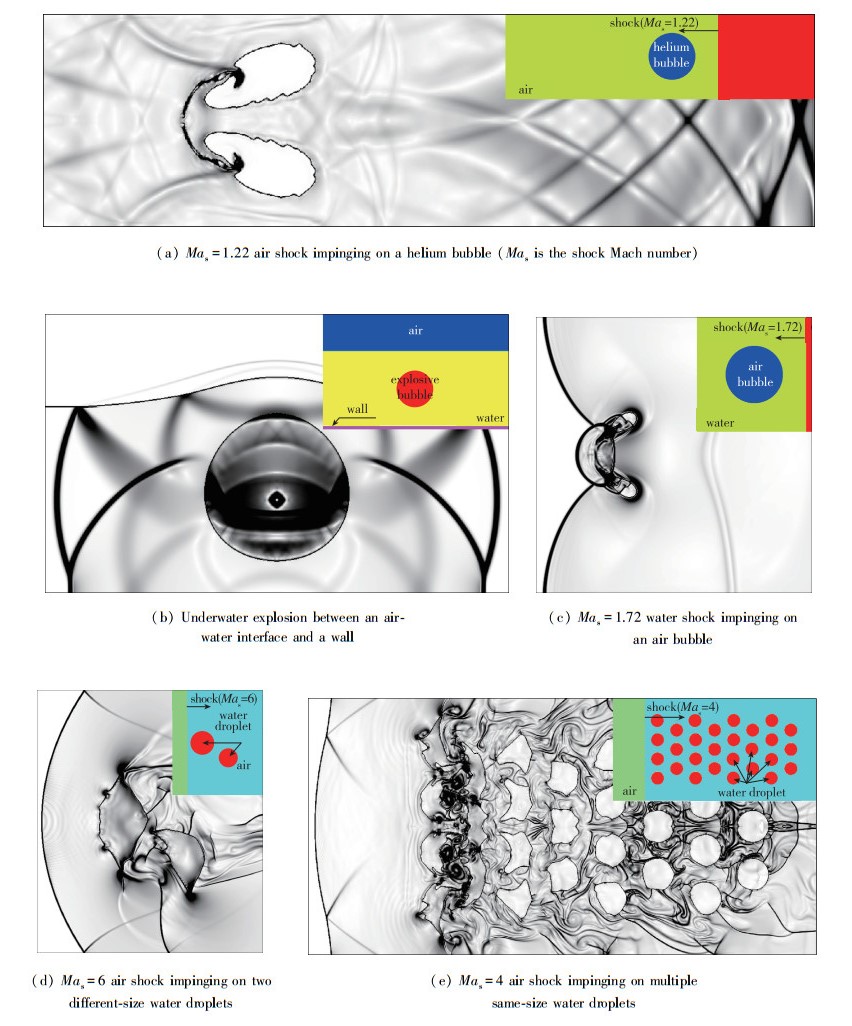
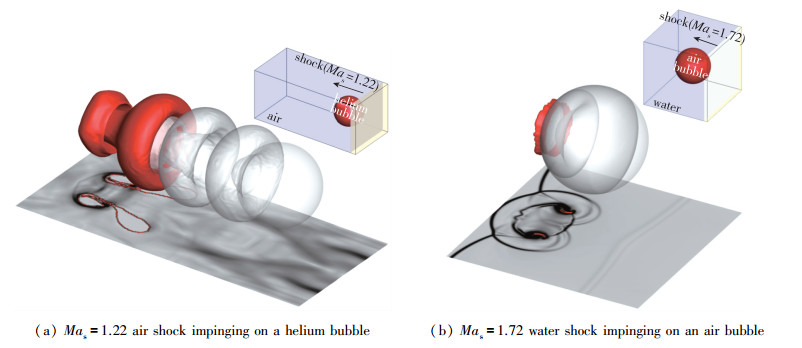
图 8和9分别给出以MGFM为代表的虚拟流体方法对一些典型的可压缩多介质问题的二维和三维模拟结果.相关研究和计算条件可参考文献[18-20, 26, 46, 48, 69, 78, 121].
|
| 图 8 MGFM类方法模拟可压缩多介质问题的二维典型算例 Fig.8 Typical examples of simulating compressible multi-medium flows with MGFM-based technique in two dimensions |
|
| 图 9 MGFM类方法模拟可压缩多介质问题的三维典型算例 Fig.9 Typical examples of simulating compressible multi-medium flows with MGFM-based technique in three dimensions |
基于Riemann解的GFM算法比OGFM或GWGFM更适用于大密度比、大压力比等强间断界面问题.本节主要回顾算法理论方面的基础性工作, 对其原因和结论进行简要概述.具体分析过程可以参见文献[48, 50, 82-85].
2.1 虚拟流体方法的设计原则文献[50]指出, 在GFM算法中, 定义的虚拟流体状态应该能够使GFM Riemann问题(4)和(5)在真实流体一侧产生正确的Riemann波.对GFM Riemann问题(4)来说, 虚拟流体状态UR*的定义理论上应该使UILG=UILe.同样, 问题(5)中UL*的定义应该使UIRG=UIRe, 见图 10的左半部分.这里上标G表示GFM Riemann问题(4)或(5)的精确解, 上标e表示多介质Riemann问题(3)的精确解.研究发现, OGFM和GWGFM在某些范围内本质上不能产生正确的Riemann波而导致计算结果不准确, 基于双激波结构ARPS的MGFM能够适用于绝大部分算例, 仅仅在接近空化条件时须特殊处理[50].

|
| 图 10 GFM Riemann问题(4)中虚拟流体区域的波系结构 Fig.10 Wave structures in the ghost fluid region for GFM Riemann problem(4) |
实际上, 传统的多介质Riemann问题解的结构通常由4个常值区域组成, 这4个常值区域与两种非线性波(激波和稀疏波)和一种线性波(接触间断或物质界面)相接.无论真实流体区域产生何种非线性波, 虚拟流体区域都可以存在各种波系结构:或者不存在Riemann波, 或者存在接触间断、激波、激波与接触间断、稀疏波、稀疏波与接触间断等波系, 见图 10的右半部分.这些虚拟流体区域中的解, 如(4)中的UIRG或(5)中的UILG, 并不是唯一的.文献[48]和[85]分别从不同角度推导并总结虚拟流体状态的合理定义方式:包括虚拟流体区域可能出现的波系结构, 以及定义虚拟流体状态需要使用的自由变量等方面.通过数值验证发现, 如果满足这些定义方式, 理论上模拟多介质Riemann问题的解完全精确, 即图 10中真实流体区域的非线性波与多介质Riemann问题解完全相同.利用这些基本设计原则可以直接推导出MGFM和PGFM两种简单有效的虚拟流体方法[48, 85].
2.2 界面精度和守恒误差近些年来, 有一系列关于应用不同版本虚拟流体方法求解多介质Riemann问题精度分析方面的研究工作.需要注意的是, 这里描述的“精度”应该被解释成内边界条件隐式地施加在物质界面的精度或者由GFM算法得到的界面状态逼近真实界面状态的精度, 而不是数值格式或最终数值解的精度. Liu等[82]证明了基于双激波结构ARPS的MGFM获得的气气Riemann问题界面状态2阶精度逼近于真实界面状态, 误差可以写成O(pIe-pK)2或O(pIe/pK-1)2(K=L, R)的形式.后来, 这个误差估计的结论由Xu等[83]进一步推广和改进.对于刚性气体状态方程[77]描述的流体, MGFM获得的界面状态都可以达到3阶精度O(pIe-pK)3.然而, 文献[82]和[83]使用的分析方法不易推广到更一般形式的状态方程. Xu等[84]因此发展了一种新的研究方法, 在不考虑真空和空化的情况下系统分析了各种GFM版本的精度. MGFM和RGFM在一般形式的状态方程(2)下都能够逼近精确解达3阶精度, 而OGFM和GWGFM仅当左右两边的状态近似相等时至多有1阶精度.基于这种分析方法, Xu等[48]证明了PGFM通过双激波ARPS得到的界面状态也有3阶精度.
通常GFM算法都是非守恒的, 这也促进了一些守恒型GFM的发展[86-87].比如, Nguyen等[87]为OGFM添加后验校正步,重新分配界面附近的守恒误差.然而, 实用有效的守恒型GFM算法还没有开发出来.数值实验表明OGFM可能产生较大的守恒误差, MGFM或RGFM可以抑制得很好[45, 47, 81].在文献[48]和[84]中, 作者系统分析了各种GFM版本的守恒误差, 同样可以得到类似的结论.
总结界面精度和守恒误差的结论可以得出:求解一维多介质Riemann问题(3)时, 通过双激波ARPS定义虚拟流体状态的GFM(MGFM,RGFM,PGFM等), 对任何形式的Riemann解都具有3阶精度的界面误差和守恒误差; 根据当地流体状态或由插值定义虚拟流体状态的GFM(OGFM,GWGFM等), 仅当左右两边的状态近似相等时至多有1阶精度的界面误差和守恒误差.至于多维问题, 目前没有完全精确的类似一维情形的Riemann解存在, 很难将界面精度和守恒误差的分析方法推广至多维.然而, 由于OGFM和GWGFM没有考虑非线性波在界面处的相互作用, 可以确定这两种方法仅能提供至多1阶精度的界面状态和守恒误差.而基于Riemann解的虚拟流体方法可以提供更加准确的结果, 这已被广泛的数值测试和应用所证实.
关于这几类GFM版本的数值结果对比可以参见文献[45, 47-48, 50, 84]. 图 11给出这些算法求解一个气水Riemann问题的压力和速度解.在刚性气体状态方程[77]描述下, 两种流体的无量纲计算参数和初始条件分别是γL=1.4,BL=0.0,ρL=0.2,uL=6.0,pL=2 000.0,γR=7.15,BR=3 309.0,ρR=1.0,uR=0.0,pR=1.0.数值上均采用5阶WENO重构的HLL空间离散格式. OGFM和GWGFM在左稀疏波和右激波的位置均产生严重的数值振荡. MGFM,RGFM和PGFM都获得了相对精确的结果, 而且几乎没有明显的差别.

|
| 图 11 不同版本虚拟流体方法的数值解与精确解的比较 Fig.11 Comparisons of numerical results from various GFMs with exact solutions |
虚拟流体方法最初用于求解可压缩多介质流的界面问题, 近年来该方法已经发展用于模拟各类更广泛和更有挑战性的界面问题.本节主要回顾算法在其他领域的应用情况.
3.1 流固耦合虚拟流体方法已经成功应用于各类流固耦合问题.不同于流体, 固体可以承受拉力, 而且在强冲击下也可能产生弹塑性变形.由于波与界面的非线性相互作用, 流固界面附近通常发生空化.不同于顺序时间步内对流体和固体交替求解的弱耦合方法, 虚拟流体方法通过一个预测步同时定义不同介质的边界条件, 将波与物质界面的相互作用和介质性质对界面运动的影响都考虑进来, 可以避免在处理强激波或强射流对结构的冲击时可能遇到的数值不稳定问题.通常根据不同的物理问题, 固体可以在Euler或Lagrange框架下描述.
在Euler框架下, 某些固体介质[13]仍可以采用刚性气体状态方程[77]描述, 但是无法分辨出是否处于弹性或塑性变形.当发生弹塑性变形时, 采用流体弹塑性(hydro-elasto-plastic)状态方程[88]描述更加准确.这样界面处理方式仍然类似于求解多流体问题的算法, 但是在不同的弹塑性变形阶段, 固体介质可能传播弹性波、塑性波中一种甚至两种非线性波, 须特别考虑固体介质产生不同波结构时界面Riemann问题的求法[81].另外, 由于流体一般不能承受负压, 当固体承受较大拉力时, 可能导致流体承受负压而产生空化.此时, 流体的状态方程应该取代为空化流的状态方程, 而且需要在求解界面Riemann问题时特殊处理固体中的负压传入流体中的情形, 避免界面压力出现负值[89].基于等熵单流体空化流模型[90]和MGFM的处理技术, 文献[91-93]定性讨论了近体水下爆炸中一系列影响结构载荷和空化演变的因素, 包括爆炸强度、爆炸源与结构的距离、结构表面曲率、结构材料或厚度等等.但此时固体被假设为可流化只适用于高压冲击下的应用, 多应用于模拟无限厚结构附近的水下爆炸等问题.
一般来说, 在Lagrange框架下描述固体最为普遍, 近年来也做了很多尝试应用虚拟流体方法处理这类问题.假设固体只发生小弹性变形, 可以将描述固体的Navier方程重新写成一个线性系统, 利用流体的非线性特征和固体的Riemann不变量构造并求解Euler-Lagrange Riemann问题来定义流固界面条件[94-95].流体的非线性特征也可以与固体的运动方程结合, 通过构建并求解耦合系统预测界面条件.这种方式已被用于各种结构模型, 如质量弹簧模型[91]、复合结构模型[96-97]、弹性板结构模型[98]等.文献[99]研究了非接触水下爆炸中板结构厚度、密度对冲击载荷和空化演变的影响.类似的虚拟流体方法应用方式也可参考文献[100].
此外, 刚性固体可以看成浸入流体内部的运动边界, 虚拟流体方法对于该问题也有一定推广.比如, 可以利用反射边界条件构造虚拟流体状态[101-102], 或者在此基础上再求解Riemann问题重新定义虚拟流体状态[103].
3.2 冲击与穿甲虚拟流体方法已经成功应用于各类固体之间的相互作用.在Euler框架下, Sambasivan等[104]将虚拟流体方法推广处理弹塑性介质的相互作用.通过水平集方法获取界面位置信息后, 将界面附近节点划分为介质-介质、介质-真空、介质-刚体3种界面类型.对于不同的界面类型, 采用注入、反射和外插等方式定义合适的边界条件或虚拟介质状态.结合自适应网格加密技术或并行算法, 这种方法成功应用于模拟各种多介质高速冲击、穿甲和破裂的多维问题[104-106]. Barton等[107]将MGFM应用于一二维超弹性滑移材料的界面变形.这种方法对固-固和固-真空Riemann问题采用线性化方法获得近似解, 但是仅考虑弹性变形.后来, Barton等[108]将其进一步推广到求解三维弹塑性材料的冲击和穿甲问题, 并加入各向异性损伤模型[109].
在Lagrange框架下, Kaboudian等[110-111]将OGFM和MGFM推广模拟弹塑性固体之间的相互作用, 虚拟流体方法模拟这种问题时称作虚拟固体方法.因此OGFM和MGFM模拟多介质固体的版本称作OGSM和MGSM(S表示固体), 但是其基本思想没有改变.在一维问题定义虚拟固体的应力和速度时, OGSM采用的是当地真实固体的应力和速度, 而MGSM是对界面附近两种介质的特征进行积分获得界面应力和速度. OGSM, 类似于原始的流体版本OGFM, 都与问题相关且有时会产生较大数值误差. Kaboudian等[110-111]给出ϑ-判据预测OGSM是否会产生较大数值误差. ϑ值量化了数值算例接近声阻抗匹配的程度.研究发现仅在ϑ < 0.1时OGSM才可以使用.
3.3 考虑黏性、表面张力、相变、化学反应等因素的复杂介质虚拟流体方法已经推广处理更复杂介质的界面跳跃条件.其难点在于考虑表面张力、黏性、相变等因素带来的影响.对于不发生相变的无黏流, 在模拟气液界面问题考虑表面张力时, 速度场跨界面连续, 压力不再连续.对于黏性流, 还须把黏性应力的跳跃加入到压力跳跃条件中[30, 54, 57, 72, 112-113].如果发生相变, 速度场也不再连续, 压力跳跃条件也应该包含这个因素[114-117].
定义虚拟流体状态时有不同的处理方式.在不可压流的计算中, 由于密度在每种介质中不同, 须求解变系数Poisson方程, 这当压力不连续时并不容易求解. Liu等[118]为变系数Poisson方程设计了一种新算法. Kang等[54]将GFM的思想[40, 118]应用于考虑黏性和表面张力影响的不可压多介质流计算.在直接数值模拟框架下对不可压多介质流黏性项的虚拟流体处理方式在最近的工作中有深入分析[119]. Desjardins等[30]也采用GFM处理不可压流压力项中的表面张力, 但是利用连续表面力法[120]使黏性项的处理更加简便.这种对黏性项缺乏锐利模型的方式并没有严重影响数值模拟结果.该跳跃条件的选取方式大多数应用于湍流模拟, 比如湍流液体射流雾化模拟[113]和湍流剪切层模拟[57].
在可压流的计算中, 传统的界面Riemann问题须因表面张力和相变带来的影响做出一些改动. Bo等[72]将表面张力影响考虑到界面Riemann问题的求解.然而这种技术没有考虑界面附近的相变和随之产生的速度跳跃, 这在汽化和多相燃烧的建模中非常关键.在多介质化学反应流中, Houim等[117]推广虚拟流体方法, 在N-S方程的双曲项中通过求解一个修正的气液界面Riemann问题将相变和表面张力考虑进来, 在抛物项中给出有关化学反应组分、黏性应力、热传导等因素的处理技术.更多的细节可以参考文献[117].
4 结论对比其他界面问题模拟技术, GFM类算法通过在虚拟流体区域内定义虚拟流体状态, 容易构造界面附近的数值通量, 将求解多介质界面流的问题转化成求解单介质流体的问题.对每种介质可以方便调用已有的单介质求解器而不需太多改动, 计算过程中不需要额外的网格变形算法或重新生成技术, 容易扩展至多维, 具有极强的简便性.尤其是以MGFM为代表的GFM类算法, 使用Riemann解定义虚拟流体状态, 还具有以下几点优势:
(1) 高保真性:结合其他界面捕获方法(如水平集方法、界面追踪方法等)可以保持界面锐利的特性, 避免界面被抹平或产生数值振荡;
(2) 强鲁棒性:与问题无关, 适合于各种多介质问题的模拟, 已被成功应用于求解各种强间断、大密度比和压力比的挑战性多介质界面难题;
(3) 广泛应用性:每种介质可以具有完全不同性质, 不同于其他只能模拟单一物理问题的算法, 理论上能够统一处理各种多介质界面问题, 包括气-液-固耦合等问题.
传统的GFM算法不具备守恒性.虽然最近发展了各种守恒型界面模拟技术, 但据作者所知, 大部分算法非常复杂, 难以扩展至三维问题.有效实用的守恒型GFM算法还在发展之中.
| [1] |
Klaseboer E, Hung K C, Wang C, et al. Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure[J]. Journal of Fluid Mechanics, 2005, 537: 387-413. DOI:10.1017/S0022112005005306 |
| [2] |
Yang J, Kubota T, Zukoski E E. Applications of shock-induced mixing to supersonic combustion[J]. AIAA Journal, 1993, 31(5): 854-862. DOI:10.2514/3.11696 |
| [3] |
Haehn N, Ranjan D, Weber C, et al. Reacting shock bubble interaction[J]. Combustion and Flame, 2012, 159(3): 1339-1350. DOI:10.1016/j.combustflame.2011.10.015 |
| [4] |
Baker J, Williams A. Hypervelocity penetration of plate targets by rod and rod-like projectiles[J]. International Journal of Impact Engineering, 1987, 5(1/4): 101-110. |
| [5] |
Kobayashi K, Kodama T, Takahira H. Shock wave-bubble interaction near soft and rigid boundaries during lithotripsy:numerical analysis by the improved ghost fluid method[J]. Physics in Medicine and Biology, 2011, 56(19): 6421-6440. DOI:10.1088/0031-9155/56/19/016 |
| [6] |
Abgrall R. How to prevent pressure oscillations in multicomponent flow calculations:a quasi conservative app-roach[J]. Journal of Computational Physics, 1996, 125(1): 150-160. |
| [7] |
Shyue K M. An efficient shock-capturing algorithm for compressible multicomponent problems[J]. Journal of Computational Physics, 1998, 142(1): 208-242. |
| [8] |
Shyue K M. A fluid-mixture type algorithm for compressible multicomponent flow with van der Waals equation of state[J]. Journal of Computational Physics, 1999, 156(1): 43-88. |
| [9] |
Shyue K M. A fluid-mixture type algorithm for compressible multicomponent flow with Mie-Grüneisen equation of state[J]. Journal of Computational Physics, 2001, 171(2): 678-707. DOI:10.1006/jcph.2001.6801 |
| [10] |
Johnsen E, Colonius T. Implementation of WENO schemes in compressible multicomponent flow problems[J]. Journal of Computational Physics, 2006, 219(2): 715-732. DOI:10.1016/j.jcp.2006.04.018 |
| [11] |
Johnsen E, Colonius T. Numerical simulations of non-spherical bubble collapse[J]. Journal of Fluid Mecha-nics, 2009, 629: 231-262. DOI:10.1017/S0022112009006351 |
| [12] |
Baer M R, Nunziato J W. A two-phase mixture theory for the deflagration-to-detonation transition (DDT) in reac-tive granular materials[J]. International Journal of Multiphase Flow, 1986, 12(6): 861-889. DOI:10.1016/0301-9322(86)90033-9 |
| [13] |
Saurel R, Abgrall R. A multiphase Godunov method for compressible multifluid and multiphase flows[J]. Journal of Computational Physics, 1999, 150(2): 425-467. DOI:10.1006/jcph.1999.6187 |
| [14] |
Kapila A K, Menikoff R, Bdzil J B, et al. Two-phase modeling of deflagration-to-detonation transition in granu-lar materials:reduced equations[J]. Physics of Fluids, 2001, 13(10): 3002-3024. DOI:10.1063/1.1398042 |
| [15] |
Allaire G, Clerc S, Kokh S. A five-equation model for the simulation of interfaces between compressible fluids[J]. Journal of Computational Physics, 2002, 181(2): 577-616. DOI:10.1006/jcph.2002.7143 |
| [16] |
Kokh S, Lagoutière F. An anti-diffusive numerical scheme for the simulation of interfaces between compressible fluids by means of a five-equation model[J]. Journal of Computational Physics, 2010, 229(8): 2773-2809. DOI:10.1016/j.jcp.2009.12.003 |
| [17] |
Movahed P, Johnsen E. A solution-adaptive method for efficient compressible multifluid simulations, with application to the Richtmyer-Meshkov instability[J]. Journal of Computational Physics, 2013, 239: 166-186. DOI:10.1016/j.jcp.2013.01.016 |
| [18] |
Nonomura T, Kitamura K, Fujii K. A simple interface sharpening technique with a hyperbolic tangent function applied to compressible two-fluid modeling[J]. Journal of Computational Physics, 2014, 258: 95-117. DOI:10.1016/j.jcp.2013.10.021 |
| [19] |
Coralic V, Colonius T. Finite-volume WENO scheme for viscous compressible multicomponent flows[J]. Journal of Computational Physics, 2014, 274: 95-121. DOI:10.1016/j.jcp.2014.06.003 |
| [20] |
Shukla R K. Nonlinear preconditioning for efficient and accurate interface capturing in simulation of multicomponent compressible flows[J]. Journal of Computational Physics, 2014, 276: 508-540. DOI:10.1016/j.jcp.2014.07.034 |
| [21] |
Beig S A, Johnsen E. Maintaining interface equilibrium conditions in compressible multiphase flows using inter-face capturing[J]. Journal of Computational Physics, 2015, 302: 548-566. DOI:10.1016/j.jcp.2015.09.018 |
| [22] |
Anderson D M, McFadden G B, Wheeler A A. Diffuse-interface methods in fluid mechanics[J]. Annual Review of Fluid Mechanics, 1998, 30: 139-165. DOI:10.1146/annurev.fluid.30.1.139 |
| [23] |
Kim J. Phase-field models for multi-component fluid flows[J]. Communications in Computational Physics, 2012, 12(3): 613-661. DOI:10.4208/cicp.301110.040811a |
| [24] |
Unverdi S O, Tryggvason G. A front-tracking method for viscous, incompressible, multi-fluid flows[J]. Journal of Computational Physics, 1992, 100(1): 25-37. |
| [25] |
Nguyen V T, Peraire J, Khoo B C, et al. A discontinuous Galerkin front tracking method for two-phase flows with surface tension[J]. Computers & Fluids, 2010, 39(1): 1-14. |
| [26] |
Terashima H, Tryggvason G. A front-tracking method with projected interface conditions for compressible multi-fluid flows[J]. Computers & Fluids, 2010, 39(10): 1804-1814. |
| [27] |
Ullah M A, Gao W B, Mao D K. Towards front-tracking based on conservation in two space dimensions Ⅲ, tracking interfaces[J]. Journal of Computational Physics, 2013, 242: 268-303. DOI:10.1016/j.jcp.2013.02.026 |
| [28] |
Osher S, Sethian J A. Fronts propagating with curvature-dependent speed:algorithms based on Hamilton-Jacobi formulations[J]. Journal of Computational Physics, 1988, 79(1): 12-49. |
| [29] |
Osher S, Fedkiw R P. Level set methods:an overview and some recent results[J]. Journal of Computational Physics, 2001, 169(2): 463-502. |
| [30] |
Desjardins O, Moureau V, Pitsch H. An accurate conservative level set/ghost fluid method for simulating turbu-lent atomization[J]. Journal of Computational Physics, 2008, 227(18): 8395-8416. DOI:10.1016/j.jcp.2008.05.027 |
| [31] |
Wang C W, Shu C W. An interface treating technique for compressible multi-medium flow with Runge-Kutta discontinuous Galerkin method[J]. Journal of Computational Physics, 2010, 229(23): 8823-8843. DOI:10.1016/j.jcp.2010.08.012 |
| [32] |
胡湘渝. 可压缩Kelvin-Helmholtz不稳定性低耗散锐界面方法直接模拟[J]. 气体物理, 2016, 1(3): 12-18. Hu X Y. Direct simulation of the compressible Kelvin-Helmholtz instability with a low-dissipation sharp-inter-face method[J]. Physics of Gases, 2016, 1(3): 12-18. (in Chinese) |
| [33] |
Barton P T, Obadia B, Drikakis D. A conservative level-set based method for compressible solid/fluid problems on fixed grids[J]. Journal of Computational Physics, 2011, 230(21): 7867-7890. DOI:10.1016/j.jcp.2011.07.008 |
| [34] |
Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. |
| [35] |
Wang Z Y, Yang J M, Stern F. A new volume-of-fluid method with a constructed distance function on general structured grids[J]. Journal of Computational Physics, 2012, 231(9): 3703-3722. DOI:10.1016/j.jcp.2012.01.022 |
| [36] |
Bo W, Grove J W. A volume of fluid method based ghost fluid method for compressible multi-fluid flows[J]. Computers & Fluids, 2014, 90: 113-122. |
| [37] |
Yang X F, James A J, Lowengrub J, et al. An adaptive coupled level-set/volume-of-fluid interface capturing method for unstructured triangular grids[J]. Journal of Computational Physics, 2006, 217(2): 364-394. DOI:10.1016/j.jcp.2006.01.007 |
| [38] |
Balcázar N, Lehmkuhl O, Jofre L, et al. A coupled volume-of-fluid/level-set method for simulation of two-phase flows on unstructured meshes[J]. Computers & Fluids, 2016, 124: 12-29. |
| [39] |
Liu T G, Khoo B C, Yeo K S. The simulation of compressible multi-medium flow:Ⅱ. Applications to 2D underwater shock refraction[J]. Computers & Fluids, 2001, 30(3): 315-337. |
| [40] |
Fedkiw R P, Aslam T, Merriman B, et al. A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method)[J]. Journal of Computational Physics, 1999, 152(2): 457-492. DOI:10.1006/jcph.1999.6236 |
| [41] |
Chang C H, Deng X L, Theofanous T G. Direct numerical simulation of interfacial instabilities:a consistent, conservative, all-speed, sharp-interface method[J]. Journal of Computational Physics, 2013, 242: 946-990. DOI:10.1016/j.jcp.2013.01.014 |
| [42] |
Glimm J, Li X L, Liu Y J, et al. Conservative front tracking with improved accuracy[J]. SIAM Journal on Numerical Analysis, 2003, 41(5): 1926-1947. DOI:10.1137/S0036142901388627 |
| [43] |
Hu X Y, Khoo B C, Adams N A, et al. A conservative interface method for compressible flows[J]. Journal of Computational Physics, 2006, 219(2): 553-578. DOI:10.1016/j.jcp.2006.04.001 |
| [44] |
Fedkiw R P. Coupling an Eulerian fluid calculation to a Lagrangian solid calculation with the ghost fluid met-hod[J]. Journal of Computational Physics, 2002, 175(1): 200-224. |
| [45] |
Liu T G, Khoo B C, Yeo K S. Ghost fluid method for strong shock impacting on material interface[J]. Journal of Computational Physics, 2003, 190(2): 651-681. DOI:10.1016/S0021-9991(03)00301-2 |
| [46] |
Hu X Y, Khoo B C. An interface interaction method for compressible multifluids[J]. Journal of Computational Physics, 2004, 198(1): 35-64. |
| [47] |
Wang C W, Liu T G, Khoo B C. A real ghost fluid method for the simulation of multimedium compressible flow[J]. SIAM Journal on Scientific Computing, 2006, 28(1): 278-302. DOI:10.1137/030601363 |
| [48] |
Xu L, Feng C L, Liu T G. Practical techniques in ghost fluid method for compressible multi-medium flows[J]. Communications in Computational Physics, 2016, 20(3): 619-659. DOI:10.4208/cicp.190315.290316a |
| [49] |
Glimm J, Marchesin D, McBryan O. A numerical method for two phase flow with an unstable interface[J]. Journal of Computational Physics, 1981, 39(1): 179-200. DOI:10.1016/0021-9991(81)90144-3 |
| [50] |
Liu T G, Khoo B C, Wang C W. The ghost fluid method for compressible gas-water simulation[J]. Journal of Computational Physics, 2005, 204(1): 193-221. |
| [51] |
Fedkiw R P, Marquina A, Merriman B. An isobaric fix for the overheating problem in multimaterial compressible flows[J]. Journal of Computational Physics, 1999, 148(2): 545-578. |
| [52] |
Terashima H, Tryggvason G. A front-tracking/ghost-fluid method for fluid interfaces in compressible flows[J]. Journal of Computational Physics, 2009, 228(11): 4012-4037. DOI:10.1016/j.jcp.2009.02.023 |
| [53] |
Tran L B, Udaykumar H S. A particle-level set-based sharp interface cartesian grid method for impact, penetration, and void collapse[J]. Journal of Computational Physics, 2004, 193(2): 469-510. DOI:10.1016/j.jcp.2003.07.023 |
| [54] |
Kang M, Fedkiw R P, Liu X D. A boundary condition capturing method for multiphase incompressible flow[J]. Journal of Scientific Computing, 2000, 15(3): 323-360. DOI:10.1023/A:1011178417620 |
| [55] |
Nguyen D Q, Fedkiw R P, Kang M. A boundary condition capturing method for incompressible flame discontinui-ties[J]. Journal of Computational Physics, 2001, 172(1): 71-98. |
| [56] |
Shin S. Internal wave computations using the ghost fluid method on unstructured grids[J]. International Journal for Numerical Methods in Fluids, 2005, 47(3): 233-251. DOI:10.1002/(ISSN)1097-0363 |
| [57] |
Desjardins O, Pitsch H. A spectrally refined interface approach for simulating multiphase flows[J]. Journal of Computational Physics, 2009, 228(5): 1658-1677. DOI:10.1016/j.jcp.2008.11.005 |
| [58] |
Caiden R, Fedkiw R P, Anderson C. A numerical method for two-phase flow consisting of separate compressible and incompressible regions[J]. Journal of Computational Physics, 2001, 166(1): 1-27. |
| [59] |
Hao Y, Prosperetti A. A numerical method for three-dimensional gas-liquid flow computations[J]. Journal of Computational Physics, 2004, 196(1): 126-144. |
| [60] |
Kim K H, Yoh J J. Shock compression of condensed matter using multimaterial reactive ghost fluid method[J]. Journal of Mathematical Physics, 2008, 49(4): 043511. DOI:10.1063/1.2905152 |
| [61] |
Zoby M R, Navarro-Martinez S, Kronenburg A, et al. Evaporation rates of droplet arrays in turbulent reacting flows[J]. Proceedings of the Combustion Institute, 2011, 33(2): 2117-2125. DOI:10.1016/j.proci.2010.05.081 |
| [62] |
Cai L, Feng J H, Xie W X, et al. Tracking discontinuities in shallow water equations and ideal magnetohydrodynamics equations via ghost fluid method[J]. Applied Numerical Mathematics, 2006, 56(12): 1555-1569. DOI:10.1016/j.apnum.2005.11.006 |
| [63] |
Xie W X, Cai L, Feng J H. Tracking entropy wave in ideal MHD equations by weighted ghost fluid method[J]. Applied Mathematical Modelling, 2007, 31(11): 2503-2514. DOI:10.1016/j.apm.2006.10.009 |
| [64] |
Van Poppel B P, Desjardins O, Daily J W. A ghost fluid, level set methodology for simulating multiphase electrohydrodynamic flows with application to liquid fuel injection[J]. Journal of Computational Physics, 2010, 229(20): 7977-7996. DOI:10.1016/j.jcp.2010.07.003 |
| [65] |
Müller S, Bachmann M, Kröninger D, et al. Comparison and validation of compressible flow simulations of laser-induced cavitation bubbles[J]. Computers & Fluids, 2009, 38(9): 1850-1862. |
| [66] |
Saurel R, Abgrall R. A simple method for compressible multifluid flows[J]. SIAM Journal on Scientific Computing, 1999, 21(3): 1115-1145. DOI:10.1137/S1064827597323749 |
| [67] |
Xie W F, Liu T G, Khoo B C. The simulation of cavitating flows induced by underwater shock and free surface interaction[J]. Applied Numerical Mathematics, 2007, 57(5/7): 734-745. |
| [68] |
Qiu J X, Liu T G, Khoo B C. Simulations of compressible two-medium flow by Runge-Kutta discontinuous Galerkin methods with the ghost fluid method[J]. Communications in Computational Physics, 2008, 3(2): 479-504. |
| [69] |
Sambasivan S K, UdayKumar H S. Ghost fluid method for strong shock interactions part 1:Fluid-fluid interfaces[J]. AIAA Journal, 2009, 47(12): 2907-2922. DOI:10.2514/1.43148 |
| [70] |
Lu H T, Zhu J, Wang D H, et al. Runge-Kutta discontinuous Galerkin method with front tracking method for solving the compressible two-medium flow[J]. Computers & Fluids, 2016, 126: 1-11. |
| [71] |
Wang C, Ding J X, Shu C W, et al. Three-dimensional ghost-fluid large-scale numerical investigation on air explosion[J]. Computers and Fluids, 2016, 137: 70-79. DOI:10.1016/j.compfluid.2016.07.015 |
| [72] |
Bo W, Liu X T, Glimm J, et al. A robust front tracking method:verification and application to simulation of the primary breakup of a liquid jet[J]. SIAM Journal on Scientific Computing, 2011, 33(4): 1505-1524. DOI:10.1137/10079135X |
| [73] |
Lu H T, Zhu J, Wang C W, et al. A Riemann problem based method for solving compressible and incompressible flows[J]. Journal of Computational Physics, 2017, 330: 1-20. DOI:10.1016/j.jcp.2016.10.047 |
| [74] |
Cocchi J P, Saurel R. A Riemann problem based method for the resolution of compressible multimaterial flows[J]. Journal of Computational Physics, 1997, 137(2): 265-298. DOI:10.1006/jcph.1997.5768 |
| [75] |
Farhat C, Rallu A, Shankaran S. A higher-order generalized ghost fluid method for the poor for the three-dimensional two-phase flow computation of underwater implo-sions[J]. Journal of Computational Physics, 2008, 227(16): 7674-7700. DOI:10.1016/j.jcp.2008.04.032 |
| [76] |
Fechter S, Jaegle F, Schleper V. Exact and approximate Riemann solvers at phase boundaries[J]. Computers & Fluids, 2013, 75: 112-126. |
| [77] |
Harlow F H, Amsden A A. Fluid dynamics: a LASL monograph[R]. Technical Report LA-4700, 1971.
|
| [78] |
Xu L, Liu T G. Explicit interface treatments for compressible gas-liquid simulations[J]. Computers & Fluids, 2017, 153: 34-48. |
| [79] |
Wang D H, Zhao N, Hu O, et al. A ghost fluid based front tracking method for multimedium compressible flows[J]. Acta Mathematica Scientia, 2009, 29(6): 1629-1646. DOI:10.1016/S0252-9602(10)60006-9 |
| [80] |
Cai L, Feng J H, Xie W X. An efficient ghost fluid method for compressible multifluids in Lagrangian coordi-nate[J]. Applied Numerical Mathematics, 2008, 58(6): 859-870. DOI:10.1016/j.apnum.2007.03.004 |
| [81] |
Liu T G, Xie W F, Khoo B C. The modified ghost fluid method for coupling of fluid and structure constituted with hydro-elasto-plastic equation of state[J]. SIAM Journal on Scientific Computing, 2008, 30(3): 1105-1130. DOI:10.1137/050647013 |
| [82] |
Liu T G, Khoo B C. The accuracy of the modified ghost fluid method for gas-gas Riemann problem[J]. Applied Numerical Mathematics, 2007, 57(5/7): 721-733. |
| [83] |
Xu L, Liu T G. Optimal error estimation of the modified ghost fluid method[J]. Communications in Computa-tional Physics, 2010, 8(2): 403-426. |
| [84] |
Xu L, Liu T G. Accuracies and conservation errors of various ghost fluid methods for multi-medium Riemann problem[J]. Journal of Computational Physics, 2011, 230(12): 4975-4990. DOI:10.1016/j.jcp.2011.03.021 |
| [85] |
许亮, 冯成亮, 刘铁钢. 虚拟流体方法的设计原则[J]. 计算物理, 2016, 33(6): 671-680. Xu L, Feng C L, Liu T G. Design principles of ghost fluid method[J]. Chinese Journal of Computational Physics, 2016, 33(6): 671-680. DOI:10.3969/j.issn.1001-246X.2016.06.007 (in Chinese) |
| [86] |
Glimm J, Li X L, Liu Y, et al. Conservative front tracking and level set algorithms[J]. Proceedings of the National Academy of Sciences of the United States of America, 2001, 98(25): 14198-14201. DOI:10.1073/pnas.251420998 |
| [87] |
Nguyen D, Gibou F, Fedkiw R. A fully conservative ghost fluid method and stiff detonation waves[C]. Proceedings of the 12th International Detonation Symposium, San Diego: IDS, 2002.
|
| [88] |
Tang H S, Sotiropoulos F. A second-order Godunov method for wave problems in coupled solid-water-gas systems[J]. Journal of Computational Physics, 1999, 151(2): 790-815. DOI:10.1006/jcph.1999.6220 |
| [89] |
Liu T G, Khoo B C, Xie W F. The modified ghost fluid method as applied to extreme fluid-structure interaction in the presence of cavitation[J]. Communications in Computational Physics, 2006, 1(5): 898-919. |
| [90] |
Liu T G, Khoo B C, Xie W F. Isentropic one-fluid modelling of unsteady cavitating flow[J]. Journal of Computational Physics, 2004, 201(1): 80-108. |
| [91] |
Xie W F, Young Y L, Liu T G, et al. Dynamic response of deformable structures subjected to shock load and cavitation reload[J]. Computational Mechanics, 2007, 40(4): 667-681. DOI:10.1007/s00466-006-0132-z |
| [92] |
刘铁钢, 谢文锋, 王成, 等. 界面曲率对空化的演变及结构载荷的影响[J]. 力学学报, 2010, 42(6): 1156-1163. Liu T G, Xie W F, Wang C, et al. Effects of surface curvature on cavitation evolution and reloading[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(6): 1156-1163. (in Chinese) |
| [93] |
Xie W F, Young Y L, Liu T G. Multiphase modeling of dynamic fluid-structure interaction during close-in explo-sion[J]. International Journal for Numerical Methods in Engineering, 2008, 74(6): 1019-1043. DOI:10.1002/(ISSN)1097-0207 |
| [94] |
Liu T G, Ho J Y, Khoo B C, et al. Numerical simulation of fluid-structure interaction using modified ghost fluid method and Naviers equations[J]. Journal of Scientific Computing, 2008, 36(1): 45-68. DOI:10.1007/s10915-007-9176-2 |
| [95] |
Liu T G, Chowdhury A W, Khoo B C. The modified ghost fluid method applied to fluid-elastic structure interaction[J]. Advances in Applied Mathematics and Mechanics, 2011, 3(5): 611-632. DOI:10.4208/aamm.10-m1054 |
| [96] |
Young Y L, Liu Z K, Xie W F. Fluid-structure and shock-bubble interaction effects during underwater explosions near composite structures[J]. Journal of Applied Mechanics, 2009, 76(5): 051303. DOI:10.1115/1.3129718 |
| [97] |
Liu Z K, Xie W F, Young Y L. Numerical modeling of complex interactions between underwater shocks and composite structures[J]. Computational Mechanics, 2009, 43(2): 239-251. DOI:10.1007/s00466-008-0301-3 |
| [98] |
Xu L, Liu T G. Modified ghost fluid method as applied to fluid-plate interaction[J]. Advances in Applied Mathematics and Mechanics, 2014, 6(1): 24-48. DOI:10.4208/aamm.2012.m50 |
| [99] |
许亮, 冯成亮, 刘铁钢. 弹性板水下爆炸冲击载荷的修正虚拟流体方法分析[J]. 计算物理, 2017, 34(1): 1-9. Xu L, Feng C L, Liu T G. Analysis of impact load on elastic plate in underwater explosions with modified ghost fluid method[J]. Chinese Journal of Computational Physics, 2017, 34(1): 1-9. DOI:10.3969/j.issn.1001-246X.2017.01.001 (in Chinese) |
| [100] |
Zeng X Y, Farhat C. A systematic approach for constructing higher-order immersed boundary and ghost fluid methods for fluid-structure interaction problems[J]. Journal of Computational Physics, 2012, 231(7): 2892-2923. DOI:10.1016/j.jcp.2011.12.027 |
| [101] |
许亮, 冯成亮, 刘铁钢. 虚拟流体方法在动边界问题中的应用[J]. 数值计算与计算机应用, 2016, 37(2): 116-124. Xu L, Feng C L, Liu T G. Ghost fluid method as applied to moving boundary problems[J]. Journal on Numerical Methods and Computer Applications, 2016, 37(2): 116-124. (in Chinese) |
| [102] |
王强, 胡湘渝, 姜宗林. 一种含运动固壁超声速流动的Descartes网格算法[J]. 计算物理, 2009, 26(4): 517-526. Wang Q, Hu X Y, Jiang Z L. A Cartesian mesh algorithm for supersonic flows around arbitrary moving bodies[J]. Chinese Journal of Computational Physics, 2009, 26(4): 517-526. DOI:10.3969/j.issn.1001-246X.2009.04.004 (in Chinese) |
| [103] |
Sambasivan S K, UdayKumar H S. Ghost fluid method for strong shock interactions part 2:immersed solid boundaries[J]. AIAA Journal, 2009, 47(12): 2923-2937. DOI:10.2514/1.43153 |
| [104] |
Sambasivan S, Kapahi A, Udaykumar H S. Simulation of high speed impact, penetration and fragmentation problems on locally refined Cartesian grids[J]. Journal of Computational Physics, 2013, 235: 334-370. DOI:10.1016/j.jcp.2012.10.031 |
| [105] |
Kapahi A, Sambasivan S, Udaykumar H S. A three-dimensional sharp interface Cartesian grid method for solving high speed multi-material impact, penetration and fragmentation problems[J]. Journal of Computational Physics, 2013, 241: 308-332. DOI:10.1016/j.jcp.2013.01.007 |
| [106] |
Kapahi A, Mousel J, Sambasivan S, et al. Parallel, sharp interface Eulerian approach to high-speed multi-material flows[J]. Computers & Fluids, 2013, 83: 144-156. |
| [107] |
Barton P T, Drikakis D. An Eulerian method for multi-component problems in non-linear elasticity with sliding interfaces[J]. Journal of Computational Physics, 2010, 229(15): 5518-5540. DOI:10.1016/j.jcp.2010.04.012 |
| [108] |
Barton P T, Deiterding R, Meiron D, et al. Eulerian adaptive finite-difference method for high-velocity impact and penetration problems[J]. Journal of Computational Physics, 2013, 240: 76-99. DOI:10.1016/j.jcp.2013.01.013 |
| [109] |
Barton P T. An Eulerian method for finite deformation anisotropic damage with application to high strain-rate problems[J]. International Journal of Plasticity, 2016, 83: 225-251. DOI:10.1016/j.ijplas.2016.04.012 |
| [110] |
Kaboudian A, Khoo B C. The ghost solid method for the elastic solid-solid interface[J]. Journal of Computational Physics, 2014, 257: 102-125. DOI:10.1016/j.jcp.2013.09.042 |
| [111] |
Kaboudian A, Tavallali P, Khoo B C. The ghost solid methods for the elastic-plastic solid-solid interface and the ϑ-criterion[J]. Journal of Computational Physics, 2015, 302: 618-652. DOI:10.1016/j.jcp.2015.09.023 |
| [112] |
Ervik Å, Lysgaard M O, Herdes C, et al. A multiscale method for simulating fluid interfaces covered with large molecules such as asphaltenes[J]. Journal of Computational Physics, 2016, 327: 576-611. DOI:10.1016/j.jcp.2016.09.039 |
| [113] |
Shao C X, Luo K, Yang Y, et al. Detailed numerical simulation of swirling primary atomization using a mass conservative level set method[J]. International Journal of Multiphase Flow, 2017, 89: 57-68. DOI:10.1016/j.ijmultiphaseflow.2016.10.010 |
| [114] |
Gibou F, Chen L G, Nguyen D, et al. A level set based sharp interface method for the multiphase incompressible Navier-Stokes equations with phase change[J]. Journal of Computational Physics, 2007, 222(2): 536-555. DOI:10.1016/j.jcp.2006.07.035 |
| [115] |
Rueda Villegas L, Alis R, Lepilliez M, et al. A ghost fluid/level set method for boiling flows and liquid evaporation:application to the Leidenfrost effect[J]. Journal of Computational Physics, 2016, 316: 789-813. DOI:10.1016/j.jcp.2016.04.031 |
| [116] |
Rueda Villegas L, Tanguy S, Castanet G, et al. Direct numerical simulation of the impact of a droplet onto a hot surface above the Leidenfrost temperature[J]. International Journal of Heat and Mass Transfer, 2017, 104: 1090-1109. DOI:10.1016/j.ijheatmasstransfer.2016.08.105 |
| [117] |
Houim R W, Kuo K K. A ghost fluid method for compressible reacting flows with phase change[J]. Journal of Computational Physics, 2013, 235: 865-900. DOI:10.1016/j.jcp.2012.09.022 |
| [118] |
Liu X D, Fedkiw R P, Kang M. A boundary condition capturing method for Poisson's equation on irregular domains[J]. Journal of Computational Physics, 2000, 160(1): 151-178. DOI:10.1006/jcph.2000.6444 |
| [119] |
Lalanne B, Rueda Villegas L, Tanguy S, et al. On the computation of viscous terms for incompressible two-phase flows with level set/ghost fluid method[J]. Journal of Computational Physics, 2015, 301: 289-307. DOI:10.1016/j.jcp.2015.08.036 |
| [120] |
Brackbill J U, Kothe D B, Zemach C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354. DOI:10.1016/0021-9991(92)90240-Y |
| [121] |
Xu L, Liu T G. Modified ghost fluid method for three-dime-nsional compressible multi-material flows with interfaces exhibiting large curvature and topological change[J]. International Journal for Numerical Methods in Fluids, submitted. |




