2. 中国科学院力学研究所高温气体动力学国家重点实验室,北京 100190;
3. 北京应用物理与计算数学研究所,北京 100088
2. State Key Laboratory of High Temperature Gas Dynamics(LHD), Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China;
3. Institute of Applied Physics and Computational Mathematics, Beijing 100088, China
Rayleigh-Taylor(RT)不稳定性在超新星爆发、星云生成等天体演化[1-3], 以及惯性约束聚变等工程研究领域[4-9]中有非常重要的作用.
当轻流体加速重流体时, 或在重力场中轻流体支撑重流体时, 两种流体交界面处的小扰动将开始增长导致发生界面不稳定性, 这种界面不稳定性就叫做RT不稳定性.对RT不稳定性已经有较多的理论研究工作.在RT不稳定性的驱动下, 界面处的小扰动先经历e指数线性增长, 进而由于高次谐波的出现, 扰动增长进入弱非线性阶段从而形成界面尖钉和气泡结构.尖钉指的是重流体进入到轻流体所形成的界面, 而气泡指的是轻流体升入到重流体中形成的界面.随着扰动进一步增长, 气泡顶部变得越来越饱满而光滑, 并以常速度增长, 而尖钉的顶部变得越来越尖而细长, 以常加速度增长.到后期, 扰动增长进入非线性乃至强非线性阶段, 此时两种流体相互掺混, 界面破碎, 出现湍流.对于线性阶段和非线性阶段的渐近行为已经有大量的理论研究工作, 有较好的理解; 由于湍流阶段的复杂性, 理论工作不便于开展, 要通过数值模拟和实验的手段进行.
RT不稳定性弱非线性阶段, 高次谐波起了非常重要的作用.由于2次、3次等高次谐波的迅速发展, 其幅值开始增加, 初始单模扰动界面变得具有多模性, 从而改变了界面的对称性, 气泡和尖钉开始形成.也就是说, 向着轻流体运动的尖钉幅值要比向着重流体运动的气泡幅值大.通常, 我们按照界面基模的增长情况划分RT不稳定性经历的线性和非线性阶段.当基模的线性幅值远远大于来自高阶的反馈幅值时, 该阶段为线性阶段.也就是说3阶、5阶等对基模的反馈幅值和基模的线性幅值相比可以忽略时, 该阶段为线性阶段, 此阶段界面向轻重流体增长的幅值相等.随着时间的推移, 3阶、5阶等高阶对基模的反馈幅值开始增加, 使得基模的非线性幅值(基模的线性幅值与高阶反馈幅值之和)偏离其线性幅值而增长.我们把基模的线性幅值与非线性幅值之差占其线性幅值10%的时刻叫做非线性饱和时间, 也就是说, 当RT不稳定性演化到非线性饱和时间时, 基模的非线性幅值就偏离线性幅值的10%了.换句话说, 就是来自高阶的反馈幅值已经达到线性幅值的10%了, 从而说明高次谐波的作用不可忽略.我们把非线性饱和时间对应的基模的线性幅值定义为非线性饱和阈值.该非线性饱和阈值通常作为划分RT不稳定性线性和非线性阶段的标志.因此, 当基模幅值远远小于非线性饱和阈值时, 为线性阶段; 当基模的幅值大于非线性饱和阈值时, 为非线性阶段; 当基模幅值接近非线性饱和阈值时, 为弱非线性阶段.考虑到3阶时, 非线性饱和阈值[13]为
| $ \frac{{{\eta _{{\rm{1s}}}}}}{\lambda } = \frac{{\sqrt 2 }}{{{\rm{ \mathsf{ π} }}\sqrt {5(3{A^2} + 1)} }} $ |
其中, λ为初始扰动波长, 无量纲Atwood数A=(ρh-ρl)/(ρh+ρl), ρh和ρl分别为重流体和轻流体密度.当重流体密度远远大于轻流体密度时, 即A=1时, 非线性饱和阈值大约是扰动波长的0.1倍.也就是说, 在Atwood数为1的情况下, 当基模的幅值达到扰动波长的1/10时, RT不稳定性就已经进入非线性阶段.在进入非线性阶段之前, 高次谐波的作用已经不可忽视.当基模的幅值接近扰动波长的1/10时, RT不稳定性正在经历弱非线性阶段, 高次谐波迅速增长, 和基模共同作用决定着界面的演化发展.
本文主要通过小参数展开法对RT不稳定性弱非线性阶段的谐波进行了理论研究.为了方便对比, 统一采用上标p, c, s分别表示直角坐标系、柱坐标系和球坐标系, 如ηp, ηc, ηs分别为直角坐标系、柱坐标系和球坐标系下的界面幅值; γp, γc, γs分别是直角坐标系、柱坐标系和球坐标系下的线性增长率.用下标L表示线性物理量,如ηL, p, ηL, c, ηL, s分别表示直角坐标系、柱坐标系和球坐标系下的线性幅值.
在直角坐标空间内, 假设在重力场中, 重力加速度为-gey, 其中重力加速度的大小为g, 方向为沿y轴负方向(竖直向下), 轻、重流体的密度分别为ρl和ρh(ρl < ρh), 重流体在轻流体的上方.由于某种原因, 两种流体的交界面处总是存在界面小扰动, 假定两流体界面为ηp(x, t=0)=εcos(kx).其中, k=2π/λ为扰动波数, λ为扰动波长, ε(ε≪λ)为扰动幅值.按照经典RT不稳定性线性理论, 界面处的初始余弦模随时间t将呈e指数形式增长, 即ηL, p=εeγpt.其中, ηL, p为界面处基模的线性扰动幅值, γp为线性增长率
| $ {\gamma ^{\rm{p}}} = \sqrt {Akg} $ |
当扰动幅值接近于初始扰动波长时, 2次和3次等高次谐波相继产生, 从而扰动进入非线性阶段.在弱非线性增长阶段, 3阶弱非线性理论[10-13]给出了演化界面: y=ηp(x, t)=η0p+η1pcos(kx)+η2pcos(2kx)+η3pcos(3kx).其中,
| $ \begin{array}{*{20}{c}} {\eta _0^{\rm{p}} = 0}\\ {\eta _1^{\rm{p}} = {\eta _{{\rm{L, p}}}} - \frac{1}{{16}}(3{A^2} + 1){k^2}\eta _{{\rm{L, p}}}^3}\\ {\eta _2^{\rm{p}} = - \frac{1}{2}Ak\eta _{{\rm{L, p}}}^2}\\ {\eta _3^{\rm{p}} = \frac{1}{2}\left( {{A^2} - \frac{1}{4}} \right){k^2}\eta _{{\rm{L, p}}}^3} \end{array} $ |
分别为0次、1次、2次和3次谐波的幅值.
可以看出, 0次谐波的幅值为零, 即没有出现0次谐波, 表明没有非振动项, 也就是说初始扰动所在的平衡界面y=0不随时间平移, 所有的扰动增长都在该平衡界面上演化.考虑到3阶时, 基模(1次谐波)的线性幅值ηL, p受到来自3阶反馈-(3A2+1)k2ηL, p3/16的修正而偏离的线性增长.由于这里的k, A和ηL, p都是正数, 所以3阶对1次谐波的修正为负反馈.该3阶负反馈使得基模的增长从原先的线性幅值增长变为非线性幅值增长, 显然, 基模的非线性增长幅值小于线性增长幅值.由于只考虑到3阶, 因此2次谐波和3次谐波的幅值没有受到其他高阶反馈的修正, 而呈现线性增长.其中, 2次谐波的幅值小于零, 表明该谐波和初始扰动相比呈反相位增长, 3次谐波幅值随Atwood数的不同而呈现不同的增长方式.当A < 0.5时, 3次谐波的幅值反相位增长; 当A>0.5时, 3次谐波的幅值同相位增长; 当A=0.5时, 3次谐波的幅值为零(即3次谐波消失).
RT不稳定性不仅仅发生在两层水平的流体层交界面上, 也发生在内外两层柱状或球壳层的流体交界面上.在柱界面或球界面上的RT不稳定性研究工作也是众多学者所关注的研究领域之一[15-17].在许多应用方面相关柱面和球面的不稳定性研究工作也相继开展.诸如由初始扰动界面曲率所引起的额外的界面不稳定性(Bell-Plesset(BP)效应), 界面的非线性演化, 包含磁效应的数值解等[18-19].
在柱坐标空间(r, θ, z), 假设重流体包围在轻流体的外围, 所受重力场为-ger (重力加速度大小为g方向为沿r向内), 两流体层之间的界面扰动为ηc(θ, t=0)=r0+εcos(κθ), 其中, κ=2πr0/λ为扰动模数, r0为初始扰动界面半径.在线性阶段, 初始余弦模随时间t呈e指数增长, ηL, c=εeγct.这里, 柱坐标空间内, 柱面线性增长率为
| $ {\gamma ^{\rm{c}}} = \sqrt {\frac{{Ag\kappa }}{{{r_0}}}} $ |
按照柱面3阶弱非线性理论[20], 扰动柱面为
| $ \begin{array}{*{20}{c}} {\eta _0^{\rm{c}} = {r_0} - \frac{1}{4}{r_0}\eta _{{\rm{L, c}}}^2}\\ {\eta _1^{\rm{c}} = {\eta _{{\rm{L, c}}}} - \frac{{3{A^2}{\kappa ^2} - A\kappa + {\kappa ^2} - 9}}{{16r_0^2}}\eta _{{\rm{L, c}}}^3}\\ {\eta _2^{\rm{c}} = - \frac{{A\kappa + 1}}{{2{r_0}}}\eta _{{\rm{L, c}}}^2}\\ {\eta _3^{\rm{c}} = \frac{{4{A^2}{\kappa ^2} + 7A\kappa - {\kappa ^2} + 3}}{{8r_0^2}}\eta _{{\rm{L, c}}}^3} \end{array} $ |
分别为柱面0次、1次、2次和3次谐波的幅值.
这里要说明的是:在3阶理论框架下, 在上述表达式中的-ηL, c2/(4r0)为2阶对0次谐波的反馈, -(3A2κ2-Aκ+κ2-9)ηL, c3/(16r02)为3阶对基模的反馈, 而2次谐波和3次谐波没有受到高阶反馈. 2阶对0次谐波的反馈表明:初始扰动所在的平衡界面随时间向内收缩. 3阶对基模的反馈因模数和Atwood数而不同, 可能是正反馈, 也可能是负反馈. 2次谐波的相位总是和初始扰动相位相同, 而3次谐波的相位和初始扰动相位要么同相位, 要么反相位, 取决于模数和Atwood数.如果保持直角坐标系下平面RT不稳定性和柱坐标系下柱面RT不稳定性初始扰动波长相同, 即满足κ=kr0的情况下, 当r0趋于无穷大时, 这些柱面RT不稳定性下的结果将再现平面RT不稳定性下的结果.
严格来讲, 通常的RT不稳定性指的是由浮力所驱动的不稳定性, 而由流体的可压缩性或几何收缩效应引起的不稳定性叫做BP效应[21-22]. RT不稳定性和BP效应对于惯性约束聚变内爆实验非常重要[23-24]. Epstein[25]基于一个按照界面扰动幅值的简单模型讨论了BP效应.紧接着, Mikaelian[26]给出了柱面和球面不稳定性微分方程, 并针对收缩流体层经历内爆和外爆时给出了线性理论.该线性理论又被Yu等[27]推广到了可压缩流体情况.此后, Forbes[28, 30],Chambers等[29]发表了一系列关于柱和球空间具有轴对称性的RT不稳定性相关论文.正如Plesset所指出:这些工作中在柱几何空间的中心轴线上假定了一个源或者汇, 或球几何中心处, 用于确保不稳定性界面向内或向外运动时, 界面内外流体质量守恒.显然这样一个源或汇的存在, 是不符合客观事实的.实际上, 无论对于天体还是惯性约束聚变, RT不稳定性总是发生在柱面或球面上.在弱非线性阶段, 空间效应和界面的曲率(BP)效应对于RT不稳定性谐波的演化都有很大的影响.为了研究这些因素对RT不稳定性界面演化的影响, 本文仅仅考虑了Atwood数A=1时球坐标空间下无黏、无旋、不可压缩流体界面的前4次谐波(0次谐波、1次谐波、2次谐波和3次谐波)的幅值演化.须要特别指出的是:本文没有假定源或者汇存在于球几何中心, 然而, 界面内仍然保持流体质量守恒, 界面外保持常压.
1 理论框架和解析结果在球坐标空间(r, φ, θ)中, r为径向坐标, φ为与z轴正向所形成的极角坐标(取值于0到π之间), θ为在xoy平面内与x轴正向所形成的方位角坐标(取值于0到2π).不可压缩液体(流体)充满界面r=r0的球面内空间, 界面外为保持常压的密度非常小(相对于液体)的气体(流体).整个空间受重力场的影响, 重力加速度为-ger.在流体界面上, 任何小幅值扰动都将引起RT不稳定性界面增长.这里, 考虑整个球界面上的初始扰动
| $ r = {\eta ^{\rm{s}}}\left( {\varphi , \theta , t = 0} \right) = {r_0} - \varepsilon P_1^1\left( {\cos \varphi } \right)\cos \theta $ |
其中, P11(cosφ)=-sinφ为1阶缔合Legendre函数.在RT不稳定性的作用下, 该球面上的小扰动将随时间增长演化.该初始扰动具有如下特点: (1)在φ方向的模数恒为1; (2)对于任意的极角φ, 方位角θ方向的模数也为1; (3)极角φ和方位角θ分别在[0, π]和[0, 2π]范围内变化时, 除φ=0或π外, 参数
对于不可压缩流体, 根据流体质量守恒, 引入球坐标空间的Laplace方程
| $ \frac{\partial }{{\partial r}}\left( {{r^2}\frac{{\partial \phi }}{{\partial r}}} \right) + \frac{1}{{\sin \varphi }}\frac{\partial }{{\partial \varphi }}\left( {\sin \varphi \frac{{\partial \phi }}{{\partial \varphi }}} \right) + \frac{1}{{{{\sin }^2}\varphi }}\frac{{{\partial ^2}\phi }}{{\partial {\theta ^2}}} = 0 $ | (1) |
其中, ϕ(r, φ, θ, t)为流体的速度势函数.
弱非线性阶段, 在演化界面上应该满足边界条件:速度连续和压力连续.速度连续指的是沿流体界面法线方向流体速度和界面速度相等.速度连续条件如下
| $ \frac{{\partial {\eta ^{\rm{s}}}}}{{\partial t}} + \frac{1}{{{r^2}}}\frac{{\partial {\eta ^{\rm{s}}}}}{{\partial \varphi }}\frac{{\partial \phi }}{{\partial \varphi }} + \frac{1}{{{r^2}{{\sin }^2}\varphi }}\frac{{\partial {\eta ^{\rm{s}}}}}{{\partial \theta }}\frac{{\partial \phi }}{{\partial \theta }} - \frac{{\partial \phi }}{{\partial r}} = 0 $ |
压力连续指的是流体界面两侧压力相等, 该条件如下
| $ \frac{{\partial \phi }}{{\partial t}} + \frac{1}{2}{\left( {\frac{{\partial \phi }}{{\partial r}}} \right)^2} + \frac{1}{{2{r^2}}}{\left( {\frac{{\partial \phi }}{{\partial \varphi }}} \right)^2} + \frac{1}{{2{r^2}{{\sin }^2}\varphi }}{\left( {\frac{{\partial \phi }}{{\partial \theta }}} \right)^2} + gr + f\left( t \right) = 0 $ |
其中, f(t)为关于时间t的任意函数.
该扰动界面受到RT不稳定性的作用, 界面小扰动开始增长.起初, 界面小扰动按照线性e指数增长, 当扰动幅值增长到一定程度后进入非线性阶段.在弱非线性阶段, 由于非线性模耦合过程, 高次谐波(即2次谐波、3次谐波等)相继产生.为此, 界面函数ηs(φ, θ, t)和速度势函数ϕ(r, φ, θ, t)可以展开为小参数
| $ \begin{array}{l} {\eta ^{\rm{s}}}\left( {\varphi , \theta , t} \right) = \mathop \sum \limits_{j = 0}^J \eta _j^{\rm{s}}\left( {\varphi , \theta , t} \right) + O({{\hat \varepsilon }^{J + 1}})\\ \phi \left( {r, \varphi , \theta , t} \right) = \mathop \sum \limits_{j = 0}^N {\phi _j}\left( {r, \varphi , \theta , t} \right) + O({{\hat \varepsilon }^{J + 1}}) \end{array} $ | (2) |
其中,
| $ \begin{array}{l} \eta _j^{\rm{s}}\left( {\varphi , \theta , t} \right) = {{\hat \varepsilon }^j}{{\tilde \lambda }^j}{{\rm{e}}^{j{\gamma ^{\rm{s}}}t}}\mathop \sum \limits_{n = 0}^j \mathop \sum \limits_{m = 0}^n {s_{j, n, m}}P_n^m\left( {\cos \varphi } \right)\cos \left( {m\theta } \right)\\ {\phi _j}\left( {r, \varphi , \theta , t} \right) = {{\hat \varepsilon }^j}{{\rm{e}}^{j{\gamma ^{\rm{s}}}t}}\mathop \sum \limits_{n = 0}^j \mathop \sum \limits_{m = 0}^n {\beta _{j, n, m}}{r^{ - (n + 1)}}P_n^m\left( {\cos \varphi } \right)\cos \left( {m\theta } \right) \end{array} $ |
其中J=3, γs为球坐标空间球面RT不稳定性线性增长率, 函数ηjs(φ, θ, t)和ϕj(r, φ, θ, t)分别为j阶扰动界面和j阶流体扰动速度势函数.速度势函数ϕ(r, φ, θ, t)满足Laplace方程(1)以及边界条件∇φ|r→+∞=0.按照初始条件, s1, 1, 1=-1和s0, 0, 0=r0.在Fourier谐波扰动幅值中的相合系数sj, n, m(j, n, m=1, 2, 3)和γs为关注的待求量.
依照已有研究工作[31]中采用的办法, 该系统可以连续从1阶到3阶逐阶进行求解.注意:由于任意时间函数f(t)的存在, 该系统0阶方程自动得到满足.经求解, 球空间球面RT不稳定性线性增长率以及部分模耦合系数如下
| $ \begin{array}{l} {\gamma ^{\rm{s}}} = \sqrt {\frac{{2g}}{{{r_0}}}} , {s_{2, 0, 0}} = - \frac{1}{{3{r_0}}}, {s_{2, 2, 0}} = \frac{{23}}{{60{r_0}}}, {s_{2, 2, 2}} = - \frac{{23}}{{120{r_0}}}\\ {s_{3, 1, 1}} = \frac{{243}}{{400r_0^2}}, {s_{3, 3, 1}} = - \frac{{71}}{{350r_0^2}}, {s_{3, 3, 3}} = \frac{{71}}{{2100r_0^2}} \end{array} $ |
其他模相合系数为0, 像s1, 1, 0, s2, 2, 1等.我们发现该线性增长率与重力加速度g和球界面初始半径r0有关:随着重力加速度的增大而增大, 随着初始半径的增大而减小.而这些非零模耦合系数与g无关, 只与初始半径有关:随着初始半径的增大而减小.
2 谐波的幅值演化为了方便和平面、柱面RT不稳定性一维扰动对比, 对球面扰动限定φ=π/2.因此, 球面演化方程即方程(2)在3阶理论框架下可以表示为
| $ r = \eta _0^{\rm{s}} + \eta _1^{\rm{s}}\cos \theta + \eta _{\rm{2}}^{\rm{s}}\cos \left( {2\theta } \right) + \eta _3^{\rm{s}}\cos \left( {3\theta } \right) $ |
其中, 前4次谐波的幅值系数分别为
| $ \begin{array}{l} \eta _0^{\rm{s}} = {r_0} - \frac{{21}}{{40{r_0}}}\eta _{{\rm{L, s}}}^2, \eta _{\rm{1}}^{\rm{s}} = {\eta _{{\rm{L, s}}}} - \frac{{2553}}{{2800r_0^2}}\eta _{{\rm{L, s}}}^3\\ \;\;\;\eta _{\rm{2}}^{\rm{s}} = - \frac{{23}}{{40{r_0}}}\eta _{{\rm{L, s}}}^2, \eta _{\rm{3}}^{\rm{s}} = - \frac{{71}}{{140r_0^2}}\eta _{{\rm{L, s}}}^3 \end{array} $ |
以及线性增长幅值为ηL, s=εeγst.
显然, 在3阶理论框架下, 2次谐波和3次谐波没有得到高阶修正, 只有0次谐波和基模分别受到2阶和3阶的反馈修正. 0次谐波在受到2阶修正之前保持常数(初始半径), 修正后则按照修正函数进行演化, 即呈e指数增长.由于反馈量总是小于零, 使得零阶扰动界面以e指数形式向内收缩.这样, 0次谐波、2次和3次谐波均按照e指数呈线性增长.其中, 2次谐波和3次谐波总是和初始扰动相位相反.对于基模而言, 由于受到来自3阶的负反馈(总是抑制e指数线性增长)使得基模偏离原先的线性增长, 而呈非线性增长.因此, 前4次谐波的幅值演化可以划分为线性幅值增长和非线性幅值增长两类.线性幅值包括0次、2次和3次谐波, 而非线性幅值指基模.
为了方便对比球面、柱面和平面RT不稳定性谐波幅值的演化, 我们选取特征量重力加速度g和扰动波长λ对谐波幅值和时间进行无量纲处理.在下列谐波幅值演化曲线图中, 球面RT不稳定性中的谐波幅值统一用实线表示, 柱面RT不稳定性谐波幅值用短线表示, 平面RT不稳定性谐波幅值用带点的短线表示. 3种RT不稳定性中, 如果没有特殊说明, 初始扰动的幅值均为0.001λ.
2.1 线性幅值演化如前所述, 线性幅值包括0次谐波、2次谐波和3次谐波的幅值, 该谐波的幅值演化曲线见图 1~3.对于柱面和球面RT不稳定性0次谐波, 该演化幅值包括两部分:初始未扰动界面r0和来自2阶的反馈幅值.然而, 对于平面RT不稳定性中的0次谐波, 其初始扰动往往施加于y0=0的平面上.为此, 我们统一取初始平衡界面为y0/λ=r0/λ=1/(2π), 即我们将平面、柱面和球面初始平衡界面取在相同位置1/(2π)处.
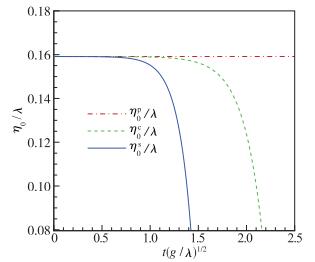
|
| 图 1 0次谐波的幅值随时间演化曲线 Fig.1 Amplitude developments of the zeroth harmonics versus time |
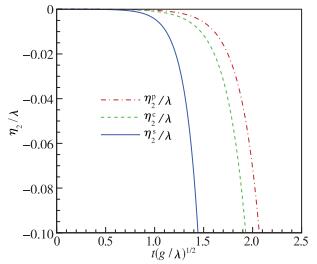
|
| 图 2 2次谐波的幅值随时间的演化曲线图 Fig.2 Amplitude developments of the second harmonic versus time |
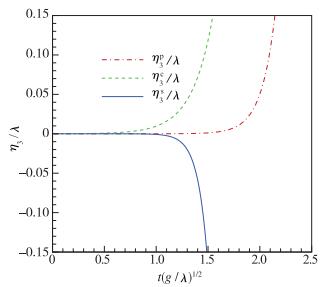
|
| 图 3 3次谐波的幅值随时间的演化曲线图 Fig.3 Amplitude developments of the third harmonic versus time |
图 1表明:对于平面RT不稳定性0次谐波, 2阶反馈为零, 而对于柱面和球面RT不稳定性0次谐波, 其2阶反馈总是小于零的.也就是说, 对于平面RT不稳定性而言, 扰动增长的同时, 所在的固定界面保持不变; 而对于柱面RT不稳定性而言, 扰动增长所在的平衡界面要向圆柱中心轴线收缩; 对于球面RT不稳定性而言, 扰动增长所在的平衡界面要向球心收缩.可见, BP效应加剧了0次谐波(扰动所在平衡界面)向内收缩.同时, 我们也看到, 球面RT不稳定性中的0次谐波的幅值增长最快, 柱面RT不稳定性中的0次谐波幅值增长较慢, 而平面RT不稳定性中0次谐波增长最慢(没有增长).也就是说从平面、柱面到球面, 空间效应加剧了平衡界面的收缩.
图 2给出了2次谐波幅值随时间的演化曲线图.可以看到, 无论对于平面、柱面还是球面RT不稳定性, 2次谐波的幅值都是反相位增长的.对于确定的某一时刻, 我们发现球面情况下2次谐波的幅值增长最快, 其次是柱面情况, 增长最慢的是平面情况下RT不稳定性的2次谐波.这就说明了BP效应和空间效应加剧了RT不稳定性2次谐波的增长.
3次谐波的幅值随时间的演化曲线见图 3.我们看到, 3次谐波的幅值随时间的演化趋势不同于0次谐波和2次谐波, 而是既有同相位增长也有反相位增长.对于平面和柱面RT不稳定性来说, 3次谐波的幅值和初始扰动相位相同, 是同相位增长; 对于球面RT不稳定性而言, 3次谐波和初始扰动相位相反, 是反相位增长.也就是说, BP效应引起了柱面RT不稳定性下3次谐波的同相位增长, 而使得球面RT不稳定性下的3次谐波反相位增长.如果不考虑相位因素, 只看3次谐波幅值的绝对值的演化关系, 我们发现:平面RT不稳定性下3次谐波的幅值增长最慢, 而柱面和球面下幅值的绝对值要大.在无量纲时间约为1.4之前, 柱面下3次谐波的幅值大于球面下3次谐波幅值的绝对值, 而无量纲时间1.4之后, 球面下3次谐波幅值的绝对值要大于柱面下3次谐波的幅值.可见, BP效应和空间效应不仅影响3次谐波的增长快慢, 也影响3次谐波的相位.
2.2 非线性幅值演化由于3阶对基模的负反馈作用, 基模增长要偏离原先的e指数线性增长, 从而完全不同于线性幅值的演化趋势, 如图 4所示.对于平面和球面情况, 基模的演化趋势大致相同:随着时间的增大, 基模的幅值先增大到饱和值, 然后开始骤然减小.在无量纲时间大约为1.3时, 球面情况下的基模幅值达到最大, 大约为0.07λ, 而平面情况下的基模幅值大约在无量纲时间为2时达到最大值0.12λ, 此后开始骤然减小.这两种情况下, 基模幅值增长阶段, 球面时的幅值总是大于平面时的幅值.其实, 在基模幅值增长阶段, 柱面时的基模幅值总是位于球面和平面时基模幅值之间.也就是说, 考虑基模的幅值增长阶段, BP和空间效应都增加了基模的非线性增长.
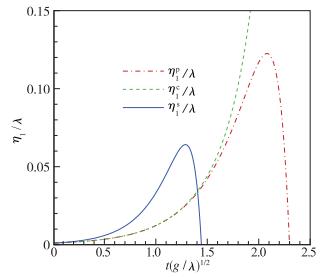
|
| 图 4 基模的幅值随时间演化曲线 Fig.4 Amplitude developments of the fundamental mode versus time |
图 4中有两处疑点须要说明: (1)为什么球面和平面情况下基模的幅值达到饱和之后会减小, 该现象存在吗?(2)为什么柱面情况下基模不会像平面和球面情况那样, 而是一直单调增长?对于问题(1), 从前面已有平面RT不稳定性弱非线性结果和本文所得球面RT不稳定性弱非线性结果可知, 3阶对基模的反馈总是负反馈.扰动刚刚开始增长时, 对基模的负反馈远远小于其线性增长, 而表现出线性增长; 随着演化时间的增大, 3阶负反馈也在增强, 使得基模的线性增长受到较大的抑制而偏离线性增长; 当演化时间达到非线性饱和时间时, 反馈幅值的绝对值等于线性幅值, 基模幅值达到最大, 即饱和幅值; 当演化时间大于非线性饱和时间时, 由于反馈幅值的绝对值大于线性幅值, 使得基模幅值开始减小.当然, 基模的幅值总是增大的, 不可能减小.之所以出现基模幅值的减小是因为没有考虑更多高阶反馈.正如平面RT不稳定性高阶效应对非线性饱和阈值的影响[13]所指出: 5阶对基模的反馈大于零, 为正反馈; 而7阶和9阶对基模的反馈为负反馈, 10阶又是正反馈等.如果所有高阶对基模的反馈都考虑到, 那么基模幅值的增长才符合实际结果.当然, 我们不可能将所有高阶反馈都考虑到, 因此, 仅仅在3阶理论框架下, 基模幅值先增大到最大, 然后开始减小是难免的.搞清楚了问题(1), 对于问题(2)的理解就容易多了.
从柱面下基模幅值一直保持增长的趋势不难推断: 3阶对基模的反馈一定是正反馈造成的.我们回到已有柱面下RT不稳定性结果η1c=ηL, c-(3A2κ2-Aκ+κ2-9)ηL, c3/16r02, 很显然, 3阶对基模的反馈是正反馈还是负反馈, 取决于Atwood数A和模数κ.我们取A=1, κ=1时, 不难发现该反馈是正反馈.因为3阶对基模的反馈是正反馈, 该反馈加剧了基模的线性增长, 从而一直保持基模幅值的增加.
3 结论采用小参数展开到3阶的方法解析研究了位于球坐标空间的无黏、无旋、不可压缩流体在常压支撑下的球面RT不稳定性前4次谐波的幅值演化.为了更好地理解由不稳定性初始扰动界面曲率所引起的BP效应, 以及包括平面、柱面和球面RT不稳定性的空间效应对RT不稳定性的影响, 将球面情况下的谐波幅值和平面以及柱面RT不稳定性谐波幅值做了对比.
我们发现不同于平面RT不稳定性, 柱面和球面RT不稳定性对0次谐波的2阶反馈均小于零, 导致扰动所在平衡界面向内收缩. BP和空间效应对弱非线性阶段谐波幅值有较大影响.为了方便对比, 选取Atwood数A=1,扰动模数κ=1.对于基模而言, 平面和球面情况下其幅值先增大到最大值(饱和幅值)然后骤然减小; 而柱面情况下的幅值保持单调增加.这种不同增长趋势的出现是由3阶对基模的反馈不同所致.平面和球面RT不稳定性中该反馈为负反馈, 抑制了基模的增长, 而柱面情况下该反馈为正反馈, 加速了基模的增长.对于2次谐波, 无论是平面、柱面还是球面RT不稳定性, 该幅值总是小于零, 该谐波和初始扰动相位相反.在同一时刻, 球面情况下的幅值增长最快, 平面幅值最慢.对于3次谐波, 球面情况下其谐波幅值小于零, 而柱面和平面时的幅值大于零.也就是说, 柱效应加剧了3次谐波幅值的正增长, 而球效应加剧了3次谐波幅值的负增长.其中, 0次谐波除了初始平衡界面(常数)外, 只有2阶反馈, 2次和3次谐波均没有受到高阶修正, 因此它们的幅值都呈e指数线性增长.只有基模受到3阶修正, 使得其幅值偏离原e指数线性增长, 呈非线性增长.可见, BP效应和空间效应对RT不稳定性谐波幅值的演化有很大影响.
致谢 本文按照匿名审稿人的宝贵意见和建议进行了修改, 提高了文章的可读性和研究的深度, 感谢匿名审稿人对本文提出的宝贵意见.本工作受到国家自然科学基金(基金号: 11472278和11372330),四川省自然基金(基金号: 18ZA0260和2018JY0454)和绵阳师范学院自然基金(基金号: HX2017007和MYSY2017JC06)的资助, 在此表示感谢!| [1] |
Hachisu I, Matsuda T, Nomoto K, et al. Nonlinear growth of Rayleigh-Taylor instabilities and mixing in SN 1987A[J]. Astrophysical Journal, 1990, 358: L57-L61. DOI:10.1086/185779 |
| [2] |
Remington B A, Drake R P, Ryutov D D. Experimental astrophysics with high power lasers and Z pinches[J]. Reviews of Modern Physics, 2006, 78(3): 755-807. |
| [3] |
王明虎, 罗喜胜.平面激波与组合倾斜空气/SF6气体界面相互作用的实验研究[C].第十五届全国激波与激波管学术交流会论文集.杭州: 中国力学学会, 2012: 31-35. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=7714600
|
| [4] |
Glendinning S G, Dixit S N, Hammel B A, et al. Measurement of a dispersion curve for linear-regime Rayleigh-Taylor growth rates in laser-driven planar targets[J]. Physical Review Letters, 1997, 78(17): 3318-3321. DOI:10.1103/PhysRevLett.78.3318 |
| [5] |
Piriz A R. Hydrodynamic instability of ablation fronts in inertial confinement fusion[J]. Physics of Plasmas, 2001, 8(3): 997-1002. DOI:10.1063/1.1344194 |
| [6] |
Ye W H, Zhang W Y, He X T. Stabilization of ablative Rayleigh-Taylor instability due to change of the Atwood number[J]. Physical Review E, 2002, 65(5): 057401. DOI:10.1103/PhysRevE.65.057401 |
| [7] |
Atzeni S, Meyer-ter-Vehn J. The physics of inertial fusion:beam plasma interaction, hydrodynamics, hot dense matter[M]. Oxford: Oxford University, 2004.
|
| [8] |
Lindl J D, Amendt P, Berger R L, et al. The physics basis for ignition using indirect-drive targets on the National Ignition Facility[J]. Physics of Plasmas, 2004, 11(2): 339-491. DOI:10.1063/1.1578638 |
| [9] |
He X T, Zhang W Y. Inertial fusion research in China[J]. The European Physical Journal D, 2007, 44(2): 227-231. DOI:10.1140/epjd/e2007-00005-1 |
| [10] |
Jacobs J W, Catton I. Three-dimensional Rayleigh-Taylor instability Part 1. Weakly nonlinear theory[J]. Journal of Fluid Mechanics, 1988, 187: 329-352. DOI:10.1017/S002211208800045X |
| [11] |
Haan S W. Weakly nonlinear hydrodynamic instabilities in inertial fusion[J]. Physics of Fluids B:Plasma Physics, 1991, 3(8): 2349-2355. DOI:10.1063/1.859603 |
| [12] |
Berning M, Rubenchik A M. A weakly nonlinear theory for the dynamical Rayleigh-Taylor instability[J]. Physics of Fluids, 1998, 10(7): 1564-1587. DOI:10.1063/1.869677 |
| [13] |
Liu W H, Wang L F, Ye W H, et al. Nonlinear saturation amplitudes in classical Rayleigh-Taylor instability at arbitrary Atwood numbers[J]. Physics of Plasmas, 2012, 19(4): 042705. |
| [14] |
Wark J S, Kilkenny J D, Cole A J, et al. Observations of the Rayleigh-Taylor instability in laser imploded microbal-loons[J]. Applied Physics Letters, 1986, 48(15): 969-971. DOI:10.1063/1.96626 |
| [15] |
Grun J, Kacenjar S. Novel x-ray backlighting method for measuring areal densities of Rayleigh-Taylor unstable, ablatively driven targets[J]. Applied Physics Letters, 1984, 44(5): 497-499. DOI:10.1063/1.94810 |
| [16] |
Amendt P. Bell-Plesset effects for an accelerating inter-face with contiguous density gradients[J]. Physics of Plasmas, 2006, 13(4): 042702. DOI:10.1063/1.2174718 |
| [17] |
Matsuoka C, Nishihara K. Vortex core dynamics and singularity formations in incompressible Richtmyer-Meshkov instability[J]. Physical Review E, 2006, 73(2): 026304. DOI:10.1103/PhysRevE.73.026304 |
| [18] |
Roderick N F, Hussey T W, Faehl R J, et al. Two-dimensional simulation of the hydromagnetic Rayleigh-Taylor instability in an imploding foil plasma[J]. Applied Physics Letters, 1978, 32(5): 273-275. DOI:10.1063/1.90045 |
| [19] |
吴俊峰, 叶文华, 张维岩. 柱几何Rayleigh-Taylor不稳定性的数值模拟[J]. 强激光与粒子束, 2003, 15(1): 64-68. |
| [20] |
Liu W H, Yu C P, Li X L. Effects of initial radius of the interface and Atwood number on nonlinear saturation amplitudes in cylindrical Rayleigh-Taylor instability[J]. Physics of Plasmas, 2014, 21(11): 112103. DOI:10.1063/1.4901088 |
| [21] |
Bell G I. Los Alamos national laboratory[R]. Report LA-1321, 1951.
|
| [22] |
Plesset M S. On the stability of fluid flows with spherical symmetry[J]. Journal of Applied Physics, 1954, 25(1): 96-98. DOI:10.1063/1.1721529 |
| [23] |
Goncharov V N, McKenty P, Skupsky S, et al. Modeling hydrodynamic instabilities in inertial confinement fusion targets[J]. Physics of Plasmas, 2000, 7(12): 5118-5139. DOI:10.1063/1.1321016 |
| [24] |
Amendt P, Colvin J D, Ramshaw J D, et al. Modified Bell-Plesset effect with compressibility:application to double-shell ignition target designs[J]. Physics of Plasmas, 2003, 10(3): 820-829. |
| [25] |
Epstein R. On the Bell-Plesset effects:the effects of uniform compression and geometrical convergence on the classical Rayleigh-Taylor instability[J]. Physics of Plasmas, 2004, 11(11): 5114-5124. DOI:10.1063/1.1790496 |
| [26] |
Mikaelian K O. Rayleigh-Taylor and Richtmyer-Meshkov instabilities and mixing in stratified cylindrical shells[J]. Physics of Fluids, 2005, 17(9): 094105. DOI:10.1063/1.2046712 |
| [27] |
Yu H D, Livescu D. Rayleigh-Taylor instability in cylindrical geometry with compressible fluids[J]. Physics of Fluids, 2008, 20(10): 104103. DOI:10.1063/1.2991431 |
| [28] |
Forbes L K. A cylindrical Rayleigh-Taylor instability:radial outflow from pipes or stars[J]. Journal of Engi-neering Mathematics, 2011, 70(1/3): 205-224. |
| [29] |
Chambers K, Forbes L K. The cylindrical magnetic Rayleigh-Taylor instability for viscous fluids[J]. Physics of Plasmas, 2012, 19(10): 102111. DOI:10.1063/1.4759453 |
| [30] |
Forbes L K. Rayleigh-Taylor instabilities in axi-symmetric outflow from a point source[J]. Anziam Journal, 2011, 53(2): 87-121. DOI:10.1017/S1446181112000090 |
| [31] |
Liu W H, Chen Y L, Yu C P, et al. Harmonic growth of spherical Rayleigh-Taylor instability in weakly nonlinear regime[J]. Physics of Plasmas, 2014, 21(11): 112112. DOI:10.1063/1.4902104 |




