2. 解放军63926部队,北京 100192;
3. 国防科技大学航天科学与工程学院,湖南长沙 410073;
4. 中国空气动力研究与发展中心,四川绵阳 621000
2. The 63926 Troop of Chinese People's Liberation Army, Beijing 100192, China;
3. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China;
4. China Aerodynamics Research and Development Center, Mianyang 621000, China
流动的分离与再附是长期以来一直受关注的研究课题.自由剪切层的非定常性是引起明显的大尺度拟序结构的主因, 对几乎所有湍流流动中存在的拟序结构都有众多报道, 这使得研究分离剪切层流动更加有趣[1].
后台阶(backward facing step, BFS)可以用在超燃冲压发动机中作为点火机构, 以增强空气与燃料之间的混合, 或者作为一种火焰稳定器[2].实际上后台阶作为流动中的一种基本几何外形, 广泛用于研究流动分离和再附[3-5], 研究工作涉及诸如低速亚声速或超声速等各种流动, 而其中关于超声速后台阶流动的研究相对较少.超声速来流在台阶处发生膨胀并产生膨胀波, 从而引起台阶附近流动分离形成回流区.由于流动分离产生了自由剪切层, 之后流动再附在台阶下游面并伴随出现再附激波.下游流动再附之后与壁面相互作用形成重新发展的边界层.
1966年, Sfeir[6]对Mach数2.4台阶高度不同的层流过渡流湍流3种方式的再附与临界点进行了实验研究, 给出了后台阶流动的压力分布, 指出湍流来流的再附点位于压力为来流35%处而层流则为60%处, 自由剪切层长度是分流流线的一半, 采用阴影流动显示手段, 没有给出流场的精细结构. 1981年, Eaton等[7]研究了后台阶流动的再附长度, 发现来流高湍流度引起再附长度减小, 指出后台阶宽度与台阶高度之比(aspect ratio)大于10时流动可以认为是二维的, 其对再附长度的影响可以忽略.在高超声速激波风洞中, Reddeppa等测量了名义Mach数为7.6时来流中台阶高度分别为2和3 mm的后台阶模型表面传热率, 采用Gai的无量纲分析方法对下游热流分布进行了理论分析, 发现对于2和3 mm台阶高度的后台阶模型流动分别近似再附于10和8个台阶高度处[8].黄伟等采用RANS方法研究了吸气式推进系统中作为稳焰器的后台阶竖直面内的速度分布, 其结果与McDaniel等[9]的实验数据进行了比较. 2012年, Mendoza等[10]对有非定常激波相互作用的后台阶流动进行了理论和数值研究, 给出了6种可能的激波入射方式, 得出了激波膨胀波激波-激波作用激波-膨胀波作用的定性结果及初始激波强度临界激波位置测量和激波传输的衰减剖面等定量数据, 研究表明这些流场固定地具有瞬时性与多维性. Biswas等[11]采用数值方法研究了低Reynolds数和中等Reynolds数条件下不同膨胀比(1.9423~3.0) 对后台阶流动的影响, Reynolds数较低时后台阶流动再附长度与之成单调递增关系, 同Reynolds数时膨胀比越大, 再附长度越小.但是这些超声速后台阶实验研究中缺乏流动的精细结构.
本文在来流Mach数3.4条件下, 基于纳米示踪的平面激光散射(nano-tracer based planar laser scattering, NPLS)技术分别研究了无控制粗糙带扰动微涡流发生器扰动3种情况下的二维后台阶模型流场, 获得了流向和展向流场结构的高分辨率瞬态图像, 分析了不同时刻的流场结构演化规律及时间平均特征, 对模型表面压力分布进行了测量并分析, 发现了流动特点及时间演化规律.
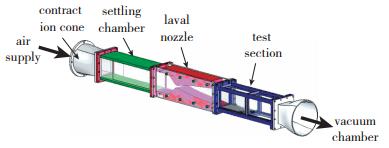
1 实验装置 1.1 超声速风洞如图 1所示, 实验使用KD-02小型吸气式低噪声超声速风洞, 气源为洁净干燥的大气, 实验段横截面尺寸为100 mm×120 mm, 喷管型面采用基于B-样条曲线的轴线配置Mach数的特征线方法设计, 能够提供均匀稳定的超声速来流.本文采用的喷管Mach数为3.4.风洞具体运行参数如表 1所示.
|
| 图 1 KD-02超声速风洞 Fig.1 KD-02 supersonic wind tunnel |
| 下载CSV 表 1 风洞运行参数 Tab.1 Parameters of wind tunnel running |
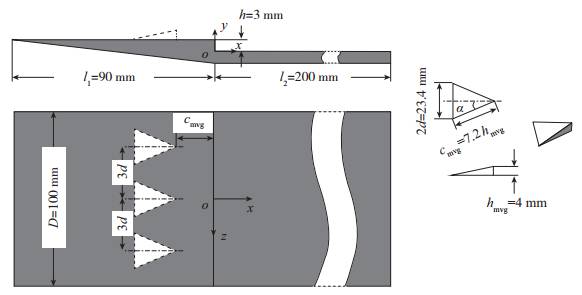
实验采用二维后台阶模型.如图 2所示, 模型台阶高度为3 mm, 上游平板长度为90 mm, 下游平板长度为200 mm, 模型的展向宽度为100 mm.分为3种实验工况:无控制加粗糙带扰动加微涡流发生器(micro-vortex generator, MVG)扰动.其中粗糙带选取36目砂纸, 尺寸90 mm×100 mm, 牢固粘贴并完整覆盖台阶上游平板表面; 微涡流发生器选用Anderson类型[12], 其几何形状及参数见图 2.
|
| 图 2 后台阶模型示意图 Fig.2 Sketch of backward facing step |
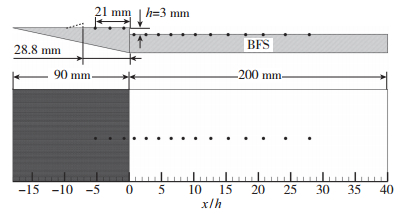
图 3为后台阶模型压力测点分布示意图, 模型从左至右依次分布了15个有效压力测点, 以台阶下缘与其对称面交点为原点, 各测点位置参数如表 2所示.
|
| 图 3 后台阶模型表面压力测点分布 Fig.3 Pressure measuring points distribution on BFS surface |
| 下载CSV 表 2 后台阶模型表面压力测点分布位置 Tab.2 Pressure measuring points positions on BFS surface |
为获得流场的高分辨率精细结构图像, 本文采用NPLS系统.纳米粒子具有良好的流动跟随性[13].纳米粒子的特征尺寸与入射光波长相当或更小, 可以产生Rayleigh散射信号,从而成像.该系统已经成功应用于超声速湍流复杂流场精细测量, 能够清晰地揭示激波膨胀波Mach盘混合层边界层等超声速典型流场结构[13-19].
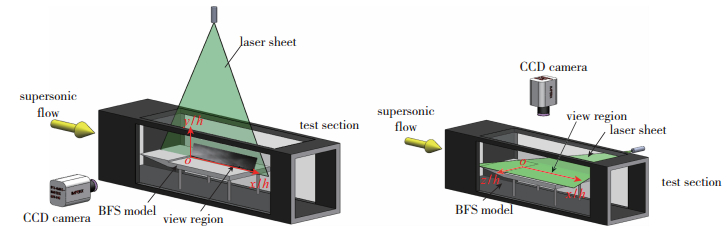
NPLS系统由计算机线间传输双曝光CCD相机粒子发生器同步控制器及Q-开关双腔Nd:YAG激光器组成.片光由Nd:YAG双腔脉冲激光器发出的激光通过相应的片光组件形成.该系统向超声速流场中均匀撒播名义粒径为50 nm的纳米粒子, Samimy等[20]指出,为使粒子能够很好跟随超声速流动特征, 粒子的Stokes数必须小于0.05.本文中粒子的Stokes数约为0.01(St=τp/τf =0.01 < 0.05, 其中粒子特征响应时间τp≈0.09 μs, 流动特征时间τf=δ/U∞≈9.3 μs, 其中δ=6 mm取自后台阶下游重新发展边界层厚度).采用波长为532 nm的激光片光照明粒子, 由垂直于片光平面放置的CCD相机接收粒子的Rayleigh散射信号, 成像激光脉冲时间为6 ns, 最大脉冲能量为350 mJ, 片光最薄处厚度小于0.5 mm, 距离片光出光口500 mm.实验采用线间传输的双曝光CCD, 双曝光时间间隔最小为0.2 μs, 获得图像大小为2048 pixel×2048 pixel, 灰度级4096. CCD和片光光源由同步控制器控制, 两次脉冲片光照射下流场中粒子的光散射信号分别记录在CCD的两次曝光时间内, 得到时间相关的两幅NPLS图像[21]. 图 4所示为本文NPLS实验测量配置, 片光照明区域为模型的法向对称面, 即xoy平面, 以及流场的展向平面, 即xoz平面, 其中原点o定于对称面内台阶下缘处, x轴平行于来流方向, y轴垂直于台阶模型表面, 指向上.相机镜头选用尼康f=60 mm定焦镜头, 拍摄光圈为2.8.
|
| 图 4 实验模型及测试示意图 Fig.4 Model and experimental setup |
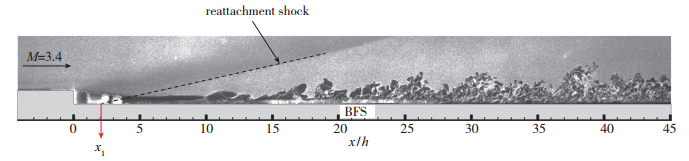
NPLS实验采用焦距60 mm定焦镜头拍摄, 光圈2.8, h=3 mm后台阶模型, 其上游平板距离实验段上壁面68 mm, 下游平板距离实验段上壁面71 mm, 膨胀比Er=71/60≈1.18. 图 5为无控制, h=3 mm, M=3.4条件下后台阶流场精细结构NPLS图像, 图像分辨率为0.0915 mm/pixel, 流动沿x方向自左向右, 流场观测区域到台阶下游45h处, 台阶上游平板实际长度为90 mm.从图中可见, 流动经过3 mm台阶膨胀作用, 形成一系列膨胀波, 如台阶上沿附近灰度较低区域所示, 流动方向向壁面倾斜, 在台阶下游平板面上形成再附后产生再附激波, 该状态下, 再附激波反向延长线与台阶下游面交于x1=2h附近.在x=10h处重新发展边界层流动开始转捩, 大尺度涡结构在10h的距离内迅速发展, 自x=20h附近涡结构逐渐破碎成大量细小结构, 这些作用均较相同流动条件下70 mm上游平板的后台阶流场作用提前且作用更充分.对大量NPLS流场图像求和取平均, 得到流场结构的时间平均场如图 6所示.从时间平均结果中可以测得流场再附激波角度约为12.6°, 再附后重新发展边界层外缘增长角度为2.5°, 增长斜率为0.044, 在流场下游x=45h附近, 湍流边界层平均厚度约为2h.
|
| 图 5 后台阶瞬态流场精细结构(无控制) Fig.5 Instantaneous fine structures of flow over BFS without control |

|
| 图 6 后台阶时间平均流场结构(无控制) Fig.6 Time-averaged structures of flow over BFS without control |
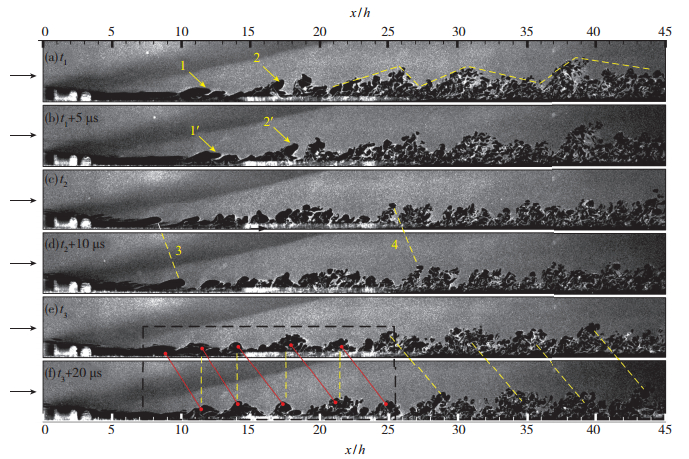
图 7为不同时间间隔内后台阶下游流场结构图像.对照这些不同时刻流场结构可以发现一些流场时间演化规律.台阶下游再附点附近, 拟序结构1经历5 μs后向下游平移了2.47 mm, 其x方向平均运动速度为494 m/s, 较主流速度低24%, 对比两个时刻该结构自身形状并未发生明显变化.而在下游x=17h处, 发卡涡结构2在5 μs内向下游平移2.93 mm, 平移速度为586 m/s, 明显比再附点附近的涡结构运动快, 并且可以观察到该发卡涡头部已经延长, 涡结构有破碎的趋势.自x=20h开始, 重新发展边界层中的涡结构破碎迅速加剧, 随着边界层发展越来越充分, 下游细小涡结构越来越明显, 但是这些细小涡结构并非完全无序, 而是分段形成一个个整体的大结构, 呈锯齿状间歇分布.随着时间间隔增大, Δt=10 μs时, 台阶下游涡结构在该间隔内平移距离更长, 自身形状变化较大, 如图中再附区拟序结构3在10 μs内向下游平移了5.95 mm, 平移速度为595 m/s, 而边界层发展的后段涡结构4则平移了6.77 mm, 对应平移速度为677 m/s.对比图(e)(f)可以发现, 后台阶重新发展边界层靠前区域的涡结构发展呈现一定的周期性规律, 如图中黑色矩形虚线框内所示, 约在x=25h之前涡结构在经历20 μs时间间隔之后基本运动到初始时刻时空间上的下游紧邻涡结构位置处, 这一现象表明在x=25h之前, 本状态下后台阶下游湍流涡结构的发展周期约为20 μs, 意味着每过20 μs空间同一位置处会出现相似涡结构, 而在x>25h的区域, 也可以发现20 μs后有相似的湍流大尺度结构出现, 但是这些大尺度结构并没有出现在上一时刻的同一位置, 尚未运动到空间上下游紧邻大尺度结构处, 而是近似出现在空间上两个大尺度结构的距离中点部位, 这说明边界层的下游流场湍流大尺度结构发展周期较长, 估计为上游部分的两倍即40 μs, 这个结论可为湍流机理研究提供一定的参考依据.
|
| 图 7 不同时刻的后台阶流场结构(无控制) Fig.7 Structures of flow over BFS at different times without control |
将激光片光以平行于后台阶模型平板壁面的方式照亮流场, 并依次调整片光距离台阶下游面的高度, 即片光高度坐标分别为y=0.5h, 1h, 1.5h, 2h, 获得不同高度处后台阶展向流场结构图像, 此外改变跨帧时间以观察展向流场结构的时间演化规律, 见图 8.各个高度均分别得到了跨帧时间5和20 μs的NPLS图像, 图像显示的流场区域大小为45h×13h, 展向以z=0为对称面两侧各6.5h, 图像分辨率为0.098 mm/pixel, 流动沿x方向自左向右, 图像的左侧起点为台阶所在位置.通过实验结果可以发现, 在距离台阶下游壁面较近的高度处, 下游重新发展边界层里的涡结构尺度较小且分布密集, 随着高度增加, 涡结构尺度有所增长且分布密度有所降低, 尤其在高度为1.5h和2h时, 边界层内涡结构的z向间距明显变大, 且涡结构自身尺度也较大.通过联系流向流场结构可以重构出流动的三维空间情景, 重新发展边界层是由大量小涡构成底部的一簇簇顶部分立的丘陵分布结构构成的.越靠近壁面, 受到壁面黏性作用影响越大, 流动能量耗散越强, 涡结构非常容易破碎;而越靠近上部主流, 流动受到的黏性作用越小, 流动能量耗散越缓慢, 大尺度涡结构破碎也较缓慢, 形成了上述现象.片光照射在台阶上游面以上高度时, 可以清晰观察到再附激波出现位置, 如图中y=1.5h及y=2h处展向NPLS图像所示, 再附激波展向整体与台阶边缘平行而局部有所弯曲, 发现离壁面越远再附激波越锐利明显, 这说明离壁面越远再附激波作用越强.可以从再附激波形成机理方面进行解释, 后台阶流动经过台阶膨胀转变方向后流向下游壁面, 受到下游壁面的压缩.但流动再附并非在同一点完成, 而是受到一段区域内的壁面压缩作用后改变流动方向和速度大小, 这些压缩点形成一系列的压缩波, 逐渐汇聚最终形成一道斜激波, 这可以从较低高度处的再附激波边缘较为模糊而远离壁面处激波边缘锐利清晰得到验证.观察台阶以下高度y=0.5h处的展向NPLS图像, 在台阶下游附近发现大量的拟序结构, 而流动再附边界层重新发展后流动拟序结构消失.研究认为, 在台阶附近存在回流区和自由剪切流动, 这里流动从台阶上游面的近层流状态开始受到膨胀加速作用, 而在台阶犄角处由于流动速度过快形成负压产生回流, 低速回流与高速主流形成强剪切, 流动迅速开始失稳转捩, 该过程很容易出现拟序结构[22].

|
| 图 8 不同高度处后台阶流场展向流动图像(无控制) Fig.8 Spanwise images in series planes of flow over BFS without control |
在后台阶模型的上游平板表面粘贴90 mm×100 mm的36目砂纸作为粗糙带,对流动进行扰动, 受粗糙带影响, 来流边界层在台阶上游附近即发生转捩, 边界层厚度增加(约2.5 mm)且流动湍流度增加.
运用NPLS技术获得上游受粗糙带扰动的超声速后台阶流场精细结构图像, 如图 9所示, 图像空间分辨率为0.092 mm/pixel.对照无控制条件下的流场结构发现, 受粗糙带影响, 台阶上游边界层发生转捩, 在台阶拐角处已经发展为一定程度的湍流边界层, 受台阶膨胀作用流动向下游壁面偏转并在短距离内再附, 流动受到壁面压缩产生再附激波, 激波角约为12.8°, 该角度与无控制条件下相当, 可见粗糙带对后台阶流动的再附激波整体影响不大.然而如果仔细观察可以发现, 由于受到湍流大尺度涡结构的诱导作用, 再附激波波足附近会有局部弯曲现象.流动再附后湍流边界层迅速增长, 在如图 10所示的时间平均NPLS图像中, 重新发展湍流边界层的增长角度约为2.8°, 增长斜率为0.0489, 在下游x=45h附近湍流边界层的厚度约为3.4h.

|
| 图 9 后台阶流场瞬态NPLS图像(粗糙带扰动) Fig.9 Instantaneous NPLS image of flow over BFS with roughness |

|
| 图 10 后台阶流场时间平均NPLS图像(粗糙带扰动) Fig.10 Time-averaged NPLS image of flow over BFS with roughness |
在Anderson三角楔微涡流发生器(MVG)控制下, 后台阶流动变得迥然不同. 图 11为有MVG控制的h=3 mm超声速后台阶流场瞬态结构NPLS图像, 空间分辨率为0.092 mm/pixel.图中流动沿水平方向自左向右, 图像显示至台阶下游45h处, 从流场图像中依次可以发现模型前缘Mach波MVG前缘尖劈作用形成的激波MVG尾迹在台阶上游平板的再附激波以及台阶下游流场的再附激波.由于MVG尾迹涡结构的强烈影响, 可以发现后台阶下游再附流动的壁面边界层明显受到抑制, MVG尾迹涡结构在台阶下游占据主要部分, 且存在大量的大尺度结构.

|
| 图 11 后台阶流场瞬态NPLS图像(MVG扰动) Fig.11 Instantaneous NPLS image of flow over BFS with MVG control |
图 12所示依次为时间间隔5, 10, 20 μs的NPLS图像序列, 揭示了受MVG扰动的Mach数3.4后台阶流动精细结构随时间演化的特征. 图 12(a)(b)及(e)(f)中台阶下游MVG尾流结构1和4在经过5和20 μs后分别向下游平移了2.8 mm和11.2 mm, 可估算出该处结构的平均平移运动速度为560 m/s.随着时间间隔的增大, 后台阶流场下游湍流结构向下游平移距离逐渐增大, 平移速度在540~585 m/s之间, 但自身形状在20 μs后几乎没有明显变化, 其相关性仍然较高.这至少可以说明MVG扰动后的流场同一湍流结构完整存在的特征时间不低于20 μs.

|
| 图 12 后台阶流场不同时间间隔NPLS图像(MVG扰动) Fig.12 NPLS images of flow over BFS with MVG control at different times |
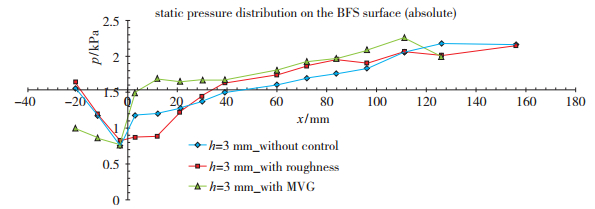
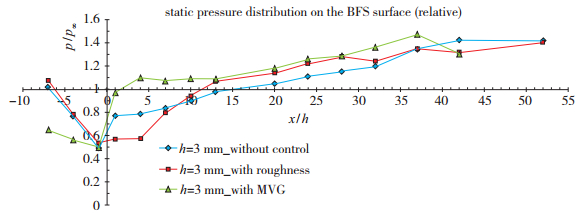
采用微型电子压力扫描系统, 对无控制条件下的h=3 mm后台阶模型表面压力进行测量, 结果如图 13所示, 测得Mach数3.4时的来流静压为p∞=1.532 kPa. 图 13为测点实际物理坐标对应的绝对壁面静压分布, 图 14为测点以台阶高度无量纲化坐标对应的相对来流压力的壁面静压分布.从表面压力测试结果来看, 台阶上游平板表面压力随着与台阶的接近迅速降低, 这是受台阶处流动发生突然膨胀加速的影响;而台阶下游的回流区内压力有所回升, 且可以观察到有一段区域压力基本维持恒定, 这段压力稳定区在x=4h上游至台阶段.这正如文献[23]中提到的回流区内的“死流区”或“静流区”, 该区域内没有质量交换, 是一片“安静”的流动区域, 一般回流区内的压力是均匀的且低于来流静压.随着流动折转后的自由剪切层发生再附并受到壁面压缩作用, 壁面压力开始逐渐回升并在台阶下游约15h处恢复至来流静压值, 在下游重新发展边界层为湍流边界层之前, 壁面静压是不断升高的.随着湍流逐渐发展, 壁面压力逐渐趋于1.4倍的来流静压并总体稳定.
|
| 图 13 后台阶模型表面静压分布(绝对压力) Fig.13 Static pressure distributions on BFS surface (absolute) |
|
| 图 14 后台阶模型表面静压分布(相对压力) Fig.14 Static pressure distributions on BFS surface (relative) |
对上游受粗糙带扰动的h=3 mm后台阶模型表面压力进行测量, 得到如图 13所示结果, 测得Mach数3.4时来流静压为p∞=1.532 kPa.从表面压力测试结果来看, 台阶上游平板表面压力随着与台阶的接近而迅速降低, 可以理解为受台阶处流动发生突然膨胀影响而压力降低, 不过台阶下游回流区内压力有所回升但不明显.而无控制条件下的流场, 回流区内压力回升较明显, 因此可以认为粗糙带有助于台阶上下游表面压力的平稳过渡.有一段区域压力基本维持恒定, 这段压力稳定区在x=4h上游至台阶之间.和无控制条件下的结果相同, 这里同样有一段区域压力基本维持稳定, 这段在x=4h上游至台阶之间的压力稳定区即为“死流区”或“静流区”[23].随着流动折转后的自由剪切层发生再附并受到壁面压缩作用, 壁面压力开始逐渐回升并在台阶下游约x=11.5h=34.5 mm附近恢复至来流静压值, 这比无控制情况较为提前.随着湍流发展的程度逐渐增大, 壁面压力逐渐趋于1.4p∞并总体稳定.
当台阶上游平板边界层有微涡流发生器(MVG)扰动时, 台阶附近的上游壁面静压逐渐降低;但受到MVG尾涡的影响, 台阶之后压力迅速升高, 并在x≈1.5h处恢复至来流静压;之后直至x=13h=39 mm压力基本维持稳定, 随后压力继续增高至1.47p∞;随着下游边界层及MVG尾涡的充分发展破碎, 壁面压力将趋于稳定值.
3 结论在Mach数3.4来流条件下, 对二维后台阶流动精细结构开展了实验研究.实验分为后台阶上游无控制加粗糙带扰动及微涡流发生器扰动3种状态, 采用NPLS方法获得了高时空分辨率的瞬态流场精细结构图像及时间演化图像, 分析了流场的瞬态结构时间平均结构及时间演化规律, 为湍流机理研究提供了参考依据.另外采用微型电子压力扫描系统测量了模型表面静压分布.
对比不同时刻的瞬态流场精细结构图像, 发现在无控制条件下, 在x=25h的上游, 后台阶下游湍流涡结构的发展周期约为20 μs, 即每经历20 μs在空间同一位置处会出现相似涡结构; 由于MVG尾迹涡结构的强烈影响, 后台阶下游再附流动的壁面边界层明显受到抑制, MVG尾迹涡结构在台阶下游占据主要部分, 且存在大量大尺度结构; MVG扰动下的后台阶下游流场大尺度结构自身形状在20 μs后几乎没有明显变化, 其相关性仍然较高, 至少说明MVG扰动后的流场同一湍流结构完整存在的特征时间不低于20 μs.有粗糙带状态相对无粗糙带台阶下游回流区压力更低, 而下游压力较高, 台阶上游区别不大; 受MVG控制后台阶下游附近区域压力突增; MVG对流动的控制改变能力较强, 粗糙带能调整台阶上下游附近流动平稳过渡, 流场壁面压力没有突变.
| [1] | Rajasekaran J. On the flow characteristics behind a backward-facing step and the design of a new axisymmetric model for their study[D]. Toronto:University of Toronto, 2011:70. |
| [2] | Huang W, Pourkashanian M, Ma L, et al. Investigation on the flameholding mechnisms in supersonic flows:backward-facing step and cavity flameholder[J]. Journal of Visualization, 2011, 14(1): 63-74. DOI:10.1007/s12650-010-0064-8 |
| [3] | Bradshaw P, Wong F Y. The reattachment and relaxation of a turbulent shear layer[J]. Journal of Fluid Mechanics, 1972, 52(1): 113-135. DOI:10.1017/S002211207200299X |
| [4] | Castro I P, Robins A G. The flow around a surface-mounted cube in uniform and turbulent streams[J]. Journal of Fluid Mechanics, 1977, 79(2): 307-335. DOI:10.1017/S0022112077000172 |
| [5] | Stokes S D, Glauser M N. An experimental investigation of the 2D backstep and two step flow geometry using laser doppler velocimetry[D]. Potsdam:Clarkson University, 1997. |
| [6] | Sfeir A. Supersonic flow separation on a backward facing step[D]. Berkeley:University of California, 1966. |
| [7] | Eaton J K, Johnston J P. A review of research on subsonic turbulent flow reattachment[R]. AIAA 1980-1438, 1980. |
| [8] | Reddeppa P, Nagashetty K, Saravanan S, et al. Measurement of heat transfer rate on backward-facing steps at hypersonic Mach number[J]. Journal of Thermophysics and Heat Transfer, 2011, 25(3): 321-328. DOI:10.2514/1.47101 |
| [9] | McDaniel J, Fletcher D, Jr Hartfield R. Staged transverse injection into Mach 2 flow behind a rearward-facingstep[R]. AIAA 1991-5071, 1991. |
| [10] | Mendoza N R, Bowersox R D. On the unsteady shock wave interaction with a backward-facing step:inviscid analysis[R]. AIAA 2012-2709, 2012. |
| [11] | Biswas G, Breuer M, Durst F. Backward-facing step flows for various expansion ratios at low and moderate Reynolds numbers[J]. Journal of Fluids Engineering, 2004, 126(3): 362-374. DOI:10.1115/1.1760532 |
| [12] | Anderson B H, Tinapple J, Surber L. Optimal control of shock wave turbulent boundary layer interactions using micro-array actuation[R]. AIAA 2006-3197, 2006. |
| [13] | Zhao Y X, Yi S H, Tian L F, et al. Supersonic flow imaging via nanopaticles[J]. Science in China Series E:Technological Sciences, 2009, 52(12): 3640-3648. DOI:10.1007/s11431-009-0281-3 |
| [14] | Zhao Y X, Yi S H, He L, et al. The experimental study of interaction between shock wave and turbulence[J]. Chinese Science Bulletin, 2007, 52(10): 1297-1301. DOI:10.1007/s11434-007-0177-1 |
| [15] | Zhao Y X, Yi S H, He L, et al. The experimental research of shocklet in supersonic turbulent mix layer[J]. Journal of National University of Defense Technology, 2007, 29(1): 12-15. |
| [16] | Zhao Y X, Yi S H, Tian L F, et al. The fractal measurement of experimental images of supersonic turbulent mixing layer[J]. Science in China Series G:Physics Mechanics and Astronomy, 2008, 51(8): 1134-1143. DOI:10.1007/s11433-008-0097-3 |
| [17] | Yi S H, He L, Zhao Y X, et al. A flow control study of a supersonic mixing layer via NPLS[J]. Science in China Series G:Physics, Mechanics and Astronomy, 2009, 52(12): 2001-2006. DOI:10.1007/s11433-009-0301-0 |
| [18] | He L, Yi S H, Zhao Y X, et al. Visualization of coherent structures in a supersonic flat-plate boundary layer[J]. Chinese Science Bulletin, 2011, 56(6): 489-494. DOI:10.1007/s11434-010-4312-z |
| [19] | Yang W B, Zhuang F G, Shen Q, et al. Experimental and numerical study on instability structure of supersonic mixing layer(Mc=0.5)[J]. Science in China Series G:Physics, Mechanics and Astronomy, 2009, 52(10): 1624-1631. DOI:10.1007/s11433-009-0189-8 |
| [20] | Samimy M, Lele S K. Motion of particles with inertia in a compressible free shear layer[J]. Physics of Fluids A:Fluid Dynamics, 1991, 3(8): 1915-1923. DOI:10.1063/1.857921 |
| [21] | Hornak J P. Encyclopedia of imaging science and tech-nology[M]. New York:Wiley, 2002:390-419. |
| [22] | Herrin J L, Dutton J C. The turbulence structure of a reattaching axisymmetric compressible free shear layer[J]. Physics of Fluids, 1997, 9(11): 3502-3512. DOI:10.1063/1.869458 |
| [23] | Deepak N R, Gai S L, Neely A J. High-enthalpy flow over a rearward-facing step-a computational study[J]. Journal of Fluid Mechanics, 2012, 695: 405-438. DOI:10.1017/jfm.2012.29 |



