微型飞行器有广泛的应用前景, 如军事侦察救援勘探空中摄影小负重物流等, 类型主要包括固定翼旋翼和扑翼.研究表明, 在小尺度(约15cm以下)下, Reynolds数很低, 固定翼和旋翼难以提供足够的高效升力和稳定性.而生物界鸟类的灵活扑翼飞行鱼类的快速摆尾前行为人类提供了灵感, 扑翼机扑翼水下航行器等成为研究热点.仿生微型扑翼飞行器Reynolds数为103~105, 属于流动从发生转捩到形成湍流的敏感区, 气动机理复杂.仿生在模仿生物运动方式的同时, 还应深层理解这些物理现象的机理, 才能有效地指导设计[1-3].
在扑翼的机理研究方面, 包括准定常和非定常空气动力学理论, 几十年来发展出了若干较明确的扑翼飞行机制.准定常空气动力学理论在抓主要矛盾的同时将复杂问题简化, 广泛应用的主要有叶元法和尾涡方法.叶元法对沿展向分布的无限多个小叶元的升力进行积分,从而获得整个扑翼的升力; 尾涡方法基于动量理论, 关心周期内的平均作用效果, 根据涡量守恒原理得知尾流与环绕扑翼的流体在动量环量上的变化等值相反, 由尾流场的变化可得出扑翼受力.非定常空气动力机制尤其关注涡的作用, 能揭示更多扑翼高升力现象, 主要包括拍-挥机制[4]前缘涡失速延迟理论[5]旋转力效应[6]尾迹捕捉作用[7]及附加质量效应[8]等.
尾流中的脱落涡是影响自身气动力飞行不稳定性以及对下游物体产生影响的重要因素[9].当扑动频率足够大时, 脱落涡排列为反向Karman涡街, 尾流速度大于前行速度, 能产生推力.同时, 尾迹捕捉作用指出, 当扑翼转动方向时, 会遇到前次扑动产生的涡, 尾流速度增加产生额外的升力峰值, 尾迹捕捉效果与涡量的分布和大小变化规律有关[10]. Ohmi等[11]通过实验测量了二维摆动和俯仰的扑翼, 发现减缩频率k是一个决定尾流结构的主要参数, 其定义为
| $ k = \frac{{{\rm{ \mathsf{ π} }}f{l_{{\rm{ref}}}}}}{{{U_{_{{\rm{ref}}}}}}} = \frac{{{\rm{ \mathsf{ π} }}f{c_{\rm{m}}}}}{{{U_\infty }}} $ |
此处参考长度lref取平均几何弦长cm, 参考速度Uref取前飞速度U∞, k与扑动频率f成正比, 是流体扰动的空间尺度与弦长的比较[2].
扑翼流场的复杂性使得理论分析和仿真更需要实验数据的支撑. 90年代以后, 粒子成像测速(particle image velocimetry, PIV)技术快速发展, PIV具备光学非接触全场测量瞬态测量的优点, 能更细致地测量扑翼尾流结构. Bomphrey[12]采用PIV测量了飞蛾的近场尾涡形态, 表明近场尾涡类似于一个椭圆形涡环. Parker等[13]利用PIV对有限翼展的扑动翼进行了测量, 精确地获得了尾流速度轮廓. Ren等[14]利用PIV得到不同相位的扑翼尾流速度场和涡量场. PIV粒子在水槽中比在风洞中散布更均匀, 因而水槽中能够测得更稳定更精细的涡结构. Lua等[15]在水槽中用PIV探究了二维摆动翼与涡的相互作用, 解释了扑翼翻转与升力增减之间的关系.宫武旗等[16]利用水洞和PIV探究了两串列扑翼的相位差对平均推力的影响机理.
扑翼的运动流场动力三者互为因果, 研究中对扑翼复杂流场物理特性的认识还存在不足, 本文利用色流实验和PIV技术定性及定量地探究了单自由度扑翼近场尾流中脱落涡的结构运动轨迹和能量变化, 促进对扑翼脱落涡的理解, 并可作为数值仿真的参考依据.
1 实验模型与研究方法 1.1 实验设备实验在厦门大学航空流体&PIV实验室的多功能流体力学实验平台上完成, 主要使用了精密循环水槽拖曳台车和PIV流场测试系统.精密循环水槽整体布局如图 1所示, 水槽为水平回流开放式, 包括进口水箱整流段测试段出口水箱以及管道设施.测试段方形截面为500mm×500mm, 测试段长度为3000mm.环流水泵由数字变频仪调节, 水流速度范围为0~0.3m/s,分辨率为0.001m/s.

|
| 图 1 多功能精密循环水槽 Fig.1 Multifunctional precise circulating tank |
本文开展实验所采用的PIV系统组件的具体信息如表 1所示. PIV图像对应实际尺寸为200 mm×145 mm, 设置互相关分析的查问域(interrogation area)大小为32×32像素.被翼翅遮挡的流场通过图片掩模(mask)的方式去掉.通过自适应互相关算法(adaptive correlation)对原始图像进行处理得到速度分布, 再对速度进行旋度计算得到涡量分布.激光片光源与来流平行的光路布局能减小误差[17], 实验台在平行来流截面的速度测量误差约1%.
| 下载CSV 表 1 PIV系统组件参数 Tab.1 Component parameters of PIV system |
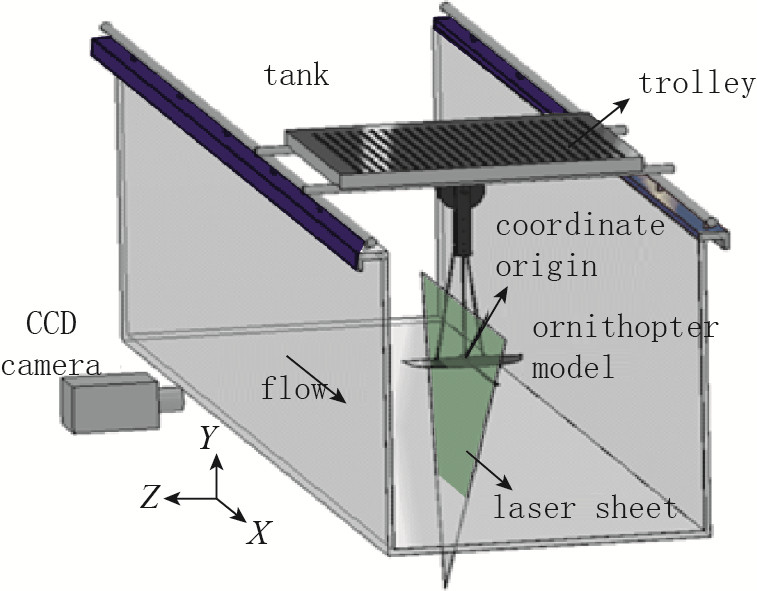
模型安装如图 2所示, 扑翼主体包括一对翅翼和中间的轴杆, 可实现挥拍幅度对称面频率和攻角的调节.轴杆的攻角即为扑翼的攻角.翅翼展开形状为半个椭圆, 展长为30cm, 根部弦长为10cm, 平均几何弦长为7.85cm.为了减小激光反射, 翅翼表面喷涂黑色哑光漆.翅翼安装在拖曳台车上, 位于水槽中央, 激光切面经过左侧翼, CCD高速摄像机位于左侧拍摄, 坐标系方向如图 2所示.
|
| 图 2 实验模型系统示意图 Fig.2 Schematic diagram of experimental system |
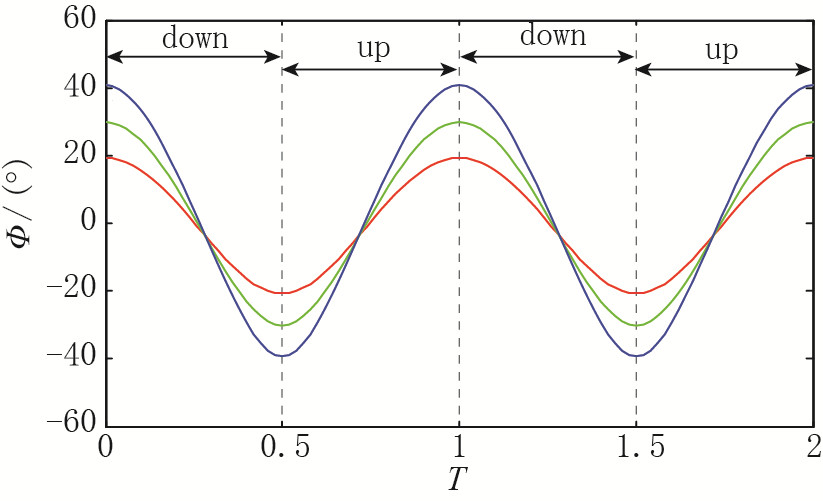
实验令上下扑对称, 来流速度扑动频率和扑动幅度可以改变.翅翼从上极点向下扑动至回到上极点的时间为一个周期, 这段时间设为无量纲周期时间T=1.扑动幅度不同时, 扑动角随时间的变化规律如图 3所示.以平均几何弦长为特征长度, 来流速度为特征速度的实验Reynolds数在3000~24000之间.
|
| 图 3 扑动角随时间的变化规律 Fig.3 Temporal variations of flapping angle |
扑翼相对于固定翼的一个重要特点就是能同时产生升力和推力[18].应用准定常叶元法对简化的扑翼模型进行了气动力生成机理分析.
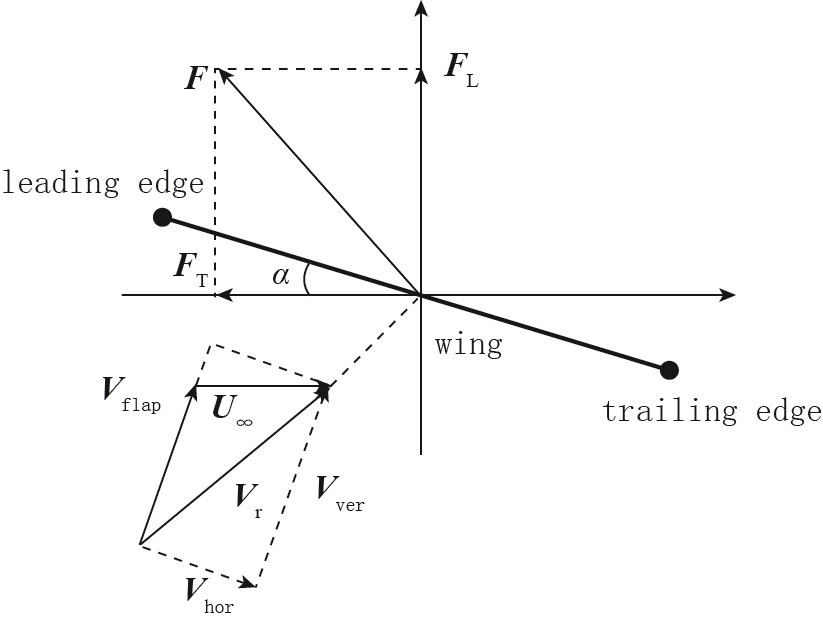
如图 4所示, 流场中低速匀直来流的速度为U∞, 扑翼攻角为α, 向下扑动时, 气流相对扑翼有垂直于翼面的速度Vflap, 因此气流相对扑翼的流动速度为Vr=U∞+Vflap, 由Kutta-Joukowski定理可知, 作用在扑翼上的气动力F方向垂直于合速度Vr, 指向前上方, 在垂直和水平方向上的分量FL, FT分别为扑翼的垂直升力和水平推力. Vr可以分解为平行于翼面的流速Vhor和垂直于翼面的矢量流速Vver, 可知其大小为:
|
| 图 4 扑翼的气动力示意图 Fig.4 Diagram of flapping wing aerodynamic forces |
下扑时:
上扑时:
Vver影响脱落涡能量大小, Vhor影响脱落涡的运动方向和脱落速度.从环量及静压来看, 由于整个流场环量守恒, 脱落涡的环量与扑翼上的环量等值反向.在正攻角时, Vver在下扑时比上扑时更大, 所以存在不同旋向脱落涡的能量差.一个周期内若脱落涡的平均环量是逆时针, 则扑翼上为平均顺时针环量, 因而在一个周期内产生了平均升力.从动能来看, 脱落涡排列为向后下方移动的反向Karman涡街, 尾流速度大于前行速度, 故产生前上方推力, 这同样可以分解为垂向升力和水平推力.脱落涡能量之和越大, 该推力就越大.值得注意的是, 简化的准定常分析能提供分析思路, 但与复杂非定常的真实流场会有一定的差异.
3 实验结果分析 3.1 扑翼脱落涡整体结构为更清晰直观地了解本模型扑翼的涡系整体结构, 首先进行色流显示实验.以攻角α=0°, 扑动幅度Φ=±10°, 频率f=0.4 Hz, 无来流和来流速度U∞=10 mm/s两种情况为例.上扑时产生下翼面涡, 下扑时产生上翼面涡, 因攻角为0°, 故下翼面涡与上翼面涡对称, 实验流场结果以上扑时下翼面涡的情况为例来展示.
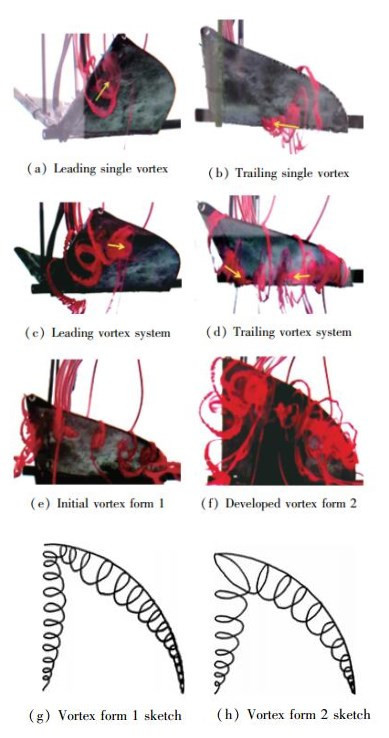
图 5为无来流时前后缘涡的发展情况. 图 5(a)和(b)分别展示前后缘单个涡的情况, 都是从边缘向内卷, 如箭头所示, 卷涡都存在朝向翼尖的展向运动, 因为翼尖处半径最大, 扑动时线速度大, 静压小, 吸引了涡向翼尖的展向运动. 图 5(c)所示的前缘涡系, 中部的涡较大, 翼尖和翼根处涡较小, 这是因为翼根处扑动线速度较小, 因此涡能量较低; 而翼尖处虽然线速度大, 但能形成压差的面积太小, 因此最初涡形态也较小, 同时, 翼尖处的涡有沿后缘向后运动的趋势. 图 5(d)展示了后缘涡系, 可见翼尖和翼根处的涡都有向中部某一点运动的趋势, 说明中部某处涡最大, 自身旋转速度大, 压力低, 吸引了周围的涡靠近, 同时观察发现这个最大的涡也在不断朝翼尖移动.如图 5(e)所示, 上扑初期和后期的前后缘涡系是两种形态, 初期呈中部涡最大的状态, 随后继续上扑, 展向流动充分, 后期形成翼尖涡最大的状态, 如图 5(f)所示. 图 5(g)和(h)对比描绘了早期中部涡最大的牛角型涡系及后期展向流动充分后翼尖涡最大的牛角型涡系.
|
| 图 5 U∞=0时脱落涡发展情况 Fig.5 Developing situations of shedding vortices at U∞=0 |
有来流时, 扑动产生的涡系发展情况与无来流时基本相同, 但存在脱落过程.如图 6所示, 从侧面观察涡系的发展, 整个过程前缘涡不断向翼尖运动, 汇聚到翼尖后与后缘涡一起脱落.上扑初期如图 6(a)所示, 后缘涡仍是中部较大的牛角型涡系; 后期如图 6(b)所示, 后缘涡在翼尖处最强, 伴随着汇聚的前缘涡随来流脱落, 在尾流中呈现形似圆柱的脱落涡系.

|
| 图 6 U∞=10mm/s时的脱落涡 Fig.6 hedding vortex system at U∞=10mm/s |
在扑动速度与来流速度之比合适的低速工况下, 展向流动充分, 前后缘涡将汇聚到翼尖后再脱落.由此可推测如果扑动速度与来流速度之比足够大(减缩频率k较大), 前缘涡在尚未充分展向流动且流向后移仍较小时, 扑翼就已经改变方向, 此时观察到的将是稳定的前缘涡, 即前缘涡失速延迟现象.反之如果扑动很慢(减缩频率k较小), 展向流动尚未充分时涡就已经脱落.
3.2 近场尾流中脱落涡的运动规律虽然涡的结构为三维, 但在靠近翼根的地方, 涡的旋转速度主要在流向平面, 一个近轴平面上的脱落涡的发展情况一定程度上能反映整体涡系的能量变化.因此, 选择激光切面为距离翼根4 cm的流向XY平面.
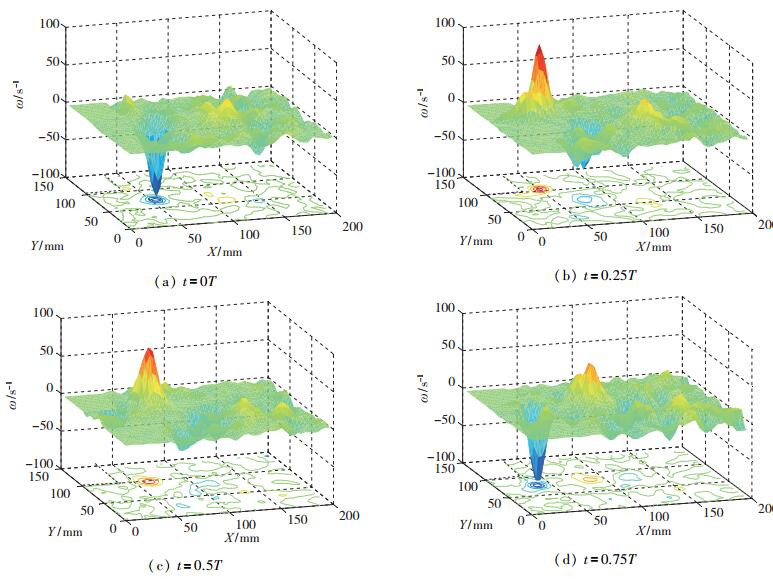
图 7展示翅翼从上极点(t=0T)开始的一个周期内近场尾流中的涡量分布, 其扑动幅度Φ=±30°, 来流速度U∞=120mm/s, 扑动频率f=0.796Hz, 减缩频率k=1.636, 0T至0.5T为下扑,0.5T至1T(0T)为上扑.图中左上方虚线内涡量为0的区域为翅翼遮光区.按规定涡量ω逆时针为正, 顺时针为负, 涡量最大处为逆时针涡的涡心, 最小处为顺时针涡心.
|
| 图 7 切面上脱落涡一周期内涡量分布(Φ=±40°, U∞=120mm/s, k=2.47) Fig.7 Vorticity distributions of shedding vortex in the sheet within a period(Φ=±40°, U∞=120mm/s, k=2.47) |
从图 7可以看出, 在上极点时, 存在一个上周期脱落了的顺时针涡, 翼边几乎没有涡, 经过0.25T的下扑, 翼边一个逆时针涡逐渐增强, 该涡到达下极点时基本脱落; 而上扑过程则是翼边出现逐渐增强的顺时针涡, 在到达上极点时基本脱落.涡脱落以后继续向下游移动, 因摩擦和碰撞涡量消散很快, 第一对脱落涡离翅翼最近, 作用最大, 且涡量比后方的涡大很多, 因此后文只分析近场尾流中的第一对脱落涡.
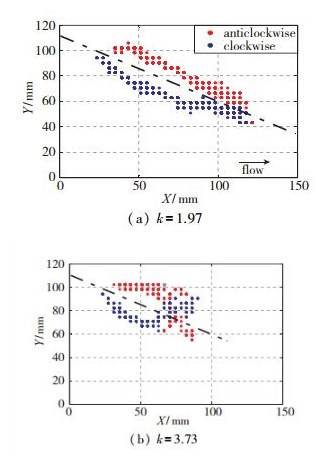
涡心能反映脱落涡的主要特征, 图 8对比了振幅Φ=±30°, 来流速度U∞=90 mm/s时, 减缩频率分别为k=1.97和k=3.73的两组实验时上下扑两阶段合成的涡心运动轨迹.在最靠近翅翼处, 逆时针涡在上方, 顺时针涡在下方, 呈反Karman涡街状, 注意两涡是交替出现的.顺时针涡和逆时针涡的运动轨迹大致呈弧形对称, 对称轴仰角约为28°, 比扑翼的24°攻角略大.反Karman涡街周期平均力的方向与沿对称轴斜向上方向大体一致, 略高于攻角.减缩频率k=1.97时, 两涡轨迹平行度更高; 而减缩频率k=3.73时, 弧度较大.两涡可穿越到轴线另一侧, 原因是翅翼附近新产生的转速较高的涡诱导了离翅翼较远的能量已耗损的涡绕其旋转, 频率越高, 两涡转速差越大, 诱导旋转越明显.
|
| 图 8 一周期内涡心运动轨迹(Φ=±30°, U∞=90mm/s) Fig.8 Trace of the vortex core within a period(Φ=±30°, U∞=90mm/s) |
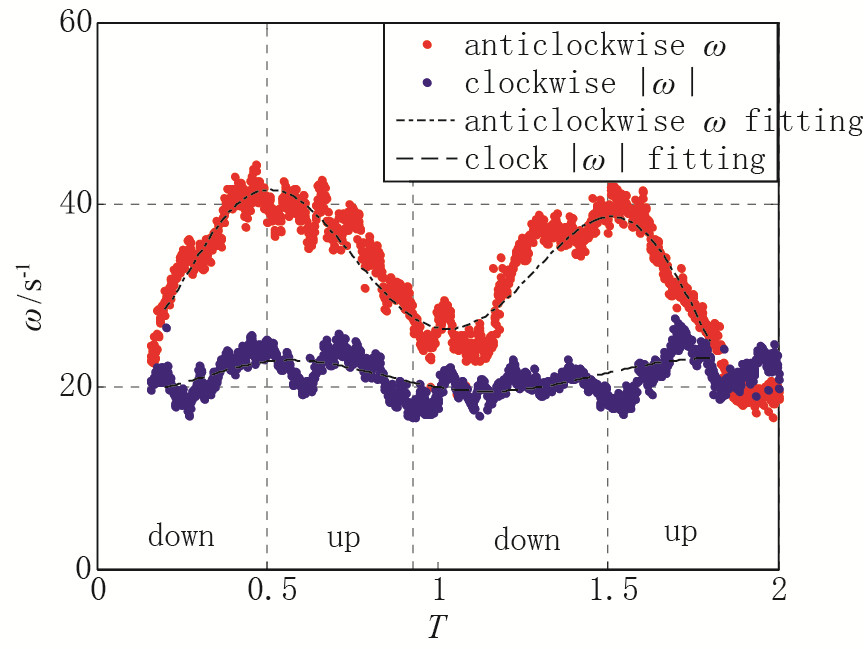
涡心涡量在一定程度上能反应涡的能量大小. 图 9以振幅Φ=±30°, 来流速度U∞=90 mm/s, 减缩频率k=1.97为例展现涡心涡量的变化.
|
| 图 9 Φ=±30°, k=1.97时涡心涡量变化 Fig.9 Variations of vortex core vorticity when Φ=±30°, k=1.97 |
同时用6阶多项式对涡心涡量变化进行拟合, 可以更清晰地看到主要规律.此时扑动频率较低, 下扑逆时针涡明显强于上扑顺时针涡, 且逆时针涡能量增强和损耗的波动大, 而顺时针涡变化不大.原因是低频率时垂直于翼面方向上的相对流动速度Vver在下扑时比上扑时更大.因此在产生涡的阶段, 下扑逆时针涡比上扑顺时针涡增强更快; 而在脱落后的耗损阶段, 转速更高的逆时针涡在摩擦力的作用下自身能量损耗很快, 同时给顺时针涡传递了旋转能量, 因此逆时针涡耗损也比顺时针涡快.
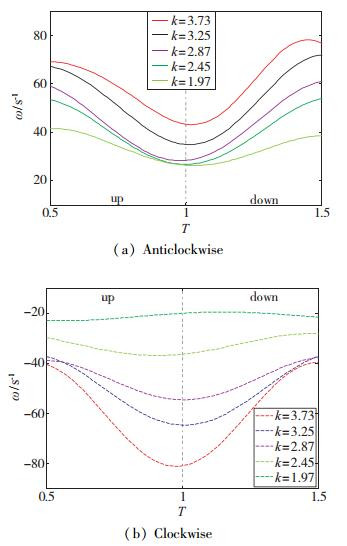
如图 10所示, 将不同减缩频率时的涡心能量变化都用6阶以上多项式曲线拟合进行对比.由图可见, 随着减缩频率增加, 逆时针涡和顺时针涡的涡心涡量都变大, 增强和衰减都更明显, 一个周期内的最大绝对值都在上下扑极点附近达到.同时可以发现, 上扑顺时针涡相比于下扑逆时针涡的能量随减缩频率的增加而增长更快.分析认为主要有两方面原因, 一是频率增大后, 扑动速度Vflap增大, 因此气流相对于翼面的垂直速度Vver在上下扑时的差距变小, 二是因为上扑时翅翼向后运动, 与涡运动方向一致, 因此上扑翅翼对涡的作用时间较长, 而下扑时翅翼作用时间范围较短, 频率越高上下扑时的翅翼作用时间范围差异越大.因此上扑脱落涡相比于下扑脱落涡, 在低频率时更小, 但高频率时增强更快.
|
| 图 10 不同减缩频率k时涡心涡量变化规律 Fig.10 Vorticity variations of vortex core at various k |
脱落涡有一定半径大小, 半径大的地方与周围流场充分接触, 涡量不断产生和消耗.某区域内的环量Γ是涡通量, 能体现脱落涡的全部能量.根据Stokes公式, 环量为
| $ \varGamma = \int\limits_l \mathit{\boldsymbol{V}} \cdot {\rm{d}}\mathit{\boldsymbol{l = }}\iint\limits_s {\nabla \times \mathit{\boldsymbol{u}}} \cdot {\rm{d}}s = \iint\limits_s \mathit{\boldsymbol{\omega }} \cdot {\rm{d}}s $ | (1) |
环量与涡量正负规定相同, 逆时针为正, 顺时针为负.统计环量的范围是以第一个涡涡心为圆心, 半径R < 40mm内的全部正涡量, 或全部负涡量.如此既能充分覆盖第一个涡, 同时又不会受上一个脱落涡影响.
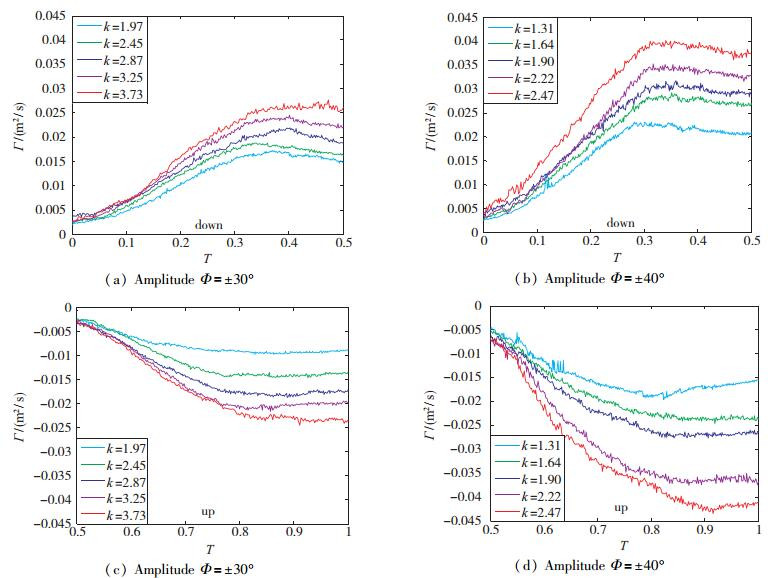
图 11以Φ=±30°和Φ=±40°为例, 展示不同减缩频率时脱落涡环量在周期内的变化规律.可知下扑和上扑环量最大值出现在0.3T~0.4T和0.8T~0.9T之间, 也就是在到达极点前的0.2T~0.4T之间.这与涡心涡量最大值在极点处到达不同, 是因为脱落涡外围摩擦损耗大, 越接近极点, 扑翼速度越慢, 翅翼扑动传递的能量小于损耗的能量, 因此环量最大值在极点前出现.环量随减缩频率的增大而增大, 且扑动幅度越大, 环量越大.
|
| 图 11 不同减缩频率k时脱落涡环量变化规律(U∞=120mm/s, Φ=±30°, Φ=±40°) Fig.11 Circulation variations of vortex at various k (U∞=120mm/s, Φ=±30°, Φ=±40°) |
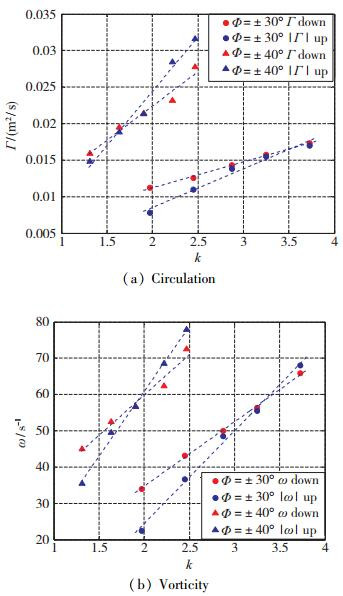
下扑半周期产生逆时针脱落涡, 上扑半周期产生顺时针脱落涡, 对不同减缩频率下产生阶段半周期内涡的平均环量和涡心涡量进行统计并拟合.如图 12所示, 下扑时逆时针涡由红色符号表示, 上扑时顺时针涡的涡量和环量为负值, 对其取绝对值, 由蓝色符号表示.半周期内产生的涡的平均涡心涡量和环量变化规律相似, 在此主要分析环量.上下扑脱落涡的环量绝对值都随减缩频率的增大而增大, 所以反Karman涡街提供的前上方的推力增大, 该推力包括的垂直升力和水平推力分量也都增大.
|
| 图 12 产生涡的半周期内平均涡心涡量和环量值 Fig.12 Average vortex core vorticity and circulation within half cycle when producing vortices |
当减缩频率低的时候, 上扑顺时针环量小于下扑逆时针环量, 随着减缩频率的增加, 上扑时的环量增速更快, 会大于下扑时的环量.因为频率越高, 上下扑时气流相对翅翼的垂直运动速度Vver越接近, 而上扑翅翼对涡的作用时间相比于下扑时越长.因此减缩频率越大, 环绕扑翼的顺时针环量则越小, 静压带来的垂直升力变小甚至为负.存在一个减缩频率的临界点kcr, 使得在该切面, 上下扑脱落的环量值相当, 无平均升力.在当前切面, Φ=±30°时, kcr约为1.7; Φ=±40°时, kcr约为3.5.由此可推测, 要得到合适的垂直升力和水平推力, 需要平衡式选择特定的减缩频率.
振幅对涡的能量也影响显著.当减缩频率相当时, 例如k为2时, Φ=±40°和Φ=±30°的两涡平均环量绝对值约为0.023和0.010, 平均涡心涡量绝对值约为60和30. k为2.5时, Φ=±40°和Φ=±30°的两涡平均环量绝对值约为0.03和0.012, 平均涡心涡量绝对值约为75和40.由此可知, k=2~2.5范围内, 涡的平均能量在Φ=±40°时大约是Φ=±30°时的两倍.并且由趋势线可见, k越大, 振幅的影响越大.
4 结论(1) 扑翼脱落涡结构因展现流体充分性的不同存在两种涡系形态, 展向流动未充分时的中部涡最大的牛角型涡系和展向流动充分时的翼尖涡最大的牛角型涡系.
(2) 上下扑时翅翼交替产生顺时针和逆时针脱落涡, 两涡运动轨迹近似弧形对称, 对称轴的仰角略大于扑翼的攻角.扑动频率越快, 轨迹弧度越大.
(3) 上下扑时第一对脱落涡的涡心涡量最大值都在上下扑极点处达到, 环量最大值出现在到达极点前的0.2T~0.4T之间.
(4) 上扑和下扑半周期内脱落涡的平均环量都随减缩频率的增大而增大, 频率较低的时候下扑环量大于上扑环量, 频率较高的时候则是上扑环量大于下扑环量.该切面存在一个上下扑环量相当的减缩频率临界点kcr, 振幅Φ=±30°时, kcr约为1.7;振幅Φ=±40°时, kcr约为3.5.
(5) 振幅对涡的能量影响显著, 当减缩频率k=2~2.5时, 涡的平均能量在振幅Φ=±40°时大约是Φ=±30°时的两倍, k越大则振幅影响越大.
| [1] |
Taha H E, Hajj M R, Nayfeh A H. Flight dynamics and control of flapping-wing MAVs: a review[J]. Nonlinear Dynamics, 2012, 70(2): 907-939. DOI:10.1007/s11071-012-0529-5 |
| [2] |
杨文青, 宋笔锋, 宋文萍, 等. 仿生微型扑翼飞行器中的空气动力学问题研究进展与挑战[J]. 实验流体力学, 2015, 29(3): 1-10. Yang W Q, Song B F, Song W P, et al. The progress and challenges of aerodynamics in the bionic flapping-wing micro air vehicle[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(3): 1-10. (in Chinese) |
| [3] |
马宏伟, 毕树生, 蔡月日, 等. 胸鳍摆动推进模式机器鱼深度控制[J]. 北京航空航天大学学报, 2015, 41(5): 885-890. Ma H W, Bi S S, Cai Y R, et al. Depth control of robotic fish propelled by oscillating paired pectoral fins[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5): 885-890. (in Chinese) |
| [4] |
Weisfogh T. Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production[J]. Journal of Experimental Biology, 1973, 59(1): 169-230. |
| [5] |
Ellington C P, Berg C V, Willmott A P, et al. Leading-edge vortices in insect flight[J]. Nature, 1996, 384(6610): 626-630. DOI:10.1038/384626a0 |
| [6] |
Dickinson M. The effects of wing rotation on unsteady aerodynamic performance at low Reynolds numbers[J]. Journal of Experimental Biology, 1994, 192(4): 179-206. |
| [7] |
Dickinson M H, Lehmann F O, Sane S P. Wing rotation and the aerodynamic basis of insect flight[J]. Science, 1999, 284(5422): 1954-1960. DOI:10.1126/science.284.5422.1954 |
| [8] |
Katz J, Plotkin A. Low-speed aerodynamics[M]. Cambridge: Cambridge University Press, 2001: 87-123.
|
| [9] |
王晓欣. 昆虫扑翼悬停飞行尾涡影响研究[D]. 北京: 清华大学, 2012: 10-12. Wang X X. Study on the wake vortex influence in insect flapping hovering flight[D]. Beijing: Tsinghua University, 2012: 10-12(in Chinese). |
| [10] |
Birch J M, Dickinson M H. The influence of wing-wake interactions on the production of aerodynamic forces in flapping flight[J]. Journal of Experimental Biology, 2003, 206(13): 2257-2272. DOI:10.1242/jeb.00381 |
| [11] |
Ohmi K, Coutanceau M, Loc T P, et al. Vortex formation around an oscillating and translating airfoil at large incidences[J]. Journal of Fluid Mechanics, 1990, 211(3): 37-60. |
| [12] |
Bomphrey R J. Application of digital partical image velocimetry to insect aerodynamics: measurement of the leading-edge vortex and near wake of a hawkmoth[J]. Experiments in Fluids, 2006, 40: 546-554. DOI:10.1007/s00348-005-0094-5 |
| [13] |
Parker K, Ellenrieder K D, Soria J. Using stereo multigrid DPIV (SMDPIV)measurements to investigate the vortical skeleton behind a finite-span flapping wing[J]. Experiments in Fluids, 2005, 39(2): 281-298. DOI:10.1007/s00348-005-0971-y |
| [14] |
Ren H, Wu Y, Huang P G. Visualization and characterization of near-wake flow fields of a flapping-wing micro air vehicle using PIV[J]. Journal of Visualization, 2013, 16(1): 75-83. DOI:10.1007/s12650-012-0152-z |
| [15] |
Lua K B, Zhang X H, Lim T T, et al. Effects of pitching phase angle and amplitude on a two-dimensional flapping wing in hovering mode[J]. Experiments in Fluids, 2015, 56(2): 1-22. |
| [16] |
宫武旗, 贾博博, 席光. 两串列扑翼的相位差对平均推力影响机理的实验研究[J]. 力学学报, 2015, 47(6): 1017-1025. Gong W Q, Jia B B, Xi G. An experimental study on the influence of the phase difference on the mean thrust of two plunging wings in tandem[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(6): 1017-1025. DOI:10.6052/0459-1879-14-378 (in Chinese) |
| [17] |
曹永飞, 顾蕴松, 程克明. 垂直于流向的截面中2D-PIV测量误差分析[J]. 实验流体力学, 2014(6): 66-72. Cao Y F, Gu Y S, Cheng K M. Analysis of the measurement error in the cross section perpendicular to flow using 2D-PIV[J]. Journal of Experiments in Fluid Mechanics, 2014(6): 66-72. (in Chinese) |
| [18] |
昂海松, 曾锐, 段文博, 等. 柔性扑翼微型飞行器升力和推力机理的风洞试验和飞行试验[J]. 航空动力学报, 2007, 22(11): 1838-1845. Ang H S, Zeng R, Duan W B, et al. Aerodynamic experimental investigation for mechanism of lift and thrust of flexible flapping-wing MAV[J]. Journal of Aerospace Power, 2007, 22(11): 1838-1845. DOI:10.3969/j.issn.1000-8055.2007.11.010 (in Chinese) |



