2. 中国科学院大学工程科学学院,北京 100049
2. School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China
旋流燃烧器是航空发动机燃烧室的核心部件之一, 精确诊断旋流火焰温度场的二维分布对于发动机燃烧机理、热声振荡、形态转变等研究具有重要意义[1-3].燃烧室内部旋流、回流的复杂流场结构, 特别是燃烧状态下旋流火焰为高温湍流燃烧, 环境更加恶劣, 使得精确测量旋流火焰二维温度场极为困难.近年来, 以可调谐激光吸收光谱技术(tunable diode laser absorption spectroscopy, TDLAS)为代表的非接触式光谱测量方法因具备对流场多参数实时诊断的能力和对流场无干扰的优点, 已成为国际上燃烧诊断领域的发展热点[4-8].
TDLAS技术是沿光程的积分测量, 即获得的是沿光程的平均值, 这不能反映实际的具有较大温度梯度及浓度梯度的流场状态, 而气流参数的二维截面分布特征对于研究燃烧组织和放热分布才更有意义.如何提高TDLAS的空间分辨能力, 已成为该光谱技术研究的前沿问题之一[9]. TDLAS结合层析成像术是提高TDLAS空间分辨能力, 实现二维断面测量的主要技术途径(tunable diode laser absorption tomography, TDLAT).根据层析成像术的具体实现方法TDLAT又可分为:优化非正交光路+双波长/单波长吸收测量方法[10]; 平行束/扇束+双波长吸收测量[11]; 正交光路+多光谱光源, 亦被称为HT(hyperspectral tomography)[12-13].前两种方法都需要大量的吸收光路(数十至数百), 这一方面增加了测量系统的复杂性, 减弱了其实用性; 另一方面, 多光束方法对于旋流燃烧器这种中小尺寸的复杂实验台, 存在光路架设空间不足, 壁面窗口奇缺的障碍, 在具体的光学系统设计中难度极大.而TDLAS-HT技术实验系统相对简单, 具有极高的时间分辨率, 在旋流燃烧诊断领域极具应用潜力.
早期的TDLAS-HT技术采用Fourier锁模光纤激光器取代传统TDLAS技术多采用的DFB激光器, 从而可实现数十kHz的频率下扫过约30 nm波长范围[13].但该型激光器价格昂贵且技术不成熟, 例如其激光波长稳定性和线性度较DFB激光器较差.除此之外, 由于光源的高频和扫描范围限制, 该TDLAS-HT系统可选谱线的低能级能量分布不够宽泛, 再耦合频率扫描速率、探测器响应、采样频率等硬件参数的匹配问题, 导致基于Fourier锁模光纤激光器的TDLAS-HT技术难以获得较优的谱线积分吸收率, 吸收数据的原始信噪比要弱于基于DFB激光的TDLAS技术.
本文基于TDLAS-HT理念, 使用4台DFB激光器分时耦合建设多光谱光源克服现有HT技术不足, 4台DFB激光器分别针对H2O分子7 185.6,7 444.3,6 807.8和7 466.3 cm-1这4条吸收谱线, 采用分时-直接吸收探测策略, 系统测量频率2.5 kHz, 采用13×13路正交光路分布(空间分辨率为7 mm), 建设TDLAS-HT测量系统.采用模拟退火算法进行数据重建, 分别反演计算4条吸收线的吸收率和吸收比分布, 进而得到甲烷/空气旋流火焰的二维温度场分布.最后结合数值模拟对该TDLAS-HT系统结果和反演算法精度进行分析.
1 基本原理及重建算法设计 1.1 TDLAS测量原理一束频率为v的单色激光通过待测流场, 激光光子被待测组分吸收, 透射光强I和入射光强I0满足Beer-Lambert关系式
| $ {\left( {I/{I_0}} \right)_v} = \exp \left( { - {K_v} \times L} \right) $ |
其中, Kv为吸收系数, L为吸收长度.其中吸收系数Kv为水蒸气分压PH2O, 吸收谱线线强度S(T), 线型函数ϕ(v)的函数.
| $ {K_v} = {P_{{{\rm{H}}_2}{\rm{O}}}}S(T)\phi (v) $ |
线型函数满足ϕ(v)归一化条件, ∫ϕ(v)dv≡1.吸收谱线线强度S(T)为温度T的函数.
| $ \begin{array}{*{20}{c}} {S(T) = S\left( {{T_0}} \right)\exp \left[ { - \left( {\frac{{hc}}{k}} \right)\left( {E_1^{\prime \prime } - E_2^{\prime \prime }} \right)\left( {\frac{1}{T} - \frac{1}{{{T_0}}}} \right)} \right] \times }\\ {\frac{{Q\left( {{T_0}} \right)}}{{Q(T)}}\left( {\frac{{{T_0}}}{T}} \right)\frac{{\left[ {1 - \exp \left( { - \frac{{hc{v_0}}}{{kT}}} \right)} \right]}}{{\left[ {1 - \exp \left( { - \frac{{hc{v_0}}}{{k{T_0}}}} \right)} \right]}}} \end{array} $ |
其中, T0为参考温度, h为Planck常数, E″为低能级能量, k为Boltzmann常数, c为真空中光速, Q(T)为配分函数.定义积分吸收率A为
| $ A = \int {{K_v}} \cdot L{\rm{d}}v = {P_{{{\rm{H}}_2}{\rm{O}}}} \cdot S(T) \cdot L $ |
本文采用模拟退火算法进行重建, 其具体表述参阅文献[14].重建程序的设计中, 首先要构建须优化的目标函数.根据吸收光谱原理, 波长为λi的吸收谱线在非均匀流场的积分吸收率Aλi表达式为
| $ {A_{{\lambda _i}}} = \int_{{L_1}}^{{L_2}} S \left( {T(l), {\lambda _i}} \right) \cdot {P_{{{\rm{H}}_2}{\rm{O}}}}(l) \cdot {\rm{d}}l $ |
S为在沿光程某位置l处温度为T的谱线强度; 同理, PH2O(l)为某位置l处温度为T时刻的水蒸气分压.
将实验获得所有光束、所有波长的Aλi的集合定义为实验吸收率分布Pm(Lj, λi), 当根据假设温度T和水蒸气浓度PH2O分布计算得到的Pc(Lj, λi)与Pm(Lj, λi)相差最小时, 将该假设分布认为是真实分布.而上述相差即为理想化的目标优化函数, 可表达为
| $ DA\left( {T, {P_{{{\rm{H}}_2}{\rm{O}}}}} \right) = \sum\limits_{j = 1}^J {\sum\limits_{i = 1}^I {{{\left( {{P_{\rm{m}}}\left( {{L_j}, {\lambda _i}} \right) - {P_{\rm{c}}}\left( {{L_j}, {\lambda _i}} \right)} \right)}^2}} } $ |
式中, i和j分别为波长和光束的序号.
在实际反演计算中, 须加入平滑度作为先验条件, 用于改善目标优化函数这一病态问题的求解, 平滑度定义为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;{R_{\rm{T}}}(T) = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left( {\frac{9}{8}{T_{m, n}} - \frac{1}{8}\sum\limits_{{k_1} = m - 1}^{m + 1} {\sum\limits_{{k_2} = n - 1}^{n + 1} {{T_{{k_1}, {k_2}}}} } } \right)}^2}} } \\ {R_P}\left( {{P_{{{\rm{H}}_2}{\rm{O}}}}} \right) = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left( {\frac{9}{8}{P_{{{\rm{H}}_2{\rm{O}}}{_{m, n}}}} - \frac{1}{8}\sum\limits_{{k_1} = m - 1}^{m + 1} {\sum\limits_{{k_2} = n - 1}^{n + 1} {{P_{{{\rm{H}}_2{\rm{O}}}{_{{k_1}, {k_2}}}}}} } } \right)}^2}} } \end{array} $ |
待优化的目标函数可表述为
| $ F\left( {T, {P_{{{\rm{H}}_2}{\rm{O}}}}} \right) = DA(T, X) + {\gamma _{\rm{T}}}{R_{\rm{T}}}(T) + {\gamma _{{P_{{{\rm{H}}_2{\rm{O}}}}}}}{R_{{P_{{{\rm{H}}_2}{\rm{O}}}}}}\left( {{P_{{{\rm{H}}_2}{\rm{O}}}}} \right) $ |
式中, γT为温度平滑系数, γPH2O为分压平滑系数.
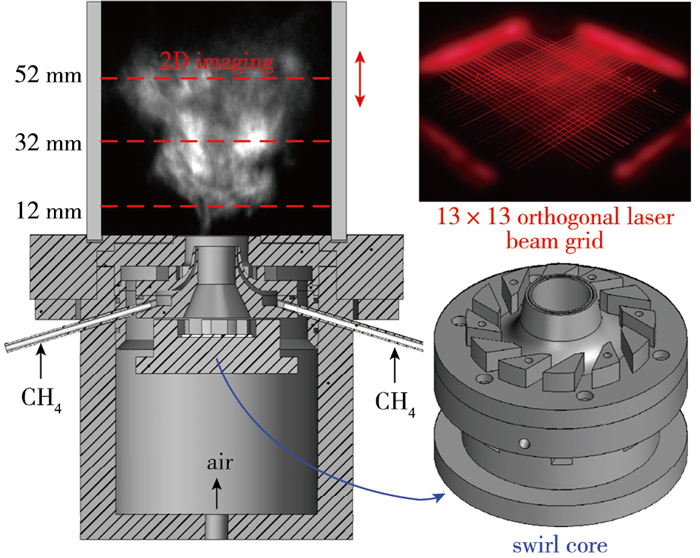
2 实验设备旋流燃烧器及TDLAS-HT系统13×13路正交光路分布如图 1所示.干燥空气分为两路, 一路经旋流器核顶部叶片与腔体之间的通道从最外层喷嘴流出, 另一路经旋流器核的侧边叶片从最内侧喷流出, 两路空气经由叶片并流出时都会产生切向速度, 从而产生旋流.甲烷由两路细管提供, 出口是外径18 mm,内径15 mm的同心环.空气、甲烷从各自喷嘴出来后进入由四面石英玻璃组成的燃烧室燃烧, 窗口均为宽85 mm,高110 mm. 图 1右上角给出本文TDLAS-HT系统13×13正交光路激光组网照片, 该网格光路通过位移机构实现高度调整, 从而实现旋流火焰出口高度不同位置截面的二维吸收光谱测量, 如图 1所示, 本实验对旋流燃烧器某典型工况下旋流火焰出口高度分别为12,32,52 mm处截面进行测量, 燃烧器工况见表 1.
|
| 图 1 旋流燃烧器及TDLAS-HT二维光路布置示意图 Fig.1 Model combustor and 13×13 orthogonal laser beams |
| 下载CSV 表 1 流量工况 Tab.1 Parameters of the four flames investigated |
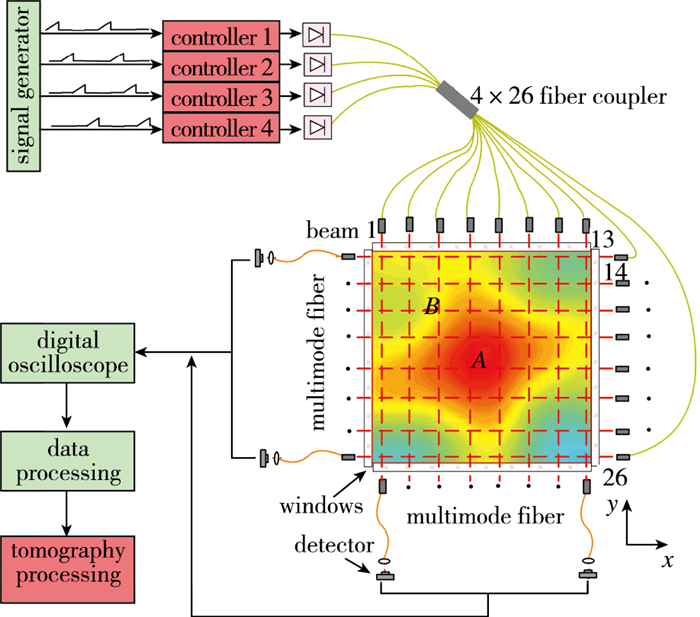
TDLAS-HT系统如图 2所示, 1台信号发生器产生4路脉冲锯齿波, 每路锯齿波频率均为10 kHz, 两两相位差90°, 同时调制4台激光控制器, 使4台DFB激光器1, 2, 3, 4分别输出7 185.6, 7 444.3, 6 807.8和7 466.3 cm-1波长的激光, 且两两激光不会叠加, 最终组合而成总调制频率为2.5 kHz的4波长激光器, 实现了HT方法的多光谱光源制备, 4路吸收波长光谱常数取自HITRAN2008数据库, 见表 2.合成HT光源由4×26光纤分路器分为26路, 每路光纤末端均装有准直器, 保证输出光束直径小于1 mm.光路1-13与光路14-26分别穿过燃烧室出口设定截面且垂直布置, 实现13×13的正交光路分布, 光束两两间隔均为7 mm, 即空间分辨率为7 mm.穿过流场的26个光束由收集器收集到多模光纤内, 分别导到26个InGaAs光电探测器, 转换为电压信号, 进而由高速数据采集仪存储, 数据整理后经反演运算程序, 重建火焰断面的温度场二维分布.
|
| 图 2 TDLAS-HT层析成像术的旋流火焰诊断示意图 Fig.2 Optical layout of the TDLAS-HT system |
| 下载CSV 表 2 4路吸收波长及其光谱常数 Tab.2 Spectroscopic line parameters used in the current study |
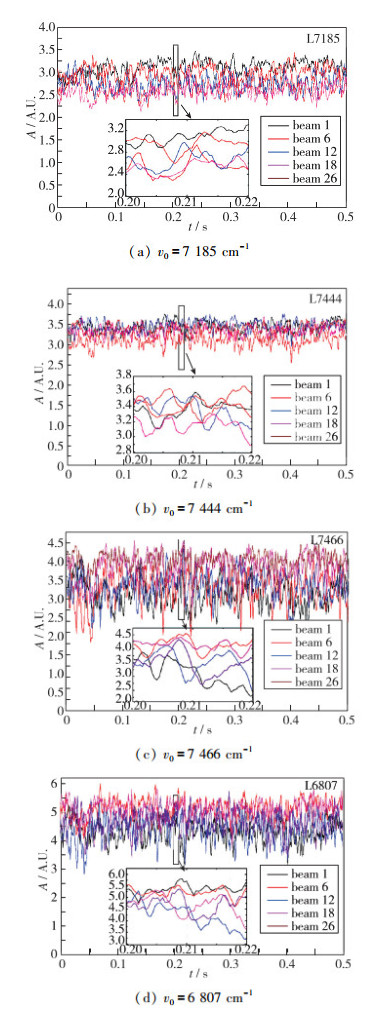
该TDLAS+HT实验方案已在平面炉及超燃直连台上验证其可行性[15-16], 值得一提的是, 在测量环境较为恶劣的超燃直连台获得的原始信号信噪比与平面炉实验中的相当, 验证该算法具备较高的重建精度和空间分辨率. 图 3为A工况下, 32 mm高度截面处x方向3路(1, 6, 12)和y方向两路(18, 26)的原始积分吸收率随时间变化, 每一路波长含有4路波长的吸收率信息.由图 3可见, 每路吸收波长吸收率信号均有明显的高低波动, 这代表火焰的振荡信息. 图 3中的局部放大图时间间隔为20 ms, 此时间段内吸收率的高低脉动有数个峰值, 一方面表明该方法具有足够高的测量频率, 可精确捕捉燃烧火焰振荡频率, 另一方面直观反映了旋流火焰的振荡燃烧特征.将26路光路中所包含4路波长的吸收率信息代入反演程序, 即可获得测量截面的温度场和水蒸气浓度二维分布.
|
| 图 3 32 mm高度截面x-1, x-6, x-12及y-18, y-26共5路波长对应4个波长吸收率的时间变化曲线 Fig.3 Absorbance evolutions of the four absorption lines corres-ponding to the five light paths(x-1, x-6, x-12, y-18 and y-26) at the 32 mm height |
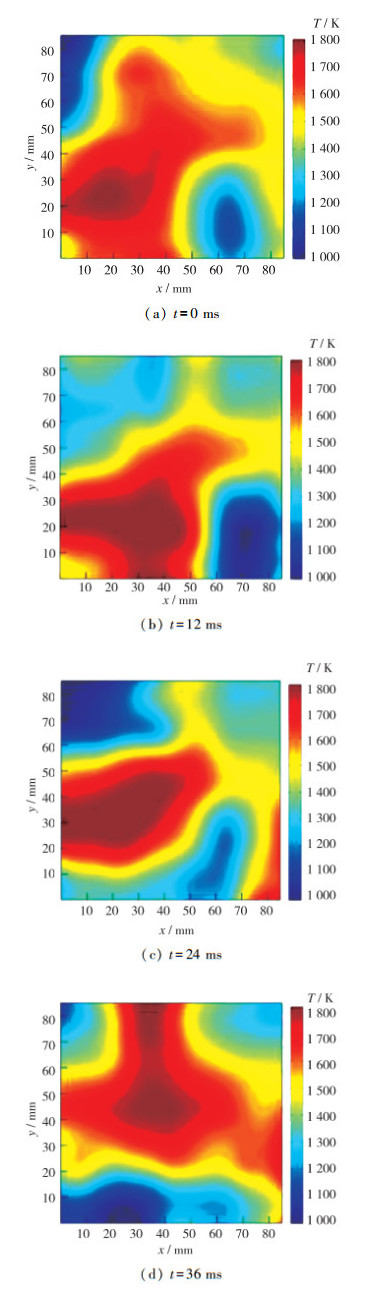
图 4展示了旋流火焰32 mm高度截面分别在0, 12, 24和36 ms时刻的温度场反演结果.由图 4可见, 12 ms时刻的燃烧核心区较0 ms时刻明显增大, 在24及36 ms时刻, 燃烧核心区出现明显的移动.上述结果表明, 该TDLAS-HT技术可清晰捕捉燃烧核心区成长及移动的动态信息, 温度场测量结果直观反映了旋流火焰的燃烧振荡.
|
| 图 4 旋流火焰32 mm高度不同时刻处二维温度场分布 Fig.4 Two-dimensional temperature fields at different times for 32 mm height |
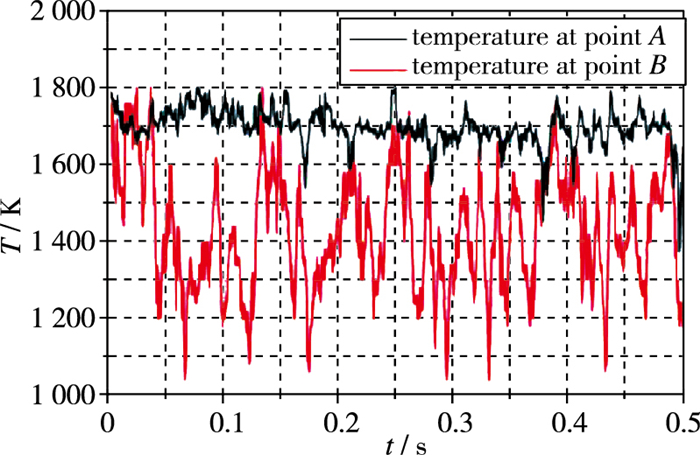
图 5给出32 mm高度截面A, B两点不同位置处温度的定量测量结果(见图 2, A点位于测量平面中心, B点偏离测量平面中心, 位于窗口与A点之间).观察图 5, 一方面, 在远离中心点处的B点温度有着较大幅度的波动, 这符合旋流火焰的燃烧振荡特性, 即燃烧核心区在不断移动; 另一方面, B处温度在该0.5 s测量周期内要整体低于中心点温度, 说明燃烧核心区虽然不停地移动, 但其区域范围基本覆盖住中心测点, 且从平均的时间尺度来看, 32 mm高度测量平面中心处温度要高于四周.
|
| 图 5 A, B两点处温度的时间变化 Fig.5 Evolution of the temperatures at two points A and B |
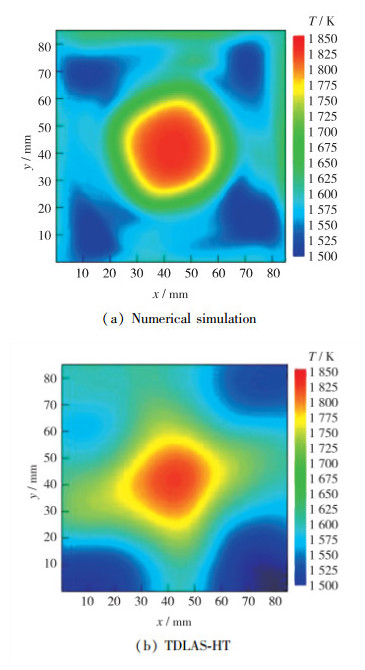
图 6展示了32 mm高度截面温度场在2 s内的平均值的数值计算(大涡模拟方法)和二维吸收光谱重建的对比.从图 6中可以看出, 温度场分布轮廓较为一致, 均为中心处最大温度, 约为1 700 K, 这也与图 5中给出结论一致; 四角温度最低, 约为1 300 K.上述结果说明重建结果较好地反映了旋流火焰的温度场的二维分布.
|
| 图 6 数值计算与重建结果温度场比较 Fig.6 Comparison of the numerical simulation with TDLAS-HT result |
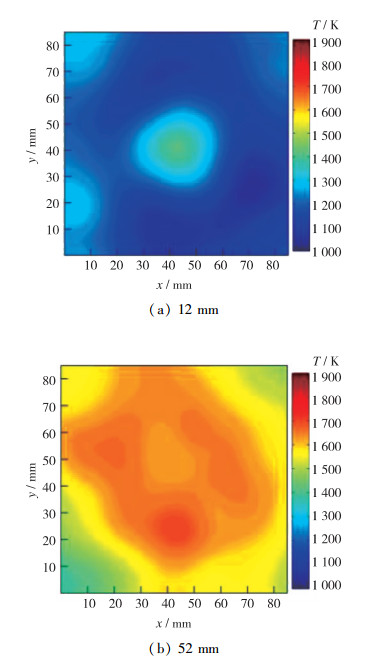
图 7展示了在12和52 mm高度截面上温度重建结果, 在12 mm高度, 核心燃烧区仅有约10 mm直径, 四角有高温区, 与高温回流区相对应; 在52 mm高度, 火焰面已基本充满整个测量截面, 说明燃烧放热已经基本完成.
|
| 图 7 旋流火焰12,52 mm高度下重建温度场 Fig.7 Two-dimensional temperature fields for 12 and 52 mm height |
本研究基于4台DFB激光器采用分时-直接吸收探测策略制备多光谱光源, 采用13×13路正交光路分布(空间分辨率为7 mm), 建设TDLAS-HT测量系统, 数据重建采用模拟退火算法.实现了旋流燃烧器某典型工况下不同高度燃烧截面二维温度场的动态分布测量, 经与数值模拟结果对比, 证明反演算法精度和重建结果可靠.该方法的应用一方面为研究旋流火焰燃烧机理开辟了新的技术手段, 另一方面可对真实航空发动机研究提供非常丰富的燃烧信息:
(1) 温度的二维截面分布能够显示燃烧影响范围, 为优化燃料喷注压力提供定量信息;
(2) 温度截面分布结合水蒸气浓度的平均值能够评估整体燃烧效率;
(3) 旋流火焰燃烧振荡可评估发动机燃烧稳定性.
| [1] |
Weigand P, Meier W, Duan X R, et al. Investigations of swirl flames in a gas turbine model combustor:Ⅰ. flow field, structures, temperature, and species distributions[J]. Combustion and Flame, 2006, 144(1/2): 205-224. |
| [2] |
See Y C, Ihme M. Large eddy simulation of a partially-premixed gas turbine model combustor[J]. Proceedings of the Combustion Institute, 2015, 35(2): 1225-1234. DOI:10.1016/j.proci.2014.08.006 |
| [3] |
Stopper U, Aigner M, Meier W, et al. Flow field and combustion characterization of premixed gas turbine flames by planar laser techniques[J]. Journal of Engineering for Gas Turbines and Power, 2009, 131(2): 021504. DOI:10.1115/1.2969093 |
| [4] |
余西龙, 曾徽, 林鑫, 等. 可调谐二极管激光吸收光谱诊断技术:原理和应用[J]. 气体物理, 2016, 1(5): 52-63. Yu X L, Zeng H, Lin X, et al. Tunable diode laser absorption spectroscopy:principle and application[J]. Physics of Gases, 2016, 1(5): 52-63. (in Chinese) |
| [5] |
Hanson R K. Applications of quantitative laser sensors to kinetics, propulsion and practical energy systems[J]. Proceedings of the Combustion Institute, 2011, 33(1): 1-40. |
| [6] |
Griffiths A D, Houwing A F. Diode laser absorption spectroscopy of water vapor in a scramjet combustor[J]. Applied Optics, 2005, 44(31): 6653-6659. DOI:10.1364/AO.44.006653 |
| [7] |
Liu X, Jeffries J B, Hanson R K, et al. Development of a tunable diode laser sensor for measurements of gas turbine exhaust temperature[J]. Applied Physics B, 2006, 82(3): 469-478. DOI:10.1007/s00340-005-2078-9 |
| [8] |
Li F, Yu X L, Gu H B, et al. Simultaneous measurements of multiple flow parameters for scramjet characterization using tunable diode-laser sensors[J]. Applied Optics, 2011, 50(36): 6697-6707. DOI:10.1364/AO.50.006697 |
| [9] |
李飞, 余西龙, 林鑫, 等. 基于TDLAS的层析成像技术TDLAT[J]. 力学学报, 2014, 46(1): 54-59. Li F, Yu X L, Lin X, et al. Parallel-beam tomography based on TDLAS[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(1): 54-59. (in Chinese) |
| [10] |
Torniainen E D, Hinz A K, Gouldin F C. Tomographic analysis of unsteady, reacting flows:numerical investiga-tion[J]. AIAA Journal, 1998, 36(7): 1270-1278. DOI:10.2514/2.509 |
| [11] |
Lindstrom C, Tam C J, Davis D, et al. Diode laser absorption tomography of two dimensional supersonic flow[R]. AIAA 2007-5014, 2007.
|
| [12] |
Ma L, Cai W W, Caswell A W, et al. Tomographic imaging of temperature and chemical species based on hyperspectral absorption spectroscopy[J]. Optics Express, 2009, 17(10): 8602-8613. DOI:10.1364/OE.17.008602 |
| [13] |
Ma L, Li X S, Sanders S T, et al. 50-kHz-rate 2D imaging of temperature and H2O concentration at the exhaust plane of a J85 engine using hyperspectral tomography[J]. Optics Express, 2013, 21(1): 1152-1162. DOI:10.1364/OE.21.001152 |
| [14] |
Cai W W, Ewing D J, Ma L. Application of simulated annealing for multispectral tomography[J]. Computer Physics Communications, 2008, 179(4): 250-255. DOI:10.1016/j.cpc.2008.02.012 |
| [15] |
李飞, 余西龙, 曾徽, 等.用于超燃论断的吸收光谱二维诊断技术[C].第六届全国高超声速科技学术会议, 腾冲, 2013.
|
| [16] |
Li F, Yu X L, Lin X, et al. Diode laser absorption tomography for supersonic combustion application[C]. Proceedings of the 4th International Conference on Experimental Fluid Mechanics, 2014.
|




