减小航空飞行器燃油消耗一个有效的途径是增加机翼的展长, 从而减小飞行器的诱导阻力.然而, 当考虑航空飞行器结构要求时, 机翼展长便受到了强烈的限制, 机翼展长增加虽然可以减小诱导阻力, 但会引起机翼重量的快速增加[1-2], 从而损害航空飞行器性能.为解决这一矛盾, 人们在主机翼下方添加支撑, 从而减小主机翼的弯曲载荷并推迟机翼的颤振[3], 该种构型称为支撑机翼构型(strut braced wing, SBW)(见图 1).由于支撑可以减轻机翼翼根承受的弯矩, 因此相对常规悬臂梁飞机可增大机翼的展弦比、减小机翼厚度、并允许机翼减小后掠角, 从而减小诱导阻力、波阻、并增加层流范围, 使飞机性能得到大幅提升[4-5].然而, 支撑机翼构型也会带来额外的气动干扰问题, 特别是飞行Mach数较高时, 该种构型方案的可行性严重依赖于机翼和支撑的气动外型的精细设计.

|
| 图 1 支撑机翼布局示意图 Fig.1 Strut braced wing concept |
多支杆支撑机翼(truss braced wing, TBW)是SBW的一个分支, TBW是在SBW基础上增加一个或多个竖直支杆[6], 增加的支杆可以使机翼和支撑的屈曲模型变得更稳固[7], 但是也会使支撑机翼气动和结构设计变得更加复杂.最近, NASA和Boeing公司通过Ultra亚声速绿色航空研究(Subsonic Ultra-Green Aircraft Research, SUGAR)项目采用实验方法和CFD方法对TBW构型进行设计分析[7-10].未来, 为减小燃油消耗, 支撑机翼构型很可能列入下一代NASA X计划之中[11], 可见, 支撑机翼构型是未来高效绿色跨声速飞机新型布局重要的可供选择方案之一.
其实, 支撑机翼概念并非是一个新概念, 早在20世纪50年代, 世界上第一架TBW飞机Hurel-Dubois HD-34成功飞行[12], 该飞机为一架空中摄影飞机.自那以后, 支撑机翼构型在商业运输机是否可行成为了一个研究热点问题, 例如, 在1980年, NASA的一个研究结果表明, SBW飞机可以明显减小燃油消耗, 但会降低巡航速度, 并且机翼尺寸和复杂结构会阻碍该布局在飞机上的应用[13].但随着对SBW研究的深入以及新的设计手段和分析工具的开发, 人们对SBW的认识也越来越深入, Efforts在20世纪末及21世纪初, 采用包含空气动力、结构、推进系统、稳定性分析等多学科方法成功证实了SBW在商业运输机上的可行性[14-15].然而由于多学科问题的复杂性, 因此在对空气动力进行计算时, 采用的是中、低阶方法或者半经验公式, 例如采用半经验公式计算阻力[16-17], 涡格法计算诱导阻力[18], Korn方程计算波阻[19]系数, 或者采用Euler方程对支撑机翼气动力进行计算[20-21]. Ivaldi等指出, 如果忽略黏性的影响, 很多采用Euler方程优化结果和采用Reynolds平均N-S方程(RANS)的优化结果并不相同[22]. Secco等也认为采用高阶方法对SBW和TBW进行分析可以对各部件气动分量、部件的干扰影响等有更清晰的认识, 可以更准确地得到SBW和TBW在空气动力方面性能收益的具体量值[3].
本文基于RANS方程对支撑机翼构型进行气动力设计及分析, 可以获得黏性对支撑机翼构型的影响, 如支撑上翼面、机翼下翼面的激波附面层分离等, 并且可以获得相对低阶方法[16-19, 21, 23-24]更精准的阻力减小量.
本文对支撑机翼气动外型设计分两个步骤进行, 第1步, 分析支撑翼型、展向位置、支撑高度、支撑后掠角、扭转角、支撑相对厚度、支撑弦长等参数对支撑机翼构型升阻比的影响, 得到支撑外型的关键性参数; 第2步, 考虑结构限制要求, 选择最终的支撑外型及位置参数, 并对机翼翼型进行匹配修型设计, 最终设计得到支撑机翼构型的外型, 对该构型进行计算分析, 并与无支撑构型升阻比进行对比, 最后得到支撑机翼设计构型的气动性能及支撑机翼构型的气动干扰量.需要注意的是:在本文支撑机翼设计中, 机翼已事先设计完毕, 机翼的一般参数见表 1, 但该机翼设计时并未考虑支撑的影响, 由于支撑的存在, 机翼翼型相对厚度可以减小, 因此在支撑机翼设计的第2步中, 对机翼翼型进行了修型设计, 但对机翼其他参数不做改变.
| 下载CSV 表 1 机翼外型参数 Tab.1 Geometric characteristics of the wing |
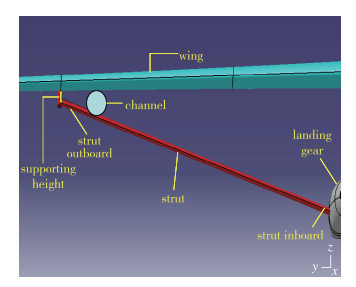
设计构型为翼身组合体构型(见图 2), 包含机身、机翼、支撑、起落架鼓包, 设计状态见表 2, 为定升力系数设计, 在给定升力系数下设计得到最大的升阻比.
|
| 图 2 支撑机翼布局设计外型图 Fig.2 Strut braced wing design configuration |
| 下载CSV 表 2 设计状态 Tab.2 Design Condition |
在本文设计中, 机翼已事先设计完毕, 机翼展弦比为17, 然而机翼设计时没有考虑加支撑的情况, 因此本文设计第2步对机翼翼型进行了修型设计, 适当减小了内机翼的翼型厚度, 使机翼和支撑更加匹配.考虑结构的限制, 不能无限地减小机翼翼型相对厚度, 因此限制修型后的机翼翼型相对厚度不得小于原机翼翼型的80%.
支撑设计约束为支撑翼型最大厚度不小于100 mm, 再考虑制造简便, 支撑设计梢根比设定为1.0.
1.2 数值方法本文数值模拟控制方程为Reynolds平均N-S方程(RANS), 计算求解器为CCFD-MB[25].
三维积分形式Reynolds平均N-S方程
| $ \frac{\partial }{\partial t}\iiint{\bar{Q}\text{d}}V+\iint{\mathit{\boldsymbol{f}}}\cdot \mathit{\boldsymbol{n}}\text{d}\mathit{S=0} $ |
其中, V为控制体体积, S为控制体表面面积, Q为守恒量, f 为矢量, 代表通过表面S的无黏通量和黏性通量之和, n 为控制体表面S的外法向单位矢量.空间半离散格式采用有限体积法构造, 无黏通量项采用2阶Roe迎风通量差分格式离散, 黏性通量项采用中心差分格式离散, 隐式时间推进, 采用多重网格技术加速收敛, 湍流模型采用一方程SA模型.
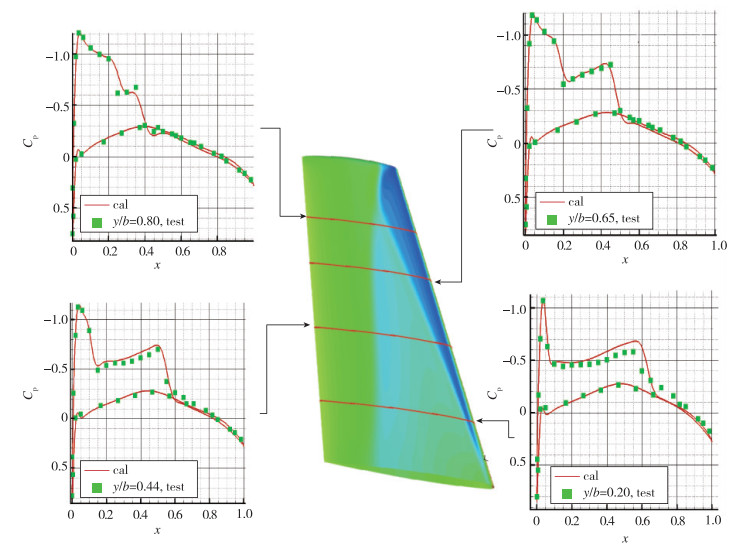
以M6机翼为例对CCFD-MB计算精度进行数值验证, 计算工况为Mach数0.839 5, Reynolds数为1.172×107, 迎角为3.06°. 图 3给出了计算得到的各剖面压力分布曲线与试验值的对比结果.从图中可以看出计算得到的压力分布与实验值吻合较好, 激波位置捕捉准确, CCFD-MB计算精度较高.
|
| 图 3 压力系数对比曲线 Fig.3 Comparisons of surface pressure distributions |
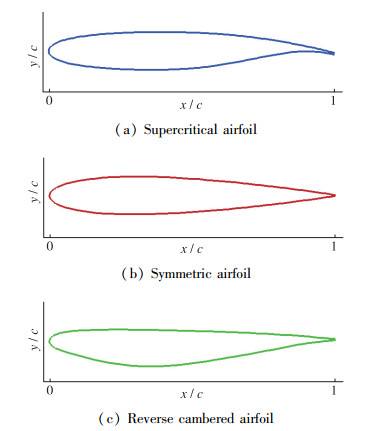
支撑外侧翼型距机翼下翼面非常近, 与机翼的气动干扰很强, 因此支撑外侧翼型设计非常重要, 本文设计了3种不同的支撑翼型(见图 4) :超临界翼型、对称翼型、反弯翼型.反弯翼型上翼面设计得较为平坦, 为保证翼型相对厚度, 翼型厚度基本集中到翼型下翼面; 3种支撑翼型的相对厚度均为13%, 机翼翼型采用跨声速飞机常见的超临界翼型, 相对厚度为11%.
|
| 图 4 支撑翼型 Fig.4 Strut airfoils |
3种支撑翼型前缘点均位于机翼翼型弦向20%处, 支撑翼上翼面与机翼下翼面高度为机翼翼型弦长的10%, 支撑翼型弦长为机翼翼型弦长的45%, 来流Mach数为0.7, 机翼翼型当地迎角均为1°, 支撑翼型当地迎角均为0°.
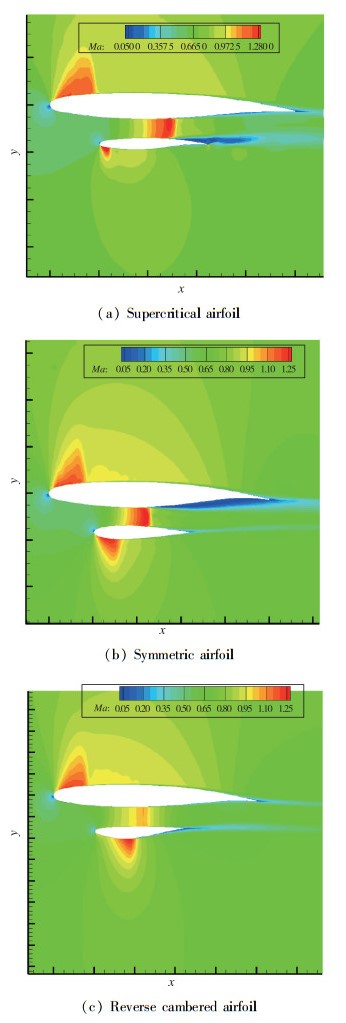
图 5为3种支撑翼型的Mach数云图, 从图中可以看出, 支撑翼型为超临界翼型和对称翼型时, 支撑翼型上翼面和机翼翼型下翼面形成的二维喷管通道内均产生了强激波, 激波后有分离区域存在.这种支撑与机翼强烈的相互干扰, 会使支撑机翼布局飞机干扰阻力大幅增加, 性能出现较大损失;而支撑翼型为反弯翼型时, 二维喷管内虽然气流仍存在加速现象, 但没有形成激波, 也没有产生分离.这是由于该反弯翼型上翼面设计得较平坦, 二维喷管内面积变化和缓.可见对于支撑机翼布局, 近翼面支撑翼型上翼面应设计得较为平坦, 上翼面损失的厚度由下翼面补齐.但也应注意的是, 下翼面过厚有可能引起支撑下翼面的强激波和分离.
|
| 图 5 支撑与机翼形成的二维喷管Mach数云图 Fig.5 2D Mach number distributions between strut and main wing |
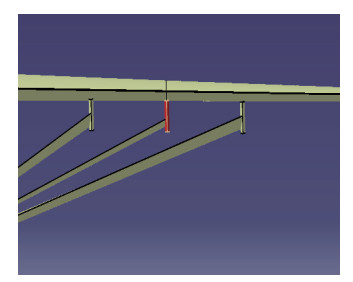
考虑3种支撑展向连接位置方案, 分别为支撑位于机翼展向40%, 50%, 60%位置处(见图 6).
|
| 图 6 不同展向位置示意图 Fig.6 Comparisons of different spanwise positions |
支撑外侧翼型采用上翼面较平的反弯翼型, 确保机翼下翼面与支撑之间的通道不产生激波和分离, 支撑内侧(与机身连接处)翼型采用对称翼型; 支撑翼型沿展向相对厚度均为13%, 弦长不变化.
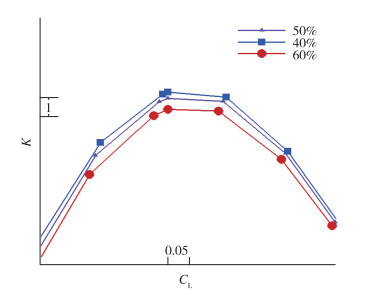
图 7为3种支撑展向连接位置方案升阻比曲线图, 从图中可以看出, 支撑展向连接位置向外侧机翼移动10%半展长, 最大升阻比降低约0.3;越靠机翼外侧, 相同升力系数下升阻比越低, 但考虑机翼结构受载情况, 支撑与机翼连接位置不能太靠内, 支撑展向位置应匹配气动和结构的要求.
|
| 图 7 不同展向位置升阻比对比图 Fig.7 Comparisons of lift-to-drag ratio among different spanwise positions |
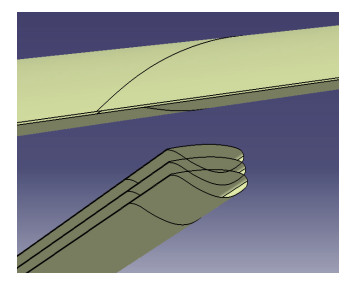
考虑3种支撑高度方案, 支撑上翼面分别为机翼下翼面5%c, 7.5%c, 10%c(见图 8, c为机翼平均气动弦长), 为显示方便, 图中隐藏了竖直支撑, 支撑外侧为反弯翼型, 内侧为对称翼型, 翼型相对厚度均为13%.
|
| 图 8 不同支撑高度位置示意图 Fig.8 Comparisons of different strut heights |
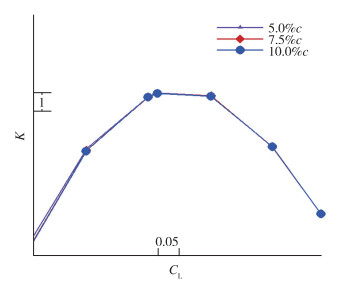
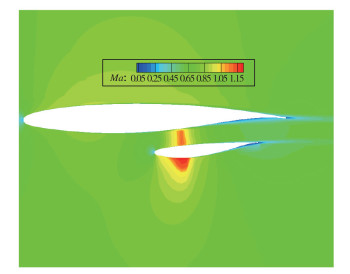
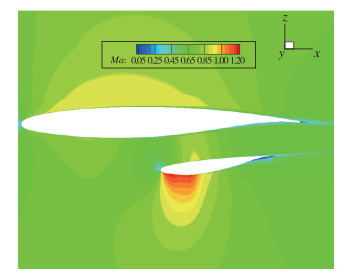
图 9为3种支撑高度方案升阻比曲线图, 从图中可以看出, 3种支撑高度方案气动力没有明显差异, 可见Ma=0.7时, 支撑高度在一定范围内对支撑机翼气动力干扰影响可以忽略, 造成这一现象的原因主要是:(1)支撑高度变化后, 近翼面支撑翼型到当地偏转角并没有进行相应变化; (2)支撑高度为5%c时, 支撑与机翼下翼面局部通道形成的激波强度非常弱(见图 10), 增加支撑高度, 通道内流动加速现象虽然减弱, 但对通道内波阻影响已很小, 并且支撑高度增加后, 支撑下翼面的激波强度增加(见图 11).
|
| 图 9 不同支撑高度升阻比对比图 Fig.9 Comparisons of lift-to-drag ratio among different strut heights |
|
| 图 10 支撑高度5%c局部通道Mach数云图 Fig.10 Mach number distribution of strut with a height of 5%c |
|
| 图 11 支撑高度10%c局部通道Mach数云图 Fig.11 Mach number distribution of strut with a height of 10%c |
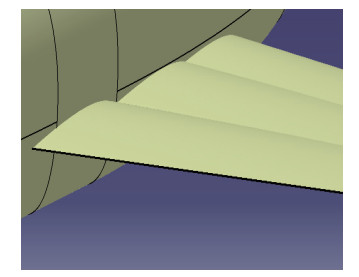
考虑3种支撑后掠角方案, 分别为支撑后掠10, 16, 20°(见图 12), 支撑近机翼面处为反弯翼型, 3种支撑后掠角方案近机翼面处支撑空间位置不变化, 远机翼面处为对称翼型, 通过变化远机翼面处支撑前后位置来改变支撑后掠角, 3种后掠角方案支撑翼型相对厚度均为13%.
|
| 图 12 不同支撑后掠角示意图 Fig.12 Comparisons of different sweep angles |
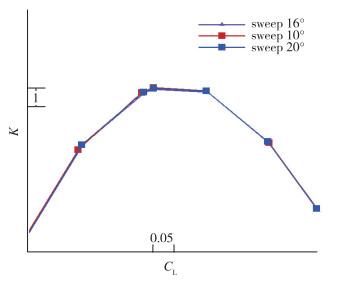
图 13为3种支撑后掠角方案升阻比曲线图.从图中可以看出, 3种支撑后掠角方案升阻比随升力系数变化曲线基本重合, 差量很小, 可见Ma=0.7时, 支撑后掠角在一定范围内对支撑机翼气动力干扰影响较小.
|
| 图 13 不同支撑后掠角升阻比对比图 Fig.13 Comparisons of lift-to-drag ratio among different sweep angles |
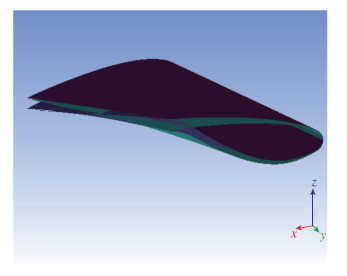
3种扭转角分布方案(见图 14)分别为:方案1, 支撑内侧安装角(远机翼面处)0°, 扭转角-8°; 方案2, 支撑内侧安装角2°, 扭转角-6°; 方案3, 支撑内侧安装角0°, 扭转角-6°. 3种扭转角方案支撑内侧均为对称翼型, 外侧均为反弯翼型, 后掠角16°, 支撑高度5%c, 相对厚度13%.
|
| 图 14 不同支撑扭转角示意图 Fig.14 Comparisons of different twist angles |
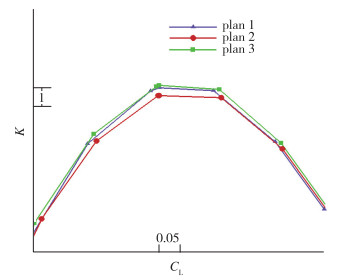
图 15为3种支撑扭转角方案升阻比曲线图, 从图中可以看出, 扭转角方案1和方案3升阻比差异不大, 看似扭转角分布对支撑机翼气动干扰不大, 但需要注意的是本节3个扭转角分布方案支撑外侧(近机翼面处)翼型均偏转了较大的负角度, 确保了支撑与机翼通道没有产生强烈的激波, 否则不合适的扭转角分布将使支撑与机翼产生的局部通道出现强激波及分离, 严重影响支撑机翼布局气动性能.扭转角分布方案2升阻比相对方案1和方案3有明显降低.可见支撑内侧安装角、扭转角分布对支撑机翼气动干扰有较明显的影响.
|
| 图 15 不同支撑扭转角升阻比对比图 Fig.15 Comparisons of lift-to-drag ratio among different twist angles |
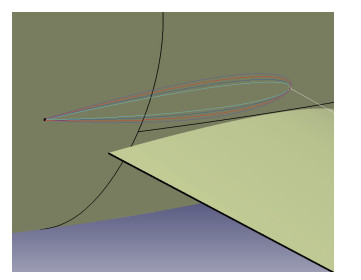
考虑4种支撑翼型相对厚度方案, 分别为相对厚度7%, 9%, 11%, 13%(见图 16), 支撑近机翼面处为反弯翼型, 远机翼面处为对称翼型, 后掠角为16°, 扭转角为-8°, 支撑高度为5%c, 支撑位于展向50%处.
|
| 图 16 不同支撑相对厚度示意图 Fig.16 Comparisons of different strut thicknesses |
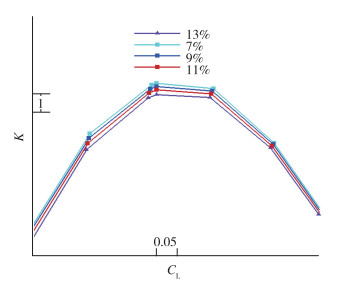
图 17为4种支撑相对厚度方案升阻比曲线图, 从图中可以看出, 随着支撑翼型相对厚度减小, 升阻比增大.
|
| 图 17 不同支撑相对厚度升阻比对比图 Fig.17 Comparisons of lift-to-drag ratio among different strut thicknesses |
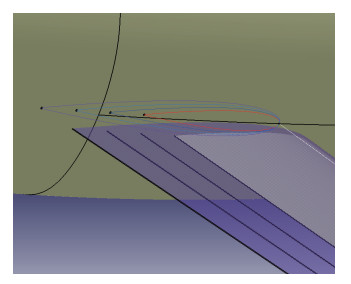
考虑4种支撑弦长方案, 分别为25%c, 31.25%c, 37.5%c, 44.25%c(见图 18), 支撑近机翼面处为反弯翼型, 远机翼面处为对称翼型, 相对厚度均为13%, 后掠角为16°, 扭转角为-8°, 支撑高度为5%c, 支撑位于展向50%处.
|
| 图 18 不同支撑弦长示意图 Fig.18 Comparisons of different strut chord lengths |
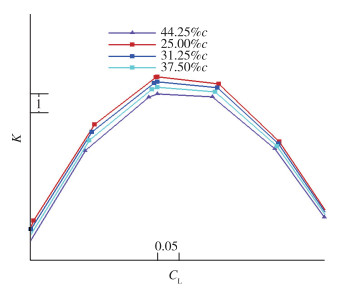
图 19为4种支撑弦长方案升力升阻比曲线图, 从图中可以看出, 随着支撑弦长减小, 升阻比增大, 这是因为支撑弦长减小, 支撑对机翼的干扰面积减小, 对机翼的干扰阻力减小, 文中支撑弦长25%c方案较44.25%c方案最大升阻比增加约0.9, 支撑弦长对升阻比影响明显, 设计中在确保支撑厚度及支撑本身不引起新的分离条件下, 尽量减小支撑弦长.
|
| 图 19 不同支撑弦长升阻比对比图 Fig.19 Comparisons of lift-to-drag ratio among different strut chord lengths |
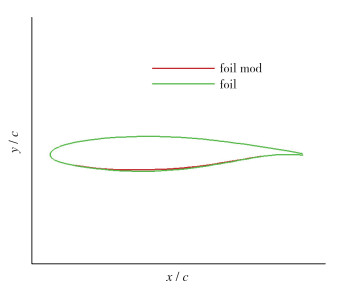
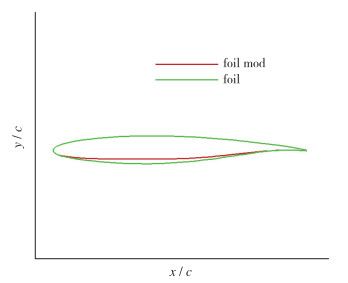
初始机翼设计时, 未充分考虑支撑的影响, 实际上, 当支撑存在时, 机翼的相对厚度可以减小[3-5].本节对初始机翼、翼根翼型和支撑与机翼连接处翼型进行了修型设计(见图 20,21), 翼根翼型对下翼面进行了小量的修型, 而支撑与机翼连接处, 支撑和机翼相对位置较近, 因此对该处机翼翼型下翼面进行了大幅度的修型, 机翼翼型下翼面进行了“拉平”设计, 这样的设计目的是使机翼和支撑之间形成的通道横截面积变化尽可能缓慢, 从而减小机翼和支撑的相互干扰.
|
| 图 20 翼根处翼型修型 Fig.20 Airfoil optimization of the main wing at root |
|
| 图 21 支撑与机翼连接处翼型修型 Fig.21 Airfoil optimization of the main wing at the conjunction point |
机翼修型设计保证了各截面处修型翼型相对厚度不小于初始翼型的80%, 修型翼型上翼面保持不变, 这样可以较大程度地保持原始翼型的设计特点.本文对支撑与机翼连接处至机翼外翼翼型均不做修改.
3.2 支撑机翼设计方案根据支撑参数规律研究及机翼修型结果, 得到了支撑机翼设计方案, 机翼及支撑外型特征参数如表 3所示, 支撑采用11%相对厚度翼型, 翼型最大厚度满足100 mm厚度限制要求.
| 下载CSV 表 3 机翼及支撑外型参数 Tab.3 Geometric characteristics of the wing and strut |
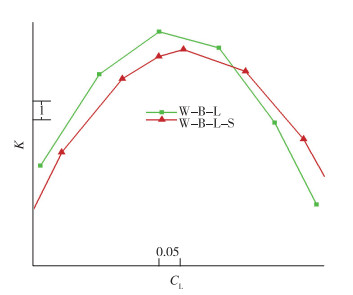
图 22为有无支撑时升阻比随升力系数变化曲线, 图中W, B, L, S分别代表机翼、机身、起落架鼓包、支撑, 在设计点升力系数为0.6时, 带支撑构型较初始非修型机翼无支撑构型升阻比减小6.3%, 升阻比减小一部分来源于支撑本身带来的阻力增加, 本文该部分阻力贡献了升阻比减小量的67%, 另外一部分来源于支撑与机翼的干扰阻力, 由此可见设计的支撑机翼构型干扰阻力较小.
|
| 图 22 有无支撑升阻比对比 Fig.22 Comparison of lift-to-drag ratio between configurations with and without strut |
需要说明的是, 初始无支撑翼身组合体构型(机翼展弦比为17)相较常规悬臂梁翼身组合体构型(相同机身、起落架鼓包, 展弦比约为8.5), 最大升阻比提高了约35%, 展弦比增加大幅提高了飞机升阻比, 尽管支撑会对升阻比有不利影响, 但在设计较好的情况下, 该不利影响较小(本文升阻比影响量为6.3%).总体来看, 支撑机翼构型升阻比相对常规悬臂梁飞机有较大提升, 是未来绿色航空飞机的一个可供选择方案.
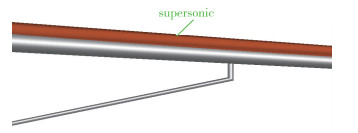
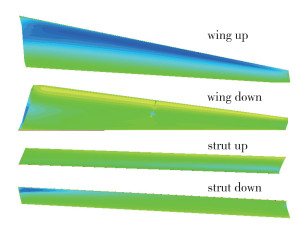
设计状态下支撑机翼构型超声速等值面区域见图 23, 超声速区主要出现在机翼上翼面, 但没有形成强激波; 机翼与支撑形成的通道内没有产生超声速, 这说明机翼与支撑形成的通道内没有产生激波及激波引起的附面层分离; 机翼及支撑上下翼面压力云图如图 24所示, 从图中可以看出, 机翼及支撑翼面压力分布变化比较平滑, 平滑的压力分布变化可以减慢边界层增长并减少黏性阻力.仅支撑下翼面内侧与起落架鼓包连接处形成了局部低压区, 该处后续还可以继续做工作.
|
| 图 23 超声速等值面 Fig.23 Supersonic region on main wing |
|
| 图 24 机翼及支撑压力云图 Fig.24 Pressure distributions on main wing and strut |
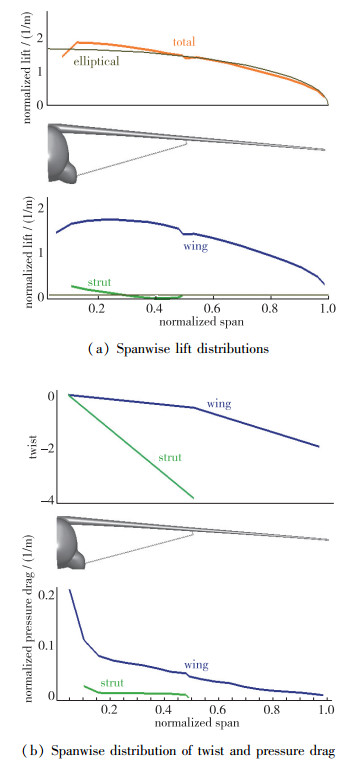
机翼与支撑扭转分布如图 25(b)上半部分所示, 支撑扭转为-4°, 支撑升力为负, 由于支撑存在负升力, 机翼内侧受其干扰影响升力会增加, 这种现象和参考文献[21, 22, 24]一致; 升力展向分布见图 25(a), 总升力分布基本符合椭圆分布, 但内翼升力分布会有一个三角形形状, 这是因为机翼和机身连接处升力有损失, 该展向升力分布现象和参考文献[3]优化结果相似; 机翼和支撑压差阻力展向分布见图 25(b)下半部分, 从图中可以看出, 机翼阻力主要出现在内翼, 外翼阻力较小, 而支撑沿展向各剖面阻力均不大, 机翼和支撑沿展向压差阻力分布并没有出现突然的上抬, 可见支撑和机翼上没有出现强激波和分离现象.
|
| 图 25 展向升力、扭转角及压差阻力分布 Fig.25 Spanwise distributions of lift, twist and pressure drag |
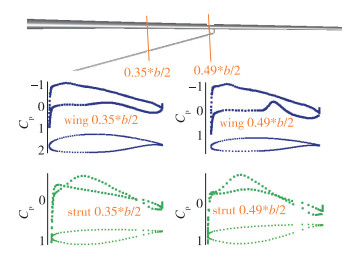
图 26为半展长35%, 49%处机翼及支撑压力分布曲线, 从图中可以看出, 设计的支撑机翼构型对机翼下翼面和支撑上翼面的抽吸效应非常小, 在半展长49%处(距离机翼与支撑连接处最近处)机翼下翼面压力仅有一个较小的凸起, 说明支撑与机翼形成的通道内气流加速较小, 这可以避免在通道内形成激波及激波引起的分离.
|
| 图 26 机翼及支撑截面压力分布 Fig.26 Pressure distributions on different wing and strut cross sections |
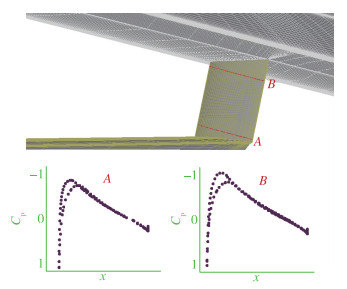
图 27为竖直支撑不同位置截面压力分布, 从图中可以看出, 竖直支撑各截面处压力恢复平滑, 压力梯度连续无阶跃, 可见支撑与机翼连接处没有形成激波和分离, 通道内流动和缓, 气流加速效应较弱, 对机翼下翼面的干扰也较弱.
|
| 图 27 竖直支撑截面压力分布 Fig.27 Pressure distributions on vertical segment of strut cross sections |
支撑机翼构型可以减轻机翼承受的弯矩, 增大机翼的展弦比和减小机翼的厚度, 这不仅减小了诱导阻力和波阻, 并允许机翼减小后掠角以增大层流流动范围, 同时也可减小机翼的结构重量.飞机的高气动力效率可减少燃油消耗和要求更小、更安静、价格更低的发动机, 使排污和噪音也更低, 可用于宽体机和窄体机, 具有巨大潜能.本文基于N-S方程对支撑机翼构型进行了气动外型设计, 设计Mach数为0.7, 设计升力系数为0.6, 由于初始无支撑翼身组合体构型(机翼展弦比为17)相较常规悬臂梁翼身组合体构型(相同机身、起落架鼓包, 展弦比约为8.5)最大升阻比提高了约35%, 而设计得到的支撑机翼构型相对初始无支撑构型在设计升力系数下升阻比仅减小6.3%, 结果显示当支撑和机翼设计较好时, 支撑机翼构型相对常规悬臂梁飞机升阻比有较大提高, 气动性能更好, 是可供未来高亚声速绿色航空飞机选择的一种新型外型; 但支撑机翼构型未来成功地在型号飞机中应用, 还须很好地解决支撑弯曲失稳、气弹等问题.
支撑和机翼通道设计是决定支撑机翼构型气动设计成功与否的一个关键, 须在实际设计中进行精细设计.本文研究结果表明支撑外侧当地翼型上翼面及机翼内侧下翼面应设计得较平, 使通道横截面积变化尽可能缓慢, 从而避免机翼与支撑通道内产生激波及分离, 并减小支撑和机翼的干扰阻力; 支撑弦长、相对厚度、展向位置、扭转角分布对支撑机翼构型气动性能影响也较大, 在支撑机翼构型设计中应对这些关键性参数重点考虑.
| [1] |
Kenway G K, Martins J R. Multipoint high-fidelity aerostructural optimization of a transport aircraft configuration[J]. Journal of Aircraft, 2014, 51(1): 144-160. DOI:10.2514/1.C032150 |
| [2] |
Kennedy G J, Kenway G W, Martins J R. High aspect ratio wing design: optimal aerostructural tradeoffs for the next generation of materials[R]. AIAA 2014-0596, 2014.
|
| [3] |
Secco N R, Martins J R. RANS-based aerodynamic shape optimization of a strut-braced wing with overset meshes[R]. AIAA 2018-0413, 2018.
|
| [4] |
Gur O, Bhatia M, Schetz J A, et al. Design optimization of a truss-braced-wing transonic transport aircraft[J]. Journal of Aircraft, 2010, 47(6): 1907-1917. DOI:10.2514/1.47546 |
| [5] |
Chakraborty I, Gross J R, Nam T, et al. Analysis of the effect of cruise speed on fuel efficiency and cost for a truss-braced wing concept[R]. AIAA 2014-2424, 2014.
|
| [6] |
Ivaldi D, Secco N R, Chen S, et al. Aerodynamic shape optimization of a truss-braced-wing aircraft[R]. AIAA 2015-3436, 2015.
|
| [7] |
Bradley M K, Droney C K, Allen T J. Subsonic ultra green aircraft research. Phase Ⅱ-volume I; truss braced wing design exploration[R]. NASA/CR-2015-218704/VOL1, 2015.
|
| [8] |
Ting E, Reynolds K, Nguyen N. Flight performance analysis of the truss-braced wing aircraft[R]. AIAA 2014-2597, 2014.
|
| [9] |
Allen T J, Sexton B W, Scott M J. SUGAR truss braced wing full scale aeroelastic analysis and dynamically scaled wind tunnel model development[R]. AIAA 2015-1171, 2015.
|
| [10] |
Scott R C, Allen T J, Funk C J, et al. Aeroservoelastic wind-tunnel test of the sugar truss braced wing wind-tunnel model[R]. AIAA 2015-1172, 2015.
|
| [11] |
Gipson L. NASA aeronautics budget proposes return of X-Planes[EB/OL]. (2016-02-19). http://www.nasa.gov/feature/nasa-aeronautics-budget-proposes-return-of-x-planes.
|
| [12] |
Carrier G, Atinault O, Dequand S, et al. Investigation of a strut-braced wing configuration for future commercial transport[C]. Proceedings of the 28th International Congress of the Aeronautical Sciences, Brisbane: ICAS, 2012.
|
| [13] |
Turriziani R V, Lovell W A, Martin G L, et al. Preliminary design characteristics of a subsonic business jet concept employing an aspect ratio 25 strut braced wing[R]. NASA CR-159361, 1980.
|
| [14] |
Grasmeyer J M. Multidisciplinary design optimization of a transonic strut-braced wing aircraft[R]. AIAA 1999-0010, 1999.
|
| [15] |
Gundlach J F, Tétrault P A, Gern F H, et al. Conce-ptual design studies of a strut-braced wing transonic tran-sport[J]. Journal of Aircraft, 2000, 37(6): 976-983. DOI:10.2514/2.2724 |
| [16] |
Gur O, Mason W H, Schetz J A. Full configuration drag estimation[R]. AIAA 2009-4109, 2009.
|
| [17] |
Gur O, Schetz J A, Mason W H. Aerodynamic considerations in the design of truss-braced wing aircraft[R]. AIAA 2010-4813, 2010.
|
| [18] |
Grasmeyer J M. A discrete vortex method for calculating the minimum induced drag and optimum load distribution for aircraft configurations with noncoplanar surfaces[C]. Proceedings of the VPIAOE-242, AOE Department, Blacksburg: Virginia Polytechnic Institute and State University, 1997.
|
| [19] |
Zhang K S, Bakar A, Ji P B, et al. Multidisciplinary optimization of truss-braced wing layout[C]. Proceedings of the 29th Congress of the international of the Aeronautical Sciences, St. Petersburg: ICAS, 2014.
|
| [20] |
Gur O, Bhatia M, Schetz J A, et al. Design optimization of a truss-braced-wing transonic transport aircraft[J]. Journal of Aircraft, 2010, 47(6): 1907-1917. DOI:10.2514/1.47546 |
| [21] |
Gagnon H, Zingg D W. High-fidelity aerodynamic shape optimization of unconventional aircraft through axial defor-mation[R]. AIAA 2014-0908, 2014.
|
| [22] |
Ivaldi D, Secco N R, Chen S, et al. Aerodynamic shape optimization of a truss-braced-wing aircraft[R]. AIAA 2015-3436, 2015.
|
| [23] |
Meadows N A, Schetz J A, Kapania R K, et al. Multidisciplinary design optimization of medium-range transo-nic truss-braced wing transport aircraft[J]. Journal of Aircraft, 2012, 49(6): 1844-1856. DOI:10.2514/1.C031695 |
| [24] |
Hwang J T, Kenway G K, Martins J R. Geometry and structural modeling for high-fidelity aircraft conce-ptual design optimization[R]. AIAA 2014-2041, 2014.
|
| [25] |
廖振荣, 郭兆电, 邓一菊, 等.航空高性能CFD计算软件CCFD研发与测试[C].第十七界全国计算流体力学会议, 杭州: 中国空气动力学会, 2017. Liao Z R, Guo Z D, Deng Y J, et al. Development and test of high performance CFD computing software CCFD[C]. Proceedings of the CARS, Hangzhou: CARS, 2017(in Chinese). |




