2. 中国航天空气动力技术研究院,北京 100074
2. China Academy of Aerospace Aerodynamics, Beijing 100074, China
反作用控制系统(reaction control system, RCS)产生直接力可用于快速改变飞行器的飞行轨迹与姿态, 特别在低动压或要求快速机动情况下, 是一种新型的气动操纵技术, 是常规舵面控制之外的重要控制手段[1]. RCS直接力控制技术已成功应用于多种飞行器, 如航天飞机、飞船、高机动导弹等, 并具有广阔的应用前景.
当RCS发动机工作时, 侧向安装的发动机喷流与超/高超声速来流相撞产生复杂的激波/边界层干扰流场, 包含复杂的波系、涡系结构以及流动的分离、再附等流动现象[2-3], 并引起表面载荷发生变化, 产生附加干扰力和力矩.而侧向喷流干扰特性受到飞行条件与喷流条件影响显著, 呈现高度非线性变化规律.侧向喷流干扰问题是反作用控制技术应用中需要解决的关键难点问题.
国内外对侧向喷流干扰流场的研究已持续了半个多世纪[4-12], 采用理论分析、数值模拟与风洞实验手段, 针对喷管出口位于表面的平板喷流模型、旋成体喷流模型及典型飞行器外形喷流干扰开展了大量的基础及应用基础研究, 涉及研究内容广泛, 包括不同来流与喷流参数以及组合参数、不同喷管布局等影响.由于飞行器外形与喷流布局的多样性、喷流干扰的复杂性以及使用环境不同, 在干扰流动机理及工程应用层面仍然存在很多问题需深入探讨.
过去的研究工作主要针对喷管出口位于弹体表面情况, 然而在导弹实际应用过程中, 在喷管迎风条件下产生力干扰因子小于0.5的不利喷流干扰现象, 甚至在攻角小于10°的力干扰因子也可能出现小于0.5的情况.这种现象主要是由喷流与弹体、控制面产生严重干扰引起的, 极大限制了RCS控制的使用范围.为避免出现上述不利干扰现象, 提出了喷管安装于翼梢方案, 减少迎风状态喷流对弹体与控制面的不利干扰.如法国的“阿斯特(Aster)”系列导弹采用翼梢处侧向喷流/尾舵复合控制方式, 喷管位于边条翼内部, 喷管出口位于翼梢, 喷管为上方下圆的非常规构型.
对于喷管位于翼或舵内部的侧向喷流干扰特性研究很少, 仅Srivastava[13]针对带有翼、舵的导弹构型, 开展了典型状态翼梢处侧向喷流干扰特性研究, 对比了喷管迎风状态弹体表面安装喷管以及翼梢安装喷管的喷流干扰结构以及喷流干扰力/力矩特性, 指出翼梢喷流干扰有效消除了不利干扰, 获得了较高的喷流干扰因子.
鉴于侧向喷流干扰的复杂性以及规律的强非线性, 在实际应用当中还须更广泛认识翼梢喷流干扰的机理以及影响规律.本文参考“阿斯特”系列导弹, 针对带长边条翼的气动布局外形, 完成了喷管位于边条翼内部的翼梢侧向喷流干扰流场数值模拟, 给出了典型条件下空间和表面的复杂流动特性, 分析了力/力矩干扰因子随飞行高度、Mach数、攻角的变化规律, 可为新型飞行器设计提供参考依据.
1 数值模拟方法 1.1 离散方法应用分区对接结构网格技术, 采用完全气体三维可压缩Reynolds平均Navier-Stokes控制方程, 通过有限体积方法进行离散.对流项离散选择2阶精度Roe格式[14], 黏性项离散采用中心差分格式, 时间项离散使用LU-SGS隐式方法[15], 采用局部时间步长加速收敛, 湍流模型采用一方程Spalart-Allmaras(S-A)湍流模型[16].
1.2 边界条件(1) 来流边界条件:给定来流Mach数Ma∞和攻角α, 根据飞行高度H确定来流的静压P∞及静温T∞;
(2) 物面边界条件:物面边界条件按无滑移绝热壁面边界条件处理;
(3) 出流边界条件:超声速出流条件;
(4) 喷流边界条件:采用喷管内外流一体化计算, 在喷管喉道处给定喷流参数.
采用的数值模拟方法已得到了大量含喷流干扰风洞实验结果验证, 见文献[17-20].
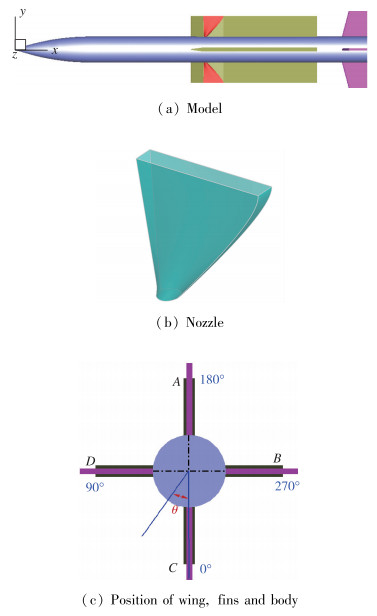
2 计算模型及计算参数 2.1 计算模型及网格借鉴法国的Aster导弹, 设计了一套由尖拱头部、圆柱弹体及边条翼和舵构成的模型, 翼前段的内部安装喷管, 喷管出口位于边条翼翼梢处, 如图 1(a)所示. 图 1(b)显示了喷管形状, 喉道为圆形、出口为长方形.
|
| 图 1 计算模型 Fig.1 Computational model |
模型柱段直径D=180 mm, 长径比L/D=14(L为全弹长, D为弹体直径), 喷管出口中心与头部理论尖点距离7.9D, 喉道面积Sthroat与出口面积Si的比为0.15.
参考面积选取弹体圆柱段截面积, 参考长度选取弹体总长度, 力矩参考点选取在头部理论尖点, x轴沿弹体纵轴向后, y轴垂直向上, z轴垂直于xoy平面(x,y,z满足右手法则).
图 1(c)中给出了从尾部向头部观看时, 边条翼、舵与弹体的相对位置, 并给出了周向角θ的定义.
计算网格采用结构网格, 并应用分区对接技术, 在边条翼、舵、喷管附近等处对生成的网格进行优化调整, 生成用于计算的网格数约为2×107, 网格结构示意见图 2.

|
| 图 2 计算网格 Fig.2 Grids of the model |
计算采用的来流参数如表 1所示, 基于直径D的来流Reynolds数ReD =1.1×106~15.3×106.计算中只考虑C喷管工作工况, 并采用空气冷喷流介质模拟.由于本项喷管为非规则喷管, 出口参数(Pj, Maj)的分布与圆形喷管相差很大.过去建立的冷、热喷转换原则都是建立在圆形出口喷管基础上的, 鉴于此, 本项采用如下方式进行冷热喷转换:
| 下载CSV 表 1 来流参数 Tab.1 Freestream parameters |
(1)将长方形出口热喷参数转换为当量圆形出口参数.其中, 保持出口面积Sj相同, 按面积平均计算Majavg, 再根据出口动量比不变, 如式(1)计算Pjavg
| $ \int_{{{S}_{\text{j}}}}{\left( {{P}_{\text{j}}}{{\gamma }_{\text{j}}}Ma_{\text{j}}^{2} \right)}\text{d}s=\left( {{P}_{\text{javg}}}{{\gamma }_{\text{j}}}Ma_{\text{javg}}^{2} \right)\times {{S}_{\text{j}}} $ | (1) |
(2) 通过出口压力比、动量比、几何相似原则进行冷热喷参数转换, 见式(2)
| $ {{\left( \frac{P_{\text{javg}}^{{}}{{\gamma }_{\text{j}}}Ma_{\text{javg}}^{2}S_{\text{j}}^{{}}}{P_{\infty }^{{}}{{\gamma }_{\infty }}Ma_{\infty }^{2}S_{\infty }^{{}}} \right)}_{\text{fs}}}={{\left( \frac{P_{\text{javg}}^{{}}{{\gamma }_{\text{j}}}M_{\text{javg}}^{2}S_{\text{j}}^{{}}}{P_{\infty }^{{}}{{\gamma }_{\infty }}Ma_{\infty }^{2}S_{\infty }^{{}}} \right)}_{\text{m}}} $ | (2) |
其中, P为压强, γ为比热比, Ma为Mach数, S为参考面积, j喷流出口参数, ∞为来流参数,fs为热喷参数, m为冷喷参数, avg为非规则喷管出口的当量平均参数.
(3) 最后按等熵管道流理论确定冷喷参数对应的喉道面积, 见式(3).并以此和原出口外形构造新的上方下圆非常规构型喷管型面
| $ S_{\text{throatm}}^{{}}=S_{\text{j}}^{{}}Ma_{\text{jm}}^{{}}{{\left\{ \left( \frac{2}{\gamma _{\text{m}}^{{}}+1} \right)\left[ 1+\left( \frac{{{\gamma }_{\text{m}}}-1}{2} \right)Ma_{\text{jm}}^{2} \right] \right\}}^{-\frac{{{\gamma }_{\text{m}}}+1}{2({{\gamma }_{\text{m}}}-1)}}} $ | (3) |
按照出口几何、动量比和压力比相似的转换原则, 得到的冷喷流总压P0j、总温T0j等参数,见表 2.
| 下载CSV 表 2 喷流参数 Tab.2 Jet parameters |
飞行高度1 km和15 km对应的喷流总压与来流静压比P0j/P∞分别为111.26, 825.64, 喷流在翼梢出口处为超声速.
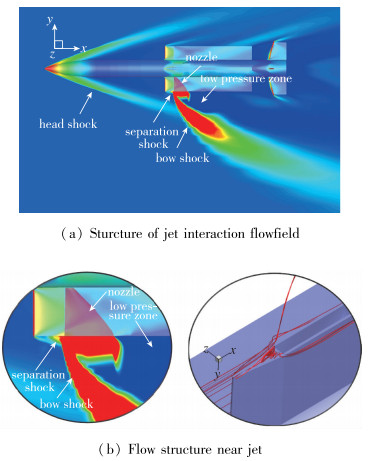
3 计算结果及讨论 3.1 典型翼梢喷流干扰流场特征图 3给出了Ma∞=4, H=15 km, α=0°条件下, C喷管工作时壁面及纵向对称平面上的等压力云图, 显示了干扰流场的空间结构特征.超声速来流流经弹体头部形成头激波, 翼、舵前缘激波, 翼梢喷流与来流干扰形成喷流弓形激波, 引起强逆压梯度使流动分离, 形成分离激波, 多种激波相互交叉形成复杂的激波系结构, 这些复杂激波系结构将导致弹体、边条翼及舵上压力分布发生变化, 影响导弹的整体气动特性和喷流控制效率.
|
| 图 3 典型流场结构 Fig.3 Typical spatial flow structure |
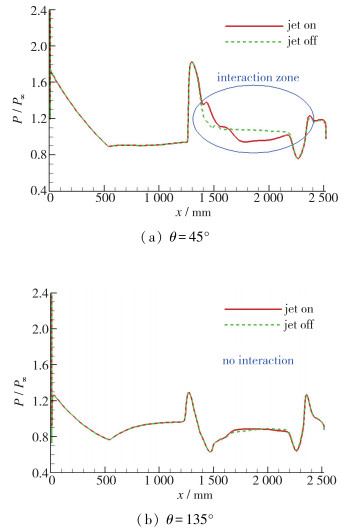
图 4给出了C喷管工作时, Ma∞=1.5, H=1 km, α=10°条件下θ=45°, 135°子午线上有、无喷流时的压力分布对比(θ的定义见图 1).从图中可以看出, 有喷与无喷时的沿弹体压力分布在迎风侧(θ=45°)存在差别, 这说明虽然将喷流出口置于翼梢, 喷流仍对边条翼、弹体、舵产生了较强的干扰.但有喷与无喷时的沿弹体压力分布在背风侧(θ=135°)基本不存在差别, 说明喷流未对无喷侧的边条翼、弹体、舵产生干扰.
|
| 图 4 子午线压力分布 Fig.4 Pressure distributions with and without jet interaction along meridian lines at H=1 km, Ma∞=1.5, α=10° |
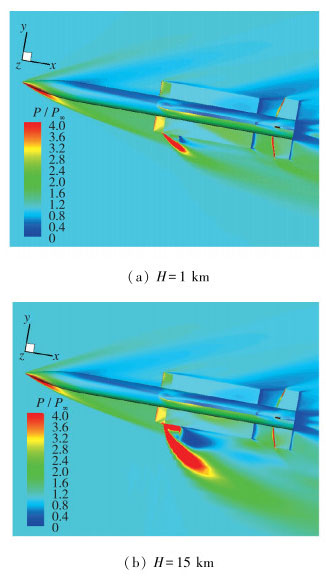
图 5给出了C喷管工作、Ma∞=4, H=1, 15 km, α=10°条件下壁面及对称面等压力云图.由于H=15 km喷流压力比大于H=1 km, 喷流穿透能力增强, 弓形激波的高度和强度以及对上下游流场干扰范围和强度都将明显增加.
|
| 图 5 不同高度计算得到的等压力云图 Fig.5 Pressure contours of different heights at Ma∞=4, α=10° |
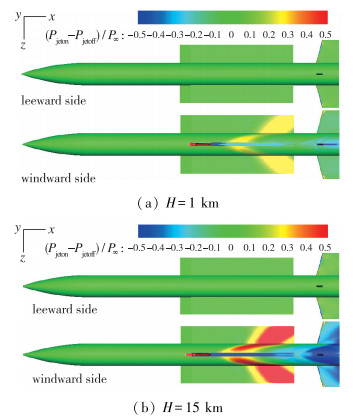
为了更清晰显示喷流对弹体、边条翼、舵迎风面和背风面影响程度, 图 6给出了Ma∞=4, H=1, 15 km, α=10°, 迎风面及背风面有无喷流表面压力差值(Pjeton-Pjetoff)/P∞分布云图.从图中可以看出在迎风面, 喷流主要干扰范围集中在边条翼、尾舵及后方弹体, H=15 km条件下喷流对弹体和边条翼干扰明显强于H=1 km条件.在背风面, 喷流对弹身、边条翼和尾舵的干扰明显弱于迎风侧.
|
| 图 6 不同高度计算得到的有喷与无喷压力差值分布 Fig.6 Distributions of (Pjeton-Pjetoff)/P∞ of different heights at Ma∞=4, α=10° |
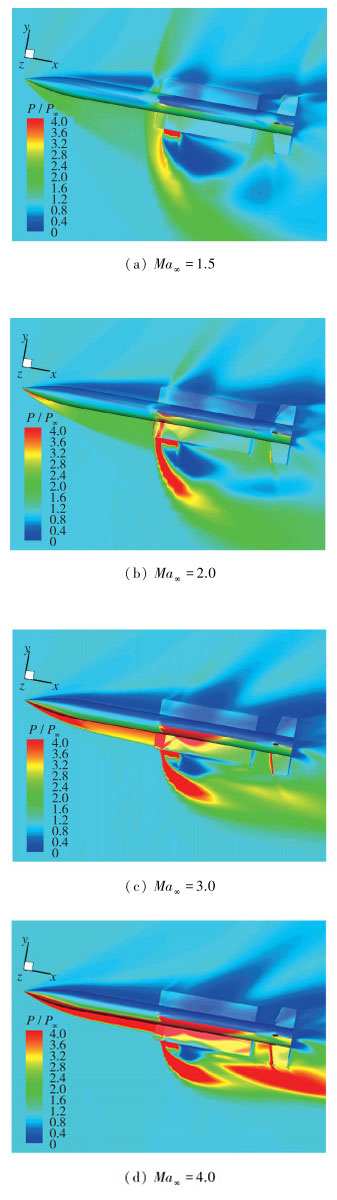
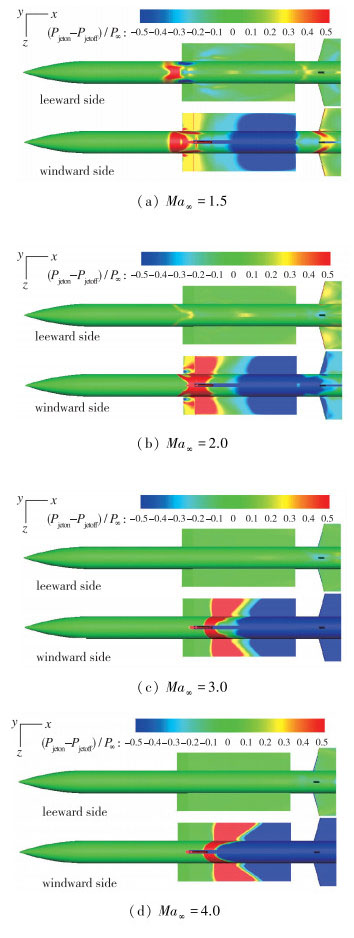
图 7给出了C喷管工作、H=15 km,α=30°时不同Mach数条件下壁面及对称面等压力云图. 图 8给出了C喷管工作、H=15 km,α=30°、不同Mach数条件下表面有无喷流压力差值分布云图.
|
| 图 7 不同Mach数计算得到的等压力云图 Fig.7 Pressure contours of different Mach numbers at H=15 km, α=30° |
|
| 图 8 不同Mach数计算得到的有无喷流压力差值分布 Fig.8 Distribution of (Pjeton-Pjetoff)/P∞ of different Mach numbers at H=15 km, α=30° |
从图中可以看出, 随着Mach数的增加, 由于来流动压增加, 喷流弓形激波逐渐靠近弹体. Ma∞= 1.5时在边条翼前段形成了大范围的脱体激波, 喷流对边条翼前至模型尾部的大范围区域产生干扰, 但随着Mach数增加, 喷流干扰的空间和表面范围逐步减小, 翼梢喷流干扰范围逐渐由边条翼前端后退至边条翼及以后区域.另一方面, 在迎风面, 随着Mach数增加, 喷流对表面压力的影响程度增加, 弹体表面有无喷流压力差(Pjeton-Pjetoff)/P∞ < 0的区域逐步增加; 在背风面, 随着Mach数增加, 由于激波范围收缩以及边条翼的阻挡效应, 背风区的干扰逐渐减弱.
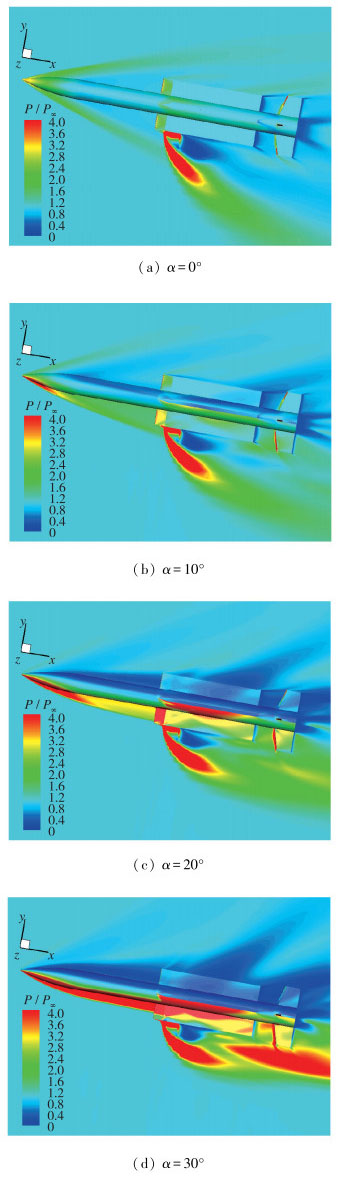
3.4 攻角对喷流干扰流场的影响图 9给出了C喷管工作、Ma∞=4, H=15 km时不同攻角条件下壁面及对称面等压力云图.对于迎风面干扰流场, 随着攻角增加, 弓形激波逐渐靠近弹体, 喷流对弹体、边条翼和尾舵的干扰增加, 在α=30°时喷流对尾舵产生了很强的干扰.
|
| 图 9 不同攻角计算得到的等压力云图 Fig.9 Pressure contours of different angles of attack at H=15 km, Ma∞=4 |
图 10给出了C喷管工作、Ma∞=4, H=15 km不同攻角条件下有无喷流压力差值分布云图, 可以看出随攻角增加, 在迎风面, 由于弓形激波逐渐靠近弹体, 喷流对表面的干扰强度逐渐增加.攻角较小时, 干扰使迎风面一部分区域压力载荷增加, 随着攻角增加, 迎风面表面压力升高、降低的程度逐渐增加, 并且弹体后段负增量(Pjeton-Pjetoff)/P∞ < 0的区域逐渐增加, 而在背风面, 喷流干扰一直较弱.
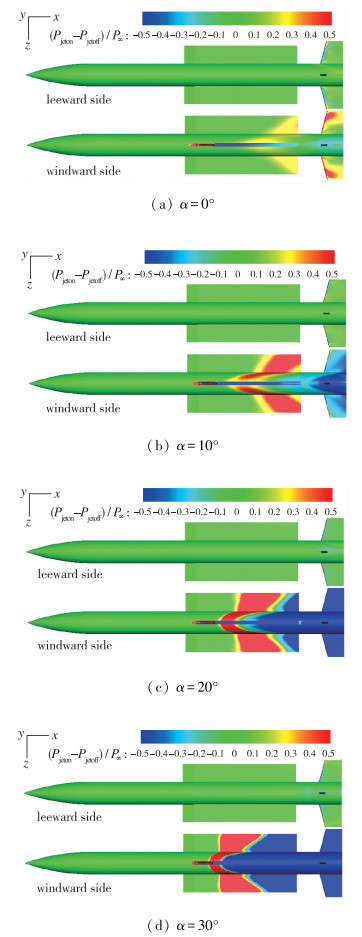
|
| 图 10 不同攻角计算得到的有喷与无喷压力差值分布 Fig.10 Distributions of (Pjeton-Pjetoff)/P∞ of different angles of attack at H=15 km, Ma∞=4 |
喷流对气动特性的影响一般采用力和力矩干扰因子的形式表征, 定义见式(4)
| $ {{K}_{i}}=\frac{{{F}_{i, {\rm jeton}}}-{{F}_{i, \text{jetoff}}}}{{{T}_{{}}}} $ | (4) |
其中, Fi, jetoff, Fi, jeton分别表示气动力六分量的无喷流值和有喷流值(有喷流值包含喷流本身产生的推力/推力矩), T表示喷流产生的总推力/力矩, i代表x, y, z, Mx, My, Mz等分量.如Ky代表法向力干扰因子, KMz代表俯仰力矩干扰因子.
图 11和图 12分别给出了C喷管工作时, 喷流干扰因子随攻角和Mach数的变化规律.
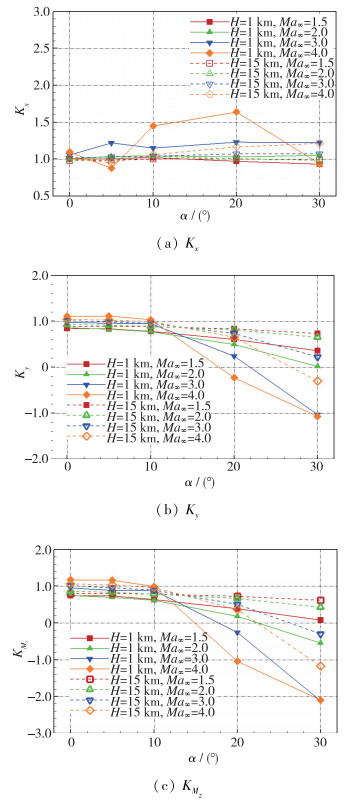
|
| 图 11 C喷管工作时干扰因子Kx, Ky, KMz随攻角的变化 Fig.11 Amplification factors Kx, Ky, KMz versus angles of attack with C jet |
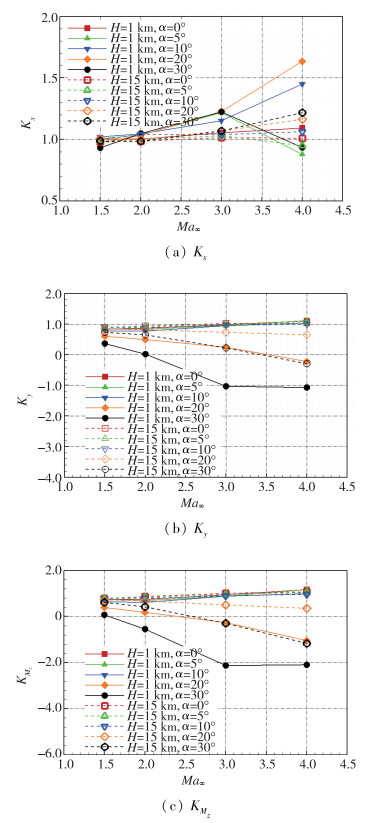
|
| 图 12 C喷管工作时干扰因子Kx, Ky, KMz随Mach数的变化 Fig.12 Amplification factors Kx, Ky, KMz versus Mach numbers with C jet |
(1) 对于轴向力干扰因子Kx而言, 在不同高度、Mach数、攻角条件下, 基本都大于或接近于1(产生有利干扰); 低飞行高度(H=1 km)下Kx随Mach数、攻角的变化幅度较高飞行高度(H=15 km)下的变化幅度大;
(2) 随攻角增加, Ky和KMz均呈现逐渐减小的趋势, 且飞行高度越低其随攻角的变化幅度越大;
(3) 不同攻角条件下, Ky和KMz随Mach数的变化规律不一致, 随攻角增加, 放大因子随Mach数变化趋势由随Mach数增加而增加变为随Mach数增加而减小, 且飞行高度越低, Ky和KMz随Mach数的变化幅度越大;
(4) 喷流干扰因子在某些条件会出现负值, 产生不利干扰.例如, H=1 km, Ma∞=3, 4下, Ky和KMz随攻角增加呈迅速减小, 出现小于0的情况, Ky最小可达-1.03, KMz最小可达-2.08.
4 结论本文数值模拟了类“阿斯特”导弹外形翼梢处侧向喷流干扰流场, 给出了典型干扰流场结构, 并分析了不同飞行参数(高度、Mach数、攻角)对喷流气动干扰特性的影响, 得出以下结论:
(1) 翼梢侧向喷流与来流干扰, 形成包含喷流弓形激波、分离激波、多类激波/激波干扰、激波/边界层干扰等复杂流场;
(2) 翼梢安装喷管方式减弱了喷流对弹体与控制面的干扰, 对比于以往表面安装方式, 干扰因子大于0.5范围明显增加, 有效增加了喷流控制使用范围;
(3) 喷流对气动特性的影响在不同飞行参数(高度、Mach数、攻角)条件呈现高度非线性变化, 尤其在低飞行高度条件下更为明显;
(4) 法向力和俯仰力矩喷流干扰因子在高Mach数、低飞行高度、大攻角条件下仍然会出现较大负值, 呈现严重不利干扰现象.
| [1] |
李素循. 近空间飞行器的气动复合控制原理及研究进展[J]. 力学进展, 2009, 39(6): 740-755. Li S X. Progress in aerodynamics of combination control for vehicles at high speed[J]. Advances in Mechanics, 2009, 39(6): 740-755. DOI:10.3321/j.issn:1000-0992.2009.06.012 (in Chinese) |
| [2] |
Price B B, Elliott G S, Ogot M. Experimental optimiza-tion of transverse jet injector geometries for mixing into a supersonic flow[C]. Proceedings of the 29th AIAA, Fluid Dynamics Conference, Albuquerque: AIAA, 1998. http://erepository.uonbi.ac.ke/handle/11295/86489
|
| [3] |
Li S X, Ni Z Y. Free jet flow and interacted jet flow[C]. Proceedings of the 7th Asian Symposium on Visualization, Singapore, 2003.
|
| [4] |
Zukoski E E, Spaid F W. Secondary injection of gases into a supersonic flow[J]. AIAA Journal, 1964, 2(10): 1689-1696. DOI:10.2514/3.2653 |
| [5] |
Aso S, Okuyama S, Kawai M. Experimental study on mixing phenomena in supersonic flows with slotinjection[C]. Proceedings of the 29th Aerospace Sciences Mee-ting, Reno: AIAA, 1991. https://arc.aiaa.org/doi/abs/10.2514/6.1991-16
|
| [6] |
Ni Z Y, Li S X, Sun Y T. Visualization of pressure contour and oil flow pattern on interactive flowfield[C]. Proceedings of the 7th Asian Symposium on Visualization, Singapore, 2003.
|
| [7] |
Chen P, Li S X, Luo S J, et al. Flow visualization on late-ral multiple jet interaction with freestream[J]. Journal of Flow Control, Measurement & Visualization, 2014, 2(1): 7-11. |
| [8] |
童木华, 李素循, 倪招勇, 等.横向喷流干扰流场结构研究[C].近代空气动力学研讨会论文集.北京: 中国空气动力学会, 2005. Tong M H, Li S X, Ni Z Y, et al. Study on flowfield structure of lateral jet interaction[C]. The Symposium on Modern Aerodynamics. Beijing: China Aeromechanics Society, 2005(in Chinese). http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGKQ200500001028.htm |
| [9] |
王军旗, 李素循, 倪招勇, 等. 数值模拟侧向超声速单喷流干扰流场特性[J]. 宇航学报, 2007, 28(3): 598-602. Wang J Q, Li S X, Ni Z Y, et al. Numerical simulation of characteristics of supersonic jet interaction flowfields[J]. Journal of Astronautics, 2007, 28(3): 598-602. DOI:10.3321/j.issn:1000-1328.2007.03.018 (in Chinese) |
| [10] |
王军旗, 李素循. 超声速多喷流干扰流场特性研究[J]. 力学学报, 2009, 41(4): 575-583. Wang J Q, Li S X. Study on the characteristics of interaction flowfields induced by supersonic multi-jets[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(4): 575-583. DOI:10.3321/j.issn:0459-1879.2009.04.014 (in Chinese) |
| [11] |
Brandeis J, Gill J. Experimental investigation of super-and hypersonic jet interaction on configurations with lifting surfaces[C]. Atmospheric Flight Mechanics Conference. AIAA, 1987. https://arc.aiaa.org/doi/10.2514/2.3354
|
| [12] |
Luo S J, Liu Y F, Cao N. Lateral jet jnteraction on a slender body in supersonic flow[C]. Proceedings of the 14th Asia Congress of Fluid Mechanic, Hanoi and Hal-ong, 2013.
|
| [13] |
Srivastava B. Aerodynamic performance of supersonic missile body-and wing tip-mounted lateral jets[J]. Journal of Spacecraft and Rockets, 1998, 35(3): 278-286. DOI:10.2514/2.3352 |
| [14] |
Roe P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computa-tional Physics, 1981, 43(2): 357-372. DOI:10.1016/0021-9991(81)90128-5 |
| [15] |
Yoon S, Jameson A. Lower-upper symmetric-gauss-seidel method for the Euler and Navier-Stokes equations[J]. AIAA Journal, 1988, 26(9): 1025-1026. DOI:10.2514/3.10007 |
| [16] |
Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flows[C]. Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno: AIAA, 1992. https://www.researchgate.net/publication/236888804_A_One-Equation_Turbulence_Model_for_Aerodynamic_Flows
|
| [17] |
刘耀峰, 李素循, 倪招勇.多喷口布局对气动特性影响[A]//吴光辉, 陈迎春.大型客机计算流体力学应用与发展[M].上海: 上海交通大学出版社, 2009. Liu Y F, Li S X, Ni Z Y. The influentce of multi-jets layout on aerodynamic characteristics[A]//Application and Development on Computational Fluid Dynamics for Large Passenger Aircraft[M]. Shanghai: Shanghai Jiaotong University Press, 2009(in Chinese). |
| [18] |
刘耀峰.多喷流干扰数值模拟研究[D].北京: 中国航天空气动力技术研究院, 2007. Liu Y F. Numerical investigation of multiple jets interac-tion characteristics[D]. Beijing: Beijing China Academy of Aerospace Aerodynamics, 2007(in Chinese). |
| [19] |
Chen P, Li S X, Liu Y F, et al. Experimental and computational study of multiple jets in crossflow on a flat plate[C]. Proceedings of the 14th Asia Congress of Fluid Mechanic, Hanoi and Halong, 2013.
|
| [20] |
Fu J, Liu Y, Ni Z, et al. Investigation of divert control jet interaction effects on aerodynamic characteristics[C]. Proceedings of the 7th Asia-Pacific International Sympo-sium on Aerospace Technology, Cairns: Curran Associates, Inc., 2015.
|



