存在扰动的两种密度不同的流体交界面, 在受到外部作用时, 扰动将发展, 界面将失稳, 导致两种流体发生混合, 即界面不稳定性.激波与不同流体界面的相互作用广泛存在于自然界和工程应用领域[1], 导致的流动失稳被称为Richtmyer-Meshkov(R-M)不稳定性.它对流体的混合具有促进作用, 从而影响流动发展进程.
对于激波加速界面导致的流体不稳定性的研究可追溯到20世纪50年代[2]. 1960年, Richtmyer对激波加速下的界面流动不稳定性给出了严格的理论推导和分析预测; 1969年, Meshkov通过激波管实验验证了Richtmyer的分析预测[3].
球形界面和平面激波是研究激波与界面作用的良好模型. Haas等[4]通过在水平激波管中观测弱激波对He和R22的球形界面的作用, 研究了激波反射折射及绕射等复杂现象, 详细分析了作用过程中的激波速度和界面速度变化规律.球形界面实验研究的不足是需要支杆支撑, 支杆会对其附近的界面发展产生影响.柱形界面也是研究R-M不稳性的基本模型之一. Tomkins等[5]运用实验测量了激波与无膜技术形成的气柱作用过程中气体混合的速率, 揭示了气体混合的机制, 并指出了二次不稳定性在界面发展后期的重要作用.单模态界面在R-M不稳定性研究中也被大量使用[6].例如, Brouillette等[7]采用厚度为0.5 μm的硝化纤维膜进行了相关研究, Sadot等[8]采用厚度为0.1 μm的薄膜形成的单模界面开展了与平面激波作用的实验.通常, 分开两种流体的薄膜破裂的碎片会影响不稳定性的发展, 且这种影响很难预测.扰动振幅增长率的激波管实验结果与理论预测之间的偏差大小取决于其强度.为了避免薄膜对实验结果的影响, 可采用薄金属板分开流体, 然后在启动激波管前通过机械装置快速抽出隔板, 将抽出隔板时产生的扰动作为界面上初始的扰动.因为分子扩散, 这样得到的是一个密度梯度为有限值的连续界面, 与密度间断界面相比不稳定性的发展会减慢.然而, 采用这种方法形成的初始扰动不具有可重复性.一种改进的生成无膜界面的方法是, 让两种介质分别从竖直激波管的两端进入观察段中形成界面, 并在实验段位置开设狭缝排出多余的气体, 通过振荡实验仪器来得到正弦的界面[9-10].
虽然实验研究比较直观, 但难度大, 重复性差, 且大多数结果都是定性的流动显示, 定量的实验数据少.随着计算机和数值计算技术的发展, 越来越多的学者运用数值模拟的方法对R-M不稳定性开展研究工作. Holmes等[11]用前缘追踪数值方法模拟了R-M不稳定性, 准确捕捉了物质界面和激波.由于要求追踪所有的波系和界面的发展, 该算法的计算量很大. Anuchina等[12]用MAH-3程序得到了R-M不稳定性线性和非线性发展阶段的结果, 对比了二维和三维的界面增长率. Latini等[13]用WENO重构方法对R-M不稳定性进行数值模拟, 发现低阶方法在不稳定性发展的后期保留了大尺度结构和对称性, 而高阶方法复现了小尺度结构, 导致对称结构被破坏, 从而增强了流体间的混合. Hu等[14]用6阶中心-迎风WENO格式模拟了R-M不稳定性, 并与相关实验结果做了对比.近年, Olson等[15]用大涡模拟方法模拟了R-M不稳定性, 讨论了数值方法网格精度Reynolds数的影响.
关于早期的R-M不稳定性研究, 可参考Holmes等[16]的综述, 文献系统而详尽地比较了实验数值模拟线性理论非线性理论, 以及脉冲理论的结果.在不稳定性发展早期, 界面以大尺度结构为主, 线性理论通常能较好地与实验和数值模拟结果吻合.在不稳定性发展后期, 界面两侧的流体出现速度差, 产生二次不稳定性, 出现一些小尺度结构, 精度越高的数值算法, 越能识别出小尺度结构, 而实验方法则难以测量.
本文针对激波与H2O和N2等混合物界面相互作用而发生的R-M不稳定性流动现象数值模拟, 主要分析界面振幅和激波强度的影响特征及规律, 为工程应用提供理论指导.
1 数值方法 1.1 基本控制方程因研究的流体由多种组分构成, 故基本控制方程由二维可压缩Navier-Stokes方程和组分质量守恒方程组成.不考虑外部体积力做功和辐射换热, 其守恒型为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho u}}{{\partial x}} + \frac{{\partial \rho v}}{{\partial y}} = 0, \\ \;\;\frac{{\partial \rho u}}{{\partial t}} + \frac{{\partial \left( {\rho {u^2} + p} \right)}}{{\partial x}} + \frac{{\partial \rho uv}}{{\partial y}} = \frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{xy}}}}{{\partial y}}, \\ \;\;\;\frac{{\partial \rho v}}{{\partial t}} + \frac{{\partial \rho uv}}{{\partial x}} + \frac{{\partial \left( {\rho {v^2} + p} \right)}}{{\partial y}} = \frac{{\partial {\tau _{yx}}}}{{\partial x}} + \frac{{\partial {\tau _{yy}}}}{{\partial y}}, \\ \;\;\;\;\;\;\frac{{\partial \rho E}}{{\partial t}} + \frac{{\partial \left( {\rho E + p} \right)u}}{{\partial x}} + \frac{{\partial \left( {\rho E + p} \right)v}}{{\partial y}} = \\ \;\frac{{\partial \left( {u{\tau _{xx}} + v{\tau _{xy}} + {q_x}} \right)}}{{\partial x}} + \frac{{\partial \left( {u{\tau _{yx}} + v{\tau _{yy}} + {q_y}} \right)}}{{\partial y}}, \\ \frac{{\partial \rho {Y_k}}}{{\partial t}} + \frac{{\partial \left[{\rho \left( {u + V_{xk}^{\rm{c}}} \right){Y_k}} \right]}}{{\partial x}} + \frac{{\partial \left[{\rho \left( {v + V_{yk}^{\rm{c}}} \right){Y_k}} \right]}}{{\partial y}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial {J_{xk}}}}{{\partial x}} + \frac{{\partial {J_{yk}}}}{{\partial y}}. \end{array} $ |
其中, ρ, (u, v), p, Yk分别为流体的密度速度分量压力第k种组分的质量分数. E为单位质量流体的总能, 表达式为
| $ E = \sum\limits_{k = 1}^N {{Y_k}\left[{\int_{{T_{{\rm{ref}}}}}^T {{c_{{\rm{p}}k}}{\rm{d}}T + h_{{\rm{f}}k}^0} } \right]} - p/\rho + u_i^2/2. $ |
其中, N为组分的总数目, hfk0为第k种组分在参考温度下的生成焓. cpk为第k种组分的定压比热, 计算公式为
| $ \frac{{{c_{{\rm{p}}k}}{W_k}}}{{{R_0}}} = {a_{1k}} + {a_{2k}}T + {a_{3k}}{T^2} + {a_{4k}}{T^3} + {a_{5k}}{T^4}. $ |
其中, Wk为第k种组分的相对分子质量, R0为普适气体常数, T为温度.多项式中的系数aik(i=1, 2, 3, 4, 5) 取自Burcat等[17]给出的拟合数据. τ, q, J分别代表黏性剪切应力、热流通量、组分扩散通量.以x方向为例, 公式分别为
| $ \begin{array}{l} \;\;\;\;\;\;\;{\tau _{xx}} = \mu \left( {\frac{4}{3}\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right), \\ \;\;\;\;\;\;\;\;\;{\tau _{xy}} = \mu \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right), \\ {q_x} = - \lambda \frac{{\partial T}}{{\partial x}} - \rho \sum\limits_{k = 1}^N {{h_k}{D_k}\frac{{{W_k}}}{W}\frac{{\partial {X_k}}}{{\partial x}}}, \\ \;\;\;\;\;{J_{xk}} = \rho {D_k}\frac{{\partial {Y_k}}}{{\partial x}}. \end{array} $ |
其中, μ, λ, W分别为混合流体的黏性系数导热系数平均分子质量; hk, Dk, Xk分别为第k种组分的静焓相对于混合流体的质量扩散系数Mole分数.
第k种组分的黏性系数采用基于Chapman-Enskog理论的公式, 第k种组分的导热系数采用改进的Eucken公式, 两种组分间的相互扩散系数计算采用Chapman和Enskog基于Boltzmann方程提出的公式, 分别为
| $ \begin{array}{l} \;\;\;{\mu _k} = \frac{{26.69{{\left( {{W_k}T} \right)}^{1/2}}}}{{\sigma _k^2{\mathit{\Omega }_{vk}}}}, \\ \frac{{{\lambda _k}{W_k}}}{{{\mu _k}{c_{vk}}}} = 1.32 + \frac{{1.77}}{{\left( {{c_{{\rm{p}}k}}/R} \right) - 1}}, \\ \;\;\;\;\;{D_{ij}} = \frac{{0.00266{T^{3/2}}}}{{pW_{ij}^{1/2}\sigma _{ij}^2{\mathit{\Omega }_{{\rm{d}}ij}}}}. \end{array} $ |
公式中各个物理量的定义和数值可查阅Reid等[18]的物性估算手册.
混合流体的黏性系数计算公式如下:
| $ \mu = \sum\limits_{i = 1}^N {\frac{{{X_i}{\mu _i}}}{{\sum\limits_{j = 1}^N {{X_j}{\mathit{\phi }_{ij}}} }}} . $ |
其中,
| $ {\mathit{\phi }_{ij}} = \frac{{{{\left[{1 + {{\left( {{\mu _i}/{\mu _j}} \right)}^{1/2}}{{\left( {{W_j}/{W_i}} \right)}^{1/4}}} \right]}^2}}}{{{{\left[{8\left( {1 + {W_i}/{W_j}} \right)} \right]}^{1/2}}}}. $ |
混合流体的导热系数计算公式如下:
| $ \lambda = \sum\limits_{i = 1}^N {\frac{{{X_i}{\lambda _i}}}{{\sum\limits_{i = 1}^N {{X_i}{A_{ij}}} }}} . $ |
其中,
| $ {A_{ij}} = \frac{{{{\left[{1 + {{\left( {{\lambda _i}/{\lambda _j}} \right)}^{1/2}}{{\left( {{W_j}/{W_i}} \right)}^{1/4}}} \right]}^2}}}{{{{\left[{8\left( {1 + {W_i}/{W_j}} \right)} \right]}^{1/2}}}}. $ |
第k种组分在混合流体中的扩散系数, 可由其与系数Dij的关系得到, 即
| $ {D_k} = \frac{{1 - {X_i}}}{{\sum\limits_j {\frac{{{X_i}}}{{{D_{ij}}}}} }}. $ |
计算中引入的修正速度Vxkc, Vykc是指第k种组分相对于混合流体的扩散速度, 公式为
| $ V_{xk}^{\rm{c}} = \sum\limits_{k = 1}^N {{D_k}} \frac{{{W_k}}}{W}\frac{{\partial {X_k}}}{{\partial x}}, \;\;\;V_{yk}^{\rm{c}} = \sum\limits_{k = 1}^N {{D_k}} \frac{{{W_k}}}{W}\frac{{\partial {X_k}}}{{\partial y}}. $ |
因各组分都为完全气体, 故混合流体满足完全气体状态方程:
| $ p = \rho RT\sum\limits_{k = 1}^N {\frac{{{Y_k}}}{{{W_k}}}} . $ |
解出守恒变量后, 依据守恒变量可以直接得到密度动能总能质量分数.压力和静焓都是温度的函数, 可使用Newton迭代法得到温度.改写混合流体状态方程和总能表达式, 得到:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;p = \rho \sum\limits_{k = 1}^N {{Y_k}{R_k}T, } \\ p = \rho h - E + \frac{1}{2}\rho \left( {{u^2} + {v^2}} \right). \end{array} $ |
构造关于T的迭代函数Q(T)为
| $ Q\left( T \right) = \rho \sum\limits_{k = 1}^N {{Y_k}{h_k} - \left( {E - \frac{1}{2}\rho u_i^2} \right)} - \rho \sum\limits_{k = 1}^N {{Y_k}{R_k}T = 0.} $ |
将迭代函数Q(T)对T求导:
| $ Q'\left( T \right) = \frac{{{\rm{d}}Q\left( T \right)}}{{{\rm{d}}T}} = \rho \sum\limits_{k = 1}^N {\left( {{Y_k}{c_{{\rm{p}}k}} - {Y_k}{R_k}} \right)} = \rho \left( {{c_{\rm{p}}} - R} \right). $ |
得到迭代公式:
| $ {T^{n + 1}} = {T^n} - \frac{{Q\left( {{T^n}} \right)}}{{Q'\left( {{T^n}} \right)}}. $ |
考虑有限差分法离散, 对流项采用5阶特征紧致-WENO混合格式[19], 输运项采用6阶对称紧致格式, 时间推进采用3阶显式Runge-Kutta方法.为此, 改写基本控制方程如下:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial {\mathit{\boldsymbol{F}}_{\rm{c}}}}}{{\partial x}} + \frac{{\partial {\mathit{\boldsymbol{G}}_{\rm{c}}}}}{{\partial y}} = \frac{{\partial {\mathit{\boldsymbol{F}}_{\rm{v}}}}}{{\partial x}} + \frac{{\partial {\mathit{\boldsymbol{G}}_{\rm{v}}}}}{{\partial y}}. $ |
其中, U为守恒变量, Fc, Gc分别为x, y方向的对流通量, Fv, Gv分别为x, y方向的输运通量.
特征紧致-WENO混合格式是紧致格式和WENO格式通过加权而形成的, 用以解决光滑流场中有间断的问题.紧致格式可用较少的模板点高精度逼近导数, 但在处理间断时会出现严重的数值振荡; WENO格式可抑制这种振荡, 但数值耗散大.于是, 通过加权因子使两者结合起来, 在光滑流场使用紧致格式, 在参数梯度比较大的间断部分使用WENO格式, 同时满足了对高精度和捕捉激波的算法要求.
省略下标“c”, 记基本控制方程x方向的对流通量F的Jacobi矩阵为
| $ {\mathit{\boldsymbol{U}}_{j + 1/2}} = \frac{1}{2}\left( {{\mathit{\boldsymbol{U}}_j} + {\mathit{\boldsymbol{U}}_{j + 1}}} \right). $ |
进而得到λj+1/2(i)和Lj+1/2(i), 则可在网格点xj上计算特征变量
| $ w_j^{\left( i \right)} = \mathit{\boldsymbol{L}}_{j + 1/2}^{\left( i \right)}{\mathit{\boldsymbol{F}}_j}. $ |
由特征紧致-WENO混合格式的定义可对半点特征变量进行差分逼近, 即
| $ \begin{array}{l} \sigma _{j + 1/2}^{\left( i \right)}\varphi _{j + 1/2}^{\left( i \right)}w_{j - 1/2}^{\left( i \right)} + w_{j + 1/2}^{\left( i \right)} + \sigma _{j + 1/2}^{\left( i \right)}\psi _{j + 1/2}^{\left( i \right)}w_{j + 3/2}^{\left( i \right)} = \hat c_{j + 1/2}^{\left( i \right)}, \\ \;\;\;\;\;\hat c_{j + 1/2}^{\left( i \right)} = \sigma _{j + 1/2}^{\left( i \right)}\hat b_{j + 1/2}^{\left( i \right)} + \left( {1 - \sigma _{j + 1/2}^{\left( i \right)}} \right)\hat w_{j + 3/2}^{\left( i \right), \;{\rm{WENO}}}. \end{array} $ |
加权函数
| $ \sigma _{j + 1/2}^{\left( i \right)} = \min \left[{1, r_{j + 1/2}^{\left( i \right)}/{r_{\rm{c}}}} \right]. $ |
其中, rc为数值模拟的经验参数.流场光滑因子rj+1/2(i)的表达式为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;r_{j + 1/2}^{\left( i \right)} = \min \left( {r_j^{\left( i \right)}, r_{j + 1}^{\left( i \right)}} \right), \\ r_j^{\left( i \right)} = \frac{{\left| {\;2\Delta w_{j + 1/2}^{\left( i \right)}\Delta w_{j - 1/2}^{\left( i \right)}\;} \right| + \varepsilon }}{{{{\left( {\Delta w_{j + 1/2}^{\left( i \right)}} \right)}^2} + {{\left( {\Delta w_{j - 1/2}^{\left( i \right)}} \right)}^2} + \varepsilon }}. \end{array} $ |
此外,
| $ \varphi _{j + 1/2}^{\left( i \right)} = \frac{1}{3} + \frac{1}{6}s_{j + 1/2}^{\left( i \right)}, \;\;\;\psi _{j + 1/2}^{\left( i \right)} = \frac{1}{3} - \frac{1}{6}s_{j + 1/2}^{\left( i \right)}. $ |
其中,
| $ s_{j + 1/2}^{\left( i \right)} = {\rm{sign}}\left( {\lambda _{j + 1/2}^{\left( i \right)}} \right). $ |
通过WENO格式得到
| $ \begin{array}{l} \hat b_{j + 1/2}^{\left( i \right)} = &\frac{1}{2}\left( {1 + s_{j + 1/2}^{\left( i \right)}} \right)\left( {\frac{1}{{18}}w_{j - 1}^{\left( i \right)} + \frac{{19}}{{18}}w_j^{\left( i \right)} + \frac{5}{9}w_{j + 1}^{\left( i \right)}} \right) + \\ &\frac{1}{2}\left( {1 - s_{j + 1/2}^{\left( i \right)}} \right)\left( {\frac{5}{9}w_j^{\left( i \right)} + \frac{{19}}{{18}}w_{j + 1}^{\left( i \right)} + \frac{1}{{19}}w_{j + 2}^{\left( i \right)}} \right). \end{array} $ |
整理以上公式, 得
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{j + 1/2}}{\mathit{\boldsymbol{F}}_{j - 1/2}} + {\mathit{\boldsymbol{L}}_{j + 1/2}}{\mathit{\boldsymbol{F}}_{j + 1/2}} + {\mathit{\boldsymbol{\varPsi}}_{j + 1/2}}{\mathit{\boldsymbol{F}}_{j + 3/2}} = {\mathit{\boldsymbol{C}}_{j + 1/2}}. $ |
其中
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{j + 1/2}^{\left( i \right)} = \sigma _{j + 1/2}^{\left( i \right)}\varphi _{j + 1/2}^{\left( i \right)}\mathit{\boldsymbol{L}}_{j + 1/2}^{\left( i \right)}, \\ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{j + 1/2}^{\left( i \right)} = \sigma _{j + 1/2}^{\left( i \right)}\psi _{j + 1/2}^{\left( i \right)}\mathit{\boldsymbol{L}}_{j + 1/2}^{\left( i \right)}, \\ \;\;\;\;\;\;\;\;\;\;\;C_{j + 1/2}^{\left( i \right)} = \hat c_{j + 1/2}^{\left( i \right)}. \end{array} $ |
通过解块三对角线性方程组获得半点的数值通量Fj+1/2, 然后求出(∂F/∂x), 即
| $ {\left( {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}}} \right)_j} = \frac{{\left( {{\mathit{\boldsymbol{F}}_{j + 1/2}} - {\mathit{\boldsymbol{F}}_{j - 1/2}}} \right)}}{{\Delta x}}. $ |
对于输运项的离散也以x方向为例.记uj′, uj″分别为(∂u/∂x)j, [∂(μ∂u/∂x)/∂x]j的近似差分, 则可由6阶对称紧致格式离散为
| $ \begin{array}{l} \frac{1}{3}{u_{j - 1}}' + {u_j}' + \frac{1}{3}{u_{j + 1}}' = \\ \;\;\;\;\frac{{28\left( {{u_{j + 1}} - {u_{j - 1}}} \right) + \left( {{u_{j + 2}} - {u_{j - 2}}} \right)}}{{36\Delta x}}, \\ \frac{1}{3}{u_{j - 1}}'' + {u_j}'' + \frac{1}{3}{u_{j + 1}}'' = \\ \frac{{28\left( {\mu {u_{j + 1}}' - \mu {u_{j - 1}}'} \right) + \left( {\mu {u_{j + 2}}' - \mu {u_{j - 2}}'} \right)}}{{36\Delta x}}. \end{array} $ |
联立上述方程, 通过解三对角线性方程组获得输运项[∂(μ∂u/∂x)/∂x].
对于时间推进, 一种3步3阶显式Runge-Kutta方法为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{U}}_j^{\left( 1 \right)} = \mathit{\boldsymbol{U}}_j^{\left( n \right)} + \Delta t\mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{U}}_j^{\left( n \right)}} \right), \\ \mathit{\boldsymbol{U}}_j^{\left( 2 \right)} = \frac{3}{4}\mathit{\boldsymbol{U}}_j^{\left( n \right)} + \frac{1}{4}\mathit{\boldsymbol{U}}_j^{\left( 1 \right)} + \frac{1}{4}\Delta t\mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{U}}_j^{\left( 1 \right)}} \right), \\ \mathit{\boldsymbol{U}}_j^{\left( {n + 1} \right)} = \frac{1}{3}\mathit{\boldsymbol{U}}_j^{\left( n \right)} + \frac{2}{3}\mathit{\boldsymbol{U}}_j^{\left( 2 \right)} + \frac{2}{3}\Delta t\mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{U}}_j^{\left( 2 \right)}} \right). \end{array} $ |
其中, Uj为j方向的守恒变量, L为空间算子.
2 算法验证选取一维Sod激波管中物质界面变化问题.初始条件为
| $ \left( {\rho, p, v} \right) = \left\{ \begin{array}{l} \left( {0.092, 0.5, 0} \right), \;\;\;\;\;\;&0 < y < 0.14\\ \left( {0.138, 0.9, - 400} \right), &0.14 < y < 0.15 \end{array} \right.. $ |
其中, 密度ρ的单位为kg/m3, 压力p的单位为atm, 速度v的单位为m/s.计算中, 采用了3000个网格. 图 1为t = 0.03 ms时流场的密度压力速度温度分布曲线.同时, 作为对比, 图中还以符号“□”给出了5阶WENO格式的计算结果.可以看出, 本文算法同5阶WENO格式的计算结果吻合良好.
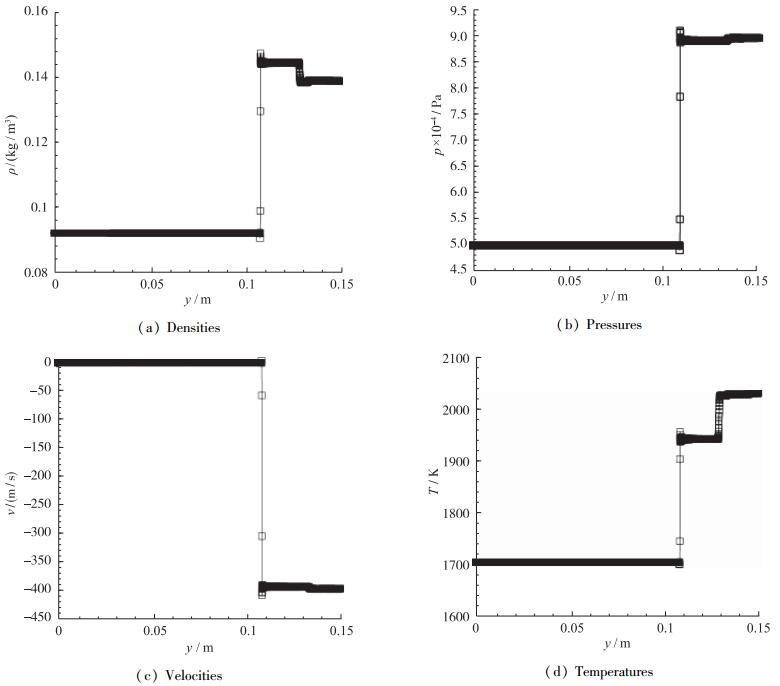
|
| 图 1 一维Sod激波管问题对比 Fig.1 Comparisons for one-dimensional Sod shock tube problem |
选取一维激波与气泡相互作用问题, 一道激波沿y方向穿过一个静止气泡.初始条件为
| $ \left( {\rho ,p,v} \right) = \left\{ {\begin{array}{*{20}{c}} {\left( {0.138,0.9, - 400} \right),}&{0.75 < y < 1.0}\\ {\left( {0.092,0.5,0} \right),}&\begin{array}{l} 0 < y < 0.4\\ 0.6 < y < 0.75 \end{array}\\ {\left( {0.476,0.5,0} \right),}&{0.4 < y < 0.6} \end{array}} \right.. $ |
计算中, 采用了3000个网格. 图 2为t = 0.03 ms时流场的密度压力速度温度分布曲线, 同时也以符号“□”给出了5阶WENO格式的计算结果.本文算法同5阶WENO格式的计算结果也吻合良好.
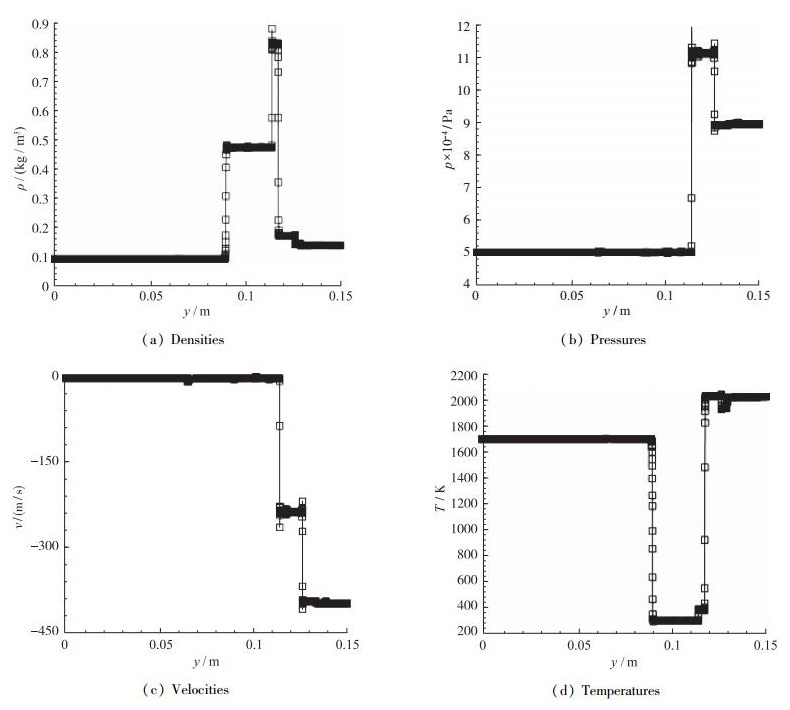
|
| 图 2 一维激波与气泡相互作用问题对比 Fig.2 Comparisons for one-dimensional shock wave and bubble interaction problem |
5阶WENO格式是经典的被广泛用来捕捉可压缩流动中激波等复杂间断的高精度格式.以上两个典型的算例均对比显示出本文算法的计算精度与其一致, 表明所引入的5阶特征紧致-WENO混合格式对于激波等复杂间断的捕捉也具有很强的适用性和有效性.
3 R-M不稳定性计算分析二维物理模型如图 3所示.计算区域中, 界面上层流体A为H2O和N2的混合物, Ab表示激波后的流体, Af表示激波前的流体; 界面下层流体B为H2, O2, N2的混合物.平面正激波从流体A中向流体B中运动, 在距离激波一定距离处有受单模态扰动的呈一定几何分布规律的界面, a为界面扰动的振幅, λa为界面扰动的波长.
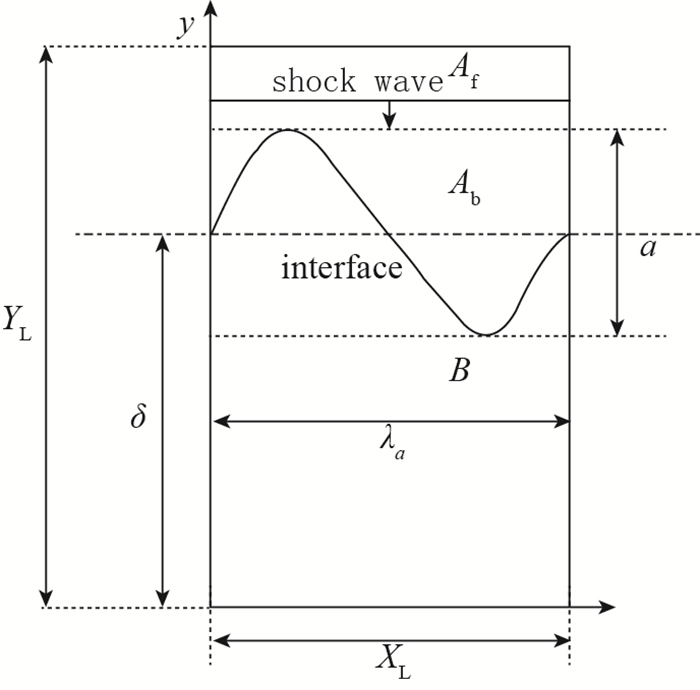
|
| 图 3 物理模型示意图 Fig.3 Schematic of the physical model |
计算区域为矩形区域, 宽XL为0.0314 m, 高YL为0.15 m.正弦型流体间断界面为[20]
| $ y\left( {t = 0} \right) = a\sin x + \delta . $ |
其中, δ为一个常数, 几何意义见图 3.根据激波Mach数Ms和Rankine-Hugoniot关系式确定激波后的流动参数, 即
| $ \begin{array}{l} \;\;\;\;\;\;\;\frac{{{p_{\rm{f}}}}}{{{p_{\rm{b}}}}} = \frac{{2\gamma }}{{\gamma + 1}}M_{\rm{s}}^2 - \frac{{\gamma - 1}}{{\gamma + 1}}, \\ \frac{{{T_{\rm{f}}}}}{{{T_{\rm{b}}}}} = \frac{{\left( {1 + \frac{{\gamma - 1}}{2}M_{\rm{s}}^2} \right) \cdot \left( {\frac{{2\gamma }}{{\gamma - 1}}M_{\rm{s}}^2 - 1} \right)}}{{\frac{{{{\left( {\gamma + 1} \right)}^2}}}{{2\left( {\gamma - 1} \right)}}M_{\rm{s}}^2}}, \\ \;\;\;\;\;\;\;\;\;\;\frac{{{\rho _{\rm{f}}}}}{{{\rho _{\rm{b}}}}} = \frac{{\left( {\gamma + 1} \right)M_{\rm{s}}^2}}{{2 + \left( {\gamma - 1} \right){M^2}}}, \\ \;\;\;\;\;\;\;\;\frac{{{u_{\rm{f}}}}}{{{u_{\rm{b}}}}} = \frac{2}{{\gamma + 1}} \cdot \frac{1}{{M_{\rm{s}}^2}} + \frac{{\gamma - 1}}{{\gamma + 1}}. \end{array} $ |
其中, 下标f, b分别表示激波后和激波前相应的物理参数.
上下边界采用流动物理量外插边界条件, 左右边界采用周期性边界条件.网格为均匀分布正交网格, 网格数为100 × 500.
流体A中物质的质量分数分别为: wH2O=0.135, wN2=0.865, 密度ρA=0.092 kg/m3; 流体B中物质的质量分数分别为: wH2= 0.015, wO2= 0.12, wN2= 0.865, 密度ρB= 0.476 kg/m3.上下层流体等压, 均为0.5 atm.
3.1 基本工况为便于参变对比分析, 设定基本工况并加以计算分析.取激波Mach数Ms=1.3, 界面扰动的振幅a=0.005 m.
图 4为瞬时密度等值云图时间序列,图 5为相应的瞬时纹影时间序列图, 计算公式为
| $ {S_h} = 0.8{{\rm{e}}^{\left( {\frac{{ - 0.8\nabla \rho }}{{\nabla {\rho _{\max }}}}} \right)}}. $ |
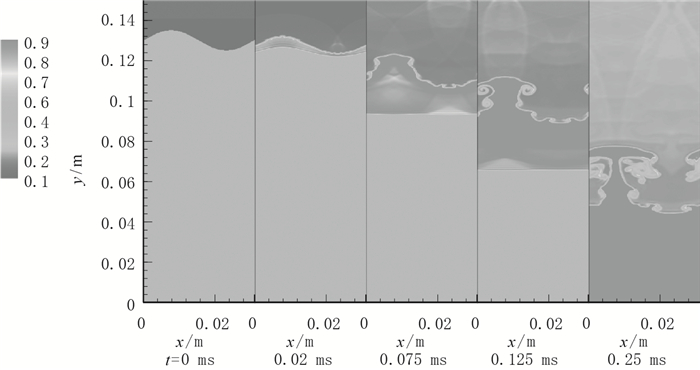
|
| 图 4 瞬时密度(Ms=1.3, a=0.005 m) Fig.4 Instantaneous densities (Ms=1.3, a=0.005 m) |
|
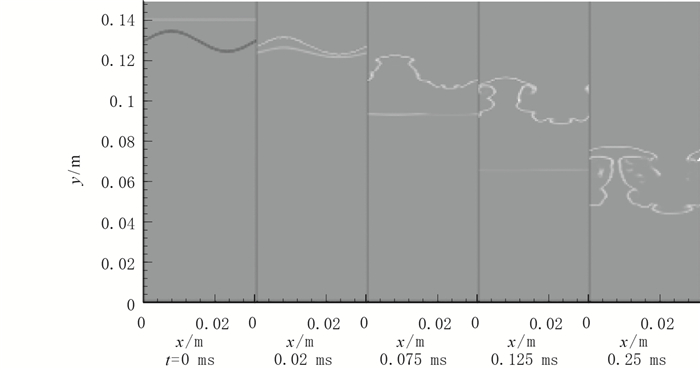
| 图 5 瞬时纹影图(Ms=1.3, a=0.005 m) Fig.5 Instantaneous schlieren (Ms=1.3, a=0.005 m) |
由图可以清晰地观察到激波与界面相互作用的过程.激波后流体的密度变大, 激波与界面相遇后继续入射. t=0.02 ms后, 激波离开界面, 平面入射波发生微弱变形, 而界面仍然是比较规则的正弦形. t=0.075 ms后, 激波基本恢复成平面波, 界面逐渐发生变形.在t=0.125 ms后可以看到, 界面已经完全失去正弦形状, 轻流体以“气泡”形式进入重流体, 重流体以“漏斗”形式进入轻流体, 且两端发生卷起, 形成“蘑菇”结构, “蘑菇杆”上出现一些小尺度结构. t=0.25 ms后, “蘑菇”结构非常明显, “蘑菇杆”上的小尺度结构会逐渐消失, 流体混合剧烈.
图 6为瞬时流向速度等值云图时间序列.在t=0.02 ms以后, 界面两侧的流体存在流向速度梯度, 所以沿界面切线方向两侧流体也存在流向速度梯度, 引起Kelvin-Helmholtz(K-H)不稳定性[21], 从而产生涡, 使界面发生变形.在t=0.125 ms的界面发展后期, K-H不稳定性的作用更为明显, 界面“漏斗”结构两侧在涡的作用下发生卷起, 形成“蘑菇”结构.
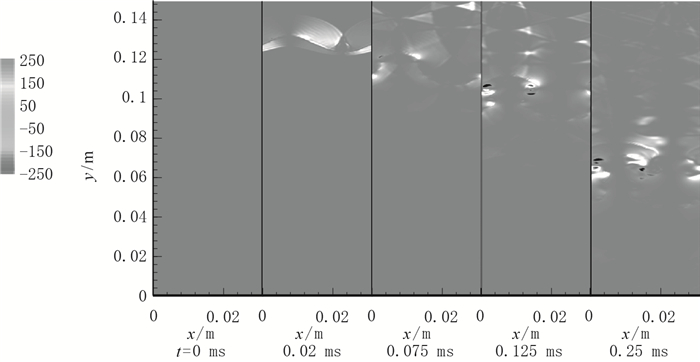
|
| 图 6 瞬时流向速度(Ms=1.3, a=0.005 m) Fig.6 Instantaneous streamwise velocities (Ms=1.3, a=0.005 m) |
图 7为瞬时涡量等值云图时间序列. t=0 ms时, 激波与界面没有接触, 流场中基本没有涡.激波与界面相遇后, 流体界面附近产生涡, 涡量有正有负, 对称分布.随时间推移, 涡量的大小和方向发生变化. “蘑菇”结构的顶部涡量最小, 两侧最大.涡量表征流体旋转运动的强度, 在涡的作用下, 不同流体不断被卷吸掺混.
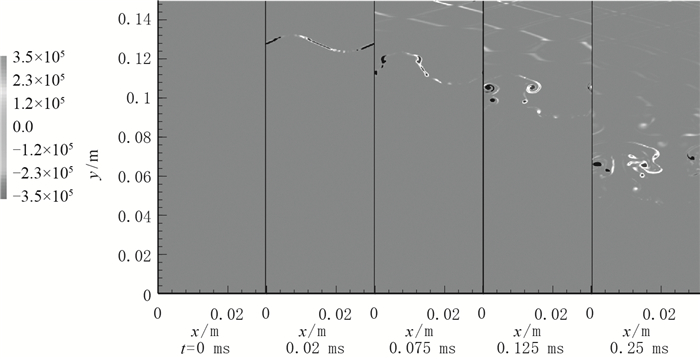
|
| 图 7 瞬时涡量(Ms=1.3, a=0.005 m) Fig.7 Instantaneous vorticities (Ms=1.3, a=0.005 m) |
在R-M不稳定性发展的前期, 激波对界面的发展起主要作用; 在中后期, 界面附近涡的产生和分布对界面变形和演化起关键作用.现分析涡动力学方程:
| $ \frac{{{\rm{D}}\mathit{\boldsymbol{\omega }}}}{{{\rm{D}}t}} = \frac{1}{{{\rho ^2}}}\nabla \rho \times \nabla p + \left( {\mathit{\boldsymbol{\omega }}\nabla } \right)\mathit{\boldsymbol{v}} - \mathit{\boldsymbol{\omega }}\left( {\nabla \cdot \mathit{\boldsymbol{v}}} \right) + v{\nabla ^2}\mathit{\boldsymbol{\omega }}\mathit{\boldsymbol{.}} $ |
右端第1项为斜压项, 是指由于密度梯度方向和压力梯度方向不在一条直线而导致涡量的变化.该项是导致涡量变化的最重要因素, 产生涡量的方向符合右手定则.一般地, 顺时针方向涡量为负, 逆时针方向涡量为正.第2项是指由于流场速度空间分布不均匀, 在平行于涡线方向和垂直于涡线方向会使涡线发生拉伸和扭曲, 从而导致涡量的变化.第3项为散度项, 是指流体微元在运动过程中, 体积变化改变了转动惯量, 从而导致转动角速度的变化, 即涡量的变化.该项只影响涡量的大小, 不影响涡量的方向.第4项为黏性项, 是指由于黏性扩散引起的涡量扩散, 即影响涡的耗散.
这里, 界面两侧流体密度的不同产生密度梯度, 激波的作用产生压力梯度.涡线的拉伸和扭曲可以忽略, 即第2项.因此, 涡量的变化主要取决于斜压项散度项黏性项. 图 8为t = 0.02, 0.075, 0.25 ms不同时刻斜压项与散度项的空间分布对比, 对应激波与界面相遇阶段界面线性发展阶段界面非线性发展阶段.对比发现, 在激波与界面作用的前中后3个时刻, 斜压项均比散度项大1个量级, 表明在激波与界面作用的过程中, 斜压项始终对涡的产生起主导作用.
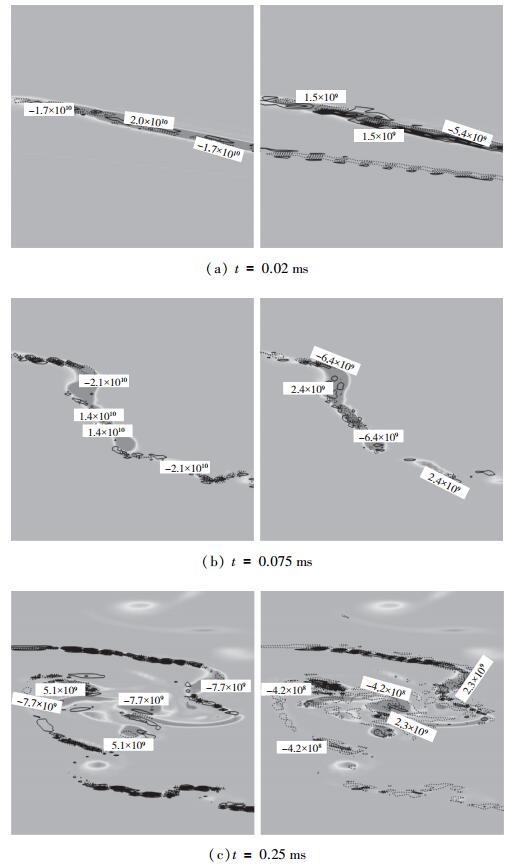
|
| 图 8 瞬时斜压项(左列)和瞬时散度项(右列)(Ms=1.3, a=0.005 m) Fig.8 Instantaneous baroclinic terms (left column) and instantaneous dilatation terms (right column) (Ms=1.3, a=0.005 m) |
定义拟涡能ε为
| $ \varepsilon = \int {\rho {\omega ^2}{\rm{d}}x{\rm{d}}y} . $ |
表征流场中激波对于涡量变化的影响.界面振幅的数值计算方法为[22]:首先判断点(i, j)处H2的质量分数是否大于初始时刻流体B中H2的质量分数的一半, 再判断点(i, j+1) 处H2的质量分数是否小于等于初始时刻流体B中H2的质量分数的一半; 若真, 则定义点(i, j)是位于界面上的点, 并记录y方向的坐标.沿着x方向依次进行该过程, 则可找到一个完整周期内的界面上所有点y方向的坐标.然后, 计算界面振幅, 即
| $ a = \frac{1}{2}\left( {{y_{\max }} - {y_{\min }}} \right). $ |
其中ymax, ymin分别为界面上的点在y方向坐标的最大值和最小值.
图 9给出了激波与界面作用过程中拟涡能和界面振幅随时间变化的曲线.初始阶段, 激波作用于界面, 斜压作用剧烈, 流场的拟涡能迅速增大; 激波离开界面后, 拟涡能在一定时间内减小, 然后又开始增大; 界面进入非线性发展阶段后, 拟涡能发生振荡, 但总体上继续增大.对于界面振幅, 先减小后增大, 且约在0.12 ms以前增长速率较大, 随后增长速率变小.激波向着界面运动, 二者没有接触时, 界面不会发生明显的变化.激波与界面相遇时, 在激波的强压缩作用下, 界面振幅有所减小, 图中曲线的第1个极值点是激波离开界面的时刻.激波离开界面后, 斜压作用在界面附近产生的涡主导界面的变形, 使界面振幅增长, 增长速率较大且呈线性增长.界面发展到后期, 伴随K-H不稳定性引起的界面“漏斗”结构向“蘑菇”结构的变化, 界面振幅增长速率有所减小, 不再呈线性变化, 而是进入非线性增长阶段.

|
| 图 9 拟涡能和界面振幅(Ms=1.3, a=0.005 m) Fig.9 Enstrophy and interface amplitude(Ms=1.3, a=0.005 m) |
基于基本工况a=0.005 m, 再增加界面扰动的振幅a=0.0025, 0.01 m算例, 计算分析界面振幅对R-M不稳定性的影响规律.
相对基本工况, 增大界面振幅. 图 10为a=0.01 m算例瞬时密度等值云图时间序列.激波与界面作用后继续入射, 激波后流体密度增大, t=0.02 ms前界面被压缩, 激波离开界面后, 界面上出现小尺度结构, 界面振幅线性增长, 随时间发展小尺度结构消失; t=0.075 ms时出现“蘑菇”结构, 界面振幅继续增大, 进入非线性发展阶段, “蘑菇”结构变明显, “蘑菇杆”结构变细, 流体不断发生混合; t=0.25 ms后混合剧烈, “蘑菇”结构明显被破坏.同图 4的基本工况相比, 两种情况在界面附近涡的分布发生了变化.
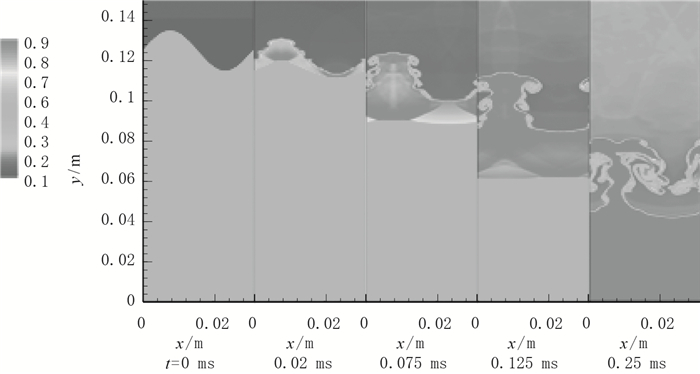
|
| 图 10 瞬时密度(Ms=1.3, a=0.01 m) Fig.10 Instantaneous densities (Ms=1.3, a=0.01 m) |
图 11为a=0.01 m算例瞬时涡量等值云图时间序列.流场中的涡始终聚集在界面附近, t=0.075 ms前流场中最大涡量较大, 分布较集中; t=0.25 ms后流场最大涡量变小, 由于流体混合, 分布较分散.同图 7的基本工况相比, a=0.01 m时激波与界面作用使界面附近产生的涡量更大, 且发展过程前后期最大涡量的变化也更大.这主要是由于a=0.01 m时混合进行得更剧烈, 使界面间密度梯度减小, 减弱了斜压作用.
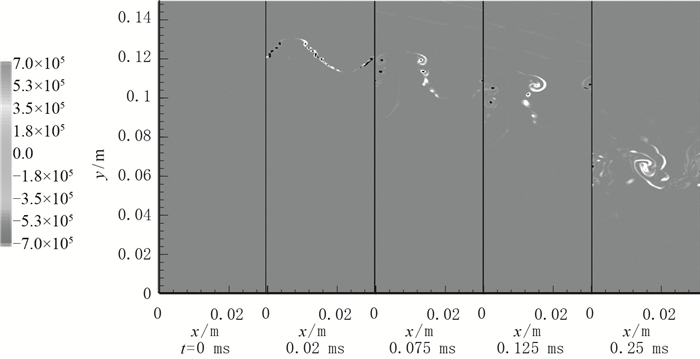
|
| 图 11 瞬时涡量(Ms=1.3, a=0.01 m) Fig.11 Instantaneous vorticities (Ms=1.3, a=0.01 m) |
图 12分别给出了a=0.01 m算例激波与界面作用过程中拟涡能和界面振幅随时间变化的曲线.初始时激波作用于界面, 斜压作用剧烈, 流场的拟涡能迅速增大; 激波离开界面后, 拟涡能在一定时间内减小, 然后继续增大, 发展后期拟涡能发生振荡, 但总体上仍保持增大趋势.界面振幅先减小后增大.在增大过程中, 约0.08 ms以前振幅增长速率较大, 为线性增长阶段; 0.08 ms之后振幅增长速率开始变小, 进入非线性发展阶段.同图 9的基本工况相比, 拟涡能变化规律相似.
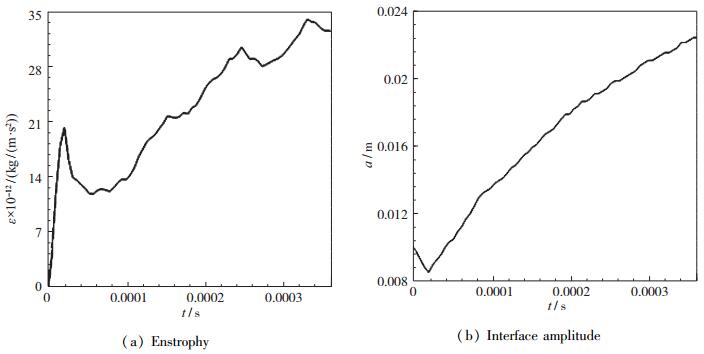
|
| 图 12 拟涡能和界面振幅(Ms=1.3, a=0.01 m) Fig.12 Enstrophy and interface amplitude (Ms=1.3, a=0.01 m) |
相对基本工况, 减小界面振幅. 图 13为a=0.0025 m算例瞬时密度等值云图时间序列.界面首先被激波压缩, 激波发生变形; 激波离开界面后, 界面较长一段时间仍然保持正弦型, 之后界面振幅开始增长; t=0.125 ms时出现“蘑菇”结构, t=0.25 ms后混合较明显, 但与另2种较大界面振幅情况相比, 混合较弱.

|
| 图 13 瞬时密度(Ms=1.3, a=0.0025 m) Fig.13 Instantaneous densities (Ms=1.3, a=0.0025 m) |
图 14为a=0.0025 m算例瞬时涡量等值云图时间序列.流场中涡量集中在界面附近, 混合发生得并不剧烈; 随时间发展, 涡量最大值增大, 发展后期最大涡量明显集中在“蘑菇”结构两侧.

|
| 图 14 瞬时涡量(Ms=1.3, a=0.0025 m) Fig.14 Instantaneous vorticities (Ms=1.3, a=0.0025 m) |
图 15分别给出了a=0.0025 m算例激波与界面作用过程中拟涡能和界面振幅随时间变化的曲线.拟涡能发展趋势与另2种较大界面振幅情况相似.界面振幅先减小后增大, t=0.14 ms左右增长速率开始有所减小, 进入非线性发展阶段.
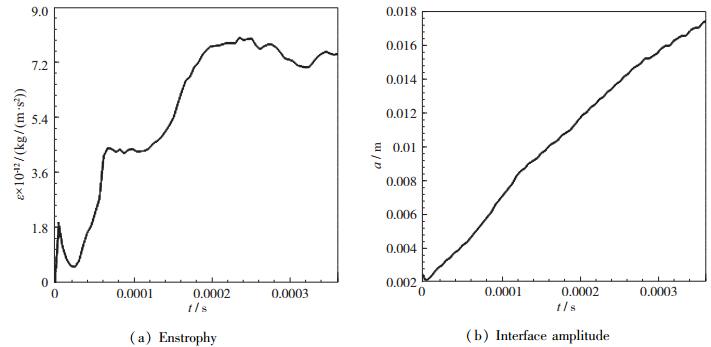
|
| 图 15 拟涡能和界面振幅(Ms=1.3, a=0.0025 m) Fig.15 Enstrophy and interface amplitude (Ms=1.3, a=0.0025 m) |
综合对比分析3种界面振幅情况可知, 当激波Mach数相同时, a=0.01 m情况的界面最先进入非线性增长阶段, 出现细小的“蘑菇”结构; 其次是a=0.005 m情况; 最后是a=0.0025 m情况.就“蘑菇”结构诱导的混合强度而言, 也呈逐渐减弱趋势.也就是说, 界面振幅越大, 界面线性发展阶段时间越短, 进入非线性增长阶段越快, 出现特征结构越快, 流体发生混合也越剧烈.另一方面, 激波与界面相遇时, 不同界面振幅对应的拟涡能变化趋势及早期增长速率相差不多, 但界面振幅越大, 激波与界面相互作用的时间越长; 界面振幅越大, 对应的拟涡能越大, 拟涡能再增长速率越大.拟涡能的增强, 强化了混合.
在3种初始界面振幅情况下, 界面振幅开始都会有一定程度的减小; 达到最小值后, 在涡的作用下逐渐增大.在界面发展前期, 界面振幅越大, 界面的变化速率越大; 在界面发展中后期, 界面振幅越大, 界面振幅增长率越早开始减小, 也越早进入非线性发展阶段, 界面变形发展得越快.
3.3 激波强度的影响基于基本工况Ms=1.3, 再增加激波Mach数Ms=1.15, 1.5算例, 计算分析激波强度对R-M不稳定性的影响规律.
相对基本工况, 增大激波强度. 图 16为Ms=1.5算例瞬时密度等值云图时间序列.激波强度变大, 激波前后流体密度比增大, 界面运动速度也变大.当激波与界面相遇时, 在激波压缩作用下, 界面振幅变小, 激波发生微弱变形, 继续运动, 经过一段时间恢复为平面波; 界面在线性增长阶段, 维持正弦型特征, 振幅增大; 然后进入非线性增长阶段, 流场出现“蘑菇”特征结构. “蘑菇”结构两侧的混合最剧烈, 混合导致混合区域流场中密度梯度变小, 界面上的结构被破坏.
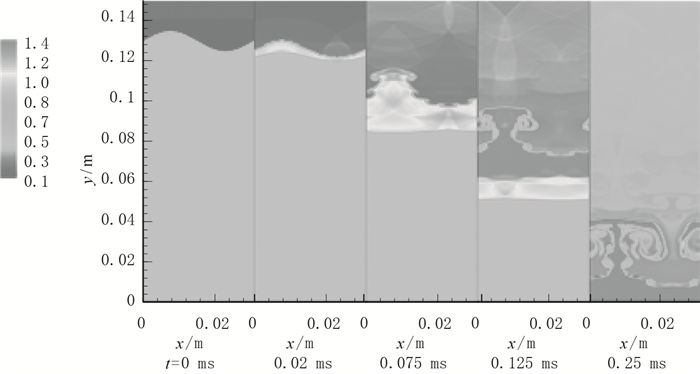
|
| 图 16 瞬时密度(Ms=1.5, a=0.005 m) Fig.16 Instantaneous densities (Ms=1.5, a=0.005 m) |
图 17为Ms=1.5算例瞬时涡量等值云图时间序列, 也显示界面附近的涡很明显, 最大涡量集中在“蘑菇”结构两侧.
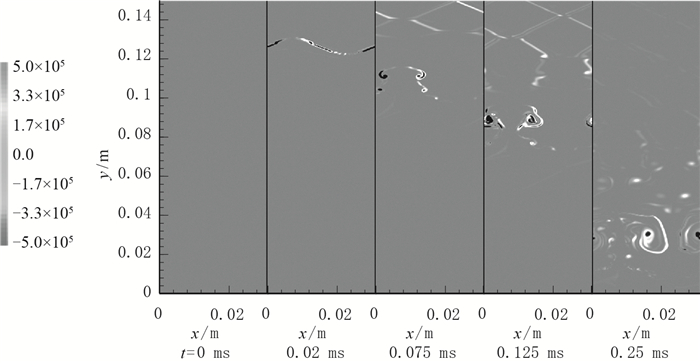
|
| 图 17 瞬时涡量(Ms=1.5, a=0.005 m) Fig.17 Instantaneous vorticities (Ms=1.5, a=0.005 m) |
图 18分别给出了Ms=1.5算例激波与界面作用过程中拟涡能和界面振幅随时间变化的曲线.拟涡能首先在激波作用下迅速增大, 激波离开界面后, 拟涡能开始减小, 然后又开始增大, 后期出现振荡, 但总体保持增大趋势.界面振幅先减小, 约在0.018 ms开始增大, 在0.1 ms增长速率变小.
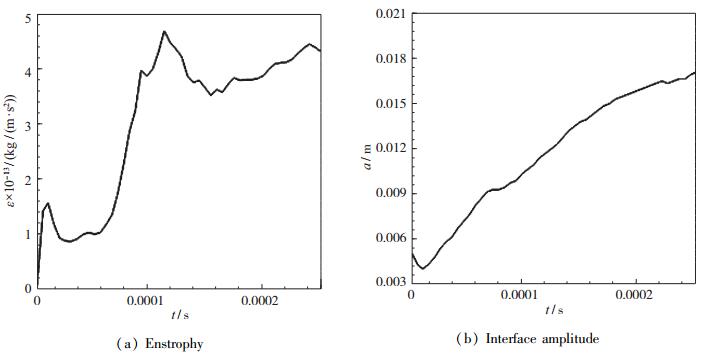
|
| 图 18 拟涡能和界面振幅(Ms=1.5, a=0.005 m) Fig.18 Enstrophy and interface amplitude (Ms=1.5, a=0.005 m) |
相对基本工况, 减小激波强度. 图 19为Ms=1.15算例瞬时密度等值云图时间序列.由图可以看出, 激波后的流体密度变大, 但是激波前后流体密度比和界面运动速度相比于另2种较大激波强度情况明显减小, 且界面变化减慢, 接近t=0.25 ms时界面才开始出现“蘑菇”结构, 混合剧烈程度也小得多. 图 20为Ms=1.15算例瞬时涡量等值云图时间序列.与另2种较大激波强度情况相比, 流场中的涡量明显较小, 在界面发展后期, 流场中最大涡量同样集中在“蘑菇”结构两侧.
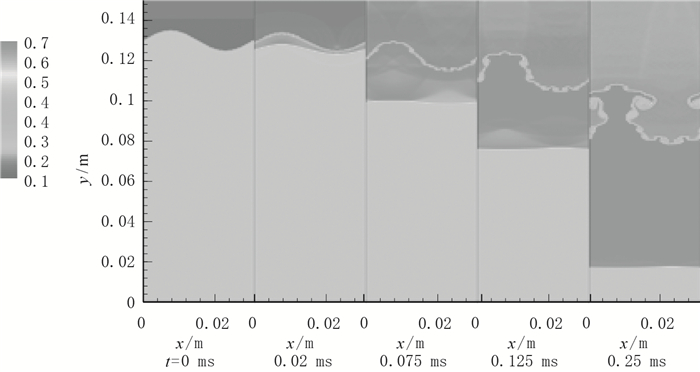
|
| 图 19 瞬时密度(Ms=1.15, a=0.005 m) Fig.19 Instantaneous densities (Ms=1.15, a=0.005 m) |

|
| 图 20 瞬时涡量(Ms=1.15, a=0.005 m) Fig.20 Instantaneous vorticities (Ms=1.15, a=0.005 m) |
图 21分别给出了Ms=1.15算例激波与界面作用过程中拟涡能和界面振幅随时间变化的曲线, 它们随时间变化的规律与另2种较大激波强度情况基本一致.

|
| 图 21 拟涡能和界面振幅(Ms=1.15, a=0.005 m) Fig.21 Enstrophy and interface amplitude(Ms=1.15, a=0.005 m) |
综合对比分析3种激波强度情况可知, 当初始界面振幅相同时, Ms=1.5情况的界面最先从线性增长阶段进入非线性增长阶段, 出现细小的"蘑菇"结构, 两种流体在"蘑菇"两侧发生混合, 界面结构被破坏.其次是Ms=1.3情况, 最后是Ms=1.15情况.激波在与界面作用过程中, 若初始界面振幅相同, 则激波强度越强, 界面线性发展阶段时间越短, 进入非线性增长阶段越快, 出现特征结构越快, 两种流体混合得越剧烈.类似地, 激波强度越大, 流场中拟涡能越大, 且拟涡能的增长速率也越大; 界面振幅均先在激波的压缩作用下一定程度地变小, 达到最小值后, 在涡的作用下开始增长.在界面发展前期, 激波强度越大, 界面振幅增长的速率越大; 界面发展中后期, 激波强度越大, 界面振幅增长率越先开始减小, 进入非线性发展阶段后, 出现特征结构, 此刻振幅增长速率会变小.总体上, 激波强度越大, 界面变形越快且越早进入非线性发展阶段, 拟涡能伴随增大可导致流体混合发生得越剧烈.
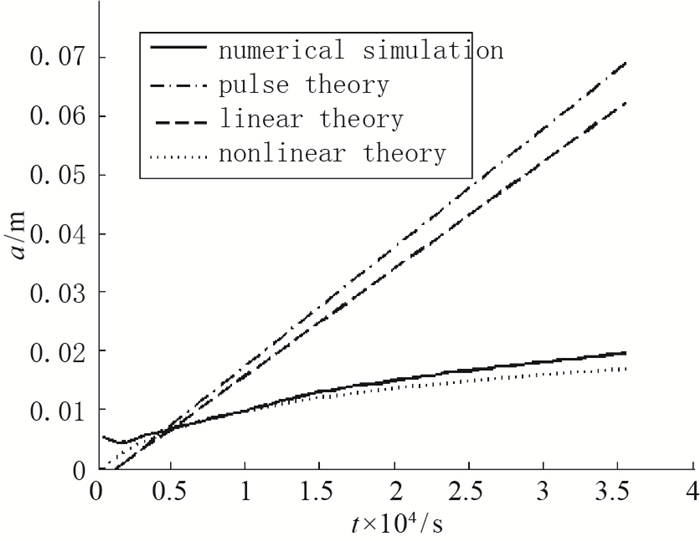
最后, 以基本工况为例, 将本文数值模拟得到的界面振幅随时间变化曲线与经典的脉冲模型[23]线性模型[24]非线性模型[25]等理论进行对比(见图 22).从图中曲线的对比可得出:各曲线整体趋势一致, 数值模拟结果与非线性理论结果定量上吻合较好, 差异较小.因此, 本文数值模拟得到的界面发展规律是合理的.
|
| 图 22 界面振幅随时间变化对比(Ms=1.3, a=0.005 m) Fig.22 Comparisons for the variations of interface amplitude(Ms=1.3, a=0.005 m) |
采用数值模拟方法, 详细研究了平面正激波与单模态正弦波界面相互作用导致的R-M不稳定性现象与强化混合流动物理机制.改变界面初始振幅和运动激波强度, 比较了不同条件下R-M不稳定性的规律.主要得到以下结论:
(1) 当激波从轻流体运动到重流体中时, 激波与界面作用, 激波发生变形.由于激波的压缩作用, 界面振幅小幅度减小.激波离开界面后, 界面发展进入线性增长阶段, 界面振幅增大, 发展到后期, 轻流体以“气泡”形式进入重流体, 重流体以“漏斗”形式进入轻流体, 出现“蘑菇”特征结构, 界面发展呈现非线性发展规律, 界面增速变小.由于斜压项和散度项作用, 界面附近产生涡, 诱导界面发生变形, 斜压作用占主导地位.由涡诱导出界面的速度差, 流动出现K-H不稳定性, 使流场中产生更多的涡.
(2) 激波Mach数不变, 比较界面初始振幅为a=0.0025, 0.005, 0.01 m时R-M不稳定性发展规律表明, 增大界面初始振幅, 能诱导界面附近产生更强的涡, 界面变形发展更快, 加快R-M不稳定性发展, 更有利于流体混合.
(3) 界面初始振幅不变, 比较激波Mach数为Ms=1.15, 1.3, 1.5时R-M不稳定性发展规律表明, 类似地, 增大激波强度, 能诱导界面附近产生更强的涡, 界面变形发展更快, 加快R-M不稳定性发展, 同样更有利于流体混合.
| [1] |
Richtmyer R D. Taylor instability in shock acceleration of compressible fluids[J]. Communications on Pure and Applied Mathematics, 1960, 13: 297-319. DOI:10.1002/(ISSN)1097-0312 |
| [2] |
Markstein G H. A shock-tube study of flame front-pressure wave interaction[J]. Symposium on Combustion, 1957, 6(1): 387-398. DOI:10.1016/S0082-0784(57)80054-X |
| [3] |
Meshkov E E. Instability of the interface of two gases accelerated by a shock wave[J]. Fluid Dynamics, 1969, 4: 101-104. |
| [4] |
Haas J F, Sturtevant B. Interaction of weak shock waves with cylindrical and spherical gas inhomogenieties[J]. Journal of Fluid Mechanics, 1987, 181: 41-76. DOI:10.1017/S0022112087002003 |
| [5] |
Tomkins C, Kumar S, Orlicz G, et al. An experimental investigation of mixing mechanisms in shock-accelerated flow[J]. Journal of Fluid Mechanics, 2008, 611: 131-150. |
| [6] |
Mikaelian K O. Richtmyer-Meshkov instability of arbitrary shapes[J]. Physics of Fluids, 2005, 17: 1-13. |
| [7] |
Brouillette M, Sturtevant B. Experiments on the Richtmyer-Meshkov instability: single-scale perturbations on a continuous interface[J]. Journal of Fluid Mechanics, 1994, 263: 271-292. DOI:10.1017/S0022112094004118 |
| [8] |
Sadot O, Erez L, Alon U, et al. Study of nonlinear evolution of single-mode and two-bubble interaction under Richtmyer-Meshkov instability[J]. Physical Review Letters, 1998, 80: 1654-1657. DOI:10.1103/PhysRevLett.80.1654 |
| [9] |
Collins B D, Jacobs J W. PLIF flow visualization and measurements of the Richtmyer-Meshkov instability of an air/SF6 interface[J]. Journal of Fluid Mechanics, 2002, 464: 113-136. |
| [10] |
Prestridge K, Orlicz G, Balasubramanian S, et al. Experiments of the Richtmyer-Meshkov instability[J]. Philosophical Transactions A: Mathematical, Physical, and Engineering Science, 2013, 371: 1-9. |
| [11] |
Holmes R L, Grove J W, Sharp D H. A numerical investigation of the Richtmyer-Meshkov instability using front tracking[J]. Journal of Fluid Mechanics, 1994, 301: 51-64. |
| [12] |
Anuchina N N, Volkov V I, Gordeychuk V A, et al. Numerical simulations of Rayleigh-Taylor and Richtmyer-Meshkov instability using MAH-3 code[J]. Journal of Computational and Applied Mathematics, 2004, 168: 11-20. DOI:10.1016/j.cam.2003.06.008 |
| [13] |
Latini M, Schilling O, Don W S. Effects of WENO flux reconstruction order and spatial resolution on reshocked two-dimensional Richtmyer-Meshkov instability[J]. Journal of Computational Physics, 2007, 221: 805-836. DOI:10.1016/j.jcp.2006.06.051 |
| [14] |
Hu X Y, Adams N A, Iaccarino G. On the HLLC Riemann solver for interface interaction in compressible multi-fluid flow[J]. Journal of Computational Physics, 2009, 228: 6572-6589. DOI:10.1016/j.jcp.2009.06.002 |
| [15] |
Olson B J, Greenough J. Large eddy simulation requirements for the Richtmyer-Meshkov instability[J]. Physics of Fluids, 2014, 26: 241-271. |
| [16] |
Holmes R L, Dimonte G, Fryxell B, et al. Richtmyer-Meshkov instability growth: experiment, simulation and theory[J]. Journal of Fluid Mechanics, 1999, 389: 55-79. DOI:10.1017/S0022112099004838 |
| [17] |
Burcat A, Ruscic B. Third millennium ideal gas and condensed phase thermochemical database for combustion with updates from active thermochemical tables[R]. ANL-05/20 and TAE 960, 2005.
|
| [18] |
Reid R C, Poling B E, Prausnitz J M. The properties of Gases and liquids[M]. New York: McGraw-Hill, 1987: 1-38.
|
| [19] |
Ren Y X, Liu M E, Zhang H X. A characteristic-wise hybrid compact-WENO scheme for solving hyperbolic conservation laws[J]. Journal of Computational Physics, 2003, 192: 365-386. DOI:10.1016/j.jcp.2003.07.006 |
| [20] |
Gupta M R, Roy S, Sarkar S, et al. Effect on Richtmyer-Meshkov instability of deviation from sinusoidality of the corrugated interface between two fluids[J]. Laser and Particle Beams, 2007, 25: 503-510. |
| [21] |
Gramer L, Noaa L G. Kelvin-Helmholtz instabilities[J]. Journal of Plasma Physics, 2007, 28: 1-11. |
| [22] |
Kilchyk V, Nalim R, Merkle C. Laminar premixed flame fuel consumption rate modulation by shocks and expansion waves[J]. Combustion and Flame, 2011, 158: 1140-1148. DOI:10.1016/j.combustflame.2010.10.026 |
| [23] |
Fraley G. Rayleigh-Taylor stability for a normal shock wave-density discontinuity interaction[J]. Physics of Fluids, 1986, 29: 376-386. DOI:10.1063/1.865722 |
| [24] |
Brouillette M. The Richtmyer-Meshkov instability[J]. Annual Review of Fluid Mechanics, 2002, 34: 445-468. DOI:10.1146/annurev.fluid.34.090101.162238 |
| [25] |
Zhang Q, Sohn S. Nonlinear theory of unstable fluid mixing driven by shock wave[J]. Physics of Fluids, 1997, 9: 1106-1124. DOI:10.1063/1.869202 |



