2. 常州大学江苏省光伏科学与工程协同创新中心,江苏常州 213164
2. Collaborative Innovation Center of Photovoltaic Science and Engineering, Changzhou University, Changzhou 213164, China
微观领域作为未来科学发展的重要方向之一已经得到越来越多的关注, 而在微机电系统(micro electro-mechanical systems, MEMS)和纳机电系统(nano electro-mechanical systems, NEMS)[1-3]、微流体器件的组成部件以及气体封装[4]和页岩气能源开采[5]等研究方向中经常出现微/纳尺度下气体的流动问题, 例如:扩散流动、Poiseuille流动[6]和Couette流动等流动类型, 而由于尺度效应的存在, 适用于常规尺度的运动方程及边界条件[7-9]都不能准确地解释微/纳尺度下的流动机理, 因此微/纳尺度下气体在纳米孔隙内的流动特性值得进行探索和研究.
由于微观领域中的研究模型一般为微/纳米级别, 在实验上很难精准地完成数据的测量和分析, 而分子动力学方法作为一种被普遍接受的数值计算方法[10], 逐渐成为研究微纳系统的重要工具[11]. Soong等[12]运用分子动力学研究了氩气在纳米孔隙内的流动特性, 并探究了壁面密度、流动取向和Lennard-Jones(L-J)势能等参数对流动特性的影响.解辉等[13-14]使用非平衡分子动力学(non-equilib-rium molecular dynamic simulation, NEMD)方法模拟了纳米孔隙内混合气体的Poiseuille流动特性, 讨论了气体疏水性与亲水性及温度效应对流动特性的影响. Kandemir等[15]模拟了氦-氩混合气体的双元扩散, 并研究混合气体的Couette流特性, 得出氩气分子的动能比氦气分子更易受上下平行板剪切速度的影响, 而在受壁面温度的影响方面却相反.目前关于纳米孔隙内气体的研究主要是以单种或者两种气体混合为研究对象[16-18], 而对于两种以上混合气体在纳米孔隙内的流动特性研究还相对较少, 需要进行相应的研究, 探索多种气体混合对纳米孔隙内气体流动特性的影响.
本文所采用的混合气体是在氮氧气体的基础上再按比例加入二氧化碳构造而成, 并利用分子动力学模拟方法研究了其在纳米孔隙内受剪切作用时的分布特性和边界滑移, 探究了气-固耦合作用强度、混合气体密度、纳米孔隙宽度以及二氧化碳配比等因素对流动特性的影响作用, 为研究纳米孔隙内混合气体的流动提供一定理论基础.
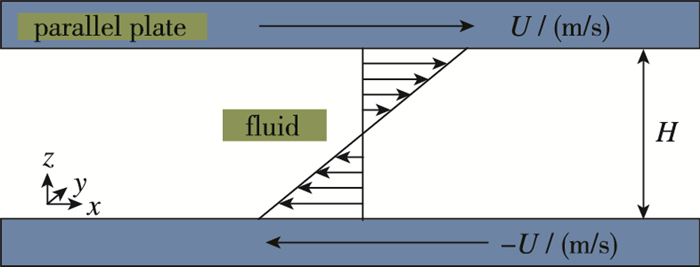
1 模型和方法本文采用的系统模型是根据前期研究[19]和参考相关文献[20-21]所得到的Couette流动系统模型, 如图 1所示.所使用的纳米孔隙的尺度大小为V=8 nm×4 nm×4.7325 nm, x和y方向设置为周期性边界.上下平行壁板沿x方向以恒定的速度做匀速相向运动, 对纳米孔隙中的混合气体进行剪切作用, z方向为纳米孔隙宽度方向.模拟系统中的混合气体由氮气、氧气和二氧化碳3部分组成, 其中氮气和氧气的混合比例保持4:1不变, 然后按照不同比例添加二氧化碳.二氧化碳则采用EPM2模型[22], 其中碳氧(C=O)键长为lC=O=0.114 9 nm, 模型的其他具体参数在表 1中列出.
|
| 图 1 Couette流模型示意图 Fig.1 Schematic of Couette model |
| 下载CSV 表 1 二氧化碳EPM2模型具体参数 Tab.1 Parameters of EPM2 model for CO2 |
采用简谐势表述二氧化碳分子的C=O键能作用, 公式为:
| $ {{E}_{r}}={{K}_{r}}{{(r-{{r}_{0}})}^{2}} $ |
式中, Kr为键能参数, r0为平衡键长.并取Kr=628.3 eV/nm2, r0=0.114 9 nm [23].对于二氧化碳分子中形成的O=C=O键角, 我们也选用相同的简谐势进行描述, 函数表达式为:
| $ {{E}_{\theta }}={{K}_{\theta }}{{(\theta -{{\theta }_{0}})}^{2}} $ |
式中Kθ为键角弹性常数, θ0为平衡键角.这里Kθ=6.416 eV/rad2, θ0=180°[22-23].构成的固体壁面的铂原子设置为面心立方(face center cubic, fcc)结构, 晶格常数a=0.392 42 nm[24].本模拟的研究主要集中在对纳米孔隙内混合气体流动特性的探索, 因此不考虑热交换对模拟的影响, 并把固体壁面设置为刚体.固体壁面原子与混合气体分子之间、氧气内部原子间、氮气内部原子间、二氧化碳内部原子间以及构成混合气体的内部分子间的相互作用势能选用L-J势能函数[25], 公式为:
| $ {{U}_{\text{LJ}}}(r)=4\varepsilon [{{(\sigma /\gamma )}^{12}}-{{(\sigma /\gamma )}^{6}}] $ |
式中, ε为势阱深度, σ为截断半径.
各原子之间的势能参数通过Lorentz-Berthelot混合法则计算得到[26].公式为:
| $ {{\varepsilon }_{ij}}=\sqrt{{{\varepsilon }_{i}}{{\varepsilon }_{ij}}}, {{\sigma }_{ij}}=({{\sigma }_{i}}+{{\sigma }_{j}})/2 $ |
式中i,j代表不同的原子.
其中, 氮气、氧气及铂原子之间的参数值在前期研究中[19]已完成, 而二氧化碳和其与氮气、氧气及铂原子之间的相互作用势能参数, 在表 2列出.
| 下载CSV 表 2 各原子间L-J势函数参数值 Tab.2 Interatomic L-J potential parameters |
本文的数据结果都是通过LAMMPS模拟软件的计算得到的, 参数的具体设置情况为:时间步长为10-3 ps (10-15 s)、L-J势函数中的σ=1.104 nm、二氧化碳分子之间的Coulomb作用的截断半径为1.2 nm.采用Verlet积分算法进行原子路径的更新[27], 由于x方向上存在速度影响, 故只在y和z方向上采用Langevin热浴法[28-29]维持系统温度为293 K.整个MD模拟持续时长为4 ns(即4×106时间步), 前1 ns用于混合气体的弛豫过程, 使其达到稳定状态; 后3 ns由于数据的输出与采集, 模拟过程中每1 ns对数据信息进行统计平均.
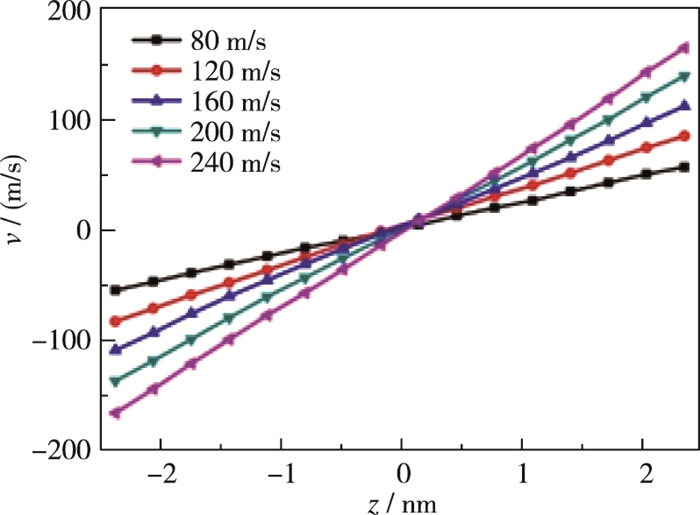
2 模拟结果讨论与分析 2.1 混合气体流动速度及密度分布运用分子动力学模拟方法, 对上下平行板施加大小不同的x方向剪切速度(80~240 m/s), 研究纳米孔隙内混合气体的Couette流特性.混合气体中氮气和氧气的比例保持4:1不变, 考虑二氧化碳由3个原子组成, 同比例加入会导致系统压强增加的因素, 故将二氧化碳的比例设为20%, 所得混合气体数密度为n=0.64. 图 2为在剪切力作用下, 混合气体的速度分布图.由图可知, 在纳米孔隙方向上混合气体流动速度近似呈线性分布趋势, 属于Newton流体范畴, 可通过带有滑移边界条件的N-S方程表征其运动形式.且随着剪切速度的增加, 剪切应变率和滑移速度都随之增加.对速度分布曲线线性拟合得到剪切应变率(
|
| 图 2 Couette流速度轮廓图 Fig.2 Velocity profiles of Couette flows |
|
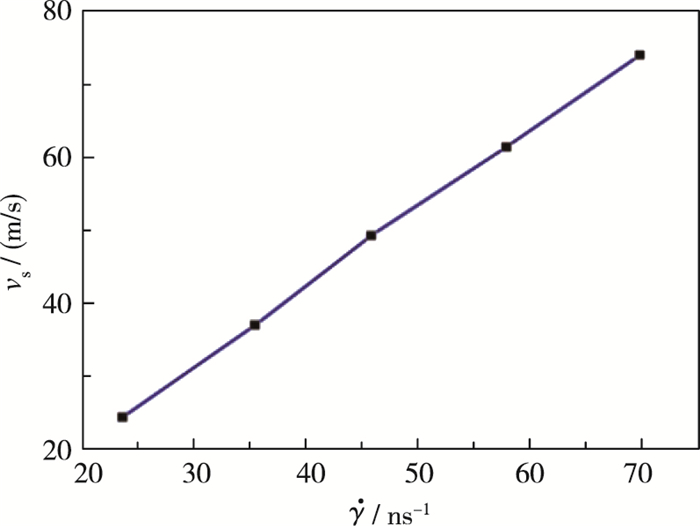
| 图 3 滑移速度随剪切应变率变化图 Fig.3 Slip velocity versus shear rate |
| $ {{L}_{\text{s}}}={{v}_{\text{s}}}/\dot{\gamma } $ |
可得, 混合气体的滑移长度(Ls)不受平行壁板剪切驱动速度的影响, 大小始终保持不变.
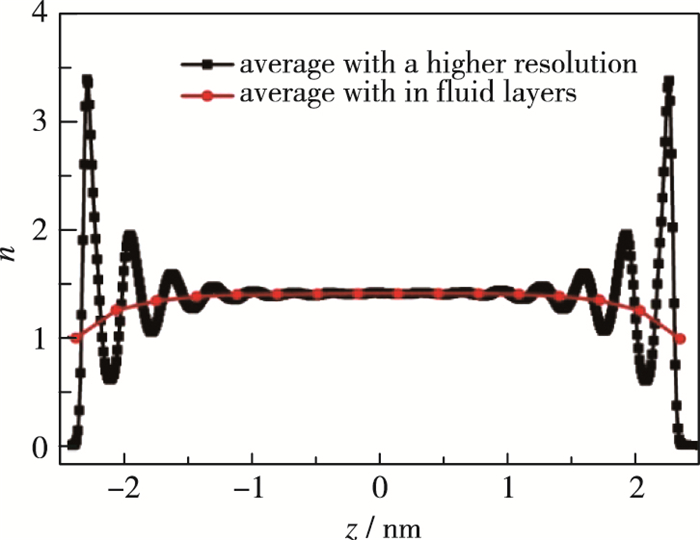
密度分布图可以直观地反映出分子的分布情况[31], 这里我们选取剪切速度为160 m/s时(其余数据趋势相同), 纳米孔隙内混合气体沿孔隙宽度方向的密度分布, 如图 4所示, 其中横坐标表示到纳米孔隙中心位置的距离(z=±H/2), 纵坐标为每σNO3体积内的分子数.图中黑色曲线代表分层的间距较小的气体的密度分布情况, 可以看出在距离固体壁面约0.6 nm的范围内气体数密度分布出现很大振荡, 这是因为平行板壁面对气体分子的吸附作用使得混合气体分子密度分布不再均匀一致, 出现了不同层次的密度堆积和明显的分层现象, 气体分子在界面处形成所谓的“类固体”效应[32].而当到壁面的距离不断增大后, 气体分子受壁面吸附作用影响减小, 分子密度分布趋于稳定.在界面处的第一个密度峰值处, 此时壁面的吸附作用和气体分子抵抗吸附作用达到平衡状态, 故此波峰处混合气体的密度值达到最大, 这是因为当气体分子距离壁面的位置小于此距离时, 壁面排斥力作用将使气体分子远离壁面, 将混合气体分子推向平衡位置聚集; 而当气体分子距离壁面的位置大于此距离时, 气体分子则受吸引而向壁面靠近, 将混合气体分子拉向平衡位置聚集, 最终使混合气体分子的密度分布值在平行板壁面附近形成一个高的峰值.而随着距离不断增大, 壁面吸附作用逐渐减小, 密度峰值也逐渐降低, 最终趋于稳定. 图 4中红色曲线为分层间距较大时气体分子的分布情况, 此时, 混合气体整体密度分布一致, 而在近壁面处密度明显低于孔隙中心处, 这是由于气固界面处存在壁面的势能作用而导致的气体稀薄效应.
|
| 图 4 混合气体沿孔隙宽度方向上的分子数密度分布图 Fig.4 Number densities of gas mixture across the channel |
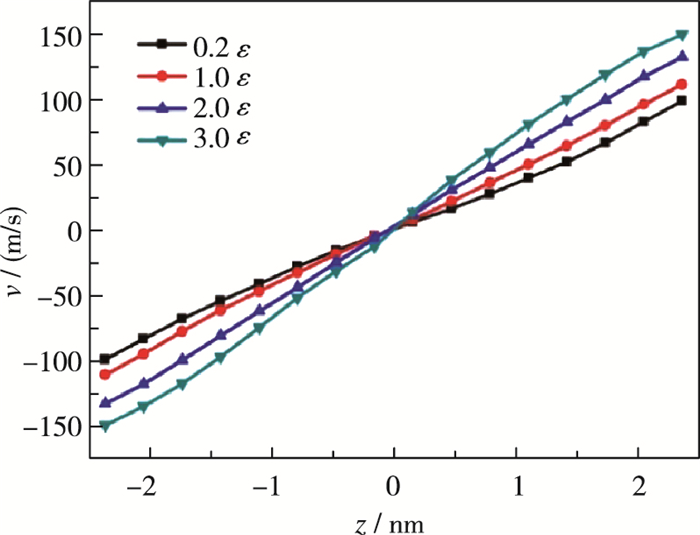
流体系统中壁面材料也是研究混合气体的流动特性所要考虑的一个因素[33], 因为每种材料对气体的吸附作用不同, 即混合气体和平行板壁面之间的耦合相互作用大小存在差异.为了体现壁面材料之间的差异, 可通过调节势函数参数中的势阱深度ε来表征, 具体方法为在原有的L-J势函数中的势阱参数ε的基础上乘以c, 通过c的不同取值体现壁面材料不同.当c取值较小时, 其对混合气体的吸附作用小于铂纳米孔隙, 反之则相反. 图 5给出了不同势能大小作用时混合气体的速度分布曲线, 从图中可以看出, 在平行板剪切驱动速度(U =160 m/s)不变的情况下, 混合气体流动速度曲线出现了差异, 随着壁面势能作用的不断增大(c取值较大), 混合气体流动速度的剪切应变率随之增大, 气体的滑移速度则逐渐减小.
|
| 图 5 不同气-固耦合强度下混合气体沿孔隙宽度方向上速度轮廓图 Fig.5 Velocity profiles of gas mixture across the channel for different gas-solid coupling strengths |
图 6为分层间距较小时, 在不同耦合强度下的混合气体沿孔隙宽度方向上的分子数密度分布图, 由于不同耦合作用下, 混合气体沿孔隙宽度方向上的分子数密度分布趋势较接近, 将不同耦合强度下的密度分布情况全部描绘出会造成重叠, 为了清晰地表现出差异, 故此处只绘制了耦合强度为0.2ε和2.0ε的两种情况.从图 6中可以看出, 当耦合作用力为2.0ε时, 其密度峰值明显要高于耦合作用为0.2ε时的情况, 并且余下数据均满足此规律, 即当作用力增大时, 气体分子在壁面附近的积聚现象更为明显.此时气体分子被吸附的概率将大大增加, 且不再直接将其反射出去, 而是在壁面处连续发生碰撞造成气体分子长时间的停留, 当其再一次获得足够大的动能时才能摆脱壁面的吸附作用.正是气体分子在界面处的这种长时间逗留导致密度分层现象的发生, 这一特点常常被称为“俘获-逃逸”[34].
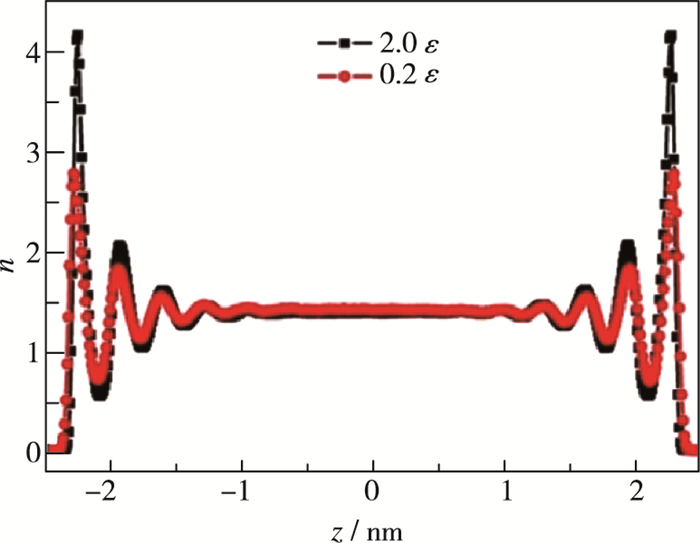
|
| 图 6 不同耦合强度下混合气体沿孔隙宽度方向上的分子数密度分布图 Fig.6 Number density profiles of gas mixture across the channel for different gas-solid coupling strengths |
已有研究表明, 流-固密度的对比也是影响流体边界滑移的一个重要因素[20], 当流体密度为一固定值时, 在改变壁面的密度时发现[35]增加壁面密度会导致流-固界面处局部剪切应变率有所降低, 而边界处的速度滑移却明显升高.这主要是由于壁面密度的增加, 在一定程度上降低了壁面粗糙度, 从而导致壁面处滑移速度的增大.这里我们通过改变流体的密度, 研究流体密度的改变对孔隙内流体边界滑移密度的影响.通过改变二氧化碳含量为20%的混合气体的密度(n=0.42~0.9), 研究不同密度下混合气体沿孔隙宽度方向上的速度分布.
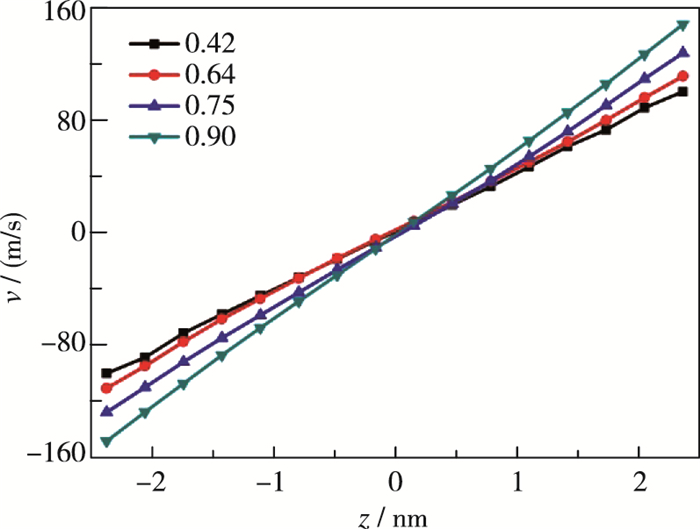
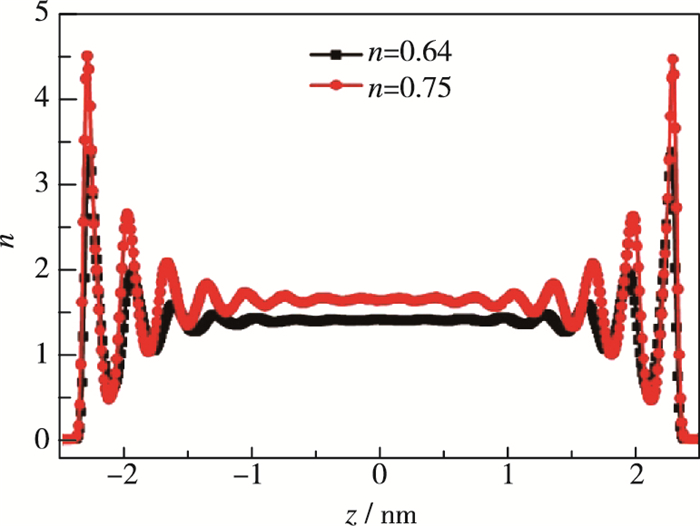
如图 7所示, 不同密度下混合气体流速在孔隙宽度方向上都为线性分布趋势, 并且随着混合气体密度的不断减小, 界面处的速度滑移现象更加明显, 滑移速度也因此不断增大.随着混合气体密度的不断减小, 一定程度上降低了气-固界面处气体分子与壁面的碰撞发生频率, 进而使得界面处的气体分子被平行板壁面势能作用所吸附的概率大大减小.因此, 随着混合气体的密度由大到小, 界面处的滑移速度出现了增大的趋势.图 8所示为混合气体分子沿纳米孔隙宽度方向上的数密度分布图, 参考图 6的处理方法, 图 8中我们也只绘制两种不同混合气体密度时(n=0.64和n=0.75)混合气体分子数密度分布对比.从图 8中可得, 当密度n=0.64时, 混合气体的分层结构明显弱于密度为0.75时, 并且余下数据均满足此规律, 既而混合气体密度越小则边界处密度堆积现象和分层结构越弱, 最终导致混合气体密度较低时边界处出现较大的滑移速度.
|
| 图 7 不同密度对应的混合气体速度分布图 Fig.7 Velocity profiles for different densities of gas mixture |
|
| 图 8 混合气体沿孔隙宽度方向上的数密度分布图 Fig.8 Number densities of gas mixture across the channel width |
为了研究含定量的二氧化碳气体(以20%为例)的混合气体流动特性随着孔隙宽度的变化规律, 并且与纯氮气和氧气组成的混合气体在不同孔隙宽度下的流动规律形成对比.我们构建4组不同的孔隙宽度(H=10σNO, 20σNO, 25σNO, 30σNO)的流动系统.
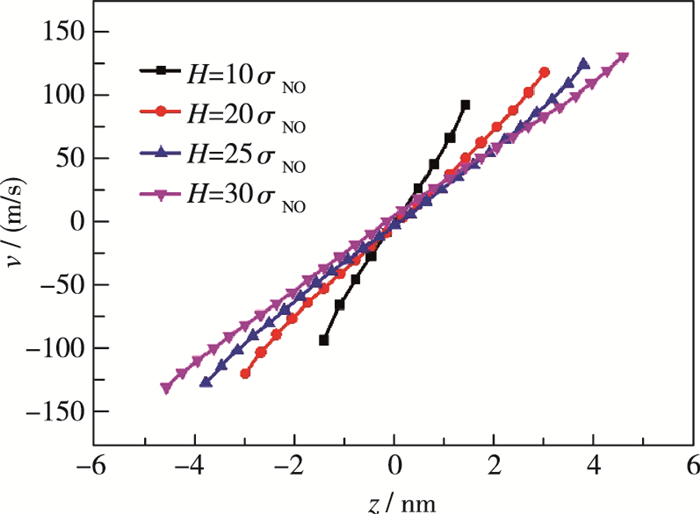
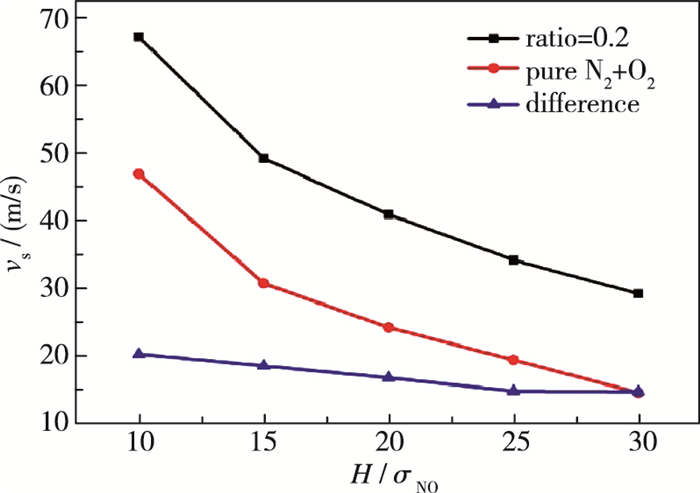
图 9给出了二氧化碳占混合气体比例为20%时, 混合气体在不同孔隙宽度下沿孔隙宽度方向上的速度分布.模拟结果显示, 当二氧化碳所占比例为20%时, 随着孔宽的不断增大, 混合气体的速度分布曲线斜率在不断增大, 即剪切应变率在不断增大, 而混合气体在界面处的滑移速度则呈减小的趋势.通过计算获得孔隙宽度为10σNO时, 其滑移速度达到67.08 m/s, 参考前期数据[19], 可得纯氮氧混合气体此时的滑移速度为46.85 m/s, 滑移速度明显降低; 当孔隙宽度为30σNO时, 其滑移速度为29.15 m/s(此时对应的纯氮氧混合气体的滑移速度为14.49 m/s).为了更加清晰地描述混合气体滑移速度随孔隙宽度的变化趋势, 其关系曲线图如图 10所示.从图 10中可观察到, 两种不同混合气体成分的滑移速度都随着孔隙宽度的增大不断减小, 且变化趋势平行一致.即对于较小的孔隙宽度, 滑移速度的减小趋势较大; 而随着孔隙宽度进一步增大, 滑移速度的下降趋势明显减缓, 并呈现近似直线的关系.从图中还可发现, 在不同的孔隙宽度下, 含有20%二氧化碳的混合气体的滑移速度都要大于纯氮气和氧气构成的混合气体, 并且两者不同孔隙宽度下的速度滑移差值因孔隙宽度变化而产生的影响较小.
|
| 图 9 不同孔隙宽度下混合气体沿纳米孔隙宽度方向上的速度分布图 Fig.9 Velocity profiles across the channel width for different channels width |
|
| 图 10 滑移速度随孔隙宽度的变化图 Fig.10 Slip velocity as a function of channel width |
为了研究混合气体中加入不同比例二氧化碳后对混合气体流动的影响规律, 分别模拟了二氧化碳占混合气体比例为0,20%,40%,60%,80%和100%这6组算例, 其中混合气体中氮气和氧气的混合比例依然保持不变(4:1).如前所述, 当同比例加入二氧化碳时, 会造成模拟体系压强的增大, 所以为了保持压强的恒定, 通过降低混合气体整体的数量密度来实现, 则调整后的混合气体数量密度分别为0.64(20%),0.56(40%),0.49(60%),0.44(80%)和0.4(100%).
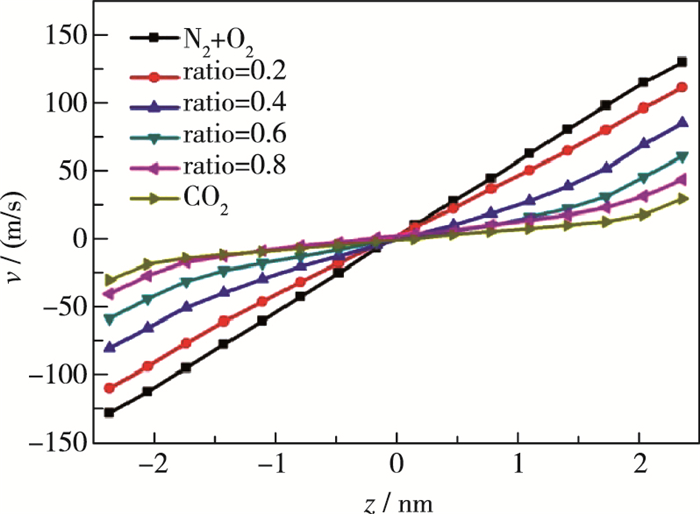
图 11给出了6组不同对比数据下混合气体沿孔隙宽度方向上的速度分布曲线图, 其中平行板的剪切驱动速度为U=160 m/s.从图 11中可以发现, 随着混合气体中二氧化碳比例的增加, 边界处的滑移速度随之不断增大.并且还发现, 随着二氧化碳比例的不断增加, 混合气体沿孔隙宽度方向上的分布不再是线性分布.即当混合气体中二氧化碳的比例低于20%时, 此时混合气体沿孔隙宽度方向上依然是线性分布, 这时其混合气体流动规律符合带有滑移边界条件的N-S方程的预测.而当二氧化碳比例达到40%及以上时, 此时混合气体在孔隙宽度方向上的速度曲线分布规律可分为两部分:孔隙内主流区域和界面处流动区域.在平行板纳米孔隙内主流区域内, 混合气体的速度曲线呈线性分布状态, 这时其分布曲线规律可用N-S方程描述, 但在混合气体与平行板壁面的界面处约0.3~0.6 nm的距离处, 混合气体的速度分布曲线不再呈线性分布, N-S方程难以对其进行合理的解释, 这主要是由于边界处固体壁面的吸附作用和气体稀薄效应所导致的.为了进一步探究滑移速度随着二氧化碳占混合气体比例的变化规律, 对于图 11中的各曲线进行线性拟合(当二氧化碳比例达到40%后只拟合曲线的线性部分), 可得到二氧化碳不同比例时对应的滑移速度, 其函数关系曲线如图 12所示.
|
| 图 11 不同比例的二氧化碳沿孔隙宽度方向上的速度分布图 Fig.11 Velocity profiles across the channel width for different component ratios of CO2 in the gas mixture |
|
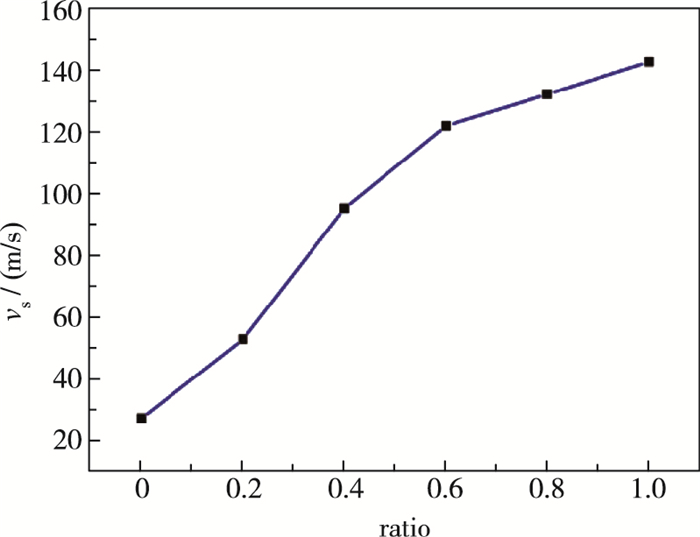
| 图 12 不同二氧化碳配比时滑移速度分布图 Fig.12 Slip velocity for different component ratios of CO2 in the gas mixture |
从图 12中可看出, 混合气体的滑移速度随着二氧化碳比例的增加整体呈现升高的趋势, 当混合气体中仅有氮气和氧气时, 滑移速度仅为27.5 m/s; 当二氧化碳的比例小于60%时, 滑移速度随着二氧化碳比例的增加出现较大的增长趋势, 且此时滑移速度达到122.3 m/s; 随着二氧化碳的比例进一步增大, 滑移速度呈现较为平缓的增长趋势, 且当混合气体的组分变为纯二氧化碳时, 滑移速度达到最大值143.1 m/s.
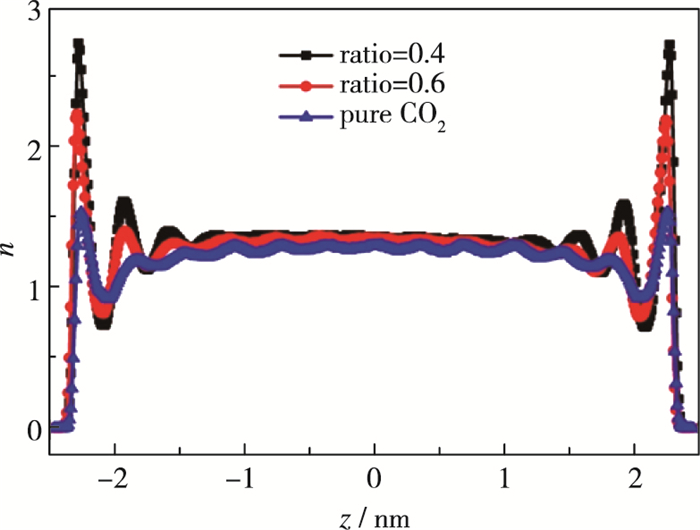
图 13给出了二氧化碳不同比例时, 混合气体沿纳米孔隙孔宽方向上的数量密度分布图.
|
| 图 13 不同比例二氧化碳对应的混合气体沿孔隙宽度方向上的数密度分布图 Fig.13 Density distributions of the gas mixture across the channel for different component ratios of CO2 |
同样参考图 6的处理办法, 这里我们只绘制了3种不同二氧化碳比例(40%, 60%, 100%)进行比较说明, 从图 13中可以看出, 当二氧化碳所占比例不同时, 混合气体在边界处都出现了不同程度的密度分层现象.对比可以发现, 混合气体分子在气-固界面处, 所形成的密度峰值的情况为:当混合气体中二氧化碳比例为40%时, 密度峰值最大, 60%次之, 100%最小.并且余下数据均满足此规律, 即随着二氧化碳比例的不断增加, 边界处的密度峰值明显降低, 固化现象减弱, 混合气体受壁面的吸附作用影响逐渐减小, 最终导致速度滑移的增大(图 11).
3 结论本文使用分子动力学方法研究了氮氧气体中引入不同比例的二氧化碳后形成的混合气体在剪切作用下的流动特性和边界滑移.研究结果表明:随着加入二氧化碳比例的不断增加, 混合气体的滑移速度不断增大, 并且当二氧化碳的比例低于20%时, 混合气体流动速度沿孔隙宽度方向依然为线性分布趋势; 而当二氧化碳比例达到40%后, 其速度运动曲线将不再呈现单一的线性分布, 而是由孔隙内主流区和近壁面流动区两部分组成.在孔隙内主流区域内依然为线性分布, 而在近壁面区出现了偏差, 此时流体已不属于Newton流.以混合气体中二氧化碳所占比例为20%为例, 研究对比发现, 当孔隙宽度发生变化时, 二氧化碳占比为20%的混合气体与氮氧混合气体的滑移速度都出现了一致的变化趋势.即整体上滑移速度随着孔隙宽度的增大而减小, 但在孔隙宽度较小时, 滑移速度的减小趋势较大; 随后, 当继续增大孔隙宽度时, 其滑移速度下降的趋势减缓, 并呈现近似直线的减小趋势.此外, 对于不同孔隙宽度下, 二氧化碳占比为20%的混合气体产生的速度滑移始终大于氮氧混合气体的滑移速度, 且两者的滑移速度差值受孔隙宽度变化的影响较弱.此外, 对于较弱的气-固耦合作用强度和较小的混合气体密度都会在界面处产生较大的滑移速度.
| [1] |
胡小唐, 李源, 饶志军, 等. 纳机电系统[J]. 纳米技术与精密工程, 2004, 2(1): 1-7. Hu X T, Li Y, Rao Z J, et al. Nanoelectromechanical systems[J]. Nanotechnology and Precision Engineering, 2004, 2(1): 1-7. (in Chinese) |
| [2] |
周兆英, 杨兴. 微/纳机电系统[J]. 仪表技术与传感器, 2003(2): 1-5. Zhou Z Y, Yang X. Micro and nano electro-mechanic systems[J]. Instrument Technique and Sensor, 2003(2): 1-5. DOI:10.3969/j.issn.1002-1841.2003.02.001 (in Chinese) |
| [3] |
严宇才, 张端. 微机电系统技术的研究现状和展望[J]. 电子工业专用设备, 2011, 40(4): 1-8, 46. Yan Y C, Zhang D. MEMS technology research status and further research works forecast[J]. Equipment for Electronic Products Manufacturing, 2011, 40(4): 1-8, 46. DOI:10.3969/j.issn.1004-4507.2011.04.001 (in Chinese) |
| [4] |
王彤, 徐洁, 谷传纲. 微尺度效应对螺旋槽干气密封性能的影响[J]. 工程热物理学报, 2004, 25(S1): 39-42. Wang T, Xu J, Gu C G. The micro scale effects on the performance of spiral grooved gas seals[J]. Journal of Engineering Thermophysics, 2004, 25(S1): 39-42. (in Chinese) |
| [5] |
Islam A, Patzek T. Slip in natural gas flow through nanoporous shale reservoirs[J]. Journal of Unconventional Oil and Gas Resources, 2014, 7: 49-54. DOI:10.1016/j.juogr.2014.05.001 |
| [6] |
Titarev V A, Shakhov E M. A higher-order conservative method for computing the Poiseuille flow of a rarefied gas in a channel of arbitrary cross section[J]. Computational Mathematics & Mathematical Physics, 2010, 50(3): 563-574. |
| [7] |
Fan J, Shen C. Statistical simulation of low-speed rarefied gas flows[J]. Journal of Computational Physics, 2001, 167(2): 393-412. |
| [8] |
Zohar Y, Lee S Y K, Lee W Y, et al. Subsonic gas flow in a straight and uniform microchannel[J]. Journal of Fluid Mechanics, 2002, 472: 125-151. |
| [9] |
Maurer J, Tabeling P, Joseph P, et al. Second-order slip laws in microchannels for helium and nitrogen[J]. Physics of Fluids, 2003, 15(9): 2613-2621. DOI:10.1063/1.1599355 |
| [10] |
Alder B J, Wainwright T E. Phase transition for a hard sphere system[J]. Journal of Chemical Physics, 1957, 27(5): 1208-1209. DOI:10.1063/1.1743957 |
| [11] |
樊康旗, 贾建援. 经典分子动力学模拟的主要技术[J]. 微纳电子技术, 2005, 42(3): 133-138. Fan K Q, Jia J Y. An overview on classical molecular dynamics simulation[J]. Micronanoelectronic Technology, 2005, 42(3): 133-138. DOI:10.3969/j.issn.1671-4776.2005.03.009 (in Chinese) |
| [12] |
Soong C Y, Yen T H, Tzeng P Y. Molecular dynamics simulation of nanochannel flows with effects of wall lattice-fluid interactions[J]. Physical Review E, 2007, 76(3): 036303. DOI:10.1103/PhysRevE.76.036303 |
| [13] |
解辉, 刘朝, 刘彬武. 纳米通道内混合气体流动的分子动力学模拟[J]. 物理化学学报, 2009, 25(5): 994-998. Xie H, Liu C, Liu B W. Molecular dynamics simulation of gas mixture flow in nanochannel[J]. Acta Physico-Chimica Sinica, 2009, 25(5): 994-998. DOI:10.3866/PKU.WHXB20090404 (in Chinese) |
| [14] |
解辉, 刘朝, 高虹. 分子动力学模拟纳米通道内混合气体流动的温度效应[J]. 工程热物理学报, 2010, 31(6): 921-924. Xie H, Liu C, Gao H. Effects of temperature on gas mixture flow in nanochannels by molecular dynamics simulations[J]. Journal of Engineering Thermophysics, 2010, 31(6): 921-924. (in Chinese) |
| [15] |
Kandemir I, Sevilgen F E. Molecular dynamics simulation of helium-argon gas mixture under various wall condi-tions[J]. Molecular Simulation, 2008, 34(8): 795-808. DOI:10.1080/08927020802275785 |
| [16] |
Kim K, Xu X B, Guo J H, et al. Ultrahigh-speed rotating nanoelectromechanical system devices assembled from nanoscale building blocks[J]. Nature Communications, 2014, 5: 3632. DOI:10.1038/ncomms4632 |
| [17] |
王沫然.微纳尺度气体流动和换热的Monte Carlo模拟[D].北京: 清华大学, 2004. Wang M R. Monte Carlo simulations on micro-and nanoscale gas flow and heat transfer[D]. Beijing: Tsinghua University, 2004(in Chinese). |
| [18] |
Roy S, Raju R, Chuang H F, et al. Modeling gas flow through microchannels and nanopores[J]. Journal of Applied Physics, 2003, 93(8): 4870-4879. DOI:10.1063/1.1559936 |
| [19] |
Zhang Z Q, Hao M L, Liu Z, et al. Flow behaviours and boundary slip of nitrogen-oxygen mixture confined in nanochannel[J]. International Journal of Materials and Structural Integrity, 2017, 11(1/3): 106. |
| [20] |
Thompson P A, Robbins M O. Shear flow near solids:epitaxial order and flow boundary conditions[J]. Physical Review A, 1990, 41(12): 6830-6837. DOI:10.1103/PhysRevA.41.6830 |
| [21] |
Barisik M, Beskok A. Molecular dynamics simulations of shear-driven gas flows in nano-channels[J]. Microfluidics and Nanofluidics, 2011, 11(5): 611-622. DOI:10.1007/s10404-011-0827-0 |
| [22] |
Harris J G, Yung K H. Carbon dioxide's liquid-vapor coexistence curve and critical properties as predicted by a simple molecular model[J]. The Journal of Physical Chemistry, 1995, 99(31): 12021-12024. DOI:10.1021/j100031a034 |
| [23] |
温伯尧, 孙成珍, 白博峰. 多孔石墨烯分离CH4/CO2的分子动力学模拟[J]. 物理化学学报, 2015, 31(2): 261-267. Wen B Y, Sun C Z, Bai B F. Molecular dynamics simulation of the separation of CH4/CO2 by nanoporous graphene[J]. Acta Physico-Chimica Sinica, 2015, 31(2): 261-267. (in Chinese) |
| [24] |
张云河, 李新海, 吴显明, 等. 合金化提高铂在PEMFC氧还原反应中的催化活性[J]. 电源技术, 2004, 28(8): 491-493, 524. Zhang Y H, Li X H, Wu X M, et al. Enhancing activity of platinum catalysts for PEMFC oxygen reduction reaction by alloying[J]. Chinese Journal of Power Sour-ces, 2004, 28(8): 491-493, 524. DOI:10.3969/j.issn.1002-087X.2004.08.010 (in Chinese) |
| [25] |
石小燕, 曾丹苓, 蔡治勇. 不同Lennard-Jones模型参数对分子动力学模拟的影响[J]. 热科学与技术, 2005, 4(3): 195-198. Shi X Y, Zeng D L, Cai Z Y. Influence of different Lennard-Jones parameters on results of molecular dynamic simulation[J]. Journal of Thermal Science and Technology, 2005, 4(3): 195-198. DOI:10.3969/j.issn.1671-8097.2005.03.002 (in Chinese) |
| [26] |
Beskok A, Karniadakis G E, Trimmer W. Rarefaction and compressibility effects in gas microflows[J]. Journal of Fluids Engineering, 1996, 118(3): 448-456. DOI:10.1115/1.2817779 |
| [27] |
Allen M P, Tildesley D J. Computer simulation of liquids[M]. Oxford: Claren-don, 1987: 385.
|
| [28] |
Cao B Y, Chen M, Guo Z Y. Liquid flow in surface-nanostructured channels studied by molecular dynamics simulation[J]. Physical Review E, 2006, 74(6): 066311. DOI:10.1103/PhysRevE.74.066311 |
| [29] |
Grest G S, Kremer K. Molecular dynamics simulation for polymers in the presence of a heat bath[J]. Physical Review A, 1986, 33(5): 3628-3631. DOI:10.1103/PhysRevA.33.3628 |
| [30] |
Thompson P A, Troian S M. A general boundary condition for liquid flow at solid surfaces[J]. Nature, 1997, 389(6649): 360-362. DOI:10.1038/38686 |
| [31] |
张程宾, 赵沐雯, 陈永平, 等. 流体密度对纳通道内流动滑移的影响[J]. 化工学报, 2012, 63(S1): 12-16. Zhang C B, Zhao M W, Chen Y P, et al. Effects of fluid density on velocity slip in nanochannels[J]. CIESC Journal, 2012, 63(S1): 12-16. (in Chinese) |
| [32] |
Granick S. Motions and relaxations of confined liquids[J]. Science, 1991, 253(5026): 1374-1379. DOI:10.1126/science.253.5026.1374 |
| [33] |
Zhang R L, Di Q F, Wang X L, et al. Numerical study of the relationship between apparent slip length and contact angle by lattice Boltzmann method[J]. Journal of Hydrodynamics, Series B, 2012, 24(4): 535-540. DOI:10.1016/S1001-6058(11)60275-8 |
| [34] |
曹炳阳.速度滑移及其对微纳尺度流动影响的分子动力学研究[D].北京: 清华大学, 2005. Cao B Y. Molecular dynamics simulation of velocity slip and its effect on micro and nanoscale flow[D]. Beijing: Tsinghua University, 2005(in Chinese). |
| [35] |
张忠强.流体在纳米微通道中的流动及传输特性研究[D].大连: 大连理工大学, 2010. Zhang Z Q. Flow and transport properties of fluids in nanochannels[D]. Dalian: Dalian University of Techno-logy, 2010(in Chinese). |




