2. 中国科学院大学工程科学学院,北京 100049
2. School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China
超燃冲压发动机被认为是吸气式高超声速飞行器中最具有潜力的推进系统, 因为它可以充分利用空气中的氧气来降低飞行器的重量, 从而降低发射成本[1-2].自1965年至今, 美国先后开展了IFTV, HRE, SCRAM, NASP, HyTech, HyFly, Hyper-X等计划.但是, 超燃冲压发动机的研究之路却充满了困难与挑战.经过50多年的艰苦历程, 超燃冲压发动机在美国才刚刚进入飞行实验验证阶段[3].俞刚等[4]对超燃冲压发动机发展50多年来遇到的问题以及以后的发展方向给出了综述.
超燃冲压发动机的研究之所以困难是因为有很多复杂的空气动力学问题和燃烧问题没有研究清楚[3-9].第一个问题是超燃冲压发动机没有足够大的推力[3].第二个问题就是超声速燃烧的不稳定问题, 严重时会引起发动机的不启动.早期的研究认为, 超燃冲压发动机的不启动是燃烧室和隔离段内的边界层分离造成的.但是, 相关实验研究表明, 发动机的不启动与热壅塞有关, 而不是由边界层分离引起的[10-12].发动机的不启动总是伴随着热壅塞的发生, 声速燃烧决定了超燃冲压发动机的当量比(Φ)和推力大小的上限. Laurence等[11],Hannemann等[12]和Oh等[13]通过风洞实验和数值模拟分别观察到了激波在隔离段内向上游传播的物理现象.
如何用理论方法来评估超燃冲压发动机的气动性能和推进性能是目前还没有解决的问题.一维加热管流理论是钱学森于1949年提出的, 目的就是为了研究超燃冲压发动机的推进性能[14].这一理论直到今天还被采用[15-17].除此之外, 还有热力学循环理论.然而, 这两个理论都是针对定常流场的, 无法用来研究非定常流场和超声速燃烧在隔离段内产生的激波强度.超燃冲压发动机的内流场总是非定常的[18-21].受发动机壁面的约束, 当燃烧室内的放热剧烈时, 燃烧产生的压力就会产生激波向上游传播, 引起燃烧流场震荡或者发动机不启动.因此须发展一种理论, 既可以预测超燃冲压发动机燃烧室内的压力变化, 又可以预测燃烧产生的激波强度.沈欢等[22]首次应用CJ爆轰理论来研究超燃冲压发动机的气动性能.既然发动机的不启动总是伴随着热壅塞现象, 而CJ爆轰波燃烧后的Mach数正好为1, 二者必然存在联系.研究结果表明, CJ爆轰理论可以预测极限状态下的燃烧放热产生的激波强度和压力大小, 因此可以用来分析发动机的极限推进性能.
本文主要包含两部分内容:第一部分是在文献[22]已有研究结果的基础上, 进一步提炼出了超燃冲压发动机和高Mach数斜爆轰发动机的5条气动设计原则.第二部分是依据该气动设计原则设计了一款斜爆轰发动机, 飞行Mach数为9, 开展了二维数值模拟研究.数值模拟只是对斜爆轰发动机的燃烧机理和流场稳定性进行了研究, 并没有涉及整个发动机的热循环效率及推进性能等.斜爆轰发动机的推进性能和热循环效率等问题还须开展更加深入的研究.第二部分内容一方面是对理论结果的应用, 另一方面也是对理论结果的验证.
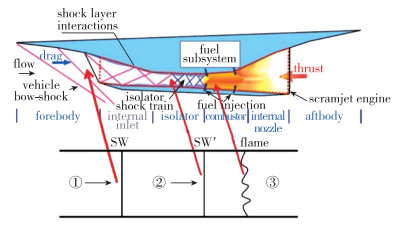
1 流动机理理论分析图 1给出了超燃冲压发动机的物理模型.发动机分为6部分, 分别为飞行器前体、内进气道、隔离段、燃烧室、尾喷管和飞行器后体.燃烧室内超声速燃烧产生的压力产生了一系列激波, 这些激波在隔离段内震荡.如果这些激波的强度足够强, 就会上传到进气道入口, 引起发动机不启动.
|
| 图 1 超燃冲压发动机物理模型 Fig.1 Physical model of scramjets |
这其中的理论问题就是如何预测这些激波的强度以及激波强度受哪些参数的影响.为了研究这一问题, 提出了一维模型.超燃冲压发动机的内流场简化成两道激波和一个火焰面, 如图 1下半部分所示, 气流从左向右流动.第一道激波SW对应的是前体压缩产生的主激波, 第二道激波SW′对应的是隔离段内的激波, 火焰面Flame对应的是燃烧室内的火焰.这两道激波既可以是正激波也可以是斜激波, 不影响结论, 因为理论分析时只用到激波传播速度, 没有涉及激波Mach数.隔离段内的激波SW′强度是主激波SW和火焰面Flame的函数.影响SW′强度的参数很多, 无法准确给出其激波强度的理论解.但是, 假设不考虑边界层分离, 在发生热壅塞的极限情况下, 会形成CJ爆轰波, 可以用CJ爆轰理论来分析超燃冲压发动机内流场的极限气动性能.
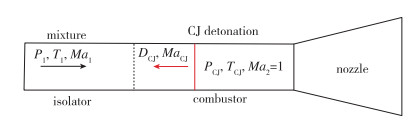
图 2给出了CJ爆轰发动机的准一维物理模型.发动机包括3部分, 分别是隔离段、燃烧室和尾喷管.隔离段内预混的爆轰气体从左向右流动, 初始压力为P1, 初始温度为T1, 初始Mach数为Ma1.预混气体在燃烧室内剧烈燃烧, 发生热壅塞, 形成CJ爆轰波, 其速度和Mach数分别为DCJ和MaCJ. Mach数为Ma2的高温高压爆轰产物从尾喷管喷出, 产生推力.显然, 爆轰产物的压力越高, 产生的推力越大.在理论分析中, 不考虑边界层的影响.
|
| 图 2 CJ爆轰发动机物理模型 Fig.2 Physical model of CJ detonation engine |
该CJ爆轰发动机如果要稳定燃烧, 理论上必须要求爆轰波的速度等于隔离段来流的速度, 即DCJ=U1, 爆轰波就会稳定在燃烧室内.如果爆轰波的速度大于隔离段来流速度, 爆轰波就会向上游传播, 引起发动机不启动.如果爆轰波的速度小于隔离段内来流的速度, 爆轰波就不能在燃烧室内保持稳定, 火焰熄灭.
在文献[22]中, 利用该理论模型和CJ爆轰理论, 讨论了燃烧室入口压力、温度、速度、当量比、燃料、氧化剂等参数对超燃冲压发动机的推进性能和超声速燃烧不稳定性问题的影响规律, 这些规律如下:
(1) 超燃冲压发动机燃烧室内燃烧前后压比随燃烧室入口静温升高呈指数下降, 燃烧室入口静温越高, 燃烧后压比越低.对于满足当量比的氢气/空气, 当燃烧室入口的静温为1 000 K时, 等截面燃烧室燃烧前后压比的最大值小于4.5, 这是理论极限值, 不可能再提高.
(2) 超声速燃烧产生内能和动能, 在运动方程上, 则表现为压力和动量, 动量的方向永远与来流方向相反.燃烧会产生激波或燃烧波, 当燃烧波速度大于来流速度时, 就会向上游传播, 超声速流场变得不稳定.对巡航Mach数为6~8的高超声速飞行器, 超燃冲压发动机隔离段内流速较低, 处于临界不稳定范围.当巡航Mach数超过9, 发动机流场将变得稳定.
(3) 采用降低当量比、多点分布释热和扩张型燃烧室的方法, 其本质都是降低燃烧波的传播速度, 使流场变得稳定.对氢气/空气混合气体, 在当量比低于0.5时, 流场是稳定的.但是降低当量比的同时燃烧压力也相应降低, 发动机推力减小.
(4) 对超燃冲压发动机, 燃烧放热产生动量和压力, 这部分动量是不能直接变成推力的, 因此采用燃烧产物压力高、动量低的燃料有利于提高发动机的综合推进性能.同氢气燃料相比, 碳氢燃料燃烧后的动量稍低、压力稍高, 因此采用碳氢燃料的超燃冲压发动机的流场要稍稳定一些, 推力稍大一些.
在上述研究结果的基础上, 结合目前国内外超燃冲压发动机的研究现状, 本文进一步提出了5条高Mach数超燃冲压发动机和斜爆轰发动机的气动设计原则:
(1) 隔离段气流速度要大于相应状态下的CJ爆轰波传播速度, 保证燃烧产生的激波不会在隔离段内上传而导致发动机不启动.从另一个角度讲, 要通过采用降低当量比、扩张型燃烧室和分布缓慢释热等方式, 降低燃烧产生的激波速度, 使其小于隔离段内气流速度, 保证激波不会上传.
(2) 对于斜爆轰发动机, 要使诱导燃烧的斜激波后面的静温达到1 400 K左右, 保证点火延迟时间足够短, 火焰不被气流吹走.点火延迟时间主要是压力、静温和当量比的函数, 但是对静温最敏感.
(3) 隔离段内的气流静温要尽可能低, 使得燃烧后压比尽可能高, 提高发动机推力.如果燃烧室入口气流静温过高, 燃烧产生的压比就会非常小, 因此推力就会非常小.
(4) 采用边界层抽吸技术, 减小边界层厚度, 避免边界层分离对流场的影响.边界层分离会产生分离泡, 分离泡产生斜激波, 与主激波发生激波/激波相互作用, 一旦发生Mach反射, 形成正激波, 就会破坏流场稳定性.
(5) 通过采用扩张型燃烧室和分布缓慢释热等方式来避免热壅塞的发生.一旦发生热壅塞, 会产生激波, 发生激波/激波相互作用, 增加激波强度, 引起激波上传.
在这5条气动设计原则中, 第1条和第5条是相互关联的.如果第一条满足, 第5条可以不用考虑.但是, 如果第1条不满足, 那么就须考虑第5条, 保证燃烧不发生热壅塞, 不产生爆轰波, 保证流场稳定.
除了上述5条气动设计原则以外, 根据理论分析结果并结合目前现有的国内外超燃冲压发动机的研究结果, 可以归纳出3条判断超燃冲压发动机极限性能的判断标准:
(1) 激波进入隔离段标准.一旦激波进入隔离段, 表明超燃冲压发动机的性能达到极限.因为激波进入隔离段后, 会增加隔离段内气流的压力和温度.根据理论分析结果, 隔离段内气流的温度太高时, 继续增加当量比, 燃烧产生的压比将不再明显增加, 推力也不再增加.
(2) 当量比Φ=0.5优化标准.综合当量比Φ=0.5是一个比较优化的标准, 继续提高当量比, 燃烧产生的压比不再明显增加, 但是超声速燃烧流场会变得更加不稳定, 因为当量比对爆轰波的速度影响非常大.
(3) 燃料多点喷射分布释热方法.与燃料单点喷射相比, 燃料多点喷射分布释热方法可以提高当量比, 但是对推力的提高是有限的, 因为下游的燃料是在上游的高温燃烧产物中燃烧的, 相当于燃烧室入口静温增加, 下游燃料燃烧后的压比很小.所以, 多点喷射方法虽然增加了当量比, 但是并没有显著地提高发动机的推力.
2 斜爆轰发动机二维数值模拟 2.1 斜爆轰发动机几何构型在这一部分中, 对斜爆轰发动机的燃烧机理开展了二维数值模拟研究, 一方面是对理论结果的应用, 另一方面也是对理论结果的检验.在高Mach数下, 相比于超燃冲压发动机, 斜爆轰发动机有一定的优势[23-25].在高Mach数下, 斜激波后面的温度高, 能够实现可燃气体的自点火燃烧, 不需要扩散、混合、热传导等过程, 因此燃烧室的长度更短, 这一过程称作激波诱导燃烧.对高Mach数斜爆轰发动机, 燃烧室入口的气流速度高, 燃烧产生的激波容易保持稳定, 同时可以保持比较低的燃烧室入口气流静温, 提高燃烧后的压力和发动机推力.
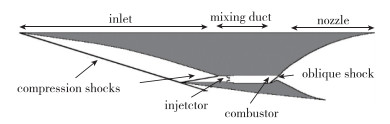
图 3给出了斜爆轰发动机的示意图, 包括进气道、燃料混合段、燃烧室、尾喷管等4个部件, 利用进气道压缩来流气体, 在混合段的前端喷入燃料, 燃料与空气在混合段内混合后到达燃烧室, 燃烧室内的楔面产生斜激波诱导燃烧, 燃烧产生的高温高压气体通过尾喷管产生推力.斜激波诱导燃烧可以极大地减小反应区长度, 进而缩短燃烧室的长度, 减轻发动机的重量, 并减小摩擦阻力.
|
| 图 3 斜爆轰发动机示意图 Fig.3 Configuration of the oblique detonation engine |
目前, 国际上已经开展了一些针对斜爆轰发动机的研究. Alexander等[24]完成了斜爆轰发动机在飞行高度为34.5 km、飞行Mach数为11条件下的三维数值模拟, 得到了斜爆轰发动机的定常流场.结果表明, 燃料在混合段中混合均匀, 燃烧室内可以产生驻定的斜爆轰波. Chan等[23]在飞行高度为34.5 km、飞行Mach数为11的条件下, 比较了两个用相同方法设计的超燃冲压发动机和斜爆轰发动机, 结果表明斜爆轰发动机的总长度和燃烧室尺寸均远小于超燃冲压发动机, 前者燃烧室的长度只有后者的1/5.
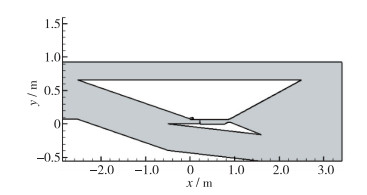
基于上面提出的斜爆轰发动机气动设计原则, 设计了一款斜爆轰发动机模型, 并开展了二维数值模拟研究, 计算域如图 4所示.整个飞行器的总长度为5 m.采用一级进气道压缩, 进气道长度为2 504 mm, 角度为13°.混合段的高度为60 mm, 膨胀角为5°.在进气道出口上壁面采用了边界层抽吸技术, 避免混合段上壁面的边界层过厚.通过混合段内的两个小支板来喷射燃料, 小支板的高度和角度分别为3 mm和5°.燃烧室前面的斜劈的角度是20°.尾喷管的长度为1 500 mm, 膨胀半角为20°.
|
| 图 4 斜爆轰发动机计算域 Fig.4 Computational domain of the oblique detonation engine |
控制方程为二维可压缩形式的Reynolds平均Navier-Stokes(RANS)方程, 湍流模型为(shear stress transport, SST)k-ω湍流模型, 并加入
可压缩形式的Reynolds平均Navier-Stokes (RANS)控制方程如下
连续性方程
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0 $ |
动量方程
| $ \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_i}}}\left( {{\tau _{ij}}} \right) $ |
能量方程
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho E} \right) + \frac{\partial }{{\partial {x_i}}}\left( {{u_i}\left( {\rho E + p} \right)} \right) = \\ \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\alpha + {\alpha _{\rm{t}}}} \right)\frac{{\partial T}}{{\partial {x_i}}} + {u_j}\left( {{\tau _{ij}}} \right)} \right] \end{array} $ |
式中, τij为应力张量, 定义如下
| $ {\tau _{ij}} = \mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}{\delta _{ij}}\frac{{\partial {u_k}}}{{\partial {x_k}}}} \right) $ |
δij为Kronecker函数.理想气体状态方程如下
| $ \mathit{p}{\rm{ = }}\rho {\mathit{R}_{\rm{c}}}\mathit{T} $ |
湍流模型为SST k-ω湍流模型.该模型兼具k-ε湍流模型的鲁棒性和k-ω湍流模型在近壁面区域的精确性, 能更好地模拟逆压梯度区.湍流动能k和比耗散率ω的输送方程如下
| $ \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\mathit{\Gamma }_\mathit{k}}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} $ | (1) |
| $ \frac{\partial }{{\partial t}}\left( {\rho \omega } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \omega {u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\mathit{\Gamma }_\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\omega } + {D_\omega } $ |
式中, Gk和Gω分别为k和ω的生成项, Γk和Γω为有效扩散项, Yk和Yω为湍流耗散项, Dω为正交发散项.
间歇因子γ和动量厚度Reynolds数
| $ \begin{array}{l} \frac{{\partial \left( {\rho \gamma } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}\gamma } \right)}}{{\partial {x_i}}} = {\mathit{P}_\mathit{r}} - {E_r} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\mu _{\rm{t}}}} \right)\frac{{\partial \gamma }}{{\partial {x_j}}}} \right]\\ \frac{{\partial \left( {\rho \mathit{\tilde R}{\mathit{e}_{\theta t}}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}\mathit{\tilde R}{\mathit{e}_{\theta t}}} \right)}}{{\partial {x_i}}} = {\mathit{P}_{\theta {\rm{t}}}} + \frac{\partial }{{\partial {x_j}}}\left[ {2\left( {\mu + {\mu _{\rm{t}}}} \right)\frac{{\partial \mathit{\tilde R}{\mathit{e}_{\theta t}}}}{{\partial {x_j}}}} \right] \end{array} $ |
式中, μt为湍流黏性, Pr和Er为转捩源项, Pθt为源项.同时, 式(1)中的Gk和Yk也作相应的修正
| $ \begin{array}{l} G_k^* = {\gamma _{{\rm{eff}}}}{G_k}\\ Y_k^* = \min \left( {\max \left( {{\gamma _{{\rm{eff}}}}, 0.1} \right), 1.0} \right){Y_k} \end{array} $ |
式中, γeff为有效间歇因子.湍流方程和边界层转捩方程的具体参数详见文献[29].
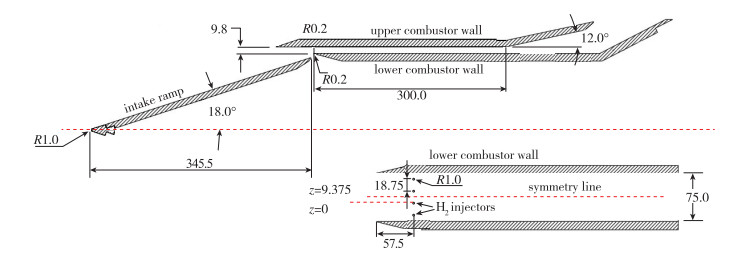
2.3 数值方法验证湍流模型对高超声速流场的影响很大, 为了验证湍流模型和转捩模型的有效性, 选用德国DLR的HyShot Ⅱ超燃冲压发动机[12, 27]模型作为算例, 进行数值模拟. HyShot Ⅱ发动机模型及尺寸如图 5所示, 模型分为进气道和燃烧室两部分, 进气道长345.5 mm, 倾角为18°, 燃烧室长300 mm, 宽75 mm, 高9.8 mm.4个氢气声速喷口位于燃烧室入口下游57.5 mm处, 喷口半径1 mm, 氢气总压460 kPa, 总温300 K, 当量比Φ=0.295. HyShot Ⅱ的实验状态为28 km高空、Mach数为7.37和攻角为3.6°. 表 1给出了HEG激波风洞的实验条件.其中pt2和qt2为文献[12]中定义的参考压力和参考热流.
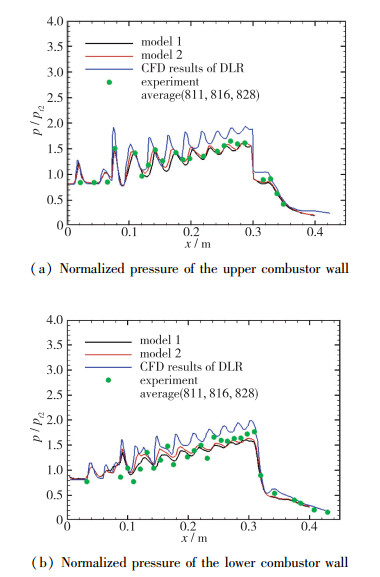
图 6给出了燃烧室上下表面压力曲线比较, 其中model 1使用了Gerlinger等[26]提出的氢氧燃烧机理, model 2使用了Burke等[28]提出的氢氧燃烧机理.数值模拟结果与实验结果吻合得非常好, 优于DLR在文献[12]中的计算结果.由于燃烧室前缘产生的激波在燃烧室内反射形成激波串以及激波与壁面边界层的相互作用, 模拟燃烧室内的流场需要合适的湍流模型.结果表明, 使用SST k-ω湍流模型和
|
| 图 6 Hyshot Ⅱ数值模拟结果与实验结果比较 Fig.6 Comparisons of CFD results of HyShot Ⅱ with DLR experimental results |
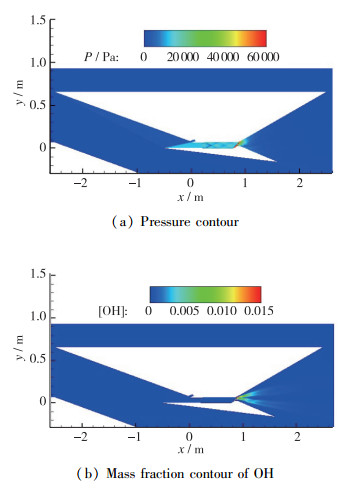
图 7给出了当量比Φ=1.0状态下的斜爆轰发动机整机的压力云图和OH质量分数云图.在当量比Φ=1.0的状态下, 数值模拟获得了稳定的燃烧流场, 燃烧波稳定在斜劈前面. Ma=9的气流经过进气道压缩后, 混合段内的气流速度大于2 000 m/s, 而当量比为1.0的氢气/空气混合气体的CJ爆轰波的速度为1 950 m/s, 根据上述气动设计原则, 流场是可以稳定的.在斜爆轰波后面燃烧产物的Mach数小于1, 发生了热壅塞, 但是对流场的稳定性不产生影响, 这是因为混合段内的气流速度大于相应状态下的CJ爆轰波速度.
|
| 图 7 斜爆轰发动机的压力云图和OH质量分数云图 Fig.7 Contours of pressure and mass fraction of OH with Φ=1.0 |
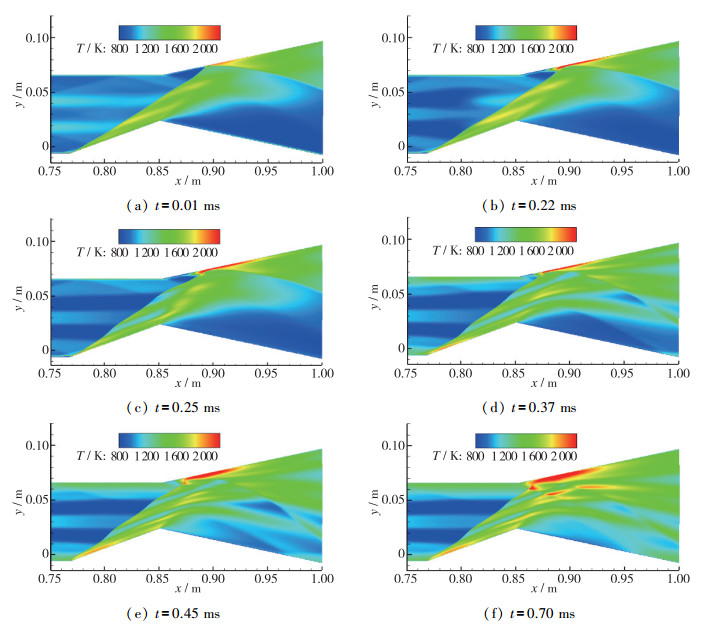
为了研究氢气射流对燃烧室内激波的影响以及激波诱导燃烧的演化过程, 以冷流工况的流场为初始流场进行计算. 图 8为0~0.7 ms内不同时刻的燃烧室温度图, t=0 ms是初始流场, 燃烧室内的楔面产生斜激波, 打到喷管上壁面处产生反射激波, 此时氢气从喷口喷出.当t=0.22 ms时, 氢气到达燃烧室, 混合段内流速U约为2 500 m/s, 混合段长度为0.5 m, 这与0.22 ms的时间十分接近.此时在燃烧室上壁面, 由于激波/边界层的相互作用, 形成一个温度较高的回流区.当t=0.25 ms时, 氢气穿过斜激波, 来流的温度、速度和组分分布不均匀, 导致激波波面出现起伏.当t=0.37 ms时, 由于激波波面的起伏, 上壁面的回流区向前移动, 同时, 随着混合段内壁面边界层的发展, 壁面附近的温度逐渐升高, 激波/边界层相互作用使回流区继续向前移动, 最终在t=0.70 ms的时刻流场变得稳定.
|
| 图 8 不同时刻燃烧室温度图 Fig.8 Temperature contours of the combustor at different instants |
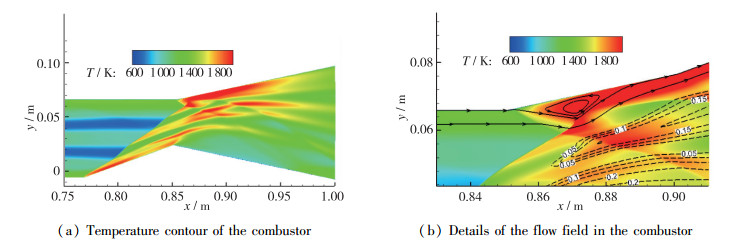
图 9给出了燃烧室和喷管局部的放大流场, 包括温度云图和H2O质量分数等值线分布.从图 9中可以看出, 斜爆轰与喷管上壁面边界层的相互作用, 引起喷管上壁面边界层局部分离, 产生一个小分离泡, 回流区内没有化学反应发生, 仅是激波边界层干扰引起的.在分离泡前面产生斜激波, 与斜爆轰波发生激波/激波相互作用.但是整个流场并没有受这个分离泡的影响, 一方面是因为喷管的扩张作用, 降低燃烧产生的逆压梯度;另一方面是因为在进气道出口上壁面采用边界层抽吸, 保证混合段内边界层很薄的效果.因此可以看出, 边界层抽吸对超燃冲压发动机和斜爆轰发动机的流场稳定起到非常关键的作用.
|
| 图 9 燃烧室内的温度云图和H2O质量分数等值线:实线为流线; 虚线为H2O质量分数 Fig.9 Temperature contours in the combustor and mass fraction of H2O :numbers and isolines |
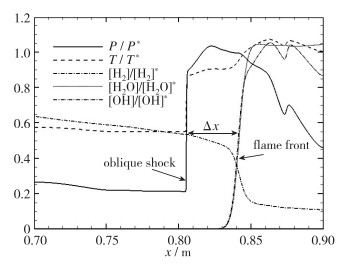
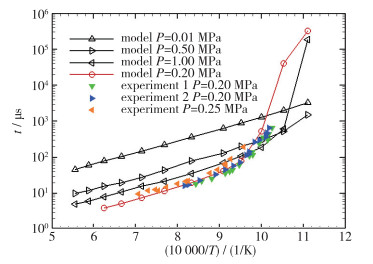
图 10给出了沿着燃烧室内一条流线的压力、温度、H2O质量分数和OH质量分数的无量纲参数分布, 图 11给出了所采用的基元反应模型在不同温度下的点火延迟时间.无量纲参数的参考量分别为P*=60 kPa, T*=1 600 K, [H2]*=0.12, [H2O]* =0.2和[OH]*=0.014.从图 10中可以看出, 燃烧室斜激波后面的温度和压力分别为1 500 K和50 kPa.从图 11中可以看出, 在相应状态下的点火延迟时间为16 μs.斜劈前诱导燃烧的斜激波后面的气流速度为2 000 m/s.因此, 激波和火焰面之间的诱导区长度为0.03 m, 与数值模拟结果吻合得非常好.
|
| 图 10 沿流线的无量纲参数分布 Fig.10 Profiles of different parameters along a stream line |
|
| 图 11 基元反应模型的点火延迟时间 Fig.11 Ignition delay time of the detailed chemical model |
本文利用CJ爆轰理论对超燃冲压发动机内流场的流动机理进行了理论分析, 给出了燃烧室气流参数随隔离段内气流参数的变化规律.在理论分析的基础上, 提出了高Mach数超燃冲压发动机和斜爆轰发动机的5条气动设计原则.根据提出的气动设计原则, 对斜爆轰发动机开展了二维数值模拟研究, 飞行Mach数为9, 飞行高度为40 km, 当量比Φ=1.0, 攻角为0°.数值模拟结果表明, 在高Mach数下斜爆轰发动机可以获得稳定的流场结构, 证明了理论分析结果的正确性.理论分析和数值模拟结果均表明, 在高Mach数下, 斜爆轰发动机具有发展潜力.
致谢 致谢本研究得到了国家自然科学基金(11672312, 11532014)的资助, 在此表示感谢.| [1] |
Ferri A. Review of problems in application of supersonic combustion[J]. The Aeronautical Journal, 1964, 68(645): 575-597. |
| [2] |
Ferri A. Review of scramjet propulsion technology[J]. Journal of Aircraft, 1968, 5(1): 3-10. DOI:10.2514/3.43899 |
| [3] |
Curran E T. Scramjet engines:the first forty years[J]. Journal of Propulsion and Power, 2001, 17(6): 1138-1148. DOI:10.2514/2.5875 |
| [4] |
俞刚, 范学军. 超声速燃烧与高超声速推进[J]. 力学进展, 2013, 43(5): 449-471. Yu G, Fan X J. Supersonic combustion and hypersonic propulsion[J]. Advances in Mechanics, 2013, 43(5): 449-471. (in Chinese) |
| [5] |
王钰涵, 王江峰, 李龙飞. 进口条件对超燃冲压发动机氢气燃烧流场特性的影响分析[J]. 气体物理, 2018, 3(3): 48-58. Wang Y H, Wang J F, Li L F. Numerical analysis of hydrogen jet combustion flows in scramjet under different inlet conditions[J]. Physics of Gases, 2018, 3(3): 48-58. (in Chinese) |
| [6] |
叶坤, 叶正寅, 武洁, 等. DMD和POD对超燃冲压发动机凹腔流动的稳定性分析[J]. 气体物理, 2016, 1(5): 39-51. Ye K, Ye Z Y, Wu J, et al. Stability analysis of scramjet open cavity flow base on POD and DMD method[J]. Physics of Gases, 2016, 1(5): 39-51. (in Chinese) |
| [7] |
乐嘉陵, 田野, 杨顺华, 等. 脉冲燃烧风洞中空气节流对煤油燃料超燃冲压发动机火焰稳定影响研究[J]. 推进技术, 2018, 39(10): 2161-2170. Le J L, Tian Y, Yang S H, et al. Study on flame stabilization in a kerosene fueled scramjet combustor with air throttling in a pulse combustion wind tunnel[J]. Journal of Propulsion Technology, 2018, 39(10): 2161-2170. (in Chinese) |
| [8] |
Shen H D, Liu Y B, Chen B Y. Control-relevant modeling and performance limitation analysis for flexible air-breathing hypersonic vehicles[J]. Aerospace Science and Technology, 2018, 76: 340-349. DOI:10.1016/j.ast.2018.02.016 |
| [9] |
Clark R J, Shrestha S B. A review of numerical simulation and modeling of combustion in scramjets[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2015, 229(5): 958-980. DOI:10.1177/0954410014541249 |
| [10] |
Mitani T, Tani K, Miyajima H. Flow choking by drag and combustion in supersonic engine testing[J]. Journal of Propulsion and Power, 2007, 23(6): 1177-1184. DOI:10.2514/1.30264 |
| [11] |
Laurence S J, Lieber D, Schramm J M, et al. Incipient thermal choking and stable shock-train formation in the heat-release region of a scramjet combustor. part I:shock-tunnel experiments[J]. Combustion and Flame, 2015, 162(4): 921-931. DOI:10.1016/j.combustflame.2014.09.016 |
| [12] |
Hannemann K, Karl S, Schramm J M, et al. Methodo-logy of a combined ground based testing and numerical modelling analysis of supersonic combustion flow paths[J]. Shock Waves, 2010, 20(5): 353-366. DOI:10.1007/s00193-010-0269-8 |
| [13] |
Oh J Y, Ma F H, Hsieh S Y, et al. Interactions between shock and acoustic waves in a supersonic inlet diffuser[J]. Journal of Propulsion and Power, 2005, 21(3): 486-495. DOI:10.2514/1.9671 |
| [14] |
Tsien H S, Beilock M. Heat source in a uniform flow[J]. Journal of Aeronautical Sciences, 1949, 16(12): 756-757. |
| [15] |
Birzer C H, Doolan C J. Quasi-one-dimensional model of hydrogen-fueled scramjet combustors[J]. Journal of Propulsion and Power, 2009, 25(6): 1220-1225. DOI:10.2514/1.43716 |
| [16] |
O'Brien T F, Starkey R P, Lewis M J. Quasi-one-dimensional high-speed engine model with finite-rate chemistry[J]. Journal of Propulsion and Power, 2001, 17(6): 1366-1374. DOI:10.2514/2.5889 |
| [17] |
Vanyai T, Bricalli M, Brieschenk S, et al. Scramjet performance for ideal combustion processes[J]. Aerospace Science and Technology, 2018, 75: 215-226. DOI:10.1016/j.ast.2017.12.021 |
| [18] |
Curran E T, Heiser W H, Pratt D T. Fluid phenomena in scramjet combustion systems[J]. Annual Review of Fluid Mechanics, 1996, 28: 323-360. DOI:10.1146/annurev.fl.28.010196.001543 |
| [19] |
Laurence S J, Karl S, Schramm J M, et al. Transient fluid-combustion phenomena in a model scramjet[J]. Journal of Fluid Mechanics, 2013, 722: 85-120. DOI:10.1017/jfm.2013.56 |
| [20] |
O'Byrne S, Doolan M, Olsen S R, et al. Analysis of transient thermal choking processes in a model scramjet engine[J]. Journal of Propulsion and Power, 2000, 16(5): 808-814. DOI:10.2514/2.5645 |
| [21] |
Liu Y F, Shen H, Zhang D L, et al. Theoretical analysis on deflagration-to-detonation transition[J]. Chinese Phy-sics B, 2018, 27(8): 084703. DOI:10.1088/1674-1056/27/8/084703 |
| [22] |
沈欢, 张子健, 刘云峰, 等. 超燃冲压发动机推进性能理论分析[J]. 气体物理, 2018, 3(1): 12-19. Shen H, Zhang Z J, Liu Y F, et al. Analysis on the propulsion performance of scramjet engine[J]. Physics of Gases, 2018, 3(1): 12-19. (in Chinese) |
| [23] |
Chan J, Sislian J P, Alexander D. Numerically simulated comparative performance of a scramjet and Shcramjet at Mach 11[J]. Journal of Propulsion and Power, 2010, 26(5): 1125-1134. DOI:10.2514/1.48144 |
| [24] |
Alexander D C, Sislian J P. Computational study of the propulsive characteristics of a Shcramjet engine[J]. Journal of Propulsion and Power, 2008, 24(1): 34-44. DOI:10.2514/1.29951 |
| [25] |
张少杰, 蔡晓东, 陈伟强, 等. 超声速气流中的爆震推进理论与研究进展[J]. 气体物理, 2018, 3(2): 27-38. Zhang S J, Cai X D, Chen W Q, et al. Theory and research progress of detonation propulsion in supersonic flow[J]. Physics of Gases, 2018, 3(2): 27-38. (in Chinese) |
| [26] |
Gerlinger P, Möbus H, Brüggemann D. An implicit multigrid method for turbulent combustion[J]. Journal of Computational Physics, 2001, 167(2): 247-276. DOI:10.1006/jcph.2000.6671 |
| [27] |
Chapuis M, Fedina E, Fureby C, et al. A computational study of the HyShot Ⅱ combustor performance[J]. Proceedings of the Combustion Institute, 2013, 34(2): 2101-2109. DOI:10.1016/j.proci.2012.07.014 |
| [28] |
Burke M P, Chaos M, Ju Y G, et al. Comprehensive H2/O2 kinetic model for high-pressure combustion[J]. International Journal of Chemical Kinetics, 2012, 44(7): 444-474. DOI:10.1002/kin.20603 |
| [29] |
Langtry R B, Menter F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J]. AIAA Journal, 2009, 47(12): 2894-2906. DOI:10.2514/1.42362 |